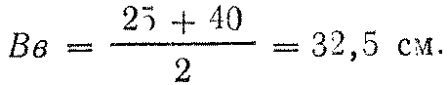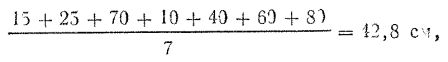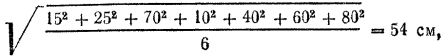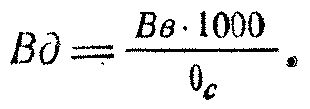Как найти меру рассеивания

В
отличии от мер центральной тенденции
меры рассеивания показывают насколько
данные неоднородны, изменчивы или
различны. По этой причине меры рассеивания
иногда называют мерами изменчивости и
вместе с мерами центральной тенденции
их называют параметрами
распределения.
Они являются не только параметрами
описания распределения случайной
величины, но и входят как составляющие
во многие другие статистические меры.

5.1.
Размах. Самой
простой из таких мер является размах
(d)–
разность между минимальным и максимальным
значением случайной величины в данном
распределении. Совершенно очевидно,
что два распределения, имеющие одинаковые
средние арифметические, медиану и моду
могут различаться по размаху, т.к. меры
центральной тенденции не показывают
насколько данные разбросаны на числовой
оси.

Размах
показывает насколько широк диапазон
значений случайной величины, но в ряде
случаев важно знать где находится
основная часть наблюдений, и тогда можно
воспользоваться другой мерой рассеивания
– полумеждуквартильным
размахом (полуинтерквартильное
отклонение).
Полумеждуквартильный размах – это
половина разности между первым и третьим
квартилем, который показывает, в каких
пределах находится около 50% наблюдений.

Недостатком
этих мер является то, что при их подсчете
не учитываются все значения случайной
величины, поэтому распределения, имеющие
равные меры центральной тенденции и
размах не обязательно будут одинаковы.
Более показательны при описании
неоднородности данных другие меры
рассеивания: среднее
отклонение (MD),
дисперсия(
),
стандартное (среднеквадратическое)
отклонение(
),.
В расчетах этих мер используется
центральное
отклонение

– разность каждого значения случайной
величины со средним арифметическим
данного распределения.

5.2.
Среднее
отклонение. Представляет
собой отношение суммы модулей центральных
отклонений к числу наблюдений и
вычисляется по формуле:

Очевидно,
что для двух разных распределений,
характеризующихся одинаковыми ранее
описанными параметрами, среднее
отклонение будет больше в том случае,
если в распределении чаще встречаются
удаленные от среднего значения.

5.3.
Дисперсия. Среднее
отклонение является полезной мерой
рассеивания, однако используется реже,
чем дисперсия – отношение суммы квадратов
центральных отклонений к числу наблюдений.
(»Байесовский» метод для вычисления
дисперсии генеральной совокупности).
В том случае, если исследователь имеет
дело не с генеральной совокупностью, а
с выборкой, формула дисперсии будет
немного иная – отношение суммы квадратов
центральных отклонений не к n,
а к n–1
(т.н. »несмещенная» оценка дисперсии):

Дисперсия
входит как параметр распределения в
ряд важных статистических
критериев,
но для описания данных психологических
экспериментов используется значительно
реже, чем стандартное
отклонение.

5.4.
Стандартное отклонение. Стандартное
отклонение представляет собой корень
из дисперсии:

Стандартное
отклонение, пожалуй, одна из наиболее
часто используемых мер рассеивания,
благодаря тем свойствам, которые оно
имеет для нормального
распределения.
В описании психологических переменных,
стандартное отклонение часто используется
как показатель границ большинства
значений или условной нормы, что является
особенно важным в психологии личности,
исследованиях интеллекта и т.д. В
настоящее время практически все важные
стандартизированные психодиагностические
шкалы (шкала Т-баллов, шкала стенов,
шкала IQ и т.д.) созданы с учетом стандартного
отклонения.

5.5.
Стандартная оценка или нормированное
отклонение. В
отличии от физики и других естественных
наук психологические переменные часто
не имеют собственных единиц измерения.
Если время реакции испытуемого можно
измерить в секундах, и сравнить результаты
исследования двух человек между собой,
а также с известными из научной литературы
данными, то показатель в 28 баллов по
вновь созданному тесту тревожности,
вряд ли кому-либо будет о чем-либо
говорить. Можно будет сказать, что этот
результат на 14 баллов меньше, чем 42
балла, полученных другим испытуемым,
но и в этом случае невозможно сравнить
эти данные с результатами этих же
испытуемых по другим тестам тревожности
и сказать, насколько велика эта разность.

Для
решения этой проблемы существуют т.н.
стандартные оценки(z).
Стандартная оценка не является мерой
рассеивания всего распределения, т.к.
существует для оценки отклонения каждого
значения от среднего в нормализованной
шкале, где среднее арифметическое равно
нулю, а стандартное отклонение – единице.
Такая шкала может быть получена путем
перевода каждого значения случайной
величины в значение, представляющее
собой отношение разности данного
значения со средним (центрального
отклонения) к стандартному отклонению
распределения:

В
таком случае, среднее арифметическое
будет равняться нулю, а основная масса
значений окажется в пределах от –1 до
+1. Стандартные оценки редко бывают
больше +2 и меньше –2, поэтому в отношении
каждого значения можно сказать – редкое
оно в данном распределении или частое,
и в какую сторону от среднего находится
– в большую, или в меньшую. Если в
рассмотренном выше примере окажется,
что баллу первого испытуемого соответствует
стандартная оценка –0.254, а второму
+1.23, то становится ясно, что первый
результат в выборке испытуемых более
частый, несколько ниже среднего и
соответствует границам условной нормы,
а второй – встречается реже и достаточно
высокий, и кроме того, разность в 14
баллов оказалась больше одного
стандартного отклонения.

5.6.
Асимметрия. Это
мера »косости» или »скошенности»
распределения. Распределения, отличающиеся
одинаковыми средними и отклонениями
могут быть, тем не менее разными, поскольку
ни модуль, ни квадрат разности не
показывают, с какой стороны от среднего
находилось отдельное значение случайной
величины. В тех случаях, когда количество
значений больших среднего превышает
количество значений меньших, чем среднее,
говорят о положительной асимметрии, в
противном случае – об отрицательной.
Асимметрия вычисляется как отношение
среднего кубов центральных отклонений
к кубу стандартного отклонения:

В
симметричном распределении асимметрия
точно равна нулю, но в зависимости от
того, как изменяются разности значений
со средним, знак асимметрии меняется
на положительный или отрицательный
(т.к. при возведении в куб знак сохраняется).

5.7.
Эксцесс.
Эта мера »выпуклости» или »крутости»
распределения. При всех одинаковых
других параметрах, два распределения
могут различаться тем, что полигон
частот будет островершинным или плоским,
т.е. мода может оказаться равной, но
встречаться с разной частотой. Эксцесс
служит для того, чтобы определить
крутизну кривой, описывающей распределение,
в окрестностях единственной моды, т.к.
предназначен только для унимодальных
распределений. Эксцесс рассчитывается
по формуле:

Особенностью всех
мер рассеивания является то, что линейное
преобразование значений случайной
величины никак не сказывается на
значениях этих мер, т.е. если к каждому
значению случайной величины прибавляется
или отнимается какое-либо число, то все
отклонения, дисперсия, асимметрия и
эксцесс останутся прежними.

Таблица
5.1. Пример расчета мер центральной
тенденции, квартилей и мер рассеивания.

Расчет
мер центральной тенденции и квартилей
распределения:

Md =
24.5 Mo
= 21 Q₁
=
21 Q₂
=
24.5 Q₃
=
35.5

Расчет
мер рассеивания:

Относительно
данного распределения можно сказать,
что:

1. Распределение
   унимодальное;

2. Основная
   масса значений находится в пределах
   (одного стандартного отклонения) от 19
   до 37, а 50% наблюдений – от 21 до 35.5;

3. Оно
   характеризуется положительной
   асимметрией, что означает, что более
   выражены отклонения в большую от
   среднего арифметического сторону;

4. Распределение
   “пологое” (отрицательный эксцесс),
   т.е. значения случайной величины
   распределены по числовой шкале достаточно
   равномерно.

Необходимо
сказать, что рассчитанные в этом примере
меры могут оказаться полезными при
сравнении между собой двух распределений
одной и той же случайной величины,
полученных в разных условиях, и тогда
можно будет заключить, в каком из двух
распределений большее среднее, где
рассеивание значений больше (или меньше),
какие значения встречаются чаще и т.д.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Меры рассеивания и зависимость между ними

67. В любых условиях стрельбы закономерность рассеивания остается неизменной, но величина площади рассеивания изменяется в зависимости от выучки стреляющего, вида оружия, боеприпасов, прицельных приспособлений, положения для стрельбы, дальности стрельбы, метеорологических и других условий стрельбы.

Для измерения величины площади рассеивания, сравнения рассеивания пуль (гранат) разных видов оружия, а также для оценки рассеивания пуль (гранат) одного и того же оружия при различных условиях стрельбы могут применяться следующие меры (единицы измерения) рассеивания: срединное отклонение, сердцевинная полоса и радиус круга, вмещающего лучшую половину попаданий или все попадания.

68. Срединным отклонением называется такое отклонение, которое в ряду всех отклонений, выписанных по абсолютной величине в возрастающем или убывающем порядке, занимает среднее место.

Срединное отклонение является основной мерой рассеивания. Оно обычно обозначается: Вд — срединное отклонение по дальности; Bв — срединное отклонение по высоте; Вб — срединное отклонение по боковому направлению.

Для определения величины срединного отклонения по одному из направлений необходимо выписать все отклонения в ряд в возрастающем или убывающем порядке по абсолютной величине. Отклонение, стоящее посредине этого ряда, и будет являться срединным отклонением.

Если ряд всех отклонений состоит из четного числа отклонений, то для определения величины срединного отклонения нужно взять два отклонения, стоящие посредине, и разделить сумму их абсолютных величин на два.

Пример. Шести пробоинам отвечают следующие величины отклонений от оси рассеивания по высоте: выше оси рассеивания 4-15; +25; + 70 см; ниже ее — 10; — 40; — 60 см. Определить срединное отклонение по высоте (Вв),

Решение. Выписав по абсолютной величине все отклонения в возрастающем порядке, получим: 10; 15; 25; 40; 60; 70 см.

Действительно, отклонение 32,5 см больше каждого из первых трех отклонений и меньше каждого из последних трех отклонений.

Примечание. При небольшом числе измерений определение величины срединного отклонения таким способом не обеспечивает необходимой точности, так как получение одного добавочного отклонения может значительно изменить величину срединного отклонения для одного и того же способа стрельбы.

Пример. Если к ряду отклонений, указанных в предыдущем примере, добавить еще одно отклонение, равное 80 см, то срединное отклонение станет равным 40 см (10; 15; 25; 40; 60; 70; 80).

В этих случаях величина срединного отклонения более точно вычисляется с помощью среднего арифметического значения. Срединное отклонение равно 0,84 или округленно 5/6, среднего арифметического значения.

Среднее арифметическое значение определяется делением суммы абсолютных значений всех отклонений на количество отклонений. Так например, по условиям предыдущего примера среднее арифметическое значение равно

а срединное отклонение

5/3*42,8=35,7 см.

В этих случаях учитываются численные значения всех отклонений, и результаты отдельных отклонений не сказываются так значительно на величине срединного отклонения.

Срединное отклонение может быть вычислено также с помощью среднего квадрэтического значения. Срединное отклонение равно 0,67 или округленно 2/3 среднего квадратического значения.

Среднее квадратическое значение при небольшом числе отклонений равно корню квадратному из суммы квадратов отклонений, деленной иа число всех отклонений без одного.

Так, по условиям предыдущего примера среднее квадратическое значение будет равно

а срединное отклонение

2/3*54=36 см

Рис. 26. Шкала рассеивания по боковому направлению с масштабом в одно среднее отклонение

69. Если от той или иной оси рассеивания отложить в обе стороны последовательно полосы, равные по ширине соответствующему срединному отклонению, то вся площадь рассеивания окажется разделенной на восемь равных полос — по четыре в каждую сторону, а полное рассеивание по любому направлению будет равно восьми срединным отклонениям.

В действительности могут быть отклонения от центра рассеивания, превышающие четыре срединных отклонения, но вероятность получения их мала (не превышает 0,7%).

При большом числе выстрелов в каждой из полос, равной по ширине одному срединному отклонению или его части, независимо от величины рассеивания содержится определенный процент точек встречи (попаданий).

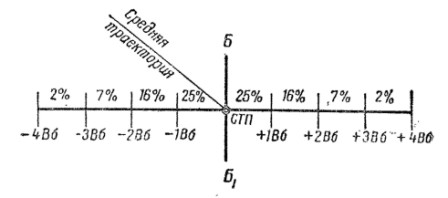
Чертеж, показывающий процентное распределение попаданий в полосы, равные по ширине одному срединному отклонению или его части, называется шкалой рассеивания (рис. 26). Шкала рассеивания в численном выражении одинакова по любому направлению и характеризует закон рассеивания.

Для полос шириной в одно срединное отклонение содержится (округленно): в первых полосах, примыкающих к оси рассеивания, по 25% точек встречи, во вторых по 16%, в третьих по 7% и в крайних по 2%.,

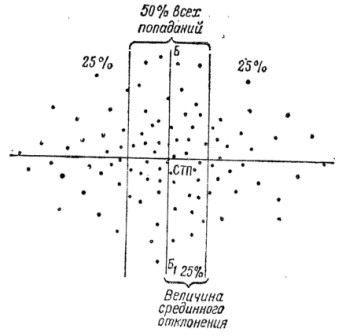
Рис. 27. Определение величины среднего отклонения по боковому направлению графическим способом

Для полос, ширина которых равна сотой части срединного отклонения, процентное распределение попаданий указано в табл. 1 приложения 4.

70. При большом числе попаданий (точек встречи) величину срединного отклонения можно определить графическим способом (рис. 27). Для этого отсчитывают справа (сверху) 25% попаданий (точек встречи) и отделяют их вертикальной (горизонтальной) линией; отсчитывают слева (снизу) 25% попаданий (точек встречи) и также отделяют их вертикальной (горизонтальной) линией. В результате этого получится полоса, вмещающая 50% попаданий (точек встречи), т. е, полоса лучшей половины попаданий. Затем измеряют расстояние между вертикальными (горизонтальными) линиями. Половину расстояния между вертикальными (горизонтальными) линиями принимают за величину срединного отклонения. В связи с этим иногда пользуются другим определением срединного отклонения: срединным отклонением называется половина ширины центральной полосы рассеивания, вмещающей 50% всех попаданий, при условии, что ось рассеивания проходит по ее середине.

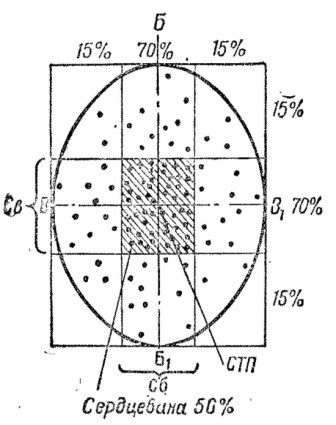
Рис. 28. Серцевинные полосы и серцевина рассеивания	Рис. 29. Определение величины серцевинной полосы по боковому направлению графическим способом

71. Полоса рассеивания, содержащая в себе 70% попаданий (точек встречи), при условии, что ось рассеивания проходит по ее середине, называется сердцевинной полосой (рис. 28).

Сердцевинные полосы обозначаются: Сд — сердцевинная полоса по дальности; Св — сердцевинная полоса по высоте; Сб — сердцевинная полоса по боковому направлению.

При пересечении двух сердцевинных полос образуется прямоугольник, включающий в себя лучшую, наиболее кучную половину всех точек встречи (0,70-0,70 = 0,49, округленно 0,50, или 50%).

Прямоугольник, образуемый пересечением двух сердцевинных полос, называется сердцевиной рассеивания.

Ширина сердцевинной полосы может быть определена графическим способом (рис. 29). Для этого надо отсчитать справа (сверху) 15% попаданий (точек встречи) и провести вертикальную (горизонтальную) линию; отсчитать слева (снизу) 15% попаданий (точек встречи) и также провести вертикальную (горизонтальную) линию. В результате этого вся площадь рассеивания окажется разделенной на три почти равные полосы, при этом центральная полоса содержит 70% попаданий, а крайние — по 15% каждая. Затем следует измерить расстояние между вертикальными (горизонтальными) линиями, которое и будет равно ширине.сердцевинной полосы.

Между сердцевинной полосой и срединным отклонением как мерами рассеивания имеется определенная зависимость. Сердцевинная полоса включает в себя 3,06 соответствующего срединного отклонения. На практике ширину сердцевинной полосы принимают округленно равной трём срединным отклонениям.

72. При стрельбе па близкие расстояния площадь рассеивания на вертикальной плоскости имеет форму круга, что означает примерное равенство характеристик рассеивания по высоте и по боковому направлению. Поэтому о величине такого рассеивания иногда судят не по двум характеристикам (Вв и Вб или Св и Сб), а по одной величине — радиусу круга, вмещающего лучшую половину (Р50) всех попаданий или все (Р100) попадания.

Для определения величины радиуса круга, включающего 50 или 100% попаданий, необходимо (рис. 30) определить среднюю точку попадания. Затем, принимая среднюю точку попадания за центр круга, провести циркулем окружность так, чтобы она вместила половину (50%) или все (100%) точки встречи. Раствор циркуля дает в первом случае величину радиуса круга, включающего 50% а во втором — 100% попаданий.

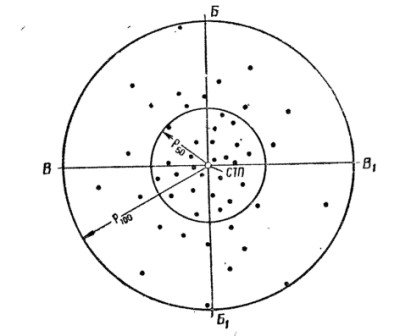
Рис. 30. Определение величины радиусов кругов, вмещающих 50 и 100% попаданий

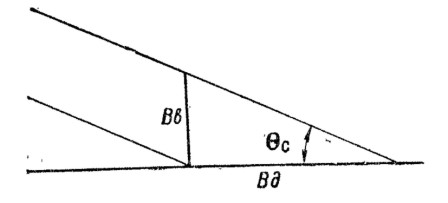
Рис. 31. Зависимость между средними отклонениями по дальности (Вб) и по высоте (Вв)

Радиус круга, вмещающего все попадания, примерно в 21/2 раза больше радиуса круга, вмещающего лучшую половину попаданий.

Между величиной радиуса круга, вмещающего лучшую половину попаданий, срединными отклонениями и сердцевинными полосами имеется определенная зависимость. Радиус круга, вмещающего лучшую половину попаданий (50%), равен 1,76 срединного отклонения или 0,6 сердцевинной полосы.

73. Между величинами рассеивания по дальности и по высоте имеется определенная зависимость: рассеивание по дальности равно рассеиванию по высоте, умноженному нз 1000 и разделенному на величину угла падения в тысячных (рис. 31), т. е,

Пример. Определить Bд, если Вв = 0,36 м, а угол падения 10 тысячных.

Решение.

Сегодня на уроке мы вспомним, что является модой, медианой и
средним арифметическим выборки. Узнаем, что называется размахом выборки.
Выясним, что называют отклонением от среднего. Познакомимся с величиной,
которую называют дисперсией. Узнаем, что называют средним квадратичным
отклонением.

Прежде, чем приступить к рассмотрению новой темы, давайте
вспомним, что совокупность данных иногда бывает полезно оценить одним числом – мерой
центральной тенденции числовых значений её элементов. К таким характеристикам
относятся мода, медиана и среднее.

Итак, мода – это значение случайной величины, имеющее
наибольшую частоту в рассматриваемой выборке.

Медиана – это число (значение
случайной величины), разделяющее упорядоченную выборку на две равные по
количеству данных части.

При этом если в упорядоченной выборке нечётное количество
данных, то медиана равна серединному из них. Если в упорядоченной выборке чётное
количество данных, то медиана равна среднему арифметическому двух
серединных чисел.

Среднее (или среднее
арифметическое) выборки – это число, равное отношению суммы всех чисел
выборки к их количеству. Если рассматривается совокупность значений случайной
величины , то её
среднее обозначают .

Отметим, что не каждую выборку имеет смысл оценивать с помощью
центральных тенденций.

Так, например, посмотрите на следующую выборку , , ,  Это выборка выигрышей (в рублях) четырёх человек. Здесь мода равна
. Медиана
также равна . Среднее
равно .

Очевидно, что ни мода, ни медиана, ни среднее не могут выступать в
роли единой объективной характеристики данной выборки. Это объясняется тем, что
наименьшие значения этой выборки существенно отличаются от наибольшего. А вот
разность наибольшего и наименьшего значений соизмерима с наибольшим значением ().

Сформулируем определение. Разность наибольшего и наименьшего
значений случайной величины выборки называется её размахом и
обозначается буквой R.

Для рассматриваемой выборки размах равен разности  и , то есть
равен .

Размах показывает, насколько велик разброс значений случайной
величины в выборке. Однако, зная размах выборки, невозможно охарактеризовать
отличие её элементов друг от друга, отличие каждого элемента от среднего
значения.

А как сравнить две выборки, которые имеют одинаковые размахи и
одинаковые средние значения?

Давайте рассмотрим пример. На место столяра претендуют двое
рабочих. Для каждого из них установили испытательный срок, в течение которого
они должны изготавливать одинаковые стулья из дерева. В следующей таблице приведены
результаты претендентов.

Каждый из рабочих за пять дней изготовил  деталей. Следовательно, средняя производительность труда за день у
обоих рабочих одинаковая и равна  стульев в
день.

Моды у предложенных совокупностей отсутствуют. Чтобы найти
медианы, расположим значения в порядке возрастания.

, , , , ; , , , , .

Количество данных в обоих случаях нечётно. Слева и справа от числа
 находятся по
два элемента. Получается, что медианы одинаковые ( и ).

В качестве критерия сравнения совокупностей в данном случае может
выступать стабильность производительности труда. Её можно оценить с
помощью отклонений от среднего значения элементов совокупности.

Давайте сформулируем определение. Отклонением от среднего
называют разность между рассматриваемым значением случайной величины и средним
значением выборки.

Например, если значение , а значение , то
отклонение  от среднего
равно .

Отклонение от среднего может быть как положительным, так и
отрицательным.

Найдём отклонение от среднего и внесём найденные значения в
таблицу.

Покажем на нашем примере, что сумма отклонений всех значений
выборки от среднего значения равна .

, .

Поэтому характеристикой стабильности элементов совокупности может
служить сумма квадратов отклонений от среднего.

Давайте найдём квадраты отклонений от среднего и суммы квадратов
отклонений.

Видим, что у второго рабочего сумма квадратов отклонений от
среднего больше, чем у первого, то есть можно записать неравенство .

На практике это означает, что второй рабочий имеет нестабильную
производительность труда: в какие-то дни он работает не в полную силу, а
какие-то навёрстывает упущенное, а это всегда сказывается на качестве
продукции.

Получается, что работодатель захочет взять на место столяра
первого рабочего, ведь у первого рабочего сумма квадратов отклонений от средней
производительности меньше.

В рассмотренном примере рабочие работали одинаковое количество
дней. Если бы рабочие работали разное количество дней и производили в среднем
за день одинаковое число деталей, то стабильность работы каждого из них можно
было бы оценить по величине среднего арифметического квадратов отклонений.
Такая величина называется дисперсией, что в переводе с латинского
означает «рассеяние», и обозначается буквой .

Для случайной величины , принимающей
 различных
значений и имеющей среднее значение , дисперсия
находится по формуле

Давайте решим задачу. Два столяра изготавливали одинаковые
стулья из дерева. При этом первый столяр трудился полную рабочую неделю, а
второй –  дня.
Сведения об их дневной выработке представлены в таблице. Сравните стабильность
работы столяров.

Итак, найдём средние значения выборок данных величин X и Y.

, .

Таким образом, мы получили, что найденные значения равны.

Далее найдём отклонения от среднего для всех значений величин X и Y.

Затем найдём квадраты отклонений от среднего. Найдём сумму
квадратов отклонений от среднего всех значений величин X и Y.

Теперь найдём дисперсию совокупности значений случайной величины X, то есть среднее
арифметическое квадратов отклонений.

Найдём дисперсию совокупности значений случайной величины Y.

Таким образом мы получили, что .

Следовательно, второй столяр работает стабильнее первого.

Отметим, что если значения , , …,  случайной
величины  повторяются
с частотами , , …,  соответственно,
то дисперсию величины  можно
вычислить по формуле

,

 где .

Используя знак суммы Ʃ, данную формулу можно записать более
компактно.

, где .

Пусть величина  имеет
некоторую размерность (например, миллиметры). Тогда её среднее значение  и отклонение
от среднего  имеют ту же
размерность, что и сама величина (в миллиметрах). А вот квадрат отклонения  и дисперсия   имеют
размерности квадрата этой величины (в квадратных миллиметрах).

Для оценки степени отклонения от среднего значения удобно иметь
дело с величиной той же размерности, что и сама величина . С этой
целью используются значения .

Сформулируем определение. Корень квадратный из дисперсии называют средним
квадратичным отклонением и обозначают , то есть .

Давайте найдём среднее квадратичное отклонение от среднего
значения выборки:

 см,  см,  см,  см,  см.

Вообще, дисперсию и среднее квадратичное отклонение в статистике
называют также мерами рассеивания значений случайной величины около
среднего значения.

Пример 6. Духовки

Выпечка пирогов проводится в двух духовках при разной температуре в зависимости от вида теста. В первой духовке выставлена температура 260 °С, а во второй — 180 °С. При измерении температуры в разных частях духовок получены следующие данные:

Определите, какая духовка прогрета более равномерно.

Комментарий к выполнению задания

Введем данные в калькулятор:

Обратите внимание на то, что мы убрали строку SUB. Формат отображения этой строки задается в строке Sub Name окна задания параметров калькулятора SET UP ([SHIFT], [MENU]). При выборе On ([F1]) таблица содержит строку SUB, при выборе OFF ([F2]) — не содержит.

Так как учащиеся уже знают и усвоили алгоритм нахождения дисперсии и стандартного отклонения, покажем им возможность получения этих величин нажатием одной клавиши.

Войдем в подменю CALC ([F2]) и активируем функцию 1VAR ([F1]) — выполнение статистических расчетов для данных одной переменной.

Мы получили расчет для данных столбца 1. Величина стандартного отклонения в этом окне обозначена как xσ_n — это среднее квадратичное отклонение (дисперсию калькулятор не вычисляет).

Имеем: среднее квадратичное отклонение для первой духовки примерно равно 4,5 В.

Чтобы провести расчет для столбца 2, нужно вернуться в подменю CALC ([EXIT]), нажать [F6] для входа в подменю выбора параметров статистических расчетов SET, и заменить в первой строке номер столбца, являющегося аргументом, на 2.

В этом подменю в первых двух строках определяются исходные данные для статистических расчетов одной переменной: в строке 1Var XList задается номер столбца с данными, в строке 1Var Freq задается частота повторения данных (по умолчанию частота равна 1, а при наличии столбца с частотой данных здесь задается его номер).

Вернемся к таблице ([EXE] или [EXIT]) и проведем расчет для второго столбца: 1VAR ([F1]):

Имеем: среднее квадратичное отклонение для второй духовки примерно равно 1,4 В.

Сравниваем средние квадратичные отклонения (4,5 В и 1,4 В) и делаем вывод: вторая духовка прогрета более равномерно.

Перейти к упражнениям

Перейти к упражнениям с решением