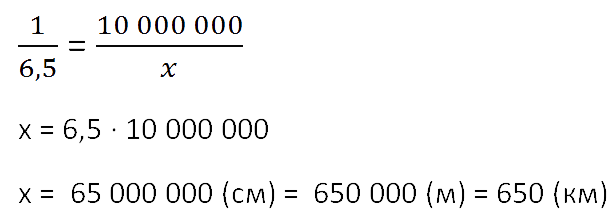Математика
6 класс
Урок № 3
Масштаб
Перечень рассматриваемых вопросов:
- Понятие масштаба.
- Находить масштаб по заданному расстоянию на местности и расстоянию на карте (плане).
- При заданном масштабе и расстоянии на местности определять расстояние на карте (плане).
- При заданном масштабе и расстоянии на карте (плане) определять расстояние на местности.
Тезаурус
Частное двух не равных нулю чисел a и b называется отношением чисел a и b.
Числа a и b называются членами отношения.
Отношения 2 к 3 и 3 к 2 называются взаимно обратными.
Отношение величин одного наименования (длины, скорости, стоимости и т. д., выраженных одинаковыми единицами измерения) есть число.
Отношение величин различных наименований (пути и времени, стоимости товара и его количества, массы тела и его объёма и т. д.) есть новая величина.
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Масштаб, выраженный отношением чисел, называется численным.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.
Теоретический материал для самостоятельного изучения
Сегодня мы с вами разберём, что означает масштаб.
Давайте сначала вспомним, что отношение величин одного наименования – это число.
Составим отношения:
Все мы хорошо знаем, что участки земной поверхности, детали машин и многое другое изображается на бумаге в уменьшенном виде.
Масштаб – это отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Рассмотрим пример:
Длина отрезка на карте равна 8 см.
Ответ: 800 м.
Ещё один пример:
Длина отрезка на местности равна 130 километров.

Ответ: 13 см.
Что же означает данный масштаб:

Говорят: карта сделана в масштабе одна двухтысячная. Объект на карте уменьшен в 2000 раз.
Что будет означать такой масштаб:

Рассмотрим ещё несколько примеров.
Огород имеет вид прямоугольника, длина которого 60 м, а ширина 10 м.

Ответ: Огород на плане будет иметь размеры: ширина 20 см, длина 12 см.

Разбор заданий тренировочного модуля
№ 1. Тип задания: Установление соответствий между элементами двух множеств.
Расстояние между двумя городами равно 150 км. Определите расстояние между изображениями этих городов на карте при трёх разных масштабах карты.

№ 2. Тип задания: Выбор элемента из выпадающего списка.
Значит, выбираем ответ 15 км.
Понятие масштаб тесно связано с отношением чисел и пропорциями.
Поэтому, если вы не уверены в своих знаниях по этим темам, настоятельно рекомендуем
изучить их еще раз.
Вы можете сделать это и на нашем ресурсе в темах
отношение чисел
и
пропорции.
Масштаб — важное понятие. Если вы научитесь его правильно понимать, он поможет
вам не только в математике, но и в географии, черчении, а порой и в физике.
Запомните!
Масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности (в реальности).
Масштаб записывают в виде отношения двух чисел. Первый член отношения обычно равен 1,
а второй член — число, показывающее во сколько раз длина единицы расстояния (см, м или км) на карте меньше
соответствующий единицы расстояния в реальности.
Разберёмся на примере:
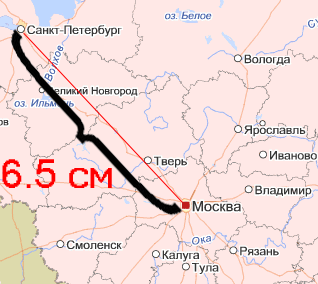
Ниже представлена часть карты с масштабом 1 : 10 000 000 (см). Такой масштаб означает, что
в 1 см на карте помещается 10 000 000 (см) реального расстояния,
или 100 000 (м), или 100 (км).
Говорят, что карта сделана в масштабе однадесятимиллионная (по названию десятичной дроби, в
которую может превратиться отношение
1 : 10 000 000 = 0,000 000 1.
Санкт-Петербург и Москва на карте соединены отрезком длиной в 6,5 (см).
Определим, сколько в реальности (км) между Москвой и Санкт-Петербургом.
Для решения этой задачи составим таблицу и занесём в неё нужные данные. Неизвестную величину обозначим за
«x».
| На карте | В реальности | |
|---|---|---|
| Масштаб | 1 (см) | 10 000 000 (см) |
| Расстояние между Москвой и Петербургом |
6,5 (см) | x (см) |
Составим и решим пропорцию:
Ответ: 650 км — приблизительное расстояние между Москвой и Санкт-Петербургом.
Теперь, зная, что такое масштаб, вы легко с помощью линейки можете измерить расстояние на карте или на чертеже и
рассчитать нужное расстояние в реальности.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2016 в 19:27
Марина Трескина
Профиль
Благодарили: 0
Сообщений: 1
Марина Трескина
Профиль
Благодарили: 0
Сообщений: 1
помогите пожайлуста я немогу найти маштаб карты, точнее я не могу понять как его находить
Например
расстояние между пунктами М и К на карте = 3.4 см, а на местности 680км. Найди маштаб карты
0
Спасибо
Ответить
20 февраля 2016 в 16:15
Ответ для Марина Трескина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Масштаб 1: 20 000 000
Подробно описано здесь.
А ещё, «масштаб» пишется с буквой «С».
0
Спасибо
Ответить
30 сентября 2016 в 14:49
Ответ для Марина Трескина
Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
Доброго времени суток. Помогите пожалуйста, я в тупике.
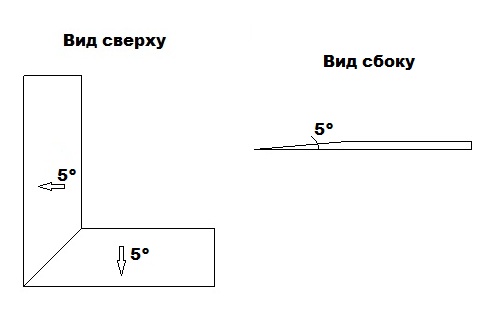
Суть вопроса: плоскости примыкают друг другу под углом 45 градусов. Сами плоскости имеют наклон 5 градусов от внутреннего угла к внешнему. При таком условии градус примыкания должен измениться. Как рассчитать точный градус примыкания?
0
Спасибо
Ответить
30 сентября 2016 в 23:43
Ответ для Марина Трескина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Попробуйте продублировать вопрос не в какой то теме, а отдельно. К сожалению, я не понимаю задачу. Может кто-нибудь на форуме сможет ответить. Удачи!
0
Спасибо
Ответить
8 февраля 2016 в 15:26
Лиана Мусилева
Профиль
Благодарили: 0
Сообщений: 1
Лиана Мусилева
Профиль
Благодарили: 0
Сообщений: 1
Какую длину имеет на карте отрезок, изображающий растояние 85км, если масштаб карты 1:1000000.
Как решить подробно с помощью таблицы?
0
Спасибо
Ответить
19 сентября 2016 в 11:55
Ответ для Лиана Мусилева
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В данной теме очень подробно расписано с примерами. Рекомендую ознакомиться.
1
Спасибо
Ответить
13 октября 2015 в 20:41
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
расстояние на местности 7целых 3 десятых изоброжено на карте отрезком в 1 см.опредилите масштаб карты.
0
Спасибо
Ответить
13 октября 2015 в 20:45
Ответ для Маргарита Помешкина
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
Маргарита Помешкина
Профиль
Благодарили: 0
Сообщений: 3
решение
0
Спасибо
Ответить
15 сентября 2016 в 9:07
Ответ для Маргарита Помешкина
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Про масштаб и его вычисление можно прочитать здесь. Ответ: 1:730 000
0
Спасибо
Ответить
28 августа 2015 в 12:10
Амина Умирова
Профиль
Благодарили: 0
Сообщений: 1
Амина Умирова
Профиль
Благодарили: 0
Сообщений: 1
На карте чей масштаб 1:25000000 расстояние между двумя городами 12 см. Найдите истенное расстояние между двумя городами
0
Спасибо
Ответить
31 августа 2015 в 15:19
Ответ для Амина Умирова
Кристина Терёшкина
Профиль
Благодарили: 0
Сообщений: 1
Кристина Терёшкина
Профиль
Благодарили: 0
Сообщений: 1
Задача решается пропорцией.
1/12=25000000/x
Значит, 12 умножаем на 25000000.
Получается 300000000 Мы превращаем см в км.
Поэтому, 300000000(см)=3000000(м)=3000(км)
Ответ: расстояние между городами 3000 км
0
Спасибо
Ответить
Помогите пожалуйста. Как найти расстояния на карте,зная на местности и МАСШТАБ
Чтобы найти масштаб, нужно разделить расстояние на местности на расстояние на карте.
При этом необходимо учитывать, что в 1 км — 100000 см.
Как найти расстояние на карте?
Всё просто.
М — масштаб, расстояние на местности, расстояние на карте.
Если , то
Отсюда следует следующее — чтобы найти расстояние на карте (), необходимо расстояние на местности () разделить на масштаб (М).
Масштаб. Измерение расстояний по планам, картам и глобусу. Урок 3
Масштаб плана или карты всегда один, но указываться он может тремя разными способами. Способы обозначения масштаба следующие:
- численные;
- именованные;
- графические (линейные и поперечные).
Численный масштаб имеет вид дроби, например 1:1000, числитель которой показывает единицу измерения на карте, а знаменатель – во сколько раз она уменьшена по сравнению с действительным расстоянием, второе число называется величиной масштаба. Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз. Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так. Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Масштаб топографическтй карты
Но, зная математику, мы легко можем перевести сантиметры в метры или километры. Чтобы делать это быстрее, переводя в метры, просто зачёркиваем 2 нуля, так как в 1м – 100 см, а в километры – убираем 5 нулей. Пример: 1:1000 – убираем 2 нуля и получаем 10 метров. Если масштаб один к ста тысячам, например, тогда уже можно перевести знаменатель и в километры – 1:100 000, для этого уберём 5 нулей, потому что в 1 км 100 000 см. Получим, что в 1 см на карте 10 км на местности, а это будет уже другой вид масштаба – именованный.
Именованный масштаб указывается на всех картах, он дополняется словами. В 1 см – 10 м, 10 м – это величина масштаба. Для примера переведём численный масштаб в именованный, пользуясь правилом, обсуждаемым выше:
- 1:25 000 000 – 1см-250 км;
- 1:10 000 000 – 1см-100 км;
- 1:20 000 – 1см-200 м.
При необходимости обратного перевода добавляем те же нули, при переводе километров в сантиметры добавим 5 нулей, метров в сантиметры – 2 нуля. Например:
- 1 см-300 м – это 1:30 000;
- 1см-250 км – это 1:25 000 000.
Для непосредственного определения расстояния по картам и планам служит линейный масштаб. Это график, помещаемый внизу карты в виде линейки (масштабная линейка), в России она разделёна на сантиметры. Справа от нуля у каждого деления линейки подписано истинное расстояние на местности, равное одному, двум или нескольким величинам масштаба. Слева от нуля сантиметр линейки разбивают на меньшие деления, например на миллиметры, для получения более точных результатов.
Понятие масштаба. Измерение расстояний на местности и на карте
Самарский областной центр технического творчества учащихся
Самарская городская общественная организация «Детско-молодежный спортивно-технический клуб Контур»
Абрамов А.В.
Самара, 2000 г.
1 часть
Пособие для учащихся учреждений дополнительного образования и для занятий спортивной радиопеленгацией в семье
1.4. Понятие масштаба. Измерение расстояний на местности и на карте.
Вспомним материал параграфа 2. Там говорилось о важнейших свойствах карты. Одно из них гласило: все объекты на карте уменьшены по сравнению с соответствующими объектами местности в одинаковое количество раз. А во сколько же раз карта уменьшена по сравнению с местностью? Наверное, разные карты уменьшены по-разному. Величина, характеризующая степень уменьшения карты, называется масштабом.
Масштаб карты — это дробь, в числителе которой стоит единица, а в знаменателе – величина, показывающая, во сколько раз уменьшены объекты карты по сравнению с соответствующими объектами местности.
Масштаб карты указывается в зарамочном оформлении. Знание масштаба позволяет нам измерять расстояния по карте и переводить их в расстояния на местности. В примере, рассмотренном в предыдущем параграфе, мы, двигаясь к лесному озеру, не знали, сколько нам до него идти. Вдруг мы отклонились от азимута и озеро давно уже позади? Такого вопроса не возникло, если бы мы, измерив расстояние от домика лесника до озера по карте, рассчитали это расстояние на местности.
Пусть масштаб карты составляет 1:15000. Это означает, что все расстояния местности уменьшены при нанесении на карту в 15000 раз. Следовательно, расстояния, измеренные по карте, при переносе на местность должны быть увеличены в 15000 раз. Каждый сантиметр карты составляет 15000 сантиметров на местности или 150 метров. Таким образом, для карты масштаба 1:15000, 1 см на карте соответствует 150 метрам на местности, а 1 мм – 15 метрам.
Как перевести расстояние, измеренное по карте, в расстояние на местности? Очень просто. Нужно расстояние в миллиметрах умножить на 15 (вспомните, ведь 1 мм это 15 м). И тогда мы получим расстояние в метрах.
Обратите внимание, что в значении масштаба не указана единица измерения (1:15000). Это не случайно. Дело в том, что нет никакой разницы в каких единицах вести измерения. Хоть в попугаях и слоненках, как это делалось в известном мультфильме. Выражение масштаба показывает, что 1 единица на карте, будь то миллиметр, сантиметр, попугай, соответствует 15000 таких же единиц на местности (миллиметров, сантиметров, попугаев).
Для удобства работы условимся измерять расстояния на карте в миллиметрах, а на местности в метрах. Тогда для перевода единиц карты в единицы местности можно воспользоваться таким соотношением:
Чтобы найти расстояние между двумя объектами местности в метрах, нужно на карте измерить это расстояние в миллиметрах, умножить на знаменатель масштаба и перевести полученный результат в метры, то есть разделить на тысячу.
Запишем соотношение в виде формулы:
где – F(m) – расстояние на местности в метрах,
K(mm) – расстояние по карте в миллиметрах, M – знаменатель масштаба.
Задания для самостоятельной работы.
- Определите расстояния между КП по картам различных масштабов.
- Выберите на карте перегон заданной длины.
- Вдоль тропы установлены КП с номерами. На карточке нарисован отрезок и указан масштаб. Добежать до «своего» КП.
- Добежать до заданного КП. Нарисовать отрезок в разных масштабах.
- Даны направления (азимуты) и расстояния. Найти КП на местности.
- Идти от КП к КП (с точки каждого КП видны другие) и рисовать маршрут в виде ломаной линии при заданном масштабе.
Как измерять расстояние по карте, плану или глобусу?
Измерять расстояния можно при помощи масштаба или градусной сетки (на плане её нет). Второй способ мы изучим немного позднее. Чтобы узнать расстояние на местности, нужно расстояние между двумя точками на карте или плане измерить при помощи линейки (этот способ подходит для прямых линий, для извилистых пользуются курвиметром или измерением малым раствором циркуля).
Измерения нужно производить очень точно, учитывая миллиметры. Затем полученные данные умножить на величину масштаба. Например, если при измерении мы получили расстояние 1,4 см, а масштаб карты в 1см 10 000 км, нужно умножить 1,4 на 10 000, получится 14 000 км – это и есть расстояние на местности. Нужно знать, что мы узнаём не действительное расстояние, а его проекцию. Линия на карте может иметь разные неточности в связи с углом наклона земной поверхности.
При помощи линейного масштаба измеряют расстояние линейкой или циркулем, переносят это расстояние на масштабную линейку и без дополнительных расчетов получают искомое расстояние. При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
Глобус – объёмная модель Земли. Он показывает шарообразную форму нашей планеты. На нём все объекты изображены в неискажённом виде. В отличие от карты, они сохраняют свою форму, площадь, длину. Направления на глобусе совпадают с направлениями на Земле. У глобуса всюду один и тот же масштаб, который обычно надписывается в южной части Тихого океана. Масштабы школьных глобусов очень мелкие: 1:50 000 000, т. е. в 1 см – 500 км, истинное расстояние на нём уменьшается в 50 миллионов раз.
Для определения расстояний по глобусу надо ниткой или полоской бумаги измерить расстояние между заданными пунктами и, зная масштаб глобуса, вычислить истинное расстояние с помощью пропорции, как по обычной карте.
Виды написания масштаба
В топографии принято указывать масштаб тремя способами.
Численный
Численный масштаб относится к самому распространенному виду, применяемому на топографических картах и различных планах. Пишется он в виде: 1:10000, где в числителе единица, а в знаменателе число, указывающее во сколько раз уменьшили реальный объект для указания его на карте. При масштабе 1: 10000 уменьшение будет в 10 тысяч раз.
Обозначение масштаба на карте
| Для карт | 1:1000000, 1:500000, 1:300000, 1:200000, 1:100000, 1:50000, 1: 25000, 1:10000 |
| Для планов | 1:5000, 1:2000, 1:1000, 1:500 |
Запомнить нужно, что чем больше цифра после дроби, тем более мелко изображен объект.
Словесный
Словесный масштаб введен для удобства пользователей. Дело в том, что на топографических материалах измерения проводятся в см, но это неудобно людям, которые, говоря о расстояниях, обычно подразумевают метры или километры. Поэтому рядом с числовым может быть написан словесный масштаб. Например, так:
- 1 : 1 000 в 1 см – 10 м,
- 1 : 20 000 в 1 см – 200 м,
- 1 : 5 000 000 в 1 см – 50 км,
- 1 : 75 000 000 в 1 см – 750 км.
Линейный
Дополнительно к числовому, может быть указан линейный масштаб. Он позволяет определить расстояние на карте или наоборот нанести линию на карту без числовых измерений.
Пример линейного масштаба
Линейный масштаб — это линия, которая делится по всей длине на одинаковые отрезки (обычно они равны 2 см). Справа от о у каждой части отрезков указывается расстояние (оно вычисляется согласно существующему масштабу). Слева от нуля также отложен отрезок с более мелкими делениями (обычно их 10).
Чтобы узнать расстояние на карте прикладываем к точке А и точке Б циркуль. Затем полученный раствор переносим на линейный масштаб, чтобы определить расстояние в метрах или километрах. Справа от нуля устанавливаем конец циркуля на полное значение отрезка, а вторым концом слева от нуля смотрим полученное значение из мелких делений. Объединив эти два значения, получаем реальное расстояние на местности.
LКарты и компас это азы ориентирования на местности. Как пользоваться компасом, вы узнаете из статьи: Ориентирование по компасу в походе – необходимая азбука для туриста-пешеходника
Масштаб и классификация карт по нему
Чем больший участок Земли нужно изобразить, тем в большее количество раз нужно уменьшить расстояния на карте по сравнению с действительным. На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Подробно можно показать небольшую площадь, посёлок, район, город. Тут будет видны уже и форма и размер зданий, расположение лесопарков, небольшие реки и др. Это возможно потому, что расстояния уменьшены несильно, масштаб карты достаточно крупный.
По масштабу карты делят на:
- мелкомасштабные (обзорные) — с масштабом менее 1: 1 000 000;
- среднемасштабные (обзорно-топографические) – в пределах 1: 200 000 до 1: 1 000 000;
- крупномасштабные (топографические) – от 1: 200 000 до 1: 10 000.
Нужно запомнить правило: чем больше величина масштаба, тем мельче масштаб карты, чем крупнее масштаб, тем подробнее карта.
как найти расстояние на карте если известен масштаб и местность?
Чтобы определить расстояние между двумя точками, вначале измеряют это расстояние на карте, а затем, пользуясь численным или линейным масштабом карты, определяют действительное значение этого расстояния на местности. Если требуется найти расстояние не по прямой, а по извилистой дороге, пользуются специальным прибором — курвиметром (рис. 43). Это прибор для измерения длины кривых линий. Основанием курвиметра служит колесико, длина окружности которого известна. Вращение колесика передается на стрелку, поворачивающуюся по круговой шкале. Зная число оборотов колесика, катящегося по измеряемой линии, легко определить и ее длину.
1 Длина отрезка на карте 3 см. Найти длину соответствующего отрезка на местности, если масштаб карты 1 : 1000000
РЕШЕНИЕ
2 Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1 : 100000
РЕШЕНИЕ
820 Определите по карте расстояние от опушки леса до точки пересечения дороги с рекой. Масштаб карты 1:100 000.
РЕШЕНИЕ
821 Расстояние между городами А и В на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты 1:1000000.
РЕШЕНИЕ
822 Длина железной дороги Москва — Петербург приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1:10 000 000.
РЕШЕНИЕ
823 Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной странице тетради это расстояние в масштабе одна десятимиллионная?
РЕШЕНИЕ
824 На рисунке дан план квартиры в масштабе 1:100. Определите по плану, какие размеры имеют кухня, ванная и комнаты и какова их площадь в действительности.
РЕШЕНИЕ
825 Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на этой карте между ними 12,6 см?
РЕШЕНИЕ
826 Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе 1:10 000 000; 1:2 000 000?
РЕШЕНИЕ
827 Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего 10 км? Какой отрезок на местности изображает на карте 1,8 см?
РЕШЕНИЕ
828 Длина детали на чертеже, сделанном в масштабе 1:5, равна 7,2 см. Чему будет равна длина этой детали на другом чертеже в масштабе 1:3; 2:1?
РЕШЕНИЕ
829 Вычислите устно.
РЕШЕНИЕ
830 Какое число надо отнять от числителя и знаменателя дроби 31/47, чтобы получить 5/9
РЕШЕНИЕ
831 Составьте три пропорции, используя верное равенство 18 : 2 — 54 : 6; 4,5 : 1,5 = 1,26 : 0,42; 2,8 · 45 = 6,3 · 20; 3,9 · 0,14 — 0.6 · 0,91
РЕШЕНИЕ
832 Две трети от двух третьих числа равны двум третьим. Какое это число?
РЕШЕНИЕ
833 Сколько гектаров в 1 м2? Сколько часов в 1 с; литров в 1 см3?
РЕШЕНИЕ
834 Известно, что объем пирамиды в 3 раза меньше объема призмы такой же высоты и с таким же основанием. Вычислите объем четырехугольной пирамиды, в основании которой прямоугольник со сторонами 2/3 дм и 9/10 дм, а высота 5 дм.
РЕШЕНИЕ
835 Чтобы приготовить 4 порции картофельной запеканки нужно взять 0,44 кг картофеля. Сколько потребуется картофеля чтобы приготовить 12 порций запеканки?
РЕШЕНИЕ
836 Некоторое расстояние ласточка пролетела за 0,5 ч со скоростью 50 км/ч. За сколько минут пролетит то же расстояние стриж, если будет лететь со скоростью 100 км/ч?
РЕШЕНИЕ
837 Начертите окружность и постройте два ее радиуса, угол между которыми 120°. Закрасьте часть круга между этими радиусами. Какая часть окажется закрашенной и останется незакрашенной?
РЕШЕНИЕ
838 1) Сумма двух чисел 7,2, причем 1/3 большего числа равна меньшему. Найдите эти числа. 2) Разность двух чисел 1,5, причем 1/4 большего равна меньшему. Найдите эти числа.
РЕШЕНИЕ
839 Решите уравнение.
РЕШЕНИЕ
840 Найдите с помощью карты расстояние от Москвы до Киева.
РЕШЕНИЕ
841 Измерьте длину и ширину своей комнаты. Начертите в тетради план этой комнаты в масштабе 1:100.
РЕШЕНИЕ
842 Расстояние на местности в 20 м изображено на плане отрезком 1 см. Определите масштаб плана.
РЕШЕНИЕ
843 Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1:300?
РЕШЕНИЕ
844 Расстояние между городами на местности равно 1300 км. Каким отрезком будет изображено это расстояние на карте, масштаб которой 1:10 000 000?
РЕШЕНИЕ
845 Длина детали на чертеже, сделанном в масштабе 1:3, равна 2,4 см. Чему будет равна длина этой детали на другом чертеже в масштабе 2:1?
РЕШЕНИЕ
846 Найдите значение выражения.
РЕШЕНИЕ
Цели урока:
- Ввести понятие масштаба, научить находить
расстояния на карте и на местности, пользуясь
масштабом, учить решать задачи, связанные с
понятием масштаба - Развивать мышление, творческую активность,
внимание, интерес к математике. - Создать условия для развития
самостоятельности.
Оборудование: компьютер, мультимедиа,
презентация (приложение 1),
учебник Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова,
С.И. Шварцбурда «Математика 6», тетрадь, линейка,
карандаши.
Тип урока — урок изучения и
первичного закрепления новых знаний
Ход урока
1. Организационный момент. (слайд 2).
Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Бороться — старательно!
И открытия нас ждут обязательно!
2. Сообщение темы урока (слайд 3)
Речь идет о трудной теме. Хотя уже
хорошо отработаны понятия: «отношение»,
«пропорция», говорилось и об отношении
расстояний. Теперь надо только по-новому назвать
одно специфическое отношение — расстояния на
карте между двумя пунктами к расстоянию между
теми же пунктами на местности.
3. Устный счет: (слайд 4)
1. Выразите в километрах:
а) 32000000 см,
б) 600000 см,
в) 32000 см,
г) 5000000 см.
2. Выразите в метрах:
а) 32000000 см,
б) 600000 см,
в) 32000 см,
г) 5000000 см.
4. Изучение нового материала.
1) Подготовительная работа. (слайд 5)
— Составьте отношения:
а) 1 см к 5000 м,
б) 1 см к 210 м,
в) 1 см к 54 см,
г) 1 см к 30000 км.
— Что нужно сначала сделать?
Решение:
а) 1 : 500000,
б) 1 : 21000,
в) 1 : 54,
г) 1 : 3000000000.
— Участки земной поверхности, детали
машин, план дома и многое другое изображают на
бумаге в уменьшенном виде.
— Если на карте, чертеже, плане
встретите такие отношения, то это масштаб карты,
чертежа, плана. (слайд 6)
2) Работа над новой темой. (слайд 7)
Определение: Отношение длины
отрезка на карте к длине соответствующего
отрезка на местности называют масштабом
карты. (Аналогично можно сказать о чертеже,
плане).
Масштаб — жезл размерный или мерило,
мерник, размерник, мера линейная, принятая для
чертежа или иной работы. (Из толкового словаря
В.И.Даля.)
— Объясните, что обозначают данные
масштабы. (слайд 
Ответ: Если масштаб карты 1 : 500000, то
на этой карте длина каждого отрезка уменьшена в
500000 раз. На такой карте расстояние, равное 5 км,
будет изображаться отрезком в 1 см.
Масштаб карты 1 : 500000 = Говорят, что карта сделана в
масштабе одна пятитысячная.
3) Работа с учебником. (слайд 9)
— Самостоятельно разберите задачу 1 на
стр. 134.
Составьте задачу по карте
масштаб карты 1 : 100000 (в 1 см — 1 км)
Задача. Длина отрезка на карте 2 см.
Найдите длину соответствующего отрезка на
местности, если масштаб карты 1 : 100000. (слайд 10)
Решение:
Пусть х (м) — расстояние на местности.
|
расстояние |
масштаб |
|
|
На карте |
2см |
1см |
|
На местности |
Х см |
100000 см |
2:х = 1:100000
х = 200000
200000см = 2000 м = 2 км
Ответ: 2 км на местности.
5. Физкультминутка.
6. Закрепление изученного материала.
Рассмотрим две задачи из учебника Н.Я.
Виленкина, В.И. Жохова, А.С. Чеснокова, С.И.
Шварцбурда «Математика 6». (слайд 11-12)
Задача. Отрезку на карте,
длина которого 3,6 см, соответствует расстояние на
местности 72 км. Каково расстояние между городами,
на этой карте расстояние между ними 12,6 см?
Решение. Составим таблицу. Запись: 72
км = 7 200 000 см — обязательна. Учащиеся должны каждый
раз видеть, что вычисляется отношение величин,
измеренных одной и той же единицей.
Таблица
|
На карте |
3,6см |
12,6см |
|
На местности |
72 км = 7 200 000 см |
Х см |
Затем, проговаривая определение
масштаба, заполняем две последние клетки в
таблице. Слева появляется запись: «3,6: 7 200 000», а
справа — «12,6: х».
— Ребята! А карта у нас одна и та же? Значит,
масштаб в обоих случаях один и тот же? Тогда мы
можем приравнять два отношения:
3,6: 7 200 000 = 12,6: х.
Вот теперь учащиеся вступают на
достаточно известную им дорогу. Они уже
отработали способ решения уравнений такого вида.
Записывают равенство произведения крайних
членов пропорции произведению ее средних членов
и находят значение х:
7 200 000 * 12,6 = 3,6 * х,
Х = (7200000 * 12,6):3,6
Здесь, как правило, учащиеся торопятся
умножать. Но этого делать не следует. Надо
попытаться сначала сократить дробь,
воспользовавшись равными отношениями 12,6:3,6 = 126:36 =
7:2. Тогда
7200000 * 7
х = ———————
2
или х = 3600000 * 7 = 25200000(см) = 252(км).
Такой подход демонстрирует учащимся
возможность отказаться от калькулятора, не
загружая себя скучной вычислительной работой.
Задача . Отрезок на местности длиной 3
км изображен на карте отрезком 6 см. Какова на
карте длина отрезка, изображающего отрезок 10 км?
Какой отрезок на местности изображает отрезок на
карте длиной 1,8 см?
Решение.
Составляем таблицу, аналогичную таблице в
предыдущей задаче, подробно разбирая, в какую
строчку какое данное записать. При этом вводим
две переменные. Это, во-первых, делает наглядной
запись условия, а во-вторых, служит подготовкой к
решению задач с двумя неизвестными.
Итак, на первом этапе решения появляется
таблица. Строка «Масштаб» пока еще не заполнена
— она заполняется по ходу решения.
Таблица
| На карте | 6 см | Х см | 1,8 см |
| На местности | 3 км=300000 см | 10 км =1 000000 см | У см |
| Масштаб |
«Что же можно узнать из второй колонки
таблицы?» — «Масштаб, он равен: 6 см: 300 000 см = 2: 100
000».
— «А как можно найти масштаб иным способом, из
третьей колонки таблицы?»
Ведя такую беседу (и каждый раз проговаривая
определение масштаба, что очень важно), получаем
вместе с классом уравнение 2: 1 00 000 = х: 1 000 000,
отсюда х = 20 (см).
Снова вспоминая понятие масштаба, получаем
уравнение
2: 100 000 = 1,8: у,
у = 90 000 (см) = 0,9 (км).
Конечно, в более сильных классах можно не
проговаривать определение масштаба каждый раз.
Но таблица, облегчающая запись решения задач,
думаю, поможет всем учащимся.
7. Самостоятельная работа. (слайд 13)
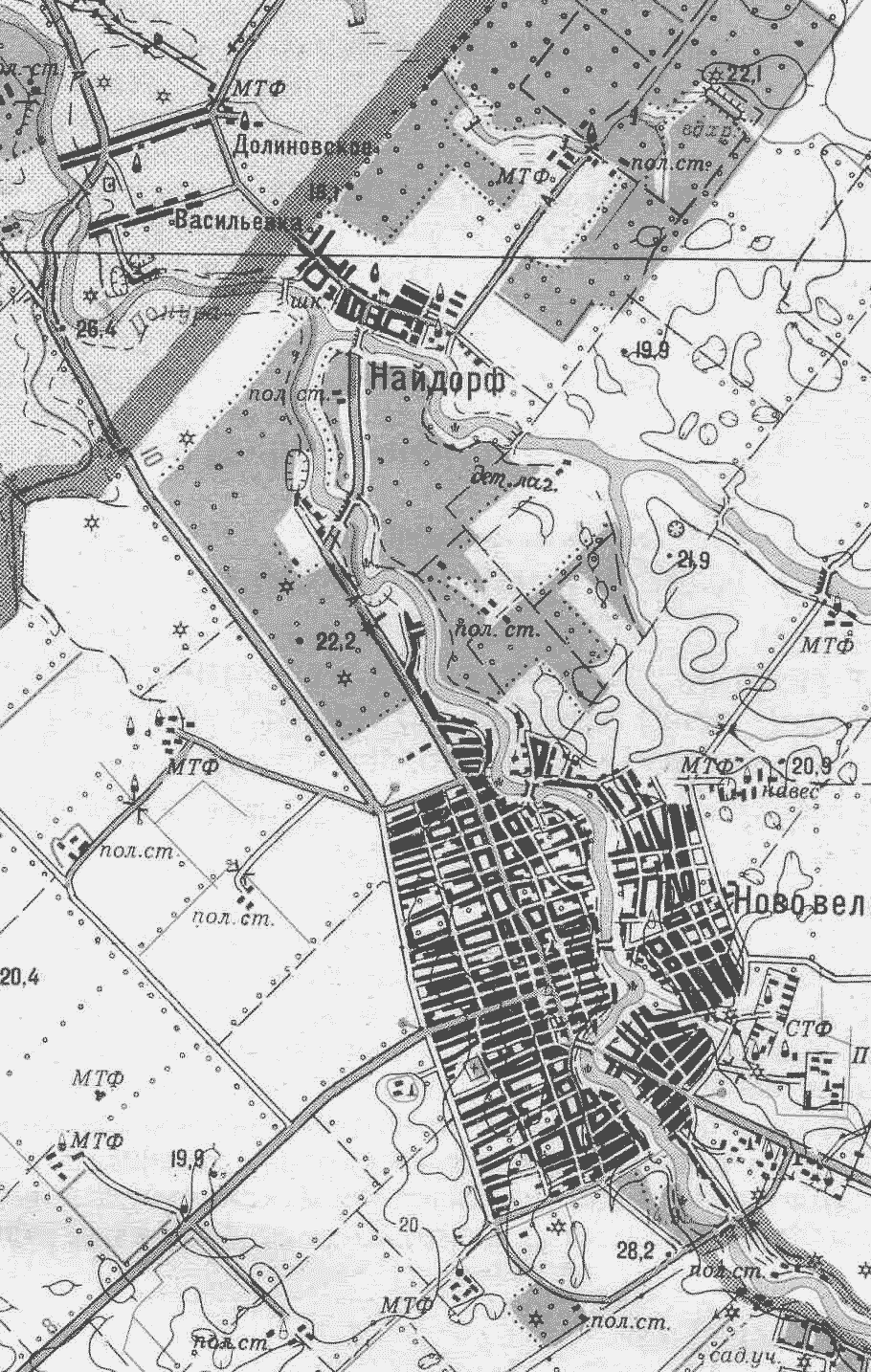
Найдите расстояние между поселком Найдорф и
станицей Нововеличковской если масштаб карты 1:
100000
8. Итог урока. (слайд 14)
— Что называют масштабом карты?
— Где в практической деятельности человек
пользуется этим понятием?
— Чему равен масштаб чертежа, если на нем детали
увеличены в 5 раз? Уменьшены в 50 раз?
9. Домашнее задание. (слайд 15)
Стр. 137 № 842, 844
Творческое задание: нарисуйте план
своего дома в масштабе 1:100 (в 1 см — 1 метр).
Приложение №1 —
Презентация к уроку по теме «Масштаб»