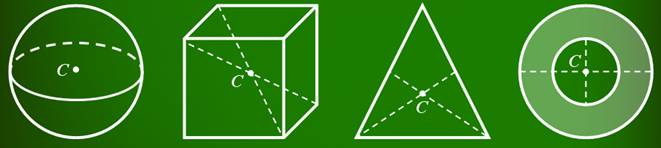
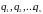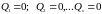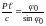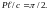Содержание:
Равновесие тел:
Представьте, что вам нужно достать книгу с верхней полки. Подставив стул, вы становитесь на него на цыпочках и… не удерживаете равновесия. А вот неваляшка всегда возвращается в вертикальное положение и никогда не теряет равновесия! Что такое равновесие и при каких условиях реальное тело (а не его модель — материальная точка) находится в равновесии?
Что такое равновесие тела
Равновесие тела — это сохранение состояния движения или состояния покоя тела с течением времени. Что значит сохранение состояния движения? Для начала определим поступательное и вращательное движения.
| Поступательное движение | Вращательное движение |
| Движение тела, при котором все точки тела движутся одинаково. | Движение тела, при котором все точки тела движутся по окружностям, центры которых распо |
|
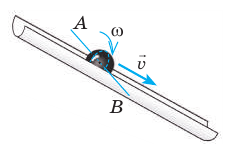
Движение шарика по наклонному желобу сложное — его можно разложить на два простых движения:
|
Центр масс тела
Если к неподвижному телу приложить некоторую силу, обычно тело начинает вращаться и одновременно двигаться поступательно. Но через некоторое время вращательное движение тела прекратится и тело будет двигаться только поступательно. Это произойдет тогда, когда линия действия силы пройдет через центр масс тела.
Центр масс тела — это точка пересечения прямых, вдоль которых направлены силы, каждая из которых вызывает только поступательное движение тела (рис. 14.1).
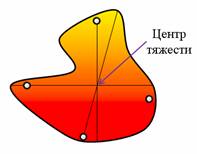
Если размеры тела гораздо меньше радиуса Земли, то центр масс тела совпадает с центром тяжести. Напомним: центр тяжести симметричных фигур расположен в их геометрическом центре; центр тяжести треугольника — в точке пересечения его медиан. (О некоторых методах определения центра масс вы узнаете в ходе лабораторной работы № 4.)
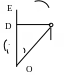
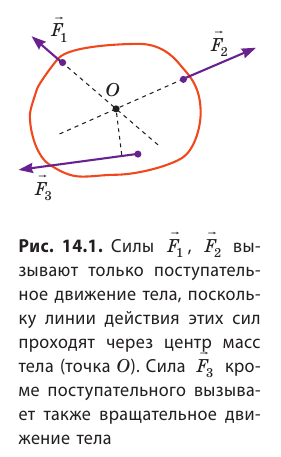
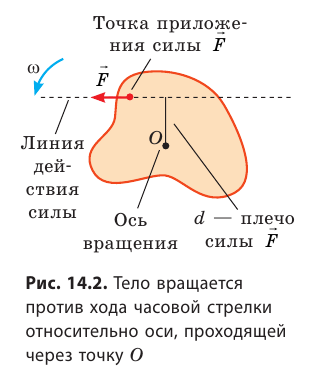
Момент силы M — это физическая величина, которая равна произведению модуля силы F, действующей на тело, на плечо d этой силы:
Единица момента силы в СИ — ньютонметр: 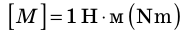
Плечо d силы F — это наименьшее расстояние от оси вращения тела до линии, вдоль которой действует сила 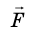
На рисунке сила 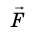
При каких условиях тело находится в равновесии
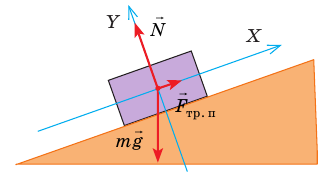
Пример. Расположенное на наклонной плоскости тело находится в состоянии равновесия, если действующие на него силы скомпенсированы: |
Пример. Рычаг находится в равновесии, если сумма моментов сил, действующих на него, равна нулю:
|
|
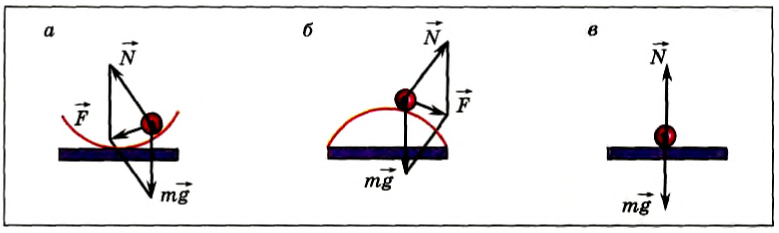
Какие существуют виды равновесия
Виды равновесия тел
| Устойчивое равновесие | Неустойчивое равновесие | Безразличное равновесие |
|
При малых отклонениях от положения равновесия тело произвольно возвращается в исходное положение |
При малых отклонениях от положения равновесия тело еще больше отклоняется от исходного положения. |
При малых отклонениях от положения равновесия тело остается в своем новом положении |
|
Равнодействующая направлена к положению равновесия тела |
Равнодействующая направлена от положения равновесия тела. |
Равнодействующая равна нулю. |
|
Сумма сил, приложенных к телу, равна нулю, но момент силы |
Сумма сил равна нулю, однако момент силы |
Силы скомпенсированы, сумма моментов этих сил равна нулю. |
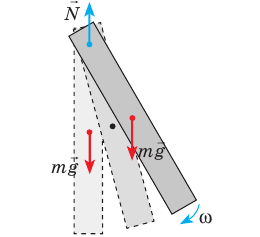
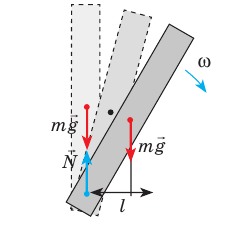
Обратите внимание! Тело, имеющее неподвижную ось вращения, будет находиться в состоянии устойчивого равновесия, если центр тяжести тела расположен ниже точки опоры или подвеса.
На практике мы часто имеем дело со случаями равновесия тел, опирающихся на несколько точек или на поверхность: человек опирается на ноги, стол и стул — на ножки, автомобиль — на колеса, дом — на фундамент и т. д. (рис. 14.3).
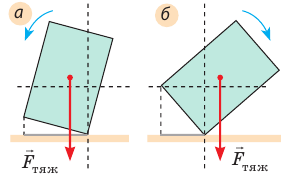
Тело, опирающееся на горизонтальную плоскость, находится в состоянии устойчивого равновесия, если вертикальная линия, проведенная через центр тяжести тела, проходит в границах площади опоры (рис. 14.3, 14.4, а).
Рис. 14.4. Если линия действия силы тяжести проходит в границах площади опоры, равновесие устойчивое (а), если вне площади опоры, равновесие нарушается — тело падает (б)
Очевидно: чем ниже расположен центр тяжести тела и чем больше площадь опоры тела, тем тело устойчивее. Именно поэтому фундаменты станков делают широкими и массивными, скоростные болиды имеют очень низкую посадку, человек или животное, чтобы принять устойчивое положение, расставляет и немного сгибает ноги (лапы). Чтобы увеличить площадь опоры, пожилой человек при ходьбе использует палку.
Пример решения задачи
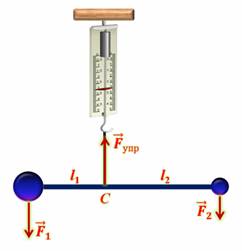
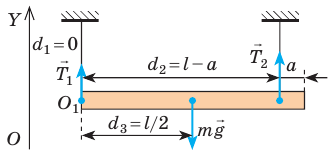
Однородный рельс длиной l =10 м и массой 900 кг поднимают на двух параллельных тросах. Определите силы натяжения тросов, если один закреплен на конце рельса, а второй — на расстоянии a =1 м от другого конца.
Анализ физической проблемы. Выполним пояснительный рисунок, где укажем силы, действующие на рельс (силы 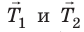
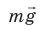
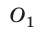
Решение:
Запишем два условия равновесия тела:
Здесь 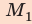
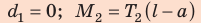
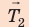
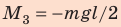
Спроецируем первое уравнение на ось ОY, подставим выражения для моментов сил и получим систему линейных уравнений:
Найдем 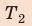
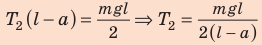
Найдем 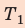
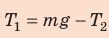
Проверим единицу, найдем значения искомых величин:
Анализ результатов. Первый трос действует на рельс с меньшей силой, поскольку сила приложена дальше от центра тяжести тела. Результат реален. Ответ:
Выводы:
- Равновесие тела — это сохранение состояния движения или покоя тела с течением времени. Сохранение состояния движения означает, что скорости поступательного и вращательного движений тела остаются неизменными.
- Тело будет в равновесии, если соблюдены два условия: 1) равнодействующая сил, приложенных к телу, равна нулю:
; 2) сумма моментов всех сил, действующих на тело, равна нулю:
.
- Различают устойчивое, неустойчивое, безразличное равновесия тел. При устойчивом равновесии тело, незначительно отклоненное от положения равновесия, возвращается в исходное положение; при неустойчивом — еще больше отклоняется от исходного положения, при безразличном — остается в своем новом положении.
Виды равновесия тела
В механике часто возникает необходимость ответить на вопрос: в каких случаях тело может сколь угодно долго оставаться в покое, если оно находилось в покое в начальный момент? Естественно, что должны выполняться условия равновесия, рассмотренные в § 33. Но практически не во всяком положении равновесия тело, находящееся в начальный момент в покое, будет оставаться в покое и в последующие моменты времени. Дело в том, что в реальных условиях, помимо учитываемых нами сил (сила тяжести, сила реакции подвеса, опоры, силы трения и т. д.), тело испытывает и неучитываемые случайные воздействия: небольшие сотрясения, колебания воздуха и т. п. Под действием таких сил тело хотя бы немного будет отклоняться от положения равновесия, а в этом случае дальнейшее поведение тела может быть различным.
При отклонении тела от положения равновесия действующие на него силы, как правило, изменяются. Возникает отличная от нуля равнодействующая сила, которая вызывает движение тела. Если равнодействующая возвращает тело в положение равновесия, то тело все время, несмотря на толчки, будет находиться вблизи положения равновесия. Такое положение равновесия называется устойчивым.
В устойчивом равновесии находится, например, шарик на вогнутой подставке (рис. 154, а). При отклонении шарика от положения равновесия равнодействующая 
Если равнодействующая сила не возвращает тело в первоначальное положение равновесия, а вызывает дальнейшее отклонение от него, то такое положение равновесия называется неустойчивым. В таком положении, например, находится шарик на выпуклой подставке (рис. 154, б). При отклонении равнодействующая сила 
Если при небольших смещениях тела из первоначального положения равнодействующая всех сил, приложенных к телу, остается равной нулю, то такое положение равновесия называется безразличным. В таком положении, например, находится шарик на горизонтальной плоскости (рис. 154, в).
Рис. 154
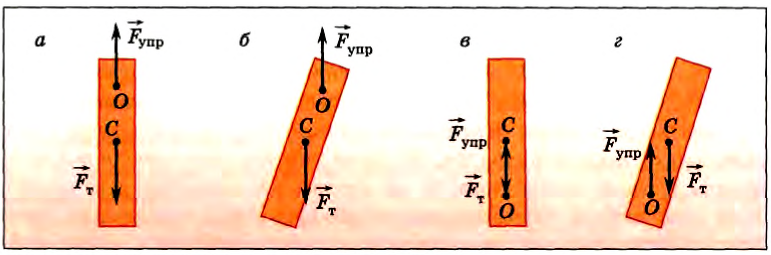
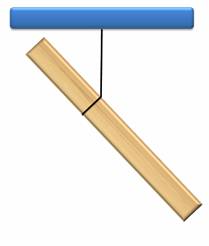
Другим примером устойчивого и неустойчивого равновесия может быть равновесие тела, имеющего ось вращения. На рисунке 155, а изображена линейка, которая может вращаться вокруг оси, проходящей через точку О. Она находится в устойчивом равновесии, если ее центр тяжести — точка C — находится ниже точки О. При отклонении от положения равновесия (рис. I55, б) возникает момент силы тяжести, который возвращает линейку в положение равновесия. Очевидно, что в отклоненном положении потенциальная энергия линейки больше, чем в положении равновесия. Таким образом, тело, имеющее ось вращения, будет находиться в устойчивом равновесии, если центр тяжести тела находится ниже оси вращения.
Если же центр тяжести находится на вертикальной прямой, проходящей через ось вращения, расположен выше оси вращения, то равновесие неустойчивое (рис. 155, в, г). В этом случае при отклонении момент силы тяжести отклоняет тело еще дальше от первоначального положения равновесия. При этом потенциальная энергия тела уменьшается. Если же ось вращения проходит через его центр тяжести, то при любом положении момент силы тяжести равен нулю, поскольку равно нулю плечо этой силы.
Рис. 155
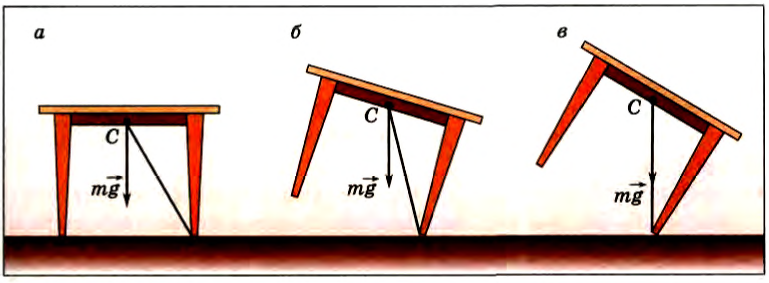
Рассмотрим теперь условия устойчивости тела, опирающегося не на одну точку, как в рассмотренных случаях, а на несколько точек (например, стол или блок, прислоненный к опоре, показанный на рисунке 156) или площадку (например, ящик, поставленный на горизонтальную плоскость). В этих случаях для равновесия тела необходимо, чтобы вертикаль, проведенная через центр тяжести, проходила внутри площади опоры тела, т. е. внутри контура. образованного линиями, соединяющими точки опоры, или внутри площадки, на которую опирается тело. При этом равновесие является устойчивым.
Рис. 154
Например, стол, стоящий на горизонтальном полу, находится в устойчивом равновесии (рис. 157, а). Если наклонять стол, то его центр тяжести будет подниматься (рис. 157,6). Однако момент силы тяжести относительно оси вращения будет стремиться вернуть его в первоначальное положение до тех пор, пока линия действия силы тяжести проходит через площадь опоры стола. Если, однако, наклонить стол так, что линия действия силы тяжести выйдет за пределы площади опоры стола, то он опрокинется вследствие действия момента силы тяжести. Очевидно, что имеется предельный угол наклона, после которого первоначальное равновесие уже не восстанавливается, и тело опрокидывается (рис. 157, в).
Рис. 157
Предельный угол тем меньше, чем выше расположен центр тяжести тела при данной площади опоры. Высоко нагруженный грузовик легче опрокинется, чем в случае, когда центр тяжести груза лежит низко.
Главные выводы
- Равновесие тела бывает устойчивым, неустойчивым и безразличным.
- Устойчивым равновесием тела является такое равновесие, при выведении тела из которого возникает равнодействующая сила, направленная в сторону первоначального положения тела, или момент сил, возвращающий тело в положение равновесия. В устойчивом положении потенциальная энергия тела минимальна.
- Неустойчивым равновесием тела называется такое равновесие, при выведении тела из которого возникает равнодействующая сила, направленная от положения равновесия, или момент сил, отклоняющий тело от положения равновесия. Потенциальная энергия тела в положении неустойчивого равновесия больше, чем потенциальная энергия тела в отклоненном положении.
- Безразличным положением равновесия является такое положение, при выведении тела из которого равнодействующая сила или момент сил остаются равными нулю. Потенциальная энергия тела при этом не меняется.
- Давление в жидкостях и газах в физике
- Закон Паскаля
- Закон Архимеда
- Движение жидкостей
- Закон электромагнитной индукции
- ЭДС индукции в движущемся проводнике
- Производство, передача и потребление электрической энергии
- Условия равновесия тел в физике
Как найти точку равновесия
Равновесием с точки зрения экономической науки называется такое состояние системы, когда каждый из участников рынка не желает изменить свое поведение. Рыночное равновесие определяется, таким образом, как ситуация, когда продавцами предлагается для продажи точно такое количество товара, какое покупатели желают приобрести. Отыскание точки равновесия заключается в построении некоторой идеальной модели рыночного поведения участников экономических отношений.

Инструкция
Воспользуйтесь для нахождения точки равновесия понятиями о функциях спроса и предложения. Это поможет определить, при каком уровне цены обе функции будут иметь равные значения. Спрос характеризует готовность покупателей приобрести товар, а предложение – готовность производителя этот товар продать.
Выразите функции спроса и предложения при помощи таблицы, состоящей из трех столбцов (см. Рис. 1). Первая колонка цифр будет включать значения цены, например, в рублях за единицу товара. Второй столбец определяет объем спроса, а третий – объем предложения за некоторый заранее определенный период.
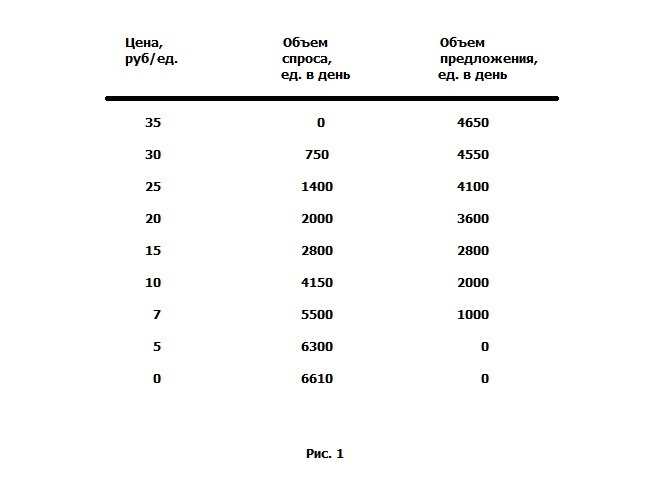
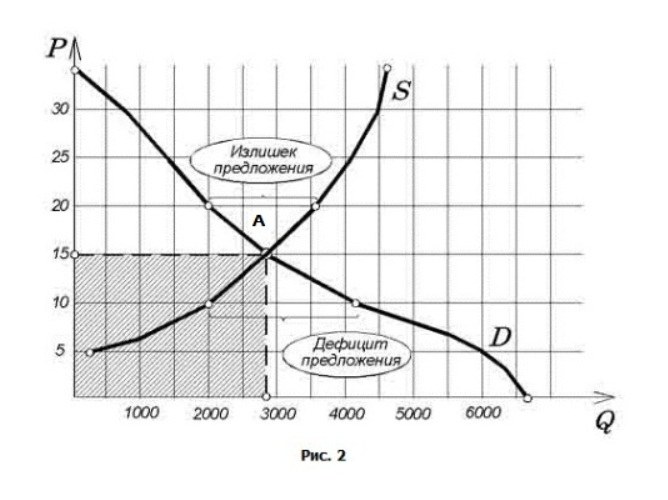
Определите по таблице, при каком уровне цены объемы спроса и предложения будут совпадать. Для приведенного учебного примера равные объемы (2800 единиц) будут наблюдаться при цене 15 рублей за единицу товара. Это и будет точкой рыночного равновесия.
Используйте для нахождения рыночного равновесия графическое отображение спроса и предложения. Данные из таблицы, аналогичной приведенной выше, перенесите в пространство двух осей, одна из которых (P) отображает уровень цены, а вторая (Q) – количество единиц товара.
Соедините линиями точки, отражающие изменение параметров в каждом столбце. В результате вы получите два графика D и S, пересекающихся в некоторой точке. Кривая D является отражением потребительского спроса на товар, а кривая S рисует картину предложения того же товара на рынке.
Отметьте точку пересечения двух кривых как A. Эта общая точка демонстрирует равновесное значение количества товара и цены на него в данном сегменте рынка. Такое графическое изображение точки равновесия делает картину спроса и предложения более объемной и наглядной.
Для каждого уровня цены определите также разницу в количестве спроса и предложения. В зависимости от расположения графиков на каждом из рассматриваемых ценовых уровней такая разница может отражать дефицит предложения или его излишек (см. Рис. 2).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Рассмотрим
механическую систему с идеальными,
стационарными и голономными связями,
положение которой определяется
независимыми обобщенными координатами
.
Для изучения колебаний около положения
равновесия,
необходимо,
прежде всего, найти эти положения.
Хорошо
известно ещё из физики, что в положении
равновесия все
обобщенные силы равны нулю:
(*)
Тогда
для консервативной системы

В
силу консервативности
и стационарности
системы
зависят только от
.
Тогда равенства (*) можно рассматривать
как уравнения относительно
.
Решая
эти уравнения,
найдем те
положения,
в которых система может
находиться в равновесии.
Если обобщенные силы зависят не только
от
,
но и от обобщенных скоростей
,
то при решении уравнений (*) все
следует
приравнять нулю.
Во
многих случаях положения равновесия
можно определить из
элементарных соображений
или с помощью обычных уравнений
статики.
Рассмотрим этот вопрос на примере.
П
ример.
Определим возможные положения
равновесия
маятника со спиральной пружиной с
угловой жесткостью С,
изображённой на Рис. 23.5. Здесь вес
маятника равен Р,
расстояние от оси подвеса О
до центра тяжести равно
.
В верхнем
вертикальном положении
маятника спиральная пружина находится
в недеформированном состоянии.
Массой пружины и трением в подшипнике
в нашей модели пренебрегаем.
З
С
аметим, что система имеет одну
степень свободы.
В качестве обобщенной координаты возьмём
угол
.
Потенциальная энергия системы П
складывается из потенциальной энергии
силы тяжести
и
Рис.
23.5
потенциальной
энергии
спиральной пружины.
За
нулевой
уровень потенциальной энергии
примем верхнее
вертикальное положение маятника.
Тогда, в текущем положении маятника
потенциальная энергия
примет вид

Из
физики известно, что для закручивания
спиральной пружины на малый угол
требуется приложить внешнюю
пару сил с
моментом
,
где с – коэффициент
угловой жесткости.
Тогда потенциальная энергия сил упругости
согласно 9.3,
будет равна
.
При
этом полная энергия маятника будет
равна

Составим
уравнение равновесия:
.
Это же уравнение можно вывести из условия
равновесия стержня.
Возникает
вопрос: Какими должны быть параметры
системы, чтобы маятник мог находиться
в заданном
положении равновесия?
Ответим
на этот вопрос. Допустим, состояние
равновесия определяется углом
.
Тогда
и
(*)
В
частности, если потребуется, чтобы
пружина удерживала маятник в горизонтальном
положении
,
будем иметь:
При таком соотношении параметров
маятник может находится в равновесии,
занимая
горизонтальное положение.
Решим
обратную
задачу.
Пусть заданы параметры
.
Определим
возможные положения равновесия маятника.
Запишем(*) в виде
,
где
.
(**)
Здесь
один корень уравнения очевиден:
!
Этому корню отвечает верхнее
вертикальное положение равновесия
маятника.
Для определения других возможных
положений равновесия нужно найти
остальные корни трансцендентного
уравнения (**). Их можно определить
различными методами, например, табличным
или графическим.
Поясним графический
способ
решения. Составим два уравнения:
;
.
Рис.23.6
Очевидно,
что второй корень уравнения
определяется абсциссой точки пересечения
обоих графиков. Причем каждому
положительному
отвечает равный по модулю, но отрицательный
корень
.
Физически это означает, что положение
равновесия маятника могут быть как
слева, так и справа
от вертикали. Кроме того, видно,
что при
(
)
прямая
не пересекает
синусоиду
.
В этом случае уравнение (**) имеет один
тривиальный корень
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Равновесие в статике – это отсутствие движения. Чтобы объект находился в равновесии, нужно, чтобы выполнялись некоторые условия, рассмотрим их.
Условие равновесия материальной точки
Чтобы материальная точка находилась в равновесии, нужно, чтобы она не двигалась поступательно.
Примечания:
- Материальная точка может двигаться только лишь поступательно.
- Точка мала и не имеет внешних границ. Поэтому, она не может двигаться вращательно вокруг оси, проходящей через её центр. Если отодвинуть ось вращения от точки на некоторое расстояние, тогда точка сможет вокруг этой оси двигаться по окружности. Но вокруг собственной оси точка вращаться не может.
Материальная точка будет находиться в равновесии, когда выполняются два условия:
1. Векторная cумма сил, действующих на точку, должна равняться нулю.
[ large boxed{ vec{F_{1}} + vec{F_{2}} + vec{F_{3}} + ldots + vec{F_{n}} = 0}]
Примечание: При выполнении этого условия, точка будет либо покоиться, либо двигаться вдоль прямой с одной и той же скоростью. Это следует из первого закона Ньютона.
2. Систему отсчета дополнительно выберем так, чтобы координаты точки в системе не менялись при выполнении условия 1.
Примечание: Такая система отсчета будет называться инерциальной, а точка будет покоиться относительно этой системы.
Условие равновесия тела
Чтобы тело находилось в равновесии, нужно, чтобы оно не двигалось поступательно и не вращалось.
Примечание: Тело, состоящее из нескольких точек, может вращаться вокруг оси, проходящей через центр этого тела. Поэтому, для тела условия равновесия нужно дополнить еще одним пунктом. Таким образом, получим три условия.
1. Алгебраическая cумма моментов сил, действующих на тело, должна равняться нулю.
[ large boxed{ M_{1} + M_{2} + M_{3} + ldots + M_{n} = 0}]
Примечания:
- При выполнении этого условия тело не будет вращаться.
- Моменты сил, вращающих тело по часовой стрелке, подставляем в это уравнение со знаком плюс. Моменты сил, вращающих против часовой стрелки – со знаком минус.
2. Векторная cумма сил, действующих на тело, должна равняться нулю.
[ large boxed{ vec{F_{1}} + vec{F_{2}} + vec{F_{3}} + ldots + vec{F_{n}} = 0}]
Примечания:
- Векторы складывают, учитывая их направления, то есть, с помощью геометрии.
- Если условие выполняется, то тело сможет двигаться равномерно прямолинейно. Чтобы тело находилось в покое, необходимо еще одно условие:
3. Систему отсчета выберем так, чтобы координаты всех точек тела не менялись в ней при равенстве нулю векторной суммы сил.
Условия равновесия применяются для решения задач статики, связанных с моментами сил.
Виды равновесия
Различают такие виды равновесия:
- неустойчивое равновесие,
- устойчивое равновесие,
- безразличное равновесие.
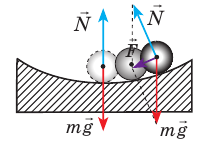
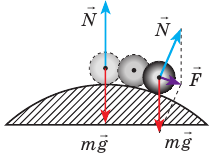
Рассмотрим однородный шар (или, например, мяч), который покоится (рис. 1) на горке – а), на горизонтальном участке – б), и в ложбинке – в).
Рис. 1. Шар находится поочередно в одном из трех положений для описания видов равновесия
Неустойчивое равновесие
На вершине горы мяч находится в неустойчивом равновесии, потому, что стоит нам подтолкнуть мяч и, он скатится с горки (рис. 1а).
Равновесие неустойчивое:
при малом отклонении
потенциальная энергия тела уменьшается
силы и моменты сил
еще больше уводят тело от положения равновесия.
В состоянии неустойчивого равновесия потенциальная энергия тела максимальна!
Безразличное равновесие
На горизонтальном участке мяч будет покоиться в любом месте, в которое мы его поместим (рис. 1б). Подтолкнем мяч, он перекатится в другое положение и там будет оставаться в безразличном равновесии.
Если потенциальная энергия тела при его перемещении из одной точки пространства в другую точку остается постоянной, равновесие можно назвать безразличным.
Устойчивое равновесие
Мяч находится в ложбинке в устойчивом равновесии (рис. 1в). Легонько подтолкнув мяч, мы выведем его из равновесия, но через непродолжительное время мяч опять вернется в ложбинку.
Равновесие устойчивое:
при малом отклонении от равновесия
потенциальная энергия тела увеличивается
силы и моменты сил
возвращают тело в положение равновесия.
Примечание: Потенциальная энергия тела будет минимально возможной, когда тело находится в устойчивом равновесии!
Равновесие тела, могущего вращаться вокруг горизонтальной оси
Рассмотрим однородный шар, изготовленный, к примеру, из пенопласта. Проткнем его спицей, после закрепим ее горизонтально, подобно перекладине на двух опорах (рис. 2).
Спица будет являться неподвижной осью вращения.
Рис. 2. Равновесие шара, могущего вращаться вокруг горизонтальной неподвижной оси
Рассмотрим три случая для тела, могущего вращаться вокруг оси. Ось вращения
- проходит через центр масс шара — равновесие безразличное (рис. 2а),
- находится выше центра масс – равновесие устойчивое (рис. 2б),
- находится ниже центра масс – равновесие неустойчивое (рис. 2в).
Примечание для случаев устойчивого и неустойчивого равновесия:
центр масс расположен на вертикальной линии (пунктир на рисунках 2б и 2в), проходящей через ось вращения.
Вокруг неподвижной оси может вращаться любое тело, в том числе, продолговатое, например, рычаг. В задачах статики для него применяют условия равновесия рычага.
Тело опирается на площадь поверхности
Условие равновесия для такого тела:
Проекция центра масс должна лежать внутри площади основания.
Допустим, зодчий захотел построить наклонную башню. Заменим для упрощения башню однородным наклонным цилиндром (рис. 3).
Рис. 3. Однородный наклонный цилиндр опирается на поверхность
Упадет ли наклонная башня?
На рисунке 3а проекция центра масс попадает внутрь площади основания. Поэтому, башня, обладающая таким наклоном, не упадет.
Если центр масс выйдет за пределы площади, на которую тело опирается, то башня опрокинется (рис 3б).
Примечание: Башня своим весом давит на площадь основания – круг. Сила давления распределяется по всему основанию тела.
Центр тяжести. Условия равновесия
«Не существует тела, у которого
бы не было этой важнейшей характеристики.
Кто-то ею доволен, кто-то не очень,
но очень хочет ее изменить»
Альберт Эйнштейн
В данной теме речь пойдет о центре тяжести и условиях равновесия твердого тела.
Вспомним материал прошлых тем. Сила тяжести — это сила, с которой Земля притягивает к себе любое тело.
Рычаг – это любое твердое тело, способное поворачиваться относительно неподвижной опоры или оси. Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
В прошлых темах было получено правило моментов, согласно которому рычаг будет находиться в равновесии, если сумма моментов сил, вращающих его по ходу часовой стрелки, равна сумме моментов сил вращающих рычаг против хода часовой стрелки.
Что такое равновесие? В физике под равновесием понимают такое состояние тела, при котором воздействие на него одних сил компенсируется воздействием других сил. Иными словами, тело находится в состоянии покоя или движется равномерно и прямолинейно.
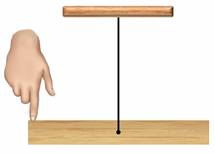
Каким образом можно добиться равновесия тела? Для ответа на это вопрос, возьмем какое-нибудь тело прямоугольной формы и, обвязав его петлей, подвесим на нити в произвольном месте. Как видим, тело начинает поворачиваться.
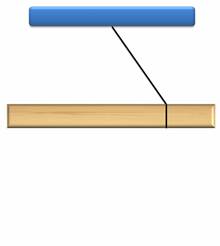
Изменим положение петли — брусок опять приходит в движение.
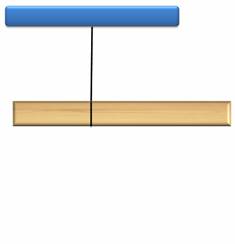
Однако можно найти такое положение петельки, при котором брусок будет находиться в состоянии покоя, т.е. в равновесии. Так вот, в этом случае говорят, что брусок подвешен в центре тяжести.
А что такое центр тяжести? До сих пор говорилось о силе тяжести как одной силе, действующей на тело целиком. Но на самом деле сила тяжести складывается из множества сил, приложенных к каждой части тела.
Можно ли заменить множество этих сил тяжести одной? А если можно, то в какой точке ее следует приложить?
Поставим опыт. Подвесим на нити динамометр, а к нему легкий жесткий стержень с двумя различными грузами на концах. Точку подвеса стержня подберем так, чтобы грузы уравновесили друг друга. Стержень с грузами будем рассматривать как одно тело, на которое действуют сила упругости нити и силы тяжести грузов.
Как показывает опыт, для того, чтобы сила тяжести всего тела заменила силы тяжести грузов, ее нужно приложить в точке, относительно которой грузы уравновешивают друг друга, — т.е. в точке подвеса стержня. Только в этом случае не изменятся ни показания динамометра, ни положение стержня. Точку приложения равнодействующей сил тяжести, действующих на отдельные части тела называют центром тяжести тела.
Как можно найти центр тяжести в различных телах?
Если тело однородно и имеет правильную форму, то все просто. У однородных тел правильной формы центр тяжести совпадает с его геометрическим центром. Так, например, центр тяжести шара лежит в его геометрическом центре, у прямоугольного параллелепипеда — в точке пересечения диагоналей, а у треугольника — на пересечении его медиан.
В некоторых случаях центр тяжести может находиться и вне тела. Например, у кольца он лежит на пересечении его диаметров.
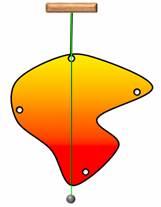
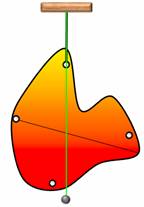
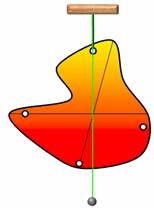
А если тело имеет неправильную форму?
Поставим опыт. Возьмем пластину неправильной формы и, по ее периметру, проделаем несколько одинаковых отверстий. Теперь подвесим пластину за одно из них. Если качать пластину, то она, после нескольких колебаний, всегда будет останавливаться в одном и том же равновесном положении. Чтобы запомнить это положение, прикрепим к оси отвес и проведем вдоль него прямую линию. Теперь подвесим пластину за другое отверстие и повторим все действия с отвесом. При этом все три отвеса проходят через одну точку — это точка и будет являться центром тяжести пластины.
За какую бы точку не подвешивали пластину, ее центр тяжести оказывается в наинизшем положении на отвесе.
Что будет, если подвесить пластину за сам центр тяжести? В этом случае, пластина может висеть в покое или вращаться.
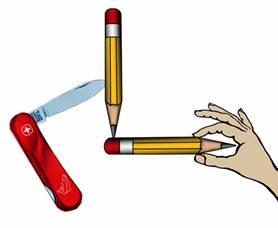
Известно, что карандаш невозможно поставить на острие, так как опорная площадка слишком мала. Однако, зная понятие центра тяжести, это можно сделать без труда. Как? Возьмем перочинный ножик, воткнем его в карандаш и поставим карандаш острием на резинку. В данном случае карандаш не падает и его даже можно слегка раскачивать. А дело все в том, что центр тяжести такой конструкции находится под опорной площадкой.
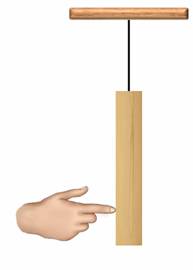
Для простоты, возьмем однородное тело прямоугольной формы. Как Центр тяжести такого тела будет располагать в его геометрическом центре — в точке пересечения диагоналей. Подвесим его так, чтобы оно заняло положение равновесия.
Теперь, если попытаться отклонить тело в сторону, то под действием силы тяжести, оно возвратится в первоначальное положение. Таким образом, равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается, называют устойчивым равновесием. При таком равновесии, центр тяжести тела располагается ниже оси вращения и находится на вертикальной прямой, проходящей через эту ось.
Если поставить тело на одну из его малых граней, то его центр тяжести будет располагаться на одной вертикальной линии с точкой опоры, но выше нее.
Если попытаться вывести тело из положения равновесия, например, толкнув его пальцем, то оно больше в начальное положение не вернется — этому будет препятствовать сила тяжести, действующая на тело. Таким образом, равновесие, при котором тело, выведенное из положения равновесия, не возвращается в начальное положение, называется неустойчивым равновесием. При неустойчивом равновесии центр тяжести тела расположен выше оси вращения и находится на вертикальной прямой, проходящей через эту ось.
Подвесим тело так, чтобы его центр тяжести совпал с точкой опоры. Толкнем его пальцем. С какой бы силой не толкать это тело, от толчков оно будет менять свое положение, но равновесия не потеряет.
Таким образом, если при отклонении или перемещении тела оно остается в равновесии, то равновесие называется безразличным. При безразличном равновесии ось вращения тела проходит через его центр тяжести, при этом центр тяжести тела остается на одном и том же уровне при любых положениях тела.
Примером устойчивого равновесия является любое тело, подвешенное на нити. Это, например, бабочки, висящие на люстре и сама люстра, лимон, висящий на лимонном дереве, маятник часов. В положении устойчивого равновесия находятся и, так называемые, висящие камни. Вот что про них пишет Александр Степанович Грин в своем произведении «Качающаяся скала»: Надо сказать, что в этих местах не редкость встретить так называемую «качающуюся скалу» — весьма любопытное явление, суть которого в том, что отдельный огромный кусок скалы в незапамятные времена получает устойчивость равновесия. Он обыкновенно стоит на каменной площадке, узким концом вниз, и, если его раскачивать, он, подобно ваньке-встаньке, принимает первоначальное положение. Такие скалы весят иногда тысячи тонн, но послушны движению руки человека средней силы. Такая скала упасть не может, если, конечно, ее не взорвут динамитом.
Примерами безразличного равновесия могут служить колеса автомобиля или мотоцикла — у них ось вращения проходит через их центр тяжести.
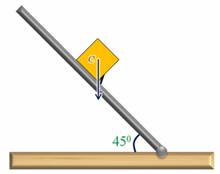
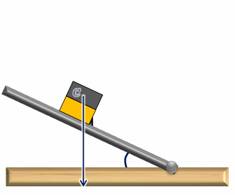
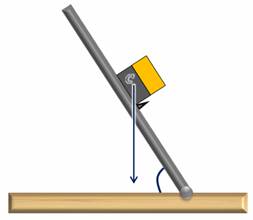
Об устойчивости положения тела можно судить и о величине угла поворота, необходимого для приведения тела в состояние неустойчивого равновесия. Для примера рассмотрим наклонную плоскость с невысокой ступенькой и два кубика. Выясним, при каком значении угла наклона произойдет опрокидывание кубика. Однородный кубик опрокинется при угле в 45 градусов.
Теперь возьмем кубик, склеенный из двух половинок — деревянной и стальной. Если поставить его деревянной частью книзу, то кубик опрокинется при значительно меньшем значении угла. Если же внизу будет стальная его часть, то опрокидывание произойдет лишь при угле больше 60 градусов.
Из этого опыта можно сделать вывод, что чем больше угол, на который нужно повернуть тело, для того, чтобы оно заняло положение неустойчивого равновесия, тем устойчивее его первоначальное положение. Величина угла поворота зависит от площади опоры тела и от положения его центра тяжести.
Упражнения.
Задача 1. Однородный массивный стержень с укрепленными на его концах грузами массой 5,5 кг и 1 кг, находится в равновесии, если подпереть его на расстоянии, равном 1/5 его длины, от более тяжелого груза. Какова масса стержня?
Основные выводы:
– Центр тяжести тела – это точка приложения равнодействующей сил тяжести, действующих на отдельные части тела.
– При любом положении тела его центр тяжести находится в одной и той же точке.
– Положение центра тяжести может измениться только при изменении относительного расположения частей тела (например, при его деформации).
– Равновесие бывает трех видов — устойчивым, неустойчивым и безразличным.
– Устойчивое равновесие — это равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается. При таком равновесии, центр тяжести тела располагается ниже оси вращения и находится на вертикальной прямой, проходящей через эту ось.
– Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия, не возвращается в начальное положение. При неустойчивом равновесии центр тяжести тела расположен выше оси вращения и находится на вертикальной прямой, проходящей через эту ось.
– При безразличном равновесии ось вращения тела проходит через его центр тяжести, при этом центр тяжести тела остается на одном и том же уровне при любых положениях тела.
Домашняя работа
Стр. 185 — 189 читать

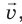
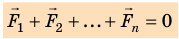
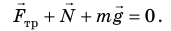
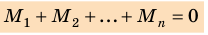
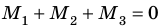 , где
, где 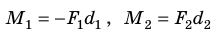 (сила
(сила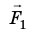 поворачивает рычаг по ходу часовой стрелки, сила
поворачивает рычаг по ходу часовой стрелки, сила 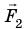 — против хода часовой стрелки);
— против хода часовой стрелки); 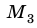 = 0 (поскольку
= 0 (поскольку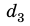 = 0 ).
= 0 ).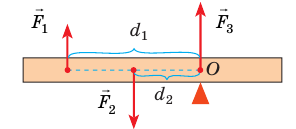
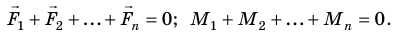
 еще больше отклоняет тело от положение равновесия
еще больше отклоняет тело от положение равновесия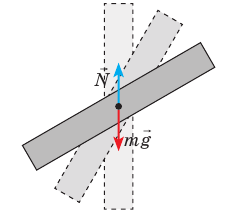

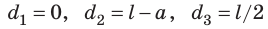
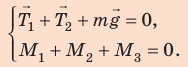
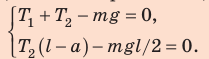
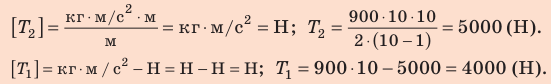
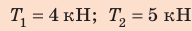
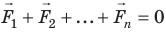 ; 2) сумма моментов всех сил, действующих на тело, равна нулю:
; 2) сумма моментов всех сил, действующих на тело, равна нулю: 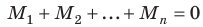 .
.