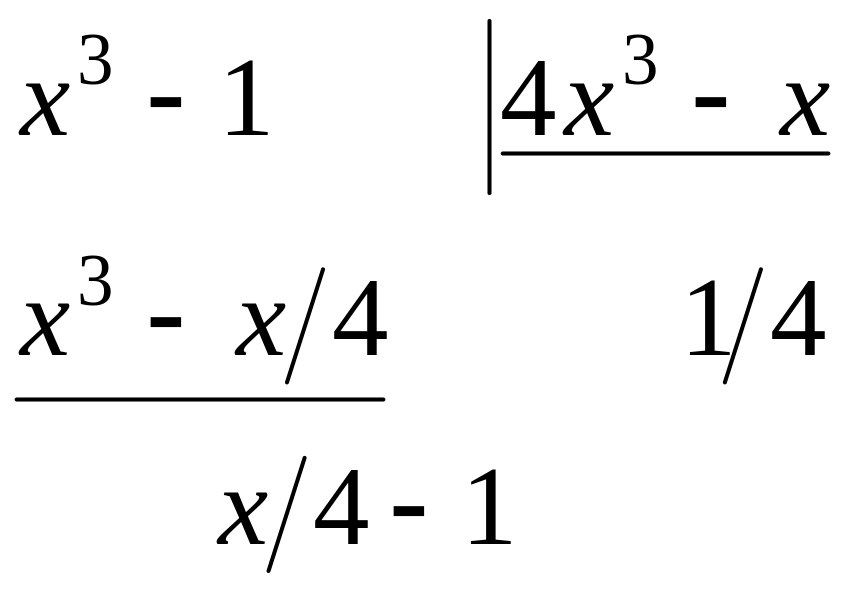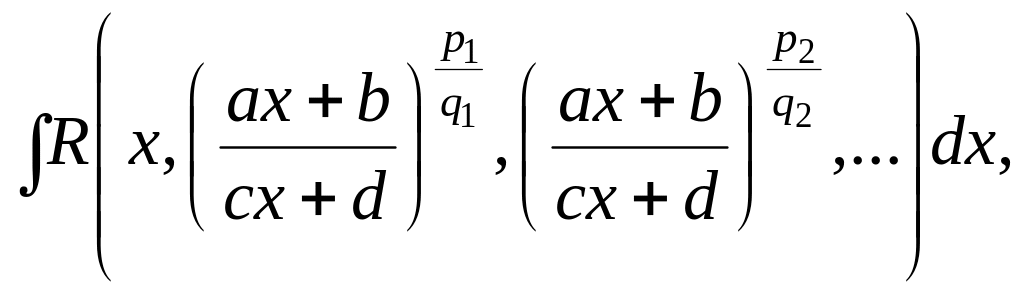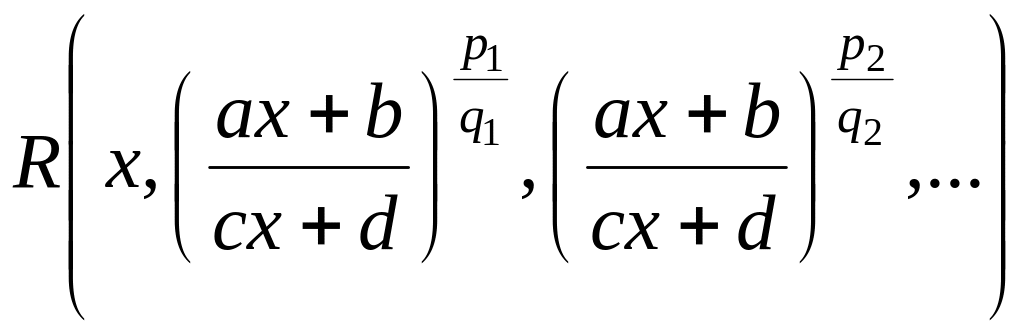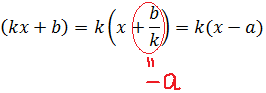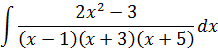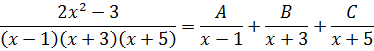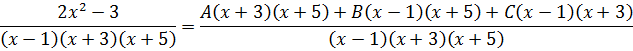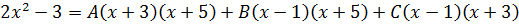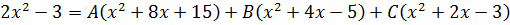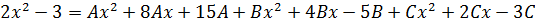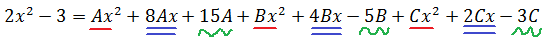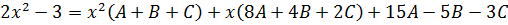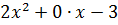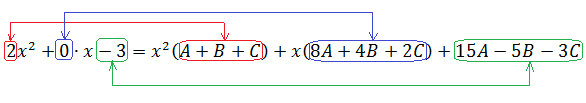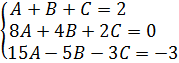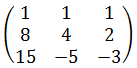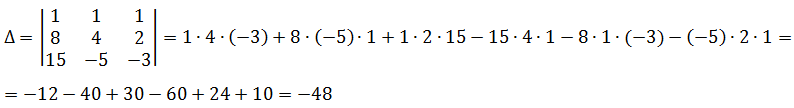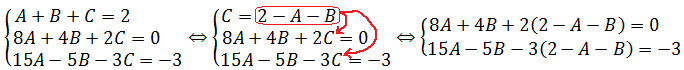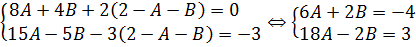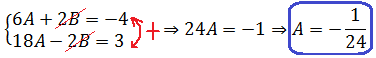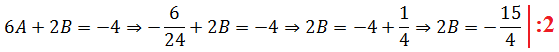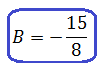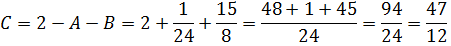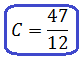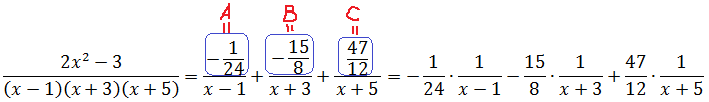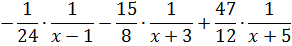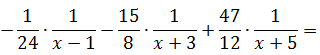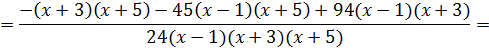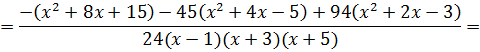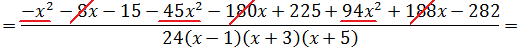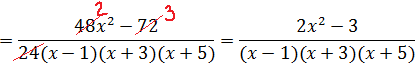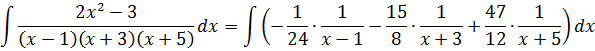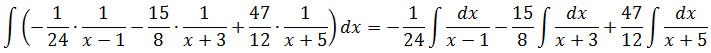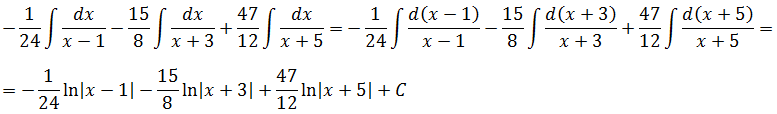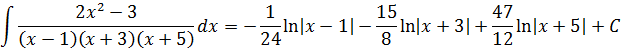Как найти метод неопределенных коэффициентов

Метод неопределённых коэффициентов

26 июля 2022

Метод неопределённых коэффициентов — это «полуолимпиадный» приём, с помощью которого вы сможете раскладывать на множители многочлены, которые не раскладываются, и решать уравнения, которые не решаются.:)

В двух словах этот метод звучит так:

В любой непонятной ситуации вводим новую переменную. А затем думаем, что с этой переменной делать.

Сегодня мы детально изучим метод неопределённых коэффициентов. Мы разберём столько разных задач, что не понять этот приём будет просто невозможно. И да: речь пойдёт не только о многочленах.:)

Содержание

1. Основная идея
2. Разложение многочлена на множители
3. Решение уравнений
4. Деление многочлена на многочлен
5. Выделение точного квадрата
6. Избавление от иррациональности
7. Зачем всё это нужно

1. Основная идея

Чтобы понять основную идею метода неопределённых коэффициентов, рассмотрим простую наводящую задачу. Допустим, у нас есть квадратный трёхчлен, разложенный на множители:

[Pleft( x right)=left( x-3 right)left( x+2 right)]

Если раскрыть скобки и привести подобные слагаемые, то получится тот же многочлен, записанный в стандартном виде:

[Pleft( x right)={{x}^{2}}-x-6]

Зная разложение на множители, легко получить стандартный вид многочлена. А вот обратный переход — от стандартного вида к множителям — является вычислительно сложной операцией, но всё ещё возможной: считаем дискриминант, находим корни, вспоминаем теорему Виета и т.д.

Немного усложним задачу. Рассмотрим разложение на множители многочлена четвёртой степени (почему именно четвёртой — см. урок. «Разложение на множители»):

[Pleft( x right)=left( {{x}^{2}}-3x+1 right)left( {{x}^{2}}+x+4 right)]

Раскроем скобки и приведём подобные. Вновь получим многочлен в стандартном виде:

[Pleft( x right)={{x}^{4}}-2{{x}^{3}}+2{{x}^{2}}-11x+4]

Но как выполнить обратную операцию? Как по стандартному виду многочлена определить, на какие множители его можно разложить? Тут на помощь и приходит метод неопределённых коэффициентов.

Проблема разложения на множители

Рассмотрим задачу в общем виде. Допустим, нам нужно разложить на множители многочлен четвёртой степени:

[Pleft( x right)= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]

Из курса алгебры мы знаем, что произвольный многочлен не всегда раскладывается на линейные двучлены вида $x-color{red}{a}$. Однако он совершенно точно раскладывается на квадратные трёхчлены вида $color{red}{a}{{x}^{2}}+color{red}{b}x+color{red}{c}$:

[Pleft( x right)=left(color{blue}{a}{{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+color{blue}{e}x+color{blue}{f} right)]

Записав такое разложение, мы уже наполовину выполнили задачу. Но нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ и $color{blue}{d}$, $color{blue}{e}$, $color{blue}{f}$. Отсюда, кстати, и название приёма — «метод неопределённых коэффициентов». И чтобы найти эти самые неопределённые коэффициенты, воспользуемся следующей теоремой.

Теорема о нулевом многочлене

Теорема (критерий многочлена, тождественно равного нулю). Многочлен

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}]

тождественно равен нулю (т.е. при любом значении переменной $x$) тогда и только тогда, когда все его коэффициенты равны нулю:

[color{blue}{{a}_{n}}= color{blue}{{a}_{n-1}}= ldots = color{blue}{{a}_{1}}= color{blue}{{a}_{0}}= color{red}{0}]

Доказательство я вынесу на отдельную страницу (см. урок «Корни многочлена»). Потому что у этой теоремы много применений, но нас сейчас интересует не сама теорема, а лишь одно-единственное следствие из неё:

Следствие (критерий равенства двух многочленов). Пусть даны два многочлена:

[begin{align}Aleft( x right) &= color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}\ Bleft( x right) &= color{blue}{{b}_{n}}{{x}^{n}}+ color{blue}{{b}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{b}_{1}}x+ color{blue}{{b}_{0}}\ end{align}]

Эти два многочлена тождественно равны друг другу (т.е. $Aleft( x right)=Bleft( x right)$ при любом $x$) тогда и только тогда, когда равны их коэффициенты при соответствующих степенях:

[color{blue}{{a}_{n}}= color{blue}{{b}_{n}}; color{blue}{{a}_{n-1}}= color{blue}{{b}_{n-1}}; ldots ; color{blue}{{a}_{1}}= color{blue}{{b}_{1}}; color{blue}{{a}_{0}}= color{blue}{{b}_{0}}]

Вот тут всё становится на свои места!

Основной алгоритм

Пусть даны два представления одного и того же многочлена. Например, в стандартном виде и разложение на множители:

[begin{align} Pleft( x right) &= color{blue}{{a}_{4}}{{x}^{4}}+ color{blue}{{a}_{3}}{{x}^{3}}+ color{blue}{{a}_{2}}{{x}^{2}}+ color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right) end{align}]

Тогда для нахождения неизвестных коэффициентов в любом из этих разложений необходимо выполнить три шага:

1. Раскрыть все скобки и привести подобные, чтобы получить две записи в стандартном виде;
2. Приравнять соответствующие коэффициенты, составить систему уравнений;
3. Решить эту систему и правильно интерпретировать ответ.

Вот и вся суть метода. Первые два пункта очевидны. Проблемы возникают лишь на третьем шаге, поскольку зачастую системы уравнений получаются нелинейными. И мы детально разберём, как решать подобные системы.

Но для начала — парочка простых задач.:)

Задача 1.1. Основная идея

Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:

[begin{align}Pleft( x right) &=2{{x}^{4}}+3{{x}^{3}}-5x-2\ Qleft( x right) &=left( ax+3 right)left( {{x}^{3}}-b right)-3x+c\ end{align}]

Решение. Согласно Теореме 1, многочлены $Pleft( x right)$ и $Qleft( x right)$ равны, когда в точности равны их коэффициенты. Поэтому раскроем скобки в многочлене $Qleft( x right)$ и найдём эти коэффициенты:

[begin{align}Qleft( x right) &=a{{x}^{4}}+3{{x}^{3}}-abx-3b-3x+c= \ &=color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right) end{align}]

Для удобства коэффициенты выделены синим цветом. Сравним их с коэффициентами многочлена $Pleft( x right)$:

[begin{align}& color{blue}{a}{{x}^{4}}+ color{blue}{3}{{x}^{3}}+left( color{blue}{-ab-3} right)x+left( color{blue}{c-3b} right)= \ = & color{red}{2}{{x}^{4}}+ color{red}{3}{{x}^{3}}+left( color{red}{-5} right)x+left( color{red}{-2} right) \ end{align}]

Чтобы многочлены были равны, должны выполняться равенства

[color{blue}{a}= color{red}{2};quad color{blue}{-ab-3}= color{red}{-5};quad color{blue}{c-3b}= color{red}{-2}]

Получили систему уравнения, которая легко решается:

[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]

Ответ: $a=2$, $b=1$, $c=1$.

Задача 1.2. Альтернативный подход

Задача. Найдите числа $a$, $b$, $c$, при которых многочлены $Pleft( x right)$ и $Qleft( x right)$ равны:

[begin{align}Pleft( x right) &=3{{x}^{4}}+7{{x}^{3}}+3{{x}^{2}}+x+2\ Qleft( x right) &=left( x+1 right)left( a{{x}^{3}}+b{{x}^{2}}-x+c right)\ end{align}]

Решение. Решим эту задачу двумя способами: «чистым» методом неопределённых коэффициентов и с привлечением схемы Горнера.

Способ 1. «Чистый» метод неопределённых коэффициентов. Раскрываем скобки в многочлене $Qleft( x right)$:

[begin{align}Qleft( x right) &=a{{x}^{4}}+b{{x}^{3}}-{{x}^{2}}+cx+a{{x}^{3}}+b{{x}^{2}}-x+c= \ &= color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c} end{align}]

Приравниваем многочлены $Qleft( x right)$ и $Pleft( x right)$:

[begin{align}& color{blue}{a}{{x}^{4}}+left( color{blue}{a+b} right){{x}^{3}}+left( color{blue}{b-1} right){{x}^{2}}+left( color{blue}{c-1} right)x+ color{blue}{c}= \= & color{red}{3}{{x}^{4}}+ color{red}{7}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{1}x+ color{red}{2} \ end{align}]

Получим набор из пяти уравнений:

[begin{array}{rrr}color{blue}{a}= color{red}{3}; & color{blue}{b-1}= color{red}{3}; & color{blue}{c}= color{red}{2}.\ color{blue}{a+b}= color{red}{7}; & color{blue}{c-1}= color{red}{1}; & {}\ end{array}]

Решаем систему из этих уравнений и получаем ответ:

[color{blue}{a}=color{red}{3}; color{blue}{b}=color{red}{4}; color{blue}{c}=color{red}{2}]

Способ 2. Привлечение схемы Горнера. Поскольку многочлен $Qleft( x right)$ разложен на множители, сделаем то же самое и с многочленом $Pleft( x right)$ — выделим из него множитель-двучлен $x+1$. Для этого заполним таблицу для $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{3} & color{blue}{7} & color{blue}{3} & color{blue}{1} & color{blue}{2}\ hline color{red}{-1} & 3 & 4 & -1 & 2 & color{green}{0}\ end{array}]

Получили остаток $r=color{green}{0}$, и многочлен $Pleft( x right)$ можно переписать так:

[Pleft( x right)=left( x+1 right)left( 3{{x}^{3}}+4{{x}^{2}}-1x+2 right)]

Приравняем многочлены $Pleft( x right)$ и $Qleft( x right)$:

[begin{align}&left( x+1 right)left( color{red}{3}{{x}^{3}}+ color{red}{4}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{2} right)= \ = &left( x+1 right)left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+left( color{blue}{-1} right)x+ color{blue}{c} right) \ end{align}]

И сразу получаем ответ:

[color{blue}{a} =color{red}{3}; color{blue}{b} =color{red}{4}; color{blue}{c} =color{red}{2}]

Ответ: $a=3$, $b=4$, $c=2$.

Если вам непонятно, как работает схема Горнера и при чём тут разложение на множители, см. урок «Схема Горнера» — это ещё один универсальный алгоритм. Который, как и метод неопределённых коэффициентов, будет полезен во многих нестандартных задачах.

2. Разложение многочлена на множители

Переходим к серьёзным задачам. Всё, что мы решали выше, сводилось к простым линейным уравнениям, которые решались обычной подстановкой.

Теперь мы разберём многочлены четвёртой степени — те самые, с которых начинали рассуждения. И заодно научимся решать нелинейные системы методом целочисленного перебора.

Задача 2.1. Самая стандартная

Задача. Разложите многочлен на множители методом неопределённых коэффициентов:

[Pleft( x right)={{x}^{4}}+2{{x}^{3}}+2{{x}^{2}}+10x+25]

Этот многочлен вообще не имеет действительных корней, в чём легко убедиться, выделив точные квадраты:

[begin{align}Pleft( x right) &=left( {{x}^{4}}+2{{x}^{3}}+{{x}^{2}} right)+left( {{x}^{2}}+10x+25 right)= \ &={{x}^{2}}{{left( x+1 right)}^{2}}+{{left( x+5 right)}^{2}} end{align}]

Полученная сумма равна нулю только если $x=-5$ и одновременно $x=0$ или $x=-1$. Что, очевидно, невозможно. Следовательно, линейных множителей в разложении не будет.

Зато квадратные множители точно будут, поэтому используем метод неопределённых коэффициентов. Предположим, что многочлен раскладывается на произведение двух квадратных трёхчленов:

[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]

Раскрываем скобки и приводим подобные:

[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ & +left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]

Сравниваем коэффициенты полученного многочлена с коэффициентами исходного:

[Pleft( x right)={{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{2}{{x}^{2}}+ color{red}{10}x+ color{red}{25}]

Выписываем равенства:

[begin{array}{rr}color{blue}{b+d}= color{red}{2}; & color{blue}{be+dc}= color{red}{10};\ color{blue}{bd+c+e}= color{red}{2}; & color{blue}{ce}= color{red}{25}.\ end{array}]

Получили систему из четырёх нелинейных уравнений. Универсального алгоритма для решения таких систем не существует. Однако здесь хорошо работает метод целочисленного перебора.

Рассмотрим последнее уравнение:

[ color{blue}{c} cdot color{blue}{e}= color{red}{25}]

Какие числа нужно перемножить, чтобы в произведении получилось 25? Вот несколько вариантов:

[begin{align}color{blue}{c} cdotcolor{blue}{e} &= color{red}{1} cdotcolor{red}{25}= color{red}{5} cdotcolor{red}{5} = \ & =left( color{red}{-1} right)cdot left( color{red}{-25} right)= \ & =left( color{red}{-5} right)cdot left( color{red}{-5} right) end{align}]

Рассмотрим вариант, когда $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$. Именно он будет правильным ответом, в чём мы сейчас убедимся.

Подставим $color{blue}{c}= color{red}{5}$ и $color{blue}{e}= color{red}{5}$ в оставшиеся три уравнения. Получим систему

[left{ begin{align}b+d &=2 \ bd+5+5 &=2 \ 5b+5d &=10 \ end{align} right.]

Последнее уравнение является следствием первого, поэтому система равносильна двум уравнениям:

[left{ begin{align}b+d &=2 \ bd &=-8 \ end{align} right.]

Эта система имеет два решения, которые легко находятся методом подбора: $color{blue}{b} = color{red}{4}$ и $color{blue}{d}= color{red}{-2}$, либо наоборот $color{blue}{b}= color{red}{-2}$ и $color{blue}{d}= color{red}{4}$. Получаем два варианта разложения:

[begin{align}{{P}_{1}}left( x right) &=left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right)left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right) \ {{P}_{2}}left( x right) &=left( {{x}^{2}}+left( color{red}{-2} right)x+ color{red}{5} right)left( {{x}^{2}}+ color{red}{4}x+ color{red}{5} right) \ end{align}]

Но ведь на самом деле это одно и то же разложение — просто множители поменялись местами. Поэтому мы вправе выбрать любой вариант.

Запишем окончательный ответ:

[Pleft( x right)=left( {{x}^{2}}+4x+5 right)left( {{x}^{2}}-2x+5 right)]

Важное замечание. После приведения подобных и сравнения коэффициентов мы получили систему из нескольких нелинейных уравнений, которые затем начали решать методом целочисленного перебора.

Такие уравнения будут преследовать нас постоянно — это основная трудность метода неопределённых коэффициентов.

Чтобы в процессе перебора не упустить из виду какой-нибудь вариант, целесообразно составлять таблицу всех возможных вариантов. Например, для равенства $color{blue}{c}cdot color{blue}{e}= color{red}{25}$ таблица выглядит так:

[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{-1} & color{red}{5} & color{red}{-5}\ hline color{blue}{e} & color{red}{25} & color{red}{-25} & color{red}{5} & color{red}{-5}\ end{array}]

Обратите внимание: в таблице нет варианта $color{blue}{c}= color{red}{25}$, $color{blue}{e}= color{red}{1}$ и $color{blue}{c}= color{red}{-25}$, $color{blue}{e}= color{red}{-1}$, потому что они получаются из первых двух вариантов перестановкой множителей в итоговом разложении.

Тем не менее, в некоторых примерах придётся рассматривать все возможные варианты. Один из таких примеров мы рассмотрим чуть позже, а пока давайте потренируемся на более адекватных задачах.:)

Задача 2.2. Снова стандартная

Задача. Разложите многочлен на множители методом неопределённых коэффициентов:

[Pleft( x right)={{x}^{4}}+5{{x}^{3}}+5{{x}^{2}}-4x-2]

Решение. Запишем искомое разложение:

[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]

Нужно найти четыре числа: $color{blue}{b}$, $color{blue}{c}$, $color{blue}{d}$, $color{blue}{e}$. Собственно, это и есть «неопределённые коэффициенты». Раскрываем скобки и приводим подобные:

[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]

Сравниваем коэффициенты этого многочлена с коэффициентами исходного:

[Pleft( x right)={{x}^{4}}+ color{red}{5}{{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-4} right)x+left( color{red}{-2} right)]

Получаем четыре уравнения, которые должны выполняться одновременно:

[begin{array}{rr}color{blue}{b+d}= color{red}{5}; & color{blue}{be+dc}= color{red}{-4};\ color{blue}{bd+c+e}= color{red}{5}; & color{blue}{ce}= color{red}{-2}.\ end{array}]

Произведение коэффициентов $color{blue}{c}cdot color{blue}{e}= color{red}{-2}$ — отрицательное число. Положим для определённости, что $color{blue}{c} gt 0$ и $color{blue}{e} lt 0$. Выпишем все возможные варианты:

[begin{array}{r|r|r}color{blue}{c} & color{red}{1} & color{red}{2}\ hline color{blue}{e} & color{red}{-2} & color{red}{-1}\ end{array}]

Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$ и $color{blue}{e}=color{red}{-2}$. Получим систему

[left{ begin{align}b+d &=5 \ bd+1-2 &=5 \ -2b+d &=-4 end{align} right.]

Вычтем почленно из последнего уравнения первое и получим

[begin{align}-3b &=-9 \ color{blue}{b} &= color{red}{3}end{align}]

Подставляем $color{blue}{b}= color{red}{3}$ в первое уравнение и получаем $color{blue}{d}= color{red}{2}$. Найденные значения $color{blue}{b}$ и $color{blue}{d}$ удовлетворяют всем трём равенствам. Следовательно, мы нашли решение системы:

[color{blue}{b}= color{red}{3}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{2}; color{blue}{e}= color{red}{-2}]

Откуда получаем искомое разложение на множители:

[Pleft( x right)=left( {{x}^{2}}+3x+1 right)left( {{x}^{2}}+2x-2 right)]

Важное замечание. К сожалению, в процессе целочисленного перебора далеко не всегда верный вариант будет попадаться сразу, на первом же шаге. Когда я собирал материалы для этого урока, иногда верным оказывался лишь четвёртый вариант из четырёх возможных.:)

Поэтому не переживайте, когда видите несовместную систему. Это нормально и даже неизбежно.

И вообще давайте посмотрим, как это выглядит на практике. Например, рассмотрим второй вариант в только что решённой задаче: $color{blue}{c}=color{red}{2}$ и $color{blue}{e}=color{red}{-1}$. Это приведёт нас к системе уравнений:

[left{ begin{align}b+d &=5 \ bd+2-1 &=5 \ -b+2d &=-4 end{align} right.]

Складываем первое уравнение с последним — и тут же получаем проблему:

[begin{align}3d &=1 \ color{blue}{d} &= color{red}{{1}/{3};} \ end{align}]

Получили дробный коэффициент $color{blue}{d}$, откуда следует, что коэффициент $color{blue}{b}$ тоже дробный:

[color{blue}{b}=5- color{blue}{d}=color{red}{{14}/{3};}]

Но тогда не выполняется второе равенство. Следовательно, система несовместна.

Задача 2.3. Упрощённые выкладки

Задача. Разложите многочлен на множители методом неопределённых коэффициентов:

[Pleft( x right)={{x}^{4}}+{{x}^{3}}+3{{x}^{2}}+32x-10]

В этот раз распишу всё кратко — только основные выкладки. Разложим многочлен $Pleft( x right)$ на два квадратных трёхчлена:

[Pleft( x right)=left( {{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{d}x+ color{blue}{e} right)]

Раскрываем скобки, приводим подобные:

[begin{align}Pleft( x right)={{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+left( color{blue}{be+d} right)x+ color{blue}{ce} \ end{align}]

Сравниваем с исходным многочленом:

[Pleft( x right)={{x}^{4}}+ color{red}{1}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{32}x+left( color{red}{-10} right)]

Получаем четыре уравнения:

[begin{array}{rr}color{blue}{b+d}= color{red}{1}; & color{blue}{be+dc}= color{red}{32};\ color{blue}{bd+c+e}= color{red}{3}; & color{blue}{ce}= color{red}{-10}.\ end{array}]

Поскольку $color{blue}{ce}= color{red}{-10} lt 0$, положим $color{blue}{c} gt 0$, $color{blue}{e} lt 0$. Возможные варианты:

[begin{array}{r|r|r|r|r}color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{5} & color{red}{10} \ hline color{blue}{e} & color{red}{-10} & color{red}{-5} & color{red}{-2} & color{red}{-1} \ end{array}]

Первые три варианта дают несовместные системы с дробными коэффициентами $color{blue}{b}$ и $color{blue}{d}$ (проверьте это!). Рассмотрим последний вариант: $color{blue}{c}= color{red}{10}$, $color{blue}{e}= color{red}{-1}$. Получим систему

[left{ begin{align}b+d &=1 \ bd+10-1 &=3 \ -b+10d &=32 end{align} right.]

Решение системы: $color{blue}{b}= color{red}{-2}$, $color{blue}{d}= color{red}{3}$. Окончательное разложение на множители:

[Pleft( x right)=left( {{x}^{2}}-2x+10 right)left( {{x}^{2}}+3x-1 right)]

3. Решение уравнений методом неопределённых коэффициентов

Одно из важнейших приложений метода неопределённых коэффициентов — это решение уравнений высших степеней. В самом деле, зачем мы раскладываем многочлен $Pleft( x right)$ на множители? Обычно по одной из двух причин:

1. Решить уравнение $Pleft( x right)=0$. Ведь произведение равно нулю, когда хотя бы один из множителей равен нулю;
2. Сократить рациональную дробь вида ${Pleft( x right)}/{Qleft( x right)};$. В этом случае многочлен $Qleft( x right)$ также придётся разложить на множители.

Про рациональные дроби мы поговорим в отдельном уроке (см. урок «Разложение на простейшие»). А вот уравнения мы разберём сейчас.

Допустим, нужно решить уравнение вида

[color{blue}{{a}_{n}}{{x}^{n}}+ color{blue}{{a}_{n-1}}{{x}^{n-1}}+ ldots + color{blue}{{a}_{1}}x+ color{blue}{{a}_{0}}=0]

В левой части равенства стоит стандартный многочлен. И если коэффициенты многочлена целые, то мы уже знаем как минимум два способа решения таких уравнений:

• Теорема Безу для отыскания рациональных корней-кандидатов;
• Схема Горнера для быстрой проверки этих кандидатов.

И эта связка отлично работает, когда многочлен имеет рациональные корни вида $x={color{blue}{p}}/{color{red}{q}};$. Вот буквально: мы найдём все такие корни и решим уравнение.

А если корни иррациональны? Безу и Горнер тут бесполезны. Зато полезным оказывается разложение на множители, когда вместо большого и страшного многочлена $Pleft( x right)$ в левой части уравнения появится произведение двух многочленов меньшей степени:

[Hleft( x right)cdot Qleft( x right)=0]

А дальше всё стандартно: произведение равно нулю, когда $Hleft( x right)=0$ или $Qleft( x right)=0$. И вот мы свели исходную задачу к двум уравнениям меньших степеней, которые наверняка легко решаются.:)

Задача 3.1. «Нерешаемое» уравнение

Задача. Решите уравнение методом неопределённых коэффициентов

[{{x}^{4}}+2{{x}^{3}}+3{{x}^{2}}+2x-3=0]

Это приведённое целочисленное уравнение, но его нельзя решить по теореме Безу и схеме Горнера. Ведь целые корни этого уравнения являются делителями свободного члена $color{blue}{{a}_{0}}=-3$. Таких делителей ровно четыре:

[x=pm 1; pm 3]

И все они дают ненулевой остаток в схеме Горнера:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{2} & color{blue}{3} & color{blue}{2} & color{blue}{-3}\ hlinecolor{red}{1} & 1 & 3 & 6 & 8 & color{red}{5}\ hlinecolor{red}{-1} & 1 & 1 & 2 & 0 & color{red}{-3}\ hlinecolor{red}{3} & 1 & 5 & 18 & 56 & color{red}{165}\ hlinecolor{red}{-3} & 1 & -1 & 6 & -16 & color{red}{45}\ end{array}]

Остаётся только метод неопределённых коэффициентов. Разложим уравнение на произведение двух квадратных трёхчленов:

[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]

Раскроем скобки и приведём подобные в правой части равенства:

[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]

Вспоминаем коэффициенты многочлена в исходном уравнении:

[{{x}^{4}}+ color{red}{2}{{x}^{3}}+ color{red}{3}{{x}^{2}}+ color{red}{2}x+left( color{red}{-3} right)=0]

Получаем уже привычный набор из четырёх уравнений:

[begin{array}{rr} color{blue}{b+d}=color{red}{2}; & color{blue}{be+dc}=color{red}{2};\ color{blue}{bd+c+e}=color{red}{3}; & color{blue}{ce}=color{red}{-3}.\ end{array}]

Рассмотрим последнее уравнение: $color{blue}{ce}=color{red}{-3}$. Произведение отрицательно, значит, множители разных знаков. Без ограничения общности положим $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Составим таблицу вариантов:

[begin{array}{r|r|r} color{blue}{c} & color{red}{1} & color{red}{3}\ hlinecolor{blue}{e} & color{red}{-3} & color{red}{-1}\ end{array}]

Итого два варианта. Рассмотрим первый вариант: $color{blue}{c}=color{red}{1}$, $color{blue}{e}=color{red}{-3}$. Получим систему

[left{ begin{align}b+d &=2\ bd+1-3 &=3\ -3b+d &=2 end{align} right.]

Вычитая из первого уравнения последнее, получаем $color{blue}{b}=color{red}{0}$, $color{blue}{d}=color{red}{2}$, что противоречит второму уравнению. Система несовместна.

Второй вариант: $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-1}$. Система уравнений:

[left{ begin{align}b+d &=2 \ bd+3-1 &=3 \ -b+3d &=2 end{align} right.]

Складывая первое и последнее уравнение, получаем $color{blue}{b}=color{red}{1}$, $color{blue}{d}=color{red}{1}$. При подстановке во второе уравнение получаем верное числовое равенство. Следовательно, мы нашли решение:

[color{blue}{b}=color{red}{1}; color{blue}{c}=color{red}{3}; color{blue}{d}=color{red}{1}; color{blue}{e}=color{red}{-1}]

Переписываем уравнение:

[left( {{x}^{2}}+x+3 right)left( {{x}^{2}}+x-1 right)=0]

Многочлен в первой скобке не имеет действительных корней, во второй — имеет:

[{{x}^{2}}+x-1=0]

Дискриминант положителен:

[D={{1}^{2}}-4cdot 1cdot left( -1 right)=1+4=5]

Корней будет два:

[x=frac{-1pm sqrt{5}}{2}]

Неудивительно, что эти корни не были обнаружены по теореме Безу. Ведь они являются иррациональными.:)

Ответ: $x=frac{-1pm sqrt{5}}{2}$.

Задача 3.2. «Нерешаемое» уравнение — 2

Задача. Решите уравнение методом неопределённых коэффициентов:

[{{x}^{4}}-4{{x}^{3}}+5{{x}^{2}}-2x-6=0]

Это задание похоже на предыдущее, поэтому распишем всё кратко. Ожидаемое разложение на множители:

[left( {{x}^{2}}+color{blue}{b}x+color{blue}{c} right)left( {{x}^{2}}+color{blue}{d}x+color{blue}{e} right)=0]

Найдём такое разложение методом неопределённых коэффициентов. Раскрываем скобки, приводим подобные:

[begin{align}{{x}^{4}}+left( color{blue}{b+d} right){{x}^{3}} &+ left( color{blue}{bd+c+e} right){{x}^{2}}+ \ &+ left( color{blue}{be+dc} right)x+ color{blue}{ce}=0 \ end{align}]

Сравниваем с коэффициентами исходного многочлена:

[{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+ color{red}{5}{{x}^{2}}+left( color{red}{-2} right)x+left( color{red}{-6} right)=0]

Выписываем четыре уравнения:

[begin{array}{rr} color{blue}{b+d}=color{red}{-4}; & color{blue}{be+dc}=color{red}{-2};\ color{blue}{bd+c+e}=color{red}{5}; & color{blue}{ce}=color{red}{-6}.\ end{array}]

Поскольку $color{blue}{ce}=color{red}{-6}$, полагаем $color{blue}{c} gt color{red}{0}$, $color{blue}{e} lt color{red}{0}$. Возможные варианты

[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{2} & color{red}{3} & color{red}{6}\ hlinecolor{blue}{e} & color{red}{-6} & color{red}{-3} & color{red}{-2} & color{red}{-1}\ end{array}]

Перебирая варианты, обнаруживаем, что правильная комбинация — это $color{blue}{c}=color{red}{3}$, $color{blue}{e}=color{red}{-2}$:

[left{ begin{align} b+d &=-4 \ bd+3-2 &=5 \ -2b+3d &=-2 end{align} right.]

Дважды прибавим к последнему уравнению первое — получим

[begin{align} 5d&=-10 \ color{blue}{d} &= color{red}{-2} \ color{blue}{b} &= color{red}{-2} end{align}]

Следовательно, исходное уравнение примет вид

[left( {{x}^{2}}-2x+3 right)left( {{x}^{2}}-2x-2 right)=0]

Многочлен в первой скобке корней не имеет (в этом легко убедиться, посчитав дискриминант). Рассмотрим вторую скобку:

[{{x}^{2}}-2x-2=0]

Дискриминант положительный:

[D={{left( -2 right)}^{2}}-4cdot1cdot left( -2 right)=4+8=12]

Уравнение имеет два корня:

[x=frac{2pm sqrt{12}}{2}=frac{2pm 2sqrt{3}}{2}=1pm sqrt{3}]

Ответ: $x=1pm sqrt{3}$.

Задача 3.3. Более сложное уравнение

Задача. Решите уравнение методом неопределённых коэффициентов:

[2{{x}^{4}}-4{{x}^{3}}+{{x}^{2}}-6x-3=0]

Это уравнение принципиально отличается от предыдущих тем, что старший коэффициент $color{blue}{{a}_{4}}=2$. Многочлен не является приведённым, поэтому разложение на множители, вообще говоря, выглядит так:

[left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( color{blue}{d}{{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]

Итого шесть неизвестных коэффициентов. Для сравнения: раньше их было всего четыре.

Однако задачу можно существенно упростить, если сделать два допущения:

1. Оба старших коэффициента — $color{blue}{a}$ и $color{blue}{d}$ — являются целыми и положительными.
2. Положим для определённости, что $color{blue}{a} gt color{blue}{d}$.

В этом и состоит ключевая идея метода неопределённых коэффициентов: мы вводим дополнительные ограничения, которые в итоге почти наверняка выполняются. Да, есть небольшой риск «промахнуться» в своих допущениях, но это компенсируется многократным упрощением дальнейших выкладок.

В нашем случае из двух допущений немедленно следует, что $color{blue}{a}=color{red}{2}$, $color{blue}{b}=color{red}{1}$, и уравнение примет вид

[left( color{red}{2}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( {{x}^{2}}+ color{blue}{e}x+ color{blue}{f} right)=0]

Осталось всего четыре неизвестных коэффициента. Раскроем скобки и приведём подобные:

[begin{align}color{red}{2}{{x}^{4}}+left( color{blue}{b+2e} right){{x}^{3}} &+left( color{blue}{be+c+2f} right){{x}^{2}}+ \ &+left( color{blue}{bf+ce} right)x+ color{blue}{cf}=0 \ end{align}]

Сравним с коэффициентами исходного уравнения:

[color{red}{2}{{x}^{4}}+left( color{red}{-4} right){{x}^{3}}+color{red}{1}{{x}^{2}}+left( color{red}{-6} right)x+left( color{red}{-3} right)=0]

Получим четыре уравнения, но из-за коэффициента $color{blue}{a}=color{red}{2}$ они отличаются от привычных:

[begin{array}{rr} color{blue}{b+2e}= color{red}{-4}; & color{blue}{bf+ce}= color{red}{-6};\ color{blue}{be+c+2f}= color{red}{1}; & color{blue}{cf}= color{red}{-3}.\ end{array}]

Многочлены в первой и второй скобке не являются взаимозаменяемыми (поскольку у них разные коэффициенты при ${{x}^{2}}$), поэтому необходимо рассмотреть все возможные комбинации, дающие $color{blue}{cf}= color{red}{-3}$:

[begin{array}{r|r|r|r|r} color{blue}{c} & color{red}{1} & color{red}{3} & color{red}{-1} & color{red}{-3}\ hlinecolor{blue}{f} & color{red}{-3} & color{red}{-1} & color{red}{3} & color{red}{1}\ end{array}]

Рассмотрим каждую комбинацию. В первом случае быстро обнаружится, что система несовместна. А вот второй случай, когда $color{blue}{c}= color{red}{3}$ и $color{blue}{f}= color{red}{-1}$, представляет интерес:

[left{ begin{align}b+2e &=-4 \ be+3-2 &=1 \ -b+3e &=-6 end{align} right.]

Складываем первое уравнение с последним — получаем

[begin{align}5e &=-10 \ color{blue}{e} &= color{red}{-2} \ color{blue}{b} &= color{red}{0} end{align}]

Итак, система совместна. Получили разложение на множители:

[left( 2{{x}^{2}}+3 right)left( {{x}^{2}}-2x-1 right)=0]

Многочлен в первых скобках принимает только положительные значения, поэтому не имеет корней:

[2{{x}^{2}}+3ge 0+3 gt 0]

Рассмотрим вторые скобки:

[{{x}^{2}}-2x-1=0]

Это квадратное уравнение. Дискриминант положительный:

[D={{2}^{2}}-4cdot 1cdot left( -1 right)=4+4=8]

Следовательно, уравнение имеет два различных корня:

[x=frac{2pm sqrt{8}}{2}=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]

Это и есть корни исходного уравнения четвёртой степени.

Ответ: $x=1pm sqrt{2}$.

4. Деление многочлена на многочлен

Ещё одна задача, где работает метод неопределённых коэффициентов — это деление одного многочлена на другой с остатком. Напомню, что разделить многочлен $Pleft( x right)$ на двучлен $Tleft( x right)$ с остатком — это значит представить его в виде

[Pleft( x right)=Qleft( x right)cdot Tleft( x right)+Rleft( x right)]

При этом степень остатка $Rleft( x right)$ должна быть меньше степени делителя $Tleft( x right)$. Кроме того,

[deg Qleft( x right)+deg Tleft( x right)=deg Pleft( x right)]

При соблюдении таких ограничений многочлены $Qleft( x right)$ и $Rleft( x right)$ всегда определяются однозначно. Их коэффициенты мы как раз и будем находить.

Задача 4.1. Деление на двучлен

Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена

[Pleft( x right)={{x}^{3}}-5{{x}^{2}}+15x-6]

на двучлен $Tleft( x right)=x-3$.

Итак, мы хотим представить многочлен $Pleft( x right)$ в виде

[Pleft( x right)=Qleft( x right)cdot left( x-3 right)+Rleft( x right)]

где $Qleft( x right)$ — неполное частное. Точнее, $Qleft( x right)$ — квадратный трёхчлен, потому что

[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)= \ &=3-1=2end{align}]

Кроме того, степень делителя $deg Tleft( x right)=1$, поэтому степень остатка $deg Rleft( x right)=0$, т.е. $Rleft( x right)$ — это просто число. С учётом этих фактов многочлен $Pleft( x right)$ примет вид

[Pleft( x right)=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x-3 right)+ color{blue}{d}]

Раскроем скобки, приведём подобные слагаемые:

[Pleft( x right)= color{blue}{a}{{x}^{3}}+left( color{blue}{b-3a} right){{x}^{2}}+left( color{blue}{c-3b} right)x+left( color{blue}{d-3c} right)]

С другой стороны, изначально тот же многочлен $Pleft( x right)$ имел вид

[Pleft( x right)= color{red}{1}{{x}^{3}}+left( color{red}{-5} right){{x}^{2}}+ color{red}{15}x+left( color{red}{-6} right)]

Приравниваем коэффициенты и получаем четыре равенства:

[begin{array}{rr} color{blue}{a}= color{red}{1}; & color{blue}{c-3b}= color{red}{15};\ color{blue}{b-3a}= color{red}{-5}; & color{blue}{d-3c}= color{red}{-6}.\ end{array}]

Это система из четырёх уравнений с четырьмя неизвестными, которая легко решается:

[color{blue}{a}= color{red}{1}; color{blue}{b}= color{red}{-2}; color{blue}{c}= color{red}{9}; color{blue}{d}= color{red}{21}]

Подставим найденные числа в $Qleft( x right)$ и $Rleft( x right)$:

[begin{align} & Qleft( x right)={{x}^{2}}-2x+9 \ & Rleft( x right)=21 \end{align}]

Ответ: $Qleft( x right)={{x}^{2}}-2x+9$, $Rleft( x right)=21$.

Поскольку мы делим $Pleft( x right)$ на двучлен $x-color{red}{3}$, составим таблицу для $x=color{red}{3}$:

[begin{array}{r|r|r|r|r} {} & color{blue}{1} & color{blue}{-5} & color{blue}{15} & color{blue}{-6}\ hlinecolor{red}{3} & 1 & -2 & 9 & color{green}{21}\ end{array}]

Перепишем многочлен $Pleft( x right)$ согласно этой таблице и сравним с записью для метода неопределённых коэффициентов:

[begin{align}Pleft( x right) &=left( color{red}{1}{{x}^{2}}- color{red}{2}x+ color{red}{9} right)left( x-color{red}{3} right)+ color{green}{21}= \ &=left( color{blue}{a}{{x}^{2}}+ color{blue}{b}x+ color{blue}{c} right)left( x- color{red}{3} right)+ color{blue}{d} end{align}]

Получили те же числа, что и при решении «напролом».

Впрочем, такие рассуждения актуальны лишь при делении на двучлен вида $x-color{red}{a}$. В следующем задании они нам уже не помогут.:)

Задача 4.2. Многочлен с параметром

Задача. При каких значениях параметров $a$ и $b$ многочлен

[Pleft( x right)={{x}^{3}}+a{{x}^{2}}-x+b]

делится без остатка на многочлен

[Tleft( x right)={{x}^{2}}+2x+5]

Решение. Если многочлен $Pleft( x right)$ делится без остатка на многочлен $Tleft( x right)$, то его можно представить в виде

[Pleft( x right)=Qleft( x right)cdot Tleft( x right)]

Здесь многочлен $Qleft( x right)$ — это частное, и его степень равна

[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=3-2=1]

Итак, $Qleft( x right)$ — линейный двучлен вида $color{blue}{c}x+color{blue}{d}$ (коэффициенты $color{blue}{a}$ и $color{blue}{b}$ уже заняты в условии задачи). Выражение для $Pleft( x right)$ можно переписать так:

[Pleft( x right)=left( color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x+5 right)]

Найдём коэффициенты $color{blue}{c}$ и $color{blue}{d}$. Раскрываем скобки (стандартная процедура для метода неопределённых коэффициентов) и приводим подобные:

[Pleft( x right)= color{blue}{c}{{x}^{3}}+left( color{blue}{2c+d} right){{x}^{2}}+left( color{blue}{5c+2d} right)x+ color{blue}{5d}]

Сравниваем с коэффициентами исходного многочлена:

[Pleft( x right)= color{red}{1}{{x}^{3}}+ color{red}{a}{{x}^{2}}+left( color{red}{-1} right)x+ color{red}{b}]

Приравниваем соответствующие «красные» и «синие» коэффициенты и получаем четыре равенства:

[begin{array}{rr}color{blue}{c}= color{red}{1}; & color{blue}{5c+2}d= color{red}{-1};\color{blue}{2c+d}= color{red}{a}; & color{blue}{5d}= color{red}{b}.\end{array}]

Итак, у нас четыре линейных уравнения и четыре переменных. Эта система имеет только одно решение:

[ color{blue}{a}= color{red}{-1}; color{blue}{b}= color{red}{-15}; color{blue}{c}= color{red}{1}; color{blue}{d}= color{red}{-3}]

Впрочем, нас интересуют лишь переменные $color{blue}{a}$ и $color{blue}{b}$.

Ответ: $a=-1$, $b=-15$.

Задача 4.3. Квадратный трёхчлен

Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена

[Pleft( x right)=2{{x}^{2}}+3x-3]

на двучлен $Tleft( x right)=2x-1$.

Решение. Частное $Qleft( x right)$ имеет степень

[deg Qleft( x right)=deg Pleft( x right)-deg Tleft( x right)=2-1=1]

Следовательно, $Qleft( x right)$ — линейный двучлен вида $color{blue}{a}x+ color{blue}{b}$, а остаток $Rleft( x right)$ — просто число $color{blue}{c}$. С учётом этого перепишем многочлен $Pleft( x right)$:

[begin{align}Pleft( x right) &=left( ax+b right)left( 2x-1 right)+c= \ &=2a{{x}^{2}}-ax+2bx-b+c= \ &= color{blue}{2a}{{x}^{2}}+left( color{blue}{2b-a} right)x+left( color{blue}{c-b} right) end{align}]

Сравним с исходным видом этого же многочлена:

[Pleft( x right)= color{red}{2}{{x}^{2}}+color{red}{3}x+left( color{red}{-3} right)]

Приравниваем соответствующие коэффициенты — получаем три уравнения:

[color{blue}{2a}=color{red}{2};quadcolor{blue}{2b-a}=color{red}{3};quadcolor{blue}{c-b}=color{red}{-3}]

Эта система легко решается:

[color{blue}{a}=color{red}{1}; color{blue}{b}=color{red}{2}; color{blue}{c}=color{red}{-1}]

Следовательно, неполное частное $Qleft( x right)=x+2$ и остаток $Rleft( x right)=-1$.

Ответ: $Qleft( x right)=x+2$, $Rleft( x right)=-1$.

Задача 4.4. Сложный многочлен

Задача. Используя метод неопределённых коэффициентов, найдите частное $Qleft( x right)$ и остаток $Rleft( x right)$ при делении многочлена

[Pleft( x right)={{x}^{5}}-1]

на квадратный трёхчлен $Tleft( x right)={{x}^{2}}+2x-1$.

Решение. На самом деле это несложная задача, но вычислений будет много. Запишем результат деления с остатком:

[Pleft( x right)=Qleft( x right)cdot left( {{x}^{2}}+2x-1 right)+Rleft( x right)]

Сразу найдём степени неполного частного и остатка:

[begin{align} deg Qleft( x right) &=deg Pleft( x right)-deg Tleft( x right)=5-2=3 \ deg Rleft( x right) & lt deg Tleft( x right)=2Rightarrow deg Rleft( x right)=1 \ end{align}]

Переходим к методу неопределённых коэффициентов. Сначала запишем общий вид многочленов $Qleft( x right)$ и $Rleft( x right)$:

[begin{align}Qleft( x right) &= color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} \ Rleft( x right) &= color{blue}{k}x+ color{blue}{l} \ end{align}]

Пусть вас не пугает большое количество переменных. Это нормально для многочленов высших степеней. Подставим наши выражения в формулу для $Pleft( x right)$:

[begin{align}Pleft( x right) &=left( color{blue}{a}{{x}^{3}}+ color{blue}{b}{{x}^{2}}+ color{blue}{c}x+ color{blue}{d} right)left( {{x}^{2}}+2x-1 right)+ \ &+ color{blue}{k}x+ color{blue}{l} \ end{align}]

Раскрываем скобки. Для удобства запишем одночлены одинаковой степени в одном и том же столбце:

[begin{array}{rrrrrr} color{blue}{a}{{x}^{5}} & + color{blue}{2a}{{x}^{4}} & — color{blue}{a}{{x}^{3}} & {} & {} & {}\ {} & + color{blue}{b}{{x}^{4}} & + color{blue}{2b}{{x}^{3}} & — color{blue}{b}{{x}^{2}} & {} & {}\ {} & {} & + color{blue}{c}{{x}^{3}} & + color{blue}{2c}{{x}^{2}} & — color{blue}{c}x & {}\ {} & {} & {} & + color{blue}{d}{{x}^{2}} & + color{blue}{2d}x & — color{blue}{d}\ {} & {} & {} & {} & + color{blue}{k}x & + color{blue}{l}\ end{array}]

Приводим подобные слагаемые:

[begin{align}Pleft( x right) &=color{blue}{a}{{x}^{5}}+left( color{blue}{2a+b} right){{x}^{4}}+left( color{blue}{-a+2b+c} right){{x}^{3}}+ \ &+left( color{blue}{-b+2c+d} right){{x}^{2}}+left( color{blue}{-c+2d+k} right)x+left( color{blue}{-d+l} right) \ end{align}]

Сравниваем эту запись с исходным многочленом:

[Pleft( x right)= color{red}{1}cdot {{x}^{5}}+ color{red}{0}cdot {{x}^{4}}+ color{red}{0}cdot {{x}^{3}}+ color{red}{0}cdot {{x}^{2}}+ color{red}{0}cdot x+left( color{red}{-1} right)]

Получаем шесть уравнений, которые последовательно решаются:

[begin{array}{ll}color{blue}{a}= color{red}{1} & color{blue}{d}=b-2c= color{red}{-12}\ color{blue}{b}=-2a= color{red}{-2} & color{blue}{k}=c-2d= color{red}{29}\ color{blue}{c}=a-2b= color{red}{5} & color{blue}{l}=d-1= color{red}{-13}\ end{array}]

Подставим найденные коэффициенты в выражения для $Qleft( x right)$ и $Rleft( x right)$:

[begin{align}Qleft( x right) &={{x}^{3}}-2{{x}^{2}}+5x-12 \ Rleft( x right) &=29x-13 \ end{align}]

Мы нашли неполное частное и остаток от деления. Это и есть окончательный ответ.

Ответ: $Qleft( x right)={{x}^{3}}-2{{x}^{2}}+5x-12$, $Rleft( x right)=29x-13$.

5. Выделение точного квадрата

Ещё одно приложение метода неопределённых коэффициентов — это «сворачивание» многочленов по формулам сокращённого умножения:

[begin{align}{{left( apm b right)}^{2}} &={{a}^{2}}pm 2ab+{{b}^{2}} \ {{left( apm b right)}^{3}} &={{a}^{3}}pm 3{{a}^{2}}b+3a{{b}^{2}}pm {{b}^{3}} \ end{align}]

Здесь всё как в разложении на множители: раскрывать скобки и привести подобные легко, а вот обратный переход — по коэффициентам «угадать» формулу сокращённого умножения — операция весьма нетривиальная.

Такие «нетривиальные операции» регулярно встречаются в задачах с параметрами и при работе с корнями. Параметрам посвящён отдельный урок, а вот корни мы рассмотрим прямо сейчас.

Задача 5.1. Избавление от корня

Задача. Упростите выражение

[sqrt{7+4sqrt{3}}]

Решение. Единственное, что здесь можно упростить — это избавиться от внешнего большого корня. Для этого нужно представить подкоренное выражение в виде точного квадрата:

[7+4sqrt{3}={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}}]

Почему именно такая конструкция возводится в квадрат? Всё просто: в исходной сумме мы видим одно слагаемое с корнем и одно слагаемое без него. Для получения такой суммы исходные слагаемые тоже должны быть разными: одно с корнем, а другое — без него.

В этом случае числа $color{blue}{a}$ и $color{blue}{b}$ будут либо рациональными, либо вообще целыми. И в этом вся суть метода неопределённых коэффициентов, потому что найти такие числа не составит особого труда — достаточно раскрыть скобки по формуле квадрата суммы:

[begin{align}{{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{2}} &={color{blue}{a}^{2}}+2color{blue}{ab}sqrt{3}+{{left( color{blue}{b}sqrt{3} right)}^{2}}= \ &=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3} end{align}]

Сравниваем полученное разложение с исходным выражением:

[color{red}{7}+color{red}{4}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)+2color{blue}{ab}sqrt{3}]

Чтобы эти выражения были гарантированно равны друг другу, достаточно потребовать, чтобы слагаемые без корня совпадали. Как и слагаемые с корнем:

[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=7 \ 2color{blue}{ab} &=4 end{align} right.]

Это нелинейная система с двумя переменными, которая легко решается методом подбора:

[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{2}^{2}}+3cdot {color{red}{1}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{2}cdotcolor{red}{1} end{align} right.]

Научиться раскладывать целые числа на «правильные» слагаемые и множители — вопрос небольшой практики. Просто попробуйте — и вы поймёте, насколько это быстро и легко.

Нам остаётся лишь записать решение:

[color{blue}{a}=color{red}{2}; color{blue}{b}=color{red}{1}]

Затем подставить найденные числа в исходное выражение:

[begin{align}sqrt{7+4sqrt{3}} &=sqrt{{{left( 2+sqrt{3} right)}^{2}}}= \ &=left| 2+sqrt{3} right|= \ &=2+sqrt{3} end{align}]

Ответ: $2+sqrt{3}$.

Важное замечание. Помните, что корень не просто «сжигает» квадрат вокруг выражения — на их месте появляется модуль:

[sqrt{{{a}^{2}}}=left| a right|]

Потому что арифметический квадратный корень — это по определению всегда неотрицательное число:

[begin{align}sqrt{{{5}^{2}}} &=left| 5 right|=5 \ sqrt{{{left( -8 right)}^{2}}} &=left| -8 right|=8 end{align}]

Когда под модулем стоит иррациональное выражение, его знак следует проверять отдельно. Иначе даже при правильном ответе его можно счесть недостаточно обоснованным.

Если вы забыли, как проверять знаки таких выражений, вернитесь к уроку «Знаки иррациональных выражений». В двух словах: для такой проверки используются либо цепочки неравенств, либо цепочки равносильных преобразований.

В следующем задании мы отработаем оба способа.

Задача 5.2. Предварительные преобразования

Задача. Упростите выражение

[sqrt{37-5sqrt{48}}]

Под корнем мы видим ещё один корень: $sqrt{48}$ — это большое число, с ним сложно работать. Поэтому прежде чем искать точный квадрат, немного упростим выражение:

[begin{align}sqrt{37-5sqrt{48}} &=sqrt{37-5sqrt{color{red}{16}cdot 3}}= \ &=sqrt{37-5cdot color{red}{4}cdot sqrt{3}}= \ &=sqrt{37-20sqrt{3}} end{align}]

Теперь представляем подкоренное выражение в виде точного квадрата

[37-20sqrt{3}={{left( color{blue}{a}- color{blue}{b}sqrt{3} right)}^{2}}]

Обратите внимание: перед нами квадрат разности. Потому что в исходном подкоренном выражении элементы не складывались, а именно вычитались. Этот факт ещё даст о себе знать, когда будем выяснять знак подмодульного выражения.

Ну а пока всё просто. Сравниваем старую запись и новую:

[color{red}{37}-color{red}{20}sqrt{3}=left( {color{blue}{a}^{2}}+3{color{blue}{b}^{2}} right)-2color{blue}{ab}sqrt{3}]

Получаем систему уравнений:

[left{ begin{align}{color{blue}{a}^{2}}+3{color{blue}{b}^{2}} &=37 \ 2color{blue}{ab} &=20 end{align} right.]

Второе уравнение перепишем в виде $color{blue}{ab}=10$, а затем разложим правые части равенств на «правильные» слагаемые и множители:

[left{ begin{align}{color{blue}{a}^{2}}+3cdot {color{blue}{b}^{2}} &={color{red}{5}^{2}}+3cdot {color{red}{2}^{2}} \ color{blue}{a}cdotcolor{blue}{b} &=color{red}{5}cdotcolor{red}{2} end{align} right.]

Получили красивое решение:

[color{blue}{a}=color{red}{5}; color{blue}{b}=color{red}{2}]

Возвращаемся к исходному выражению и извлекаем корень:

[sqrt{37-20sqrt{3}}=sqrt{{{left( 5-2sqrt{3} right)}^{2}}}=left| 5-2sqrt{3} right|]

Чтобы раскрыть модуль, нужно выяснить знак иррационального числа $5-2sqrt{3}$. Для этого можно заметить, что $sqrt{3} lt 2$, поэтому

[5-2sqrt{3} gt 5-2cdot 2=1 gt 0]

Это и есть цепочка неравенств. Также можно напрямую сравнить число $5-2sqrt{3}$ с нулём:

[begin{align}5-2sqrt{3} &vee 0 \ 5 &vee 2sqrt{3} \ 25 &vee 12 end{align}]

Очевидно, что $25 gt 12$, поэтому мы ещё раз убеждаемся, что исходное число положительное, и модуль раскрывается со знаком «плюс»:

[left| 5-2sqrt{3} right|=5-2sqrt{3}]

Ответ: $5-2sqrt{3}$.

Но всё это были довольно простые примеры с квадратным корнем. Как насчёт корней $n$-й степени?

Задача 5.3. Проблема с корнем

Задача. Упростите выражение

[sqrt[3]{sqrt{10}-3}cdot sqrt[6]{19+6sqrt{10}}]

Решение. Для начала вспомним свойства корней $n$-й кратности. Их можно умножать:

[sqrt[n]{a}cdot sqrt[n]{b}=sqrt[n]{acdot b}]

А также извлекать корень из корня:

[sqrt[k]{sqrt[m]{a}}=sqrt[mcdot k]{a}]

В частности, второй корень из задачи можно переписать так:

[sqrt[6]{19+6sqrt{10}}=sqrt[3]{sqrt{19+6sqrt{10}}}]

Чтобы избавиться от внутреннего квадратного корня, представим подкоренное выражение в виде точного квадрата. Но поскольку $sqrt{10}=sqrt{5}cdot sqrt{2}$, возможны два варианта:

[begin{align}19+6sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}} \ 19+6sqrt{10} &={{left( color{blue}{a}sqrt{2}+ color{blue}{b}sqrt{5} right)}^{2}} \ end{align}]

Однако в исходном выражении (т.е. прямо в условии задачи) есть ещё один $sqrt{10}$, который пока никак не преобразуется и никуда не денется, поэтому целесообразно рассмотреть лишь первый вариант:

[begin{align} color{red}{19}+ color{red}{6}sqrt{10} &={{left( color{blue}{a}+ color{blue}{b}sqrt{10} right)}^{2}}= \ &=ldots =left( {color{blue}{a}^{2}}+10{color{blue}{b}^{2}} right)+ 2color{blue}{ab}sqrt{10} end{align}]

Получаем стандартную систему:

[left{ begin{align}{color{blue}{a}^{2}}+10{color{blue}{b}^{2}} &=19 \ 2 color{blue}{ab} &=6 end{align} right.]

Второе уравнение равносильно $color{blue}{ab}=3$, и всю систему можно переписать так:

[left{ begin{align}{color{blue}{a}^{2}}+10cdot {color{blue}{b}^{2}} &={color{red}{3}^{2}}+10cdot {color{red}{1}^{2}} \ color{blue}{a} cdotcolor{blue}{b} &= color{red}{3}cdotcolor{red}{1} end{align} right.]

Очевидно, что $color{blue}{a}=color{red}{3}$, $color{blue}{b}=color{red}{1}$, поэтому

[begin{align}sqrt{19+6sqrt{10}} &=sqrt{{{left( 3+sqrt{10} right)}^{2}}}= \ &=left| 3+sqrt{10} right|= \ &=3+sqrt{10} end{align}]

Возвращаемся к исходному заданию:

[sqrt[3]{sqrt{10}-3}cdot sqrt[3]{3+sqrt{10}}=sqrt[3]{{{left( sqrt{10} right)}^{2}}-{{3}^{2}}}=1]

Ответ: 1.

Наконец, рассмотрим задание, где требуется выделить куб суммы и куб разности. Как вы понимаете, это задание совершенно другого уровня сложности.:)

Задача 5.4. Куб суммы и куб разности

Задача. Упростите выражение

[sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}]

Чтобы «красиво» извлечь корень третьей степени, нужно представить подкоренное выражение в виде точного куба. Начнём с суммы:

[begin{align}color{red}{10}+ color{red}{6}sqrt{3} &={{left( color{blue}{a}+ color{blue}{b}sqrt{3} right)}^{3}}= \ &={color{blue}{a}^{3}}+3{color{blue}{a}^{2}} color{blue}{b}sqrt{3}+3color{blue}{a}{color{blue}{b}^{2}}cdot 3+{color{blue}{b}^{3}}cdot 3sqrt{3}= \ &=left( {color{blue}{a}^{3}}+9color{blue}{a}{color{blue}{b}^{2}} right)+left( 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} right)sqrt{3} end{align}]

Получаем систему с двумя неизвестными:

[left{ begin{align}{color{blue}{a}^{2}}+9color{blue}{a}{color{blue}{b}^{2}} &=10 \ 3{color{blue}{a}^{2}}color{blue}{b}+3{color{blue}{b}^{3}} &=6 end{align} right.]

Методом подбора находим решение: $color{blue}{a}=color{red}{1}$, $color{blue}{b}=color{red}{1}$. Несмотря на грозный внешний вид, такие системы часто легко решаются простым перебором с проверкой:

[{{left( 1+1cdot sqrt{3} right)}^{3}}=1+3sqrt{3}+9+3sqrt{3}=10+6sqrt{3}]

Возвращаемся к исходному выражению:

[begin{align}& sqrt[3]{10+6sqrt{3}}+sqrt[3]{10-6sqrt{3}}= \ = &sqrt[3]{left( 1+sqrt{3} right)}+sqrt[3]{left( 1-sqrt{3} right)}= \ = & 1+sqrt{3}+1-sqrt{3}=2 \ end{align}]

Ответ: 2.

6. Избавление от иррациональности в знаменателе

Последний приём, который мы рассмотрим в этом уроке — избавление от иррациональностей в знаменателе с помощью неопределённых коэффициентов.

Из курса алгебры мы помним, как избавлять от простых иррациональностей. Например, домножение на квадратный корень:

[frac{1}{sqrt{2}}=frac{1cdotcolor{red}{sqrt{2}}}{sqrt{2}cdotcolor{red}{sqrt{2}}}=frac{sqrt{2}}{2}]

Или домножение на сопряжённое:

[frac{1}{sqrt{3}-1}=frac{1cdot left( color{red}{sqrt{3}+1} right)}{left( sqrt{3}-1 right)cdot left( color{red}{sqrt{3}+1} right)}=frac{sqrt{3}+1}{2}]

Но всё это касается лишь самых простых корней — квадратных. Уже в случае с кубическими корнями такой фокус не пройдёт. Тут-то на помощь к нам и приходят коэффициенты-переменные.

Задача 6.1. Корень третьей степени

Задача. Избавьтесь от иррациональности в знаменателе:

[frac{10}{1+sqrt[3]{9}}]

Поскольку это иррациональное число, то никакие преобразования не избавят нас от корней полностью.

Заметим, что $sqrt[3]{9}=sqrt[3]{3}cdot sqrt[3]{3}$. Попробуем возвести число $sqrt[3]{3}$ в разные степени:

[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{3} right)}^{n}} & sqrt[3]{3} & sqrt[3]{9} & 3 & 3sqrt[3]{3} & 3sqrt[3]{9} & 9\ end{array}]

Итак, все степени числа $sqrt[3]{3}$ можно разделить на три типа:

1. Целые числа $color{blue}{a}in mathbb{Z}$;
2. Иррациональные выражения вида $color{blue}{b}sqrt[3]{3}$ где $color{blue}{b}in mathbb{Z}$;
3. Выражения вида $color{blue}{c}sqrt[3]{9}$, где $color{blue}{c}in mathbb{Z}$.

Логично предположить (и это можно доказать), что результат деления на $1+sqrt[3]{9}$ можно представить в виде комбинации слагаемых этих трёх типов:

[frac{10}{1+sqrt[3]{9}}=color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]

Однако нам неизвестны коэффициенты $color{blue}{a}$, $color{blue}{b}$ и $color{blue}{c}$. Найти их — в этом и состоит суть задачи.:)

И тут к делу подключается метод неопределённых коэффициентов. Преобразуем уравнение так, чтобы найти эти коэффициенты. Для начала умножим обе части на $1+sqrt[3]{9}$:

[10=left( 1+sqrt[3]{9} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)]

Раскрываем скобки:

[color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}+ color{blue}{a}sqrt[3]{9}+ 3color{blue}{b}+ 3color{blue}{c}sqrt[3]{3}=10]

Группируем слагаемые относительно одинаковых корней:

[begin{align}& left( color{blue}{a}+ 3color{blue}{b} right)+left( color{blue}{b}+ 3color{blue}{c} right)sqrt[3]{3}+left( color{blue}{a} + color{blue}{c} right)sqrt[3]{9}= \ = &color{red}{10}+ color{red}{0}cdot sqrt[3]{3}+ color{red}{0}cdot sqrt[3]{9} \ end{align}]

Выше мы предположили, что все коэффициенты $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ — целые (в крайнем случае рациональные). Следовательно, множители при корнях $sqrt[3]{3}$ и $sqrt[3]{9}$ должны быть равны нулю (иначе число слева будет иррациональным):

[begin{align}color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align}]

С учётом этих двух условий само уравнение примет вид

[color{blue}{a}+ 3color{blue}{b}= color{red}{10}]

Получили систему из трёх уравнений с тремя неизвестными:

[left{ begin{align}color{blue}{a}+ 3color{blue}{b} &= color{red}{10} \ color{blue}{b}+ 3color{blue}{c} &= color{red}{0} \ color{blue}{a}+ color{blue}{c} &= color{red}{0} end{align} right.]

Все уравнения линейные, система решается элементарно. Решением будут числа $color{blue}{a}= color{red}{1}$, $color{blue}{b}= color{red}{3}$, $color{blue}{c}= color{red}{-1}$, поэтому исходное выражение можно переписать так:

[frac{10}{1+sqrt[3]{9}}= color{red}{1}+ color{red}{3}cdot sqrt[3]{3}- color{red}{1}cdot sqrt[3]{9}]

Ответ: $1+3sqrt[3]{3}-sqrt[3]{9}$.

Важное замечание. Чтобы избавиться от иррациональности конкретно в этой задаче, достаточно было домножить числитель и знаменатель дроби на недостающую часть куба суммы:

[begin{align} frac{10}{1+sqrt[3]{9}} &=frac{10cdot left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}{left( 1+sqrt[3]{9} right)left( color{red}{1-sqrt[3]{9}+sqrt[3]{{{9}^{2}}}} right)}= \ &=ldots =1+3sqrt[3]{3}-sqrt[3]{9} end{align}]

Однако такой подход не работает, когда в знаменателе стоит конструкция вида $color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}$. А метод неопределённых коэффициентов работает всегда.:)

Попробуем решить ещё одну задачу такого же типа.

Задача 6.2. То же самое, но чуть сложнее

Задача. Избавьтесь от иррациональности в знаменателе:

[frac{46}{2-3sqrt[3]{2}}]

Решение. Найдём несколько степеней числа $sqrt[3]{2}$:

[begin{array}{c|c|c|c|c|c|c}n & 1 & 2 & 3 & 4 & 5 & 6\ hline{{left( sqrt[3]{2} right)}^{n}} & sqrt[3]{2} & sqrt[3]{4} & 2 & 2sqrt[3]{2} & 2sqrt[3]{4} & 4\ end{array}]

На будущее: для корня $n$-й степени достаточно рассмотреть первые $n$ степеней. В нашем случае достаточно было выписать $sqrt[3]{2}$, $sqrt[3]{4}$ и $sqrt[3]{8}=2$ — новых иррациональных чисел мы уже не получим.

Итак, решаем задачу методом неопределённых коэффициентов. Попробуем подобрать целые (или рациональные) числа $color{blue}{a}$, $color{blue}{b}$, $color{blue}{c}$ такие, что

[frac{46}{2-3sqrt[3]{2}}= color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4}]

Умножаем обе части уравнения на $2-3sqrt[3]{2}$:

[left( 2-3sqrt[3]{2} right)left( color{blue}{a}+ color{blue}{b}sqrt[3]{2}+ color{blue}{c}sqrt[3]{4} right)=46]

Раскрываем скобки, приводим подобные:

[begin{align}2color{blue}{a}+ 2color{blue}{b}sqrt[3]{2}+ 2color{blue}{c}sqrt[3]{4} -3color{blue}{a}sqrt[3]{2} -3color{blue}{b}sqrt[3]{4} -6color{blue}{c} &= color{red}{46} \ left( 2color{blue}{a}- 6color{blue}{c} right)+left( 2color{blue}{b}- 3color{blue}{a} right)sqrt[3]{2}+left( 2color{blue}{c}- 3color{blue}{b} right)sqrt[3]{4} &= color{red}{46}end{align}]

Это равенство верно при соблюдении трёх условий:

[left{ begin{align}2color{blue}{a}- 6color{blue}{c} &= color{red}{46} \ 2color{blue}{b}- 3color{blue}{a} &=color{red}{0} \ 2color{blue}{c}- 3color{blue}{b} &=color{red}{0} \ end{align} right.]

Это система из трёх линейных уравнений с тремя неизвестными. Её решение:

[color{blue}{a}= color{red}{-4}; color{blue}{b}= color{red}{-6}; color{blue}{c}= color{red}{-9}]

Следовательно, исходное выражение можно переписать так:

[frac{46}{2-3sqrt[3]{2}}= color{red}{-4-6}cdot sqrt[3]{2} color{red}{-9}cdot sqrt[3]{4}]

Ответ: $-4-6sqrt[3]{2}-9sqrt[3]{4}$.

Важное замечание. Здесь тоже можно «составить» куб суммы в знаменателе:

[begin{align}frac{46}{2-3sqrt[3]{2}} &=frac{46cdot left( color{red}{{{2}^{2}}+2cdot 3sqrt[3]{2}+9sqrt[3]{4}} right)}{{{2}^{3}}-{{left( 3sqrt[3]{2} right)}^{3}}} \ &= ldots =-4-6sqrt[3]{2}-9sqrt[3]{4} end{align}]

Почему не использовать этот приём всегда? Потому что в следующей задаче он уже не сработает. Там помогут только неопределённые коэффициенты и решение системы уравнений.

Задача 6.3. Когда кубы уже не помогают

Это задание чуть сложнее, потому что здесь не помогут формулы сокращённого умножения. Да и сами вычисления будут чуть сложнее, чем в предыдущих задачах.

Задача. Избавьтесь от иррациональности в знаменателе:

[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}]

Мы уже встречались с числами $sqrt[3]{3}$ и $sqrt[3]{9}$, поэтому знаем, что исходное выражение можно представить в виде

[frac{2}{1+sqrt[3]{3}-sqrt[3]{9}}= color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9}]

Преобразуем выражение, избавившись от дроби:

[left( color{blue}{a}+ color{blue}{b}sqrt[3]{3}+ color{blue}{c}sqrt[3]{9} right)cdot left( 1+sqrt[3]{3}-sqrt[3]{9} right)= color{red}{2}]

Раскроем скобки, приведём подобные:

[begin{align}left( color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} right) &+left( color{blue}{a}+ color{blue}{b} -3color{blue}{c} right)sqrt[3]{3}+ \ &+left( -color{blue}{a}+ color{blue}{b}+ color{blue}{c} right)sqrt[3]{9}= color{red}{2} \ end{align}]

Это равенство возможно при соблюдении трёх условий:

[left{ begin{align}color{blue}{a}- 3color{blue}{b}+ 3color{blue}{c} &= color{red}{2} \ color{blue}{a}+ color{blue}{b}- 3color{blue}{c} &= color{red}{0} \ -color{blue}{a}+ color{blue}{b}+ color{blue}{c} &= color{red}{0} end{align} right.]

Три линейных уравнения, три переменных. Всё решается легко:

[color{blue}{a}= color{red}{2}; color{blue}{b}= color{red}{1}; color{blue}{c}= color{red}{1}]

Следовательно, исходное выражение перепишется так:

[frac{2}{1+ sqrt[3]{3}- sqrt[3]{9}}= color{red}{2}+ color{red}{1}cdot sqrt[3]{3}+ color{red}{1}cdot sqrt[3]{9}]

Ответ: $2+sqrt[3]{3}+sqrt[3]{9}$.

Как видите, никакие кубы суммы здесь уже не помогут.:)

7. Зачем всё это нужно

В этом уроке мы рассмотрели пять типов задач, которые можно решить методом неопределённых коэффициентов. У внимательного читателя наверняка возник вопрос: зачем вообще нужен этот метод, когда многие из этих задач можно решить проще и быстрее с помощью отдельных специальных приёмов?

В самом деле:

• Большинство многочленов отлично раскладываются на множители с помощью теоремы Безу и схемы Горнера — об этом мы говорили в отдельном уроке. Но только при условии, что среди корней есть рациональные.
• То же самое можно сказать и про решение уравнений.
• Делить многочлены друг на друга с остатком вообще лучше столбиком. Это самый быстрый и самый надёжный способ — при условии, что среди коэффициентов нет параметров.
• Точные квадраты зачастую можно подобрать, если немного подумать. Как и дополнительные множители для избавления от иррациональности. Если только это не «тяжёлый» случай, где формулы сокращённого умножения не работают.

Так зачем же нужен метод неопределённых коэффициентов? Всё дело в тех самых оговорках: «при условии», «только если не тяжёлый случай» и т.д.

Основная сила этого метода — в его универсальности. Да, считать придётся чуть больше, чем при использовании более специализированных приёмов. И да: целочисленный перебор не всегда приводит нас к успеху.

Но перед нами прежде всего универсальный алгоритм. Который точно работает — всегда, везде, без всяких оговорок. И если задача не решается методом неопределённых коэффициентов, то «специализированные» приёмы тем более не помогут.

Более того: область применения этого метода намного шире. Например, мы не рассмотрели разложение рациональных дробей в простейшие, а это очень важный приём, например, в интегрировании — и ему тоже нет альтернативы.

Поэтому берите на вооружение всё, что вы сегодня узнали, практикуйтесь — и да прибудут с вами решённые задачи, олимпиады и университетские зачёты и экзамены.:)

Смотрите также:

1. Бином Ньютона
2. Схема Горнера
3. Сравнение дробей
4. Четырехугольная пирамида в задаче C2
5. Задача B5: площадь кольца
6. Сечения и двугранные углы

Метод неопределенных коэффициентов

ЛИТЕРАТУРА:
[6] п. 24.3 – 24.4

Метод
неопределенных коэффициентов используется
для вычисления интегралов от рациональных
дробей вида

многочлены степени m
и n
соответственно.

Рассмотрим
основные этапы нахождения интегралов
данным методом.

1).
Если дробь

неправильная, т.е. m
> n,
то необходимо выделить целую часть,
представив

в виде

где

— многочлены и степень многочлена

меньше n.

2).
Раскладываем знаменатель

на множители:

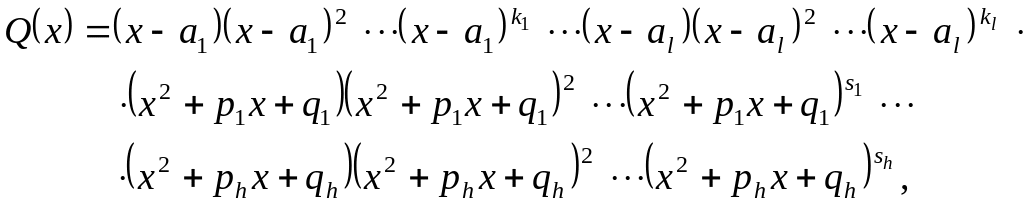
где

являются
корнями многочлена

кратности

соответственно, а квадратные трехчлены

не раскладываются на множители.

3).
Дробь

записывается как сумма элементарных
дробей:

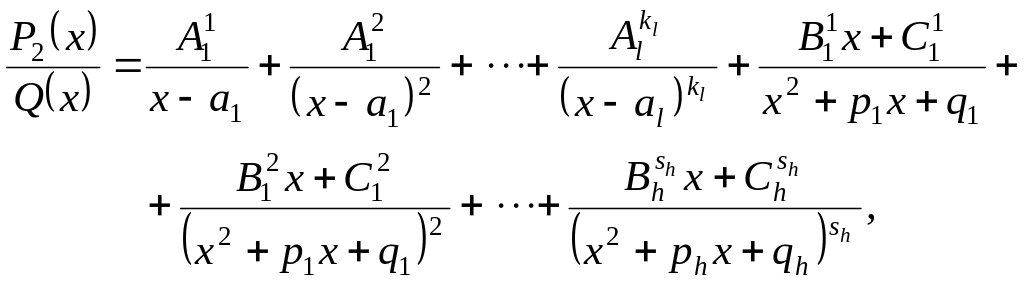
где
коэффициенты

не
определены.

Пример
1.
Найти

Решение.
Так как степени многочленов

равны, выделим целую часть:

Получим:

— целая часть,

— числитель дробной части. Т.е.

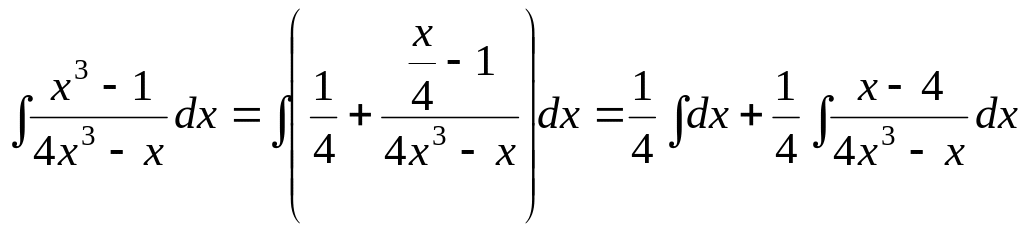
Разложим
знаменатель

на множители:

тогда

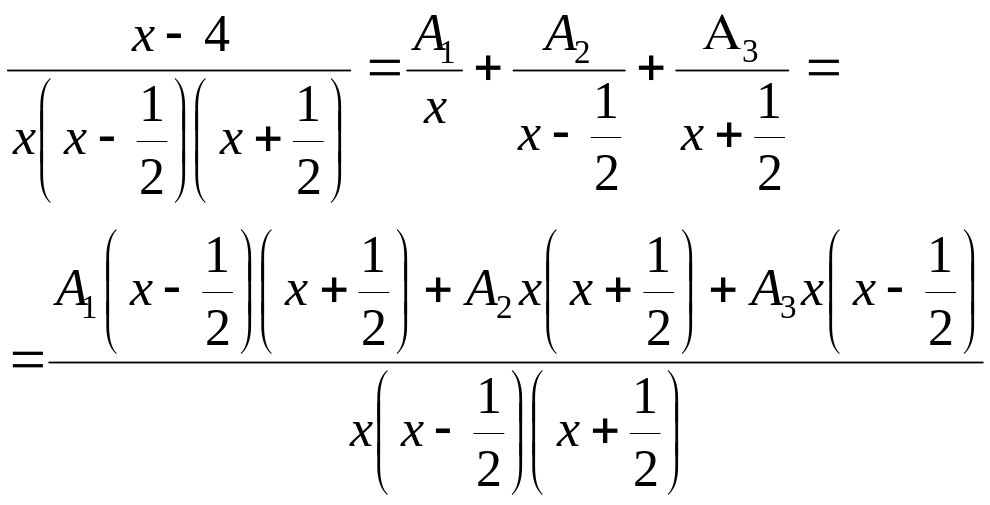
Приравниваем
числители левой и правой дробей:

Пусть

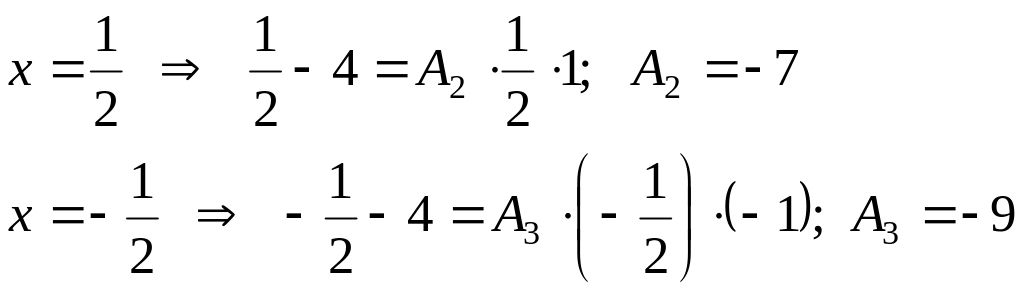
Подставляя
найденные значения в разложение на
элементарные дроби, получим:

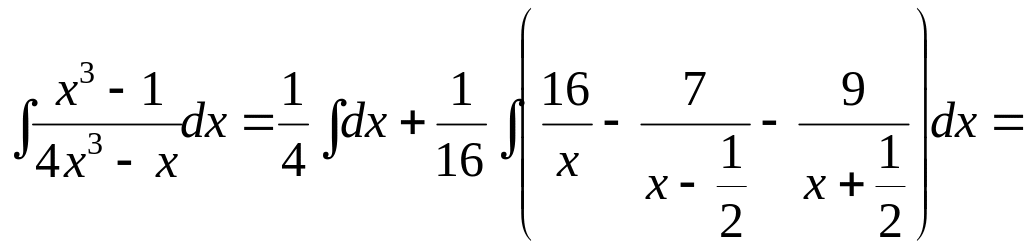
Пример
2.
Найти

Решение.
Выделяем целую часть:

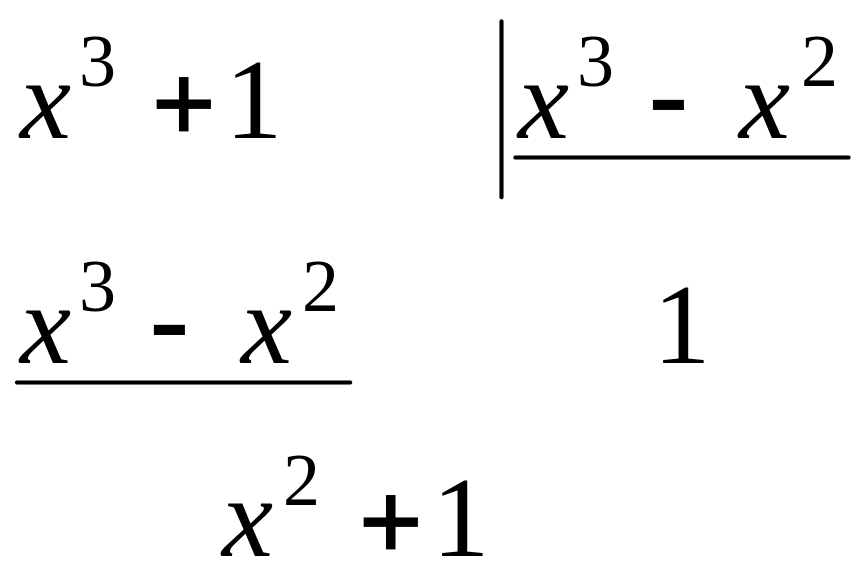
Следовательно:

так
как корень x=0
кратности 2, то получим следующее
разложение на сумму дробей:

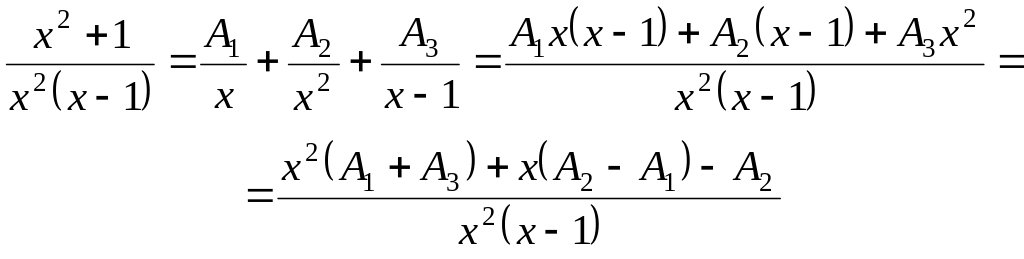
и
получаем систему для нахождения

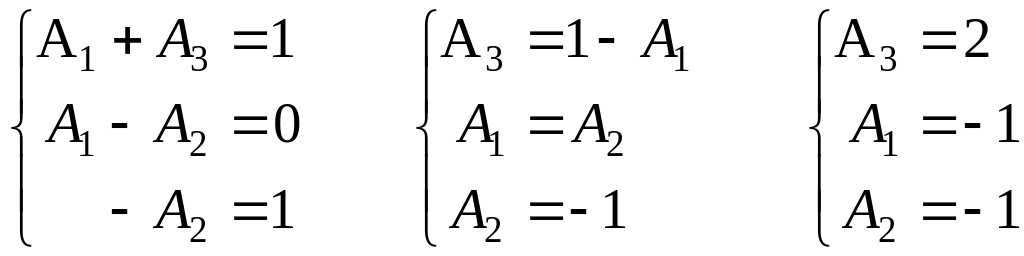
Задачи:

Найти интегралы:

1).	2).
3).	4).
5).	6).
7).	8).
9).	10).

Интегрирование некоторых иррациональных функций

ЛИТЕРАТУРА:
[6] п. 25.3 – 25.5

1). Интегралы вида

где

— рациональная функция своих аргументов;

—
целые числа, вычисляются с помощью
подстановки

где s
– наименьший общий знаменатель дробей

В
частности, для вычисления

применяется подстановка

где s
– наименьший общий знаменатель дробей

Пример
1.
Найти

.

Решение.
Делаем подстановку

тогда

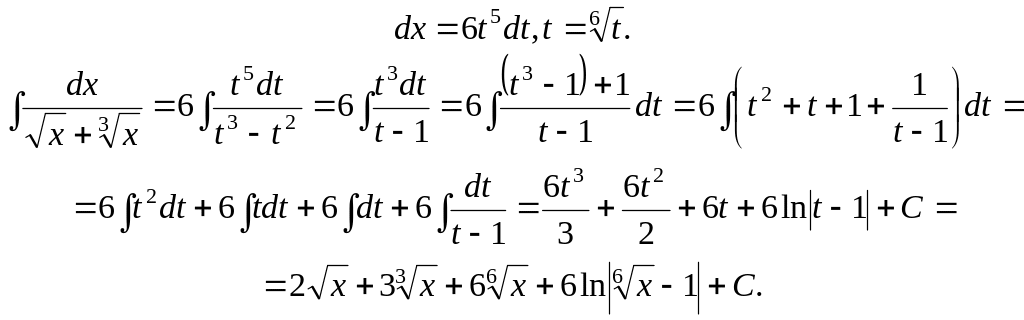
Пример
2.
Найти интеграл

Решение.

Делаем
подстановку

тогда

.

Методом неопределенных
коэффициентов получаем

2).
Интеграл от дифференциального бинома

где m,
n,
p
— рациональные
числа, может быть приведен к интегралу
от рациональных функций лишь в следующих
трех случаях (теорема Чебышева):

а)
p
– целое число. Полагаем

где N
– общий знаменатель дробей m
и n.

б)

целое.
Полагаем

где N
– знаменатель дроби p.

в)

целое.
Применяем подстановку

где N
– знаменатель дроби p.

Если
n
= 1, то эти случаи эквивалентны
следующим:

1)
p
– целое;

2)
m
– целое;

3)
(m
+ p)
– целое.

Пример
3. Найти
интеграл

Решение.
В нашем случае

Так как p
– целое (случай а), то полагаем

тогда

и интеграл примет вид:

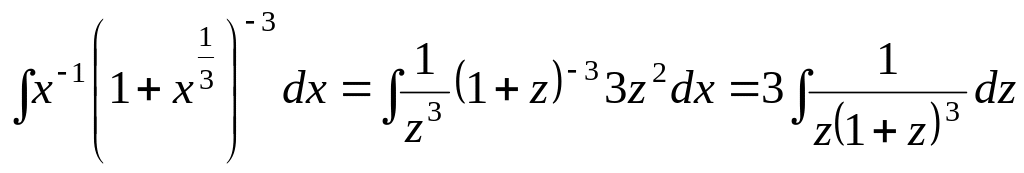
Для
дальнейшего нахождения интеграла
используем метод неопределенных
коэффициентов

т.е.

Пусть

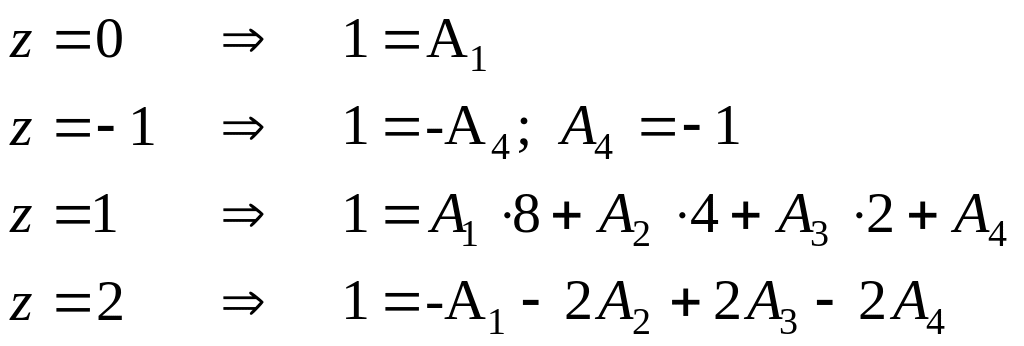
Тогда

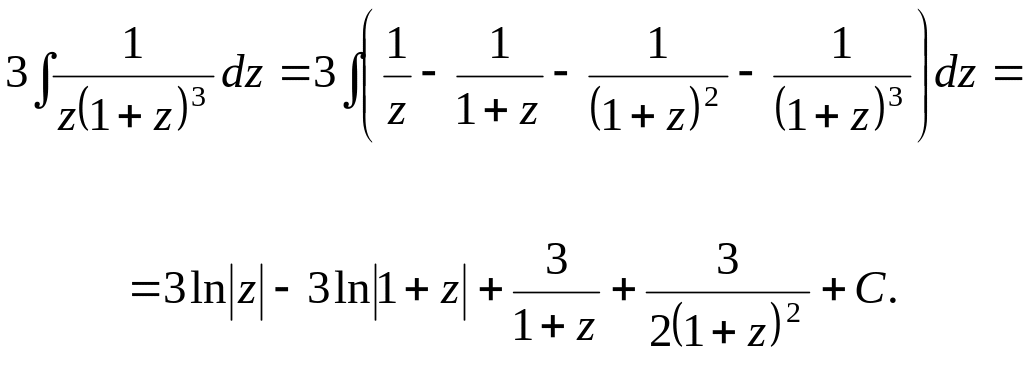
Подставляя

получим окончательный ответ:

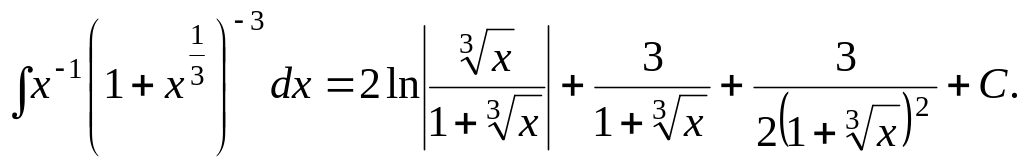
3).
Для интегралов вида

можно использовать
подстановки Эйлера:

1).
Если a
> 0, то

2).
Если с
> 0, то

3).Если

и

— действительные корни трехчлена

то

Пример
4. Найти
интеграл

Решение.
В нашем случае а
= 1 > 0, используем подстановку :

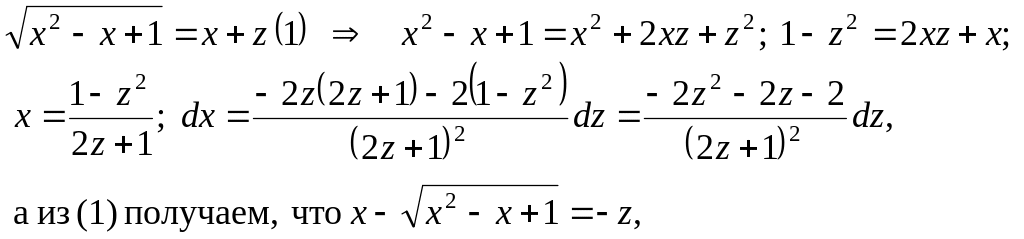
тогда интеграл

Для
дальнейшего решения используем метод
неопределенных коэффициентов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

• Первый способ нахождения коэффициентов
• Второй способ нахождения коэффициентов

Для нахождения неизвестных коэффициентов в разложении

$frac{P_{m}(x)}{Q_{n}(x)}=frac{A_{1}}{x-x_{1}}+ldots+frac{A_{n}}{left(x-x_{1}right)^{n}}+frac{B_{1}}{x-x_{2}}+ldots+frac{B_{m}}{left(x-x_{2}right)^{m}}+$

$+frac{C_{1} x+D_{1}}{x^{2}+p_{1} x+q_{1}}+ldots+frac{F_{k} x+G_{k}}{left(x^{2}+p_{1} x+q_{1}right)^{k}}+ldots$

используется метод неопределенных коэффициентов, суть которого состоит в следующем:

Метод неопределенных коэффициентов позволяет проинтегрировать любую
рациональную дробь. При этом могут получиться лишь
многочлены, рациональные дроби, логарифмы и арктангенсы.

Второй способ нахождения коэффициентов

Второй способ нахождения искомых коэффициентов состоит в том, что в получаемом относительно
$x$ тождестве аргументу
$x$ придают значения корней, в результате чего
получаются уравнения для нахождения неизвестных коэффициентов. Данный метод более удобен, если корни знаменателя некратные.
На практике чаще всего используется комбинация обоих способов.

Читать дальше: интегрирование правильных рациональных дробей.

        Приветствую всех, дорогие друзья!

        Ну что, поздравляю! Мы с вами благополучно добрались до основного материала в интегрировании рациональных дробей — метода неопределённых коэффициентов. Великого и могучего.) В чём же заключается его величество и могущество? А заключается оно в его универсальности. Имеет смысл ознакомиться, правда? Предупреждаю, что уроков по данной теме будет несколько. Ибо тема очень длинная, а материал крайне важный. )

        Сразу скажу, что в сегодняшнем уроке (и последующих тоже) мы будем заниматься не столько интегрированием, сколько… решением систем линейных уравнений! Да-да! Так что те у кого проблемы с системами, повторите матрицы, определители и метод Крамера. А тех товарищей, у кого и с матрицами туго, призываю, на худой конец, освежить в памяти хотя бы «школьные» методы решения систем — метод подстановки и метод почленного сложения/вычитания.

        Для начала нашего знакомства отмотаем плёнку немного назад. Ненадолго вернёмся к прошлым урокам и проанализируем все те дроби, которые мы с вами интегрировали до этого. Напрямую, безо всякого метода неопределённых коэффициентов! Вот они, эти дроби. Я рассортировал их по трём группам.

        Группа 1

        В знаменателе — линейная функция либо сама по себе, либо же в степени. Одним словом, в знаменателе стоит произведение одинаковых скобок вида (х-а).

        Например:

        (x+4)¹ = (x+4)

        (x-10)² = (x-10)(x-10)

        (2x+5)³ = (2x+5)(2x+5)(2x+5)

        И так далее. Кстати, пусть вас не смущают скобки (4х+5) или (2х+5)³ с коэффициентом k внутри. Это всё равно, по своей сути, скобки вида (х-а). Ибо это самое k из таких скобок всегда можно вынести наружу.

        Вот так:

        

        Вот и всё.) И неважно, что именно при этом стоит в числителе — просто dx или же многочлен какой. Мы всегда раскладывали числитель по степеням скобки (x-a), превращали большую дробь в сумму маленьких, подводили (где надо) скобку под дифференциал и интегрировали.

        Группа 2

        

        Что общего у этих дробей?

        А общее то, что во всех знаменателях стоит квадратный трёхчлен ax²+bx+c. Но не просто, а именно в единственном экземпляре. И неважно здесь, положительный у него дискриминант или отрицательный.

        Такие дроби всегда интегрировались одним из двух способов — либо разложением числителя по степеням знаменателя, либо выделением полного квадрата в знаменателе с последующей заменой переменной. Всё зависит от конкретной подынтегральной функции.

        Группа 3

        

        Это были самые нехорошие для интегрирования дроби. В знаменателе — неразложимый квадратный трёхчлен, да ещё и в степени n. Но, опять же, в единственном экземпляре. Ибо, кроме трёхчлена, других множителей в знаменателе нету. Такие дроби интегрировались по рекуррентной формуле. Либо напрямую, либо сводились к ней после выделения полного квадрата в знаменателе и последующей замены переменной.

        Однако, к сожалению, всё богатое многообразие рациональных дробей не ограничивается только лишь этими тремя рассмотренными группами.

        А как быть, если в знаменателе стоят разные скобки? Например, что-нибудь типа:

        (х-1)(х+1)(х+2)

        Или одновременно скобка (х-а) и квадратный трёхчлен, что-то типа (х-10)(х²-2х+17)? И в других подобных случаях? Вот, именно в таких случаях и приходит на помощь метод неопределённых коэффициентов!

        Сразу скажу: работать мы пока что будем только с правильными дробями. Теми, у которых степень числителя строго меньше степени знаменателя. Как быть с неправильными дробями, подробно рассказано в первом уроке по дробям. Надо выделять целую часть (многочлен). Делением уголком числителя на знаменатель или разложением числителя — как хотите. И даже пример разобран. А многочлен вы уж как-нибудь худо-бедно проинтегрируете. Не маленькие уже поди.) Но на неправильные дроби тоже порешаем примеры!

        А теперь начинаем знакомиться. В отличие от большинства учебников по высшей математике, наше знакомство мы начнём не с сухой и грузной теории про основную теорему алгебры, теорему Безу, про разложение рациональной дроби на сумму простейших (об этих дробях позже) и прочего занудства, а начнём мы с несложного примера.

        Например, нам требуется найти вот такой неопределённый интеграл:

        

        Первый взгляд на подынтегральную дробь. В знаменателе стоит произведение трёх скобок:

        (x-1)(x+3)(x+5) 

        Причём все скобки разные. Поэтому наша старая технология с разложением числителя по степеням знаменателя в этот раз уже не прокатывает: какую именно скобку выделять в числителе? (х-1)? (х+3)? Непонятно… Выделение полного квадрата в знаменателе — тоже не в кассу: там многочлен третьей степени (если перемножить все скобки). Что делать?

        При взгляде на нашу дробь возникает вполне естественное желание… Прямо-таки непреодолимое! Из нашей большой дроби, которую неудобно интегрировать, как-то сделать три маленьких. Хотя бы вот так:

        

        Почему именно такой вид надо искать? А всё потому, что в таком виде наша исходная дробь уже удобна для интегрирования! Подводим знаменатель каждой маленькой дроби под дифференциал и — вперёд.)

        А можно ли вообще получить такое разложение? Новость хорошая! Соответствующая теорема математики гласит — да, можно! Такое разложение существует и единственно.

        Но есть одна проблемка: коэффициенты А, В и С мы пока не знаем. И сейчас нашей основной задачей как раз и будет их определить. Узнать, чему же равны наши буковки А, В и С. Отсюда и название — метод неопределённых коэффициентов. Начнём наше сказочное путешествие!

        Итак, у нас есть равенство, от которого мы начинаем плясать:

        

        Давайте приведём справа все три дроби к общему знаменателю и сложим:

        

        Теперь можно смело отбросить знаменатели (ибо они одинаковы) и просто приравнять числители. Всё как в обычном дробно-рациональном уравнении:

        

        Следующим шагом раскрываем все скобки (коэффициенты А, В и С пока лучше оставить снаружи):

        

        Далее вставляем все коэффициенты внутрь скобок и избавляемся от этих самых скобок:

        

        А теперь (важно!) выстраиваем всю нашу конструкцию справа по старшинству степеней: сначала собираем в кучку все члены с х², потом — просто с иксом и, наконец, собираем свободные члены. Фактически, просто приводим подобные и группируем слагаемые по степеням икс.

        Вот так:

        

        

        А теперь осмысливаем результат. Слева — наш исходный многочлен. Второй степени. Числитель нашей подынтегральной дроби. Справа — тоже некоторый многочлен второй степени. Но с неизвестными коэффициентами. Данное равенство должно быть справедливо при всех допустимых значениях икс. Дроби-то слева и справа были одинаковые (по нашему условию)! Это означает, что их числители (т.е. наши многочлены) — тоже одинаковые. Стало быть, коэффициенты при одинаковых степенях икс у этих многочленов обязательно должны быть равны!

        Начинаем с самой старшей степени. С квадрата. Смотрим, что за коэффициенты у нас стоят при х² слева и справа. Справа у нас стоит сумма коэффициентов А+В+С, а слева — двойка. Так у нас рождается первое уравнение.

        Записываем:

        А+В+С = 2

        Есть. Первое уравнение готово.)

        Далее идём по снижающейся траектории — смотрим на члены с иксом в первой степени. Справа при икс у нас стоит 8А+4В+2С. Хорошо. А что у нас при икс стоит слева? Гм… Слева вообще никакого слагаемого с иксом нету! Там только 2х² — 3. Как быть? Очень просто! Это значит, что коэффициент при икс слева у нас равен нулю! Мы же можем записать нашу левую часть вот так:

        

        А что? Имеем полное право.) Отсюда второе уравнение выглядит так:

        8A+4B+2C = 0

        Ну вот, практически, и всё. Осталось приравнять свободные члены:

        15А-5В-3С = -3

        Одним словом, приравнивание коэффициентов при одинаковых степенях икса происходит по такой схеме:

        

        Все три наших равенства должны выполняться одновременно. Поэтому собираем из наших выписанных уравнений систему:

        

        Системка не самая трудная для прилежного студента — три уравнения и три неизвестных. Как хотите, так и решайте. Можно методом Крамера через матрицы с определителями, можно методом Гаусса, можно даже обычной школьной подстановкой.

        Для начала я решу эту систему так, как обычно решают такие системы культурные студенты. А именно — методом Крамера.

        Решение начинаем с составления матрицы системы. Напоминаю, что эта матрица — просто табличка, составленная из коэффициентов при неизвестных. 

        Вот она:

        

        А вот дальше начинаем вычислять определители. Муторно немного, но ничего не поделать. Не школьники уже поди.)

        Первым делом вычисляем определитель матрицы системы. Или, коротко, определитель системы. Обычно он обозначается греческой буквой ∆ («дельта»):

        

        Отлично, определитель системы не равен нулю (-48≠0). Из теории систем линейных уравнений этот факт означает, что наша система совместна и имеет единственное решение.

        Следующим шагом вычисляем определители неизвестных ∆_A, ∆_B, ∆_C. Напоминаю, что каждый из этих трёх определителей получается из основного определителя системы путём замены столбцов с коэффициентами при соответствующих неизвестных на столбец свободных членов.

        Вот и составляем определители и считаем:

        

        

        

        Подробно объяснять технику вычисления определителей третьего порядка я здесь не буду. И не просите. Это уже совсем отклонение от темы будет.) Кто в теме, тот понимает, о чём речь. И, возможно, уже догадался, каким именно способом я вычислил эти три определителя.)

        А дальше уже находим неизвестные А, B и С по формулам Крамера:

        

        Вот всё и готово.)

        Так обычно решают системы культурные студенты. Но… Не все студенты дружат с матрицами и определителями. К сожалению. Для кого-то эти простые понятия высшей математики так навсегда и остаются китайской грамотой и таинственным монстром в тумане…

        Что ж, специально для таких некультурных студентов предлагаю более привычный способ решения — метод последовательного исключения неизвестных. Фактически, это продвинутый «школьный» метод подстановки. Только шагов побольше будет.) Но суть та же самая. Первым делом я исключу переменную С. Для этого я выражу С из первого уравнения и подставлю во второе и третье:

        

        Упрощаем, приводим подобные и получаем новую систему, уже с двумя неизвестными:

        

        Теперь, в этой новой системе, тоже можно выразить одну из переменных через другую. Но самые внимательные студенты, возможно, заметят, что коэффициенты перед переменной B — противоположны. Два и минус два. Стало быть, очень удобно будет сложить между собой оба уравнения, чтобы исключить переменную В и оставить только букву А.

        Складываем левые и правые части, мысленно сокращаем 2B и -2B и решаем уравнение только относительно А:

        

        Есть. Первый коэффициент найден: А = -1/24.

        Определяем второй коэффициент В. Например, из верхнего уравнения:

        

        Отсюда получаем:

        

        Отлично. Второй коэффициент тоже найден: B = -15/8. Осталась ещё буковка С. Для её определения используем самое верхнее уравнение, где она у нас выражена через А и В:

        

        Итак:

        

        Ну вот и всё. Неизвестные коэффициенты найдены! Неважно, через Крамера или через подстановку. Главное, правильно найдены.)

        Стало быть, наше разложение большой дроби в сумму маленьких будет выглядеть вот так:

        

        И пусть вас не смущают полученные дробные коэффициенты: в данной процедуре (методе неопределённых коэффициентов) это самое обычное явление.

        А теперь крайне желательно проверить, правильно ли мы нашли наши коэффициенты A, B и С. Поэтому сейчас берём черновик и вспоминаем восьмой класс — складываем обратно все три наши маленькие дроби.

        

        Если мы получим исходную большую дробь — значит, всё хорошо. Нет — значит, бейте меня ищите ошибку.

        Общий знаменатель, очевидно, будет 24(х-1)(х+3)(х+5).

        Поехали:

        

        

        

        

        

        Йес!!! Получили исходную дробь. Что и требовалось проверить. Всё гуд. Так что прошу не бить.)

        А теперь возвращаемся к нашему исходному интегралу. Легче он за это время не стал, да. Но теперь, когда наша дробь разложена в сумму маленьких, её интегрирование стало сплошным удовольствием!

        Смотрите сами! Вставляем наше разложение в исходный интеграл.

        Получаем:

        

        Пользуемся свойствами линейности и разбиваем наш большой интеграл в сумму маленьких, все константы выносим за знаки интеграла.

        Получаем:

        

        А полученные три маленьких интеграла уже легко берутся подведением знаменателя под знак дифференциала.

        Продолжаем интегрирование:

        

        Вот и всё.) И не надо в данном уроке спрашивать меня, откуда в ответе взялись логарифмы! Кто помнит таблицу интегралов, тот в теме и всё поймёт. А кто не помнит — гуляем по ссылочкам. Я их не просто так ставлю.

        Окончательный ответ:

        

        Вот такая красивая троица: три логарифма — трус, бывалый и балбес. И попробуй, догадайся до такого хитрого ответа с ходу! Только метод неопределённых коэффициентов и выручает, да.) Собственно, с этой целью и разбираемся. Что, как и откуда.

        В качестве тренировочного упражнения, предлагаю вам попрактиковаться в методе и проинтегрировать вот такую дробь:

        

        Потренируйтесь, найдите интеграл, не сочтите за труд! Должен получиться вот такой ответ:

        

        Метод неопределённых коэффициентов — штука мощная. Спасает даже в самой безнадёжной ситуации, когда и так дробь преобразовываешь, и эдак. И вот тут у некоторых внимательных и интересующихся читателей, возможно, возник целый ряд вопросов:

        — Что делать, если многочлен в знаменателе вообще не разложен на множители?

        — КАК надо искать разложение любой большой рациональной дроби на сумму маленьких? В каком виде? Почему именно в таком, а не сяком?

        — Что делать, если в разложении знаменателя есть кратные множители? Или скобки в степенях типа (х-1)²? В каком виде искать разложение?

        — Что делать, если, помимо простых скобок вида (х-а), знаменатель одновременно содержит и неразложимый квадратный трёхчлен? Скажем, х²+4х+5 ? В каком виде искать разложение?

        Что ж, пришла пора основательно разбираться, откуда ноги растут. В следующих уроках.)