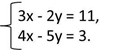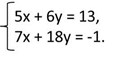Как найти метод постановки

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».

Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).

	x = 7 − 5y
3(7 − 5y) − 2y = 4  (*)

(*)   3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
                 − 17y = − 17     | :(−17)
y = 1

Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
	+          =>	x + 5y + 3x − 2y = 11
3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».

Для этого умножим первое уравнение на «−3».

	x + 5y = 7 | ·(−3)
3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
3x − 2y = 4

	−3x −15y = −21
3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
	+          =>	−3x −15y + 3x − 2y = −21 + 4
3x − 2y = 4		−17y = −17 |:(−17)
		y = 1

Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения «x».

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».

	x = 17 + 3 · (−30)
y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
2x −2y = 4 − 3y

	8x − 3y − 6x = −4
2x −2y + 3y = 4

Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4      |·(−1)
2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
	+          =>	−2x + 3y + 2x + y = 4 + 4
2x + y = 4		4y = 8         | :4
		y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».

Ответ: x = 1; y = 2

---

Ваши комментарии

Оставить комментарий:

---

Давайте разберемся, как же решать системы уравнений способом подстановки?

1)    Выразим из первого или второго уравнения системы неизвестное х или у (как нам удобнее);

2)    Подставим в другое уравнение (в то, из которого не выражали неизвестное) вместо неизвестного х или у (если выражали х, подставляем вместо х; если выражали у, подставляем вместо у) полученное выражение;

3)    Решаем уравнение, которое получили. Находим х или у;

4)    Подставляем полученное значение неизвестного и находим второе неизвестное.

Правило записано. Теперь давайте попробуем применить его при решении системы уравнений.

Пример 1.

Внимательно посмотрим на систему уравнений. Замечаем, что из первого уравнения легче выразить у.

Выражаем у:

–2у = 11 – 3х

у = (11 – 3х)/(–2)

у = –5,5 + 1,5х

Теперь аккуратно подставим во второе уравнение вместо у выражение –5,5 + 1,5х.

Получим: 4х – 5(–5,5 + 1,5х) = 3

Решаем это уравнение:

4х + 27,5 – 7,5х = 3

–3,5х = 3 – 27,5

–3,5х = –24,5

х = –24,5/(–3,5)

х = 7.

Подставляем в выражение у = – 5,5 + 1,5х вместо х значение, которое мы нашли. Получаем:

у = – 5,5+ 1,5 · 7 = –5,5 + 10,5 = 5.

Ответ: (7; 5)

Интересно, а если выразить из первого уравнения не у, а х, измениться ли ответ?

Давайте попробуем выразить х из первого уравнения.

3х = 11 + 2у

х = (11 + 2у)/3

Подставим вместо х во второе уравнение  выражение (11 +2у)/3, получим уравнение с одним неизвестным и решим его.

4(11 + 2у)/3 – 5у = 3, умножим обе части уравнения на 3, получим

4(11 + 2у) – 15у=9

44 + 8у – 15у = 9

–7у = 9 – 44

–7у = –35

у = –35/(–7)

у = 5.

Находим переменную х, подставляя 5 в выражение х = (11 +2у)/3.

х = (11 +2·5)/3 = (11+10)/3 = 21/3 = 7

Ответ: (7; 5)

Как видите, ответ получился такой же. Если вы будете внимательны и аккуратны, то независимо от того, какую переменную вы выражаете  –  х или у, ответ получите правильный.

Довольно часто ученики спрашивают: «Есть ли еще другие способы решения систем, кроме сложения и подстановки?»

Есть некоторое видоизменение способа подстановки – способ сравнивания неизвестных.

1)    Надо из каждого уравнения системы выразить одно и то же неизвестное через второе.

2)    Полученные неизвестные сравнивают, получают уравнение с одним неизвестным.

3)    Находят значение одного неизвестного.

4)    Подставляют полученное значение неизвестного и находят второе неизвестное.

Пример 2.  Решить систему уравнений

Из двух уравнений выразим переменную х через у.

Получим из первого уравнения х = (13 – 6у) / 5, а из второго х = (–1 – 18у) / 7.

Сравнивая эти выражения, получаем уравнение с одним неизвестным и решаем его:

(13 – 6у) / 5 = (–1 – 18у) / 7

7 (13 – 6у)  = 5 (–1 – 18у)

91 – 42у = –5 – 90у

–42у + 90у = –5 – 91

48у = – 96

у = – 96 / 48

у = – 2.

Неизвестное х найдем подставив значение у в одно из выражений для х.

(13 – 6(– 2)) / 5= (13+12) / 5 = 25/5 = 5

Ответ: (5; –2).

Думаю, что и у вас все получиться. Если остались вопросы, приходите ко мне на уроки. 

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

п.1. Метод подстановки

Например:
( left{ begin{array}{ l } mathrm{x^2+y=10} & \ mathrm{x-y=2} & end{array}right. )
Шаг 1. Из второго уравнения x = y + 2
Шаг 2. Подставляем в первое уравнение:
(mathrm{ (y+2)^2+y=10Rightarrow y^2+4y+4+y-10=0Rightarrow y^2+5y-6=0Rightarrow })
( mathrm{(y+6)(y-1)=0Rightarrow} left[ begin{array}{ l } mathrm{y_1=-6} & \ mathrm{y_2=1} & end{array}right. )
Шаг 3. Находим x₁ = –6 + 2 = –4, x₂ = 1 + 2 = 3
Ответ: {(–4; –6); (3; 1)}.

п.2. Метод сложения

Шаг 1. Умножить одно и второе уравнение на уравнивающие коэффициенты (если необходимо).
Шаг 2. Сложить (вычесть) левые и правые части уравнений.
Шаг 3. Решить полученное уравнение относительно одной переменной.
Шаг 4. Найти соответствующие значения второй переменной.

Например:
( left{ begin{array}{ l } mathrm{x^2+y=10} & \ mathrm{x-y=2} & end{array}right. )
Сразу переходим к шагу 2, складываем оба уравнения, получаем:
(mathrm{ x^2+x=12Rightarrow x^2+x-12=0Rightarrow (x+4)(x-3)=0Rightarrow } left[ begin{array}{ l } mathrm{x_1=-4} & \ mathrm{x_2=3} & end{array}right. )
Находим соответствующие y:
y₁ = x₁ – 2 = –4 – 2 = –6,    y₂ = x₂ – 2 = 3 – 2 = 1
Ответ: {(–4; –6); (3; 1)}.

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) ( left{ begin{array}{ l } mathrm{x+y=8} & \ mathrm{x^2+xy-3=37} & end{array}right. )
Решаем методом подстановки: ( left{ begin{array}{ l } mathrm{y=8-x} & \ mathrm{x^2+x(8-x)-3=37} & end{array}right. )
Для нижнего уравнения: ( mathrm{x^2+8x-x^2-3=37Rightarrow 8x=40 Rightarrow x=5} )
Подставляем в верхнее уравнение: ( mathrm{y=8-5=3} )

Ответ: (5; 3).

б) ( left{ begin{array}{ l } mathrm{x^2+y=1} & \ mathrm{x^2-y=10} & end{array}right. )
Решаем методом сложения: ( mathrm{2x^2=8Rightarrow x^2=4Rightarrow x=pm 2} )
Находим y: y = 1 – x² = 1 – 4 = –3

Ответ: {(–2; –3); (2; –3)}.

в) ( left{ begin{array}{ l } mathrm{x+xy=15} & \ mathrm{x-3xy=-25} & end{array}right. )
Решаем методом сложения: $$ left{ begin{array}{ l } mathrm{x+xy=15 |times 3} & \ mathrm{x-3xy=-25} & end{array}right.Rightarrow (+) left{ begin{array}{ l } mathrm{3x+3xy=45} & \ mathrm{x-3xy=-25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{4x=20} & \ mathrm{xy=15-x} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=5} & \ mathrm{y=frac{15-x}{x}=frac{15-5}{5}=2} & end{array}right. $$

Ответ: (5; 2).

г) ( left{ begin{array}{ l } mathrm{x^2+y^2=13} & \ mathrm{x-4y+5=0} & end{array}right. )
Решаем методом подстановки: ( left{ begin{array}{ l } mathrm{x=4y-5} & \ mathrm{(4y-5)^2+y^2=13} & end{array}right. )
Для нижнего уравнения: ( mathrm{16y^2-40y+25+y^2=13Rightarrow 17y^2-40y+12=0} ) $$ mathrm{D=40^2-4cdot 17cdot 12=1600-816=784=28^2}\ mathrm{y=frac{40pm 28}{34}=} left[ begin{array}{ l } mathrm{y_1=frac{6}{17}} & \ mathrm{y_2=2} & end{array}right. $$ Подставляем в верхнее уравнение: $$ mathrm{x_1=4cdotfrac{6}{17}-5=frac{24-85}{17}=-frac{61}{17}=-3frac{10}{17}, x_2=4cdot 2-5=3} $$

Ответ: ( mathrm{left{(3; 2); left(-3frac{10}{17}; frac{6}{17}right)right}} ).

д*) ( left{ begin{array}{ l } mathrm{x^2+2xy+3y^2=17} & \ mathrm{5x^2-3xy+y^2=3} & end{array}right. )
Умножим первое уравнение на 3, второе – на 17, и отнимем одно из другого. $$ (-)left{ begin{array}{ l } mathrm{3x^2+6xy+9y^2=51} & \ mathrm{85x^2-51xy+17y^2=51} & end{array}right.Rightarrow 82x^2-57xy+8y^2=0 $$ Получили однородное уравнение. Поделим его на ( mathrm{y^2: 82left(frac{x}{y}right)^2-57left(frac{x}{y}right)+8=0} )
Решаем полученное квадратное уравнение: $$ mathrm{D=57^2-4cdot 82cdot 8=3249-2624=625=25^2,} mathrm{left(frac{x}{y}right)=frac{57pm 25}{164}}= left[ begin{array}{ l } mathrm{frac{8}{41}} & \ mathrm{frac12} & end{array}right. $$ Получаем: ( left[ begin{array}{ l } mathrm{x=frac{8}{41}y} & \ mathrm{2x=y} & end{array}right. )
Подставляем первую пропорцию в первое уравнение системы: begin{gather*} mathrm{ left(frac{8}{41}yright)^2+2cdotfrac{8}{41}ycdot y+3y^2=17Rightarrow left(frac{64}{1681}+frac{16}{41}+3right)y^2=17Rightarrow }\ mathrm{ y^2=frac{17cdot 1681}{5763}=frac{1681}{339}=frac{41^2}{339}Rightarrow y=pmfrac{41}{sqrt{339}}, x=pmfrac{8}{41}cdotfrac{41}{sqrt{339}}=pmfrac{8}{sqrt{339}} } end{gather*} Подставляем вторую пропорцию в первое уравнение системы: $$ mathrm{ x^2+2xcdot 2x+3cdot(2x)^2=17Rightarrow 17x^2=17Rightarrow x^2=1Rightarrow x=pm 1, y=pm 2 } $$

Ответ: ( mathrm{left{(1; 2); (-1; -2); left(frac{8}{sqrt{339}}; frac{41}{sqrt{339}}right); left(-frac{8}{sqrt{339}}; -frac{41}{sqrt{339}}right)right}} ).

Пример 2*. Решите систему уравнений с помощью замены переменной:
a) ( left{ begin{array}{ l } mathrm{x+y+xy=26} & \ mathrm{xy(x+y)=160} & end{array}right. )
Замена переменных: ( left{ begin{array}{ l } mathrm{a=x+y} & \ mathrm{b=xy} & end{array}right. ) begin{gather*} left{ begin{array}{ l } mathrm{a+b=26} & \ mathrm{ab=160} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{a=26-b} & \ mathrm{(26-b)b=160} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{a=26-b} & \ mathrm{-b^2+26b-160=0} & end{array}right.Rightarrow \ Rightarrow left{ begin{array}{ l } mathrm{a=26-b} & \ mathrm{-b^2-26b+160=0} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{a=26-b} & \ mathrm{(b-10)(b-16)=0} & end{array}right.Rightarrow left[begin{array}{ l } left{begin{array}{ l } mathrm{a_1=16} & \ mathrm{b_1=10} & end{array}right.& \ left{begin{array}{ l } mathrm{a_2=10} & \ mathrm{b_2=16} & end{array}right. end{array}right. end{gather*} Возвращаемся к исходным переменным: (left[begin{array}{ l } left{begin{array}{ l } mathrm{x+y=16} & \ mathrm{xy=10} & end{array}right.& \ left{begin{array}{ l } mathrm{x+y=10} & \ mathrm{xy=16} & end{array}right. end{array}right. )
Решаем первую систему: ( left{ begin{array}{ l } mathrm{x+y=16} & \ mathrm{xy=10} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=16-y} & \ mathrm{(16-y)y=10} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=16-y} & \ mathrm{16y-y^2=10} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{x=16-y} & \ mathrm{y^2-16y+10=0} & end{array}right. )
$$ mathrm{ D=16^2-40=216, y_{1,2}=frac{16pmsqrt{216}}{2}=8pmsqrt{54} } $$ $$ mathrm{ x_{1,2}=16-(8pmsqrt{54})=8pmsqrt{54} } $$ Решаем вторую систему: ( left{ begin{array}{ l } mathrm{x+y=10} & \ mathrm{xy=16} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=10-y} & \ mathrm{(10-y)y=16} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=10-y} & \ mathrm{10y-y^2=16} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{x=10-y} & \ mathrm{y^2-10y+16=0} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=10-y} & \ mathrm{(y-2)(y-8)=0} & end{array}right.Rightarrow left[begin{array}{ l } left{begin{array}{ l } mathrm{x_3=8} & \ mathrm{y_3=2} & end{array}right.& \ left{begin{array}{ l } mathrm{x_4=2} & \ mathrm{y_4=8} & end{array}right. end{array}right. )

Ответ: (mathrm{left{(8-sqrt{54}; 8+sqrt{54}); (8+sqrt{54}; 8-sqrt{54}); (8; 2); (2; 8)right}}).

Ответ: {(2; 1) ; (1; 2)}.