Как найти мгновенную скорость 10 класс - Исправление недочетов и поиск решений вместе с Examum.ru

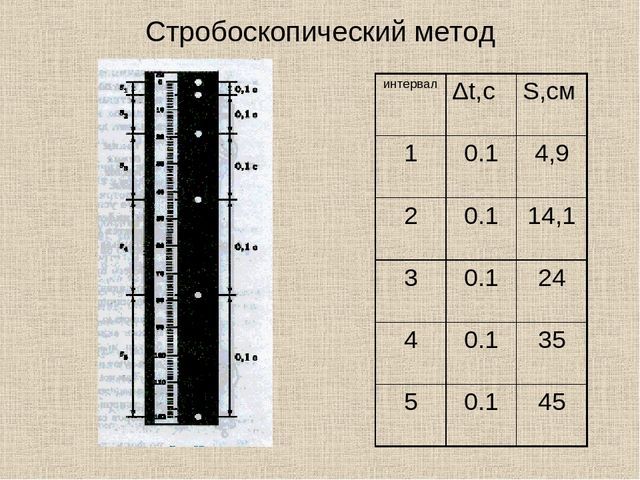
Загрузить PDF

Скорость — это быстрота перемещения объекта в заданном направлении. ^[1] В общих целях нахождение скорости объекта (v) — простая задача: нужно разделить перемещение (s) в течение определенного времени (s) на это время (t), то есть воспользоваться формулой v = s/t. Однако таким способом получают среднюю скорость тела. Используя некоторые вычисления, можно найти скорость тела в любой точке пути. Такая скорость называется мгновенной скоростью и вычисляется по формуле v = (ds)/(dt), то есть представляет собой производную от формулы для вычисления средней скорости тела.^[2]

1
Начните с уравнения. Для вычисления мгновенной скорости необходимо знать уравнение, описывающее перемещение тела (его позицию в определенный момент времени),^[3] то есть такое уравнение, на одной стороне которого находится s (перемещение тела), а на другой стороне — члены с переменной t (время).^[4] Например:

s = -1.5t² + 10t + 4
- В этом уравнении:
  
  Перемещение = s. Перемещение — пройденный объектом путь. Например, если тело переместилось на 10 м вперед и на 7 м назад, то общее перемещение тела равно 10 — 7 = 3 м (а на 10 + 7 = 17 м).
  
  Время = t. Обычно измеряется в секундах.
2
Вычислите производную уравнения. Чтобы найти мгновенную скорость тела, чьи перемещения описываются приведенным выше уравнением, нужно вычислить производную этого уравнения. Производная — это уравнение, позволяющее вычислить наклон графика в любой точке (в любой момент времени). Чтобы найти производную, продифференцируйте функцию следующим образом: если y = a*xⁿ, то производная = a*n*x^n-1. Это правило применяется к каждому члену многочлена.
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
  
  s = -1.5t² + 10t + 4
  (2)-1.5t^(2-1) + (1)10t^{1 — 1} + (0)4t⁰
  -3t¹ + 10t⁰
  -3t + 10
3
Замените «s» на «ds/dt», чтобы показать, что новое уравнение — это производная от исходного уравнения (то есть производная s от t). Производная — это наклон графика в определенной точке (в определенный момент времени). Например, чтобы найти наклон линии, описываемой функцией s = -1.5t² + 10t + 4 при t = 5, просто подставьте 5 в уравнение производной.
- В нашем примере уравнение производной должно выглядеть следующим образом:
  
  ds/dt = -3t + 10
4
В уравнение производной подставьте соответствующее значение t, чтобы найти мгновенную скорость в определенный момент времени.^[5] Например, если вы хотите найти мгновенную скорость при t = 5, просто подставьте 5 (вместо t) в уравнение производной ds/dt = -3 + 10. Затем решите уравнение:

ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 м/с
- Обратите внимание на единицу измерения мгновенной скорости: м/с. Так как нам дано значение перемещения в метрах, а время — в секундах, и скорость равна отношению перемещения ко времени, то единица измерения м/с — правильная.
Реклама

1
Постройте график перемещения тела. В предыдущей главе вы вычисляли мгновенную скорость по формуле (уравнению производной, позволяющему найти наклон графика в определенной точке).^[6] Построив график перемещения тела, вы можете найти его наклон в любой точке, а следовательно определить мгновенную скорость в определенный момент времени.
- По оси Y откладывайте перемещение, а по оси X — время. Координаты точек (x,у) получите через подстановку различных значений t в исходное уравнение перемещение и вычисления соответствующих значений s.
- График может опускаться ниже оси X. Если график перемещения тела опускается ниже оси X, то это значит, что тело движется в обратном направлении от точки начала движения. Как правило, график не распространяется за ось Y (отрицательные значения x) — мы не измеряем скорости объектов, движущихся назад во времени!
2
Выберите на графике (кривой) точку P и близкую к ней точку Q. Чтобы найти наклон графика в точке P, используем понятие предела. Предел — состояние, при котором величина секущей, проведенной через 2 точки P и Q, лежащих на кривой, стремится к нулю.
- Например, рассмотрим точки P(1,3) и Q(4,7) и вычислим мгновенную скорость в точке P.
3

Найдите наклон отрезка PQ. Наклон отрезка PQ равен отношению разницы значений координат «у» точек P и Q к разнице значений координат «х» точек P и Q. Другими словами, H = (y_Q — y_P)/(x_Q — x_P), где H — наклон отрезка PQ. В нашем примере наклон отрезка PQ равен:

H = (y_Q — y_P)/(x_Q — x_P)
H = (7 — 3)/(4 — 1)
H = (4)/(3) = 1.33
4

Повторите процесс несколько раз, приближая точку Q к точке P. Чем меньше расстояние между двумя точками, тем ближе значение наклона полученных отрезков к наклону графика в точке P. В нашем примере проделаем вычисления для точки Q с координатами (2,4.8), (1.5,3.95) и (1.25,3.49) (координаты точки P остаются прежними):

Q = (2,4.8): H = (4.8 — 3)/(2 — 1)
H = (1.8)/(1) = 1.8

Q = (1.5,3.95): H = (3.95 — 3)/(1.5 — 1)
H = (.95)/(.5) = 1.9

Q = (1.25,3.49): H = (3.49 — 3)/(1.25 — 1)
H = (.49)/(.25) = 1.96
5
Чем меньше расстояние между точками P и Q, тем ближе значение H к наклону графика в точке P При предельно малом расстоянии между точками P и Q, значение H будет равно наклону графика в точке P Так как мы не можем измерить или вычислить предельно малое расстояние между двумя точками, графический способ дает оценочное значение наклона графика в точке Р.
- В нашем примере при приближении Q к P мы получили следующие значения H: 1.8; 1.9 и 1.96. Так как эти числа стремятся к 2, то можно сказать, что наклон графика в точке P равен 2.
- Помните, что наклон графика в данной точке равен производной функции (по которой построен этот график) в этой точке. График отображает перемещение тела с течением времени и, как отмечалось в предыдущем разделе, мгновенная скорость тела равна производной от уравнения перемещения этого тела. Таким образом, можно заявить, что при t = 2 мгновенная скорость равна 2 м/с (это оценочное значение).
Реклама

1
Вычислите мгновенную скорость при t = 4, если перемещение тела описывается уравнением s = 5t³ — 3t² + 2t + 9. Этот пример похож на задачу из первого раздела с той лишь разницей, что здесь дано уравнение третьего порядка (а не второго).
- Сначала вычислим производную этого уравнения:
  
  s = 5t³ — 3t² + 2t + 9
  s = (3)5t^{(3 — 1)} — (2)3t^{(2 — 1)} + (1)2t^{(1 — 1) + (0)9t^{0 — 1}
  15t⁽²⁾ — 6t⁽¹⁾ + 2t^{(0)
  15t⁽²⁾ — 6t + 2}}
- Теперь подставим в уравнение производной значение t = 4:
  
  s = 15t⁽²⁾ — 6t + 2
  15(4)⁽²⁾ — 6(4) + 2
  15(16) — 6(4) + 2
  240 — 24 + 2 = 22 м/с
2
Оценим значение мгновенной скорости в точке с координатами (1,3) на графике функции s = 4t² — t. В этом случае точка P имеет координаты (1,3) и необходимо найти несколько координат точки Q, лежащий близко к точке P. Затем вычислим H и найдем оценочные значения мгновенной скорости.
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
  
  s = 4t² — t
  
  t = 2: s = 4(2)² — (2)
  4(4) — 2 = 16 — 2 = 14, so Q = (2,14)
  
  t = 1.5: s = 4(1.5)² — (1.5)
  4(2.25) — 1.5 = 9 — 1.5 = 7.5, so Q = (1.5,7.5)
  
  t = 1.1: s = 4(1.1)² — (1.1)
  4(1.21) — 1.1 = 4.84 — 1.1 = 3.74, so Q = (1.1,3.74)
  
  t = 1.01: s = 4(1.01)² — (1.01)
  4(1.0201) — 1.01 = 4.0804 — 1.01 = 3.0704, so Q = (1.01,3.0704)
- Теперь вычислим H:
  
  Q = (2,14): H = (14 — 3)/(2 — 1)
  H = (11)/(1) = 11
  
  Q = (1.5,7.5): H = (7.5 — 3)/(1.5 — 1)
  H = (4.5)/(.5) = 9
  
  Q = (1.1,3.74): H = (3.74 — 3)/(1.1 — 1)
  H = (.74)/(.1) = 7.3
  
  Q = (1.01,3.0704): H = (3.0704 — 3)/(1.01 — 1)
  H = (.0704)/(.01) = 7.04
- Так как полученные значения H стремятся к 7, то можно сказать, что мгновенная скорость тела в точке (1,3) равна 7 м/с (оценочное значение).
Реклама

Советы

Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.

Об этой статье

Эту страницу просматривали 83 497 раз.

Была ли эта статья полезной?

Источник

Самым простым видом механического движения является
прямолинейное движение с постоянной по модулю и направлению скоростью:

Однако не будем забывать о том, что равномерно движение — это
модель реального движения. В действительности же реальные тела чаще всего
движутся не равномерно. Например, все вы знаете, что автомобиль в начале своего
движения из состояния покоя постепенно увеличивает свою скорость. Где-то в середине
пути он, возможно, будет недолго двигаться с постоянной скоростью. А при
торможении его скорость будет постепенно уменьшаться. То есть движение автомобиля
является неравномерным. Поэтому описать его с помощью уравнения движения мы не
можем, так как скорость тела постоянно меняется.

Но нам на помощь приходить понятие мгновенной скорости, то
есть скорости точки в данный момент времени (или в данной точке траектории).

Чтобы понять, как определяется мгновенная скорость,
рассмотрим неравномерное движение материальной точки по криволинейной
траектории. Пусть в некоторый момент времени t
она занимает положение М. А спустя некоторый промежуток времени Δt₁ — положение М₁.

Укажем на рисунке перемещение, которое совершила точка за
этот промежуток времени.

Если теперь мы с вами разделим это перемещение на промежуток
времени, в течение которого оно произошло, то тем самым найдём такую скорость равномерного
прямолинейного движения, с которой должна была бы двигаться точка, чтобы
попасть из начального положения в конечное за определённый промежуток времени.
Эта скорость называется средней скоростью перемещения. Она
показывает, какое перемещение в среднем совершала точка за единицу времени.

Направление этой скорости совпадает с направлением вектора
перемещения точки.

Но как же нам определить скорость точки в положении М?
Давайте попробуем уменьшить рассматриваемый промежуток времени. Из рисунка
видим, что в этом случае точка совершит меньшее перемещение. Средняя же
скорость точки на этом участке хотя и не равна скорости в точке М, но
уже ближе к ней.

Если мы продолжим уменьшать промежутки времени и,
соответственно, перемещения, то очень скоро мы придём к тому, что средние
скорости будут незначительно отличаться друг от друга и от скорости точки в
положении М. В конце концов промежуток времени станет так мал, что можно
будет пренебречь изменением скорости за это время. Следовательно, при
стремлении промежутка времени к нулю отношение будет
стремиться к своему некоторому предельному значению.

Физическая векторная величина, равная пределу
отношения перемещения к промежутку времени, в течение которого это перемещение
произошло, при стремлении промежутка времени к нулю, называется мгновенной
скоростью:

Направление вектора мгновенной скорости зависит от вида
движения точки. Так, если точка движется прямолинейно, то направление
мгновенной скорости совпадает с направлением движения. А вот в случае
криволинейного движения вектор мгновенной скорости направлен по касательной к
траектории.

В этом легко убедиться, если понаблюдать за раскалёнными
частицами, отрывающимися от точильного камня. Или за частицами грязи,
вылетающими из-под колеса буксующего автомобиля.

Для описания неравномерного движения точки, помимо понятия
средней скорости перемещения, в физике чаще используют понятие средней
путевой скорости. Она определяется отношением пути к промежутку времени, за
который этот путь пройдён:

Проще говоря, средняя путевая скорость показывает, какой путь
в среднем проходило тело за единицу времени.

Однако не стоит забывать о том, что средняя путевая скорость
характеризует движение за весь промежуток времени в целом. Например, когда мы слышим,
что расстояние между двумя городами автомобиль преодолел за 5 ч со скоростью
100 км/ч, мы понимаем, что в среднем он за каждый час проезжал сто километров. Но
во время движения он мог заехать на заправку, где-то двигаться с бо́льшей
или меньшей скоростью. Иными словами, средняя путевая скорость не даёт
информации о скорости движения точки в каждый момент времени.

Для примера давайте с вами определим среднюю путевую скорость
движения точки, если первую половину пути она преодолела со скоростью 15 м/с, а
вторую — со скоростью 25 м/с.

Мы уже с вами не раз говорили о том, что характер движения
точки зависит от того, относительно каких тел мы рассматриваем это движение (то
есть от выбора системы отсчёта). Но так как тело
отсчёта мы можем выбирать совершенно произвольно, то положение одного и того же
тела можно одновременно рассматривать в разных системах координат.

Рассмотрим такой опыт. Пусть у нас есть стеклянная трубка,
заполненная вязкой жидкостью. Опустим в неё тяжёлый шарик и будем перемещать
трубку относительно школьной доски в горизонтальном направлении, не меняя
ориентации трубки. Одновременно будем наблюдать за движением шарика и отмечать
его положения через равные интервалы времени.

Теперь выберем две системы координат: одну свяжем с доской и
назовём неподвижной, а вторую — с трубкой и назовём движущейся.

Из рисунка видно, что перемещение точки относительно
неподвижной системы отсчёта равно векторной сумме её перемещения относительно
движущейся системы и перемещения движущейся системы отсчёта относительно
неподвижной:

В этом состоит принцип независимости движений.

Теперь разделим записанное нами уравнение на промежуток
времени, в течение которого произошли эти перемещения:

И учтём, что отношения перемещений к промежутку времени равны
скоростям:

Таким образом получаем, что скорость тела относительно
неподвижной системы отсчёта равна векторной сумме его скорости относительно
подвижной системы отсчёта и скорости подвижной системы отсчёта относительно
неподвижной.

Данное утверждение называется законом сложения
скоросте́й Галилея. Он справедлив как для равномерного, так и для
неравномерного движения. Только в этом случае складываются мгновенные скорости.

Однако этот закон нельзя применять для точек, движение
которых происходит со скоростями, близкими к скорости света в вакууме.

Для примера решим такую задачу. На какой угол следует
отклонится от перпендикуляра к течению реки и сколько времени нужно плыть на
лодке, чтобы пересечь реку перпендикулярно её течению, если скорость лодки
относительно воды 3 м/с, скорость течения реки — 1,5 м/с, а ширина русла — 400
м?

Источник

Рассмотрим движение тела из точки (A) в точку (B) (рис. (1)). Траектория (AB) является криволинейной.

Введём понятие «средняя скорость».

На рисунке (1) показаны вектора перемещений тела (Delta{vec{r_3}}), (Delta{vec{r_2}}) и (Delta{vec{r_1}}) за различные сокращающиеся промежутки времени (Delta{t_3}), (Delta{t_2}) и (Delta{t_1}).

Рис. (1). Перемещения тела при криволинейном движении

Средняя скорость равна отношению перемещения за конечный промежуток времени:

Средняя скорость является векторной величиной:

направление средней скорости υ ср→↑↑Δr→ находится согласно математической формуле определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу средней скорости);
числовое значение средней скорости (модуль, проекции на координатные оси) определяется согласно геометрическим правилам работы с векторами;
физические понятия отличаются от математических понятий наличием единиц измерения ([(v_{ср})] (=) [(frac{м}{с})]).

Участки траектории (AB), (AD) и (AE) (рис. (1)) характеризуются, соответственно, средними скоростями:

(vec{v_{ср3}}), (vec{v_{ср2}}), (vec{v_{ср1}}).


(vec{v_{ср3}}) = (frac{Delta{vec{r_3}}}{Delta{t_3}})	(vec{v_{ср2}}) = (frac{Delta{vec{r_2}}}{Delta{t_2}})	(vec{v_{ср1}}) = (frac{Delta{vec{r_1}}}{Delta{t_1}})

Если уменьшать неограниченно промежуток времени (Delta{t}), то быстрота движения тела характеризуется понятием «мгновенная скорость» (или «скорость»).

Математическая запись уменьшения промежутка времени:

Δt→0

(в математике существует понятие «предел», символ данного понятия — «lim»).

Физический смысл принципа уменьшения промежутка времени: на определённом этапе данной процедуры значения средней скорости будут приблизительно одинаковыми и определение физического понятия «средняя скорость» изменится на физическое понятие «мгновенная скорость»

υ→=limΔt→0υ ср→=limΔt→0Δr→Δt

Мгновенная скорость является векторной величиной:

вектор мгновенной скорости (далее — скорости) направлен по касательной к траектории в исследуемой точке (проверь, как на рисунке (1) «хорды — перемещения (Delta{vec{r_3}}), (Delta{vec{r_2}}) и (Delta{vec{r_1}})» при уменьшении промежутков времени (Delta{t_3}), (Delta{t_2}) и (Delta{t_1}) изображаются касательными, которые соответствуют векторам скоростей (vec{v_3}), (vec{v_2}), (vec{v_1})).

На рисунке (1) тело движется из точки (E) в точку (D), изменяя скорость от (v_2) до (v_3). Параллельным переносом перенесём вектор (vec{v_{3}}) к (vec{v_{2}}), тогда изменение скорости за промежуток времени (Delta{t}) равно разности векторов

((vec{v_{3}})(-)(vec{v_{2}})), что на рисунке (1) соответствует вектору ускорения (vec{a_{2}}).

Среднее ускорение равно отношению изменения скорости к промежутку времени:

Примечание:

1) в физических задачах при написании символа aср → индекс «ср», как правило, не прописывается;

2) в ситуации прямолинейного неравномерного движения используется термин «ускорение».

Характеристики физического понятия «среднее ускорение»:

направление вектора среднего ускорения определяется согласно правилу aср→↑↑Δυ→;
числовое значение ускорения (модуль, проекции на координатные оси) определяется согласно геометрическим правилам работы с векторами;
единица измерения ([(a_{ср})] (=) [(frac{м}{с^2})]).

Участки траектории (AB), (AD) и (AE) (рис. (1)) характеризуются, соответственно, средними ускорениями (vec{a_{3}}), (vec{a_{2}}), (vec{a_{1}}).


(vec{a_{3}}) (=) (frac{Delta{vec{v_3}}}{Delta{t_3}})	(vec{a_{2}}) (=) (frac{Delta{vec{v_2}}}{Delta{t_2}})	(vec{a_{1}}) (=) (frac{Delta{vec{v_1}}}{Delta{t_1}})

Если уменьшать неограниченно промежуток времени (Delta{t}), то изменение скорости движения тела в конкретный момент времени характеризуется физическим понятием «мгновенное ускорение».

Вектор мгновенного ускорения при движении тела по криволинейной траектории представляет векторную сумму компонентов данного вектора, которые направлены по касательной и нормали (перпендикуляр к касательной).

Векторное и скалярное уравнения скорости материальной точки

1) Общий вид:

векторное уравнение — (vec{v}) (=) (vec{v}(t));
числовые (скалярные) уравнения — (v_x) (=) (v_x(t)), (v_y) (=) (v_y(t)), (v_z) (=) (v_z(t)).

2) Прямолинейное равноускоренное движение:

векторное уравнение — (vec{v}(t)) (=) (vec{v}{_0}) (+) (vec{a}(t — t_0)),

где (vec{v}{_0}) — скорость тела в начальный момент времени ({t_0}), (vec{v}(t)) — скорость тела в произвольный момент

времени (t);

числовые (скалярные) уравнения — (v_x(t)) (=) (v_{0x}) (+) (a_x(t — t_0)), (v_y(t)) (=) (v_{0y}) (+) (a_y(t — t_0)),

(v_z(t)) (=) (v_{0z}) (+) (a_z(t — t_0)).

Графическое изображение зависимости проекции скорости от времени ({v_х}(t))

При движении тела с постоянным ускорением проекция скорости изменяется по линейному закону в зависимости от времени (t): (v_x(t)) (=) (v_{0x}) (+) (a_x(t — t_0)) (рис. (2)).

Рис. (2). График зависимости проекции скорости от времени

Значение проекции ускорения по графику определяется как тангенс угла: (a_x) (=) (tgα) (=) (frac{Delta{v}}{Delta{t}}).

Перемещение

Проекции перемещений при равнопеременном движении в момент времени (t) определяются формулами:

(s_x(t)=x(t) — x_0), (s_y(t)=y(t) -y_0), (s_z(t)=z(t) — z_0).

(A)

(B)

Рис. (3). Определение модуля и проекций перемещения по графику зависимости проекции скорости от времени

Модуль и проекции перемещения тела определяются графическим способом с

использованием графика зависимости (v_x(t)).

Рисунок (3) (A) ((v_0) (=) (0))

Рисунок (3) (B) ((v_0) (≠) (0))

Модуль перемещения определяется как площадь прямоугольного треугольника (ABC) с катетами

Модуль перемещения определяется как площадь трапеции (ABCD) с основаниями (d) (=) (v_0), (b) (=) (v_0+at) и высотой (h) (=) (t).

S=12b+dh⇒S=υ0⋅t+a⋅t22

Проекция перемещения: (s_x) (=) (S)

Примечание: если график проекции скорости состоит из участков, где площадь трапеции имеет отрицательное значение (например, (s_{x1}) (>) (0), (s_{x2}) (<) (0)), то модуль перемещения тела равен:

s=sx1+sx2

Источники:

Рис. 1. Перемещения тела при криволинейном движении. © ЯКласс.

Рис. 2. График зависимости проекции скорости от времени. © ЯКласс.

Рис. 3. Определение модуля и проекций перемещения по графику зависимости проекции скорости от времени. © ЯКласс.

Источник

Мгновенная скорость

4.3

Средняя оценка: 4.3

Всего получено оценок: 79.

4.3

Средняя оценка: 4.3

Всего получено оценок: 79.

Большинство движений в природе являются неравномерными. При описании таких движений большое значение имеет параметр «мгновенная скорость». Рассмотрим его подробнее.

Скорость при неравномерном движении

Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

$$v= {Sover t}$$

Рис. 1. Скорость равномерного прямолинейного движения.

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.

В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:

$$v={20over 2.02}=9.9(м/с)$$

Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.9м ниже.

Однако, проведя реальное измерение, можно убедиться, что это совсем не так. За первую секунду предмет пройдет только 4.9м. А за первые полсекунды – всего лишь 1.23м ! Если же высота падения будет больше, то за три секунды путь составит не 29.7м, как следует из формулы, а больше 40м !

Рис. 2. Стробоскопическое фото свободного падения.

Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.

Свести неравномерное движение к равномерному невозможно.

Мгновенная скорость

Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.

Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:

Время	Координата	Скорость
1.000	4.905	–
2.000	19.620	14.715
1.500	11.036	12.263
1.100	5.935	10.301
1.050	5.408	10.055
1.010	5.004	9.859
1.001	4.915	9.815

Можно видеть, что с уменьшением рассматриваемого отрезка времени, изменение вычисленной скорости между строками таблицы также становится меньше.

Приведенный пример показывает главный прием, который используется для изучения непрерывных величин – изучаемый диапазон разбивается на мелкие участки, на которых изменение скорости невелико, и движение мало отличается от непрерывного. В пределе время прохождения каждого такого участка стремится к нулю, а скорость на его протяжении постоянна.

Скорость материальной точки в данный момент времени при прохождении данного малого участка пути называется мгновенной скоростью.

Рис. 3. Мгновенная скорость.

Мгновенная скорость материальной точки равна отношению малого перемещения на пути движения к времени прохождению этого перемещения. Формула мгновенной скорости:

$$v={ΔSover Δt}, при Δt rightarrow 0$$

Если для моментов времени, приведенных выше, измерить точные значения мгновенной скорости падающего предмета, то получим следующую таблицу (с отличиями от предыдущей таблицы):

Время	Мгновенная скорость	Отличие,%
2.000	19.620	25.00
1.500	14.715	16.67
1.100	10.791	4.55
1.050	10.301	2.38
1.010	9.908	0.5
1.001	9.820	0.05

Можно видеть, что по мере уменьшения рассматриваемых отрезков времени отличия между первой и второй таблицей уменьшаются.

Что мы узнали?

Мгновенная скорость – это скорость прохождения данного малого участка пути за малый промежуток времени. В идеале мгновенная скорость определяется на текущем бесконечно малом промежутке времени, за который совершается бесконечно малое перемещение.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 79.

А какая ваша оценка?

Источник

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

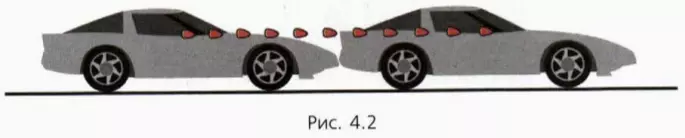
Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

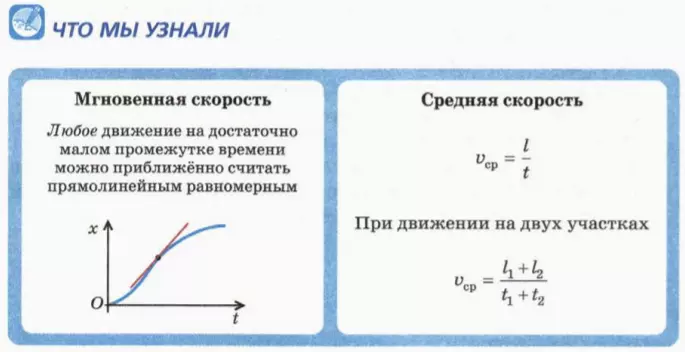
Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

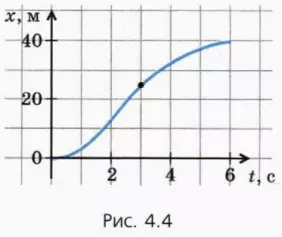
На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

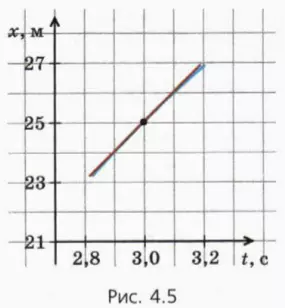
На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

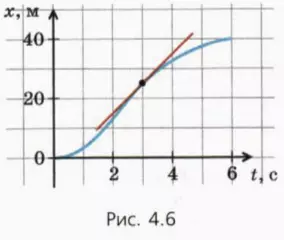
Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

v_ср = l/t. (1)

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

v_ср = (l₁ + l₂)/(t₁ + t₂), (2)

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

16. Тело движется вдоль оси x. Зависимость координаты тела от времени выражается формулой x = 0,2 * t².
а) Выберите удобный масштаб и изобразите график зависимости x(t) в течение первых 6 с.
б) С помощью этого графика найдите момент времени, в который мгновенная скорость тела была равна средней скорости за все время движения.

Источник