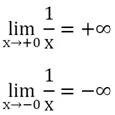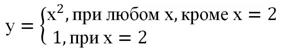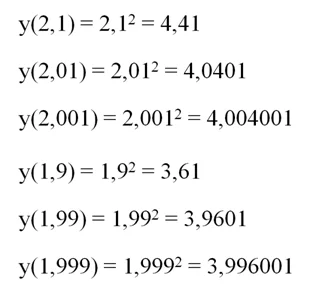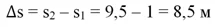Загрузить PDF
Загрузить PDF
Скорость — это быстрота перемещения объекта в заданном направлении. [1]
В общих целях нахождение скорости объекта (v) — простая задача: нужно разделить перемещение (s) в течение определенного времени (s) на это время (t), то есть воспользоваться формулой v = s/t. Однако таким способом получают среднюю скорость тела. Используя некоторые вычисления, можно найти скорость тела в любой точке пути. Такая скорость называется мгновенной скоростью и вычисляется по формуле v = (ds)/(dt), то есть представляет собой производную от формулы для вычисления средней скорости тела.[2]
-
1
Начните с уравнения. Для вычисления мгновенной скорости необходимо знать уравнение, описывающее перемещение тела (его позицию в определенный момент времени),[3]
то есть такое уравнение, на одной стороне которого находится s (перемещение тела), а на другой стороне — члены с переменной t (время).[4]
Например:s = -1.5t2 + 10t + 4
- В этом уравнении:
-
- Перемещение = s. Перемещение — пройденный объектом путь. Например, если тело переместилось на 10 м вперед и на 7 м назад, то общее перемещение тела равно 10 — 7 = 3 м (а на 10 + 7 = 17 м).
- Время = t. Обычно измеряется в секундах.
-
- В этом уравнении:
-
2
Вычислите производную уравнения. Чтобы найти мгновенную скорость тела, чьи перемещения описываются приведенным выше уравнением, нужно вычислить производную этого уравнения. Производная — это уравнение, позволяющее вычислить наклон графика в любой точке (в любой момент времени). Чтобы найти производную, продифференцируйте функцию следующим образом: если y = a*xn, то производная = a*n*xn-1. Это правило применяется к каждому члену многочлена.
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
s = -1.5t2 + 10t + 4
(2)-1.5t(2-1) + (1)10t1 — 1 + (0)4t0
-3t1 + 10t0
-3t + 10
- Другими словами, производная каждого члена с переменной t равна произведению множителя (стоящему перед переменной) и степени переменной, умноженному на переменную в степени, равную исходной степени минус 1. Свободный член (член без переменной, то есть число) исчезает, потому что умножается на 0. В нашем примере:
-
3
Замените «s» на «ds/dt», чтобы показать, что новое уравнение — это производная от исходного уравнения (то есть производная s от t). Производная — это наклон графика в определенной точке (в определенный момент времени). Например, чтобы найти наклон линии, описываемой функцией s = -1.5t2 + 10t + 4 при t = 5, просто подставьте 5 в уравнение производной.
- В нашем примере уравнение производной должно выглядеть следующим образом:
ds/dt = -3t + 10
- В нашем примере уравнение производной должно выглядеть следующим образом:
-
4
В уравнение производной подставьте соответствующее значение t, чтобы найти мгновенную скорость в определенный момент времени.[5]
Например, если вы хотите найти мгновенную скорость при t = 5, просто подставьте 5 (вместо t) в уравнение производной ds/dt = -3 + 10. Затем решите уравнение:ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 м/с- Обратите внимание на единицу измерения мгновенной скорости: м/с. Так как нам дано значение перемещения в метрах, а время — в секундах, и скорость равна отношению перемещения ко времени, то единица измерения м/с — правильная.
Реклама
-
1
Постройте график перемещения тела. В предыдущей главе вы вычисляли мгновенную скорость по формуле (уравнению производной, позволяющему найти наклон графика в определенной точке).[6]
Построив график перемещения тела, вы можете найти его наклон в любой точке, а следовательно определить мгновенную скорость в определенный момент времени.- По оси Y откладывайте перемещение, а по оси X — время. Координаты точек (x,у) получите через подстановку различных значений t в исходное уравнение перемещение и вычисления соответствующих значений s.
- График может опускаться ниже оси X. Если график перемещения тела опускается ниже оси X, то это значит, что тело движется в обратном направлении от точки начала движения. Как правило, график не распространяется за ось Y (отрицательные значения x) — мы не измеряем скорости объектов, движущихся назад во времени!
-
2
Выберите на графике (кривой) точку P и близкую к ней точку Q. Чтобы найти наклон графика в точке P, используем понятие предела. Предел — состояние, при котором величина секущей, проведенной через 2 точки P и Q, лежащих на кривой, стремится к нулю.
- Например, рассмотрим точки P(1,3) и Q(4,7) и вычислим мгновенную скорость в точке P.
-
3
Найдите наклон отрезка PQ. Наклон отрезка PQ равен отношению разницы значений координат «у» точек P и Q к разнице значений координат «х» точек P и Q. Другими словами, H = (yQ — yP)/(xQ — xP), где H — наклон отрезка PQ. В нашем примере наклон отрезка PQ равен:
H = (yQ — yP)/(xQ — xP)
H = (7 — 3)/(4 — 1)
H = (4)/(3) = 1.33 -
4
Повторите процесс несколько раз, приближая точку Q к точке P. Чем меньше расстояние между двумя точками, тем ближе значение наклона полученных отрезков к наклону графика в точке P. В нашем примере проделаем вычисления для точки Q с координатами (2,4.8), (1.5,3.95) и (1.25,3.49) (координаты точки P остаются прежними):
Q = (2,4.8): H = (4.8 — 3)/(2 — 1)
H = (1.8)/(1) = 1.8Q = (1.5,3.95): H = (3.95 — 3)/(1.5 — 1)
H = (.95)/(.5) = 1.9Q = (1.25,3.49): H = (3.49 — 3)/(1.25 — 1)
H = (.49)/(.25) = 1.96 -
5
Чем меньше расстояние между точками P и Q, тем ближе значение H к наклону графика в точке P При предельно малом расстоянии между точками P и Q, значение H будет равно наклону графика в точке P Так как мы не можем измерить или вычислить предельно малое расстояние между двумя точками, графический способ дает оценочное значение наклона графика в точке Р.
- В нашем примере при приближении Q к P мы получили следующие значения H: 1.8; 1.9 и 1.96. Так как эти числа стремятся к 2, то можно сказать, что наклон графика в точке P равен 2.
- Помните, что наклон графика в данной точке равен производной функции (по которой построен этот график) в этой точке. График отображает перемещение тела с течением времени и, как отмечалось в предыдущем разделе, мгновенная скорость тела равна производной от уравнения перемещения этого тела. Таким образом, можно заявить, что при t = 2 мгновенная скорость равна 2 м/с (это оценочное значение).
Реклама
-
1
Вычислите мгновенную скорость при t = 4, если перемещение тела описывается уравнением s = 5t3 — 3t2 + 2t + 9. Этот пример похож на задачу из первого раздела с той лишь разницей, что здесь дано уравнение третьего порядка (а не второго).
- Сначала вычислим производную этого уравнения:
s = 5t3 — 3t2 + 2t + 9
s = (3)5t(3 — 1) — (2)3t(2 — 1) + (1)2t(1 — 1) + (0)9t0 — 1
15t(2) — 6t(1) + 2t(0)
15t(2) — 6t + 2 - Теперь подставим в уравнение производной значение t = 4:
s = 15t(2) — 6t + 2
15(4)(2) — 6(4) + 2
15(16) — 6(4) + 2
240 — 24 + 2 = 22 м/с
- Сначала вычислим производную этого уравнения:
-
2
Оценим значение мгновенной скорости в точке с координатами (1,3) на графике функции s = 4t2 — t. В этом случае точка P имеет координаты (1,3) и необходимо найти несколько координат точки Q, лежащий близко к точке P. Затем вычислим H и найдем оценочные значения мгновенной скорости.
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
s = 4t2 — t
t = 2: s = 4(2)2 — (2)
4(4) — 2 = 16 — 2 = 14, so Q = (2,14)t = 1.5: s = 4(1.5)2 — (1.5)
4(2.25) — 1.5 = 9 — 1.5 = 7.5, so Q = (1.5,7.5)t = 1.1: s = 4(1.1)2 — (1.1)
4(1.21) — 1.1 = 4.84 — 1.1 = 3.74, so Q = (1.1,3.74)t = 1.01: s = 4(1.01)2 — (1.01)
4(1.0201) — 1.01 = 4.0804 — 1.01 = 3.0704, so Q = (1.01,3.0704) - Теперь вычислим H:
Q = (2,14): H = (14 — 3)/(2 — 1)
H = (11)/(1) = 11Q = (1.5,7.5): H = (7.5 — 3)/(1.5 — 1)
H = (4.5)/(.5) = 9Q = (1.1,3.74): H = (3.74 — 3)/(1.1 — 1)
H = (.74)/(.1) = 7.3Q = (1.01,3.0704): H = (3.0704 — 3)/(1.01 — 1)
H = (.0704)/(.01) = 7.04 - Так как полученные значения H стремятся к 7, то можно сказать, что мгновенная скорость тела в точке (1,3) равна 7 м/с (оценочное значение).
Реклама
- Сначала найдем координаты Q при t = 2, 1.5, 1.1 и 1.01.
Советы
- Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
- Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
- Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.
Реклама
Об этой статье
Эту страницу просматривали 83 536 раз.
Была ли эта статья полезной?
Download Article
Download Article
Velocity is defined as the speed of an object in a given direction.[1]
In many common situations, to find velocity, we use the equation v = s/t, where v equals velocity, s equals the total displacement from the object’s starting position, and t equals the time elapsed. However, this technically only gives the object’s average velocity over its path. Using calculus, it’s possible to calculate an object’s velocity at any moment along its path. This is called instantaneous velocity and it is defined by the equation v = (ds)/(dt), or, in other words, the derivative of the object’s average velocity equation.[2]
-
1
Start with an equation for velocity in terms of displacement. To get an object’s instantaneous velocity, first we have to have an equation that tells us its position (in terms of displacement) at a certain point in time. This means the equation must have the variable s on one side by itself and t on the other (but not necessarily by itself), like this:
s = -1.5t2 + 10t + 4
- In this equation, the variables are:
-
-
Displacement = s . The distance the object has traveled from its starting position.[3]
For example, if an object goes 10 meters forward and 7 meters backward, its total displacement is 10 — 7 = 3 meters (not 10 + 7 = 17 meters). - Time = t . Self explanatory. Typically measured in seconds.
-
Displacement = s . The distance the object has traveled from its starting position.[3]
-
- In this equation, the variables are:
-
2
Take the equation’s derivative. The derivative of an equation is just a different equation that tells you its slope at any given point in time. To find the derivative of your displacement formula, differentiate the function with this general rule for finding derivatives: If y = a*xn, Derivative = a*n*xn-1.This rule is applied to every term on the «t» side of the equation.[4]
- In other words, start by going through the «t» side of your equation from left to right. Every time you reach a «t», subtract 1 from the exponent and multiply the entire term by the original exponent. Any constant terms (terms which don’t contain «t») will disappear because they be multiplied by 0. This process isn’t actually as hard as it sounds — let’s derive the equation in the step above as an example:
s = -1.5t2 + 10t + 4
(2)-1.5t(2-1) + (1)10t1 — 1 + (0)4t0
-3t1 + 10t0
-3t + 10
Advertisement
- In other words, start by going through the «t» side of your equation from left to right. Every time you reach a «t», subtract 1 from the exponent and multiply the entire term by the original exponent. Any constant terms (terms which don’t contain «t») will disappear because they be multiplied by 0. This process isn’t actually as hard as it sounds — let’s derive the equation in the step above as an example:
-
3
Replace «s» with «ds/dt.» To show that our new equation is a derivative of the first one, we replace «s» with the notation «ds/dt». Technically, this notation means «the derivative of s with respect to t.» A simpler way to think of this is just that ds/dt is just the slope of any given point in the first equation. For example, to find the slope of the line made by s = -1.5t2 + 10t + 4 at t = 5, we would just plug «5» into t in its derivative.
- In our running example, our finished equation should now look like this:
ds/dt = -3t + 10
- In our running example, our finished equation should now look like this:
-
4
Plug in a t value for your new equation to find instantaneous velocity.[5]
Now that you have your derivative equation, finding the instantaneous velocity at any point in time is easy. All you need to do is pick a value for t and plug it into your derivative equation. For example, if we want to find the instantaneous velocity at t = 5, we would just substitute «5» for t in the derivative ds/dt = -3 + 10. Then, we’d just solve the equation like this:ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 meters/second- Note that we use the label «meters/second» above. Since we’re dealing with displacement in terms of meters and time in terms of seconds and velocity in general is just displacement over time, this label is appropriate.
Advertisement
-
1
Graph your object’s displacement over time. In the section above, we mentioned that derivatives are just formulas that let us find the slope at any point for the equation you take the derivative for.[6]
In fact, if you represent an object’s displacement with a line on a graph, the slope of the line at any given point is equal to the object’s instantaneous velocity at that point.[7]
- To graph an object’s displacement, use the x axis to represent time and the y axis to represent displacement. Then, just plot points by plugging values for t into your displacement equation, getting s values for your answers, and marking the t,s (x,y) points on the graph.
- Note that the graph can extend below the x axis. If the line representing your object’s motion drops below the x axis, this represents your object moving behind where it started. Generally, your graph won’t extend behind the y axis — we don’t often measure velocity for objects moving backward in time!
-
2
Choose one point P and a point Q that is near it on the line. To find a line’s slope at a single point P, we use a trick called «taking a limit.» Taking a limit involves taking two points (P, plus Q, a point near it) on the curved line and finding the slope of the line linking them over and over again as the distance between P and Q gets smaller.
- Let’s say that our displacement line contains the points (1,3) and (4,7). In this case, if we want to find the slope at (1,3), we can set (1,3) = P and (4,7) = Q.
-
3
Find the slope between P and Q. The slope between P and Q is the difference in y-values for P and Q over the difference in x-values for P and Q. In other words, H = (yQ — yP)/(xQ — xP), where H is the slope between the two points. In our example, the slope between P and Q is:
H = (yQ — yP)/(xQ — xP)
H = (7 — 3)/(4 — 1)
H = (4)/(3) = 1.33 -
4
Repeat several times, moving Q nearer to P. Your goal here is to make the distance between P and Q smaller and smaller until it gets close to a single point. The smaller the distance between P and Q gets, the closer the slope of your tiny line segments will be to the slope at point P. Let’s do this a few times for our example equation, using the points (2,4.8), (1.5,3.95), and (1.25,3.49) for Q and our original point of (1,3) for P:
Q = (2,4.8): H = (4.8 — 3)/(2 — 1)
H = (1.8)/(1) = 1.8Q = (1.5,3.95): H = (3.95 — 3)/(1.5 — 1)
H = (.95)/(.5) = 1.9Q = (1.25,3.49): H = (3.49 — 3)/(1.25 — 1)
H = (.49)/(.25) = 1.96 -
5
Estimate the slope for an infinitely small interval on the line. As Q gets closer and closer to P, H will get closer and closer to the slope at point P. Eventually, at an infinitely small interval, H will equal the slope at P. Because we aren’t able to measure or calculate an infinitely small interval, we just estimate the slope at P once it’s clear from the points we’ve tried.[8]
- In our example, as we moved Q closer to P, we got values of 1.8, 1.9, and 1.96 for H. Since these numbers appear to be approaching 2, we can say that 2 is a good estimate for the slope at P.
- Remember that the slope at a given point on a line is equal to the derivative of the line’s equation at that point. Since our line is showing our object’s displacement over time and, as we saw in the section above, an object’s instantaneous velocity is the derivative of its displacement at a given point, we can also say that 2 meters/second is a good estimate for the instantaneous velocity at t = 1.
Advertisement
-
1
Find the instantaneous velocity at t = 4 given the displacement equation s = 5t3 — 3t2 + 2t + 9. This is just like our example in the first section, except that we’re dealing with a cubic equation rather than a quadratic equation, so we can solve it in the same way.
- First, we’ll take our equation’s derivative:
s = 5t3 — 3t2 + 2t + 9
s = (3)5t(3 — 1) — (2)3t(2 — 1) + (1)2t(1 — 1) + (0)9t0 — 1
15t(2) — 6t(1) + 2t(0)
15t(2) — 6t + 2 - Then, we’ll plug in our value for t (4):
s = 15t(2) — 6t + 2
15(4)(2) — 6(4) + 2
15(16) — 6(4) + 2
240 — 24 + 2 = 218 meters/second
- First, we’ll take our equation’s derivative:
-
2
Use graphical estimation to find the instantaneous velocity at (1,3) for the displacement equation s = 4t2 — t. For this problem, we’ll use (1,3) as our P point, but we’ll have to find a few other points near it to use as our Q points. Then, it’s just a matter of finding our H values and making an estimation.
- First, let’s find Q points at t = 2, 1.5, 1.1 and 1.01.
s = 4t2 — t
t = 2: s = 4(2)2 — (2)
4(4) — 2 = 16 — 2 = 14, so Q = (2,14)t = 1.5: s = 4(1.5)2 — (1.5)
4(2.25) — 1.5 = 9 — 1.5 = 7.5, so Q = (1.5,7.5)t = 1.1: s = 4(1.1)2 — (1.1)
4(1.21) — 1.1 = 4.84 — 1.1 = 3.74, so Q = (1.1,3.74)t = 1.01: s = 4(1.01)2 — (1.01)
4(1.0201) — 1.01 = 4.0804 — 1.01 = 3.0704, so Q = (1.01,3.0704) - Next, let’s get our H values:
Q = (2,14): H = (14 — 3)/(2 — 1)
H = (11)/(1) = 11Q = (1.5,7.5): H = (7.5 — 3)/(1.5 — 1)
H = (4.5)/(.5) = 9Q = (1.1,3.74): H = (3.74 — 3)/(1.1 — 1)
H = (.74)/(.1) = 7.3Q = (1.01,3.0704): H = (3.0704 — 3)/(1.01 — 1)
H = (.0704)/(.01) = 7.04 - Since our H values seem to be getting very close to 7, we can say that 7 meters/second is a good estimate for the instantaneous velocity at (1,3).
- First, let’s find Q points at t = 2, 1.5, 1.1 and 1.01.
Advertisement
Add New Question
-
Question
What is the difference between instantaneous and average velocity?
Instantaneous is at that moment, whereas average is the mean of the entire time span.
-
Question
How do I calculate instantaneous acceleration?
Instantaneous acceleration can be considered as the value of the derivative of the instantaneous velocity. For example:
s = 5(t^3) — 3(t^2) + 2t + 9
v = 15(t^2) — 6t + 2
a = 30t — 6If we want to know the instantaneous acceleration at t = 4, then a(4) = 30 * 4 — 6 = 114 m/(s^2)
-
Question
When is instantaneous velocity and average velocity the same?
Instantaneous velocity tells you the velocity of an object at a single moment in time. If the object is moving with a constant velocity, then the average velocity and instantaneous velocity will be the same. In all situations, they are not likely to be the same.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
To find acceleration (the change in velocity over time), use the method in part one to get a derivative equation for your displacement function. Then, take another derivative, this time of your derivative equation. This will give you an equation for finding acceleration at a given time — all you have to do is plug in your value for time.
-
The equation which relates Y (displacement) to X (time) might be really simple, like, for instance, Y= 6x + 3. In this case the slope is constant and it is not necessary to find a derivative to find the slope, which is, following the Y = mx + b basic model for linear graphs, 6.
-
Displacement is like distance but it has a set direction, this makes displacement a vector and speed a scalar. Displacement can be negative while distance will only be positive.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate instantaneous velocity, start with an equation for velocity in terms of displacement, which should have an «s» on one side for displacement and a «t» on the other for time. Then, take the equation’s derivative and replace the «s» with the notation «ds» over «dt.» Finally, plug in a «t» value and solve the equation to find the instantaneous velocity at any point in time. To learn how to estimate instantaneous velocity graphically, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,051,346 times.
Did this article help you?
План урока:
Предел функции на бесконечности
Предел функции в точке
Приращение аргумента и функции
Средняя скорость изменения функции
Мгновенная скорость и понятие производной
Предел функции на бесконечности
Рассмотрим довольно простую функцию
y = 1/x
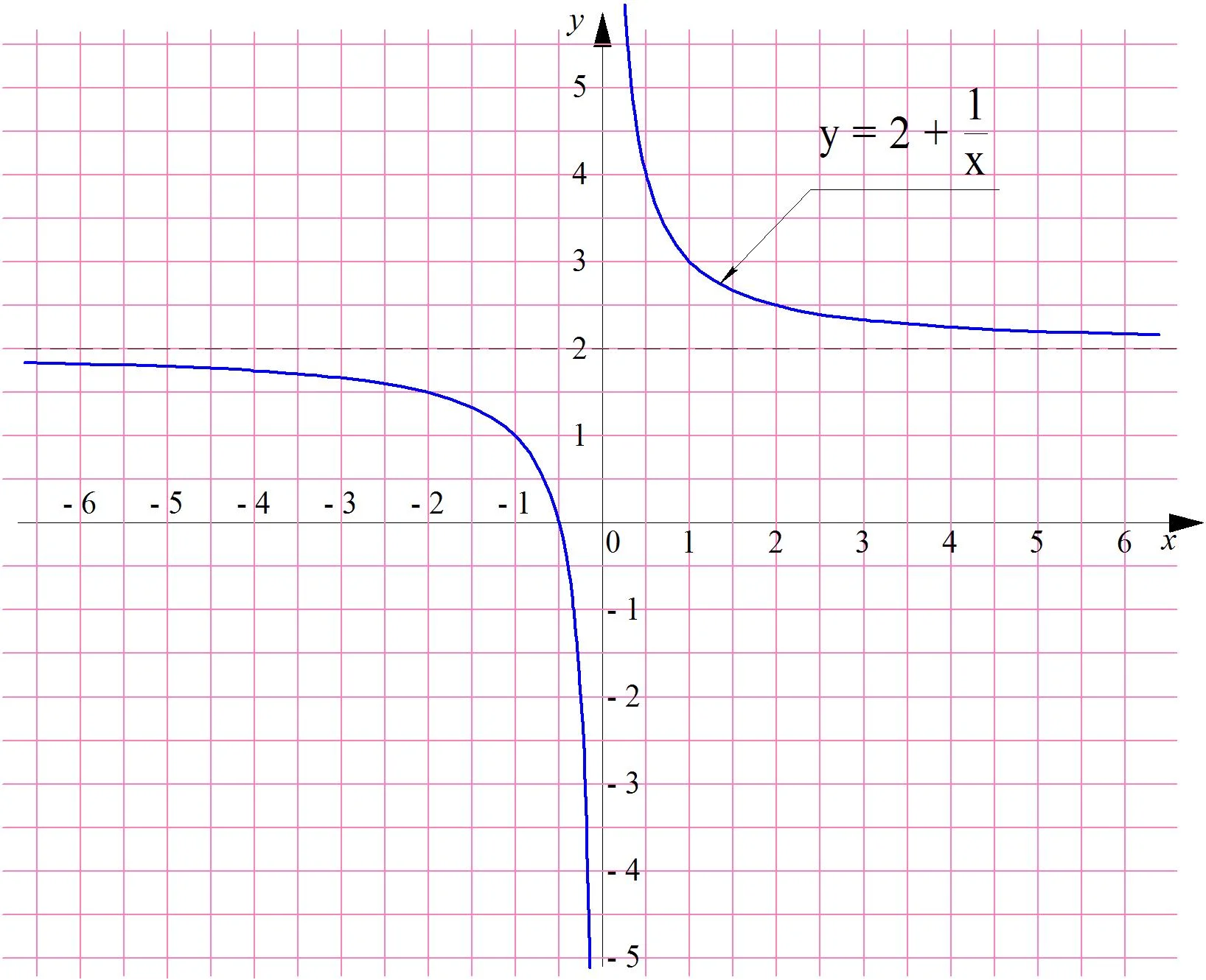
Её график называется гиперболой и выглядит так:
Можно заметить, что при больших положительных значениях х график функции приближается к горизонтальной оси Ох, но не пересекает её. Действительно, если мы будем вычислять значение у при всё больших значениях х, то будем получать всё меньшие, но всё же положительные числа:
Получается, что при бесконечном росте аргумента х функция стремится к нулю. Можно ли эту особенность функции как-то записать, используя математические символы? Оказывается, можно, и выглядит это запись так:
которая означает, что х стремится к бесконечности. После символа lim записана сама функция 1/х. В целом вся запись читается так: «предел функции у = 1/х при х, стремящемся к бесконечности, равен нулю».
Вернемся к графику функции у = 1/х. Видно, что если мы будем брать всё меньшие отрицательные значения х, то функция также будет стремится к нулю. Действительно, попробуем подставлять в нее как можно меньшие значения аргумента:
Чтобы записать эту особенность функции, используется следующая запись:
который может быть получен параллельным переносом графика у = 1/х на две единицы вверх:
Очевидно, что пределы этой функции при х → + ∞ и х → – ∞ равны 2:
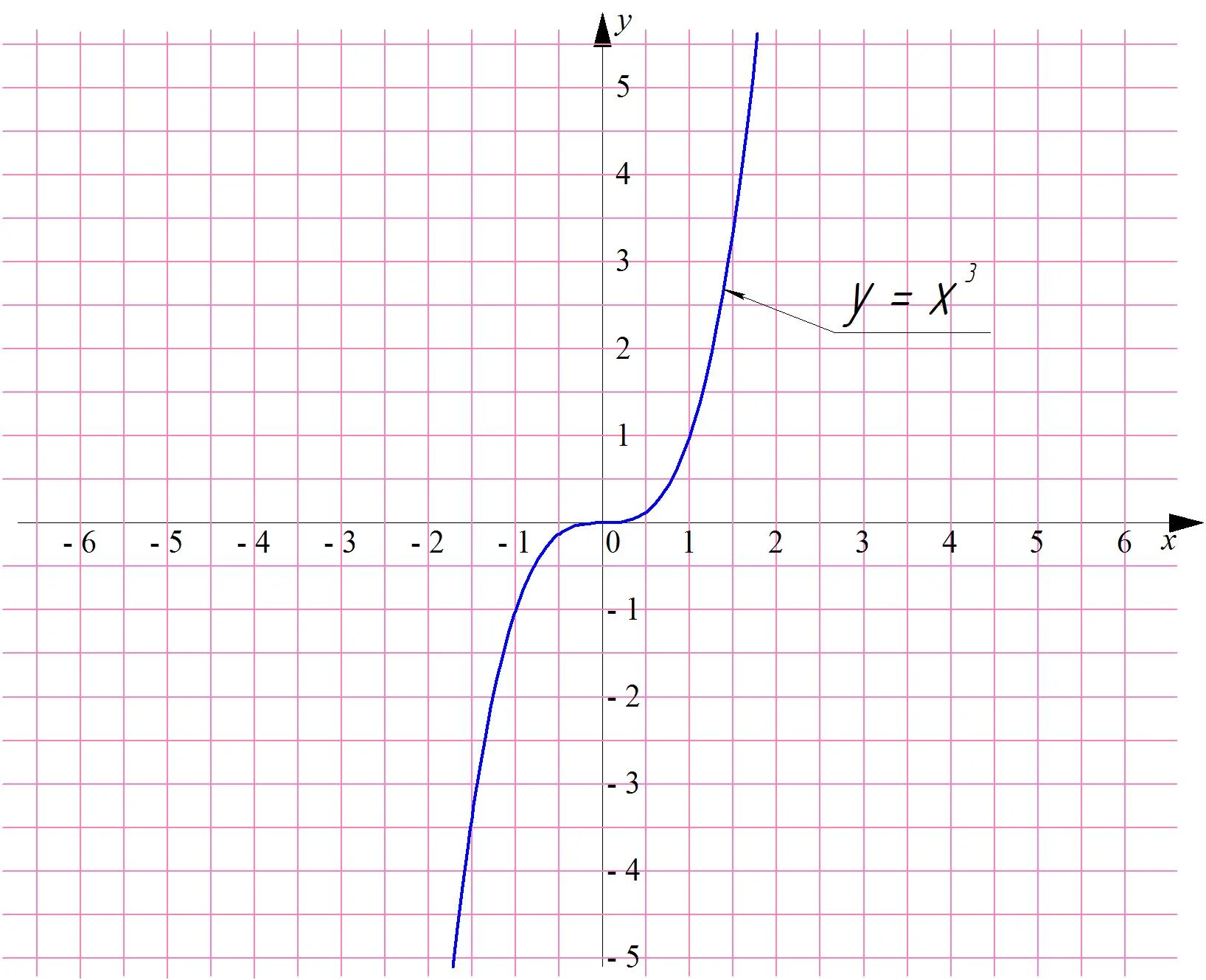
Возможны случаи, когда при бесконечном увеличении аргумента функции она не стремится к какому-то конкретному числу, а сама также неограниченно возрастает. Для примера посмотрим на график у = х3:
Видно, что при х → ∞ сама функция неограниченно растет, что можно показать расчетами:
Возникает вопрос – для всякой ли функции можно указать ее предел на бесконечности? Оказывается, что нет. Для примера рассмотрим тригонометрическую функцию у = sinx, графиком которой является синусоида:
С одной стороны, sinx явно не стремится к какому-то конкретному числу при увеличении х, он «колеблется» между числами 1 и (– 1). С другой стороны, нельзя и сказать, что он стремится к бесконечности. Получается, что у этой функции просто нет пределов на бесконечности.
Предел функции в точке
Порою нас интересует поведение функции не на бесконечности, а вблизи конкретной точки х0. Конечно, в большинстве случае можно просто вычислить функцию в этой точке, однако иногда это невозможно сделать. Для примера рассмотрим функцию
Очевидно, что точка х = 2 не входит в ее область определения, ведь при подстановке этого значения в функцию знаменатель дроби обратится в ноль. Однако в любой другой точке значение функции будет равняться единице:
График такой функции будет выглядеть как прямая у = 1, у которой есть одна «выколотая точка», соответствующая х = 2:
Итак, функция не определена в точке х = 2, однако можно вычислить предел функции в точке х = 2. Действительно, при любом, сколь угодно близком к 2 значении х функция будет равна единице:
Попробуем также приблизиться к точке 2 с другой стороны, подставляя в функцию числа, меньшие двух:
Снова всё время получается единица. Поэтому мы можем уверенно записать, что
Значительно чаще приходится иметь дело с пределами в точке, которые равны бесконечности. Снова посмотрим на график функции у = 1/х:
Видно, график не пересекает ось Оу, ведь число х = 0 не входит в область определения функции. Однако можно заметить, что при приближении х к нулю функция неограниченно возрастает:
Обратите внимание, что под пределом мы использовали запись «х → + 0», а не «х → 0». Почему? Дело в том, что если мы будем приближаться к нулю с «противоположной» стороны, подставляя в функцию не положительные, а отрицательные числа, то функция будет стремится к – ∞:
Получается, что предел функции в точке х = 0 зависит от того, с какой стороны мы приближаемся к этой точке, слева или справа. В связи с этим в математике существует понятие односторонних пределов. Для обозначения пределов, получаемых при приближении к нулю справа, то есть со стороны бОльших чисел, перед ним ставят знак плюс, а при указании предела слева, то есть со стороны мЕньших чисел – знак минус:
Предел и односторонние пределы – это два разных понятия. Считается, что функция имеет предел в точке только тогда, когда оба односторонних предела в этой точке совпадают.
В качестве ещё одного примера предела функции в точке можно привести зависимость у = tg х, график которой выглядит следующим образом:
В точке х = π/2 функция не определена. Однако видно, что при приближении к этой точке слева функция неограниченно возрастает, а при приближении справа – неограниченно убывает. Это записывается следующим образом:
До этого мы вычисляли пределы функций в точках, где сами функции не определены. Однако пределы можно вычислять и в тех точках, где функция определена. В большинстве случаев (но не всегда) они как раз равны значению функции в этой точке. Например, найдем предел
В точке х = 2 значение функции будет равно 4:
Будут ли односторонние пределы в этой точке также равняться 4? Сначала проверим предел справа
Действительно, получаем значения у, всё более близкие к 4. Аналогично можно убедиться, что и предел слева также равен 4:
Приведем несколько искусственный пример функции, у которой предел в точке не совпадает со значением функции в этой точке. Пусть функция задается с помощью такого графика
Он представляет собой параболу у = х2 с выколотой точкой (2; 4). При этом функция определена в точке х = 2, но имеет там значение, равное единице. Аналитически эту функцию можно описать так:
Понятно, что у(2) = 1, однако попытаемся приблизиться к точке х = 2 справа и слева и посмотрим, что получится:
Мы видим, что при х→2 функция и справа, и слева стремится к четверке, а не к единице. То есть получается, что предел функции в точке х = 2 не совпадает со значением функции этой функции в этой же точке. Такая ситуация произошла именно из-за того, что точка х = является выколотой.
Сразу заметим, что непосредственно в практических задачах пределы почти не используются. В связи с этим эта тема изучается в школьном курсе довольно поверхностно, не дается строгое определение предела функции (предполагается, что это понятие интуитивно понятно), а также не рассматриваются примеры на вычисление пределов функций. С другой стороны, на понятии предела построены почти все строгие рассуждения и доказательства в математическом анализе. В частности, определение понятие производной (которая имеет огромное практическое применение) дается именно с помощью предела. Поэтому полностью исключить пределы из школьного курса нельзя.
Приращение аргумента и функции
Часто нас интересует, как изменяется функция при изменении аргумента. Например, известно, что объем куба вычисляется по формуле
где а – ребро куба. Предположим, что мы провели измерения какого-то куба и выяснили, что длина его ребра равна 2 см. Тогда объем куба составит 23 = 8 см3. Но ведь любое измерение производится не с абсолютной точностью, а с некоторой погрешностью. Как оценить погрешность вычисления объема, если известна погрешность измерения его ребра?
Пусть с учетом погрешности линейки, составляющей 0,1 см, известно, что длина ребра находится в диапазоне от 2 до 2 + 0,1 = 2,1 см. Тогда максимально возможный объем куба составит 2,13 = 9,261 см3. Получается, что погрешность в измерении объема куба составляет 9,261 – 8 = 1,261 см3.
С точки зрения математического анализа мы в данном случае рассматривали поведение функции у = х3 в точке х = 2. Мы допустили некоторое изменение величины х, которое называют приращением аргумента и обозначают как ∆х. Далее мы высчитали, какое изменение величины у, или приращение функции, обозначаемое как ∆у, соответствует этому приращению аргумента. Выяснилось, что приращению ∆х = 0,1 соответствует приращение ∆у = 1,261.
В более общем случае произвольной функции у = f(x) можно дать некоторое приращение ∆х в некоторой точке х0. В результате этого изменится и само значение f(x), причем величину этого изменения обозначают как ∆у. Это можно проиллюстрировать графически:
Задание. Дана функция у = 3х2 + х + 4. Вычислите приращение функции в точке х0 = 5, если ∆х = 1.
Решение. Сначала вычислим новое значение аргумента функции, с учетом данного ему приращения:
Далее вычислим значения функции, соответствующие старому и новому аргументу:
Задание. Радиус круга, измеренный с погрешностью не более 0,5 см в меньшую сторону, равен 10 см. Оцените погрешность вычисления его площади.
Решение. Площадь круга рассчитывается по формуле:
Средняя скорость изменения функции
Часто в физике и других естественнонаучных дисциплинах одни величины характеризуют изменение других величин. Классический случай – это скорость, которая характеризует, насколько быстро изменилось положение тела (или материальной точки в пространстве). Рассмотрим пример. Пусть пешеход движется по прямой улице с постоянной скоростью 2 м/с. Попытаемся построить график, который иллюстрирует зависимость пройденного пешеходом пути и его скорости от времени. Известно, что при равномерном прямолинейном движении пройденный путь можно найти по формуле:
S = v*t
Где s – путь;
V – скорость;
t – время.
Так как скорость равна 2 м/с, то зависимость пути от времени будет выглядеть так:
s(t) = 2t
которая является прямой пропорциональностью. Поэтому ее график будет прямой линией:
Так как скорость во время всего движения остается равной 2 м/с, то зависимость скорости от времени будет иметь вид v = 2, а выглядеть она будет как горизонтальная линия:
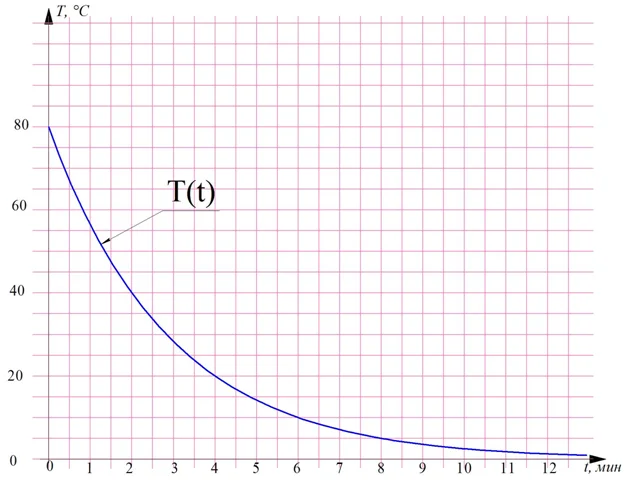
В данном случае найти зависимости s(t) и v(t) было очень легко. Но теперь усложним задачу. Пусть зависимость s(t) задается не прямой линией, а некоторой кривой:
Можно ли теперь что-то сказать о скорости движения пешехода?
Ясно, что в различные моменты времени скорость пешехода различна. Но мы можем найти среднюю скорость пешехода в какой-то момент времени. Например, рассмотрим промежуток времени со 2-ой по 10-ую секунду.
Его протяженность, очевидно, равна 10 – 2 = 8 секундам. Если первый момент времени обозначить как t1, а второй как t2, то протяженность этого промежутка времени (∆t) можно вычислить по формуле
Судя по графику, к моменту времени t1 пешеход прошел только 1 метр, а на момент t2он преодолел уже 9,5 м. Сколько же метров он прошел за промежуток времени ∆t? Если первое расстояние обозначить как s1, а второе как s2, то пройденное расстояние (∆s) можно рассчитать так:
Тогда средняя скорость на рассматриваемом участке можно вычислить, поделив ∆s на ∆t
В данной ситуации мы рассматривали функцию, которая задает зависимость между перемещением пешехода и временем. Средняя скорость характеризует, как быстро двигается пешеход, то есть как быстро функция s(t) меняет своё значение. Очевидно, что в данном случае величина ∆t – это некоторое приращение аргумента функции s(t), в то время как ∆s– это приращение самой функции. Получается, что с помощью приращений можно вычислять среднюю скорость объектов.
Однако в физике рассматривается не только скорость перемещения вточек пространстве. Например, можно говорить о скорости остывания горячего чайника. Пусть его температура меняется по закону, график которого представлен на рисунке:
Можно ли узнать, с какой средней скоростью остывал чайник на промежутках от 2-ой до 4-ой минуты? Да, для этого надо в точке t = 2 мин дать приращение аргумента ∆t = 2мин и посмотреть, какое приращение ∆T получит сама функция:
Пусть t1 = 2 мин, а t2 = 4 мин. Тогда
По графику видно, что в момент t1 температура чайника составляет Т1 = 40°С. Через две минуты она уже упала до отметки Т2 = 20°С. Получается, что за промежуток ∆t функция T(t) получила приращение
Обратите внимание, что приращение оказалось отрицательным. Дело в том, что температура чайника падала, то изменялась в меньшую сторону. Знак минус указывает именно на направление изменения функции. Если бы чайник нагревался, то приращение оказалось бы положительным.
Теперь мы можем вычислить среднюю скорость остывания чайника на промежутке между 2-ой и 4-ой минутой:
Знак минус указывает на то, что температура на этом промежутке времени уменьшается, а не возрастает.
В более общем случае, когда у нас есть произвольная функция у = f(x), с помощью приращений можно вычислить среднюю скорость её изменения на каком-нибудь промежутке. Пусть первая точка промежутка обозначается как х0, а его протяженность составляет ∆х. Тогда первой точке соответствует значение функции у(x0), а концу промежутка – значение у(x0 + ∆x):
Тогда средняя скорость изменения функции на промежутке [x0;x0 + ∆x] рассчитывается по формуле:
Мгновенная скорость и понятие производной
Итак, зная функцию, можно вычислить среднюю скорость ее изменения на любом промежутке. Но, когда автомобиль едет по шоссе, его спидометр показывает не среднее, а конкретное значение скорости в каждый момент времени. Другими словами, у автомобиля есть мгновенная скорость, и именно ее показывает спидометр. Как же узнать ее?
Пусть у нас есть функция s(t), определяющая пройденной машиной путь, и нам требуется найти мгновенную скорость в некоторый момент времени t1. Мы можем дать функции s(t) приращение ∆t, а потом найти и среднюю скорость на промежутке [t1; t1 + ∆t]. Естественно, она будет являться лишь некоторым приближением, с помощью которого мы оцениваем мгновенную скорость в момент t1. Однако далее мы можем уменьшить промежуток ∆t. Тогда у нас получится иное значение средней скорости, которое будет более близким к мгновенной скорости. Чем меньший промежуток ∆t мы возьмем, тем ближе к мгновенной скорости в точке t0 будет полученное нами значение средней скорости.
Например, пусть путь, пройденный машиной, задается функций s = t2. Нас интересует скорость автомобиля в момент t1 = 5 сек. Мы можем найти среднюю скорость на интервале от 5-ой до 6-ой секунды. Так, к пятой секунде машина успеет проехать 52 = 25 метров, а к шестой секунде она проедет 62 = 36 метров. Получится, что за промежуток ∆t, равный 6 – 5 = 1 секунде, машина проедет путь ∆s = 36 – 25 = 11 метров. Тогда средняя скорость на промежутке составит
Теперь возьмем более короткий промежуток ∆t, равный всего лишь 0,1 с. То есть мы рассмотрим период времени между моментом t1 = 5 cи t2 = 5,1 c. Снова-таки, к 5-ой секунде машина проедет 25 метров, а к моменту 5,1 сона пройдет 5,12 = 26,01 м. То есть за 0,1 с автомобиль преодолеет 26,01 – 25 – 1,01 м, а средняя скорость при этом составит
Ещё раз уменьшим промежуток ∆t. Пусть теперь он составляет всего 0,01с. Тогда средняя скорость будет определяться так:
Видно, что при уменьшении промежутка ∆t средняя скорость стремится к величине 10 м/с. Поэтому логично считать именно эту величину мгновенной скоростью машины в момент времени t = 5 c. Однако возникает вопрос – уверены ли мы, что мгновенная скорость стремится именно к 10 м/с, а не, скажем, к 10,001 м/с? Как точно определить это число? Здесь как раз помогают пределы. Можно записать, что мгновенная скорость – это предел отношения ∆s/∆t при ∆t, стремящемся к нулю. То есть
Получили, что мгновенная скорость в момент t1 = 5 действительно равна 10 м/с.
Задание. Вычислите мгновенную скорость разгоняющегося самолета через 10 секунд после начала разгона, если пройденное им расстояние задается законом s(t) = 5t2.
Решение. За 10 секунд самолет успеет преодолеть
Дадим функции s(t) приращение ∆t и обозначим как t1 момент времени, когда со старта прошло 10 секунд. Тогда к моменту t1 + ∆t самолет успеет пройти
Решая данную задачу, мы дали функции s(t) приращение ∆t и записали отношение ∆s/∆t. Далее мы устремили величину ∆t к нулю и посмотрели, к какому числу устремится отношение ∆s/∆t. Это число и оказалось мгновенной скоростью. В более общем случае произвольной функции у = f(x)в точке х0 можно дать приращение аргумента ∆х, которому будет соответствовать некоторое приращение функции ∆у. Далее можно вычислить предел отношения ∆у/∆х, который будет характеризовать, как быстро в точке х0 функция меняет свое значение. Этот предел называют производной функции в точке х0. Для обозначения производной над функцией ставят штрих.
В общем случае алгоритм вычисления производной в некоторой точке следующий:
1.Фиксируем точку х0, вычисляем для нее значение функции у(х). Это значение будет конкретным числом
- Даем функции приращение аргумента ∆х, переходим в новую точку х0 + ∆х, вычисляем в ней значение функции у(х0 + ∆х). Это значение будет не числом, а выражением, содержащим переменную ∆х.
- Находим приращение функции ∆у, используя формулу
Это приращение также должно содержать величину ∆х.
- Составляем соотношение ∆у/∆х.
- Находим предел этого отношения при ∆х→0. Этот предел и есть значение производной.
Задание. Найдите производную функции у = 4х2 + 7х в точке х0 = 2.
Решение. Сначала вычислим значение функции в точке х0:
Далее определяем величину у(х0 + ∆х) (это будет не конкретное число, а некоторое выражение, содержащее переменную ∆х):
Задание. Найдите производную функции у = 1/х в точке х0 = 5.
Решение. Высчитаем у(х0):
Пусть у функции есть приращение ∆х, тогда в точке х0 + ∆х ее значение составит:
В рассмотренных примерах для вычисления производной мы использовали ее определение. Однако на практике такой метод почти не используется. В будущем мы узнаем более эффективные способы для нахождения производной.
Мы уже убедились, что использование производной помогает находить мгновенную скорость тел. По этой причине понятие производной функции играет огромную роль в механике (разделе физике, изучающем движение). Однако этим ее практическое применение не ограничивается. По сути, она является основой для всей классической физики, и именно ее появление в XVII в. обеспечило выдающийся прогресс в науке вплоть до конца XIX в. При этом производная используется и в геометрии для анализа графиков функций. Более подробно ее применение будет также рассмотрено позже.
Определение
Скорость — это термин, который характеризует изменение заданной координаты в движении.
В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.
Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого в конкретную единицу времени, и направлена совместно я с векторным перемещением.
Средняя скорость – довольно простое понятие в разделе кинематика.
Определение
Следовательно, средняя скорость – это конкретная величина, которая равна отношению пройденного пути, к величине времени, за которое данный путь пройден телом.
[v_{mathrm{cp}}=frac{S}{t}]
Основные моменты, на которые следует уделить внимание при определении средней скорости:
- Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
- Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.
Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.
Определение
Мгновенная скорость — это некий числовой предел, к которому стремится показатель средней скорости.
Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.
Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.
Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.
Формула
Мгновение скорости можно определить по следующей формуле: v=s/Δt
где:
v – скорость мгновения, м/с
s – движение, перемещение тела, м ( если Δt→0 )
Δt – временной интервал, который стремится к нулевому значению, с.
Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.
Временной интервал движения тела – это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение, всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.
Нет времени решать самому?
Наши эксперты помогут!
Направление и перемещение действия средней и мгновенной скорости относительно координатной оси
Средняя скорость всегда направлена вместе с перемещением:
Для мгновенной скорости характерно движение в конкретный момент времени.
Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.
Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.
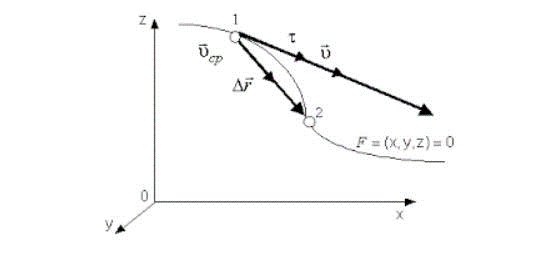
Примеры решения задач по определению мгновенной и средней скорости
Пример №1:
Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.
Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:
- Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
- Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
- Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
- Расстояние и скорость имеют одинаковые значения по модулю и, следовательно, равны 5 м/с.
[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]
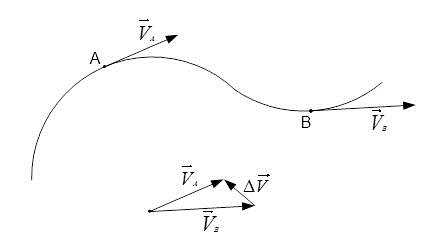
Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.
В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.
Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.
Пример №2:
Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.
Алгоритм решения:
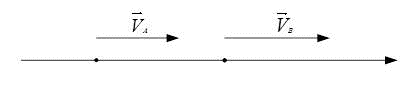
Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:
- в точке А и в точке В направление движения мгновенной скорости одинаково;
- рассматриваемое тело, которое осуществляет движение, делает это с равным ускорением, следовательно:
[vec{V}_{A}=vec{V}_{B}]
Содержание материала
- Советы
- Видео
- Что такое мгновенная скорость на реальных примерах
- Как найти мгновенную скорость из средней скорости
- Мгновенная скорость при криволинейном движении
- Ускорение. Касательное ускорение. Центростремительное ускорение
- Об особенностях понятия мгновенной скорости
- Что мы узнали?
Советы
- Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
- Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
- Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.
Видео
Что такое мгновенная скорость на реальных примерах
Реальные примеры мгновенной скорости
Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; в это время полное смещение и средняя скорость будут равны нулю. В таких случаях движение рассчитывается по формуле мгновенная скорость.
Как найти мгновенную скорость из средней скорости
Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.
Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить Vinst.
Мгновенная скорость при криволинейном движении
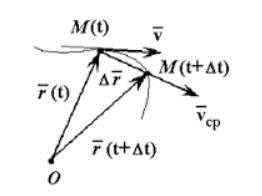
Положение материальной точки на траектории зададим радиус-вектором $overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:
скорость — это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.
Единицы измерения ускорения:

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Об особенностях понятия мгновенной скорости
Для того чтобы вычислить мгновенную скорость на практике, следует понимать, что она представляет собой функцию времени. Следует определить на какое расстояние переместился объект в течение крайне малого промежутка времени, который называют моментом времени. Насколько же мал этот допустимый интервал? Если рассматривать совершенные приборы, например радиолокационные станции, то даже самые точные из них позволяют отслеживать скорость за время, которое примерно составляет около 10-6 с. Согласитесь, что несмотря на ничтожную малость этого значения, оно ни в коей мере не является моментом времени, а представляет собой временной промежуток. По этой причине отношение физиков к понятию скорости в определенный момент времени неоднозначное, и оно считается не наделенным конкретным физическим смыслом. Хотя на практике термин «мгновенная скорость» широко используется при управлении навигацией в авиации и космонавтике.
Подобным образом можно рассуждать и о мгновенном ускорении, которое представляет собой зависимость, а точнее производную от скорости и имеет с ней одно направление.
Что касается мгновенной скорости физического тела, находящегося в состоянии покоя относительно выбранной системы отсчета, то она будет равняться нулю.
Что мы узнали?
Мгновенная скорость – это скорость прохождения данного малого участка пути за малый промежуток времени. В идеале мгновенная скорость определяется на текущем бесконечно малом промежутке времени, за который совершается бесконечно малое перемещение.