Как найти мгновенную скорость материальной точки

Была ли эта статья полезной?

Mодуль средней скорости по пути равен: $leftlangle vrightrangle =frac{S}{triangle t}$

Мгновенная скорость дает точную информацию о движении в определенный момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.

Мгновенная скорость (или просто скорость) есть предел, к которому стремится средняя скорость $leftlangle vrightrangle $ при стремлении промежутка времени $triangle t$ к нулю:

$v={mathop{lim}_{triangle t} frac{triangle r}{triangle t} }=frac{dr}{dt}=dot{r}$ (1)

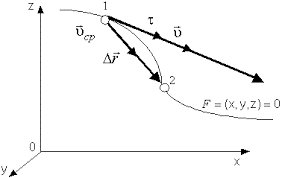
Вектор $v$ направлен по касательной к криволинейной траектории, так как бесконечно малое (элементарное) перемещение dr совпадает с бесконечно малым элементом траектории ds.

Рисунок 2. Вектор мгновенной скорости $v$

В декартовых координатах уравнение (1) эквивалентно трем уравнениям

$left{ begin{array}{c}
v_x=frac{dx}{dt}=dot{x} \
v_y=frac{dy}{dt}=dot{y} \
v_z=frac{dz}{dt}=dot{z} end{array}
right.$ (2)

Модуль вектора $v$ в этом случае равен:

$v=left|vright|=sqrt{v^2_x+v^2_y+v^2_z}=sqrt{x^2+y^2+z^2}$ (3)

Переход от декартовых прямоугольных координат к криволинейным осуществляется по правилам дифференцирования сложных функций. Пусть радиус-вектор r есть функция криволинейных координат: $r=rleft(q_1,q_2,q_3right) $. Тогда скорость $v=frac{dr}{dt}=sum^3_{i=1}{frac{partial r}{partial q_i}frac{partial q_i}{partial t}}=sum^3_{i=1}{frac{partial r}{partial q_i}}dot{q_i}$

Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат

В сферических координатах, полагая $q_1=r; q_2=varphi ; q_3=theta $, получаем представление $v$ в следующий форме:

$v=v_re_r+v_{varphi }e_{varphi }+v_{theta }e_{theta }$, где $v_r=dot{r}; v_{varphi }=rdot{varphi }sintheta ;; v_{theta }=rdot{theta } ;;$

[dot{r}=frac{dr}{dt};; dot{varphi }=frac{dvarphi }{dt};; dot{theta }=frac{dtheta }{dt}; v=rsqrt{1+{varphi }^2sin^2theta +{theta }^2}]

Мгновенная скорость — это значение производной от функции перемещения по времени в заданный момент времени, и связана с элементарным перемещением следующим соотношением: $dr=vleft(tright)dt$

План урока:

Закон сложения скоростей

Мгновенная скорость, направление мгновенной скорости

Ускорение. Касательное ускорение. Центростремительное ускорение

Равноускоренное движение

Свободное падение

Равномерное движение точки по окружности

Закон сложения скоростей

Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью    относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена  (см. рисунок 1).

Рисунок 1 – Первоначальная скорость пчелы и ветра

Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):

Рисунок 2 – Изменившаяся скорость пчелы

Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v₂ системе отсчета.

Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.

Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.

То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.

Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt₁, Δt₂,…Δt_n,  и найти средние скорости за эти отрезки времени:

А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δt_b направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.

Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.

Ускорение. Касательное ускорение. Центростремительное ускорение

Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить  на маленькие отрезки времени и рассматривать ускорение на каждом из них.

Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2

Равноускоренное движение

Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении

Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:

Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.

При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:

v = v₀ + a * t

Если же ускорение противонаправлено начальной скорости, это выражение станет таким:

v = v₀ — a * t

Рассмотрим график зависимости скорости от времени при равноускоренном движении (см. рисунок 8). Считаем, что тело совершает движение вдоль оси ОХ, а все величины – начальная скорость (v_ox) , ускорение (a_x)  – взяты в проекции на эту ось.

Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении

Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.

Свободное падение

Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение

Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.

• Свободное падение

Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).

Рисунок 9 – Свободное падение тела

Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:

• Движение тела, брошенного вертикально вверх

Представим, что тело подкинули вертикально наверх с начальной скоростью v₀ (см. рисунок 10).

Рисунок 10 – Тело бросили вертикально вверх

Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v₀ (вообще нужно было бы писать v_oy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).

Отсюда можно найти полное время полета:

• Движение тела, брошенного под углом к горизонту

Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью  под углом α к горизонту.

Рисунок 11 – Тело брошено под углом к горизонту

Уравнения движения в общем виде по двум осям выглядят так:

Еще время полета можно посчитать, учитывая что  в двух моментах – в начале полета и в конце. Значит можно посчитать:

Равномерное движение точки по окружности

Центростремительное ускорение

Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).

Рисунок 12 – Изменение направления скорости при равномерном движении по окружности

За изменение направления скорости отвечает центростремительное ускорение (  Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:

где R – радиус окружности, по которой циклически движется тело.

В прошлой статье мы немножко разобрались с тем, что такое механика  и зачем она нужна. Мы уже знаем, что такое система отсчета,  относительность движения и материальная точка. Что ж, пора двигаться дальше!  Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики  и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной  от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь  — x нулевое- начальная координата. v нулевое — начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.