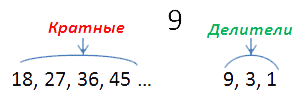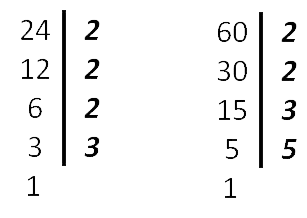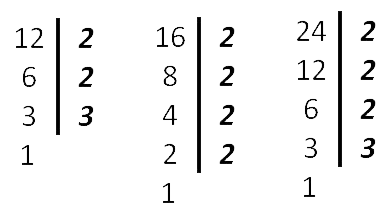Как найти минимальное число кратное двум числам - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.

1
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.
2
Запишите ряд чисел, которые кратны первому числу. Кратное число – это число, которое делится на данное число без остатка.^[1] Кратные числа можно посмотреть в таблице умножения..
- Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.
3
Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.
- Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.
4
Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.^[2]
- Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.
Реклама

1
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.
2

Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.
3

Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.
4

Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).
5

К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.^[3]
6
Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.
- Например, . Таким образом, наименьшее общее кратное 20 и 84 равно 420.
Реклама

1
Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.^[4]
- Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.
2
Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.
3

Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.
4
Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.
- Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.
5

Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.
6

Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.
7
Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.^[5]
- Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: .
8
Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.^[6]
- Например, . Таким образом, наименьшее общее кратное 18 и 30 равно 90.
Реклама

1
Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят. Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.^[7]
- Например, в выражении ост. 3:
  15 – это делимое
  6 – это делитель
  2 – это частное
  3 – это остаток.
2
Запишите выражение, которое описывает операцию деления с остатком. Выражение: .^[8] Это выражение будет использовано, чтобы записать алгоритм Евклида и найти наибольший общий делитель двух чисел.
- Например, .
- Наибольший общий делитель (НОД) – это наибольшее число, на которое делятся все данные числа.^[9]
- В этом методе сначала нужно найти наибольший общий делитель, а затем вычислить наименьшее общее кратное.
3
Большее из двух чисел рассматривайте в качестве делимого. Меньшее из двух чисел считайте делителем. Для этих чисел запишите выражение, которое описывает операцию деления с остатком.
- Например, найдите наименьшее общее кратное чисел 210 и 45. Запишите такое выражение: .
4
Первый делитель превратите в новое делимое. Остаток используйте в качестве нового делителя. Для этих чисел запишите выражение, которое описывает операцию деления с остатком.
- Например, .
5
Повторяйте описанные действия до тех пор, пока остаток не будет равен 0. Предыдущий делитель используйте в качестве нового делимого, а предыдущий остаток – как новый делитель; для этих чисел записывайте соответствующее выражение.^[10]
- Например, . Так как остаток равен 0, дальше делить нельзя.
6
Посмотрите на последний делитель. Это наибольший общий делитель двух чисел.^[11]
- Например, последним выражением было , поэтому последний делитель – это число 15. Таким образом, 15 – это наибольший общий делитель чисел 210 и 45.
7

Перемножьте два числа. Затем разделите произведение на наибольший общий делитель. Так вы вычислите наименьшее общее кратное двух чисел.^[12][[[Image:Find the Least Common Multiple of Two Numbers Step 25.jpg|center]]

Реклама

Советы

Если нужно найти НОК трех и более чисел, упросите себе задачу. Например, чтобы вычислить НОК чисел 16, 20 и 32, сначала найдите наименьшее общее кратное чисел 16 и 20 (оно равно 80), а потом найдите НОК чисел 80 и 32, которое равно 160.
НОК имеет множество применений. Например, чтобы сложить или вычесть дроби, они должны иметь одинаковый знаменатель. Если у дробей разные знаменатели, нужно преобразовать дроби так, чтобы привести их к общему знаменателю. А это проще сделать, если найти наименьший общий знаменатель, который равен наименьшему общему кратному чисел, которые находятся в знаменателях дробей.

Об этой статье

Эту страницу просматривали 69 224 раза.

Была ли эта статья полезной?

Источник

Download Article

A multiple is the result of multiplying a number by an integer. The least common multiple (LCM) of a group of numbers is the smallest number that is a multiple of all the numbers. To find the least common multiple you need to be able to identify the factors of the numbers you are working with. You can use a few different methods to find the least common multiple. These methods also work when finding the LCM of more than two numbers.

1
Assess your numbers. This method works best when you are working with two numbers that are less than 10. If you are working with larger numbers, it’s best to use a different method.
- For example, you might need to find the least common multiple of 5 and 8. Since these are small numbers, it is appropriate to use this method.
2
Write out the first several multiples of the first number. A multiple is a product of any number and an integer.^[1] In other words, they are the numbers you would see in a multiplication table.
- For example, the first several multiples of 5 are 5, 10, 15, 20, 25, 30, 35, and 40.
Advertisement
3
Write out the first several multiples of the second number. Do this near the first set of multiples, so that they are easy to compare.
- For example, the first several multiples of 8 are 8, 16, 24, 32, 40, 48, 56, and 64.
4
Find the smallest multiple the numbers have in common. You might need to extend your list of multiples until you find one both numbers share. This number will be your least common multiple.^[2]
- For example, the lowest multiple 5 and 8 share is 40, so the least common multiple of 5 and 8 is 40.

1
Assess your numbers. This method works best when both of the numbers you are working with are greater than 10. If you have smaller numbers, you can use a different method to find the least common multiple more quickly.
- For example, if you need to find the least common multiple of 20 and 84, you should use this method.
2

Factor the first number. You want to factor the number into its prime factors; that is, find the prime factors you can multiply together to get this number. One way to do this is by creating a factor tree. Once you are done factoring, rewrite the prime factors as an equation.^[3]
3

Factor the second number. Do this in the same way you factored the first number, finding the prime factors you can multiply together to get the number.
4

Write down the factors each number shares. Write the factors as a multiplication sentence. As you write each factor, cross it off in each numbers factorization equation.^[4]
5

Add any leftover factors to the multiplication sentence. These are the factors you did not cross out when comparing the two groups of factors. Thus, these are factors that the two numbers do not share.^[5]
6
Calculate the least common multiple. To do this, multiply together all of the factors in your multiplication sentence.^[6]
- For example, . So, the least common multiple of 20 and 84 is 420.

1
Draw a tic-tac-toe grid. A tic-tac-toe grid is two sets of parallel lines that intersect each other perpendicularly. The lines form three rows and three columns and looks like the pound key (#) on a phone or keyboard. Write your first number in the top-center square of the grid. Write your second number in the top-right square of the grid.^[7]
- For example, if you are trying to find the least common multiple of 18 and 30, write 18 in the top center of your grid, and 30 in the top right of your grid.
2
Look for a factor that is common to both numbers. Write this number in the top-left square of your grid. It is helpful to use prime factors, but you don’t necessarily have to.
- For example, since 18 and 30 are both even numbers, you know that that they both have a factor of 2. So write 2 in the top-left of the grid.
3

Divide the factor into each number. Write the quotient in the square below either number. A quotient is the answer to a division problem.^[8]
4
Find a factor that is common to the two quotients. If there is no factor common to both quotients, you can skip this and the next step. If there is a common factor, write it in the middle-left square of the grid.^[9]
- For example, 9 and 15 both have a factor of 3, so you would write 3 in the middle-left of the grid.
5

Divide this new factor into each quotient. Write this new quotient below the first ones.
6

Extend your grid if necessary. Follow this same process until you reach a point where the last set of quotients have no common factor.
7
Draw a circle around the numbers in the first column and last row of your grid. You can think of it as drawing an “L” for “least common multiple.” Write a multiplication sentence using all of these factors.^[10]
- For example, since 2 and 3 are in the first column of the grid, and 3 and 5 are in the last row of the grid, you would write the sentence .
8
Complete the multiplication. When you multiply all of these factors together, the result is the least common multiple of your two original numbers.^[11]
- For example, . So, the least common multiple of 18 and 30 is 90.

1
Understand the vocabulary of division. The dividend is the number being divided. The divisor is the number the dividend is being divided by. The quotient is the answer to the division problem. The remainder is the amount left over after a number is divided by another.^[12]
- For example, in the equation :
  15 is the dividend
  6 is the divisor
  2 is the quotient
  3 is the remainder.
2
Set up the formula for the quotient-remainder form. The formula is .^[13] You will use this form to set up Euclid’s algorithm to find the greatest common divisor of two numbers.
- For example, .
- The greatest common divisor is the largest divisor, or factor, that two numbers share.^[14]
- In this method, you first find the greatest common divisor, and then use it to find the least common multiple.
3
Use the larger of the two numbers as the dividend. Use the smaller of the two numbers as the divisor. Set up an equation in quotient-remainder form for these two numbers.
- For example, if you are trying to find the least common multiple of 210 and 45, you would calculate .
4
Use the original divisor as the new dividend. Use the remainder as the new divisor. Set up an equation in quotient-remainder form for these two numbers.
- For example, .
5
Repeat this process until you have a remainder of 0. For each new equation, use the previous equation’s divisor as the new dividend, and the previous remainder as the new divisor.^[15]
- For example, . Since the remainder is 0, you do not need to divide any further.
6
Look at the last divisor you used. This is the greatest common divisor for the two numbers.^[16]
- For example, since the last equation was , the last divisor was 15, and so 15 is the greatest common divisor of 210 and 45.
7

Multiply the two numbers. Divide the product by the greatest common divisor. This will give you the least common multiple of the two numbers.^[17]

Add New Question

Question

What’s the formula of the least common multiple?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

The formula is lcm(a, b) = a × b / gcd(a, b), where a and b are the numbers for which you want to find the LCM, and GCD is the greatest common divisor.
Question

Is there a least common multiple calculator?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

Yes, there are multiple LCM calculators online. Try websites like CalculatorSoup.com or Calculator.net to find calculators for finding the LCM and doing a variety of other common calculations.
Question

What’s the fastest way to find the least common multiple of two numbers?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

One quick and easy way to do it is to start by finding the greatest common factor (GCF) of the 2 numbers. Divide the GCF into either one of the 2 numbers, then multiply the result by the other number. This will give you the LCM.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

If you need to find the LCM of more than two numbers, the above methods can be tweaked. For instance, to find the LCM of 16, 20, and 32, you could start by finding the LCM of 16 and 20 (which is 80), and then find the LCM of 80 and 32, which turns out to be 160.
The LCM has many uses. The most common is that, whenever you add or subtract fractions, they must have the same denominator; if they do not, you need to convert each fraction to some equivalent fraction so they will share the same denominator. The best way to do that is to find the lowest common denominator (LCD) — which is just the LCM of the denominators.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To find the least common multiples of two numbers, start by writing out the first several multiples for each number. For example, the first several multiples of 5 would be 5, 10, 15, 20, 25, 30, 35, and 40. Once you’ve written out the first several multiples for both numbers, find the smallest multiple that they have in common, which is the least common multiple. If they don’t have a common multiple, keep listing the multiples for each number until you find one. If you want to know how to use prime factorization or an algorithm to find the least common multiple, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,235,502 times.

Did this article help you?

Источник

Наименьшее о́бщее кратное (HOK) двух целых чисел — это наименьшее натуральное число, которое делится на оба без остатка, то есть кратно им обоим. К примеру, для чисел 6 и 4, наименьшим общим кратным будет 12.

Как найти НОК?

Способов найти НОК несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОК при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

разложить оба числа на простые множители;
выбрать одну группу множителей;
добавить к ним множители из второй группы, которые отсутствуют в выбранной;
найти их произведение.

Примеры нахождения наименьшего общего кратного

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОК 4 и 6

1. Раскладываем 6 и 4 на простые множители:

2. Возьмем первую группу множителей: 2 · 3.

3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2

4. Вычисляем произведение: 2 · 3 · 2 = 12.

Ответ: НОК (6; 4) = 12

Пример 2: найти НОК 32 и 20

1. Раскладываем 32 и 20 на простые множители:

2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.

3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2

4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.

Ответ: НОК (32; 20) = 160

Источник

Наименьшее общее кратное двух и более чисел (НОК) — это самое маленькое целое число, которое делится нацело на любое из этих чисел.

К примеру, узнаем наименьшее общее кратное чисел 6 и 9.

Числа, кратные 6-ти: 6, 12, 18, 24 …
Числа, кратные 9-ти: 9, 18, 27…

Самое меньшее число, которое в этих разложениях совпадает — это 18.

НОК(6;9) = 18

Как найти наименьшее общее кратное (НОК:

Чтобы найти НОК, сначала нужно разложить данные вам числа на простые множители, как и при нахождении НОД.

Пример 1. Найдем НОК(6;9).

6 = 2 · 3
9 = 3 · 3

Затем выписываем простые множители из первого разложения 2 · 3 и добавляем к ним недостающие из второго разложения.
Во втором разложении две тройки. Одна тройка у нас уже записана. Осталась еще одна, выписываем ее: 3.
Записываем наименьший общий делитель, перемножив выписанные числа.

НОК(6;9) = 2 · 3 · 3 = 18

Как себя проверить?
НОК(6;9) получился равным 18. 18 делится и на 6, и на 9 без остатка.
А если бы мы выписали множители 2 · 3 · 3 · 3 и получили бы НОК = 54?
54 тоже делится на 6 и 9 без остатка, но он больше, чем 18, а значит правильный ответ — 18.

Пример 2. Найдите НОК(а;b), если а = 3 · 5 · 11, b = 3 · 5 · 2

Наши числа уже разложены на простые множители, осталось лишь выписать те, которые участвуют в нахождении НОК.

а = 3 · 5 · 11
b = 3 · 5 · 2

НОК(а;b) = 3 · 5 · 11· 2 = 330

Пример 3. Найдите НОК(3;13).

3 и 13 — простые числа, они сами и есть простые множители.

НОК(3;13) = 3 · 13 = 39

Пример 4. Найдите НОК(44;25).

44 = 2·2·11
25 = 5·5

НОК(44, 25) = 2·2·11 · 5·5 = 44 · 25 = 1100

Из примера 3 и 4 следует, что НОК простых и взаимно простых чисел можно найти, перемножив эти числа.

Пример 5. Найдите НОК(108;144).

144 = 2·2·2·2·3·3
108 = 2·2·3·3·3

НОК(108;144) = 2·2·2·2·3·3·3 = 432

Нахождение НОК трех, четырех и более чисел

Алгоритм точно такой же, как и при нахождении НОК двух чисел.

1 — раскладываем числа на простые множители.
2 — переписываем все множители самого длинного разложения.
3 — дописываем недостающие множители из разложений других чисел.

Найдите НОК(240; 144; 480)

480 = 2·2·2·2·2·3·5
240 = 2·2·2·2·3·5
144 = 2·2·2·2·3·3

Выпишем все множители числа 480: 2·2·2·2·2·3·5 (пять двоек, одна 3 и одна 5)
Смотрим на множители числа 240 и видим, что каждый из них (а это четыре двойки, одна 3 и одна 5) повторяется, можно их зачеркнуть 2·2·2·2·3·5.
Смотрим на число 144, повторяются четыре двойки и одна 3 ( 2·2·2·2·3 ) , но у нас в этом разложении две тройки, а выписана пока только одна, поэтому вторую 3 тоже выписываем.

НОК(240; 144; 480) = 2·2·2·2·2·3·5·3 = 1440

Найдите наименьшее общее кратное пяти чисел 84, 6, 48, 7, 143.

Сначала разложим данные числа на простые множители:

84 = 2 · 2 · 3 · 7
6 = 2 · 3
48 = 2 · 2 · 2 · 2 · 3
7 (7 – простое число, оно совпадает со своим разложением на простые множители)
143 = 11 · 13

К множителям числа 84 (2, 2, 3 и 7) нужно добавить недостающие множители из разложения числа 6. Разложение числа 6 не содержит недостающих множителей, так как 2 и 3 уже присутствуют в разложении первого числа.
Дальше к множителям 2, 2, 3, 7 добавляем недостающие множители 2, 2 из разложения числа 48, получаем набор множителей 2, 2, 3, 7, 2, 2 .
К этому набору на следующем шаге не придется добавлять множителей, так как 7 уже содержится в нем.
Наконец, к множителям 2, 2, 2, 2, 3 и 7 добавляем недостающие множители 11 и 13 из разложения числа 143.
Получаем произведение 2 · 2 · 3 · 7 · 2 · 2 · 11 · 13 , которое равно 48048.

НОК(84, 6, 48, 7, 143) = 2·2·2·2·3·7·11·13 = 48 048.

Задачи на нахождение НОК

Мальчик хочет купить несколько пачек мороженного по 8 рублей, но у него только 5 рублевые монеты, а у продавца нет сдачи. Какое наименьшее число пачек мороженного он сможет купить?

1 способ. Нахождение НОК подбором:

Эта сумма должна делиться и на 8 рублей, и на 5 рублей без остатка.
1) Выпишем числа кратные 8: 8, 16, 24, 32, 40
2) Выпишем числа кратные 5: 5, 10, 15, 20, 25, 30, 35, 40
Выбираем наименьшее общее кратное.
Нашли, эта сумма = 40 рублей.
Теперь надо узнать сколько пачек можно купить на эту сумму:
40:8=5
Ответ: мальчик может купить 5 пачек мороженного.

2 способ (общепринятый). Нахождение НОК в общем случае:

Эта сумма должна делиться и на 8 рублей, и на 5 рублей без остатка.

1) Выполним разложение 8 и 5 на простые множители.

8 | 2 5 | 5
4 | 2 1 |
2 | 2
1

НОК(8,5) = 8 * 5 = 40

2) Поскольку у нас нет одинаковых множителей, то для нахождения наименьшего общего кратного мы перемножаем эти числа между собой. Нашли НОК, т.е. эта сумма = 40 рублей. Теперь узнаем количество пачек мороженного

40 : 8 = 5 (п.)

Не забываем размерность и пишем ответ

Ответ: мальчик может купить 5 пачек мороженного.

Вдоль дороги от города (пункт А) до деревни (пункт В) были поставлены столбы через каждые 50 м. Их заменили другими, поставив на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который стоит на месте старого.

60 = 2·2·3·5
50 = 2·5·5

НОК(50;60) = 2·2·3·5·5 = 300 (м)

Ответ: 300 м от пункта А до ближайшего столба, который стоит на месте старого.

В одном городе начинаются три туристических теплоходных рейса. Первый длится 12 суток, второй — 18 суток, а третий — 21 сутки. Сегодня из города вышли теплоходы по всем трем маршрутам. Через сколько суток они снова вместе уйдут в плавание?

12 = 2·2·3
18 = 2·3·3
21 = 3·7

НОК(12;18;21) = 2·2·3·3·7 = 252 (сут.)

Ответ: через 252 суток они снова вместе уйдут в плавание.

В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 и третий – 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трём маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? Какое количество рейсов сделает каждый теплоход?

Решение:

1) НОК (15,20 и 12) = 60 (суток) – время встречи.
2) 60 : 15 = 4 (рейса) – 1 теплоход.
3) 60 : 20 = 3 (рейса) – 2 теплоход.
4) 60 : 12 = 5 (рейсов) – 3 теплоход.
Ответ: 60 суток, 4 рейса, 3 рейса, 5 рейсов.

Маша для Медведя купила в магазине яйца. По дороге в лес она сообразила, что число яиц делится на 2,3,5,10 и 15. Сколько яиц купила Маша?

Решение:

НОК (2;3;5;10;15) = 30 (яиц)
Ответ: Маша купила 30 яиц.

Требуется изготовить ящик с квадратным дном для укладки коробок размером 16 ͯ 20 см. Какова должна быть наименьшая длина стороны квадратного дна, чтобы уместить коробки в ящик вплотную?

Решение:

1) НОК (16 и 20) = 80 (коробок).
2) S = a ∙ b – площадь 1 коробки.
S = 16 ∙ 20 = 320 ( см ² ) – площадь дна 1 коробки.
3) 320 ∙ 80 = 25600 ( см ² ) – площадь квадратного дна.
4) S = а² = а ∙ а
25600 = 160 ∙ 160 – размеры ящика.
Ответ: 160 см — сторона квадратного дна.

Вдоль дороги от пункта К стоят столбы электролинии через каждые 45 м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Сколько столбов было и сколько будут стоять?

Решение:

1) НОК (45 и 60) = 180.
2) 180 : 45 = 4 – было столбов.
3) 180: 60 = 3 – стало столбов.
Ответ: 4 столба, 3 столба.

Сколько солдат маршируют на плацу, если они будут маршировать строем по 12 человек в шеренге и перестраиваться в колонну по 18 человек в шеренге?

Решение:

1) НОК (12 и 18) = 36 (человек) – маршируют.
Ответ: 36 человек.

Бегун Коля знает, что через каждые 400 м от старта стоит наблюдатель, а через каждые 700 м от старта можно попить воды. На каком минимальном расстоянии от старта можно попить воды и задать вопрос наблюдателю?

НОК(400;700) = 2800 (м)
Ответ: 2800 м.

Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре?

НОК(50;70)= 350 см, а не 3 метра
Ответ: прав папа.

Заведующая хозяйством Раиса Максимовна дала поручение учителю труда Ильдару Олеговичу закупить доски, которые можно распилить на равные части и по 30 см, и по 40 см. Какой длины и сколько потребуется досок, если нужно 16 кусочков по 30 см и 12 кусочков по 40 см.

1) НОК(30; 40) = 120 (см)
2) 16:(120:30) = 4 (д.)
3) 12:(120:40) = 4 (д.)
Ответ: всего 8 досок по 120 см.

Родители Артема – люди очень интересных профессий. Мама – стюардесса, а папа – машинист скорого поезда. Мама бывает дома один раз в четыре дня, а папа – один раз в семь дней. Так получилось, что оба они 1 января 2015 года уходят в рейс. Когда Артем увидит своих родителей дома вместе?

НОК(4;7) = 28
Ответ: семья будет дома вместе 28 января.

Калькулятор определения НОД и НОК

Для тех, кто уже отчаялся понять тему, НОД и НОК — калькулятор:

Если что-либо осталось для вас непонятным, задавайте вопросы в комментариях.

Источник

Для того, чтобы находить общий знаменатель
при
сложении
и
вычитании дробей с разными
знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).

Кратное числу «a» — это число, которое
само делится на число «a» без остатка.

Числа кратные 8
(то есть, эти числа разделятся на 8 без остатка):
это числа 16, 24, 32 …

Кратные 9: 18, 27, 36, 45 …

Чисел, кратных данному числу a бесконечно много, в отличии от делителей
этого же числа. Делителей —
конечное количество.

Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.

Запомните!

Наименьшим общим кратным (НОК) двух и более натуральных
чисел называется наименьшее натуральное число, которое само
делится нацело на каждое из этих чисел.

Как найти НОК

НОК можно найти и записать двумя способами.

Первый способ нахождения НОК

Данный способ обычно применяется для небольших чисел.

Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое
для обоих чисел.
Кратное числа «a»
обозначаем большой буквой «К».

К (a) = {…, …}

Пример. Найти НОК 6 и 8.

К (6) = {12, 18, 24, 30, …}

К (8) = {8, 16, 24, 32, …}

НОК (6, = 24

Второй способ нахождения НОК

Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.

Разложить данные числа на простые множители.
Подробнее правила разложения на
простые множители вы можете прочитать в теме
как найти наибольший общий делитель (НОД).
Выписать в строчку множители, входящие в разложение
самого большого из чисел, а под ним —
разложение остальных чисел.

Запомните!

Количество одинаковых множителей в разложениях чисел может быть разное.

60 = 2 · 2 · 3 · 5

24 = 2 · 2 · 2 · 3
Подчеркнуть в разложении
меньшего числа (меньших чисел) множители,
которые не вошли в разложение бóльшего числа
(в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.

НОК (24, 60) = 2 · 2 · 3 · 5 · 2
Полученное произведение записать в ответ.

Ответ: НОК (24, 60) = 120

Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24).

24 = 2 · 2 · 2 · 3

16 = 2 · 2 · 2 · 2

12 = 2 · 2 · 3

Как видим из разложения чисел, все множители 12 вошли в
разложение 24
(самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из
разложения числа 16.

НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48

Ответ: НОК (12, 16, 24) = 48

Особые случаи нахождения НОК

Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.
Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее
кратное равно произведению этих чисел.

Пример.

НОК (8, 9) = 72

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

5 сентября 2020 в 15:37

Елена Елена
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Елена Елена
Профиль
Благодарили: 0

Сообщений: 1

НОК(360,102)

0
Спасибо thanks
Ответить

6 сентября 2020 в 13:42
Ответ для Елена Елена

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

360 = 2³· 3²· 5; 102 = 2 · 3 · 17.
НОК(360; 102) = 2³· 3²· 5 · 17 = …

0
Спасибо thanks
Ответить

30 мая 2018 в 17:34

Тамара Татарникова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Тамара Татарникова
Профиль
Благодарили: 0

Сообщений: 1

Найдите четырёхзначное число, которое кратно 24, а произведение цифр этого числа равно 16, в ответ дайте какое-нибудь одно число.
Я написала 1242, но 1242 при делении на 24 дает в ответе 51,75 будет ли это верным ответом?

0
Спасибо thanks
Ответить

3 июня 2018 в 1:58
Ответ для Тамара Татарникова

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

1128 1224 8112

0
Спасибо thanks
Ответить

29 ноября 2016 в 14:47

Анвар Тынайбеков
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анвар Тынайбеков
Профиль
Благодарили: 0

Сообщений: 1

НОК(344и170)=

0
Спасибо thanks
Ответить

2 декабря 2016 в 8:23
Ответ для Анвар Тынайбеков

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

1
Спасибо thanks
Ответить

15 февраля 2016 в 19:02

Кирилл Журавлёв
(^-^)
Профиль
Благодарили: 1

Сообщений: 3

(^-^)
Кирилл Журавлёв
Профиль
Благодарили: 1

Сообщений: 3

число 123 454 321 делится на 11 111. найдите нок этих чисел

1
Спасибо thanks
Ответить

15 февраля 2016 в 19:08
Ответ для Кирилл Журавлёв

Кирилл Журавлёв
(^-^)
Профиль
Благодарили: 1

Сообщений: 3

(^-^)
Кирилл Журавлёв
Профиль
Благодарили: 1

Сообщений: 3

12132211

0
Спасибо thanks
Ответить

19 сентября 2016 в 12:55
Ответ для Кирилл Журавлёв

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Здесь подробно описано нахождение НОК.

А в супер-решателе можно себя проверить.

0
Спасибо thanks
Ответить

15 февраля 2016 в 18:51

Кирилл Журавлёв
(^-^)
Профиль
Благодарили: 1

Сообщений: 3

(^-^)
Кирилл Журавлёв
Профиль
Благодарили: 1

Сообщений: 3

ЧИСЛО 123 454 321 ДЕЛИТСЯ 11 111. НАЙДИТЕ НОК ЭТИХ ЧИСЕЛ НЕ ВЫПОЛНЯЯ РАЗЛОЖЕНИЯ ЧИСЕЛ НА ПРОСТЫЕ МНОЖИТЕЛИ

0
Спасибо thanks
Ответить

19 сентября 2016 в 12:56
Ответ для Кирилл Журавлёв

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

0
Спасибо thanks
Ответить

27 января 2016 в 18:15

Lera Kuchinskaya
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Lera Kuchinskaya
Профиль
Благодарили: 0

Сообщений: 1

НОК 100 150 250 cry

0
Спасибо thanks
Ответить

27 января 2016 в 22:36
Ответ для Lera Kuchinskaya

Виктория Казимирова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Виктория Казимирова
Профиль
Благодарили: 0

Сообщений: 1

А что за цифры!!!?

0
Спасибо thanks
Ответить

28 января 2016 в 16:00
Ответ для Lera Kuchinskaya

Anton Wuckert
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Anton Wuckert
Профиль
Благодарили: 0

Сообщений: 1

НОК = 1500

0
Спасибо thanks
Ответить

19 сентября 2016 в 11:42
Ответ для Lera Kuchinskaya

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Для решения можно воспользоваться решателем на сайте.

0
Спасибо thanks
Ответить

22 января 2016 в 13:46

Андрей Алексеев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Андрей Алексеев
Профиль
Благодарили: 0

Сообщений: 1

числа 4,5,6,7,10,12,15,16,20,50, которые являются делителями 24 и кратными 2

0
Спасибо thanks
Ответить

23 января 2016 в 13:33
Ответ для Андрей Алексеев

Александра Сирота
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Александра Сирота
Профиль
Благодарили: 0

Сообщений: 2

ОТВЕТ: 4 и 12

0
Спасибо thanks
Ответить

24 января 2016 в 13:41
Ответ для Андрей Алексеев

Инна Шабрашина
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Инна Шабрашина
Профиль
Благодарили: 0

Сообщений: 5

6 ,2, 12

0
Спасибо thanks
Ответить

25 января 2016 в 19:52
Ответ для Андрей Алексеев

Нелия Ахмедова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Нелия Ахмедова
Профиль
Благодарили: 0

Сообщений: 1

6,12.

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:59
Ответ для Андрей Алексеев

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Чтобы не запутаться, необходимо каждое из чисел проверить на оба условия:
1) 4 — 24/4=6 — делитель 24. 4/2=2 — кратно 2.
2) 5 — 24/5=не делится без остатка — не делитель. 5/2 — не делится без остатка — не кратно 2.
И так далее.
Ответ: 4,6,12.

0
Спасибо thanks
Ответить

23 декабря 2015 в 17:00

Евгений Мухамедшин
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Евгений Мухамедшин
Профиль
Благодарили: 0

Сообщений: 1

1) (4/15+5/8)-3/5

2) (1/5+13/16)-9/20

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:01
Ответ для Евгений Мухамедшин

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Для нахождения НОК можно воспользоваться супер-решателем. Раскрываем скобки и приводим к общему знаменателю.
1) ===0
2) ===

0
Спасибо thanks
Ответить

17 ноября 2015 в 6:29

Светлана Каблучко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Светлана Каблучко
Профиль
Благодарили: 0

Сообщений: 1

запишите числа удовлетворяющие двойное неравенство 354<х<361 если известно что они кратны 2,5,10

0
Спасибо thanks
Ответить

24 ноября 2015 в 17:56
Ответ для Светлана Каблучко

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8

360

0
Спасибо thanks
Ответить

Источник