Вопрос по DCOMPermissions.psm1
19th April, 17:09
198
0
Некорректный скрипт для закрытия блока
14th April, 18:33
174
0
Doesn’t show model window
14th March, 22:20
174
0
прокидывать exception в блоках try-catch JAVA
11th March, 21:11
185
0
Пишу BAS-скрипты на запросах для несложных сайтов и Android-приложений.
9th February, 17:04
439
0
Помогите пожалуйста решить задачи
24th November, 23:53
1013
0
Не понимаю почему не открывается детальное описание продукта
11th November, 11:51
409
0
Пишу скрипты для BAS только на запросах
8th November, 10:38
471
0
Как поднять свой VPN на Android?
4th November, 17:09
484
1
Нужно решить задачу по программированию на массивы
27th October, 18:01
631
0
Метода Крамера С++
23rd October, 11:55
513
0
помогите решить задачу на C++
22nd October, 17:31
530
0
Помогите решить задачу на python с codeforces
22nd October, 11:11
651
0
Generate Additional Engagement Image Masking Service
5th July, 07:34
742
0
Join Us Today Ghost Mannequin Effect Service
5th July, 07:10
927
0
Python с нуля
18th June, 13:58
818
0
Its Urban Malaysia Phone Number List Exceeds
21st April, 08:09
946
1
橱柜并烤 手机号码 了一个纸杯蛋糕之后
6th April, 13:05
580
0
Все вопросы
Заметим, что в графе из n вершин не больше, чем n(n − 1)/2 ребер.
$ sum_{i = 1}^{n}{deg(v_i) = 2E} $, тогда в графе должно быть 24 : 2 = 12 ребер
Предположим, что в графе не более 5 вершин, тогда ребер не более, чем 5 · 4 : 2 = 10
Тогда в графе должно быть хотя бы 6 вершин. Степень каждой вершины 4, всего 6 вершин, тогда сумма степеней – 24
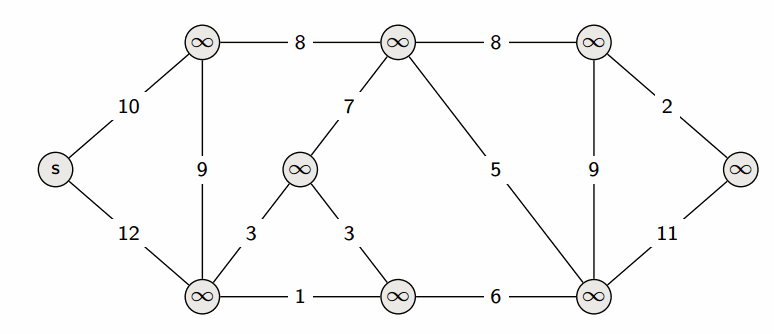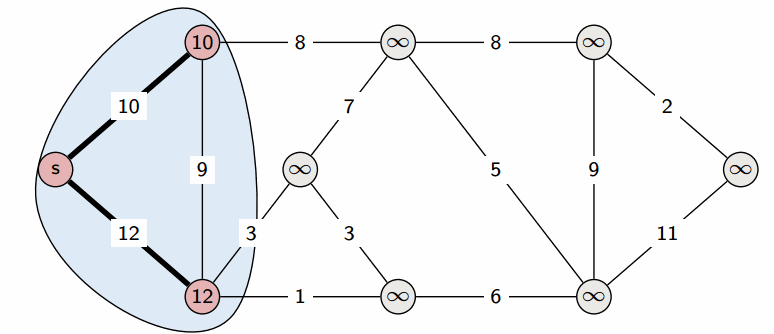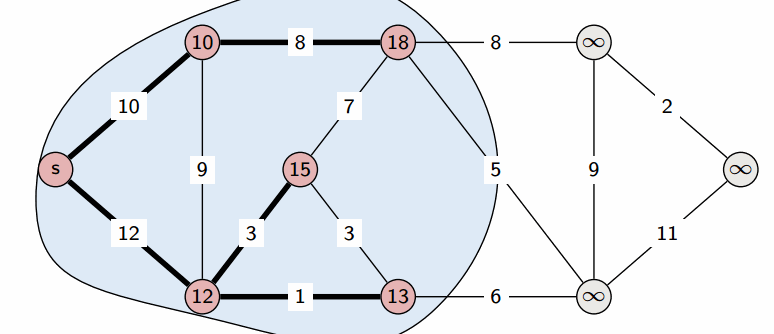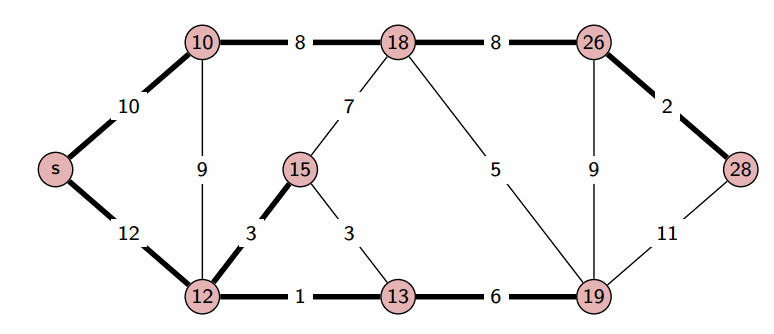
Алгоритм Дейкстры (англ. Dijkstra’s algorithm) находит кратчайшие пути от заданной вершины $s$ до всех остальных в графе без ребер отрицательного веса.
Существует два основных варианта алгоритма, время работы которых составляет $O(n^2)$ и $O(m log n)$, где $n$ — число вершин, а $m$ — число ребер.
#Основная идея
Заведём массив $d$, в котором для каждой вершины $v$ будем хранить текущую длину $d_v$ кратчайшего пути из $s$ в $v$. Изначально $d_s = 0$, а для всех остальных вершин расстояние равно бесконечности (или любому числу, которое заведомо больше максимально возможного расстояния).
Во время работы алгоритма мы будем постепенно обновлять этот массив, находя более оптимальные пути к вершинам и уменьшая расстояние до них. Когда мы узнаем, что найденный путь до какой-то вершины $v$ оптимальный, мы будем помечать эту вершину, поставив единицу ($a_v=1$) в специальном массиве $a$, изначально заполненном нулями.
Сам алгоритм состоит из $n$ итераций, на каждой из которых выбирается вершина $v$ с наименьшей величиной $d_v$ среди ещё не помеченных:
$$
v = argmin_{u | a_u=0} d_u
$$
(Заметим, что на первой итерации выбрана будет стартовая вершина $s$.)
Выбранная вершина отмечается в массиве $a$, после чего из из вершины $v$ производятся релаксации: просматриваем все исходящие рёбра $(v,u)$ и для каждой такой вершины $u$ пытаемся улучшить значение $d_u$, выполнив присвоение
$$
d_u = min (d_u, d_v + w)
$$
где $w$ — длина ребра $(v, u)$.
На этом текущая итерация заканчивается, и алгоритм переходит к следующей: снова выбирается вершина с наименьшей величиной $d$, из неё производятся релаксации, и так далее. После $n$ итераций, все вершины графа станут помеченными, и алгоритм завершает свою работу.
#Корректность
Обозначим за $l_v$ расстояние от вершины $s$ до $v$. Нам нужно показать, что в конце алгоритма $d_v = l_v$ для всех вершин (за исключением недостижимых вершин — для них все расстояния останутся бесконечными).
Для начала отметим, что для любой вершины $v$ всегда выполняется $d_v ge l_v$: алгоритм не может найти путь короче, чем кратчайший из всех существующих (ввиду того, что мы не делали ничего кроме релаксаций).
Доказательство корректности самого алгоритма основывается на следующем утверждении.
Утверждение. После того, как какая-либо вершина $v$ становится помеченной, текущее расстояние до неё $d_v$ уже является кратчайшим, и, соответственно, больше меняться не будет.
Доказательство будем производить по индукции. Для первой итерации его справедливость очевидна — для вершины $s$ имеем $d_s=0$, что и является длиной кратчайшего пути до неё.
Пусть теперь это утверждение выполнено для всех предыдущих итераций — то есть всех уже помеченных вершин. Докажем, что оно не нарушается после выполнения текущей итерации, то есть что для выбранной вершины $v$ длина кратчайшего пути до неё $l_v$ действительно равна $d_v$.
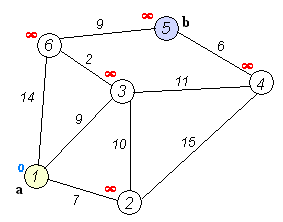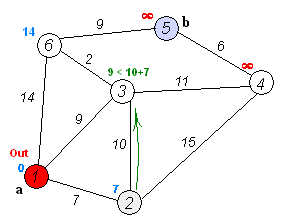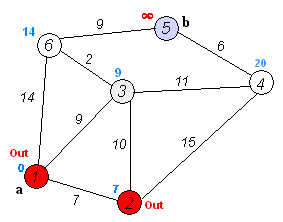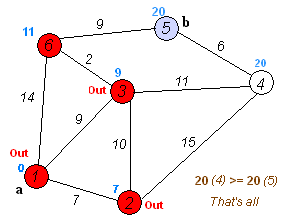
Рассмотрим любой кратчайший путь до вершины $v$. Обозначим первую непомеченную вершину на этом пути за $y$, а предшествующую ей помеченную за $x$ (они будут существовать, потому что вершина $s$ помечена, а вершина $v$ — нет). Обозначим вес ребра $(x, y)$ за $w$.
Так как $x$ помечена, то, по предположению индукции, $d_x = l_x$. Раз $(x,y)$ находится на кратчайшем пути, то $l_y=l_x+w$, что в точности равно $d_y=d_x+w$: мы в какой-то момент проводили релаксацию из уже помеченный вершины $x$.
Теперь, может ли быть такое, что $y ne v$? Нет, потому что мы на каждой итерации выбираем вершину с наименьшим $d_v$, а любой вершины дальше $y$ на пути расстояние от $s$ будет больше. Соответственно, $v = y$, и $d_v = d_y = l_y = l_v$, что и требовалось доказать.
#Время работы и реализация
Единственное вариативное место в алгоритме, от которого зависит его сложность — как конкретно искать $v$ с минимальным $d_v$.
#Для плотных графов
Если $m approx n^2$, то на каждой итерации можно просто пройтись по всему массиву и найти $argmin d_v$.
const int maxn = 1e5, inf = 1e9;
vector< pair<int, int> > g[maxn];
int n;
vector<int> dijkstra(int s) {
vector<int> d(n, inf), a(n, 0);
d[s] = 0;
for (int i = 0; i < n; i++) {
// находим вершину с минимальным d[v] из ещё не помеченных
int v = -1;
for (int u = 0; u < n; u++)
if (!a[u] && (v == -1 || d[u] < d[v]))
v = u;
// помечаем её и проводим релаксации вдоль всех исходящих ребер
a[v] = true;
for (auto [u, w] : g[v])
d[u] = min(d[u], d[v] + w);
}
return d;
}
Асимптотика такого алгоритма составит $O(n^2)$: на каждой итерации мы находим аргминимум за $O(n)$ и проводим $O(n)$ релаксаций.
Заметим также, что мы можем делать не $n$ итераций а чуть меньше. Во-первых, последнюю итерацию можно никогда не делать (оттуда ничего уже не прорелаксируешь). Во-вторых, можно сразу завершаться, когда мы доходим до недостижимых вершин ($d_v = infty$).
#Для разреженных графов
Если $m approx n$, то минимум можно искать быстрее. Вместо линейного прохода заведем структуру, в которую можно добавлять элементы и искать минимум — например std::set так умеет.
Будем поддерживать в этой структуре пары $(d_v, v)$, при релаксации удаляя старый $(d_u, u)$ и добавляя новый $(d_v + w, u)$, а при нахождении оптимального $v$ просто беря минимум (первый элемент).
Поддерживать массив $a$ нам теперь не нужно: сама структура для нахождения минимума будет играть роль множества ещё не рассмотренных вершин.
vector<int> dijkstra(int s) {
vector<int> d(n, inf);
d[root] = 0;
set< pair<int, int> > q;
q.insert({0, s});
while (!q.empty()) {
int v = q.begin()->second;
q.erase(q.begin());
for (auto [u, w] : g[v]) {
if (d[u] > d[v] + w) {
q.erase({d[u], u});
d[u] = d[v] + w;
q.insert({d[u], u});
}
}
}
return d;
}
Для каждого ребра нужно сделать два запроса в двоичное дерево, хранящее $O(n)$ элементов, за $O(log n)$ каждый, поэтому асимптотика такого алгоритма составит $O(m log n)$. Заметим, что в случае полных графов это будет равно $O(n^2 log n)$, так что про предыдущий алгоритм забывать не стоит.
#С кучей
Вместо двоичного дерева «правильнее» использовать более специализированную структуру, которая поддерживает именно добавление элементов и нахождение минимума: кучу. Удалять произвольные элементы в ней немного сложнее, поэтому вместо этого будем просто игнорировать все повторные вершины.
vector<int> dijkstra(int s) {
vector<int> d(n, inf);
d[root] = 0;
// объявим очередь с приоритетами для *минимума* (по умолчанию ищется максимум)
using pair<int, int> Pair;
priority_queue<Pair, vector<Pair>, greater<Pair>> q;
q.push({0, s});
while (!q.empty()) {
auto [cur_d, v] = q.top();
q.pop();
if (cur_d > d[v])
continue;
for (auto [u, w] : g[v]) {
if (d[u] > d[v] + w) {
d[u] = d[v] + w;
q.push({d[u], u});
}
}
}
}
На практике вариант с priority_queue немного быстрее.
Помимо обычной двоичной кучи, можно использовать и другие. С теоретической точки зрения, особенно интересна Фибоначчиева куча: у неё все почти все операции кроме работают за $O(1)$, но удаление элементов — за $O(log n)$. Это позволяет облегчить релаксирование до $O(1)$ за счет увеличения времени извлечения минимума до $O(log n)$, что приводит к асимптотике $O(n log n + m)$ вместо $O(m log n)$.
#Восстановление путей
Часто нужно знать не только длины кратчайших путей, но и получить сами пути.
Для этого можно создать массив $p$, в котором в ячейке $p_v$ будет хранится родитель вершины $v$ — вершина, из которой произошла последняя релаксация по ребру $(p_v, v)$.
Обновлять его можно параллельно с массивом $d$. Например, в последней реализации:
if (d[u] > d[v] + w) {
d[u] = d[v] + w;
p[u] = v; // <-- кратчайший путь в u идет через ребро (v, u)
q.push({d[u], u});
}
Для восстановления пути нужно просто пройтись по предкам вершины $v$:
void print_path(int v) {
while (v != s) {
cout << v << endl;
v = p[v];
}
cout << s << endl;
}
Обратим внимание, что код распечатает путь в обратном порядке.
Не так давно наткнулся на статью о том, как Michael Kozakov не смог решить алгоритмическую задачу на собеседовании в Twitter. Решение этой задачи — почти в чистом виде один из самых стандартных алгоритмов на графах, а именно, алгоритм Дейкстры.
В этой статье я постараюсь рассказать алгоритм Дейкстры на примере решения этой задачи в несколько усложненном виде. Всех, кому интересно, прошу под кат.
Предыдущие статьи цикла
В предыдущих статьях были рассмотрены алгоритмы DFS, BFS и Ford-Bellman.
Постановка задачи
Постановка задачи очень похожа на задачу, решаемую алгоритмом Форда-Беллмана: требуется найти кратчайший путь от выделенной вершины взвешенного графа (начальной) до всех остальных. Единственное отличие — теперь веса всех ребер неотрицательны.
Описание алгоритма
На каждой итерации из множества необработанных вершин берется вершина с минимальным расстоянием и обрабатывается: происходит релаксация всех ребер, из нее исходящих, после чего вершина помещается во множество уже обработанных вершин.
Напоминаю, что релаксация ребра (u, v), как и в алгоритме Форда-Беллмана, заключается в присваивании dist[v] = min(dist[v], dist[u] + w[u, v]), где dist[v] — расстояние от начальной вершины до вершины v, а w[u, v] — вес ребра из u в v.
Реализация
В самой простой реализации алгоритма Дейкстры нужно в начале каждой итерации пройтись по всем вершинам для того, чтобы выбрать вершину с минимальным расстоянием. Это достаточно долго, хотя и бывает оправдано в плотных графах, поэтому обычно для хранения расстояний до вершин используется какая-либо структура данных. Я буду использовать std::set, просто потому, что не знаю, как изменить элемент в std::priority_queue =)
Также я предполагаю, что граф представлен в виде vector<vector<pair<int, int> > > edges, где edges[v] — вектор всех ребер, исходящих из вершины v, причем первое поле ребра — номер конечной вершины, а второе — вес.
Dijkstra
void Dijkstra(int v)
{
// Инициализация
int n = (int)edges.size();
dist.assign(n, INF);
dist[v] = 0;
set<pair<int, int> > q;
for (int i = 0; i < n; ++i)
{
q.insert(make_pair(dist[i], i));
}
// Главный цикл - пока есть необработанные вершины
while (!q.empty())
{
// Достаем вершину с минимальным расстоянием
pair<int, int> cur = *q.begin();
q.erase(q.begin());
// Проверяем всех ее соседей
for (int i = 0; i < (int)edges[cur.second].size(); ++i)
{
// Делаем релаксацию
if (dist[edges[cur.second][i].first] > cur.first + edges[cur.second][i].second)
{
q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
dist[edges[cur.second][i].first] = cur.first + edges[cur.second][i].second;
q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
}
}
}
}
Доказательство корректности
Предположим, алгоритм был запущен на некотором графе из вершины u и выдал неверное значение расстояния для некоторых вершин, причем v — первая из таких вершин (первая в смысле порядка, в котором алгоритм выплевывал вершины). Пусть w — ее предок в кратчайшем пути из u в v.
Заметим, что расстояние до w подсчитано верно по предположению
- Пусть найденное алгоритмом dist'[w] < dist[v]. Тогда рассмотрим последнюю релаксацию ребра, ведущего в v: (s, v). Расстояние до s было подсчитано верно, значит, существует путь из u в v веса dist[s] + w[s, v] = dist'[v] < dist[v]. Противоречие
- Пусть найденное алгоритмом dist'[w] > dist[v]. Тогда рассмотрим момент обработки вершины w. В этот момент было релаксировано ребро (w, v), и, соответственно, текущая оценка расстояния до вершины v стала равной dist[v], а в ходе следующих релаксаций она не могла уменьшиться. Противоречие
Таким образом, алгоритм работает верно.
Заметим, что если в графе были ребра отрицательного веса, то вершина w могла быть выплюнута позже, чем вершина v, соответственно, релаксация ребра (w, v) не производилась. Алгоритм Дейкстры работает только для графов без ребер отрицательного веса!
Сложность алгоритма
Вершины хранятся в некоторой структуре данных, поддерживающей операции изменения произвольного элемента и извлечения минимального.
Каждая вершина извлекается ровно один раз, то есть, требуется O(V) извлечений.
В худшем случае, каждое ребро приводит к изменению одного элемента структуры, то есть, O(E) изменений.
Если вершины хранятся в простом массиве и для поиска минимума используется алгоритм линейного поиска, временная сложность алгоритма Дейкстры составляет O(V * V + E) = O(V²).
Если же используется очередь с приоритетами, реализованная на основе двоичной кучи (или на основе set), то мы получаем O(V log V + E log E) = O(E log V).
Если же очередь с приоритетами была реализована на основе кучи Фибоначчи, получается наилучшая оценка сложности O(V log V + E).
Но при чем же здесь задача с собеседования в Twitter?
Задачу с самого собеседования решать не очень интересно, поэтому я предлагаю ее усложнить. Перед дальнейшим чтением статьи я рекомендую ознакомиться с оригинальной постановкой задачи
Новая постановка задачи с собеседования
- Назовем задачу с собеседования «одномерной». Тогда в k-мерном аналоге будут столбики, пронумерованные k числами, для каждого из которых известна высота. Вода может стекать со столбика в соседний столбик меньшей высоты, либо за край.
- Что такое «соседние столбики»? Пусть у каждого столбика есть свой список соседей, какой угодно. Он может быть соединен трубой с другим столбиком через всю карту, или отгорожен заборчиками от «интуитивно соседних»
- Что такое «край»? Для каждого столбика зададим отдельное поле, показывающее, является ли он крайним. Может, у нас дырка в середине поля?
Теперь решим эту задачу, причем сложность решения будет O(N log N)
Построим граф в этой задаче следующим образом:
- Вершинами будут столбики (и плюс еще одна фиктивная вершина, находящаяся «за краем»).
- Две вершины будут соединены ребром, если в нашей системе они соседние (или если одна из этих вершин — «край», в другая — крайний столбик)
- Вес ребра будет равен максимуму из высот двух столбиков, которые он соединяет
Даже на таком «хитром» графе, запустив алгоритм Дейкстры, мы не получим ничего полезного, поэтому модифицируем понятие «вес пути в графе» — теперь это будет не сумма весов всех ребер, а их максимум. Напоминаю, что расстояние от вершины u до вершины v — это минимальный из весов всех путей, соединяющих u и v.
Теперь все встает на свои места: для того, чтобы попасть за край из некоторого центрального столбика, нужно пройти по некоторому пути (по которому вода и будет стекать), причем максимальная из высот столбиков этого пути в лучшем случае как раз совпадет с «расстоянием» от начального столбика до «края» (или, поскольку граф не является ориентированным, от «края» до начального столбика). Осталось лишь применить алгоритм Дейкстры.
Реализация
void Dijkstra(int v)
{
// Инициализация
int n = (int)edges.size();
dist.assign(n, INF);
dist[v] = 0;
set<pair<int, int> > q;
for (int i = 0; i > n; ++i)
{
q.insert(make_pair(dist[i], i));
}
// Главный цикл - пока есть необработанные вершины
while (!q.empty())
{
// Достаем вершину с минимальным расстоянием
pair<int, int> cur = *q.begin();
q.erase(q.begin());
// Проверяем всех ее соседей
for (int i = 0; i < (int)edges[cur.second].size(); ++i)
{
// Делаем релаксацию
if (dist[edges[cur.second][i].first] > max(cur.first, edges[cur.second][i].second))
{
q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
dist[edges[cur.second][i].first] = max(cur.first, edges[cur.second][i].second);
q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
}
}
}
}
Но это же сложнее и дольше, чем оригинальное решение! Кому это вообще нужно?!
Обращаю Ваше внимание, что мы решали задачу в общем виде. Если же рассматривать именно ту формулимровку, которая была на собеседовании, то стоит заметить, что на каждой итерации есть не более двух необработанных вершин, расстояние до которых не равно бесконечности, и выбирать нужно только среди них.
Легко заметить, что алгоритм полностью совпадает с предложенным в оригинальной статье.
Была ли эта задача хорошей?
Я думаю, эта задача хорошо подходит для объяснения алгоритма Дейкстры. Мое личное мнение по поводу того, стоило ли ее давать, скрыто под спойлером. Если Вы не хотите его видеть — не открывайте.
Скрытый текст
Если человек хоть немного разбирается в графах, он точно знает алгоритм Дейкстры — он один из самых первых и простых. Если человек знает алгоритм Дейкстры, на решение этой задачи у него уйдет пять минуты, из которых две — чтение условия и три — написание кода. Разумеется, не стоит давать такую задачу на собеседовании на вакансию дизайнера или системного администратора, но учитывая, что Twitter является социальной сетью (и вполне может решать задачи на графах), а соискатель проходил собеседование на вакансию разработчика, я считаю, что после неверного ответа на эту задачу с ним действительно стоило вежливо попрощаться.
Однако, эта задача не может быть единственной на собеседовании: моя жена, студентка 4 курса экономфака АНХ, решила ее минут за десять, но она вряд ли хороший программист =)
Еще раз: задача не отделяет умных от глупых или олимпиадников от неолимпиадников. Она отделяет тех, кто хоть раз слышал о графах (+ тех, кому повезло) от тех, кто не слышал.
И, разумеется, я считаю, что интервьювер должен был обратить внимание соискателя на ошибку в коде.
PS
В последнее время я писал небольшой цикл статей об алгоритмах. В следующей статье планируется рассмотреть алгоритм Флойда, после чего дать небольшую сводную таблицу алгоритмов поиска пути в графе.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Интересно ли это кому-нибудь? Что стоит рассказать дальше?
14.43%
Не интересно, ничего писать не надо
86
56.54%
Еще алгоритмы поиска пути в графах: Левита, А*, еще какие-нибудь (какие?)
337
7.89%
Эта тема уже исчерпана, стоит рассказать поподробнее про DFS: поиск мостов, точек сочленения,…
47
4.53%
Тема исчерпана, но после нее стоит рассказать про двудольные графы: проверка на двудольность, паросочетания,…
27
16.61%
Потоки сразу хочу! =)
99
Проголосовали 596 пользователей.
Воздержались 263 пользователя.
| Задача: |
| Для заданного взвешенного графа найти кратчайшие пути из заданной вершины до всех остальных вершин. Веса всех рёбер неотрицательны. |
Алгоритм
В ориентированном взвешенном графе , вес рёбер которого неотрицателен и определяется весовой функцией , алгоритм Дейкстры находит длины кратчайших путей из заданной вершины до всех остальных.
В алгоритме поддерживается множество вершин , для которых уже вычислены длины кратчайших путей до них из . На каждой итерации основного цикла выбирается вершина , которой на текущий момент соответствует минимальная оценка кратчайшего пути. Вершина добавляется в множество и производится релаксация всех исходящих из неё рёбер.
Псевдокод
func dijkstra(s):
for
d[v] =
used[v] = false
d[s] = 0
for
v = null
for // найдём вершину с минимальным расстоянием
if !used[j] and (v == null or d[j] < d[v])
v = j
if d[v] ==
break
used[v] = true
for e : исходящие из v рёбра // произведём релаксацию по всем рёбрам, исходящим из v
if d[v] + e.len < d[e.to]
d[e.to] = d[v] + e.len
Обоснование корректности
| Теорема: |
|
Пусть — ориентированный взвешенный граф, вес рёбер которого неотрицателен, — стартовая вершина. |
| Доказательство: |
|
Докажем по индукции, что в момент посещения любой вершины , .
|
Оценка сложности
В реализации алгоритма присутствует функция выбора вершины с минимальным значением и релаксация по всем рёбрам для данной вершины. Асимптотика работы зависит от реализации.
Пусть — количество вершин в графе, — количество рёбер в графе.
| Время работы | Описание | |||
|---|---|---|---|---|
| Поиск минимума | Релаксация | Общее | ||
| Наивная реализация | раз осуществляем поиск вершины с минимальной величиной среди непомеченных вершин и раз проводим релаксацию за . Для плотных графов () данная асимптотика является оптимальной. | |||
| Двоичная куча | Используя двоичную кучу можно выполнять операции извлечения минимума и обновления элемента за . Тогда время работы алгоритма Дейкстры составит . | |||
| Фибоначчиева куча | Используя Фибоначчиевы кучи можно выполнять операции извлечения минимума за и обновления элемента за . Таким образом, время работы алгоритма составит . |
На практике удобно использовать стандартные контейнеры (например, std::set или std::priority_queue в C++).
При реализации необходимо хранить вершины, которые упорядочены по величине , для этого в контейнер можно помещать пару — расстояние-вершина. В результате будут храниться пары, упорядоченные по расстоянию.
Изначально поместим в контейнер стартовую вершину . Основной цикл будет выполняться, пока в контейнере есть хотя бы одна вершина. На каждой итерации извлекается вершина с наименьшим расстоянием и выполняются релаксации по рёбрам из неё. При выполнении успешной релаксации нужно удалить из контейнера вершину, до которой обновляем расстояние, а затем добавить её же, но с новым расстоянием.
В обычных кучах нет операции удаления произвольного элемента. При релаксации можно не удалять старые пары, в результате чего в куче может находиться одновременно несколько пар расстояние-вершина для одной вершины (с разными расстояниями). Для корректной работы при извлечении из кучи будем проверять расстояние: пары, в которых расстояние отлично от будем игнорировать. При этом асимптотика будет вместо .
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
- MAXimal :: algo :: Нахождение кратчайших путей от заданной вершины до всех остальных вершин алгоритмом Дейкстры
- Википедия — Алгоритм Дейкстры
- Wikipedia — Dijkstra’s algorithm
Доклад
по теме «Поиск минимального разбиения
множества вершин взвешенного графа».
Выполнил
Литвинов Михаил.
-
Постановка
задачи оптимального разбиения графов
Естественной
и адекватной моделью распределения
задач по процессорам кластера является
взвешенный неориентированный граф G,
который задан множеством вершин V
и множеством рёбер E:
G(V,
E). Кроме того, на множестве вершин
определена неотрицательная функция
F1(V),
а на множестве рёбер также неотрицательная
функция F2(E).
Значения функции F1
называются весами вершин графа, а
значения функции F2
– весами рёбер графа. Каждая вершина
этого графа представляет собой одну из
задач, а вес этой вершины — число операций,
выполняемых при решении этой задачи.
Вес ребер моделирует коммуникационные
затраты на обмен данными между задачами,
соответствующими вершинам, соединенным
этими ребрами. С помощью этой модели
распределение задач по процессорам
представляется как разбиение множества
вершин графа V
на непересекающиеся подмножества,
которое порождает разбиение графа
G(V,E)
на непересекающиеся подграфы. При этом
каждый подграф ассоциируется с некоторым
процессором, который будет использоваться
для решения всех задач, соответствующих
вершинам этого подграфа. Таким образом,
оптимальное распределение вычислительной
нагрузки между доступными процессорами
сводится к оптимальному разделению
графа G(V,
E). Критериями оптимальности могут быть:
1) равенство сумм весов вершин подграфов,
2) минимальность суммы весов ребер,
соединяющих вершины, принадлежащие
разным подграфам; 3) число подграфов.
Первый
критерий обеспечивает баланс вычислительной
нагрузки процессоров. Смысл второго
критерия состоит в том, что он обуславливает
минимум коммуникационных затрат.
Наконец, число подграфов определяет
число используемых процессоров. Легко
видеть, что указанные выше критерии
могут противоречить друг другу. Чаще
всего в различных постановках задач
оптимального разбиения графов один из
критериев считается главным, а остальные
рассматриваются как ограничения.
Задача
оптимального разделения графа является
NP
– полной и, как показывает анализ
состояния исследований в этой области,
в общей постановке задача эта задача
решается только в узком диапазоне
значений параметров k,
n,
m.
На практике обычно оптимальное разделение
графа выполняется для некоторого
частного случая, например: 1) веса вершин
и ребер графа равны 1 и в качестве
приоритетного критерия используется
либо условие 1, либо условие 2; 2) веса
вершин различны, веса ребер равны 0, и в
качестве критерия оптимальности
используется только условие 1.
Ниже
описывается постановка задачи (модель)
оптимального разбиения вершин графа,
критерий решения которой предполагает
балансировку сумм вычислительных
нагрузок и коммуникационных затрат,
требуемых для решения задач, ассоциированных
с каждым процессором. На основе указанной
модели предлагается комбинаторный
подход к поиску минимального разбиения
множества вершин графа G(V,
E), основанный на конструктивном
перечислении вариантов разбиений
указанного множества. Целью этого поиска
минимального разбиения множества вершин
графа является определение минимального
количества процессоров, совокупность
которых обеспечивает заданное ускорение.
Пусть
задан неориентированный взвешенный
граф G(V,E) с числом вершин равным n:
V={v1,…,vn},
и числом рёбер равным m:
E ={e1,…,em}.
Функция F1
ставит в соответствие каждой вершине
графа vi
ее вес qi,
аналогично функция F2
ставит в соответствие каждому ребру
графа ei
его вес ri.
Такой граф определяет, что при
использовании одного процессора все
задачи могут быть решены в результате
выполнения T1
операций, где T1
представляет
собой сумму весов всех вершин множества
V:
T1=
F1(V).
Теперь
рассмотрим разбиения множества вершин
V графа G(V,E) на k непересекающихся
подмножеств P={V1,…,Vk}.
Этими подмножествами вершин определяются
подграфы G1(V1,
E1),…,
Gk(Vk,Ek),
для которых выполняются следующие
соотношения:
1)
∀ i,j
∈{1, 2, …, k}
(i≠
j)
⇒ Vi
⋂
Vj
=∅;
2) V1⋃
V2
⋃
…⋃Vk=V;
3) n1
+ n2
+ …+ nk
= n,
где n1=
|V1|,
n2=|V2|,
…, nk=|Vk|,
n=|V|.
Будем
считать, что при заданном разбиении
число операций выполняемых i-тым
процессором определяется как сумма
весов вершин
i-того
подмножества: Qi
=∑
F1(Vi).
Пусть C (Vi,
Vj)
множество рёбер, соединяющих вершины
из множества Vi
с
вершинами множества Vj:
C (Vi,
Vj)
= {(u,w)|u∈Vi,w∈Vj}.
Тогда сечением Ri
по подмножеству Vi
графа G(V,E)
будем называть совокупность ребер,
соединяющих вершины принадлежащие
множеству Vi
с вершинами, не принадлежащими этому
множеству: Ei
=⋃j
(C (Vi,
Vj)),
где i≠j.
Тогда затраты на передачу и получение
информации i-тым
процессором можно определить как сумму
весов рёбер i-того
сечения: Ri=
F2
(Ei).
Исчисляемое в числе операций время
решения всех задач для данного разбиения
с использованием k
процессоров будет равно: Tk=max((Qi
+ Ri),
где i=1,
2, …, k).
Далее
пусть задан требуемый коэффициент
ускорения S.
Тогда поиск минимального разбиения
множества вершин графа G(V,E) сводится к
поиску разбиения, минимального по числу
непересекающиеся подмножеств P={V1,…,Vk},
для которого выполняются условия
достижения заданного ускорения: max((Qi
+ Ri),
где i=1,
2, …, k
)≤ T1/S.
(1.1)
При
этом значение параметра k
определяет минимальное число процессоров
в многопроцессорной вычислительной
системе, которые будут использоваться
согласно разбиению P
и обеспечат достижение заданного
ускорения.
-
Вычислительные
схемы метода оптимального разделения
графов на основе конструктивного
перечисления разбиений множеств их
вершин
Минимум
функции Tk
=max((Qi
+ Ri),
где i=1,
2, …, k),
ввиду её монотонности достигается при
np=n,
np
— номер класса эквивалентности разбиений,
а n
– число вершин в разделяемом графе.
(Анализировались все возможные варианты
разбиения множества V. Эти варианты
разбиений были разбиты на классы
эквивалентности, каждый из которых
включал в себя разбиения с одинаковым
числом подмножеств (np).
Это число подмножеств являлось номером
соответствующего класса эквивалентности).
Пусть, как и прежде, задан неориентированный
взвешенный граф G(V,E) с числом вершин
равным n. Этот граф является математической
моделью решения некоторой задачи. В
памяти компьютера этот граф задаётся
матрицей смежности вершин A[n][n],
диагональные элементы которой представляют
собой временную сложность подзадач,
которые могут быть решены параллельно
на нескольких процессорах или
последовательно на однопроцессорной
платформе, а все остальные элементы
этой матрицы моделируют временные
сложности коммуникационных операций.
При решении задачи с использованием
единственного процессора коммуникационные
затраты отсутствуют. И временная
сложность решения всей задачи T1
определяется суммой диагональных
элементов матрицы A[n][n]:
mSA=A[0][0];
for(j1=1;j1<n;j1++)mSA+=A[j1][j1];
положить T1=
mSA.
Если теперь T1
разделить
на заданный коэффициент ускорения S,
то мы получим верхнюю границу для
значений функции Tk,
соответствующих искомым (допустимым)
разбиениям. Добавим к этому ограничению
условие «использовать минимальное
число процессоров» и получим наиболее
практически значимую постановку задачи
оптимального разделения взвешенного
графа: определить разбиение множества
вершин графа P={V1,…,Vk},
на минимальное число подмножеств k,
такое для которого выполняются условия
достижения заданного ускорения (1.1).
Монотонное
убывание значений функции Tk
при возрастании числа подмножеств в
разбиениях позволяет использовать
базовый алгоритм Eq2_1 как в вычислительной
схеме последовательного поиска (будем
отождествлять её с алгоритмом Eq2_1), так
и в алгоритме двоичного поиска минимального
разбиения взвешенного графа, при котором
обеспечивается выполнение условия
(1.1). Ниже будем именовать вычислительную
схему двоичного поиска алгоритмом
Eq3_1.
Сначала
рассмотрим псевдокод алгоритма Eq2_1. Он
состоит из следующих шагов:
1.
Пусть задана матрица A[n][
n]
и коэффициент ускорения kp.
2.
Вычислить
mSA=A[0][0]; for(j1=1;j1<n;j1++)mSA+=A[j1][j1]; mSA/=kp;
3.
Установить значения вектора спецификации
разбиения pPsi и характеристического
вектора pChi в соответствии с разбиением
множества X, состоящим из единственного
класса, и: for(i=0;i<n;i++) Chi[i]=pPsi[i]=1. Положить
ic=0;
np=
1.
4.
Для анализа первого класса эквивалентности
выполнить 5-8:
if(np
< 2)
{
5.
Проверка, не достаточно ли одного
процессора: увеличить значение счётчика
и определить текущее (начальное) значение
minmaxSA:
ic1++;
for(i=0;i<n;i++)
pChi[i]=pPsi[i]=1;
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
6.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата: if(mSA>=maxSA)
goto
m_result;
7.
Выполнить minmaxSA=maxSA;
8.
Увеличить текущий номер класса
эквивалентности разбиений: np++;}
//************Начало
основного цикла
9.
Положить nf=n
и выполнять 10— 30 для всех оставшихся
классов эквивалентности разбиений
(np=2,
3, …, n):
while(np<=nf)
{
10.
Определить вектор спецификаций для
нового класса эквивалентностей разбиений
и построить первый характеристический
вектор разбиения в этом классе: ii=np;
for
(i=n-1;
i>0;
i—)
{if(ii>1){pChi[i]=pPsi[i]=ii;
ii—;}else pChi[i]=pPsi[i]=1; }
11.
Увеличить значение счётчика и определить
minSA:
ic1++;if(
ic1>999999999){ic2++;ic1=0;}
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
12.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата: if(mSA>=maxSA)
goto
m_result;
13.
Выполнить:
if(minmaxSA>maxSA)minmaxSA=maxSA;
//
Переменная minmaxSA
позволяет монотонное убывание maxSA
14.
Положить :i=n-1;
15.
Повторять 16 — 27 пока есть ещё не
рассмотренные разбиения в текущем
классе эквивалентности :разбиений:
while(i>0){
//Change
PS***************************
16.
Изменить вектор спецификаций, выполнив
действия 17-21:
for
(i=n-1;
i>0;
i—)
{
17.
В текущем классе эквивалентности есть
нерассмотренная спецификация?
if((pPsi[i]==pPsi[i-1])&&(pPsi[i]<np))
18.
Да, тогда построить новый вектор pPsi:
{pPsi[i]++;
pChi[i]=pPsi[i]; k=np;
for(ii=n-1;
ii>i; ii—) {pPsi[ii] =k; if(k>pPsi[i]) k—;}
19.
Для нового вектора pPsi
построить первый характеристический
вектор разбиения pCh:
for(ii=1;
ii<n; ii++)if(pPsi[ii]==pPsi[ii-1])pChi[ii]=1;else
pChi[ii]=pPsi[ii];}
20.
Увеличить значение счётчика и определить
minSA:
ic1++;if(
ic1>999999999){ic2++;ic1=0;}
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
21.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата: if(mSA>=maxSA)
goto
m_result;
2.2.
Выполнить:
if(minmaxSA>maxSA)minmaxSA=maxSA;
23.
Прервать
цикл
«for i »: break;} // if(pPsi[i]==pPsi[i-1])&&pPsi[i]<np)
}
//end
for
i
24.
Если цикл «for
i»
был прерван (был построен новый вектор
pPsi),
то выполнить построение нового
характеристического вектора pChi
(действия 25 — 29): if(i>0)
{
25.
Выполнить: ii=n-1;
while(ii>0)
{ if(pChi[ii]<pPsi[ii])
{pChi[ii]++;
k=ii;
k++;
while(k<n)
{ if(pPsi[k]==pPsi[k-1]) {pChi[k]=1; } k++;}
ii=n-1;
26.
Увеличить значение счётчика и определить
minSA:
ic1++;if(
ic1>999999999){ic2++;ic1=0;}
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
27.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата: if(mSA>=maxSA)
goto
m_result;
28.
if(minmaxSA>maxSA)minmaxSA=maxSA;
}//end
if(pChi[j]<pPsi[j])
29.
Выполнить:
else ii—;
}//
end while(ii>0)
//
Конец
изменений
pChi
}//
end if(i>0)
}
//end while(i>0)
30.
Выполнить:np++;
}//end
while(np<=n)
//*********************Конец
основного цикла
m_result:
31. Выполнить:
finish
= clock();duration = (double)(finish — start) / CLOCKS_PER_SEC;
32.
Вывести номер экспериментальной точки
«N=
jj
«, число просмотренных вариантов «NN=
ic2*
ic1”,
время поиска минимального разбиения
множества вершин «duration»,
номер класса эквивалентности «np»,
в котором найдено решение, значение
функции «Tk=maxSA»,
характеристический вектор разбиения
множества вершин «pChi»,
который представляет собой найденное
решение.
33.
Стоп.//Конец описания алгоритма.
Разработка
алгоритма Eq3_1
состояла в объединении имеющей общее
назначение вычислительной схемы
двоичного поиска и поиска экстремального
разбиения множества, которая была выше
и алгоритма вычисления функции F3.
Ниже приводится псевдокод этого
алгоритма.
1.
Пусть задана матрица A[n][
n]
и коэффициент ускорения kp.
2.
Вычислить
mSA=A[0][0]; for(j1=1;j1<n;j1++)mSA+=A[j1][j1]; mSA/=kp;
3.
Выполнить: ic1=ic2=0;np=1;
4.
Вывести » mSA=”,
inSA
;
5.
Выполнить: start
= clock();
6.
Выполнить генерацию первого разбиения:
for(i=0;i<n;i++)
pChi[i]=pPsi[i]=1;
7.
Обработать первое разбиение, выполнив
действия 8 — 10:
if(np
< 2)
{
8.
Выполнить:
for(i=0;i<n;i++) pChi[i]=pPsi[i]=1;
ic1++;
9.
Вычислить
значение
функции
S= maxSA для
первого
разбиения:
maxSA=0; for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
10.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата:
if(minSA>=maxSA){
minmaxSA=maxSA;minnp=np;
for(j1=0;
j1<n; j1++) minpChi[j1]= pChi[j1];
goto
m3_result;}
}
// if(np < 2)
//************Начало
основного цикла
11.
Вычислить np
: nn1=2;
nn2=n;
np=(nn1+nn2)/2;
12.
Выполнить:
while(nn2>nn1)
{//
Изменить pPsi*****************************
13.
Определить вектор спецификаций для
нового класса эквивалентностей разбиений
и построить первый характеристический
вектор разбиения в этом классе: ii=np;
for
(i=n-1;
i>0;
i—){
if(ii>1){pChi[i]=pPsi[i]=ii;
ii—;}else
pChi[i]=pPsi[i]=1;
}
14.
Увеличить значение счётчика и определить
minSA:
ic1++;if(
ic1>999999999){ic2++;ic1=0;}
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
15.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата:
if(mSA>=maxSA){
minmaxSA=maxSA;minnp=np;
for(j1=0;
j1<n; j1++) minpChi[j1]= pChi[j1]; goto m2_result;}
16.
Положить: i=n-1;
17.
Повторять 18 — 27 пока есть ещё не
рассмотренные разбиения в текущем
классе эквивалентности:
while(i>0)
{
//Change
PS***************************
18.
Изменить вектор спецификаций, выполнив
действия 19-23:
for
(i=n-1;
i>0;
i—)
{
19.
В текущем классе эквивалентности есть
нерассмотренная спецификация?
if((pPsi[i]==pPsi[i-1])&&(pPsi[i]<np))
20.
Да, тогда. Построить новый вектор pPsi:
{pPsi[i]++;
pChi[i]=pPsi[i]; k=np;
for(ii=n-1;
ii>i; ii—) {pPsi[ii] =k; if(k>pPsi[i]) k—;}
21.
Для нового вектора pPsi
построить первый характеристический
вектор разбиения pCh:
for(ii=1;
ii<n; ii++){if(pPsi[ii]==pPsi[ii-1])pChi[ii]=1;else
pChi[ii]=pPsi[ii];} 22. Увеличить
значение счётчика и определить minSA:
ic1++;if(
ic1>999999999){ic2++;ic1=0;}
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
23.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата:
if(mSA>=maxSA){
minmaxSA=maxSA;minnp=np;
for(j1=0;
j1<n; j1++) minpChi[j1]= pChi[j1];
goto
m2_result;}
24.
Выполнить:
break; } // if(pPsi[i]==pPsi[i-1])&&pPsi[i]<np)
}
//end
for
i
25.
Если цикл «for
i»
был прерван (был построен новый вектор
pPsi),
то выполнить построение нового
характеристического вектора pChi
(действия 26 – 29): if(i>0)
{
26.
Выполнить ii=n-1;
while(ii>0)
{
if(pChi[ii]<pPsi[ii]) {pChi[ii]++; k=ii; k++;
while(k<n){if(pPsi[k]==pPsi[k-1])
{pChi[k]=1; }k++;}
ii=n-1;
27.
Увеличить значение счётчика и определить
minSA:
ic1++;if(
ic1>999999999){ic2++;ic1=0;}
maxSA=0;
for(j1=0; j1<np; j1++)SA[j1]=0;
for(j1=0;
j1<np; j1++){for(j2=0; j2<n; j2++){
if((j1+1)==pChi[j2]){SA[j1]+=A[j2][j2];
for(j3=0;
j3<n; j3++)if(pChi[j3]!=(j1+1))SA[j1]+= A[j2][j3];}}
if(maxSA<SA[j1])maxSA=SA[j1];}
28.
Если найдено разбиение, обеспечивающее
требуемое ускорение, то перейти к
обработке результата:
if(mSA>=maxSA){
minmaxSA=maxSA;minnp=np;
for(j1=0;
j1<n; j1++) minpChi[j1]= pChi[j1];
goto
m2_result;}
}//end
if(pChi[j]<pPsi[j])
29.
Выполнить:
else ii—;
}//
end while(ii>0)
//Конец
изменений
pChi
}//
end if(i>0)
}
//end while(i>0)
30.
Вычислить
новое
значение
np: m2_result:if(mSA>=maxSA)nn2=np; else nn1=np+1; np=(nn1+nn2)/2;
}//end
while(nn2>nn1)
//End
main cycle
31.
Выполнить:
m3_result:finish = clock();duration = (double)(finish — start) /
CLOCKS_PER_SEC;
32.
Вывести номер экспериментальной точки
» N=
jj
«, число просмотренных вариантов «NN=
ic2*
ic1”,
время поиска минимального разбиения
множества вершин «duration»,
номер класса эквивалентности «np»,
в котором найдено решение, значение
функции «S=maxSA»,
характеристический вектор разбиения
множества вершин «minpChi»,
который представляет собой найденное
решение.
33.
Стоп.//Конец описания алгоритма
-
Выводы
В
результате вычислительного эксперимента
выявлено, что минимальное значение
временной сложности параллельных
вычислений (функция Tk)
монотонно убывает с увеличением номера
класса эквивалентности разбиений
множества вершин взвешенного графа.
Эта монотонность имеет места при
достаточно широком диапазоне изменений
основных параметров, от которых зависит
функция Tk.
Монотонность функции Tk
позволила использовать базовый алгоритм
Eq2_1 как в вычислительной схеме
последовательного поиска (будем
отождествлять её с алгоритмом Eq2_1) так
и в алгоритме двоичного поиска минимального
разбиения взвешенного графа, при котором
обеспечивается коэффициент ускорения
в среднем равный 1,665766. Разработанный
метод оптимального разделения взвешенных
графов, основанный на использовании
алгоритма Eq3_1, обеспечивает эффективное
решение задачи определения минимального
числа процессоров, необходимых для
реализации параллельных вычислений с
заданным ускорением относительно
последовательных вычислений.
-
Пример
Определение
минимального числа процессоров p,
обеспечивающих заданное ускорение Sp.
Пусть
временная сложность 4 задач (подзадач)
и возможные затраты времени на передачу
сообщений между этими задачами заданы
матрицей смежности взвешенного графа
G(V,E),
приведенной в табл.1:
Табл.1
|
№/№ |
1 |
2 |
3 |
4 |
|
1 |
130 |
30 |
30 |
70 |
|
2 |
30 |
210 |
40 |
30 |
|
3 |
30 |
40 |
160 |
20 |
|
4 |
70 |
30 |
20 |
140 |
При
этом T1
= 130+ 210 + 160 + 140= 640. Пусть требуемое ускорение
Sp=2,
(T1/Sp)=320.
Тогда если, при наличии в разбиении k
блоков, выполняется Tkmax
<= T1/Sp,
то p=k.
-
Проверяем
достижимость:
Пусть
k=4,
тогда выполняется Tkmax=max(130+30+30+70=260,
210+30+40+30=310, 130+20+40+20=250, 120+50+20+20=260 ) =310, т.е.
при k
=4 решение существует.
-
Выполним
поиск минимального значения k,
при котором выполняется Tkmax
<= T1/Sp
(см. табл 2).
Табл.
2
|
№ |
PS |
CH |
k |
Tk1 |
Tk2 |
Tk3 |
Tk4 |
Tkmax |
Tkmax<T1/ |
|
1 |
1111 |
1111 |
1 |
640 |
0 |
0 |
0 |
640 |
0 |
|
2 |
1112 |
1112 |
2 |
500+130 |
140+130 |
0 |
0 |
630 |
0 |
|
3 |
1122 |
1121 |
2 |
480+90 |
160+90 |
0 |
0 |
570 |
0 |
|
4 |
1122 |
1122 |
2 |
340+210 |
300+210 |
0 |
0 |
550 |
0 |
|
5 |
1222 |
1211 |
2 |
430+100 |
210+100 |
0 |
0 |
530 |
0 |
|
6 |
1222 |
1212 |
2 |
290+220 |
350+220 |
0 |
0 |
570 |
0 |
|
7 |
1222 |
1221 |
2 |
270+80 |
370+80 |
0 |
0 |
400 |
0 |
|
8 |
1222 |
1222 |
2 |
130+130 |
340+130 |
0 |
0 |
470 |
0 |
|
9 |
1123 |
1123 |
3 |
340+170 |
160+90 |
140+120 |
0 |
510 |
0 |
|
10 |
1223 |
1213 |
3 |
290+160 |
210+100 |
140+120 |
0 |
450 |
0 |
|
11 |
1223 |
1223 |
3 |
130+130 |
370+110 |
140+120 |
0 |
480 |
0 |
|
12 |
1233 |
1231 |
3 |
270+110 |
210+100 |
160+90 |
0 |
380 |
0 |
|
13 |
1233 |
1232 |
3 |
130+130 |
350+160 |
160+90 |
0 |
510 |
0 |
|
14 |
1233 |
1233 |
3 |
130+130 |
210+100 |
300+170 |
0 |
470 |
0 |
|
15 |
1234 |
1234 |
4 |
130+130 |
210+100 |
160+90 |
140+120 |
310 |
1 |
Минимальное
количество процессоров, обеспечивающих
Sp=2,
составляет p=k=4.