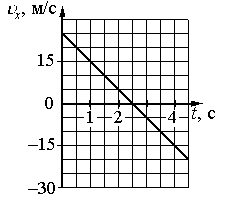Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.
Что такое мгновенная скорость? Мгновенная скорость — скорость тела в данный момент времени. Обозначается vмгн. Далее, когда мы будем говорить о скорости, мы будем понимать под ней мгновенную скорость тела и обозначать ее просто — v.
Определение
Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t0 и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:
v = v0 + at
v — скорость тела в данный момент времени, v0 —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось
Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.
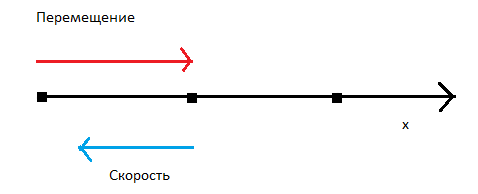
Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.
Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.
Скалярная формула скорости
В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:
v = v0 ± at
Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.
Проекция скорости
Проекция скорости при равноускоренном прямолинейном движении имеет вид:
vx = v0x + axt
Знак проекции скорости зависит от того, в какую сторону движется тело:
- Знак проекции скорости имеет знак «+», если тело движется в сторону направления оси ОХ.
- Знак проекции скорости имеет знак «–», если тело движется противоположно направлению оси ОХ.
Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.
График скорости
График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.
Определение направления движения тела относительно оси ОХ по графику скорости
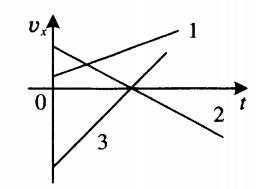
- Если график скорости лежит выше оси времени, то тело движется в направлении оси ОХ. На рисунке этому утверждению соответствует график 1.
- Если график скорости пересекает ось времени, то модуль скорости тела сначала уменьшался, и тело тормозило. Но с момента пересечения оси времени оно меняло направление движения в противоположную сторону и двигалось ускоренно. На рисунке этому соответствуют графики скорости 2 и 3.
- Если график скорости лежит ниже оси времени, тело движется в направлении, противоположном направлению оси ОХ. На рисунке тело 3 до пересечения с осью времени двигалось противоположно направлению ОХ. Но тело 2 двигалось противоположно оси только после пересечения с этой осью.
Сравнение модулей ускорения по графикам скоростей
Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.
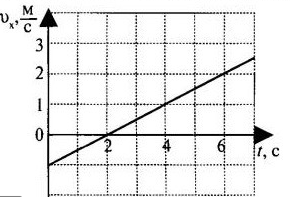
Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.
На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.
Полезные факты
- Если тело начинало движение из состояния покоя, его начальная скорость равна 0, а его ускорение положительно: v0 = 0, a > 0.
- Если тело заканчивает движение остановкой, то его мгновенная скорость в конечный момент времени равна 0, а его ускорение отрицательно: v = 0, a < 0.
- Если тело покоится, его скорость и ускорение равны 0: v0 = 0, a = 0.
Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.
Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:
v = v0 – at
Выразим начальную скорость:
v0 = v + at
Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:
v0 = 0 + 2 ∙ 5 = 10 (м/с)
Задание EF18553

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
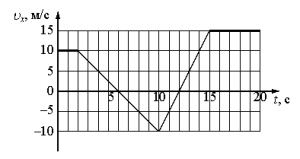
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.1k
Страница 5 из 6
3 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
В этой главе приводится ряд задач по динамике для демонстрации эффективности применения векторного способа при решении задач.
3.1 Задачи типа «брусок на наклонной плоскости»
3.1.1 Простейший случай
Брусок массой находится на гладкой наклонной плоскости с углом наклона к горизонту (рисунок 3). Найти ускорение бруска .
Решение.
В условии задачи обозначены брусок и гладкая наклонная плоскость (т.е. трением в данном случае можно пренебречь). На брусок будет действовать сила тяжести вследствие притяжения к Земле и сила реакции опоры наклонной плоскости, возникшая как результат её деформации бруском. Сила тяжести может считаться известной, т.к. мы знаем массу бруска и ускорение свободного падения вблизи поверхности Земли как по величине, так и по направлению. Величина реакции опоры нам неизвестна, известно лишь её направление – перпендикулярно поверхности вверх. Обозначим это пока просто отрезком (рисрисунок 4). Но очевидно следующее: сила реакции опоры должна в точности компенсировать приложенную нагрузку. Также очевидно следующее: движение бруска будет происходить вдоль плоскости. Поэтому есть смысл рассмотреть две составляющие силы тяжести : параллельную поверхности плоскости и перпендикулярную ей (красные векторы на рис. 4). Перпендикулярная компонента характеризует воздействие бруска на плоскость, и в движении не участвует. Сила реакции опоры будет по модулю равна этой составляющей, а по направлению противоположна ей. А вот параллельная компонента полностью отвечает за движение бруска по плоскости. Найти значения этих компонент несложно, они представляют собой катеты прямоугольного треугольника, а гипотенуза – сам вектор . Тогда:
. (1)
Ускорение бруска найдём по второму закону Ньютона. С учётом формул (1) запишем ответ задачи:
; .
Хотя условие задачи не требует нахождения силы реакции опоры, опишем процесс её нахождения в этой задаче, чтобы в дальнейших задачах не повторяться.
; . (2)
Анализ решения.
При решении этой задачи мы обошлись исключительно геометрическими построениями, нам не пришлось решать системы алгебраических уравнений.
Стоит заметить следующее: вклад в движение тел вносят только те силы, которые имеют ненулевые составляющие к предполагаемому направлению движения. Координатный метод решения позволяет не проводить такой тщательный анализ сил, в векторном методе он необходим!
3.1.2 Учёт силы трения
Брусок массой находится на наклонной плоскости с углом наклона к горизонту (рис. 3). Найти ускорение бруска , если коэффициент трения бруска о плоскость равен .
Решение.
Частично пропустим анализ условия задачи – он приведён в предыдущем пункте. Отметим только новое. Вдоль направления движения теперь будут действовать две силы: параллельная составляющая силы тяжести и сила трения (рисунок 5). Величина силы трения нам также пока неизвестна. Но известно следующее: . Другими словами: сила трения всегда пропорциональна силе реакции опоры! В таких случаях бывает весьма полезным введение обобщающей силы реакции опоры . Её направление не будет зависеть от величины силы реакции опоры , а будет только определяться величиной коэффициента трения скольжения . Действительно:
или . (3)
Если , то это значит, что сила трения покоя достигла своего максимального значения и превратилась в силу трения скольжения, но этой силы недостаточно для предотвращения соскальзывания – тело придёт в движение. Если же , то это значит, что сила трения покоя ещё не достигла своего максимального значения и ещё может удерживать брусок в покое. Тогда ответ запишется следующим образом:
;
.
где учтено, что .
Анализ решения.
В этой задаче мы выявили очень важную и полезную зависимость (3). В дальнейшем будем часто ей пользоваться.
При наличии силы трения может существовать целый диапазон значений углов , при которых брусок будет покоиться.
Полученный ответ более общ по сравнению с предыдущей. Предыдущая задача является частным случаем данной – её решение можно получить, если подставить в ответ . Проделайте это самостоятельно.
3.1.3 Учёт ускоренного движения наклонной плоскости без учёта силы трения
Брусок массой находится на гладком клине с углом наклона к горизонту (рисунок 6). Найти ускорение бруска (относительно клина), если клин движется по основанию ускоренно с ускорением .
Решение.
За основу возьмём задачу 3.1.1. Теперь клин, а, значит, и система отсчёта, связанная с ним, движется ускоренно. Это значит, что к силам тяжести и реакции опоры, действующих на брусок, добавится ещё одна – сила инерции , обусловленная ускоренным движением клина зелёная на рисунке 7. В условии задачи направление ускоренного движения клина не указано, поэтому сразу укажем два равновозможных направления вектора силы инерции. В дальнейшем рассмотрим каждый случай по отдельности. Эта сила не перпендикулярна плоскости клина, поэтому также как и сила тяжести внесёт вклад в движение бруска. Этот вклад будет определяться параллельной составляющей вектора силы к наклонной плоскости. Перпендикулярная составляющая, так же как и сила тяжести будет только влиять на величину силы реакции опоры. Компоненты вектора силы инерции указаны на рисунке 7 красными векторами. Выпишем величины составляющих (их найдём так же, как и составляющие вектора силы тяжести в задаче 1):
(4)
Вектор результирующей силы запишется в виде:
(5)
(не забываем о направлении силы инерции!)
Тогда ускорение тела будет равно:
(6)
А вот модуль ускорения существенно зависит от того, куда будет двигаться клин. Поэтому рассмотрим два возможных варианта.
1) Клин движется ускоренно влево (рисунок 8).
В этом случае сила инерции будет направлена вправо. Две параллельные компоненты сил тяжести и инерции направлены в одну сторону, поэтому определено направление ускорения бруска . Он будет двигаться вниз вдоль наклонной плоскости клина с ускорением, модуль которого будет равен:
(7)
(это следует из формул (6) и (4)).
Но так будет не всегда. При увеличении ускорения клина увеличится и ускорение бруска. В конце концов компонента вектора ускорения , сонаправленная вектору , станет равной самому вектору (рисунок 9). В этот момент брусок оторвётся от клина и будет двигаться далее только под действием силы тяжести. Из построения видно, что . Тогда с учётом формулы (7):
Действительно, при – невозможно заставить двигаться брусок с ускорением свободного падения, вытаскивая из-под него горизонтально расположенную доску. Наоборот, при – вдоль вертикальной стены брусок и так движется с ускорением свободного падения.
1) Клин движется ускоренно вправо (рисунок 9).
В этом случае компоненты векторов сил тяжести и инерции, обозначенные нами как параллельные, направлены противоположно друг другу. Поэтому направление ускорения бруска неочевидно. Оно может быть направлено как вниз, так и вверх. А если названные компоненты компенсируют друг друга, то брусок вообще будет покоиться. Исходя из уравнения (6), найдём модуль ускорения для всех случаев.
Если , то ускорение бруска направлено вниз вдоль клина и по имеет величину .
Если , то ускорение бруска направлено вверх вдоль клина и по имеет величину .
Если , то ускорение бруска равно нулю. Это возможно при условии, когда .
Анализ решения.
Мы получили несколько различных движений в зависимости от величины и направления ускорения клина, а также прямо в тексте решения провели и их анализ на правильность и допустимость. Опять-таки, все выводы довольно просты, очевидны и в большей мере используют физику нежели традиционный координатный способ.
Представленное решение не единственно. Рассмотрим ещё одно, на наш взгляд, более простое и элегантное. По аналогии с обобщающей силой реакции опоры (см. предыдущую задачу) введём обобщающую силу действия – сумму сил тяжести и инерции (рисунок 10). Формально это можно рассматривать как изменение ускорения свободного падения на некоторое . Преимущества этого подхода заключается в том, что рассматривается только одно компонента – параллельная плоскости клина, которая вносит вклад в движение. В зависимости от ориентации вектора суммарного действия, тело будет либо покоиться, либо двигаться ускоренно вверх или вниз. Из построения на рис. 10 видно, что:
Если , то тело будет двигаться ускоренно вверх по клину с ускорением, равным по модулю .
Если , то брусок будет покоиться.
Если , то брусок соскользнёт вниз с ускорением .
Обозначенные три условия касались случая, когда ускорение клина направлено вправо. Если же ускорение клина направлено влево, то независимо от величины угла , тело будет соскальзывать вниз по клину с ускорением по величине .
В этих формулах .
Выведенные здесь формулы полностью совпадают с полученными ранее после их преобразовании. Рассмотрим общий случай:
.
Выразим неизвестные пока и через полученный ранее :
.
Тогда:
.
Такие же ответы были получены ранее. Значит, предложенные решения верны, но второе, несомненно, более изящно. Собственно говоря, именно данное решение в большей степени можно рассматривать, как применение векторного способа.
Следует заметить, что мы нашли в задаче ускорение бруска относительно клина, а не относительно стола, по которому движется клин. Самостоятельное решение поставленной задачи позволить глубже разобраться в происходящем. Но уже сейчас видно, как нужно действовать – нужно сложить полученное ускорение с ускорением самого клина. Нарисовать схему векторов будет несложно, а вот для нахождения модуля результирующего ускорения нужно будет «попотеть» – используется теорема косинусов.
Также возможно рассмотрение более общей задачи с учётом силы трения бруска о клин, которое характеризуется коэффициентом трения скольжения . Решение задачи в данной работе представлено не будет, т.к. оно является объединением решений двух предыдущих задач. Продуктивным будет решение, заключающееся в рассмотрении не 4 векторов, а только двух обобщённых (обобщённой силы действия, равной сумме силы тяжести и силы инерции, и обобщённой силы реакции опоры, равной сумме силы реакции опоры и силы трения).
3.2 Задачи на нахождение минимальной силы, действующей на тело.
3.2.1 Простейший случай
Брусок массой лежит на плоскости (рисунок 11). Коэффициент трения скольжения бруска о плоскость . С какой минимальной силой нужно действовать на брусок, чтобы сдвинуть его с места.
Решение.
В задаче присутствуют следующие материальные тела: брусок, плоскость, Земля. Взаимодействие бруска и Земли выражается посредством силы тяжести, действующей на брусок. Взаимодействие бруска и плоскости описывается с помощью силы реакции опоры. При любой попытке сдвинуть тело с места возникнет сила трения (сперва покоя, а потом и скольжения). Сделаем чертёж и расставим обозначенные силы (рисунок 12).
Из условия задачи понятно, что брусок будет двигаться по плоскости. Но минимальная сила, вызвавшая движение, не обязательно должно быть направлена горизонтально. Это станет понятным из следующих соображений. Сила должна преодолеть силу трения скольжения, которая зависит от силы реакции опоры, которая, в свою очередь будет зависеть от силы тяжести и, самое главное, приложенной силы. Прикладывая силу горизонтально, мы не компенсируем силу реакции опоры, поэтому и сила трения максимальна. Наоборот, прикладывая силу под большим углом, мы будем больше поднимать тело, чем его тащить. Оптимальный вариант заключается в том, чтобы мы приложенной силой слегка приподняли тело, чтобы уменьшить силу реакции опоры и, соответственно, силу трения.
По условию задачи тело должно двигаться равномерно. Тогда по второму закону Ньютона, сумма сил, действующих на тело должна быть равна нулю.
. (8)
Введём в рассмотрение обобщённую силу реакции опоры , равную сумме сил реакции опоры и сил трения. Вектора и перпендикулярны друг другу, и их можно рассматривать как катеты, а вектор — как гипотенузу. Её величина пока неизвестна, но зато вполне определено направление этой силы. Действительно, вектора и пропорциональны друг другу, поэтому отношение модулей силы трения и реакции опоры будет однозначно определённым.
или .
В этом случае формула (8) примет вид:
. (9)
Исследуем формулу (9) графически (рисунок 13). Отобразим вектор силы тяжести. От его конца отложим известный нам угол наклона вектора обобщённой силы реакции опоры. Сам вектор будет лежать на полученном луче. Вектор приложенной силы будет начинаться в конце вектора , а заканчиваться в начале вектора силы тяжести. Этот вектор будет минимален только в одном случае – когда он будет перпендикулярен вектору , или тройка векторов , и должны составлять перпендикулярный треугольник. Любое другое положение вектора (черные отрезки на рисунке 13) приведёт только к увеличению силы. Из анализа полученного треугольника находим: минимальная сила должна быть направлена под углом к горизонту. Вычислим модуль этой силы:
.
Анализ решения.
Приведём решение задачи с использованием традиционного координатного способа.
За основу возьмём расположение сил на рисунке 12 и формулу (8). Выберем систему отсчёта (рисунке 14). Ось направлена горизонтально, а ось — вертикально. Спроецируем формулу (8) на оси системы координат:
.
Решим систему:
(10)
Величина приложенной силы весьма сложным образом зависит от угла наклона силы к горизонтали. Для нахождения экстремального значения нужно вычислить производную функции и приравнять её к нулю. Потом нужно вычислить вторую производную, чтобы узнать, с каким экстремумом мы имеем дело: точкой минимума или максимума. Далее полученное значение подставляется в функцию и находится его значение. Краткое обозначение дальнейшей деятельности совсем не добавило оптимизма, наоборот, один вид анализируемой функции отбивает всякое желание выполнять названные этапы. Но мы всё же приведём дальнейшее решение.
Произведение равно нулю, когда один из сомножителей равен нулю. Но , (т.к. знаменатель не может быть равным нулю). Остаётся только следующее: . Решая, получаем: — точно такой же ответ мы получили раньше гораздо проще и понятнее. Находя вторую производную, убеждаемся что это действительно точка минимума. Тогда подставим полученное решение в формулу (10) и найдём ответ:
.
Ответы совпадают, но второй был получен гораздо более сложным образом и совсем ненагляден. Ещё раз убеждаемся в простоте, элегантности и эффективности векторного способа решения физических задач.
3.2.2 Движение бруска с заданным ускорением
Брусок массой лежит на плоскости (рисунок 15). Коэффициент трения скольжения бруска о плоскость . С какой минимальной силой нужно действовать на брусок, чтобы он начал двигаться с ускорением .
Решение.
За основу возьмём решение предыдущей задачи и внесём в него необходимые изменения.
Во-первых, это касается уравнения (8). Теперь оно запишется в виде:
. (11)
Через обозначим обобщённую реакцию опоры. Как показано в предыдущих задачах, этим мы добиваемся определённости в направлении вектор, а это не так уж и мало.
Дальнейшее решение также проведём графически и с применением векторного подхода (рисунке 16). Искомый вектор должен заканчиваться в конце вектора . Он будет минимален только в одном случае, если будет перпендикулярен вектору обобщённой реакции опоры. Вектор стал больше, а вот вектор — меньше.
Из уравнения (11) выразим вектор :
.
Вектора и известны по условию задачи. Поэтому целесообразно их объединить в один. Обозначим его через .
.
Модуль вектора равен , а между составляющими существует следующее соотношение .
После этого векторная диаграмма существенно упрощается, и становится возможным её решить (рисунок 17). Вектор — гипотенуза прямоугольного треугольника, а векторы и — его катеты. Тогда:
Как и следовало ожидать, ответ должен быть похожим на ответ предыдущей задачи. Если в условии задачи принять, что ускорение равно нулю, то мы получим ответ предыдущей задачи.
Из рисунка 16 видно, что вполне возможна ситуация, когда вектор вообще превратится в нуль. Определим, какую силу нужно приложить к бруску в этом случае и с каким ускорением от при этом будет двигаться. В полученном прямоугольном треугольнике вектор силы тяжести уже не будет гипотенузой – это уже противолежащий катет. Гипотенузой стала сама приложенная сила. Тогда:
.
Результирующая сила будет являться прилежащим катетом. Между катетами существует следующее соотношение:
;
откуда
. (12)
При ускорениях, больших, чем определяются формулой (12) брусок оторвётся от поверхности и взлетит. Дальше будет двигаться только под действием двух сил: приложенной силы и силы тяжести.
Анализ решения.
Проверка полученных формул на граничные условия показала, что они верны. Практически вся задача была решена практически устно, за исключением момента преобразования ответа. Но если бы мы решали задачу традиционным способом, то всё равно не избежали бы таких громоздких преобразований. Более того, они были бы значительно усложнёнными.
Вариацией на тему может быть также задача следующего содержания: «Найти минимальную силу, которую нужно приложить к бруску, чтобы тот сдвинулся с места в случае, когда плоскость, на которой находится брусок, движется горизонтально с ускорением ». Нетрудно заметить, что ответ будет полностью похож на ответ решённой задачи за исключением того, что в числителе в скобках вместо знака «плюс» должен стоять знак «плюс-минус». Это определяется направлением ускоренного движения основания: движется ли оно влево или вправо. Приведём ответ:
.
3.2.3 Движение бруска по клину
На наклонной стороне клина с углом наклона лежит брусок массой . Какую минимальную силу следует приложить к бруску, чтобы начать тащить его равномерно вверх по клину, если коэффициент трения скольжения бруска по клину равен (риунок. 18)?
Решение.
Задача похожа на предыдущие, поэтому должны быть похожи подходы в решении и, собственно говоря, ответы.
Изобразим диаграмму сил и сразу введём обобщающую силу реакции опоры (рисунок 19).
Брусок поднимают равномерно, поэтому результирующая сила равна нулю. Запишем второй закон Ньютона для данных сил:
.
Решим полученное уравнение графически (рис. 20). Начнём с известной силы тяжести. Далее определимся с направлением обобщённой силы реакции опоры. Она будет повёрнута теперь на угол (составные силы – реакции опоры и трения – сами наклонены на угол , а угол определяется исключительно величиной коэффициента трения скольжения ), а вот величина её нам по-прежнему не известна. Поэтому поступим, как поступали ранее: проведём в обозначенном направлении луч, а из точки начала вектора силы тяжести опустим на проведённый луч перпендикуляр. Полученный перпендикуляр будет искомой силой, а отрезок луча от конца вектора силы тяжести до точки пересечения будет являться вектором обобщённой силы реакции опоры. Тогда:
(13)
Сила будет направлена также под углом к поверхности клина.
Если в полученную формулу (13) подставить угол , то получим ответ задачи 3.2.1.
Анализ решения.
Ответ опять-таки получен практически устно. Проверка на граничные условия показала его правильность.
Теперь не составит труд решить задачу ещё более общего вида: «На наклонной плоскости клина с углом наклона покоится брусок массы , удерживаемый силой трения покоя. С какой минимальной силой нужно тащить брусок равномерно вверх, если клин двигается горизонтально с ускорением . Коэффициент трения скольжения между бруском и клином равен ». Ответом, как нетрудно догадаться, будет обобщение ответов рассмотренных выше задач. Решение приводить не будем.
3.3 Задачи о равновесии бруска
3.3.1 Простейший случай
К вертикальной стене горизонтальной силой прижат брусок массой . Какова должна быть эта сила по величине, чтобы брусок покоился, если коэффициент трения скольжения бруска о стену равен (рисунок 21)?
Решение.
Расставим все силы, действующие на брусок (рисунок 22). В этой задаче тоже будем использовать обобщённую силу реакции опоры – как было неоднократно показано, этим мы добьёмся определённости в её направлении. Также можно ввести в рассмотрение обобщённую силу действия , равную сумме сил тяжести и приложенной силы: . Это позволит анализировать только две силы вместо четырёх. Равновесие наступит в случае равенства сил и , а это возможно только в том случае, когда они лежат на одной прямой. Но направление обобщённой реакции опоры зафиксировано и определяется исключительно коэффициентом трения скольжения. Это значит, что между векторами приложенной силы и обобщённого действия должен быть точно такой же угол. А это возможно только в том случае, когда для векторов и будет выполняться условие:
.
Отсюда следует, что
. (14)
Действительно, сила реакции опоры будет равна приложенной силе, а сила трения равна . Действие силы тяжести компенсируется противодействием возникшей силы трения.
Анализ решения.
Если приложенная сила по величине будет меньше, чем вычисленная по формуле (14), то это будет означать, что направления векторов обобщённых сил действия и реакции опоры не будут противоположно направлены, а это, в свою очередь, будет означать, что существует ненулевая результирующая сила, которая стремиться сдвинуть тело с места вниз. Если же величина приложенной силы будет больше вычисленной, то тогда по нашим рассуждениям должна возрасти и сила реакции опоры, а вслед за ней и сила трения. Т.е. появится сила, стремящаяся сдвинуть тело вверх??? На самом деле в этом случае помимо изменения величины силы измениться и её направление (это проявится в уменьшении угла наклона). Это значит, что сила трения не будет уже силой трения скольжения, она будет ещё силой трения покоя, которая в точности равна силе тяжести. Напомним, что угол наклона результирующих сил действия и реакции опоры мы вычисляли для силы трения скольжения, и в данном случае такой метод определения направления будет неприменим.
3.3.2 Нахождение минимальной силы
Слегка изменим условие предыдущей задачи, а именно, найдём минимальную силу, которую нужно приложить к бруску, чтобы тот не соскользнул.
Решение.
Ясно, что она совсем не должна быть направлена горизонтально – она будет направлена под некоторым углом к вертикали. Рассмотрим треугольник сил, действующих на тело: это сила тяжести , обобщённая сила реакции опоры и приложенная сила (рисунок 23). Как обычно, начнем рассуждения с известных – это сила тяжести. Через конец этой силы проведём прямую под углом к горизонтали (напомним, что именно такой угол составляет вектор с вектором реакции опоры , т.е. с горизонталью). А из начала вектора силы тяжести опустим перпендикуляр на проведённую прямую (это и будет минимальное расстояние между точкой и прямой), величина и направление которого определят приложенную силу. Нетрудно видеть, что она равна
. (15)
Анализ решения.
Немного удивляет тот факт, что величина полученной силы оказалась меньше силы тяжести.
Если величина коэффициента трения будет стремиться к 1, то величина приложенной силы будет стремиться к . Угол между вертикалью и вектором приложенной силы при этом будет стремиться к 45°.
Если же коэффициент трения скольжения станет равным нулю, то величина приложенной силы в этом случае станет равной силе тяжести и будет направлена вертикально вверх (т.е. под тело поставили подставку). Это хорошо согласуется с тем, что наблюдается наяву.
Задания
Версия для печати и копирования в MS Word
Автомобиль движется прямолинейно. На графике представлена зависимость скорости автомобиля от времени. Чему равен минимальный модуль ускорения? Ответ выразите в метрах на секунду в квадрате.
Спрятать решение
Решение.
На всех рассматриваемых интервалах времени скорость автомобиля меняется равномерно, следовательно, ускорение на каждом интервале постоянно. Рассчитаем ускорения:
в интервале от 0 до 10 с:
в интервале от 10 до 20 с:
в интервале от 20 до 30 с:
в интервале от 30 до 40 с:
Минимальный модуль ускорения равен 0,5 м/с2.
Ответ: 0,5.
Гость 13.10.2012 16:25
здравствуйте) а почему не с 20 до 30?
там же вроде убывает о.о
Гость
Добрый день!
В данной задаче спрашивают не о минимальном значении проекции ускорения, а о минимальном значении модуля ускорения. Поэтому необходимо сравнивать абсолютные величины.
КАК НАЙТИ МОДУЛЬ МИНИМАЛЬНОГО УСКОРЕНИЯ ?
2 Ответы
оставил комментарий
18 Май, 18
от
Fredi2005_zn
Начинающий
(166 баллов)