Как найти минимальное значение в матлабе

Minimum elements of array

Syntax

Description

example

M = min(A)
returns the minimum elements of an array.

  • If A is a vector, then
    min(A) returns the minimum of
    A.

  • If A is a matrix, then
    min(A) is a row vector containing the minimum
    value of each column of A.

  • If A is a multidimensional array, then
    min(A) operates along the first dimension of
    A whose size is greater than
    1, treating the elements as vectors. The size
    of M in this dimension becomes
    1, while the sizes of all other dimensions
    remain the same as in A. If A
    is an empty array whose first has zero length, then
    M is an empty array with the same size as
    A.

  • If A is a
    table or timetable, then min(A) returns a one-row
    table containing the minimum of each variable. (since R2023a)

example

M = min(A,[],"all")
returns the minimum over all elements of A.

example

M = min(A,[],dim)
returns the minimum element along dimension dim. For example,
if A is a matrix, then min(A,[],2) returns
a column vector containing the minimum value of each row.

example

M = min(A,[],vecdim)
returns the minimum over the dimensions specified in the vector
vecdim. For example, if A is a matrix,
then min(A,[],[1 2]) returns the minimum over all elements in
A because every element of a matrix is contained in the
array slice defined by dimensions 1 and 2.

example

M = min(A,[],___,missingflag)
specifies whether to omit or include missing values in A for
any of the previous syntaxes. For example,
min(A,[],"includemissing") includes all missing values
when computing the minimum. By default, min omits missing
values.

example

[M,I] =
min(___)
also returns the index into the operating dimension that corresponds to the
first occurrence of the minimum value of A.

example

[M,I] =
min(A,[],___,"linear")
also returns the linear index into A that corresponds to the
minimum value in A.

example

C = min(A,B)
returns an array with the smallest elements taken from A or
B.

C = min(A,B,missingflag)
also specifies how to treat missing values.

___ = min(___,"ComparisonMethod",method)
optionally specifies how to compare elements for any of the previous syntaxes.
For example, for a vector A = [-1 2 -9], the syntax
min(A,[],"ComparisonMethod","abs") compares the elements
of A according to their absolute values and returns a minimum
value of -1.

Examples

collapse all

Smallest Vector Element

Create a vector and compute its smallest element.

A = [23 42 37 15 52];
M = min(A)

Smallest Complex Element

Create a complex vector and compute its smallest element, that is, the element with the smallest magnitude.

A = [-2+2i 4+i -1-3i];
min(A)

Smallest Element in Each Matrix Column

Create a matrix and compute the smallest element in each column.

Smallest Element in Each Matrix Row

Create a matrix and compute the smallest element in each row.

A = [1.7 1.2 1.5; 1.3 1.6 1.99]
A = 2×3

    1.7000    1.2000    1.5000
    1.3000    1.6000    1.9900

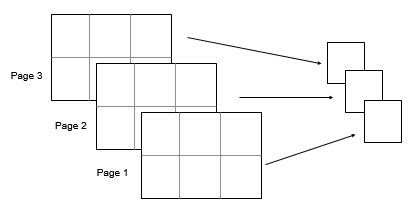
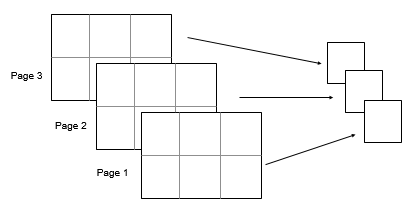
Minimum of Array Page

Create a 3-D array and compute the minimum over each page of data (rows and columns).

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
M1 = min(A,[],[1 2])
M1 = 
M1(:,:,1) =

    -2


M1(:,:,2) =

    -5


M1(:,:,3) =

    -3

To compute the minimum over all dimensions of an array, you can either specify each dimension in the vector dimension argument or use the "all" option.

Smallest Element Including Missing Values

Create a matrix containing NaN values.

A = [1.77 -0.005 3.98 -2.95; NaN 0.34 NaN 0.19]
A = 2×4

    1.7700   -0.0050    3.9800   -2.9500
       NaN    0.3400       NaN    0.1900

Compute the minimum value of the matrix, including missing values. For matrix columns that contain any NaN value, the minimum is NaN.

M = min(A,[],"includemissing")
M = 1×4

       NaN   -0.0050       NaN   -2.9500

Smallest Element Indices

Create a matrix A and compute the smallest elements in each column as well as the row indices of A in which they appear.

Return Linear Indices

Create a matrix A and return the minimum value of each row in the matrix M. Use the "linear" option to also return the linear indices I such that M = A(I). 

[M,I] = min(A,[],2,"linear")

Smallest Element Comparison

Create a matrix and return the smallest value between each of its elements compared to a scalar.

Input Arguments

collapse all

A — Input array
scalar | vector | matrix | multidimensional array | table | timetable

Input array, specified as a scalar, vector, matrix, multidimensional array, table, or
timetable.

  • If A is complex, then min(A) returns
    the complex number with the smallest magnitude. If magnitudes are
    equal, then min(A) returns the value with the smallest
    magnitude and the smallest phase angle.

  • If A is a scalar, then min(A) returns A.

  • If A is a 0-by-0 empty array, then min(A) is
    as well.

If A has type categorical, then it
must be ordinal.

Complex Number Support: Yes

dim — Dimension to operate along
positive integer scalar

Dimension
to operate along, specified as a positive integer scalar. If you do not specify the dimension,
then the default is the first array dimension of size greater than 1.

Dimension dim indicates the dimension whose
length reduces to 1. The size(M,dim) is 1,
while the sizes of all other dimensions remain the same, unless size(A,dim) is 0.
If size(A,dim) is 0, then min(A,dim) returns
an empty array with the same size as A.

Consider an m-by-n input matrix,
A:

  • min(A,[],1) computes the minimum of the
    elements in each column of A and returns a
    1-by-n row
    vector.

    min(A,[],1) column-wise operation

  • min(A,[],2) computes the minimum of the
    elements in each row of A and returns an
    m-by-1 column
    vector.

    min(A,[],2) row-wise operation

vecdim — Vector of dimensions
vector of positive integers

Vector of dimensions, specified as a vector of positive integers. Each
element represents a dimension of the input array. The lengths of the output
in the specified operating dimensions are 1, while the others remain the
same.

Consider a 2-by-3-by-3 input array, A. Then
min(A,[],[1 2]) returns a 1-by-1-by-3 array whose
elements are the minimums computed over each page of
A.

Mapping of a 2-by-3-by-3 input array to a 1-by-1-by-3 output array

missingflag — Missing value condition
"omitmissing" (default) | "omitnan" | "omitnat" | "omitundefined" | "includemissing" | "includenan" | "includenat" | "includeundefined"

Missing value condition, specified as one of the values in this
table.

Value Input Data Type Description
"omitmissing" All supported data types Ignore missing values in the input arrays,
and compute the minimum over fewer points. If all elements
in the operating dimension are missing, then the
corresponding element in M is
missing.
"omitnan" double, single,
duration
"omitnat" datetime
"omitundefined" categorical
"includemissing" All supported data types

Include missing values in the input
arrays when computing the minimum. If any element in the
operating dimension is missing, then the corresponding
element in M is
missing.
"includenan" double, single,
duration
"includenat" datetime
"includeundefined" categorical

B — Additional input array
scalar | vector | matrix | multidimensional array | table | timetable

Additional input array, specified as a scalar, vector, matrix, multidimensional array, table,
or timetable. Inputs A and B must
either be the same size or have sizes that are compatible (for example,
A is an M-by-N
matrix and B is a scalar or
1-by-N row vector). For more
information, see Compatible Array Sizes for Basic Operations.

  • If A and B are both arrays,
    then they must be the same data type unless one is a
    double. In that case, the data type of the
    other array can be single,
    duration, or any integer type.

  • If A and B are ordinal
    categorical arrays, they must have the same
    sets of categories with the same order.

  • If either A or B is a table
    or timetable, then the other input can be an array, table, or
    timetable.

Complex Number Support: Yes

method — Comparison method
"auto" (default) | "real" | "abs"

Comparison method for numeric input, specified as one of these values:

  • "auto" — For a numeric input array
    A, compare elements by
    real(A) when A is real,
    and by abs(A) when A is
    complex.

  • "real" — For a numeric input array
    A, compare elements by
    real(A) when A is real or
    complex. If A has elements with equal real parts,
    then use imag(A) to break ties.

  • "abs" — For a numeric input array
    A, compare elements by
    abs(A) when A is real or
    complex. If A has elements with equal magnitude,
    then use angle(A) in the interval (-π,π] to break
    ties.

Output Arguments

collapse all

M — Minimum values
scalar | vector | matrix | multidimensional array | table

Minimum values, returned as a scalar, vector, matrix, multidimensional array or table.
size(M,dim) is 1, while the sizes
of all other dimensions match the size of the corresponding dimension in
A, unless size(A,dim) is
0. If size(A,dim) is
0, then M is an empty array with
the same size as A.

I — Index
scalar | vector | matrix | multidimensional array | table

Index, returned as a scalar, vector, matrix, multidimensional array, or
table. I is the same size as the first output.

When "linear" is not specified, I is
the index into the operating dimension. When "linear" is
specified, I contains the linear indices of
A corresponding to the minimum values.

If the smallest element occurs more than once, then I
contains the index to the first occurrence of the value.

C — Minimum elements from A or B
scalar | vector | matrix | multidimensional array | table | timetable

Minimum elements from A or B, returned as a scalar,
vector, matrix, multidimensional array, table, or timetable. The size of
C is determined by implicit expansion of the
dimensions of A and B. For more
information, see Compatible Array Sizes for Basic Operations.

The data type of C depends on the data types
of A and B:

  • If A and B are
    the same data type, then C matches the data type
    of A and B.

  • If either A or B is single,
    then C is single.

  • If either A or B is
    an integer data type with the other a scalar double,
    then C assumes the integer data type.

  • If either A or B is a
    table or timetable, then C is a table or
    timetable.

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

This function fully supports tall arrays. For
more information, see Tall Arrays.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

  • If you specify an empty array for the second argument in order to
    supply dim or missingflag, the
    second argument must be of fixed-size and of dimension
    0-by-0.

  • If you specify dim or
    missingflag, then they must be constants.

  • If the input is a variable-size array, the length of the dimension to
    operate along must not be zero at run-time.

  • See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).

  • See Code Generation for Complex Data with Zero-Valued Imaginary Parts (MATLAB Coder).

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

  • If you specify an empty array for the second argument in order to
    supply dim or missingflag, the
    second argument must be of fixed-size and of dimension
    0-by-0.

  • If you specify dim or
    missingflag, then they must be constants.

  • See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).

  • See Code Generation for Complex Data with Zero-Valued Imaginary Parts (MATLAB Coder).

HDL Code Generation
Generate Verilog and VHDL code for FPGA and ASIC designs using HDL Coder™.

Usage notes and limitations:

  • Inputs of 3-D matrices or greater are not supported.

  • Inputs that have complex data types are not supported.

  • Input matrices or vectors must be of equal size.

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a

expand all

R2023a: Specify missing value condition

Omit or include all missing values in the input arrays when computing the minimum
value by using the "omitmissing" or
"includemissing" options. Previously,
"omitnan", "includenan",
"omitnat", "includenat",
"omitundefined", and "includeundefined"
specified a missing value condition that was specific to the data type of the input
arrays.

R2023a: Perform calculations directly on tables and timetables

The min function can calculate on all variables within a table or
timetable without indexing to access those variables. All variables must have data types
that support the calculation. For more information, see Direct Calculations on Tables and Timetables.

R2021b: Specify comparison method

Specify the real or absolute value method for determining the minimum value of the
input by using the ComparisonMethod parameter.

R2018b: Operate on multiple dimensions

Operate on multiple dimensions of the input arrays at a time. Specify a vector of
operating dimensions, or specify the "all" option to operate on
all array dimensions.

Источник

Минимальные элементы массива

Синтаксис

Описание

пример

M = min(A) возвращает минимальные элементы массива.

  • Если A вектор, затем min(A) возвращает минимум A.

  • Если A матрица, затем min(A) вектор-строка, содержащий минимальное значение каждого столбца.

  • Если A многомерный массив, затем min(A) действует вдоль первого измерения массива, размер которого не равняется 1, обработка элементов как векторы. Размер этой размерности становится 1 в то время как размеры всех других размерностей остаются то же самое. Если A пустой массив с первой размерностью 0, затем min(A) возвращает пустой массив с тем же размером как A.

пример

M = min(A,[],dim) возвращает минимальный элемент по измерению dim. Например, если A матрица, затем min(A,[],2) вектор-столбец, содержащий минимальное значение каждой строки.

пример

M = min(A,[],nanflag) задает, включать ли или не использовать NaN значения в вычислении. Например, min(A,[],'includenan') включает весь NaN значения в A в то время как min(A,[],'omitnan') игнорирует их.

M = min(A,[],dim,nanflag) также задает размерность, которую задает направление расчета при использовании nanflag опция.

пример

[M,I] =
min(___) также возвращает индекс в операционную размерность, которая соответствует минимальному значению A для любого из предыдущих синтаксисов.

пример

M = min(A,[],'all') находит минимум по всем элементам A. Этот синтаксис допустим для MATLAB® версии R2018b и позже.

пример

M = min(A,[],vecdim) вычисляет минимум по размерностям, заданным в векторном vecdim. Например, если A матрица, затем min(A,[],[1 2]) вычисляет минимум по всем элементам в A, поскольку каждый элемент матрицы содержится в срезе массивов, заданном размерностями 1 и 2.

M = min(A,[],'all',nanflag) вычисляет минимум по всем элементам A при использовании nanflag опция.

M = min(A,[],vecdim,nanflag) задает несколько размерностей, которых задают направление расчета при использовании nanflag опция.

[M,I] =
min(A,[],'all',___) возвращает линейный индекс в A это соответствует минимальному значению в A при определении 'all'.

пример

[M,I] =
min(A,[],___,'linear') возвращает линейный индекс в A это соответствует минимальному значению в A.

пример

C = min(A,B) возвращает массив с самыми маленькими элементами, взятыми из A или B.

C = min(A,B,nanflag) также задает, как обработать NaN значения.

___ = min(___,'ComparisonMethod',method) опционально задает, как сравнить элементы для любого из предыдущих синтаксисов. Например, для векторного A = [-1 2 -9], синтаксис min(A,[],'ComparisonMethod','abs') сравнивает элементы A согласно их абсолютным значениям и возвращает -1.

Примеры

свернуть все

Самый маленький векторный элемент

Создайте вектор и вычислите его самый маленький элемент.

A = [23 42 37 15 52];
M = min(A)

Самый маленький комплексный элемент

Создайте комплексный вектор и вычислите его самый маленький элемент, то есть, элемент с наименьшей величиной.

A = [-2+2i 4+i -1-3i];
min(A)

Самый маленький элемент в каждом столбце матрицы

Создайте матрицу и вычислите самый маленький элемент в каждом столбце.

Самый маленький элемент в каждой матричной строке

Создайте матрицу и вычислите самый маленький элемент в каждой строке.

A = [1.7 1.2 1.5; 1.3 1.6 1.99]
A = 2×3

    1.7000    1.2000    1.5000
    1.3000    1.6000    1.9900

Самое маленькое включение элемента NaN

Создайте вектор и вычислите его минимум, исключая NaN значения.

A = [1.77 -0.005 3.98 -2.95 NaN 0.34 NaN 0.19];
M = min(A,[],'omitnan')

min(A) также приведет к этому результату начиная с 'omitnan' опция по умолчанию.

Используйте 'includenan' отметьте, чтобы возвратить NaN.

M = min(A,[],'includenan')

Самые маленькие индексы элемента

Создайте матричный A и вычислите самые маленькие элементы в каждом столбце, а также индексах строки A в котором они появляются.

Минимум страницы массивов

Создайте трехмерный массив и вычислите минимум по каждой странице данных (строки и столбцы).

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
M1 = min(A,[],[1 2])
M1 = 
M1(:,:,1) =

    -2


M1(:,:,2) =

    -5


M1(:,:,3) =

    -3

Начиная в R2018b, вычислять минимум по всем размерностям массива, можно или задать каждую размерность в векторном аргументе размерности или использовать 'all' опция.

Возвратите линейные индексы

Создайте матричный A и возвратите минимальное значение каждой строки в матричном M. Используйте 'linear' опция, чтобы также возвратить линейные индексы I таким образом, что M = A(I). 

[M,I] = min(A,[],2,'linear')

Самое маленькое сравнение элемента

Создайте матрицу и возвратите наименьшее значение между каждым из его элементов по сравнению со скаляром.

Входные параметры

свернуть все

A — Входной массив
скаляр | вектор | матрица | многомерный массив

Входной массив, заданный как скалярный, векторный, матричный или многомерный массив.

  • Если A является комплексным, затем min(A) возвращает комплексное число с наименьшей величиной. Если величины равны, то min(A) возвращает значение с наименьшей величиной и самым маленьким углом фазы.

  • Если A скаляр, затем min(A) возвращает A.

  • Если A пустой массив 0 на 0, затем min(A) также.

Если A имеет вводят categorical, затем это должно быть порядковым.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | categorical | datetime | duration
Поддержка комплексного числа: Да

dim — Размерность, которая задает направление расчета
положительный целочисленный скаляр

Величина для работы, заданная как положительный целый скаляр. Если значение не задано, то по умолчанию это первый размер массива, не равный 1.

Размерность dim указывает на размерность, длина которой уменьшает до 1. size(M,dim) 1, в то время как размеры всех других размерностей остаются то же самое, если size(A,dim) 0. Если size(A,dim) 0, затем min(A,dim) возвращает пустой массив с тем же размером как A.

Рассмотрите двумерный входной массив, A:

  • Если dim = 1, затем min(A,[],1) возвращает вектор-строку, содержащий самый маленький элемент в каждом столбце.

  • Если dim = 2, затем min(A,[],2) возвращает вектор-столбец, содержащий самый маленький элемент в каждой строке.

min возвращает A если dim больше ndims(A).

vecdim — Вектор из размерностей
вектор из положительных целых чисел

Вектор из размерностей в виде вектора из положительных целых чисел. Каждый элемент представляет размерность входного массива. Продолжительности выхода в заданных операционных размерностях равняются 1, в то время как другие остаются то же самое.

Рассмотрите 2 3х3 входным массивом, A. Затем min(A,[],[1 2]) возвращает 1 1 3 массивами, элементами которых являются минимумы, вычисленные по каждой странице A.

Типы данных: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

B — Дополнительный входной массив
скаляр | вектор | матрица | многомерный массив

Дополнительный входной массив в виде скаляра, вектора, матрицы или многомерного массива. Входные параметры A и B должен или быть одного размера или иметь размеры, которые совместимы (например, A M— N матрица и B скаляр или 1— N вектор-строка). Для получения дополнительной информации см. «Совместимые размеры массивов для основных операций».

  • A и B должен быть совпадающий тип данных, если каждый не double. В этом случае типом данных другого массива может быть singleдлительность, или любой целочисленный тип.

  • Если A и B порядковый categorical массивы, у них должны быть те же наборы категорий с тем же порядком.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | categorical | datetime | duration
Поддержка комплексного числа: Да

nanflag NaN условие
'omitnan' (значение по умолчанию) | 'includenan'

NaN условие в виде одного из этих значений:

  • 'omitnan' — Проигнорируйте весь NaN значения во входе. Если всеми элементами является NaN, затем min возвращает первый.

  • 'includenan' — Включайте NaN значения во входе для вычисления.

Для datetime массивы, можно также использовать 'omitnat' или 'includenat' не использовать и включать NaT значения, соответственно.

Для categorical массивы, можно также использовать 'omitundefined' или 'includeundefined' не использовать и включать неопределенные значения, соответственно.

Типы данных: char

method ‘ComparisonMethod’
'auto' (значение по умолчанию) | 'real' | 'abs'

Метод сравнения для числового входа в виде одного из этих значений:

  • 'auto' — Для числового входного массива A, сравните элементы real(A) когда A действительно, и abs(A) когда A является комплексным.

  • 'real' — Для числового входного массива A, сравните элементы real(A) когда A является действительным или комплексным. Если A имеет элементы с равными действительными частями, затем используйте imag(A) повредить связи.

  • 'abs' — Для числового входного массива A, сравните элементы abs(A) когда A является действительным или комплексным. Если A имеет элементы с равной величиной, затем используйте angle(A) в интервале (-π,π], чтобы повредить связи.

Выходные аргументы

свернуть все

M — Минимальные значения
скаляр | вектор | матрица | многомерный массив

Минимальные значения, возвращенные как скаляр, вектор, матрица или многомерный массив. size(M,dim) 1, в то время как размеры всех других размерностей совпадают с размером соответствующей размерности в A, если size(A,dim) 0. Если size(A,dim) 0, затем M пустой массив с тем же размером как A.

I — Индекс
скаляр | вектор | матрица | многомерный массив

Индексируйте, возвращенный как скаляр, вектор, матрица или многомерный массив. I одного размера с первым выходом.

Когда 'linear' не задан, I индекс в операционную размерность. Когда 'linear' задан, I содержит линейные индексы A соответствие минимальным значениям.

Если самый маленький элемент происходит несколько раз, то I содержит индекс к первому вхождению значения.

C — Минимальные элементы от A или B
скаляр | вектор | матрица | многомерный массив

Минимальные элементы от A или B, возвращенный как скаляр, вектор, матрица или многомерный массив. Размер C определяется неявным расширением размерностей A и BДля получения дополнительной информации см. «Совместимые размеры массивов для основных операций».

Тип данных C зависит от типов данных A и B:

  • Если A и B совпадающий тип данных, затем C совпадает с типом данных A и B.

  • Если любой A или B single, затем C single.

  • Если любой A или B целочисленный тип данных с другим скалярный double, затем C принимает целочисленный тип данных.

Расширенные возможности

«Высокие» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

  • Если вы задаете пустой массив для второго аргумента для того, чтобы предоставить dim или nanflag, второй аргумент должен иметь фиксированный размер и размерности 0— 0.

  • Если вы задаете dim или nanflag, затем они должны быть константами.

  • Если вход является массивом переменного размера, длина размерности, которой задает направление расчета не должна быть нулем во времени выполнения.

  • «Смотрите информацию о генерации кода функций Toolbox (MATLAB Coder) в разделе «»Ограничения переменных размеров»».».

  • Смотрите генерацию кода для комплексных данных с мнимыми частями с нулевым знаком (MATLAB Coder).

Генерация кода графического процессора
Сгенерируйте код CUDA® для NVIDIA® графические процессоры с помощью GPU Coder™.

Указания и ограничения по применению:

  • Если вы задаете пустой массив для второго аргумента для того, чтобы предоставить dim или nanflag, второй аргумент должен иметь фиксированный размер и размерности 0— 0.

  • Если вы задаете dim или nanflag, затем они должны быть константами.

  • «Смотрите информацию о генерации кода функций Toolbox (MATLAB Coder) в разделе «»Ограничения переменных размеров»».».

  • Смотрите генерацию кода для комплексных данных с мнимыми частями с нулевым знаком (MATLAB Coder).

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).

Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает распределенные массивы. Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).

Представлено до R2006a

Источник

Matrices in MATLAB are 2-dimensional arrays that store mostly numeric data at different indices. Now, to find the indices of maximum and minimum values of a given matrix, MATLAB does not provide any direct functionality however, we can do the same by using two other functionalities. Firstly, we will find the maximum or minimum value of a given matrix and then, we will find the indices of those two values. In this scenario, MATLAB does offer simple functions to perform the former tasks. In this article, we shall see how to do the same for a magic square.

Maximum and Minimum Values in a Matrix:

The max() and min() functions find the maximum and minimum values respectively in an array, along a given dimension. The output of these commands will be a row vector(default) which will have max/min values of each column in that array/matrix. Then we can apply the max()/min() function again to find the max/min values from that 1D vector. 

Syntax:

To get row vectors with extreme values

max-row = max(matrix)

min-row = min(matrix)

To get extreme value from a given row vector of extreme values

max(max-row)

min(min-row)

Now let us see the same in action.

Maximum Value:

We will create a 5×5 magic square and find its maximum value, which should be 25.

Example 1:

Matlab

matrix = magic(5)

max_val = max(max(matrix))

Output:

Minimum Value:

Similarly, we will now find the minimum value of the same magic square, which should be 1.

Example 2:

Matlab

matrix = magic(5)

min_val = min(min(matrix))

Output:

Finding Indices of Max/Min Values in the Same Magic Square:

Now we will use the find() function to get the indices of the max/min values.

Syntax:

max-index = find(matrix==max_val)

min-index = find(matrix==min_val)

Example 3:

Matlab

matrix = magic(5);

min_val = min(min(matrix));

max_val = max(max(matrix));

[minx,miny] = find(matrix==min_val);

[maxx,maxy] = find(matrix==max_val);

fprintf("minimum index")

disp([minx,miny])

fprintf("maximum index")

disp([maxx,maxy])

Output:

Finding Max/Min Values With Multiple Occurrences:

We can also find the indices of all occurrences of the max/min value of a matrix in a similar way. See the following code for understanding the same.

Example 4:

Matlab

matrix = [1 2 3;

        1 23 4;

        2 23 5]

min_val = min(min(matrix));

max_val = max(max(matrix));

[minx,miny] = find(matrix==min_val);

[maxx,maxy] = find(matrix==max_val);

fprintf("minimum indexn")

disp([minx,miny])

fprintf("maximum indexn")

disp([maxx,maxy])

Output:

As can be seen, the minimum value 1 occurs at (1,1) and (2,1), and the maximum value 23 occurs at (2,2) and (3,2) indices. The same results are given by the above code.

Last Updated :
21 Nov, 2022

Like Article

Save Article

Источник

Image

I want to extract the two points (i.e their values) which are marked with black outline in figure. These minima points are 2 and 5. Then after extraction these marked points coordinates I want to calculate the distance between them.

The code that I am using to plot average values of image, calculate minimas and locations is

I1=imread('open.jpg');
I2=rgb2gray(I1);
figure, title('open');
plot(1:size(I2,1), mean(I2,2));
hold on
horizontalAverages = mean(I2 , 2);
plot(1:size(I2,1) , horizontalAverages)
[Minimas locs] = findpeaks(-horizontalAverages) 
plot(locs , -1*Minimas , 'r*')

Minima 

-86.5647
-80.3647
-81.3588
-106.9882
-77.0765
-77.8235
-92.2353
-106.2235
-115.3118
-98.3706

locs =

    30
    34
    36
    50
    93
    97
   110
   121
   127
   136

Источник

min

Minimum elements of an array

Syntax 

  • C = min(A)
C = min(A,B)
C = min(A,[],dim)
[C,I] = min(...)

Description

C = min(A)
 returns the smallest elements along different dimensions of an array.

If A is a vector, min(A) returns the smallest element in A.

If A is a matrix, min(A) treats the columns of A as vectors, returning a row vector containing the minimum element from each column.

If A is a multidimensional array, min operates along the first nonsingleton dimension.

C = min(A,B)
 returns an array the same size as A and B with the smallest elements taken from A or B.

C = min(A,[],dim)
 returns the smallest elements along the dimension of A specified by scalar dim. For example, min(A,[],1) produces the minimum values along the first dimension (the rows) of A.

[C,I] = min(...)
 finds the indices of the minimum values of A, and returns them in output vector I. If there are several identical minimum values, the index of the first one found is returned.

Remarks

For complex input A, min returns the complex number with the largest complex modulus (magnitude), computed with min(abs(A)), and ignores the phase angle, angle(A). The min function ignores NaNs.

See Also

max, mean, median, sort

   mfilename   minres 

Источник

Понравилась статья? Поделить с друзьями:
  • Как найди долевую нить на ткани
  • Как юридически правильно составить доверенность
  • Как составить план придуманной сказки
  • Как найти максимальное значение в информатике
  • Как найти фотки человека паука