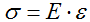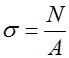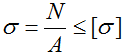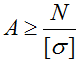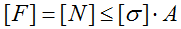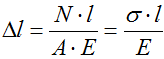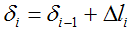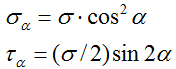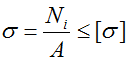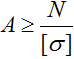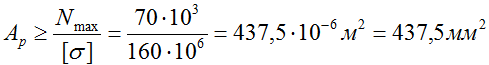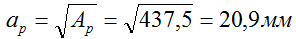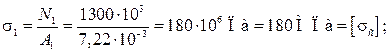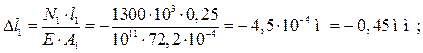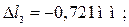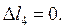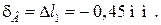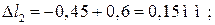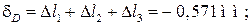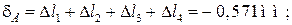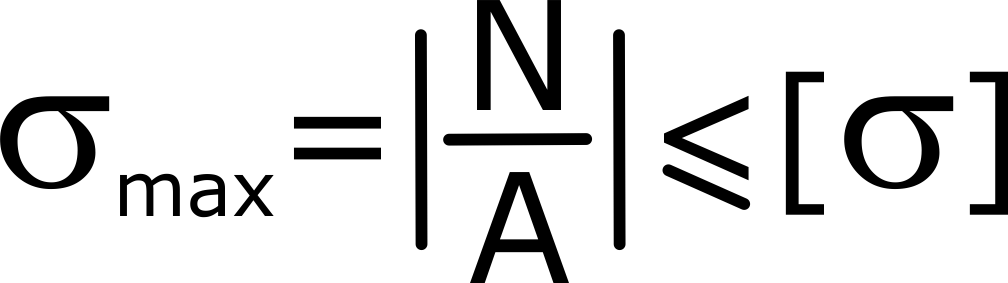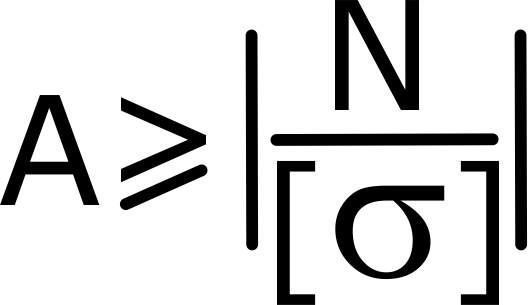Как найти минимальную площадь поперечного сечения

Определить минимальную площадь поперечного сечения стержня из хрупкого материала

Определить минимальную площадь поперечного сечения стержня из хрупкого материала, который растягивается силой F равной 45кН, если временное сопротивление равно 300МПа, а коофициэнт  запаса прочности равен 5.

F=45кН                                         [G]=F/A                         A=F/[G]

Gвр=300МПа=30кН/см²                     [G]= Gвр/[S]               A=45/(30/5)=7.5см²

[S]=5

A=?

Учитывая, что

,
а
,

условие устойчивости,
получим в виде:

.
(14.26)

Если
стержень сжат одной силой
,
то в этом случае продольная силаи выражение (14.26) приобретает вид:

.
(14.27)

Местные
ослабления практически не изменяют
величину критической силы. Поэтому в
формулах (14.26), (14.27) вводится полная
площадь поперечного сечения.

Условие устойчивости
(14.27) решает три задачи:

1. Проверочный расчет
   сжатых стержней.

2. Подбор величины
   сжимающей нагрузки.

3. Проектировочный
   расчет.

Рассмотрим порядок решения каждой из
этих задач.

Задача 1:

1. Так как условия закрепления концов
стержня, длина стержня, форма поперечного
сечения и его размеры известны, находим
минимальный осевой момент инерции
,
площадь,
вычисляем минимальный радиус инерции
сеченияи гибкость стержня.

2. По таблице 14.2 определяем коэффициент
продольного изгиба
и вычисляем напряжение в стержне по
формуле:

.

3. Сравниваем полученное напряжение с
допускаемым напряжением:

.

Задача 2:

1. Выполняем пункт 1, изложенный в
предыдущей задаче.

2. По таблице 14.2 находим коэффициент
продольного изгиба
и определяем допускаемое значение силыпо
формуле:

.

Задача 3:

1. При решении этой задачи используем
метод последовательных приближений
(метод итераций) путем варьирования
величиной коэффициента продольного
изгиба
.
Так как в расчетной формуле на устойчивостьимеются две неизвестные величиныкоэффициенти искомая площадь поперечного сечения,
принимаем в первой попытке значение
для коэффициента продольного изгиба.

2. Определяем площадь поперечного сечения
,
находим размеры поперечного сечения,
минимальный осевой момент инерции и
минимальный радиус инерции.

3. Определяем гибкость стержня
,
и по таблице 14.2 находим коэффициент
продольного изгиба.
Еслизначительно
отличается от,
то и напряжение в стержне будет существенно
отличаться от допускаемого. В этом
случае повторяем расчет: вычисляем
среднее значениеи обращаемся к пункту 2. Если требуется
третья попытка, то определяеми т.д. Обычно при подборе сечений требуется
не более двух-трех попыток.

Рассмотрим несколько примеров определения
величины критической силы для сжатого
стержня и расчета сжатых стержней на
устойчивость.

Пример 14.1. Определить наименьшую
гибкость стержня, при которой для
вычисления критического усилия еще
применима формула Эйлера, если стержень
выполнен из стали с пределом
пропорциональностиМПа
и модулем упругостиМПа.

Решение:

1. Формула Эйлера применима,
если критические напряжения, действующие
в стержне, не превышают предела
пропорциональности:

.

Отсюда предельная величина гибкости,
при которой применима формула Эйлера,
равна:

.

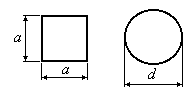
Пример 14.2.Какой из двух стержней
одинаковой длины, условия закрепления
и нагружения которых также одинаковы,
является более гибким – стержень
квадратного или круглого сечения с
равной площадью (Рис.14.6)?

Решение:

1. По условию задачи площади поперечных
сечений стержня, приведенные на рис.14.6,
одинаковы:
или.
Откуда.

Рис.14.6

2. Отношение гибкостей двух стержней с
одинаковыми условиями закрепления
концов и одинаковой длины обратно
пропорционально отношению минимальных
радиусов инерции их поперечных сечений
или при одинаковой площади поперечных
сечений обратно пропорционально корню
квадратному из отношения минимальных
моментов инерции сечений:

.

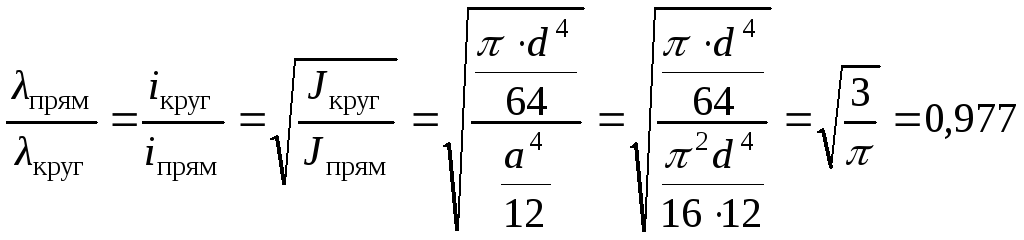
3. Таким образом, гибкость стержня с
прямоугольным сечением составляет:

или
гибкость стержня с прямоугольным
сечением составляет 97,7% от гибкости
стержня с круглым сечением. Иными
словами, гибкость стержня с круглым
сечением оказалась на 2,3% больше.

Пример.14.3.
Определить величину критического
усилия и критическое напряжение для
стойки прямоугольного поперечного
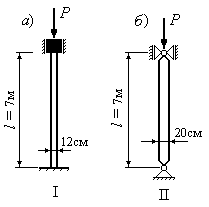
сечения 1220см²длиной 7м из дерева с модулем упругостиМПа.
В плоскости наименьшей жесткости оба
конца стойки защемлены (положение 1), а
в перпендикулярном положении (положение
2) – оба конца стойки шарнирно оперты
(Рис.14.7).

Решение

1. Определим величину критической силы
для первого положения стержня (Рис.14.7,а):

кН.

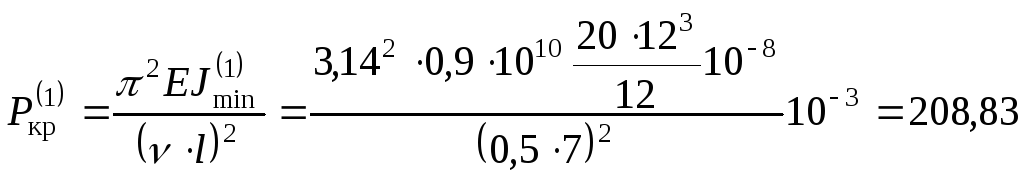
Рис.14.7

2. Определим величину критической силы
для второго положения стержня (Рис.14.7,б):

кН.

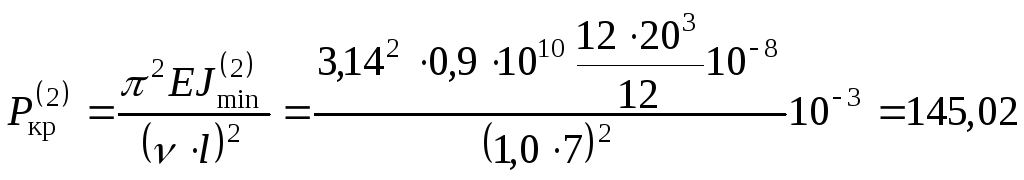
3. Из двух значений критической силы
принимаем меньшее:
кН.
Определяем критическое напряжение:

МПа.

4. Определим правомерность применения
формулы Эйлера для решения этой задачи.
Для этого определим предельное значения
гибкости для дерева, если предел
пропорциональности для дерева
МПа.

.

Гибкость стержня для первого положения
стержня равна:

.

Гибкость стержня для второго положения
стержня равна:

.

Здесь:
см;см.

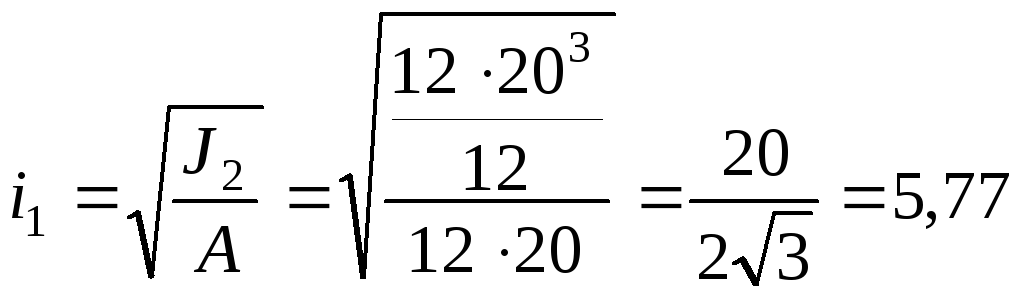
Таким образом, гибкость стержня для
обоих его положений оказалась выше
предельной для дерева и, следовательно,
применение формулы Эйлера для определения
критической силы было оправданным.

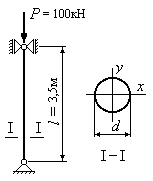
Пример 14.4.Произвести проверку
устойчивости сжатой деревянной колонны
(Рис.14.8) круглого поперечного сечения
диаметромсм
длинойм,
если основное допускаемое напряжениеМПа,
а сжимающая силакН.

Рис.14.8

Решение:

1. Определяем площадь поперечного
сечения:

см².

2. Определяем радиус инерции сечения:

см.

1. Определяем
   гибкость стержня:

.

1. По
   таблице 14.2 находим с помощью линейной
   интерполяции:

.

1. Определяем
   величину допускаемого напряжения
   устойчивости:

МПа.

1. Вычисляем
   нормальные ноапряжения в сечении от
   сжатия:

МПа.

8. Сравнивая
с,
получаем:МПа
<
МПа.
Значит, устойчивость колонны обеспечена.

Пример 14.5.Для предыдущей задачи
найти величину критической силы,
доускаемое значение нагрузки и величину
коэффициента запаса устойчивости, если
для дерева модуль упругостиМПа,
предел пропорциональностиМПа.

Решение:

1. Определяем
   предельную гибкость для дерева:

.

2. Определяем величину критической силы.
Гибкость стержня в предыдущем примере
составила
.
Следовательно, для определения критической
силы можно применять формулу Эйлера:

кН.

3. Находим допускаемое значение для
сжимающей силы. Значение для коэффициента
продольного изгиба берем из предыдущего
примера
:

кН.

4. Определяем коэффициент запаса
устойчивости:

.

Пример 14.6.Как изменятся величины
критической и допускаемой силы и
коэффициент запаса устойчивости, если
длину стержня уменьшить вдвое. Для
решения задачи взять данные из примера
14.5.

Решение:

1. Если длину стержня уменьшить вдвое
до
м,
сохранив при этом условия закрепления
концов стержня, гибкость стержня также
уменьшится в два раза:

.

Это значение гибкости меньше предельного,
равного
.
Следовательно, формулу Эйлера для
определения критической силы использовать
нельзя, а следует использовать для этой
цели формулу Ясинского.

1. Определяем
   величину коэффициента продольного
   изгиба:

.

3. Из таблицы 14.1 берем значения эмпирических
коэффициентов для дерева
МПа,МПа
и вычисляем величину критической силы:

кН.

1. Определяем
   допускаемое значение сжимающей силы:

кН.

1. Находим
   коэффициент запаса устойчивости:

.

Таким образом, с уменьшением длины
стержня вдое значения для критической
и допускаемой силы увеличились,
коэффициент запаса устойчивости стал
меньше.

Пример 14.7. Подобрать из сортамента
прокатной стали двутавр для стержня
длиной 4м, сжатого центрально приложенной
силойкН.
Оба конца стержня защемлены. Материал
– Ст.3. Основное допускаемое напряжениеМПа.

Решение:

1. Принимаем
   и находим площадь поперечного сечения:

см².

Из сортамента прокатной стали выбираем
двутавр №22а с площадью
см²и минимальным радиусом инерциисм.

Находим гибкость стержня:

.

Из таблицы 14.2 определяем коэффициент
продольного изгиба:
.
Так как междуиимеется значительная разница, переходим
ко второ й попытке.

2. Принимаем
и находим площадь поперечного сеченния
двутавра:

см².

Из сортамента прокатной стали выбираем
двутавр №18а с площадью
см²и минимальным радиусом инерциисм.

Находим гибкость стержня:

.

Определяем коэффициент продольного
изгиба, используя данные таблицы 14.2:

.

Поскольку разница между
ине очень большая, найдем напряжения,
возникающие в стержне:

МПа.

Стержень недогружен. Определяем
относительную величину недогруза:

.

Обычно относительная величина недогруза
или перегруза должна составлять порядка
3% по абсолютной величине. Поэтому
переходим к третьей попытке.

3. Принимаем
и находим площадь поперечного сеченния
двутавра:

см².

В сортаменте прокатной стали имеется
двутавр №18 с площадью
см²и минимальным радиусом инерциисм.

Площадь этого двутавра меньше требуемой.
Проверим его. Находим гибкость стержня:

.

Определяем коэффициент продольного
изгиба:

.

Находим напряжение в стержне:

МПа.

Стержень оказался перегруженным.
Относительная величина перенапряжения
составляет:

.

Такое перенапряжение недопустимо.
Поэтому окончательно принимаем для
сечения стержня двутавр №18а.

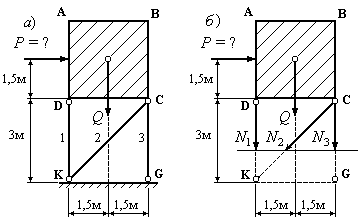
Пример 14.8. Водонапорный бак АВСD
весом
кН
поддерживается стержнями DK, CK, CGи
испытывает действие ветровой нагрузки(Рис.14.9,а).
В узлахC, D, K, Gкрепления
стержней шарнирные. Поперечные сечения
всех стержней одинаковы. При каком
наименьшем значении ветровой нагрузкистержень №1 не следует проверять на
устойчивость?

Рис.14.9

Решение:

1. Будем исходить из того, что
проверять стержень №1 на устойчивость
не следует, если этот стержень будет
либо растянут, либо не нагружен вообще.
Наименьшее значение силы
,
при котором стержень №1 не следует
проверять на устойчивость, будет таким,
при котором усилие в стержне №1 будет
равно нулю. Во всех остальных случаях
при большем значении силыстержень №1 будет растянут.

2. Рассечем стержни №1, №2, №3 горизонтальным
сечением (Рис.14.9,б) и рассмотрим равновесие
верхней части конструкции. Для нахождения
усилий в стержнях применим метод
моментных точек. Выберем в качестве
моментной точки для стержня №1 точку С
и составим относительно нее сумму
моментов сил, действующих на верхнюю
часть конструкции. Получим:

.

Принимая
,
из уравнения равновесия находимкН.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

iSopromat.ru

Пример решения задачи по расчету размеров поперечного сечения прямого стального стержня по условию прочности на растяжение-сжатие.

Для прямого стержня постоянного сечения подобрать размер стороны a квадратного сечения по условию прочности. Материал стержня – сталь. Допустимые напряжения [ σ ]=160 МПа.

Полученные размеры принять согласно ГОСТ 6636.

Пример решения

Предыдущие пункты решения задачи

Рассматриваемый стержень нагружен исключительно продольными силами, поэтому для подбора размеров его поперечного сечения воспользуемся условием прочности при растяжении-сжатии.

где N – внутренние продольные силы (найдены ранее),
A — площадь поперечного сечения стержня.

Чтобы найти размеры поперечного сечения стержня рассчитаем площадь A. Для этого запишем условие прочности относительно площади:

Площадь сечения в данном случае постоянна по всей длине стержня и должна обеспечивать прочность на всех его силовых участках. Поэтому расчет будем вести по самому нагруженному из них, т.е. где внутренняя сила максимальна (N_max).

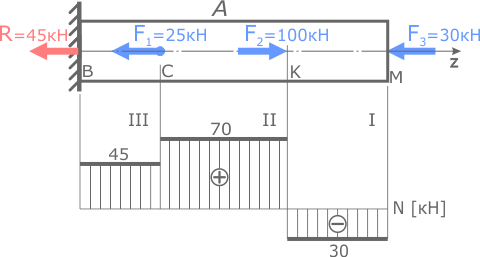
По построенной эпюре внутренних сил видно, что наиболее нагруженным является II участок, где N=N_max=70кН.

Тогда расчетная площадь сечения стержня:

Таким образом для обеспечения необходимой прочности стержня площадь его поперечного сечения должна быть не менее 437,5 мм 2 .

Теперь, зная площадь квадрата, рассчитаем его сторону

Это соответственно минимальный размер поперечного сечения стержня, обеспечивающий его прочность.

В случаях, когда в задании не ставится дополнительных условий полученный размер можно округлить до целого миллиметра, но только в большую сторону.

По ГОСТ 6636 окончательно принимаем ближайший в сторону увеличения линейный размер а =22мм.

Все дальнейшие расчеты стержня будем вести по этому размеру.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

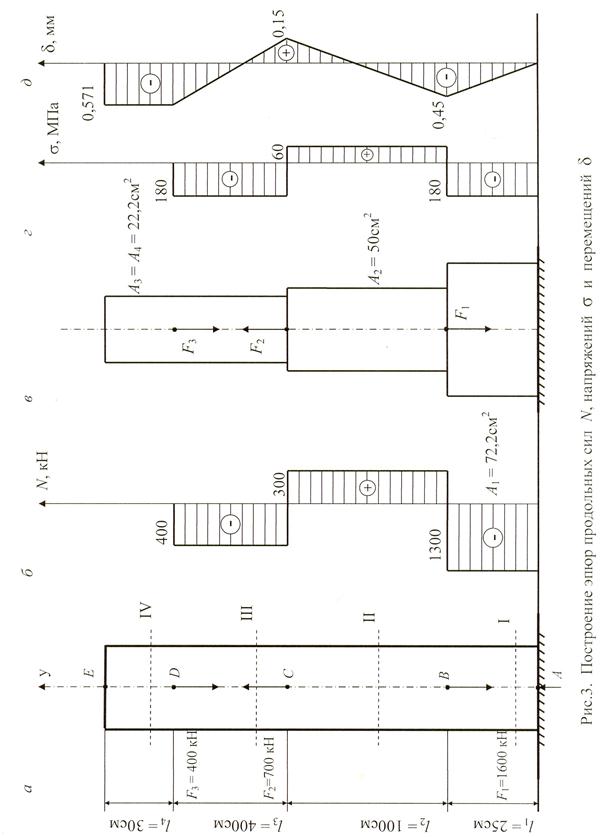
Пример 1. Определить площадь поперечных сечений на всех участках чугунного стержня (рис

Определить площадь поперечных сечений на всех участках чугунного стержня (рис. 3, а). Построить эпюры продольных сил N, напряжений σ и перемещений δ. Принять для чугуна [σ_с] = 180 МПа, [σ_р] = 60 МПа, Е = 10 5 МПа = 10 11 Па.

Рассматриваемый стержень имеет одну опорную реакцию R, и для него можно составить лишь одно уравнение статики: ΣY = 0. Значит, эта система статически определима:

Стержень подвергается растяжению – сжатию. Выделяем участки нагружения 1 – 4 (между точками приложения внешних сил), в пределах которых намечаются сечения I – IV.

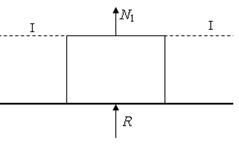
Для определения N₁ на первом участке рассмотрим равновесие части стержня, расположенной ниже сечения I – I. На нее действует реакция R (рис. 4). Уравнение статики ΣY = 0 имеет вид

Полученный в результате подсчета знак минус при N₁ указывает,

что N₁ имеет направление, противоположное заданному, и что первый участок сжат.

Рис. 4. Определение внутренних сил N₁

На часть стержня, расположенную ниже сечения II — II, действуют реакция R и сила F₁. Тогда продольная сила в сечении II — II равна

Аналогично определяются N₃, N₄: N₃ = – 400 кН; N₄ = 0. По вычисленным значениям N строится эпюра продольных сил (см. рис. 3, б).

Из условия прочности 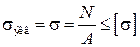определяем площади поперечных сечений на участках стержня:

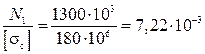
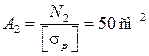
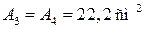
A₁ = м 2 = 72,2 см 2 ;

;

.

Вычисления сделайте самостоятельно.

Рассчитываемый стержень с найденными площадями поперечных сечений показан на рис.3, в.

; ; .

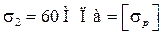
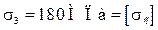
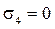
Проделанные расчеты напряжений являются проверочными.

На рис. 3, г показана эпюра нормальных напряжений. Вычислим

деформации участков стержня:

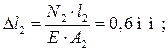
Перемещение любого сечения стержня равно сумме деформаций участков, расположенных между сечением и опорой.

Перемещение δ_А точки А: δ_А = 0. Перемещение точки В обусловлено деформацией участка I:

Перемещение точки С складывается из деформаций участков I и II:

Перемещение точки D складывается из деформаций участков I, II

Перемещение точки E складывается из деформаций участков I, II, III

По вычисленным значениям δ строится эпюра перемещений (см. рис. 3, д).

Задача 1. Растяжение и сжатие

(статически определимая система)

Произвести расчет стержня постоянного поперечного сечения (рис. 5) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ], равным 210 МПа и модулем продольной упругости Е, равным 200 ГПа. Данные к задаче приведены в табл. 1.

1) вычислить продольные силы на участках стержня и построить эпюру N;

2) определить размеры поперечного сечения (сторону квадрата или диаметр);

3) вычислить нормальные напряжения на участках стержня и пос­троить эпюру σ по длине стержня;

4) вычислить деформацию участков стержня и построить эпюру перемещений δ.

Источник

iSopromat.ru

Условие прочности при растяжении и сжатии: нормальные напряжения σ в сечениях бруса не должны превышать заданных допустимых напряжений [σ].

При продольном осевом нагружении (растяжении-сжатии) в поперечных сечениях бруса имеют место только нормальные напряжения σ . Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:

Здесь
σ _max – максимальные расчетные нормальные напряжения в стержне,
N – внутренние продольные силы (принимаются с построенных эпюр),
А – соответствующая площадь поперечного сечения бруса,
[ σ ] – допустимые напряжения (расчетное сопротивление) для материала стержня, определяемое как:

n – коэффициент запаса прочности, устанавливаемый нормативными документами.

Данное условие означает что для того чтобы стержень при растяжении-сжатии оставался прочным, напряжения σ в его сечениях не должны превышать допустимых значений [ σ ].

В случаях, когда для материала стержней допустимые напряжения на растяжение [ σ ]_р и на сжатие [ σ ]_сж отличаются, при сравнении необходимо учитывать знак напряжений σ , который зависит только от знака соответствующих внутренних сил N.

Так, положительные значения напряжений σ сравниваются с [ σ ]_р, отрицательные напряжения по модулю не должны превышать значения [ σ ]_сж.

Три задачи расчета на прочность

Данное условие прочности позволяет решать три основных задачи сопротивления материалов и технической механики:

Проверка на прочность.

В случае, когда известны внешние нагрузки, а также размеры и материал стержня можно выполнить проверку его прочности. Для этого по каждому участку рассчитывается величина нормальных напряжений σ , после чего максимальная из них сравнивается с заданным допустимым значением [ σ ].

Ответ в данной задаче дается в виде заключения:

• если σ _max ≤ [ σ ] стержень прочный,
• если σ _max > [ σ ] стержень непрочный.

Подбор размеров сечения (проектировочный расчет)

Эта задача является основной в технической механике. Здесь, по известным схеме нагружения и материалу стержня определяется минимально необходимая площадь поперечного сечения A обеспечивающая его прочность.

Для этого условие прочности записывается относительно искомой величины.

Полученные размеры в случае необходимости можно только увеличивать. Уменьшение размеров приведет к превышению напряжениями допустимых значений.

Определение грузоподъемности стержня.

Данная формула позволяет по известным размерам и материалу рассчитать величину допустимой внутренней силы, которую может выдержать стержень, оставаясь прочным.

В данном случае условие прочности записано относительно внутренней силы N.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Расчет на прочность

Задача на построение эпюр поперечной силы Q, изгибающего момента M и подбор сечения (проектный расчет)

Для заданной схемы консольной балки требуется построить эпюры поперечной силы Q и изгибающего момента M, выполнить проектировочный расчет, подобрав круглое сечение.

Материал — дерево, расчетное сопротивление материала R=10МПа, М=14кН·м,q=8кН/м

Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. Построим эпюры обычным способом.

1. Определим опорные реакции.

Равномерно распределенную нагрузку q заменим условной силой Q= q·0,84=6,72 кН

В жесткой заделке три опорные реакции — вертикальная, горизонтальная и момент, в нашем случае горизонтальная реакция равна 0.

Найдем вертикальную реакцию опоры R_A и опорный момент М_A из уравнений равновесия.

На первых двух участках справа поперечная сила отсутствует. В начале участка с равномерно распределенной нагрузкой (справа) Q=0, в заделеке — величине реакции R_A.3. Для построения эпюры изгибающих моментов M составим выражения для их определения на участках. Эпюру моментов построим на растянутых волокнах, т.е. вниз.

4.Проектировочный расчет, то есть подбор размеров поперечного сечения.

Максимальный изгибающий момент с эпюры М=14 кН·м. Определим осевой момент сопротивления сечения

Таким образом, подбираем сечение с диаметром 25 см.

Задача на подбор сечения и проверку прочности. Касательное напряжение и энергетический критерий прочности

Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:

Покажем балку с построенными эпюрами Q и М

Согласно эпюре изгибающих моментов опасным является сечение С, в котором М_С=М_max=48,3кНм.

Условие прочности по нормальным напряжениям для данной балки имеет вид σ_max=M_C/W_X≤σ_adm. Требуется подобрать сечение из двух швеллеров.

Определим необходимое расчетное значение осевого момента сопротивления сечения:

Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера I_x=1670см 4 , тогда осевой момент сопротивления всего сечения:

Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Тогда получим недонапряжение:

Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Q_max=48,9 кН.

Условие прочности по касательным напряжениям имеет вид:

Для швеллера №20 а: статический момент площади S_x1=95,9 см 3 , момент инерции сечения I_x1=1670 см 4 , толщина стенки d₁=5,2 мм, средняя толщина полки t₁=9,7 мм, высота швеллера h₁=20 см, ширина полки b₁=8 см.

Для поперечного сечения из двух швеллеров:

b=2d₁=2·0,52=1,04 см.

Определяем значение максимального касательного напряжения:

τ_max=48,9·10 3 ·191,8·10 −6 /3340·10 −8 ·1,04·10 −2 =27МПа.

Как видно, τ_max Схема сечения балки и эпюры напряжений для анализа напряженного состояния

Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых:

Используя энергетический критерий прочности, получим

Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется

(135,3 МПа Запись опубликована 08.03.2015 автором admin в рубрике Расчет на прочность.

Построение эпюр Q и М , проектный расчет (подбор сечения)

Требуется построить эпюры Q и M и подобрать стальную балку двутаврового поперечного сечения при расчетном сопротивлении R=160 МПа.

1.Определение реакций:

Сумма моментов относительно опор:

Сумма проекций всех сил на ось У (проверка):

2.Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.

1) Первый участок:

2) Второй участок:

3) Третий участок:

3.Проектировочный расчет, то есть подбор размеров поперечного сечения.

Подобрать стальную балку двутаврового поперечного сечения при R=160 МПа:

С эпюры берем максимальный момент:

По сортаменту подбираем двутавр № 20 с

Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:

Построение эпюр Q и М, проектировочный расчет (подбор сечения)

Для заданной балки требуется построить эпюры Q и M, найти M_max и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала R_u=10 МПа.

1.Определение реакций:

Сумма проекций всех сил на ось z:

Сумма проекций всех сил на ось y:

Сумма моментов относительно точки А:

После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).

2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.

Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.

M— изгибающий момент, считается положительным, если растягивает нижние волокна.

1)Первый участок:

2) Второй участок:

3) Третий участок:

Следует отметить ,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.

3.Проектировочный расчет, то есть подбор размеров поперечного сечения.

Подберем деревянную балку круглого поперечного сечения при R_u=10 МПа

С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки.

Расчёт балок на прочность при изгибе

В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.

а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,

б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.

а) Для определения σ_(К), τ_(К) и _maxσ,_maxτ потребуется знать величины осевого момента инерции всего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсечённой части и статического момента половины сечения S_max:

б) Проверка прочности:

— по условию прочности нормальных напряжений:

— по условию прочности касательных напряжений:

В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.

Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:

– уравнение прямой.

— уравнение параболы.

z₂=3м: М = 30 · 3 – 5 · 3 2 = 90 — 45 = 45кНм,

z₂=6м: М = 30 · 6 – 5 · 6 2 = 180 — 180 = 0.

Определение аналитического максимума изгибающего момента второго участка:

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.

Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.

В данном случае максимальный момент по модулю М = 60кНм

а) сечение круглой формы d=?

б) сечение прямоугольной формы при h/b = 2:

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:

Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:

— для круглого сечения

— для прямоугольного сечения

Воспользуемся этими формулами. Тогда

— для балки круглого сечения при :

— для балки прямоугольного сечения

Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:

А_{прямоугольного} = 865,3см 2 2 , следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.

Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.

Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:

∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.

z₂=2м: М = 40+ 104 · 2 – 10 · 2 2 = 208 кНм.

III участок

z₃=2м: М = 24 + 136·2 — 10 (2+2) 2 = 24 + 272 – 160 = 136кНм,

z₃=4м: М = 24 + 136·4 – 10 (2+4) 2 = 24 + 544 – 360 = 208 кНм.

z₃ = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.

Проверяем скачки в эпюрах:

а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М₂=24, приложенному в этом месте.

первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,

второй – под силой F=80кН и равен ей (64+16=80кН),

третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)

Наконец, проектируем двутавровое сечение.

Подбор его размеров производится из условия прочности по нормальным напряжениям :

В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления W_х нет. Есть № 40 а с W_х=1190 см 3 и № 45 а с W_х=1430 см 3

Попробуем меньший из них. Если принять двутавр № 40 а , у которого W_х=1190 см 3 , то наибольшее напряжение в опасном сечении будет:

и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.

Поэтому приходится принимать ближайший больший размер двутавра, а именно №45 а , у которого W_х=1430 см 3 . В этом случае балка будет работать с недонапряжением:

Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :

Это условие прочности выполняется, даже с избыточным запасом.

Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).

1.Определение опорных реакций

∑М(А) = F · 2 + М₁ — М₂— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М₁— М₂ – А · 8 + q·6·1 =0,Проверка:

∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.

2.Построение эпюр изгибающих моментов и поперечных сил.

z₂=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.

III участок

z₃=2м: М = 210·2 — 20·(2+2) 2 = 420 – 320 = 100кНм,

z₃=4м: М = 210·4 – 20 · (2+4) 2 = 840 – 720 = 120кНм.

3. Подбор сечений (опасное сечение по σ: |_maxМ|=131,25кНм,

опасное сечение по τ: |_maxQ|=130кН).

Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)

Принимаем: В=0,24м,

Вариант 2. Деревянное круглое

Принимаем d=0,45м,

Вариант 3. Чугун : ([σ_Р]=30МПа, [σ_с]=120МПа, [τ]=15МПа)

Принимаем b=0,19м, тогда h=0,38м, d=0,076м.

Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).

Вариант 5. Сталь, круглая труба

Принимаем D=0,22м → d = 0,6·D =0,132м.

Вариант 6. Сталь, прямоугольная труба

Принимаем b=0,13м, h=0,26м.

Кстати: какое из сечений стальной балки выгодней по расходу материала?

Двутавр — А = 72,6см 2 = 72,6·10 -4 = 0,00726м 2 ,

круглая труба –

прямоугольная труба —

Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.

Источник

Цитата: Goran от 08.02.16, 16:47:50
Есть же уточнение…Автор пытается найти не несущую способность шва, а формулу определяющую допустимые параметры дефектов (плошадь непровара)

Именно. Хочу понять, как закладываются нормы допустимости дефектов для неразрушающих методов контроля. Особенно для ультразвука. За основу берется, в основном, предельно допустимая «площадь» плоского дна отверстия. Для ГПМ нормы существуют. Но в моей практике очень много нестандартных ситуаций и контролируемых изделий, на которые нет никаких норм. Лично для себя хочу найти механизм подачи полезной информации «заказчику» контроля. Хотя и не обязан….

Цитата: Valery-Moscow от 08.02.16, 16:32:07
ВСЕ зависит от требуемой достоверности результатов расчетов….

без конкретного описания задачи и чертежа — советы бесполезны

Ваш вопрос:
Каким расчетом можно определить минимальное сечение, которое приведет к необратимым последствиям при различных нагрузках?

простите — некорректный…

в дополнение к тому, что нет чертежа, нагрузки у Вас не конкретные, а «различные»…… — т.е. поди туда, не знаю куда….

важным является вопрос:

Вам нужно знать РЕАЛЬНУЮ ситуацию с напряжениями или нужны просто красивые картинки «а-ля расчеты»…. или даже просто числа полученные по «сертифицированным» формулам?

если просто числа   — берите «сертифицированные» формулы и ВПЕРЕД!

если же нужны РЕАЛЬНЫЕ расчеты — то нужно описание задачи + геометрия = на основании этого придумать постановку и нужно писать техническое задание на расчет.

чуть-чуть информации об одной модельной задачке — которую только вчера пришлось решать для строителей — да бы объяснить им ЗНАЧИМОСТЬ выбора типа КЭ:
металлическая колонна — квадратное сечение, с боку приварен уголок для опирания фермы.

вот две картинки — приведенные напряжения по Мизесу

1-ая картинка — КЭ с линейной апроксимацией        — 5.019ЕПа
2-ая картинка — КЭ с квадратичной апроксимацией — 3.199Е7 Па

геометрия, назгрузки и пр. = одинаковы

тем не менее — разница в полученных результатах очевидна

на самом деле — расчет сварных швов — если к этому подходить серьезно — весьма сложен, так как область сварки имеет температурную анизотропию — которую «анулировать» весьма не просто, кроме того — ЛЮБАЯ сварка — подразумевает что в области варки металла — всегда присутствуют поры, инородные включения и пр… — которые являются концентраторами напряжений и так далее….

Цитата: Kirilius83 от 08.02.16, 16:55:50
Автор пытается понять, как вообще ведутся расчеты на прочность (даже вообще — расчеты), он никогда ничего не считал вообще.

Ну это Вы зря. А Вы что, можете рассчитать все на свете? Так помогите с примером, как другие.

Цитата: Valery-Moscow от 08.02.16, 16:32:07
ВСЕ зависит от требуемой достоверности результатов расчетов….

без конкретного описания задачи и чертежа — советы бесполезны

Ваш вопрос:
Каким расчетом можно определить минимальное сечение, которое приведет к необратимым последствиям при различных нагрузках?

простите — некорректный…

в дополнение к тому, что нет чертежа, нагрузки у Вас не конкретные, а «различные»…… — т.е. поди туда, не знаю куда….

важным является вопрос:

Вам нужно знать РЕАЛЬНУЮ ситуацию с напряжениями или нужны просто красивые картинки «а-ля расчеты»…. или даже просто числа полученные по «сертифицированным» формулам?

если просто числа   — берите «сертифицированные» формулы и ВПЕРЕД!

если же нужны РЕАЛЬНЫЕ расчеты — то нужно описание задачи + геометрия = на основании этого придумать постановку и нужно писать техническое задание на расчет.

чуть-чуть информации об одной модельной задачке — которую только вчера пришлось решать для строителей — да бы объяснить им ЗНАЧИМОСТЬ выбора типа КЭ:
металлическая колонна — квадратное сечение, с боку приварен уголок для опирания фермы.

вот две картинки — приведенные напряжения по Мизесу

1-ая картинка — КЭ с линейной апроксимацией        — 5.019ЕПа
2-ая картинка — КЭ с квадратичной апроксимацией — 3.199Е7 Па

геометрия, назгрузки и пр. = одинаковы

тем не менее — разница в полученных результатах очевидна

на самом деле — расчет сварных швов — если к этому подходить серьезно — весьма сложен, так как область сварки имеет температурную анизотропию — которую «анулировать» весьма не просто, кроме того — ЛЮБАЯ сварка — подразумевает что в области варки металла — всегда присутствуют поры, инородные включения и пр… — которые являются концентраторами напряжений и так далее….

Согласен. мало информации. Попробую разузнать больше информации для более конкретной задачи. Спасибо за пример!

Цитата: Kirilius83 от 08.02.16, 16:43:00
Ну, считать нужно сечение, а не нагрузку — значит расчет нагрузки отдельно.
Имеем нагрузку, допускаемые напряжения, нужно посчитать площадь…

Да, расчет нагрузки и допускаемые напряжения — тут все сложно (если конечно коэф запаса небольшой). Но сам подбор площади при их известных — несложно.

Вот про подбор площади и «несложно» по подробней.  Литературу почитаю обязательно, но как вспомню школьную математику, я ее особо не знал, но хорошо воспринимал примеры и потом просто ассоциативно хорошо решал задачи ( на 4-5) . Вот и сейчас сколько не читай, но пару раз увидишь наглядный пример или услышишь пояснение простым языком — легче дальше вникать.