Как найти минимальную скорость электронов

0 Пользователей и 1 Гость просматривают эту тему.

Электрон влетает в
пространство между обкладками плоского воздушного конденсатора под α к нижней
обкладке. Определите минимальное значение модуля скорости электрона, при
которой он достигнет верхней обкладки конденсатора, если напряжение между
обкладками 60 В.

Решение.

Предположим, что
обкладки конденсатора покоятся относительно инерциальной системы отсчета,
связанной с лабораторией, и расположены горизонтально. Ось OX направим вдоль нижней обкладки конденсатора, ось OY –
вертикально вверх. Отсчет времени начнем в момент влета электрона в пространство
между обкладками конденсатора.

В качестве физической
системы рассмотрим «электрон». Будем считать его материальной точкой.
Выделенная система не замкнута, поэтому для решения задачи воспользуемся
кинематико-динамическим способом описания.

Движущийся в
пространстве между обкладками конденсатора электрон взаимодействует с
электростатическим полем конденсатора, с гравитационным и магнитным полями
Земли и с воздухом. Взаимодействие электрона с электростатическим полем можно
описать силой F_эл = eE, модуль которой, если пренебречь краевыми эффектами и явлением
электростатической индукции, не изменяется. Эта сила направлена против поля
(заряд электрона отрицательный). Взаимодействие электрона с гравитационным
полем Земли можно описать силой тяжести mg.
Если взаимодействием с воздухом и с магнитным полем пренебречь, то динамическое
уравнение движения электрона имеет вид: ma
= mg + eE. Принимая во внимание, что F_эл >> mg , получим ma = eE, т.е. движение электрона будет равноускоренным. Поэтому
кинематические законы движения электрона имеют следующий вид.

Проецируем векторы,
изображающее соответствующие величины, на оси координат.

Решив данную систему
уравнений относительно v₀ , с учетом того, что E
= U/d, где d
– расстояние между обкладками
конденсатора, получим v₀ .

Так как все величины,
входящие в формулу, за исключением v_y
, постоянны, то v₀ = f(v_y). Вертикальная составляющая скорости электрона у верхней
обкладки должна удовлетворять условию v_y
>= 0, т.е. в противном случае электрон
повернет обратно, так и не долетев до нее. Поэтому скорость влета электрона в
конденсатор будет минимальной, если v_y
= 0.

Задачу можно решить,
применив к рассматриваемой физической системы теорему об изменении кинетической
энергии, согласно которой изменение кинетической энергии электрона при перемещений
из начального состояния в конечное в электростатическом поле конденсатора равно
работе внешних сил, действовавших на него во время движения. При сделанных допущениях
DW_кин = A_{эл.поля} . если в качестве
начального состояния физической системы выбрать состояние в момент влета
электрона в конденсатор, а в качестве конечного – момент подлета к верхней
обкладки, то получаем.

Работа сил
электростатического поля A = —eU.

Так как v_y >= 0, то получаем такую же самую формулу как и в первом
случае.

Этот же результат можно
получить, рассмотрев физическую систему «электрон – электрической поле
конденсатора», которая, если пренебречь взаимодействием с внешними объектами,
является замкнутой и  может быть описана
законом сохранений энергии, в соответствии с которым энергия системы в момент
влета электрона в конденсатор равна ее энергии в тот момент времени, когда
электрон окажется у верхней обкладки.

Выбираем нулевой
уровень потенциала на верхней обкладке конденсатора.

Где eU –
потенциальная энергия взаимодействия электрона с электростатическим полем
конденсатора. Энергия системы в конечном состоянии – W­_кон .

Таким образом,
использование различных вариантов теоретического базиса решения задачи и
различный выбор физических систем приводят к одному и тому же результату, что
свидетельствует о правильности ее решения.

Заметим, что полученное
значение v_0min
является ответом задачи при условии, что
угол α удовлетворяет условию α >= arctg 2d/l.

Ответ: 

Источник: Физика. Полный курс подготовки к ЦТ.  Под общей редакцией проф. В.А. Яковенко.

Условия существования токов в газах

Газ, в котором нет заряженных частиц, не является проводником электрического тока (он изолятор). Газ будет проводником только в том случае, если возникнут носители электрических зарядов (свободные электроны и ионы), то есть газ будет ионизирован. Положительные ионы могут быть однозарядными и многозарядными, это зависит от количества потерянных электронов. Отрицательные ионы, обычно однозарядны, образованы присоединением одного электрона к атому.

Так, необходимо существование постороннего фактора ионизации, не связанного с наличием электрического поля для того, чтобы газ являлся проводником. Это может быть, например, высокая температура, излучение, столкновения атомов газа с быстро движущимися элементарными частицами. Надо отметить, что и в нормальных условиях газы, например воздух, имеют электрическую проводимость, правда, весьма малую. Эта проводимость вызвана излучением радиоактивных веществ, которые присутствуют на поверхности Земли, и космическими лучами, которые приходят на планету из пространства. В том случае, если напряжённость поля мала, то течение тока через газ останавливается практически сразу, как перестает работать внешний фактор ионизации. Подобный ток называют несамостоятельным.

После того, как прекращает действовать ионизирующий фактор, положительные и отрицательные ионы газа объединяются и образуют нейтральные молекулы. Этот процесс носит название — рекомбинация. В результате рекомбинации проводимость газа возвращается к первоначальному значению. При этом проводимость газа уменьшается постепенно.

В том случае, когда напряженность поля довольно большая, то само поле может вызывать ионизацию газа, при которой газ становится проводником. В таких условиях ток называют самостоятельным. Универсальной зависимости силы самостоятельного тока от напряжения не выявлено. Все определяют конкретные условия. Сила самостоятельного тока может и увеличиваться и уменьшаться с ростом напряжения.

Несамостоятельный газовый разряд (несамостоятельный ток)

Допустим, что газ, который находится между электродами, постоянно ионизируется. Пусть $N$ — концентрация зарядов каждого знака (или число пар ионов каждого знака), тогда ${(frac{dN}{dt})}_{obr}$ — скорость изменения (образования) концентрации зарядов внешним источником ионизации. Параллельно с процессом ионизации идет процесс рекомбинации.

Если внешнего поля нет, то через некоторое время устанавливается динамическое равновесие, при котором скорость образования ионов становится равной скорости рекомбинации. При этом $N=N^+=N^-$, где полагаем, что ионы однозарядные. В равновесии можно записать, что:

где $r$ — коэффициент рекомбинации, концентрация ионов одного знака равна:

Когда присутствует внешнее электрическое поле, то часть электронов долетает до электродов и там нейтрализуется. Условием динамического равновесия в этом случае станет выражение:

где $(frac{dN}{dt})$- число пар ионов исчезающих в результате нейтрализации на электродах в единицу времени.

Плотность тока определяется как:

где $v_d=bE$- скорость дрейфа заряда в электрическом поле, $b^+, b^-$ — подвижности положительных и отрицательных зарядов. В таком случае, равенство (2) перепишем в виде:

Формула (3) эквивалентна закону Ома только в том случае, если выражение $qleft(b^++ b^-right)N$ не зависит от $E$ и $j$. В газах зависимость $qleft(b^++ b^-right)N$ обычно существует, поэтому выражение (4) не эквивалентно закону Ома.

В том случае, если расстояние между электродами принять равным d, то плотность тока насыщения ($j$) можно выразить как:

если считать, что все возникающие ионы попадают на электроды раньше, чем успевают рекомбинировать. С учетом выражения (5) формулу (2) запишем как:

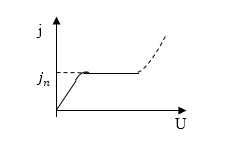
Рассмотрим два предельных случая. Пусть плотность ток очень мала. Этот случай соответствует малым внешним электрическим полям. В этом случае количество ионов, которые нейтрализованы на электродах существенно меньше, чем нейтрализованных за счет рекомбинации, тогда их число не изменяется. Разряд подчиняется закону Ома. На вольт — амперной характеристике (рис.1) это соответствует участку ОА.

Другой предельный случай, когда мы получаем ток насыщения ($j_n$) из уравнения (6) при $rN^2ll frac{j}{qd}$, тогда:

где плотность тока насыщения ($j_n$) не зависит от внешнего поля, создается всеми ионами, которые образованы в результате работы ионизатора. Этому условию отвечает участок BC рис.1.

При промежуточных значениях напряжения внешнего поля происходит плавный переход от линейной зависимости между током и напряжением к насыщению (участок АВ).

Выражение для плотности тока, имеющее вид:

называют характеристикой несамостоятельного тока.

Самостоятельный ток

В том случае, если при плотности тока, равной току насыщения увеличивать напряженность внешнего поля, то плотность тока снова начнет расти. Это происходит от того, что электроны газа до рекомбинации с ионами успевают приобрести энергию, при которой они ионизируют молекулы газа благодаря высокой напряженности внешнего поля. Как результат, скорость ионизации зависит от напряженности внешнего поля. Появляющийся при этом ток называют самостоятельным. Начальная часть характеристики этого тока показана на рис.1 пунктиром.

К видам самостоятельных газовых разрядов относят:

• тлеющий разряд

• дуговой разряд

• искровой разряд

• коронный разряд.

Условие задачи:

Потенциал заряженного металлического шара 45 В. Какой минимальной скоростью должен обладать электрон, чтобы улететь с поверхности шара на бесконечно далёкое расстояние?

Задача №6.3.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(varphi=45) В, (upsilon-?)

Решение задачи:

Система “заряженный металлический шар – электрон” является замкнутой, то есть на неё не действуют никакие внешние силы. Запишем закон сохранения энергии для системы до (то есть когда электрон находится на поверхности шара) и после (когда электрон уже будет находиться на бесконечно большом расстоянии от шара).

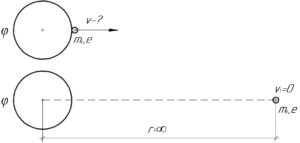
[{W_{п0}} + {W_{к0}} = {W_п} + {W_к}]

Здесь (W_{п0}) – начальная потенциальная энергия взаимодействия заряженного металлического шара и электрона, (W_{к0}) – начальная кинетическая энергия электрона, (W_{п}) – конечная потенциальная энергия взаимодействия, (W_{к}) – кинетическая энергия электрона на бесконечно большом расстоянии от шара. Первые две указанные величины можно найти по формулам:

[left{ begin{gathered}
{W_{п0}} = – varphi e hfill \
{W_{к0}} = frac{{{m_e}{upsilon ^2}}}{2} hfill \
end{gathered} right.]

В этих формулах (e) – модуль заряда электрона, равный 1,6·10^-19 Кл, (m_e) – масса электрона, равная 9,1·10^-31 кг.

Понятно, что (W_{п}) будет равна нулю, поскольку энергия взаимодействия обратно пропорциональна расстоянию. Кинетическая энергия (W_{к}) равна нулю из-за условия минимальности скорости электрона (upsilon). Учитывая всё написанное, а также вышеуказанную систему, имеем:

[ – varphi e + frac{{{m_e}{upsilon ^2}}}{2} = 0]

[varphi e = frac{{{m_e}{upsilon ^2}}}{2}]

[upsilon = sqrt {frac{{2varphi e}}{{{m_e}}}} ]

Посчитаем численный ответ:

[upsilon = sqrt {frac{{2 cdot 45 cdot 1,6 cdot {{10}^{ – 19}}}}{{9,1 cdot {{10}^{ – 31}}}}} approx 4 cdot {10^6};м/с]

Ответ: 4·10⁶ м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.24 Какая совершается работа при перенесении точечного заряда 20 нКл из бесконечности
6.3.26 Две равномерно заряженные проводящие пластины образовали однородное поле
6.3.27 Напряженность поля внутри конденсатора равна E. Найти работу перемещения заряда

Спрятать решение

Источник: Гельф­гат И. М. Сбор­ник задач по фи­зи­ке для 11 клас­са, Х.: «Гим­на­зия», 2004 (№ 11.15)