106
Упростив, взяв частные производные L по а и b и задав результаты равными нулю, получаем:
(2.14а)
(2.14b)
В матричной форме:
|
(2.15) |
||
|
Таблица 2.7 Свертка входного импульса [1, |
Таблица 2.8 Ошибки при двухэлементной обратной |
|
|
(-0.5)] с коэффициентами фильтра [( |
20 ), |
фильтрации и фильтрации методом наименьших квад- |
|
ратов. |
||
|
21 |
( 218 )].
Решая относительно коэффициентов фильтра, получаем (а, b) = [(- 1021 ), (- 214 )].
Втаблице 2.10 показан результат применения этого фильтра к входному импульсу.
Втаблице 2.11 показан результат применения обратного фильтра и фильтра, действующего по методу наименьших квадратов, причем ошибка, допущенная обрат-
ным фильтром намного больше. Однако, для входного импульса [(- 12 ), 1] оба фильтра
дают большие ошибки (таблица 2.11) сравнительно с ошибками для импульса [1, (- 12 )] (таблица 2.8). Причина этого рассматривается в Разделе 2.5.
В двух предыдущих разделах для числового анализа обратного фильтра, действующего по принципу наименьших квадратов использовались два входных импульса:
[1, (- 12 )] и [(- 12 ), 1]. Результаты показывают, что ошибка при преобразовании первого
импульса в единичный импульс с нулевой задержкой меньше, чем при преобразовании второго импульса (см. таблицы 2.8 и 2.11). Первый импульс ближе к одиночному импульсу с нулевой задержкой (1, 0, 0), чем второй импульс. С другой стороны, второй импульс ближе к единичному импульсу с нулевой задержкой (0, 1, 0), чем первый импульс. Мы приходим к выводу, что ошибка уменьшается, если результат сильно напоминает распределение энергии во входной последовательности. Первый импульс ха-

107
рактеризуется большей энергией в начале, а у второго импульса основная энергия сосредоточена в конце.
На рис.2.15 показаны три импульса с одним и тем же амплитудным спектром, но с различными фазовыми спектрами с задержкой. Основная энергия верхнего импульса сконцентрирована в начале, у среднего импульса – в центре и у нижнего – в конце. Из Раздела 1.2.2 мы знаем, что форма импульса может быть модифицирована путем изменения фазового спектра при постоянном амплитудном спектре.
Рис.2.15 Импульс имеет конечную длину. Если максимум энергии приходится на начало импульса, он является минимально-фазовым (вверху). Если энергия сконцентрирована главным образом в середине импульса, он является смешанно-фазовым (в середине). Если энергия сконцентрирована в конце импульса, он является максимально-фазовым. Количественный анализ этого показан на рис.2.16.
Рис.2.9 Свертка фильтра (а, b) с входным импуль-
сом [(-0.5), 1].
Рис.2.10 Свертка входного импульса [(-0.5), 1] с ко-
эффициентом фильтра [(- 1021 ), (- 214 )].
|
Рис.2.11 Ошибки, |
допущенные |
при двухэле- |
Рис.2.12 Кумулятивная энергия |
|
ментной обратной |
фильтрации |
и фильтрации |
|
|
методом наименьших квадратов. |
Мы говорим, что импульс минимально-фазовый, если максимум его энергии сконцентрирован в начале. Аналогично, импульс является максимально-фазовым, если максимальная энергия сосредоточена в конце этого импульса. Наконец, во всех промежуточных ситуациях импульс является смешанно-фазовым. Отметим, что импульс оп-
108
ределяется как переходная форма волны конечной длины, т.е. импульс является реализуемым. Минимально-фазовый импульс является односторонним в том смысле, что он нулевой до времени t = 0. Импульс, равный нулю для t < 0, называется каузальным (causal). Эти определения согласуются с пониманием того, что физические системы реагируют на возбуждение только после возбуждения. Отклик также имеет конечную продолжительность. Можно сделать вывод, что минимально-фазовый импульс является реализуемым и казуальным. Эти наблюдения можно охарактеризовать количественно, рассматривая четыре трехточечных импульса (Robinson, 1966):
А: (4, 0, -1) В: (2, 3, -2) С: (-2, 3, 2) D: (-1, 0, 4)
Рассчитаем кумулятивную энергию каждого импульса в какой-либо один момент времени. Кумулятивная энергия рассчитывается путем сложения амплитуд, возведенных во вторую степень, как показано на рис.2.16. Отметим, что все четыре импульса характеризуются одинаковой полной энергией (17 единиц), но скорость повышения энергии у каждого импульса своя. Например, в случае импульса А энергия возрастает почти до полной величины при самой первой временной задержке. Для импульсов В и С энергия возрастает относительно медленно. Наконец, импульс D характеризуется наименьшей скоростью возрастания энергии. На рис.2.16 можно видеть, что кривые энергии для импульсов А и D образуют верхнюю и нижнюю границы. Импульс А имеет наименьшую задержку энергии, а импульс D – наибольшую. При данном фиксированном амплитудном спектре, как на рис.2.17, импульс с наименьшей задержкой энергии называется минимально задержанным, а импульс с наибольшей задержкой энергии называется максимально задержанным. Это является основой теоремы задержки энергии Робинсона: минимально-фазовый импульс имеет наименьшую задержку энергии.
Временная задержка эквивалентна задержке по фазе. На рис.2.18 показаны фазовые спектры четырех импульсов (Robinson, 1966). Отметим, что импульс А характеризуется наименьшим изменением по оси частот и мы говорим, что это минимальнофазовый импульс. Импульс D характеризуется наибольшим изменением, и мы говорим, что это максимально-фазовый импульс. Наконец, импульсы В и С характеризуются изменениями большими, чем импульс А и меньшими, чем импульс D; следовательно, они являются смешанно-фазовыми. Поскольку все четыре импульса имеют один и тот же амплитудный спектр (рис.2.17) и энергетический спектр, они должны иметь один и ту же ФАК. Это можно видеть из таблицы 2.13, где сведение в таблицы только одна сторона ФАК, поскольку последовательность реального времени имеет симметричную ФАК (Раздел 1.2.3).
Отметим, что нулевая задержка на ФАК равна полной энергии, содержащейся в каждом импульсе, т.е. 17 единиц. Это действительно для любого импульса; площадь под кривой энергетического спектра равна величине нулевой задержки ФАК, это утверждается теоремой Парсеваля (Приложение А).
Процесс, посредством которого сейсмический импульс сжимается в единичный импульс с нулевой задержкой, деконволюцией сжатия. В Разделах 2.3 и 2.4 были рассмотрены фильтры, предназначенные для достижения этой цели. Их рабочие характеристики зависят не только от длины (сравните результаты двух- и трехточечного фильтров в Разделе 2.3), но от того, является ли входной импульс минимальнофазовым. Оператор деконволюции является результатом обращения импульса. Если импульс был минимально-фазовым, результатом деконволюции также будет устойчивый минимально-фазовый импульс. Термин “устойчивый” означает, что коэффициенты фильтра образуют сходящийся ряд. В частности, коэффициенты убывают во времени (и

109
равны нулю при t = ∞); следовательно, фильтр характеризуется конечной энергией. Это относится к импульсу [1, (- 12 )] результат обращения которого [1, ( 12 ), ( 14 ), …]. Резуль-
тат обращения представляет собой устойчивый фильтр деконволюции сжатия. С другой стороны, если импульс был минимально-фазовым, результат его обращения не будет устойчивым.
|
Таблица 2.13 Задержка ФАК А, В, С, D. |
Таблица 2.14 Задержка ФАК входного импульса |
|
[1, (-0.5)]. |
Таблица 2.15 Задержка ФВК желаемого результата (1, 0, 0) с входным импульсом [1, (-0.5)].
Это действительно для импульса [(- 12 ), 1], результат обращения которого зада-
ется расходящимся рядом [-2, -4, -8, …]. Наконец, смешанно-фазовый импульс не имеет устойчивого результата обращения. Эта дискуссия приводит нас к допущению 6.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.2k
Лекция 5 НАЧАЛЬНЫЙ ИМПУЛЬС И ЧУВСТВИТЕЛЬНОСТЬ ВВ Начальный импульс – это определенное количество внешней энергии, которое необходимо приложить к заряду для начала процесса взрывчатого превращения ВВ. Инициированием называется процесс приложения начального импульса к заряду. Виды начального импульса — механический (удар, трение и пр. ); — тепловой (разогрев и поджигание ВВ); -электрический; — химический; — энергия другого типа ВВ (взрывной начальный импульс). Разрушение горных пород взрывом, 2010 1
Механический начальный импульс, широко используемый в военных целях (взрыватели ударного действия, мины и пр. ), не применяется в промышленности из-за повышенной опасности, несмотря на то, что многие виды взрывчатых материалов могут взорваться от механического начального импульса. Исключение составляют капсюли-воспламенители, применяющиеся в специфической области взрывного дела – прострелочно-взрывных работах в нефтяных и газовых скважинах. Тепловой начальный импульс применяется только для взрывания черного дымного пороха. Большинство ВВ при поджигании горят с участием кислорода атмосферы, не переходя от горения к детонации. В то же время тепловой начальный импульс используется при производстве взрывных работ в специальных устройствах для инициирования зарядов – детонаторах (капсюлях-детонаторах, электродетонаторах), необходимых для возбуждения начального импульса в зарядах ВВ. Так, в капсюлях-детонаторах инициирование первичного инициирующего вещества происходит с помощью снопа искр из огнепроводного шнура (ОШ), а в электродетонаторах – посредством снопа искр от капельки зажигающего состава, воспламеняющейся от нагревающейся нити накаливания. Разрушение горных пород взрывом, 2010 2
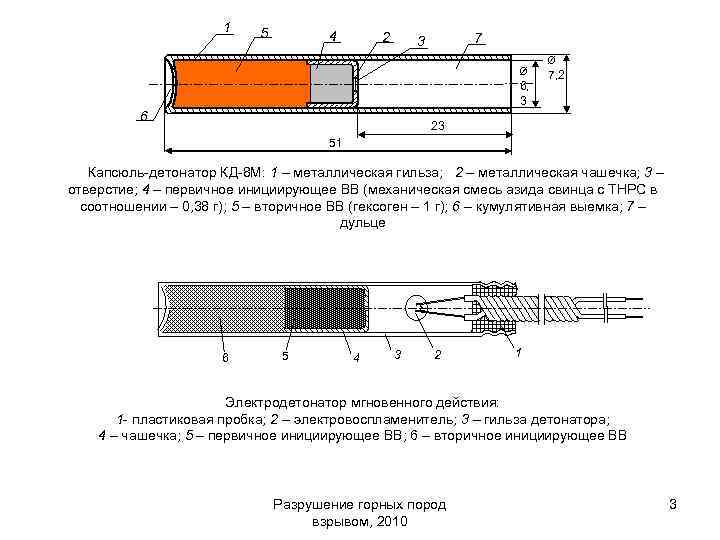
1 5 4 2 7 3 Ø 6, 3 6 Ø 7, 2 23 51 Капсюль-детонатор КД-8 М: 1 – металлическая гильза; 2 – металлическая чашечка; 3 – отверстие; 4 – первичное инициирующее ВВ (механическая смесь азида свинца с ТНРС в соотношении – 0, 38 г); 5 – вторичное ВВ (гексоген – 1 г); 6 – кумулятивная выемка; 7 – дульце 6 5 4 3 2 1 Электродетонатор мгновенного действия: 1 — пластиковая пробка; 2 – электровоспламенитель; 3 – гильза детонатора; 4 – чашечка; 5 – первичное инициирующее ВВ; 6 – вторичное инициирующее ВВ Разрушение горных пород взрывом, 2010 3
Сущность электрического начального импульса состоит в инициировании заряда ВВ электрической дугой высокого напряжения (15 -25 к. В), возникающей между двумя электродами, помещенными в ВВ. Данный способ инициирования зарядов применяется в высоковольтных электродетонаторах для обработки материалов энергией взрыва (ЭДВ-1, ЭДВ 2). Химический начальный импульс обеспечивается химической реакцией двух или нескольких компонентов, при соединении которых между собой происходит реакция в форме взрывного превращения. Разрушение горных пород взрывом, 2010 4
Основным видом начального импульса, применяемым в промышленности, является энергия другого типа ВВ (взрывной импульс). Промышленные взрывчатые вещества, за исключением черного дымного пороха, взрываются только от взрывного импульса (энергии другого типа ВВ). В качестве примера использования взрывного начального импульса можно привести взрывание скважинных зарядов ВВ с помощью детонирующего шнура. Инициирование скважинного заряда: 1 2 1 – электродетонатор (первичное инициирующее ВВ – гремучая ртуть, вторичное инициирующее ВВ – 3 гексоген); 2 – детонирующий шнур 4 (взрывчатое вещество – ТЭН); 3 – промежуточный детонатор (тротиловые шашки Т-400 Г); 4 – гранулированное ВВ (граммонит 79/21) Взрывной начальный импульс передается от электродетонатора 1 к детонирующему шнуру 2, от детонирующего шнура – к промежуточному детонатору 3, а от него – к основному заряду ВВ 4. Разрушение горных пород взрывом, 2010 5
Чувствительность ВВ – его восприимчивость к определенному виду внешнего воздействия. Она зависит от свойств ВВ, его структуры (порошкообразное, гранулированное, литое), температуры, влажности и др. Для оценки чувствительности ВВ проводят определенные виды условных испытаний – пробы на чувствительность. Для оценки взрывчатых веществ проводят следующие основные испытания их чувствительности: — к инициирующему импульсу и к капсюлю-детонатору; — удару; — трению; — нагреванию; — действию открытого пламени; — передаче детонации. Разрушение горных пород взрывом, 2010 6
Проба на чувствительность к инициирующему импульсу и к капсюлю-детонатору Всем ВВ, нечувствительным к первичным средствам инициирования, дают оценку чувствительности к детонации по величине минимального начального импульса, необходимого для возбуждения в них устойчивого взрывчатого разложения. Для этого подрывают серию открытых цилиндрических патронов испытуемого ВВ в бумажной оболочке диаметром, заведомо большим его критического, и длиной в 5 -10 раз больше этого диаметра. В качестве инициатора используют тетриловые или тротиловые прессованные шашки массой от 5 до 100 г, чувствительные к капсюлю-детонатору КД № 8, которые полностью углубляют в патрон или подводят вплотную к его торцу. Заряды взрывают в вертикальном положении на грунтовой площадке. Находят такую минимальную массу шашки-детонатора, при которой во всех трех параллельных опытах фиксируется полная детонация патронов испытуемого ВВ. Выраженная в граммах инициатора, она и служит характеристикой чувствительности ВВ к детонации. Разрушение горных пород взрывом, 2010 7
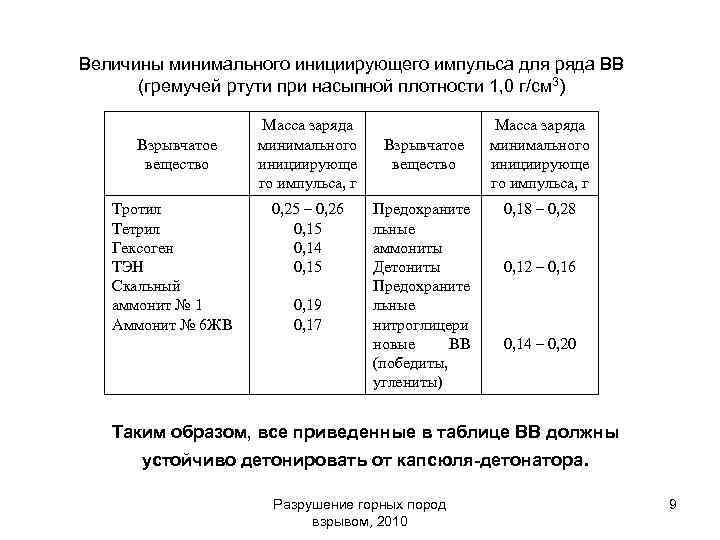
Для ВВ, заведомо чувствительных к КД № 8, минимальный начальный импульс находят иным способом. В мельхиоровые колпачки диаметром 6 мм запрессовывают различные навески (от 0, 1 до 0, 5 г) гремучей ртути. Колпачки помещают в гильзы из-под КД № 8 (без 1 -граммовой тетриловой начинки). Изготовленные таким образом инициаторы с отрезком ОШ помещают в заряды исследуемого ВВ диаметром 40 мм и массой 50 или 100 г. Заряды взрывают на свинцовых столбиках по методу определения бризантности. За величину импульса принимают наименьшую навеску гремучей ртути, при которой достигается обжатие свинца, близкое к обжатию при инициировании заряда ВВ от стандартного капсюля-детонатора. Величины минимального инициирующего промышленных ВВ приведены в таблице. Разрушение горных пород взрывом, 2010 импульса для ряда 8
Величины минимального инициирующего импульса для ряда ВВ (гремучей ртути при насыпной плотности 1, 0 г/см 3) Взрывчатое вещество Тротил Тетрил Гексоген ТЭН Скальный аммонит № 1 Аммонит № 6 ЖВ Масса заряда минимального инициирующе го импульса, г 0, 25 – 0, 26 0, 15 0, 14 0, 15 0, 19 0, 17 Взрывчатое вещество Предохраните льные аммониты Детониты Предохраните льные нитроглицери новые ВВ (победиты, углениты) Масса заряда минимального инициирующе го импульса, г 0, 18 – 0, 28 0, 12 – 0, 16 0, 14 – 0, 20 Таким образом, все приведенные в таблице ВВ должны устойчиво детонировать от капсюля-детонатора. Разрушение горных пород взрывом, 2010 9
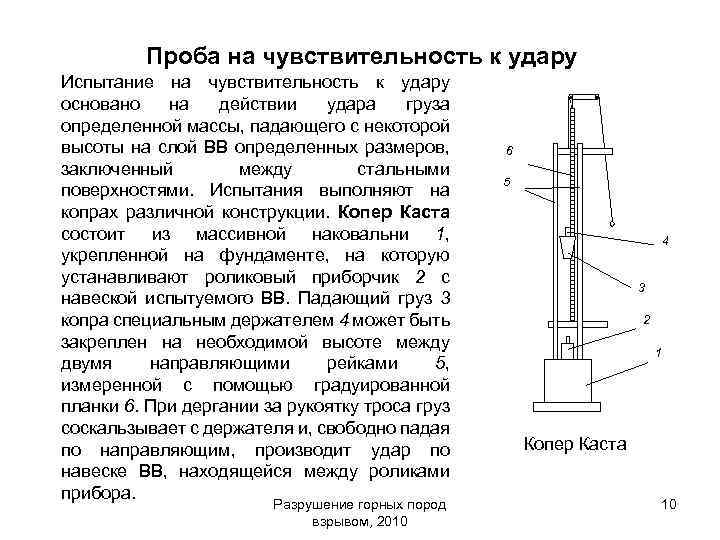
Проба на чувствительность к удару Испытание на чувствительность к удару основано на действии удара груза определенной массы, падающего с некоторой высоты на слой ВВ определенных размеров, заключенный между стальными поверхностями. Испытания выполняют на копрах различной конструкции. Копер Каста состоит из массивной наковальни 1, укрепленной на фундаменте, на которую устанавливают роликовый приборчик 2 с навеской испытуемого ВВ. Падающий груз 3 копра специальным держателем 4 может быть закреплен на необходимой высоте между двумя направляющими рейками 5, измеренной с помощью градуированной планки 6. При дергании за рукоятку троса груз соскальзывает с держателя и, свободно падая по направляющим, производит удар по навеске ВВ, находящейся между роликами прибора. Разрушение горных пород взрывом, 2010 6 6 55 4 4 3 3 2 2 1 1 Копер Каста 10
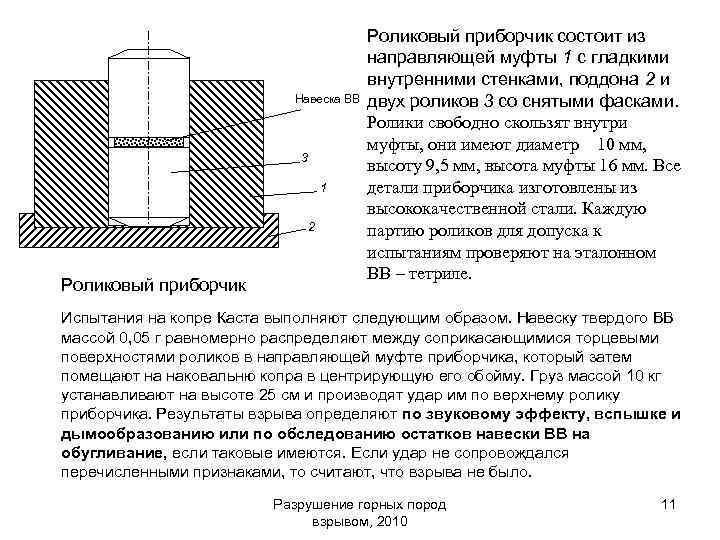
Навеска ВВ 3 1 2 Роликовый приборчик состоит из направляющей муфты 1 с гладкими внутренними стенками, поддона 2 и двух роликов 3 со снятыми фасками. Ролики свободно скользят внутри муфты, они имеют диаметр 10 мм, высоту 9, 5 мм, высота муфты 16 мм. Все детали приборчика изготовлены из высококачественной стали. Каждую партию роликов для допуска к испытаниям проверяют на эталонном ВВ – тетриле. Испытания на копре Каста выполняют следующим образом. Навеску твердого ВВ массой 0, 05 г равномерно распределяют между соприкасающимися торцевыми поверхностями роликов в направляющей муфте приборчика, который затем помещают на наковальню копра в центрирующую его обойму. Груз массой 10 кг устанавливают на высоте 25 см и производят удар им по верхнему ролику приборчика. Результаты взрыва определяют по звуковому эффекту, вспышке и дымообразованию или по обследованию остатков навески ВВ на обугливание, если таковые имеются. Если удар не сопровождался перечисленными признаками, то считают, что взрыва не было. Разрушение горных пород взрывом, 2010 11
Характеристики чувствительности к удару ВВ Показатели чувствительности Взрывчатое вещество Гремучая ртуть Азид свинца Нитроглицерин ТНРС Динамиты ТЭН Гексоген Тетрил Аммониты Тротил минимальная высота падения груза массой 2 кг, при которой происходит взрыв, см число взрывов при падении груза массой 10 кг с высоты 25 см 2 3– 4 4 11 17 28 29 30 30 – 75 60 – 70 100 100 100 65 – 70 50 – 60 10 – 60 2– 8 Разрушение горных пород взрывом, 2010 12
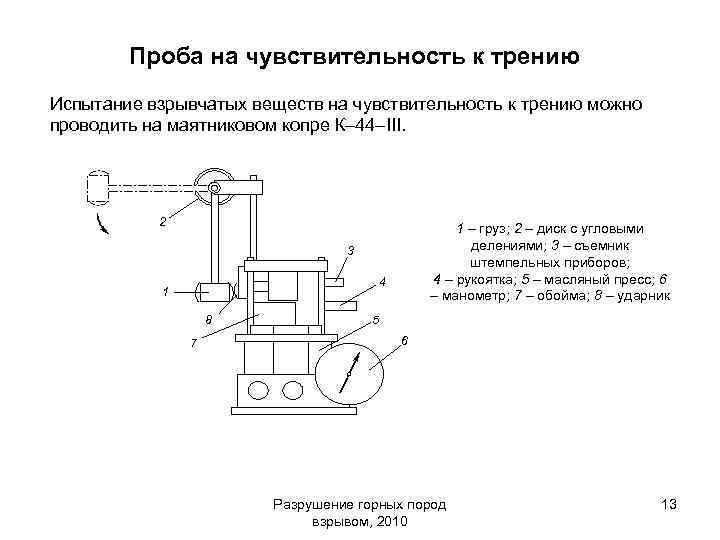
Проба на чувствительность к трению Испытание взрывчатых веществ на чувствительность к трению можно проводить на маятниковом копре К– 44–III. 2 1 – груз; 2 – диск с угловыми делениями; 3 – съемник штемпельных приборов; 4 – рукоятка; 5 – масляный пресс; 6 – манометр; 7 – обойма; 8 – ударник 3 4 1 8 7 5 6 Разрушение горных пород взрывом, 2010 13
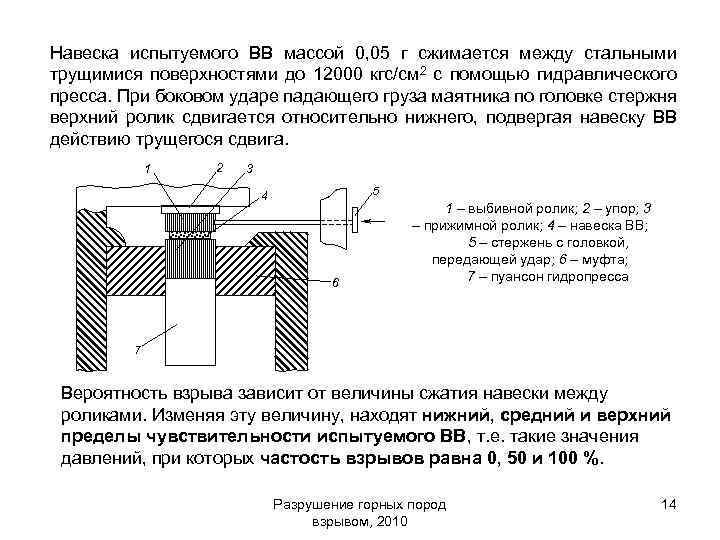
Навеска испытуемого ВВ массой 0, 05 г сжимается между стальными трущимися поверхностями до 12000 кгс/см 2 с помощью гидравлического пресса. При боковом ударе падающего груза маятника по головке стержня верхний ролик сдвигается относительно нижнего, подвергая навеску ВВ действию трущегося сдвига. 1 2 3 5 4 6 1 – выбивной ролик; 2 – упор; 3 – прижимной ролик; 4 – навеска ВВ; 5 – стержень с головкой, передающей удар; 6 – муфта; 7 – пуансон гидропресса 7 Вероятность взрыва зависит от величины сжатия навески между роликами. Изменяя эту величину, находят нижний, средний и верхний пределы чувствительности испытуемого ВВ, т. е. такие значения давлений, при которых частость взрывов равна 0, 50 и 100 %. Разрушение горных пород взрывом, 2010 14
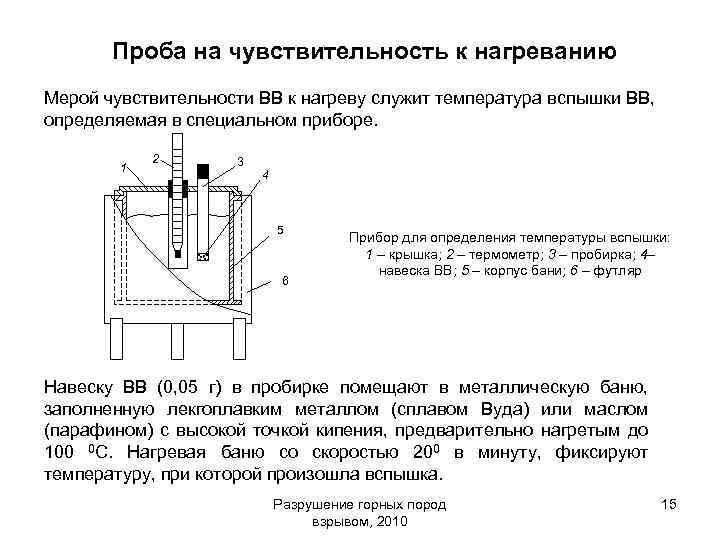
Проба на чувствительность к нагреванию Мерой чувствительности ВВ к нагреву служит температура вспышки ВВ, определяемая в специальном приборе. 1 2 3 4 5 6 Прибор для определения температуры вспышки: 1 – крышка; 2 – термометр; 3 – пробирка; 4– навеска ВВ; 5 – корпус бани; 6 – футляр Навеску ВВ (0, 05 г) в пробирке помещают в металлическую баню, заполненную лекгоплавким металлом (сплавом Вуда) или маслом (парафином) с высокой точкой кипения, предварительно нагретым до 100 0 С. Нагревая баню со скоростью 200 в минуту, фиксируют температуру, при которой произошла вспышка. Разрушение горных пород взрывом, 2010 15
Температура вспышки некоторых ВВ Взрывчатое вещество Тротил Гексоген ТЭН Нитроглицерин Гремучая ртуть Азид свинца Температура вспышки, 0 С 290 – 300 215 – 230 205 – 215 200 – 205 175 – 180 230 – 340 Взрывчатое вещество ТНРС Дымный порох Аммониты Предохранительные аммониты Пироксилин Разрушение горных пород взрывом, 2010 Температура вспышки, 0 С 275 290 280 – 320 250 – 350 195 16
Проба на чувствительность к действию открытого пламени Чувствительность к действию открытого пламени определяют следующим образом: навеску ВВ массой 1, 0 г помещают в пробирку, в которую вводят отрезок огнепроводного шнура (ОШ) таким образом, чтобы его торцевая часть располагалась на расстоянии 1 см от навески ВВ, длина отрезка ОШ составляет 5 – 10 см 1 – пробирка; 2 – отрезок огнепроводного шнура; 3 – навеска ВВ 1 2 1 см 3 Навеска ВВ подвергается воздействию снопа искр от сгорания пороховой сердцевины ОШ, во время проведения опыта определяют, происходит или нет воспламенение испытуемого ВВ. Разрушение горных пород взрывом, 2010 17
Проба на чувствительность к передаче детонации Испытание основано на возбуждении детонации одного патрона взрывом другого, уложенных на грунте соосно на некотором расстоянии друг от друга. Определяется максимальное расстояние передачи детонации между ними, величина которого является одной из важнейших характеристик детонационной способности ВВ, она характеризует качество их изготовления. Активный заряд (патрон-боевик) ОШ Пассивны й заряд КД О передаче детонации судят по отсутствию остатков ВВ и оболочки пассивного заряда и по наличию углубления и следов взрыва в грунте на месте расположения патронов. Разрушение горных пород взрывом, 2010 18
Важность таких испытаний состоит в том, что при заряжании шпуров патронированными ВВ между патронами могут оставаться воздушные промежутки. При взрыве такого заряда детонационная волна на границе «ВВ» — «воздух» переходит в ударную волну, которая интенсивно затухает в воздухе. Если ВВ обладает нормальным качеством, то энергии ударной воздушной волны, прошедшей через существующий промежуток, будет достаточно для того, чтобы возбудить детонацию в торце следующего патрона. Взаимные переходы детонационной волны в ударную и обратно при передаче детонации на расстояние схематично показаны на рисунке. 1 – активный заряд; 2 – воздушный промежуток; 3 — пассивный заряд; I – III – зоны распространения детонации Разрушение горных пород взрывом, 2010 19
Для изменения (повышения или уменьшения) чувствительности в состав ВВ вводятся специальные добавки. Сенсибилизаторами называются добавки, повышающие чувствительность ВВ. Существует два основных типа сенсибилизаторов. К I типу относятся инертные вещества, температура плавления и твердость которых выше, чем у компонентов самого ВВ (мелкоизмельченное стекло, кварцевый песок, буровая пыль, металлическая стружка). На острых гранях частиц сенсибилизатора концентрируется энергия удара и трения, вызывающая локальные очаги воспламенения и взрыва. Например, примесь к тротилу 0, 1– 0, 2 % кварцевого песка повышает его чувствительность в 3 – 5 раз. Данный тип сенсибилизаторов не допускается для применения в промышленных ВВ из-за возможности неуправляемого повышения чувствительности в отдельных частях объема ВВ. Разрушение горных пород взрывом, 2010 20
II тип сенсибилизаторов – это более мощные, более чувствительные к внешним воздействиям ВВ (жидкие нитроэфиры, гексоген и др. ), которые в смеси с малочувствительными взрывчатыми (аммиачная селитра и др. ) или невзрывчатыми веществами обеспечивают нормальную чувствительность смесевого ВВ к инициированию капсюлем-детонатором и одновременно повышают энергетические характеристики этого смесевого ВВ. Флегматизаторами называют добавки, снижающие чувствительность ВВ к внешним воздействиям. В качестве флегматизаторов используются мягкие и легкоплавкие примеси, а также компоненты ВВ с высокой теплопоглащающей способностью (индустриальные масла, парафин и др. ). Вода также оказывает флегматизирующее действие на взрывчатые вещества. Действие флегматизаторов связано с затратой части тепловой энергии начального импульса на нагревание и плавление данных добавок. Разрушение горных пород взрывом, 2010 21
2.4.2. Экспоненциальный
импульс.
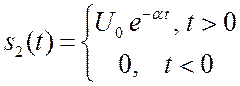
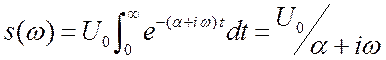
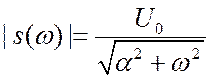
Импульс и его спектр изображены на рисунках 2.9 и 2.10. Длительность импульса
на уровне равна
.
убывает монотонно с ростом
, но достаточно медленно. Для определения
ширины спектра примем уровень 0,1 от . Тогда:
;
.
2.4.3. Косинусоидальный импульс (непрерывный).
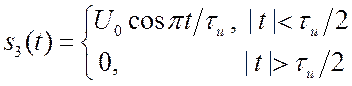
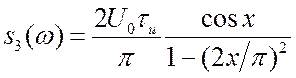
. (2.10)
Импульс и его спектр изображены на рис. 2.7 и 2.8. есть «площадь» импульса.
убывает с ростом
немонотонно, но уже быстрее, как
(сигнал непрерывен). Ширина спектра до
первого нуля равна
. Тогда
.
2.4.4. «Колокольный» импульс (гладкий).
. Рис. 2.11. Сигнал
бесконечен во времени, но он очень быстро стремится к нулю с ростом . Поэтому он служит хорошей моделью
гладкого импульса конечной длительности. Длительность импульса условно (для оценок)
определяется на уровне . Тогда
.
Вычислим спектр этого сигнала.
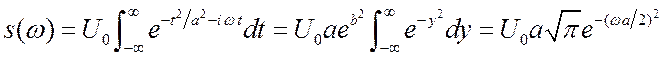
), (2.11)
где выбирается из условия
. Последний интеграл равен
.
есть
«площадь» импульса. Плотность спектра, рис. 2.12, определяется такой
же функцией, как и импульс, и очень быстро, монотонно убывает с ростом . Определим условно ширину спектра
тоже на уровне
. Тогда
или
.
2.4.5. Связь длительности импульса и ширины спектра.
Из приведённых примеров следует, что произведение
длительности импульса на ширину спектра
даёт величину порядка единицы. Интересно
определить для какого импульса это произведение будет минимальным. Важность
этого вопроса связана с выбором оптимальной формы импульса для кодирования
информации.
Предварительно мы должны принять некоторый единый,
удобный способ определения длительности импульса и ширины спектра. Такой общий
способ был предложен на энергетической основе. Для всех рассмотренных импульсов,
кроме последнего, мы можем считать при
. «Колокольный» импульс
описывается четной функцией времени, и при вычислении полной энергии сигнала мы
можем снова интегрировать по промежутку , удвоив
результат. Тогда полная энергия сигнала ( для
«колокольного» и для всех остальных
импульсов) 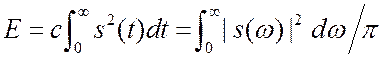
При интегрировании по конечным
интервалам мы получим часть полной энергии. Определим длительность импульсов и ширину спектров
так, чтобы получить, например, 0,9 полной
энергии из равенств: 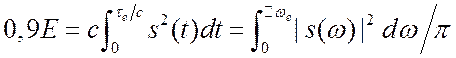
произведения . Интересные результаты такого сравнения
приведены в таблице, которая заимствована из книги Харкевича «Спектры и
анализ».
|
Импульс |
Длительность |
Ширина спектра |
|
|
Экспоненциальный |
|
|
|
|
Прямоугольный |
|
|
|
|
Треугольный |
|
|
|
|
Косинусоидальный |
|
|
|
|
Колокольный |
|
|
|
Импульсы с разрывами самые плохие.
Непрерывные импульсы лучше. При той же эффективной длительности их спектр
примерно в два раза уже. Для «гладких» импульсов спектр будет ещё уже,
но всегда . Значение произведения для колокольного
импульса получается очень близким к теоретическому пределу.
2.5. Идеализированные сигналы. Обобщённые спектры.
При анализе линейных цепей широко используются
идеализированные сигналы, которые не могут быть реализованы, такие, как
ступенчатая функция (прямоугольный импульс бесконечной длительности), предельно
короткий импульс — функция, линейно растущее
(неограниченно) напряжение и другие. Несмотря на это, первые два сигнала
находят очень широкое применение по причинам, которые скоро станут понятны.
Такие сигналы не удовлетворяют условию абсолютной интегрируемости, их энергия
бесконечна. Приходится вводить обобщенные спектры, поскольку обычное преобразование
Фурье для них неприменимо.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Импульсы минимальной длительности (к настоящему времени вплоть до 16 фс) можно получить, как указывалось выше путем последующей компрессии. [c.227]
Импульсы минимальной длительности 227 [c.363]
При достижении максимума отнощения сигнал/шум полезный сигнал никогда не успевает нарастать до максимальной величины, так как при этом обеспечивается передача лишь основных, несущих наибольшую энергию, гармонических составляющих спектра. Очевидно, при оптимальной выявляемости сигнала на выходе датчика всегда содержится дополнительная динамическая погрешность измерения, так как при изменении длительности сигнала и неизменной амплитуде меняется уровень р. Для исключения этой погрешности необходимо, чтобы при регистрации импульса минимальной длительности сигнал на выходе 7 С-фильтра успевал нарастать до максимальной величины. Так как для выполнения этого требования расчетные значения к очень велики, то минимально допустимая величина к определяется из условия передачи активной ширины спектра сигнала. [c.151]
Следует подчеркнуть, что указанное преобразование зарегистрированных сведений осуществляется чрезвычайно быстро. Минимальное время,необходимое для восстановления изображения, можно оценить с помощью следующих рассуждений. Пусть просвечивающая волна представляет собой световой импульс с длительностью т. Импульс ограниченной длительности можно рассматривать как набор монохроматических волн, причем спектральная ширина импульса бv, согласно изложенному в 21, связана с т универсальным соотношением бvт = 1. Голограмма, будучи, по существу, дифракционной решеткой, произведет спектральное разложение импульса, и изображение каждой точки предмета будет соответствующим образом расширено. Для того чтобы такое уширение практически не было заметным, спектральная ширина импульса должна быть меньше интервала частот, разрешаемого голограммой-решеткой (см. 50). На основе высказанных соображений легко показать, что длительность импульса должна удовлетворять условию [c.268]
Полагая D = 9 см, sin фо — sin ф = 1/3 в (67.3), находим чрезвычайно малое значение необходимой длительности импульса т лг 10 1 с. При снижении требований к качеству изображения минимальную длительность импульса можно еще более уменьшить. [c.269]
Диапазон контролируемых толщин. Минимальную толщину изделия, контролируемого эхо-методом, определяет мертвая зона толщиномера. Она аналогична мертвой зоне дефектоскопа (см. подразд. 5.2). Для ее сокращения в приборах групп А и В добиваются минимальной длительности зондирующего импульса, а в приборах группы Б применяют РС-преобра-зователи. В результате мертвая зона для толщиномеров групп А и В составляет 0,2. .. 0,3 мм, для толщиномеров группы Б — 0,5. .. 1,5 мм. [c.405]
Коммутационная способность тиристорных ключей по напряжению 100 В, по току 0,1 А контактных ключей соответственно 30 В и 0,5 А (для РПИ-1). Зона нечувствительности 0,2—2%. Постоянные времени демпфирования О—20 с, интегрирования 5—500 с, дифференцирования О—200 с. Минимальная длительность импульса 0,1—1 с. Коэффициент пропорциональности для РПИ-1 0,1—10. Изменение коэффициента масштабирования 0—1 [c.761]
Отсюда видно, что квадратичный член в частотной модуляции приводит к уменьшению эффективной дисперсионной длины. Вследствие этого минимальная длительность импульса достигается на длинах [c.35]
Нетрудно убедиться, что из этого соотношения следует формула (8) для длины компрессии L . Выполняя обратное фурье-преобразование, из (23) при учете (25) для минимальной длительности импульса Тп, получаем выражение (7). [c.39]
Для устойчивости синхронного режима работы солитонного лазера требуется весьма точное согласование (до 1 мкм) длин основного и вспомогательного резонаторов. В [38] сообщается о создании автоматизированной системы стабилизации режима работы солитонного лазера, минимальная длительность импульсов доведена до 100 фс. [c.215]
Минимальная длительность импульсов синхронно-накачиваемых лазеров. Процесс генерации в растворах красителей хорошо описывается четырехуровневой моделью активной среды (рис. 6.9)[20]. Квант накачки [c.250]
Теоретический предел длительности импульсов, генерируемых в режиме синхронной накачки, связан с невозможностью создания на рабочем переходе инверсии населенности за время, меньше времени колебательной релаксации Тр 1 пс в данном возбужденном состоянии молекулы красителя. Если длительность импульса накачки заключена в интервале Тто, как показывают расчеты [24], минимальная длительность импульса генерации ограничивается величиной [c.251]
Зависимость средней по цугу длительности импульсов генерации <т > от числа импульсов накачки М приведена на рис. 6.14. Видно, что увеличение М до 40—60 приводит к установлению стационарного значения <т >. Основным фактором, ограничивающим минимальную длительность выходных импульсов, является временная модуляция цуга накачки, приводящая к неодновременности достижения порога генерации для разных импульсов, что, в свою очередь, уширяет импульс генерации. Отметим, что перспективными с точки зрения генерации длинных цугов (М 10 ) пикосекундных импульсов с постоянной амплитудой являются твердотельные лазеры с самосинхронизацией мод и электронным управлением добротностью резонатора. [c.256]
Подчеркнем, что с точки зрения достижения минимальной длительности усиление частотно-модулированного импульса и последующее [c.270]
Уже в начале 80-х годов стало ясно, что перспективы генерации сверхкоротких импульсов УФ диапазона связаны с удвоением частоты лазеров на красителях и их последующем усилении в эксимерных усилителях. Трудности в осуществлении пассивной или активной синхронизации мод эксимерных лазеров вызваны, прежде всего, малыми временами существования инверсии в активной среде (10 —10 с), что резко ограничивает число проходов излучения по резонатору. К настоящему времени минимальная длительность, реализованная в режиме активной синхронизации мод, составляет 120 пс [74]. Итоги развития пикосекундных эксимерных систем подведены в обзоре [75]. [c.271]
Метод двухкаскадной генерации разностной частоты позволяет достаточно просто и с высокой эффективностью формировать сверхкороткие ИК импульсы. Изменяя интенсивности взаимодействующих в первом каскаде волн и длину нелинейных кристаллов, можно управлять длительностью импульсов. Предельные возможности схемы, с точки зрения достижения минимальной длительности, определяются полосой пропускания параметрического преобразователя. Так при длине кристалла L=22 мм можно преобразовывать импульсы с длительностью, превышающей 4 пс. Уменьшение длины кристалла приводит к уширению полосы преобразования, но снижает его эффективность. [c.278]
Это и означает, что излучение имеет форму короткого и интенсивного импульса. Длительность этого импульса больше характерного времени резонатора Травного по меньшей мере нескольким временам полного обхода резонатора. Следовательно, минимальные длительности импульса составляют, например, в твердотельных лазерах с модуляцией добротности и с обычной длиной резонатора (L 1 м) несколько десятков наносекунд. [c.90]
Применение лазерных импульсов минимально достигнутой к настоящему времени длительности (т , 0,1 пс) и безынерционных оптических затворов, например, на основе преобразования во вторую гармонику или параметрического эффекта позволяет довести пространственное разрешение Ах до величины порядка 10 мкм. [c.127]
Как видно из рисунков, увеличение энергии накачки и коэффициента отражения позволяет получать более короткие и интенсивные импульсы. При малых коэффициентах отражения или малых энергиях накачки обратная длительность импульсов и интенсивность меняются монотонно. Они достигают максимальных значений у границы области синхронизации, соответствующей максимально допустимой длине резонатора. При несколько больших коэффициентах отражения или энергиях накачки обратная длительность импульсов и их интенсивность достигают внутри области синхронизации мод максимума. Этот экстремум представляет особый интерес при выборе параметров лазера, так как в экстремуме длительность импульсов минимальна и малые флуктуации длины резонатора не оказывают заметного влияния на процесс синхронизации мод и характеристики излучения лазера. Выбирая в качестве примера опти- [c.166]
В последнее время ведется много работ по исследованию этого явления для разработки технологии шокового упрочнения (sho k hardening) [71, 75]. Для этих целей используется излучение твердотельных неодимовых лазеров и газовых ОКГ с длиной волны 10,6 мкм, работающих в импульсном режиме. Авторы ряда работ измеряли давления, возникающие на поверхности образца при действии гигантских импульсов ОКГ. В частности, производилось измерение давления при использовании СОз-лазера, генерирующего излучения с длиной волны 10,6 мкм [75]. Длительность импульса изменялась путем регулирования состава газовой смеси лазера. Минимальная длительность импульса составляла 100 нс. Давление определялось путем измерения перемещений обратной стороны мишени, которая одновременно являлась одним из зеркал [c.23]
Электроэрозионная обработка использует расплавление и испарение малых порций металла импульсами электрической энергии, которые вырабатываются периодически специальными генераторами. Обработка ведется в жидкой среде, и развивающиеся в межэлектрод-ном промежутке в момент прохождения разряда гидродинамические силы выбрасывают расплавленную порцию металла из зоны обработки. Это позволяет электроду постепенно внедряться в обрабатываемую заготовку, последняя присоединяется к тому полюсу, на котором выделяется больше тепла. Разряд, т. е. пробой межэлек-тродного промежутка, возникает каждый раз между наиболее сближенными точками анода и катода. В результате каждого импульса на поверхности электродов образуются небольшие углубления, форма и размеры которых зависят от мощности импульса, его длительности и свойств обрабатываемого материала. Следует обратить внимание на то, что удаление материала происходит на обоих электродах (с заготовки и с инструмента). Разрушение электрода-ин-струмента (или износ) явление нежелательное не только потому, что на него затрачивается бесполезно энергия, но и из-за снижения точности обработки и экономичности процесса. Уменьшения износа электрода-инструмента добиваются выбором для их изготовления соответствующих материалов, применением униполярных импульсов, подключением электрода-инСтрумента к тому из полюсов источника тока, на котором его износ будет минимальным. [c.145]
На рисунке приняты следующие обозначения а — ударное ускорение (Oojraax — максимальное ударное ускорение при ограничении по скорости соударения (iZs)min — минимальное ударное ускорение при ограничении по деформации (/ )тт — минимальная длительность переднего фронта ударного импульса (4)тах — максимальная длительность переднего фронта ударного импульса tz, = f (й) — зависимость изменения длительности переднего фронта ударного импульса от ударного ускорения при ограничении по скорости соударения = = / (o ) — зависимость изменения длительности переднего фронта ударного импульса от ударного ускорения при ограничении по пути торможения а,, ZI — ударное ускорение, удовлетворяющее обоим ограничениям (5,0 — длительность переднего фронта ударного импульса, удовлетворяющая обоим ограничениям. [c.339]
Выходные сигналы при сопротивлении нагрузки 2 кОм — 10 В (24 В для РБИ1-П). Коммутационная способность тиристорных ключей по напряжению <127 В. по току <0,1 А. Зона нечувствительности 0,2—2 %. Постоянные времени демпфирования 0—20 с, интегрирования 5—500 или 10—20000 с. Скорость связи 0,2—2,5 %/с. Минимальная длительность импульса 0,1 — [c.468]
Из этого выражения очевидно, что длительность импульса минимальна при а = /AaL это условие совпадает с выражением (8.5.9), полученным полуинтуитивным методом. Подставляя аЬ = = 1/4а в (8.5.25), находим следующее выражение для минимальной длительности импульса [c.332]
Если ao 2<0, то ФМ импульс расплывается быстрее, чем немодули-рованный. В случае a k >0 ФМ импульс сначала сжимается, а затем расширяется (ср. кривые 2 и 5 на рис. 1.3а). Минимальная длительность импульса [c.34]
Lk= (ао/гз) . Минимальная длительность сжатого импульса (см. (18)) T i 2/A of = (ао Го) На рис. 1.7 приведены графики, характеризующие связь вида частотной модуляции и дисперсии среды, обеспечивающей компрессию импульсов. [c.38]
Для рассматриваемой нами модели гауссовского ФМ импульса (1) ответ очевиден. Прошедший через диспергирующую среду ФМ импульс будет иметь максимальную амплитуду и, следовательно, минимальную длительность при условии, что все его спектральные компоненты точно сфазированы ) [c.39]
Из (30) следует, что чем ближе форма начального импульса к прямоугольному (чем больше т), тем больше минимальная длительность ктш- другими словами, для супергауссовских импульсов коэффициент компрессии оказывается меньше, нежели для гауссовского. С ростом т уменьшается и длина компрессии. [c.41]
Время Тпр определяет минимальную длительность импульса в фокусе линзы. Формула (7) справедлива в первом приближении теории дисперсии. Заметим, что для импульсов длительностью в несколько фемтосекунд существенным оказывается дисперсионное расплывание в материале линзы, описываемое вторым приближением. [c.60]
Реальные количественные закономерности дисперсионного режима сжатия были установлены в [17, 19] методами математического моделирования. В численных экспериментах нелинейное уравнение Шредингера (4.3.1) интегрировалось по t, при различных параметрах нелинейности R. Вычислялись профили интенсивности, распределения текущей частоты в различных сечениях световода и результаты сжатия час-тотпо-модулированных импульсов при оптимальной настройке решеточного компрессора. На рис. 4.7 приведены зависимости минимальной длительности импульса от длины световода. Видно, что для каждого значения R существует оптимальная длина световода Lonr, при которой достигается максимальная степень сжатия Наличие экстремума связано с тем, что на малых рас стояниях 2 Lф форма импульса еще практически не изменилась и нелинейное ушире-ние спектра растет пропорционально р асстоя нию (2). Н а р ас-стоянии расплывание [c.180]
| Рис. 5.1. Самосжатие УУ-солитонного импульса при N=4. На вставке приведена зависимость минимальной длительности импульса от (сплошная линия — теория, точки — эксперимент [10]) | ![Рис. 5.1. Самосжатие УУ-солитонного импульса при N=4. На вставке приведена зависимость минимальной длительности импульса от (<a href="/info/232485">сплошная линия</a> — теория, точки — эксперимент [10])](https://mash-xxl.info/pic1/080209068140037061173070036163127170210180240078.png) |
На выходе системы формируются импульсы с длительностью 0,8 пс на стоксовой частоте (Х(,= 1,10 мкм). В этой схеме синхронно-накачи-ваемый волоконный световод играет роль активной среды и безынерционного фазового модулятора, а наличие решеточного компрессора позволяет стабилизировать длительность выходного импульса на минимальном уровне. Минимальная длительность в подобных устройствах ограничивается шириной полосы рамановского усиления и может быть, в принципе, доведена до 100 фс. [c.217]
К форме импульса разрядного тока через лампу. накачки твердотельного излучателя не предъявляется. жестких требований. Фронт стремятся сделать длительностью не менее 100 мкс, чтобы избежать возникновения ударной волны, способной вывести лампу накачки из строя [5, 36]. Вместе с тем, минимальная длительность лмпульса должна превышать время, необходимое для создания условий генерации излучения, а максимальная определяться требованиями к продолжительности излу- чения и может составлять единицы и даже десятки миллисекунд. [c.32]
При малом отличии частоты модуляции сот от то расчет может быть выполнен аналогично сделанному выше. Здесь член разложения экспоненты (4.22), прямо пропорциональный времени, ответствен за сдвиг частоты. Не вдаваясь в детали расчета, приведем на рис. 4.3 рассчитанные для случая фазовой модуляции зависимости длительности импульсов от расстройки 6югп = ато — Ют [4.5]. Минималь-ная длительность импульсов имеет место при некоторой малой отрицательной расстройке, в то время как с увеличением положительной расстройки длительность импульсов монотонно растет. В случае амплитудной модуляции длительность импульсов минимальна при бсот = 0 и монотонно нарастает с увеличением как положительной, так и отрицательной расстройки. [c.143]
Для каждого значения длины волны длительность импульсов может плавно меняться за счет перемещения призмы, что. вызывает изменение оптического пути, проходимого импульсом внутри стекла. Как видно из рис. 6.16, для каждой длины волны при определенном значении длины пути в стекле обеспечивается полная компенсация чирпа и длительности импульсов минимальны. Оптическая длина пути, соответствующая минимальной длительности импульсов, меняется в зависимости от концентрации поглотителя и в свою очередь обеспечивает минимальную длительность импульсов при определенной концентрации или соответствующей длине волны излучения лазера. Наиболее короткие импульсы длительностью менее 100 фс были при этом получены в диапазоне длин волн от 605 до 620 нм, причем минимум длительности импульсов достигался при 617 нм. Основные экспериментальные результаты могут быть описаны в рамках теории, изложенной в п. 6.2.7. [c.225]