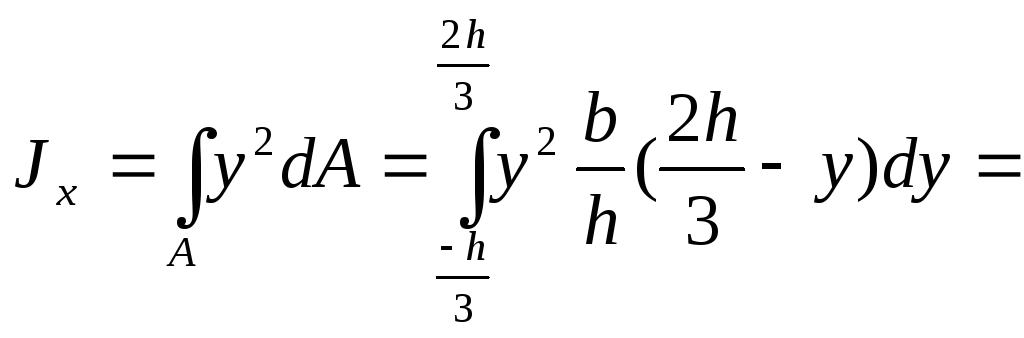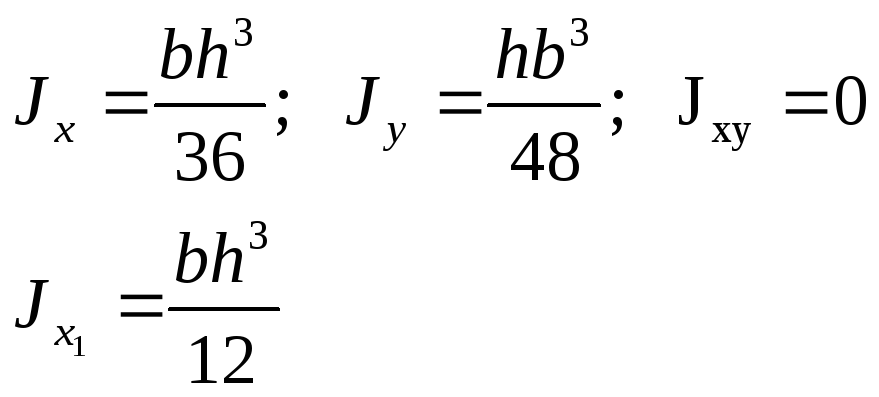Как найти минимальный момент инерции

Прямоугольное
сечение.

Прямоугольное
сечение имеет две оси симметрии, а
главные центральные оси Сx
и Cy
проходят через середины параллельных
сторон.

Главный
центральный момент инерции относительно
оси x

Элементарную
площадку dA
в этом случае можно представить в виде
полоски во всю ширину сечения и толщиной
dy,
значит dA=b*dy.
Подставим под знак интеграла значение
dA
и проинтегрировав по всей площади, т.е.
в пределах изменения ординаты y
от –h/2
до +h/2,
получим

Окончательно

Аналогично
получим формулу главного центрального
момента инерции прямоугольника
относительно оси y:

Круглое
сечение

Для
круга главные центральные моменты
инерции относительно осей x
и y
равны между собой.

Поэтому
из равенства

Треугольник

2.Изменение моментов инерции при переходе от центральных осей к параллельным:

J_x1=J_x
+ a²А;

J_y1=J_y
+ b²А;

момент
инерции относительно любой оси равен
моменту инерции относительно центральной
оси, параллельной данной, плюс произведение
площади фигуры на квадрат расстояния
между осями. J_y1x1=J_yx
+ abF;
(«a»
и «b»
подставляют в формулу с учетом их знака).

3.Изменение моментов инерции при повороте осей

J_x1=J_xcos²
+ J_ysin²
— J_xysin2;
J_y1=J_ycos²
+ J_xsin²
+ J_xysin2;

J_x1y1=(J_x
— J_y)sin2
+ J_xycos2
;

Угол
>0,
если переход от старой системы координат
к новой происходит против час.стр. J_y1
+ J_x1=
J_y
+ J_x

Экстремальные
(максимальное и минимальное) значения
моментов инерции называются главными
моментами инерции.
Оси, относительно которых осевые моменты
инерции имеют экстремальные значения,
называются главными
осями инерции.
Главные оси инерции взаимно перпендикулярны.
Центробежные моменты инерции относительно
главных осей = 0, т.е. главные оси инерции
— оси, относительно которых центробежный
момент инерции = 0. Если одна из осей
совпадает или обе совпадают с осью
симметрии, то они главные. Угол,
определяющий положение главных осей:
,
если

₀>0

оси поворачиваются против час.стр. Ось
максимума всегда составляет меньший
угол с той из осей, относительно которой
момент инерции имеет большее значение.
Главные оси, проходящие через центр
тяжести, называются главными
центральными осями инерции.
Моменты инерции относительно этих осей:

J_max
+ J_min=
J_x
+ J_y.
Центробежный момент инерции относительно
главных центральных осей инерции равен
0. Если известны главные моменты инерции,
то формулы перехода к повернутым осям:

J_x1=J_maxcos²
+ J_minsin²;
J_y1=J_maxcos²
+ J_minsin²;
J_x1y1=(J_max
— J_min)sin2;

4.Классификация элементов конструкций

Стержнем
наз. Геом тела у которых один из размеров
много больше других.

Пластины
или оболочки
– это геом тела у которых один из размеров
<< других

Массивные
тела—
все размеры одного порядка

5.Основные
допущения о свойствах материала

Однородные
– в люб. точке материалы имеют одинак.
физико-химич. св-ва;

Сплошная
среда – кристаллич. строение и микроскопич.
дефекты не учитываются;

Изотропны
– механич. св-ва не зависят от направления
нагружения;

Идеальная
упругость – полностью восстанавливают
форму и размеры после снятия нагрузки.

6.Типы
опор

а)
Шарнирно – неподвижная (двухсвязная)
опора: Воспринимает как вертикальные,
так и горизонтальные усилия (усилия под
углом).

б)
Шарнирно – подвижная опора – воспринимает
только вертикальные нагрузки. Реакция
опоры всегда направлена вдоль опорного
стержня, перпендикулярно опорной
поверхности

в)
Жесткая заделка (трехсвязная)

Реакции
в опорах определяют из условия равновесия
(уравнение статики).

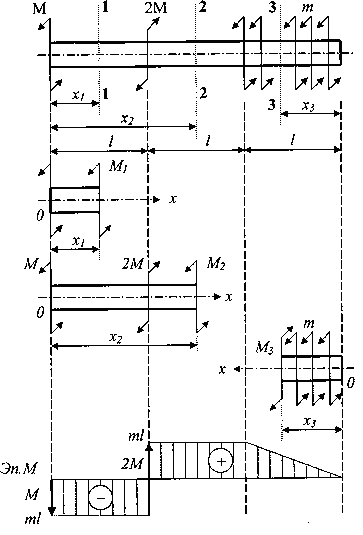
7.Классификация
нагрузок

1. По
   месту действия

Поверхностные
и объемные

а)
сосредоточенная сила

б)
распределенная сила

прямоугольная
Rq=
qa

треугольная
Rq=
½ qa

в)
сосредоточенный момент

изгибающий

скручивающий

г)
распределенный момент

Rmz=
mz a –равнодейств распр мом

1. По
   времени действия

Постоянные
и временные

1. По
   характеру действия

Статические
и динамические

1. По
   характеру возникновения

Активная(известны)
и реактивная (неизвестны)

8.Основные
принципы изучаемого курса

При
расчете сложного сопротивления
используется принцип
независимости действия сил.
Сложный вид нагружения представляется
как система простых видов нагружения
действующих независимо друг от друга.
Решение при сложном сопротивлении
получается в результате сложения решений
полученных при простых видах нагружения.

принцип
Сен-Венана

на
достаточном удалении от места приложения
нагрузки характер её воздействия не
зависит от способа её приложения, а
зависит от величины равнодействующей.

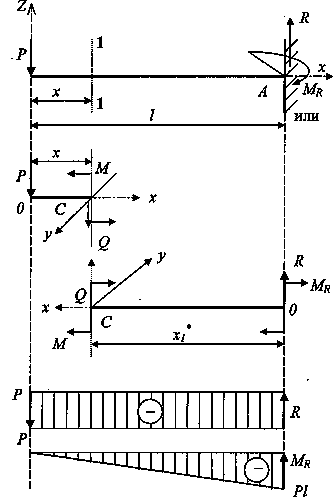
9.Внутренние
усилия. Метод сечений (Метод РОЗУ)

Nz=∑z
(pi)
нормальная с

Qx=∑x
(pi)
поперечная с

Qy=∑y
(pi)

Mz=∑mz
(pi) крутящий
момент

Mx=∑mx
(pi) изгибающий

My=∑my
(pi)

Разрезаем
мысл тело плоск

Отбрасываем
одну из г внутр усил

Заменяем
внутр усилиями

Уравновешив
внутр ус внеш нагр

10.Правило
знаков внутренних усилий

Правило
знаков поперечных сил при изгибе:

Крутящий
момент

Против
ЧС при взгляде со стороны сеч то +

Правило
знаков изгибающих моментов:

Правило
проверки правильности построения эпюр
нагружения:

В
сечениях балки, где приложены внешние
сосредоточенные нагрузки на эпюре д.б.
скачёк на величину этой нагрузки.

11.Эпюры
внутренних усилий

ПРИ
РАСТЯЖЕНИИ-СЖАТИИ

ПРИ
КРУЧЕНИИ

при
прямом изгибе

12.Дифференциальные
зависимости при изгибе

;
;

13.Следствия
из дифференциальных зависимостей

1. Если
   на участке нет распр нагр (q=0)
   то поперечная сила на этом участке
   имеет пост вел., а эпюры изгиб мом
   меняются по лин закону

2. На
   уч на котором присутст распр нагр пост
   интенсивн. Поперечная сила меняется
   по лин зак , а эпюры по закону квадр
   параболы. Причем эпюра мх всегда напр
   навстречу распр нагрузке. Где Qy равно
   0 эпюра мх имеет экстремум. Если Qy равно
   0 на всем участке, то мх постоян величину

4.
На участке где Qy>0 эпюра мх возрастает
слева направо

5.
В том сеч. где приложена сосред сила
эпюра Qy
имеет скачок на вел этой силы. В сеч где
сосред момент эпюра мх имеет скачок на
величену этого момента

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В прошлый раз мы поговорили о такой величине, как статические моменты. Теперь можем двигаться дальше: сегодня на повестке моменты инерции. 

Внимательный читатель уже может возмутиться:
 “И зачем мы изучаем эти моменты? Какой в этом прок?
Причём же тут инерция, если сопромат — по сути статика?»

На первый вопрос у меня есть два ответа — краткий и не очень. Пока ограничусь кратким:

Статические моменты и моменты инерции  широко используются для определения нормальных и касательных напряжений, определении прогибов и деформаций конструкций. Читая о том, как все это вычислить,  вы будете сталкиваться с геометрическими характеристиками постоянно. Поэтому лучше сразу понимать, о чем идёт речь, а, при необходимости, подсматривать тут.

В изгибаемом элементе от момента сил возникают напряжения, для определения которых нам и нужен момент инерции (хотя и опосредованно. Впрочем, если вы читали статью про моменты, то это уже знаете). При этом сам элемент деформируется, и величина этих деформаций (прогибов) также определяется с помощью момента инерции. 

Для ответа на второй вопрос перейдем уже к моментам инерции.

Что такое момент инерции

Суть и смысл моментов инерции в общем случае походит на статические моменты, однако корни нужно искать в описании вращения тела. Для вращательного движения одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Рассмотрим вращающееся тело, как совокупность точек с предельно малыми размером и массой, которые находятся на расстояниях Ri (от нуля до R):

Тут видно, что также, как в формуле кинетической энергии при линейном движении мера инертности — масса, при вращательном движении мера инертности — момент инерции. Впрочем, я немного забегаю вперёд.

Угловая скорость вращающегося тела — угол поворота, пройденный за единицу времени

Тут начальный угол поворота φ₀ может быть равен нулю, если мы рассматриваем начало движения. 

Линейная скорость тела:

Ускорение вращающегося тела (а нас интересует нормальное) тогда:

Я не буду затрагивать динамику вращающегося тела, и расскажу только о жизненно необходимом.

Сила (которая по второму закону Ньютона — произведение массы на ускорение):

и момент:

И вот тут вспомним уже третий закон Ньютона — действию всегда есть равное и противоположное противодействие, а значит действию найденного нами момента будет сопротивляться — момент инерции.

Вспомним также, что, как и со статическими моментами, на разные точки тела, удаленные от оси вращения на разные расстояния будет действовать разный момент, а общий момент можно получить их просуммировав:

При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. Но, как я уже показал, рассказывая про статические моменты, массу точек для изотропных (в данном случае имеющих одинаковую плотность) объектов можно выносить за скобки и рассматривать исключительно геометрию. Формула момента инерции примет следующий вид:

Почему I_р? Потому что мы с вами оперировали радиусом и углом поворота (в формуле угловой скорости) — т.е. использовали полярную систему отсчета (что и демонстрирует индекс p).

Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.

Как найти момент инерции

Чтобы немного упростить себе операции со всеми этими величинами перейдем к родной и понятной  системе отсчета: перпендикулярным осям X и Y. Возьмем случайное сечение стержня и рассмотрим интегралы, как мы уже делали со статическими моментами:

Первые два интеграла называются осевыми моментами инерции относительно осей x и y, а третий — центробежным моментом инерции сечения относительно осей x, y. Теперь рассмотрим случай параллельного переноса осей , не вдаваясь глубоко в вычисление интегралов.

Для осей  x₁=x+a, y₁=y+b моменты инерции будут равны: 

Если вы, как и часть прочитавших эту статью перед публикацией, не имеете черного пояса и седьмого дана в интегральных преобразованиях, то:

т.к. 

и 

Тут первый интеграл — Ix1, второй интеграл — Sx1, а третий раскрывается в площадь при нулевом свободном члене.

Надеюсь, понятно, что при параллельном переносе по y изменяется только ось (буква). 

В последнем случае мы рассматриваем перенос по обеим осям сразу.

Где:
Ix — очевидно, момент инерции относительно оси x
Sx — статический момент сечения относительно оси y
F — площадь сечения

А теперь предположим, что некие оси x₁ и y₁  являются центральными, тогда и выражения упрощаются и принимают вид:

Немного проясню обозначение осей:

Центральными называются оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.

Главными называются оси, в которых центробежный момент инерции (I_xy) равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

 И теперь можно уже коснуться практики: речь о моментах инерции простых сечений.

Момент инерции прямоугольника

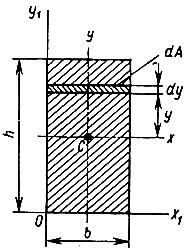
Определим осевые моменты инерции прямоугольника со сторонами b и h относительно осей x и y, проходящих через его центр тяжести. В качестве элементарной площадки dA возьмем полоску шириной b и высотой . Тогда будем иметь:

Не прибегая к вычислениям, замечу, что для момента инерции относительно оси Y изменится только положение сторон b и h. Следовательно:

Момент инерции квадрата

Прямоугольник со сторонами b=h=a. Следовательно:

Момент инерции круга

Тут воспользуемся полярным моментом инерции относительно центра круга. Определим его, как сумму колец с толщиной dp:

Момент инерции кольца

А здесь – явная аналогия с моментом инерции круга:

Как мы видим, момент инерции кольца это разность моментов инерции большего и меньшего кругов.

Пример нахождения момента инерции тавра

Найдём осевые моменты инерции тавра (рисунок 5), приведенного на рисунке, относительно центральных осей x_c и y_c.

Рисунок 8. Тавр, положение осей

Так как оси x₁ и x₂ являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси x_c воспользуемся формулой.

Момент инерции относительно оси y_c получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось y_c является общей центральной осью для простых фигур и для всей фигуры.

Центробежный момент инерции относительно осей x_c и y_c равен нулю, так как ось инерции y_c является главной осью (осью симметрии фигуры).

Обобщение и подведение итогов

Момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении. В статике момент инерции применяется в определении прогибов, расчетах конструкций на касательные и нормальные напряжения. Момент инерции также, как и статические моменты, характеризует положение осей относительно сечения элемента. Так у нас появляются:

Центральные оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.

Главные оси, в которых центробежный момент инерции (I_xy) равен нулю, а осевые моменты инерции — максимальны. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

При этом главные и центральные оси могут совпадать!

Список использованных источников

1. Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
3. Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3

Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников

5 449

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.