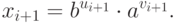Перейти к содержимому
Формулировка. Дано натуральное число. Найти его наименьший нетривиальный делитель или вывести само это число, если такового нет.
Решение. Задача решается аналогично предыдущей. При этом необходимо начать обычный цикл с увеличением, при котором переменная цикла i изменяется от 2 до n (такая верхняя граница нужна для того, чтобы цикл всегда заканчивался, так как когда i будет равно n, выполнится условие n mod i = 0). Весь остальной код при этом не отличается.
Код:
- program SmallestDiv;
- var
- i, n: word;
- begin
- readln(n);
- for i := 2 to n do begin
- if n mod i = 0 then begin
- writeln(i);
- break
- end
- end
- end.
Найти наибольший нетривиальный делитель натурального числа
Формулировка. Дано натуральное число. Найти его наибольший нетривиальный делитель или вывести единицу, если такового нет.
Примечание 1: делителем натурального числа a называется натуральное число b, на которое a делится без остатка. То есть выражение «b – делитель a» означает: a / b = k, причем k – натуральное число.
Примечание: нетривиальным делителем называется делитель, который отличен от 1 и от самого числа (так как на единицу и само на себя делится любое натуральное число).
Решение. Пусть ввод с клавиатуры осуществляется в переменную n. Попробуем решить задачу перебором чисел. Для этого возьмем число на единицу меньшее n и проверим, делится ли n на него. Если да, то выводим результат и выходим из цикла с помощью оператора break. Если нет, то снова уменьшаем число на 1 и продолжаем проверку. Если у числа нет нетривиальных делителей, то на каком-то шаге проверка дойдет до единицы, на которую число гарантированно поделится, после чего будет выдан соответствующий условию ответ.
Хотя, если говорить точнее, следовало бы начать проверку с числа, равного n div 2 (чтобы отбросить дробную часть при делении, если n нечетно), так как ни одно натуральное число не имеет делителей больших, чем половина это этого числа. В противном случае частное от деления должно быть натуральным числом между 1 и 2, которого просто не существует.
Данная задача также решается через for, но через другую его разновидность, и теперь счетчик будет убывать от n div 2 до 1. Для этого do заменится на downto, при позиции начального и конечного значений остаются теми же.
Алгоритм на естественном языке:
1) Ввод n;
2) Запуск цикла, при котором i изменяется от n div 2 до 1. В цикле:
- Если n делится на i (то есть, остаток от деления числа n на i равен 0), то выводим i на экран и выходим из цикла с помощью break.
Код:
- program GreatestDiv;
- var
- i, n: word;
- begin
- readln(n);
- for i := n div 2 downto 1 do begin
- if n mod i = 0 then begin
- writeln(i);
- break
- end
- end
- end.
Кстати, у оператора ветвления if в цикле отсутствует else-блок. Такой условный оператор называется оператором ветвления с одной ветвью.
Задача № 14. Найти наибольший нетривиальный делитель натурального числа
Формулировка. Дано натуральное число. Найти его наибольший нетривиальный делитель или вывести единицу, если такового нет.
Примечание 1: делителем натурального числа a называется натуральное число b, на которое a делится без остатка. То есть выражение «b – делитель a» означает: a / b = k, причем k – натуральное число.
Примечание: нетривиальным делителем называется делитель, который отличен от 1 и от самого числа (так как на единицу и само на себя делится любое натуральное число).
Решение. Пусть ввод с клавиатуры осуществляется в переменную n. Попробуем решить задачу перебором чисел. Для этого возьмем число на единицу меньшее n и проверим, делится ли n на него. Если да, то выводим результат и выходим из цикла с помощью оператора break. Если нет, то снова уменьшаем число на 1 и продолжаем проверку. Если у числа нет нетривиальных делителей, то на каком-то шаге проверка дойдет до единицы, на которую число гарантированно поделится, после чего будет выдан соответствующий условию ответ.
Хотя, если говорить точнее, следовало бы начать проверку с числа, равного n div 2 (чтобы отбросить дробную часть при делении, если n нечетно), так как ни одно натуральное число не имеет делителей больших, чем половина это этого числа. В противном случае частное от деления должно быть натуральным числом между 1 и 2, которого просто не существует.
Данная задача также решается через for, но через другую его разновидность, и теперь счетчик будет убывать от n div 2 до 1. Для этого do заменится на downto, при позиции начального и конечного значений остаются теми же.
Алгоритм на естественном языке:
1) Ввод n;
2) Запуск цикла, при котором i изменяется от n div 2 до 1. В цикле:
1. Если n делится на i (то есть, остаток от деления числа n на i равен 0), то выводим i на экран и выходим из цикла с помощью break.
Код :
1. program GreatestDiv; 2. 3. var 4. i, n: word; 5. 6. begin 7. readln(n); 8. for i := n div 2 downto 1 do begin 9. if n mod i = 0 then begin 10. writeln(i); 11. break 12. end 13. end 14. end.
Кстати, у оператора ветвления if в цикле отсутствует else-блок. Такой условный оператор называется оператором ветвления с одной ветвью.
Задача № 15. Найти наименьший нетривиальный делитель натурального числа
Формулировка. Дано натуральное число. Найти его наименьший нетривиальный делитель или вывести само это число, если такового нет.
Решение. Задача решается аналогично предыдущей. При этом необходимо начать обычный цикл с увеличением, при котором переменная цикла i изменяется от 2 до n (такая верхняя граница нужна для того, чтобы цикл всегда заканчивался, так как когда i будет равно n, выполнится условие n mod i = 0). Весь остальной код при этом не отличается.
Код :
1. program SmallestDiv; 2. 3. var 4. i, n: word; 5. 6. begin 7. readln(n); 8. for i := 2 to n do begin 9. if n mod i = 0 then begin 10. writeln(i); 11. break 12. end 13. end 14. end.
Задача № 16. Подсчитать общее число делителей натурального числа
Формулировка. Дано натуральное число. Подсчитать общее количество его делителей.
Решение. Задача достаточно похожа на две предыдущие. В ней также необходимо провести перебор в цикле некоторого количества натуральных чисел на предмет обнаружения делителей n, но при этом необходимо найти не первый из них с какого-либо конца отрезка [1, n] (это отрезок, содержащий все числа от 1 до n включительно), а посчитать их. Это можно сделать с помощью счетчика count, который нужно обнулить непосредственно перед входом в цикл. Затем в условном операторе if в случае истинности условия делимости числа n (n mod i = 0) нужно увеличивать счетчик count на единицу (это удобно делать с помощью оператора inc).
Алгоритм на естественном языке:
1) Ввод n;
2) Обнуление переменной count (в силу необходимости работать с ее значением без предварительного присваивания ей какого-либо числа)
3) Запуск цикла, при котором i изменяется от 1до n. В цикле:
1. Если n делится на i (то есть, остаток от деления числа n на i равен 0), то увеличиваем значение переменной count на 1;
4) Вывод на экран значения переменной count.
Код :
1. program CountDiv; 2. 3. var 4. i, n, count: word; 5. 6. begin 7. readln(n); 8. count := 0; 9. for i := 1 to n do begin 10. if n mod i = 0 then inc(count) 11. end; 12. writeln(count) 13. end.
Задача № 17. Проверить, является ли заданное натуральное число простым
Формулировка. Дано натуральное число. Проверить, является ли оно простым.
Примечание: простым называется натуральное число, которое имеет ровно два различных натуральных делителя: единицу и само это число.
Решение. Задача отличается от предыдущей только тем, что вместо вывода на экран числа делителей, содержащегося в переменной count, необходимо выполнить проверку равенства счетчика числу 2. Если у числа найдено всего два делителя, то оно простое и нужно вывести положительный ответ, в противном случае – отрицательный ответ. А проверку через условный оператор, как мы уже знаем, можно заменить на вывод результата самого булевского выражения с помощью оператора write (writeln).
Код:
Дата добавления: 2018-10-25 ; просмотров: 1436 ; Мы поможем в написании вашей работы!
Что такое нетривиальный делитель

Тип 25 № 29673
Назовём нетривиальным делителем натурального числа его делитель, не равный единице и самому числу. Например, у числа 6 есть два нетривиальных делителя: 2 и 3. Найдите все натуральные числа, принадлежащие отрезку [123456789; 223456789] и имеющие ровно три нетривиальных делителя. Для каждого найденного числа запишите в ответе его наибольший нетривиальный делитель. Ответы расположите в порядке возрастания.
Например, в диапазоне [5; 16] ровно три различных нетривиальных делителя имеет число 16, поэтому для этого диапазона вывод на экране должна содержать следующие значения:
Если решать задачу перебором — программа будет существенно неэффективна по времени. Заметим, что у каждого делителя числа имеется пара, например, пары делителей числа 16 будут выглядеть так: 1 и 16, 2 и 8, 4 и 4, всего пять различных делителей. Отсюда можно заключить, что имеет смысл перебирать возможные делители числа от единицы до корня от самого числа и, находя очередной делитель, прибавлять к переменной numDel 2. Также заметим, что поскольку число должно иметь три нетривиальных делителя, можно рассматривать только числа, квадратной корень из которых равен целому числу. Также отдельно будем учитывать квадратный корень числа, накапливая при этом в переменной numDel единицу.
|
0 / 0 / 0 Регистрация: 26.06.2012 Сообщений: 14 |
|
|
1 |
|
Найти и вывести на экран наибольший нетривиальный делитель числа26.06.2012, 22:17. Показов 8042. Ответов 2
Пользователь вводит с клавиатуры натуральное число, найти и вывести на экран наибольший нетривиальный (т.е. не равный введённому числу или единице) делитель числа, либо сообщить, что число простое. Например, если пользователь ввёл 17, то на экран выводится сообщение «число простое»; если пользователь ввёл 24, то на экран выводится сообщение «наибольший нетривиальный делитель: 12».
0 |
|
Invader_Zim Twilight Parasite 154 / 150 / 7 Регистрация: 21.07.2011 Сообщений: 908 |
||||
|
26.06.2012, 22:25 |
2 |
|||
|
РешениеНикНик, проверяй сначала на простоту.
0 |
|
rinat_w 92 / 88 / 17 Регистрация: 13.11.2011 Сообщений: 193 |
||||
|
26.06.2012, 22:33 |
3 |
|||
|
НикНик,
0 |
Задача № 15. Найти наименьший нетривиальный делитель
натурального числа
Формулировка. Дано натуральное число. Найти его
наименьший нетривиальный делитель или вывести само это число, если такового
нет.
Решение. Задача решается аналогично предыдущей. При
этом необходимо начать обычный цикл с увеличением, при котором переменная цикла
i изменяется от 2 до n (такая верхняя граница нужна для того, чтобы цикл
всегда заканчивался, так как когда i будет равно n, выполнится
условие n mod i
= 0). Весь остальной код при этом не отличается.
Код:
1.
program SmallestDiv;
2.
3.
var
4.
i, n: word;
5.
6.
begin
7.
readln(n);
8.
for i := 2 to n do begin
9.
if n mod i = 0 then begin
10.
writeln(i);
11.
break
12.
end
13.
end
14.
end.
Скачано с www.znanio.ru
2.1 Парадокс дней рождения
Теорема 2.3 Пусть 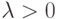




Следствие 2.1 (Парадокс дней рождения) Чтобы с вероятностью 
Этот парадокс допускает следующие применения в криптографии.
2.2.1 Алгоритм Полларда для факторизации натурального числа
Пусть нам требуется факторизовать натуральное число 
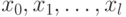




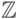







Если 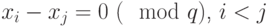
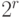





Для сравнения среди таких пар достаточно хранить 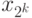
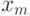
Правда, такая хитрость требует увеличить длину последовательности. Допустим, наименьшие 




Поскольку мы сравниваем 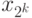
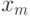

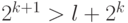





- Взять многочлен
с целыми коэффициентами и случайное число
. Положить
.
- Вычислить
.
- Если
— степень двойки, положить
,
, перейти к предыдущему шагу.
- (Теперь
— не степень двойки). Если
, то
— нетривиальный делитель числа
.
- Положить
. Если
, перейти к шагу 2.
Отметим, что при фиксированном 




Пример 2.2 С помощью 

На первом шаге алгоритма требуется выбрать многочлен 









Допустим, в последовательности 
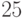

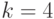

Выберем 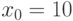
Итак, нам повезло найти нетривиальный делитель 31 числа 2449. Если бы мы досчитали до 


2.2.2 Алгоритм Полларда для дискретного логарифмирования
Изменим алгоритм предыдущего параграфа так, чтобы с его помощью решать задачу дискретного логарифмирования. Его идея остаётся прежней: мы будем вычислять последовательность 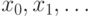

Найдём 


Определим последовательности 
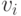

Тогда если 

Коллизия 
Отметим, что данный алгоритм может быть также обобщен для дискретного логарифмирования в произвольной циклической группе, и даже для поиска коллизий хэш-функций.




 Сообщение было отмечено НикНик как решение
Сообщение было отмечено НикНик как решение
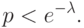


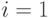 .
. .
. ,
,  , перейти к предыдущему шагу.
, перейти к предыдущему шагу. , то
, то  — нетривиальный делитель числа
— нетривиальный делитель числа  , перейти к шагу 2.
, перейти к шагу 2.