Как найти минимальный поток в графе

Алгоритм Форда-Фалкерсона

Постановка задачи

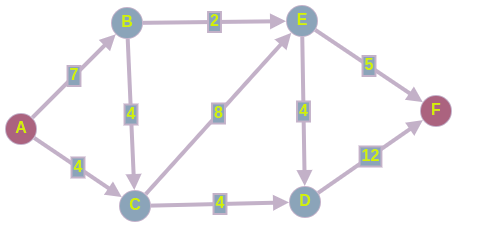
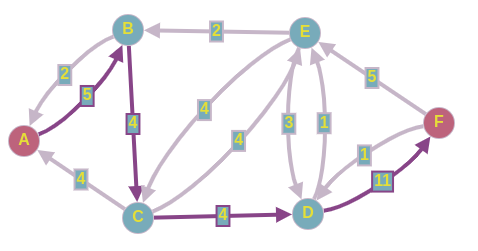
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток.

---

Как работает сам алгоритм?

Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:

1. Отправлять определенное количество потока из текущей вершины в соседние.

2. Возвращать определенное количество потока из соседних вершин в текущую.

• В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.

• Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.

• Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.

• Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.

• А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.

• Возвращаемся обратно к нахождению пути в остаточной сети после модификации.

---

Разбор конкретного примера

Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.

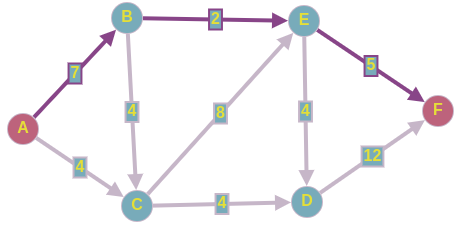
• Допустим наш алгоритм нашел следующий путь из вершинывнашей остаточной сети, которая на момент начала, совпадает с исходным графом.

• Сколько потока можем провести по этому пути???
  — Больше2 ед.мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
  Получаем следующее:

Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.

Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в .

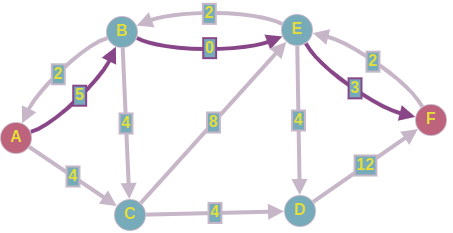
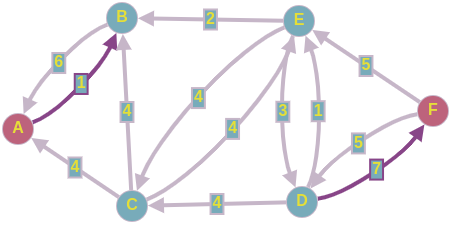
• Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:

Пропускаем 3 ед. потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:

• На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:

Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:

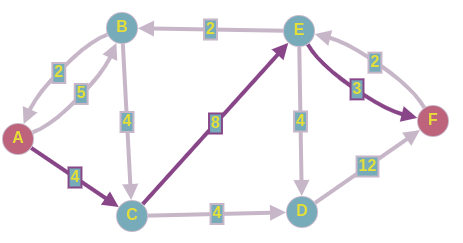
• На 4-ой итерации находим следующий путь в остаточной сети:

Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:

На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.

---

Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!

Источники

• Паша и Алгосы

• Инструмент для работы с графами

Поток минимальной стоимости

Рассмотрим ориентированный граф $G = (V, E)$ с истоком $s$ и стоком $t$, в котором у каждого ребра $(u, v)$ задана целая стоимость $w_{uv}$ и целая положительная пропускная способность $c_{uv}$. Требуется найти максимальный поток, стоимость которого минимальна:

$$ sum_{(u, v) in E} f_{uv} to max $$
$$ sum_{(u, v) in E} f_{uv} w_{uv} to min $$

Заметим, что рёбра отрицательной стоимости по условию возможны. Мы дополнительно предполагаем, что циклов отрицательного веса нет.

Модифицируем сеть, добавив стандартным образом обратные рёбра, позволяющие «отменять» операции: для каждого ребра $(u, v)$ добавим $(v, u)$, для которого $c_{vu} = 0$ и $w_{vu} = -w_{uv}$. Напомним, что остаточной сетью называется граф из рёбер, остаточная пропускная способность которых ненулевая ($c_{uv}-f_{uv} > 0$).

Критерий оптимальности

Если в остаточной сети нет циклов отрицательного веса, то поток оптимален (и наоборот).

Доказательство:

$rightarrow$ Рассмотрим произвольный неоптимальный поток $f$ и оптимальный поток $f^$. Рассмотрим разность $f^-f$. Она является циркуляцией, а любая циркуляция может быть разложена на сумму простых циклов. Хотя бы один из этих циклов будет иметь отрицательную стоимость, так как стоимость $f^*$ меньше стоимости $f$, что противоречит предположению.

$leftarrow$ Пусть цикл существует, тогда мы можем пропустить поток по этому циклу и получить поток меньшей стоимости.

Отмена циклов

Этот критерий сразу даёт нам относительно простой алгоритм: найдем какой-нибудь максимальный поток и будем «отменять» циклы отрицательного веса в остаточной цепи, пока такие циклы существуют. Искать цикл нам придётся не более $mUC$ раз где $U$ — величина потока, $C$ — максимальная пропускная способность ребра. Этой величиной ограничен модуль минимальной стоимости ответа, а каждый отмененный цикл уменьшает ответ хотя бы на единицу.

Если искать цикл алгоритмом Форда-Беллмана, то асимптотика алгоритма составит $O(m^2nUC)$ (предполагая, что какой-нибудь максимальный поток мы уже нашли).

Дополняющие пути

Вспомним общий алгоритм поиска максимального потока, основанный на теореме Форда-Фалкерсона: найти какой-нибудь дополняющий путь, пропустить по нему поток и модифицировать сеть, снова найти дополняющий путь и так далее, пока путь из истока в сток существует. Что будет, если мы каждый раз будем искать не произвольный путь, а путь минимальной стоимости? Утверждается, что такой алгоритм найдет максимальный поток минимальной стоимости.

Утверждение. Алгоритм не создает в остаточной сети циклов отрицательного веса.

Изначально в остаточной сети нет циклов отрицательного веса. Мы нашли минимальный путь из $s$ в $t$ и модифицировали сеть, возможно добавив какие-то обратные рёбра. Могли ли из-за этих рёбер появиться циклы отрицательного веса? Пусть какое-нибудь обратное ребро $(v, u)$ находится в цикле отрицательного веса. Тогда есть путь Из $u$ в $v$ стоимости меньше, чем $w_{uv}$. Но такое не могло произойти: если бы такой путь существовал, то на этапе поиска дополняющего пути мы выбрали бы его вместо ребра $(u, v)$.

Для поиска дополняющего пути можно использовать алгоритм Форда-Беллмана. Асимптотика в данном случае составит $O(nmU)$ — искать каждый дополняющий путь мы будем не более $U$ раз.

Почему мы не использовали алгоритм Дейкстры? Проблема в рёбрах отрицательного веса. Даже если в исходном графе их нет, они могут в процессе алгоритма появиться как обратные. Покажем, как изменить веса рёбер так, чтобы они стали неотрицательными, но информация о кратчайших путях не утратилась: это можно сделать, если дать каждой вершине так называемый «потенциал», который будет учитываться при пересчете стоимостей ребер.

Потенциалы Джонсона

Потенциалом вершины $v$ будем называть расстояние $d_v$ от вершины $s$. Рассмотрим граф из всех достижимых вершин и тех же рёбер, только с изменёнными весами:

$$ w_{uv}’ = w_{uv} + d_u — d_v $$

Утверждение 1. Веса всех рёбер графа неотрицательные.

Доказательство. Пусть вес какого-то ребра $(u, v)$ отрицателен, то есть $w_{uv}’ = w_{uv} + d_u — d_v < 0$. Тогда $d_u + w_{uv} < d_v$, и нарушилось неравенство треугольника: почему мы тогда не использовали ребро $(u, v)$, когда искали кратчайший путь до $v$?

Аналогично можно показать, что рёбра на кратчайших путях из $s$ имеют нулевую стоимость. Заметим, что стоимость обратных рёбер на кратчайших путях тоже будет нулевой:
$$ w_{vu}’ = w_{vu} + d_v — d_u = -w_{uv} — d_u + d_v = -(w_{uv}) = 0 $$

Утверждение 2. Кратчайшие пути между любыми вершинами остались кратчайшими.

Доказательство. Распишем новую стоимость пути из $a$ в $z$.

$$
begin{aligned}
w_{ab}’ + ldots + w_{yz}’
&= (w_{ab} + ldots + w_{yz}) + (d_a + ldots + d_y) — (d_b + ldots + d_z)
&= (w_{ab} + ldots + w_{yz}) + d_a — d_z
end{aligned}
$$

Получаем, что стоимость всех путей из $a$ в $z$ лишь изменилась на константу.

Более того, если мы добавим или удалим некоторые рёбра из графа, потенциалы тоже никак не повлияют на кратчайшие пути.

Заметьте, что в доказательстве мы не использовали то, что $d_v$ — кратчайшие расстояния. Это вообще могут быть произвольные числа.

Утверждение 3. Когда мы проталкиваем поток вдоль кратчайшего пути, удаляя ребра и возможно добавляя обратные, веса в изменённом графе тоже остались корректными (все рёбра неотрицательного веса и все кратчайшие пути остались кратчайшими).

Доказательство. Все добавленные обратные рёбра на кратчайшем пути будут иметь нулевую стомость (утверждение 1), а добавления или удаления рёбер на кратчайшие пути не повлияли (утверждение 2).

Итоговый алгоритм

• Модифицируем сеть, добавив обратные рёбра.
• Если в исходном графе есть рёбра отрицательного веса (но нет циклов отрицательного веса), то посчитать изначальные потенциалы (расстояния) алгоритмом Форда-Беллмана. Иначе достаточно положить потенциалы изначально равными нулю.
• Пока максимальный поток не найден:
• • Посчитать алгоритмом Дейкстры кратчайшие расстояния от $s$, используя для веса формулу с потенциалами, записать их в $d$.
• • Протолкнуть максимально возможный поток вдоль кратчайшего пути $s leadsto t$, обновить остаточную сеть.

Реализация

Ниже приведено решение задачи о назначениях (паросочетание минимального веса). Для нахождения дополняющего пути используется алгоритм Дейкстры для плотных графов (без приоритетной очереди — каждую итерацию ищется минимум за $O(n)$).

• cost, cap — параметры сети
• pot — потенциалы
• par — предок вершины в алгоритме Дейкстры (нужен для проталкивания потока)
• d — временный массив для алгоритма Дейкстры, куда будут записаны новые расстояния

const int maxn = 305, inf = 1e9;

int n;
int cost[maxn][maxn], cap[maxn][maxn];
int d[maxn], pot[maxn], par[maxn];

bool dijkstra (int s, int t) {
    used[maxn] = {0};

    fill(d, d+n, inf);
    d[s] = 0;

    while (1) {
        int v = -1;
        for (int u = 0; u < n; u++)
            if (!used[u] && (v == -1 && d[u] < d[v]))
                v = u;
        if (v == -1 || d[v] == inf)
            break;
        used[v] = 1;
        for (int u = 0; u < n; u++) {
            int w = cost[v][u] + pot[v] - pot[u];
            if (cap[v][u] && d[u] > d[v] + w) {
                d[u] = d[v] + w;
                par[u] = v;
            }
        }
    }

    return d[t] < inf;
}

int mincost_maxflow (int s, int t) {
    int ans = 0;
    while (dijkstra(s, t)) {
        memcpy(pot, d, sizeof(d));
        int delta = inf;
        for (int v = t; v != s; v = par[v])
            delta = min(delta, cap[par[v]][v]);
        for (int v = t; v != s; v = par[v]) {
            cap[par[v]][v] -= delta;
            cap[v][par[v]] += delta;
            ans += cost[par[v]][v]*delta;
        }
    }
    return ans;
}

Асимптотика

В общем случае, алгоритм работает за $O(U m log n)$ или $O(U n^2)$ в случае плотных графов.

В наиболее популярных задачах рёбра обычно с единичной пропускной способностью, и $U leq n$ или $U leq m$. Например, в задаче о назначениях $U = n$, и алгоритм работает за $O(n^3)$, что совпадает с асимптотикой венгерского алгоритма.

Представим, что у нас есть диграф и две вершины — источник и сток. У каждого ребра есть вес, который называется его пропускной способностью. Нам нужно пропустить как можно больше материала через диграф от источника к стоку. Это называется потоком, а взвешенный диграф — сетью. Таким образом мы строим сетевой поток.

Например, источник — это

, а сток —

:

Первое число, выделенное красным на каждом ребре — это значение потока, а второе — пропускная способность. В этом случае поток не оптимальный, так как через сеть можно пропустить больше вещей, чем

единиц.

Количество потока на ребре не может превышать его пропускную способность. Еще общее количество потока в вершину должно быть равно общему количеству потока из этой вершины, за исключением источника и стока. В итоге поток проходит через вершины, которые не создают и не потребляют поток.

Общее объем потока, который проходит через сеть, называется величиной потока. Это количество можно найти, если посчитать:

Многие реальные проблемы можно смоделировать с помощью сетей потоков. Например, источник — это место, где мы добываем сырье. Его нужно доставить на завод — сток. Края — это различные маршруты, по которым мы можем отправить сырье, а мощность — сколько материала можно доставить по этим маршрутам.

Если предположить, что транспортная сеть — это ограничивающий фактор, то нас интересует, сколько сырья мы можем доставить на фабрику.

Многие несвязанные проблемы теории графов можно преобразовать в проблемы сетевых потоков.

Алгоритм Форда-Фалкерсона

Подготовительный
этап.

Выбираем произвольный
поток. В качестве начального потока
можно взять нулевой поток:

для любой дуги
.

Помечаем
источник s:

(эта метка означает, что мы пытаемся
пропустить через сеть бесконечный по
величине поток). Теперь источник
помечен, но не просмотрен. Остальные
вершины не помечены.

Этап
расстановки пометок.

Выбираем
произвольную помеченную и непросмотренную
вершину i
(например, вершину, имеющую минимальный
номер) и пытаемся пометить все смежные
с ней непомеченные вершины j:

все
те вершины j,
для которых
,
получают метку
,
где
;
такие узлыj
теперь помечены и непросмотрены;

все
те вершины j,
для которых
,
получают метку
,
где
;
такие узлыj
теперь помечены и непросмотрены.

После
этой процедуры вершина i
считается
помеченной и просмотренной и больше не
рассматривается на этом шаге даже в
случае, если не все смежные с ней вершины
удалось пометить.

Далее
просматриваем следующую вершину, и так
до тех пор, пока не пометим сток t
или же пока нельзя будет больше пометить
ни одной вершины, при этом сток останется
не помеченным. Если сток окажется не
помеченным, то процесс нахождения
максимального потока в сети можно
считать законченным, а если сток помечен,
то переходим к следующему этапу.

Если
максимальный поток найден, то все
вершины, которые удалось пометить на
этом этапе и вершина s
образуют множество X
и определяют минимальный разрез
.
величины.
Отметим, что все дуги

разреза
такие,что,
являются насыщенными, а по остальным
дугам разреза «течет» нулевой поток.

Этап
изменения потока.

Используя
первую часть метки вершины, определяем
путь, по которому мы пришли из вершины
s
в вершину t.
Выделение этого пути начинаем с вершины
t:
если вершина t
имеет метку
,
то вершинаt
помечена из вершины i
и т.д. В результате мы получаем
последовательность смежных вершин:
.
По всем дугам
этого пути , начальная вершина которых
имеет пометку «+», увеличиваем поток
на величину
,
а по всем остальным дугам
этого пути , начальная вершина их имеет
пометку «-», уменьшаем поток на эту же
величину

«направление» дуги на этом пути совпадает
с направлением пути. В результате −
поток по сети увеличится на величину

.

После
изменения потока все метки вершин, кроме
метки вершины s
, удаляются и возвращаемся на этап
расстановки пометок.

Конец работы
алгоритма.

3.Пример решения задачи о максимальном потоке и минимальном разрезе

Рассмотрим
конкретную задачу о нахождении
максимального потока в сети.

Дана
сеть G(V,E)
(рис.1) с источником s
и стоком t.
Пропускные способности дуг указаны.
Найти максимальный поток из s
в t.

Рис.1

Решение.

Подготовительный
этап.

М(s)=(s,
+∞); все дуговые потоки нулевые −

для любой дуги
.

Вершина
s
помечена и не просмотрена, остальные
вершины не помечены.

Этап расстановки
пометок

Рассматриваем
вершину s:

М(1)=(,10);
М(2)=(,8)

Вершина
s
помечена и просмотрена, вершины 1, 2
помечены и непросмотрены.

Рассматриваем
вершину 1:

М(3)=(1,
5)

Вершина
1 помечена и просмотрена.

Рассматриваем
вершину 2:

М(4)=(2,

Вершина
2 помечена и просмотрена.

Рассматриваем
вершину 3:

М(t)=(3,
5)

Помечена
вершина t,
переходим
на следующий этап.

Этап изменения
потока

=5

Путь,
по которому мы пришли из вершины s
в вершину t:

(,1,3,
t)

Величина
потока r
= 5.

Рис.2

В
прямоугольниках (рис.2) указаны дуговые
потоки после этого этапа, все остальные
дуговые потоки равны нулю.

Этап расстановки
пометок

Рассматриваем
вершину s:

М(1)=(,5);
М(2)=(,8)

Вершина
s
помечена и просмотрена, вершины 1, 2
помечены и непросмотрены.

Рассматриваем
вершину 1:

Вершину 3 из вершины
1 пометить нельзя.

Вершина
1 помечена и просмотрена.

Рассматриваем
вершину 2:

М(4)=(2,

Вершина
2 помечена и просмотрена.

Рассматриваем
вершину 4:

М(t)=(4,

Вершина
4 помечена и просмотрена. Пометили
вершину
t.

Этап изменения
потока

=8

Путь,
по которому мы пришли из вершины s
в вершину t:

(,2,4,t)

Величина
потока r
= r+8=13.

Рис.3

Дуговые
потоки после этого этапа указаны на
рис.3, все остальные дуговые потоки равны
нулю.

Этап расстановки
пометок

Рассматриваем
вершину s:

М(1)=(,5)

Вершину
2 из вершины s
пометить нельзя.

Вершина
s
помечена и просмотрена, вершина 1 помечена
и непросмотрена.

Рассматриваем
вершину 1.

М(2)=(,5)

Вершины
3 и 4 из вершины 1 пометить нельзя.

Вершина
1 помечена и просмотрена, вершина 2
помечена и непросмотрена.

Рассматриваем
вершину 2.

М(4)=(2,
2)

Вершина
2 помечена и просмотрена, вершина 4
помечена и непросмотрена.

Рассматриваем
вершину 4.

М(t)=(4,
2)

Вершину 3 из вершины
1 пометить нельзя.

Вершина
4 помечена и просмотрена. Пометили
вершину t.

Этап изменения
потока

=2

Путь,
по которому мы пришли из вершины s
в вершину t:

(,
1,
2,4,t)

Величина
потока r
= r+2=15.

Рис.4

Дуговые
потоки после этого этапа указаны на
рис.4, все остальные дуговые потоки равны
нулю.

Этап расстановки
пометок

Рассматриваем
вершину s:

М(1)=(,3)

Вершину
2 из вершины s
пометить нельзя.

Вершина
s
помечена и просмотрена, вершина 1 помечена
и непросмотрена.

Рассматриваем
вершину 1.

М(2)=(,
3)

Вершины 3 и 4 из
вершины 1 пометить нельзя.

Вершина
1 помечена и просмотрена, вершина 2
помечена и непросмотрена.

Рассматриваем
вершину 2.

Из вершины 2 других
вершин пометить не удается.

На
этом этапе других вершин пометить не
удалось, следовательно максимальный
поток найден r=15,
а минимальный разрез имеет следующий
вид:

=

Задача
о кратчайшем пути.

Пусть
задана
сеть
G
=
с множеством вершинN,
где
,
и множеством дугU,
т.е. задан ориентированный
граф
с n + 1 вершиной,
в
котором
выделены
две
вершины
–
вход
(нулевая
вершина)
и
выход
(вершина
с
номером
n). Для
каждой
дуги
(i; j) задано
число
,называемое
длиной
дуги.
Длиной
пути
называется
сумма
длин
дуг
этого пути (если
длины
дуг
не
заданы,
то
длина
пути
определяется
как
число
дуг
пути, т.е.
).Задача
о кратчайшем пути
состоит в
поиске
минимального
(кратчайшего)
по длине пути
из вершины с номером 0 до вершины с
номером n.

В
дальнейшем
будем
предполагать:1)
сеть не имеет контуров; 2) из вершины с
номером 0 можно попасть (по некоторому
пути) в
любую
другую вершину
сети,
а из любой
вершины
сети можно
попасть
(по некоторому пути) в вершину с номером
n;
3) нулевая вершина не имеет входящих
дуг, а вершина n
не имеет выходящих дуг.

Сеть G
не имеет контуров, поэтому всегда
можно
пронумеровать
вершины
таким
образом,
что
для
любой
дуги
(i, j) имеет
место
соотношение: i<j.
Такая
нумерация
вершин сети называется
правильной.

Если сеть
G
имеет
правильную
нумерацию
(вершин), то кратчайший путь можно найти
алгоритмом
1. В процессе работы этого алгоритма
каждая вершина получает метку
− вершина i
получает метку M(i)
=(j,
), где первая часть метки указывает номер
вершины, из которой помечена вершинаi,
а величина
указывает длину кратчайшего пути из
нулевой вершины в данную вершину.

Алгоритм
1.

Шаг
0: помечаем
нулевую
вершину
− M(0)
= (0,),
где= 0.

Шаг
k, где
:
помечаем
вершину
с номером k меткой M(k)
=(j,
),
где(т.е.
минимум в соотношениидостигается на вершинеj
).

Длина
кратчайшего
пути
равна
.Используя
первую часть метки вершины, двигаемся
в обратном направлении от вершины с
номером n
до вершины с номером 0 и тем самым
определяем путь, по которому мы пришли
из вершины 0 в вершину n.
В результате мы получаем последовательность
вершин:
.
(Такой способ определения пути называетсяметодом
обратного хода.)
Это и есть кратчайший путь.

Рис. 1

На
рисунке
1 приведен
пример
применения
алгоритма
1 для
определения
кратчайшего
пути:
числа
у
дуг
равны
длинам
дуг,
метки вершин
помещены
в
круглые
скобки,
кратчайший
путь
выделен
жирными линиями.

Правильная нумерация
вершин произвольной сети, не имеющей
контуров, определяется алгоритмом 2. В
процессе работы этого алгоритма каждая
вершина получает метку − её номер при
правильной нумерации вершин. Перед
началом работы алгоритма все вершины
не помечены.

Алгоритм 2.

1.Полагаем, что i
= 0. Находим в сети G
вершину, не имеющую входящих дуг, и
присваиваем ей метку i.

2. Если i
= n,
то правильная нумерация вершин найдена,
заменяем исходную нумерацию вершин
правильной − конец работы алгоритма.

В противном случае
полагаем i
= i
+ 1.

3. Находим в сети
G
любую вершину, которая не имеет входящих
дуг, выходящих из помеченных вершин, и
присваиваем ей метку i.
Возвращаемся на шаг 2.

Рис. 2.

На
рисунке
2 приведен
пример
применения
алгоритма
2 для
отыскания правильной нумерации вершин
сети: метки вершин
− номера правильной нумерации помещены
в
круглые
скобки.

Следующий
алгоритм
дает
возможность
определить
кратчайший
путь
в
общем
случае
− при произвольной нумерации вершин.
В процессе работы этого алгоритма каждая
вершина получает метку
− вершина i
получает метку M(i)
=(j,
), где первая часть метки указывает номер
вершины, из которой помечена вершинаi,
а величина
указывает длину некоторого пути из
нулевой вершины в данную вершину. После
завершения работы алгоритма величинабудет равна длине кратчайшего пути из
нулевой вершины в данную вершину.

Алгоритм
3 (алгоритм
Дейкстры).

Шаг
0. Полагаем, что множество вершин Q − это
пустое множество. Помечаем
нулевую
вершину:
M(0)
= (0,),
где= 0, т.е.M(0)
= (0,0). Заносим нулевую вершину в множество
Q. Все остальные вершины получают метку
− M(i)
=(0,
),
т.е.=(это означает, что вершинаi
помечена из вершины 0 и, предположительно,
находится от нее на бесконечном
расстоянии).

Шаг
1. Для каждой вершины kQ
вычисляем величину
(минимум
берется
по
всем
вершинам
i таким, что iQ
и в сети имеется дуга (i,k),
и этот
минимум достигается на вершине j).
Среди всех
таких вершин k
выбираем ту, которая имеет минимальную
величину
,
помечаем ее −M(k)
=(j,
)
и заносим в множествоQ.

Подобную
процедуру
повторяем
до
тех
пор,
пока
не
будет
помечена
вершина
n.

Длина
кратчайшего
пути
равна
.
Используя
первую часть метки вершины, находим сам
кратчайший путь методом обратного хода.

Конец работы
алгоритма.

Рис.3.

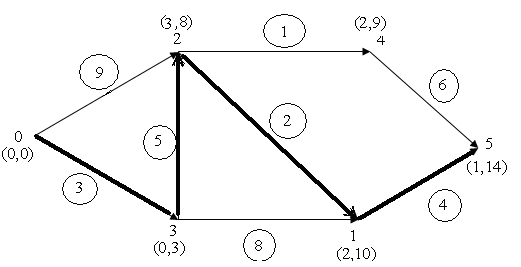
Применим алгоритм
Дейкстры к графу на рис. 3, числа
в кружочках равны
длинам
дуг.

Шаг
0.

M(0) =
(0,0),

M(i) =(0,

)
для
i = 1,2,…,n

Q = {0}

Шаг
1.

;

;

M(3) =(0,
3)

Q = {0, 3}

;

;

M(2) =(3,
8);

Q = {0, 3, 2}

;

;

Q = {0, 3, 2, 4}

;

;

Q = {0, 3, 2, 4, 1}

;

Q = {0, 3, 2, 4, 1, 5}

Рис.4

На
рисунке
4 приведен
пример
применения
алгоритма
1 для
определения
кратчайшего
пути:
числа
у
дуг
равны
длинам
дуг,
метки вершин
помещены
в
круглые
скобки,
кратчайший
путь
выделен
жирными линиями.

Задача о потоке минимальной стоимости

Определение:

Пусть дана сеть . — источник и сток. Ребра имееют пропускную способность поток и цену за единицу потока . Тогда общая стоимость потока из в :

Свойства сети

• Поток не может превысить пропускную способность.

• Поток из в должен быть противоположным потоку из в .

• Сохранение потока. Для каждой вершины, сумма входящего и исходящего потоков равно .

Задача:

Дана сеть . — источник и сток. Ребра имееют пропускную способность поток — и цену за единицу потока . Требуется найти максимальный поток, суммарная стоимость которого минимальна.

Алгоритмы решения

Метод устранения отрицательных циклов в остаточной сети

Воспользуемся леммой об эквивалентности свойства потока быть минимальной стоимости и отсутствии отрицательных циклов в остаточной сети. Получим следующий алгоритм:

Алгоритм

• Начало.
• Шаг 1. Определим для каждого прямого ребра обратное ребро . Определим его характеристики: , , .
• Шаг 2. Для каждого ребра зададим поток равный .
• Шаг 3. Найдем произвольный максимальный поток(любым алгоритмом нахождения максимального потока), построим для него остаточную сеть, где каждому ребру будет соответствовать величина .
• Шаг 4. При помощи алгоритма Форда-Беллмана найдем отрицательный цикл в построенной сети (отрицательный цикл ищется по стоимости ребра, т.е. ребра имеют вес ). Если отрицательный цикл не нашелся — перейдем к шагу 6.
• Шаг 5. Избавимся от отрицательного цикла, для этого пустим по нему максимально возможный поток. Величина потока равна минимальной остаточной пропускной способности в цикле. Перейдем к шагу 4.
• Шаг 6. Отрицательных циклов в остаточной сети нет, значит, максимальный поток минимальной стоимости найден.
• Конец.

Асимптотика

Алгоритм Форда-Беллмана работает за , улучшение цикла за . Если обозначить максимальную стоимость потока как , а максимальную пропускную способность как , то алгоритм совершит итераций поиска цикла, если каждое улучшение цикла будет улучшать его на 1. В итоге имеем , где — асимптотика поиска максимального потока.

Метод дополнения потока вдоль путей минимальной стоимости

Использование потенциалов Джонсона

См. также

• Сведение задачи о назначениях к задаче о потоке минимальной стоимости
• Венгерский алгоритм решения задачи о назначениях

Источники информации

• Википедия — Поток минимальной стоимости
• Визуализатор алгоритма нахождения максимального потока минимальной стоимости
• Хабрахабр — Максимальный поток минимальной стоимости
• Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом «Вильямс», 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)