Как найти минимальный промежуток времени

Чему равен минимальный промежуток времени между двумя последовательными совпадениями координат?

#python #mysql #sql #performance #timestamp

#python #mysql #sql #Производительность #временная метка

Вопрос:

Итак, представьте, что у меня есть база данных с идентификаторами и меткой времени:

 ID.      Time_Stamp_Col

id1.     2017-10-16 17:54:28
id2.     2016-09-13 17:14:17
id3.     2019-10-01 19:30:37
id4.     2017-08-27 20:55:30
id5.     2017-11-19 10:56:15
id6.     2018-02-12 09:59:24
  

и произвольное количество временных меток (2 для этого примера):

 2018-02-12 09:55:29
2017-11-19 10:21:12
  

Как мне вернуть столбец, содержащий минимальный timestampdiff между Time_stamp_Col и произвольным количеством временных меток?

(Я использую python, поэтому я полностью согласен с созданием цикла для генерации повторяющегося текста в соответствии с произвольным количеством временных меток)

У меня это пока:

 SELECT 
    LEAST(DATEDIFF('2018-02-12 09:55:29',
                    b.Time_Stamp_Col),
            DATEDIFF('2017-11-19 10:21:12',
                    b.Time_Stamp_Col)),
FROM
    DataBaseInQuestion b
  

Но это так невероятно медленно. DataBaseInQuestion содержит 14 миллионов строк. Есть ли более быстрый способ?

Комментарии:

1. Если вам нужно вернуть 14 миллионов строк, ваш запрос будет медленным.

Ответ №1:

Найдите «средний диапазон временных меток», который имеет минимальную итоговую разницу для заданного «произвольного количества временных меток».

Если количество «произвольных временных меток» нечетное, то это средняя временная метка. Возьмите временную метку, равную этой медиане. Если такая временная метка не существует, тогда возьмите любую временную метку в диапазоне временных меток, прилегающих к средней временной метке, или, если такой временной метки нет, возьмите временную метку, ближайшую к этому диапазону.

Если количество «произвольных временных меток» равно, то это диапазон между двумя средними временными метками. Возьмите любую временную метку в этом диапазоне или, если такой временной метки нет, возьмите временную метку, ближайшую к этому диапазону.

В обоих вариантах «ближайшая временная метка» означает «временную метку, которая имеет минимальное количество произвольных временных меток между self и ближайшей границей диапазона, если есть пара таких временных меток, тогда возьмите ближайший по разнице».

---

Нам нужна не формула / теория, а практическое решение. Шаги:

1. У нас есть массив «временных меток данных». Допустим, это DTS [1..X], он содержит X временных меток.
2. У нас есть массив «произвольных временных меток». Допустим, это ATS[1..N], он содержит N временных меток.
3. Вычислите индексы двух медианных элементов в ATS (для массива с нечетным количеством это будет один и тот же элемент). N ₁ = (N 1) MOD 2 ; N ₂ = (N 2) MOD 2.
4. В DTS — найдите временную метку DTS [K ₁], ближайшую, но не выше ATS [N ₂], и временную метку DTS [K ₂], ближайшую, но не ниже ATS [N ₁].
5. Вычислите «суммарное расстояние» для DTS [K ₁] и DTS [K ₂].

Если суммы равны, то оба элемента и все элементы между ними (да, в этом случае они могут быть не смежными!) Являются решением.

Если они отличаются, то элемент с наименьшей суммой является решением. Кажется, что в этом случае не может быть пары решений (но вы можете проверить его соседей, чтобы убедиться).

---

Почему это должно работать?

Представьте, что AST содержит только 2 ts. Возьмите одно летнее время между ними, оно имеет некоторую сумму различий. Переместите его на 1 секунду влево. Расстояние до левого ATS уменьшается на 1 с, до правого — увеличивается на 1 с, а общая сумма не меняется. Переместите еще один, и снова … и сумма будет постоянной, пока мы не достигнем левого ATS. Когда мы пересечем его, сумма будет увеличиваться на 2 за каждый 1-й ход.

Теперь представьте, что у нас есть 3-элементный ATS. Снова возьмите одно летнее время и поместите его поверх среднего AST. Переместитесь влево или вправо на 1 секунду — частичная сумма для левых / правых точек не изменится, расстояние до середины увеличится на 1 секунду, общая сумма увеличится на 1 секунду. Двигайтесь дальше — когда мы пересекаем крайние точки, сумма будет увеличиваться на 3 для каждого шага…

Расширьте это до 4, 5, … элемента в ATS. Временная метка с минимальной суммой соответствует средней временной метке или среднему диапазону временных меток. Отклонение от него увеличивает сумму, пересечение метки времени увеличивает скорость увеличения.

Комментарии:

1. Я не уверен, что полностью понимаю /: Как это приведет к кратчайшей разнице во времени между строкой и произвольными временными метками?

2. @Travasaurus Добавлены некоторые пояснения.

Минимальный промежуток — время

Cтраница 2

Интервалом между поездами в пакете при автоблокировке называется минимальный промежуток времени, разделяющий два поезда, следующие друг за другом по участку.
 [16]

Оптимальным содержанием жидкости, при котором обеспечивается полнота разделения за минимальный промежуток времени, оказалось 23 % вес.
 [18]

Разрешающим временем т счетчика или регистрирующей установки в целом называют минимальный промежуток времени между двумя последовательными импульсами, которые регистрируются раздельно. Разрешающее время имеет размерность сек / имп или мин / имп, однако для краткости его выражают обычно в секундах или минутах Обусловленные разрешающим временем потери при регистрации импульсов складываются из потерь ча счет разрешающего времени отдельных блоков регистрирующего устройства. Разрешающее время счетчиков Гейгера — Мюллера составляет примерно 10 — 2 — 10 — 4 сек, а усилительных блоков — от 5 — 10 — 5 до 1 10 — 6 сек для разных типов приборов. Общее разрешающее время регистрирующего устройства определяется, в конечном счете, разрешающим временем того из блоков, для которого т максимально.
 [20]

Время выключения ( запирания) / выкл, мксек — минимальный промежуток времени между моментом прохождения мгновенного значения прямого тока вентиля через нуль и моментом, когда повторное приложение прямого напряжения не вызывает включения тиристора. Время выкл играет важную роль при расчете инверторов и высокочастотных выпрямителей. Оно определяется обычно при Фр п 20 н — 25 С и выключении номинального тока. Однако при максимальном нагреве р-п структуры величина Выкл может существенно возрастать.
 [21]

Оптимальным содержанием жидкости, при котором обеспечивается полнота разделения за минимальный промежуток времени, оказалось 23 % вес.
 [23]

Оценим параметры электронно-лучевого ЗУ при считывании информации с заданной вероятностью ошибки за минимальный промежуток времени. Очевидно, и быстродействие, и вероятность ошибки зависят от плотности записи информации и параметров электронного луча, применяемого для считывания. Определим связь между плотностью записи информации и быстродействием при заданных вероятности ошибки, токе и геометрических параметрах электронного луча.
 [24]

Для обеспечения стабильного горения дуги необходимо, чтобы восстановление сварочного режима происходило в минимальный промежуток времени.
 [25]

В терминах обобщенных решений этих уравнений, допускающих существование конечной энергии, был найден минимальный промежуток времени Т, за который можно с помощью граничных управлений перевести процесс из произвольно заданного начального состояния ( и ( ж 0) р ( ж) иг ( ж 0) tjj ( x в произвольно заданное финальное состояние и ( х Т) pi ( x) ut ( xT ipi ( x), и эти граничные управления были предъявлены в явном аналитическом виде.
 [26]

По отношению к кредиту — это доходность к погашению, рассчитанная исходя из величины минимального промежутка времени между выплатами. Данный промежуток берется в качестве рас-счетного интервала для начисления сложного процента.
 [27]

Измерения электропроводности указывают не только на температурную зависимость образования структуры кокса, но и определяют минимальный промежуток времени, необходимый для завершения этого процесса, что едва ли можно осуществить какими-либо другими методами. Несомненно, что эти два момента важны при определении технологических условий коксования того или иного угля.
 [28]

Вследствие этого наметилась тенденция к преодолению трудностей путем ввода в теорию нек-рой минимальной длины и нек-рого минимального промежутка времени, что должно отразить прерывный характер пространственно-временных свойств материи в микромире. Сам термин квантование пространства и времени не точен. Он вызывает представление о неких элементарных, весьма малых частях, кирпичиках), из к-рых складываются пространство и время. На самом же деле реальный смысл гипотезы прерывности пространства и времени заключается в том, что в микромире существует определ. Указанное изменение, по-видимому, состоит в том, что в микрообластях, лежащих ниже определ.
 [29]

Задача быстродействия заключается в переводе управляемого объекта или процесса из некоторого множества начальных состояний в заданное множество конечных состояний за минимальный промежуток времени. К таким задачам относятся задачи о быстрейшем перелете из одной точки пространства в другую точку, о быстрейшем нагреве стержня, о быстрейшем успокоении струны и др. Эти и многие другие прикладные задачи быстродействия могут трактоваться как частный случай более общей задачи быстродействия, когда управления и траектории представляют собой элементы некоторых подходящим образом выбранных функциональных пространств.
 [30]

Страницы:  

   1

   2

   3

   4

Амплитуда, период, частота колебаний.

Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша­рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах, санти­метрах и т. д. На графике колебаний амплитуда определяется как макси­мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша­ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т) — это время, за которое совершается одно полное ко­лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы­рем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей­ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес­ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю­щихся величин, например, для затухающих колебаний.

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.

Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

.

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

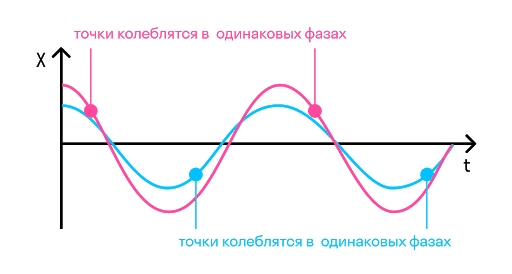
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

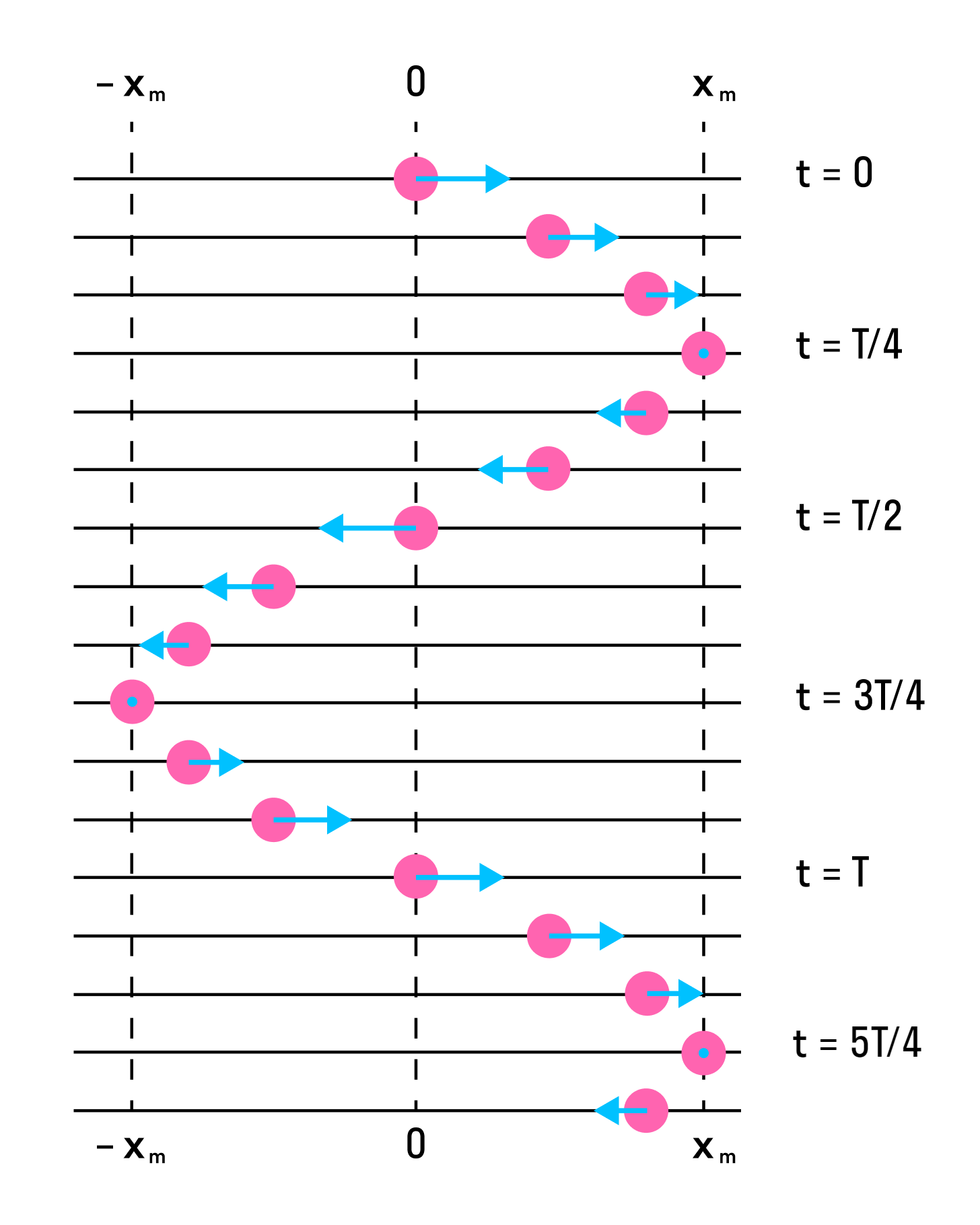
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

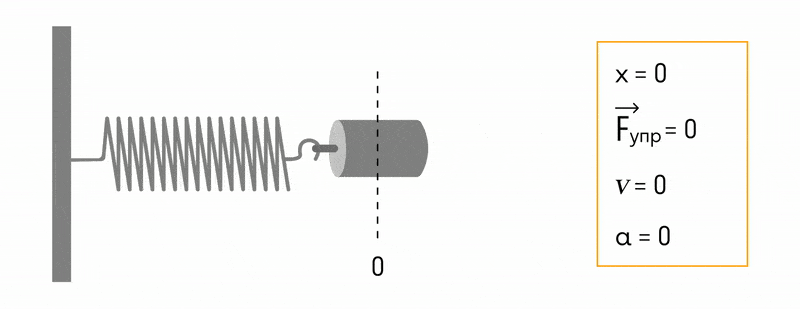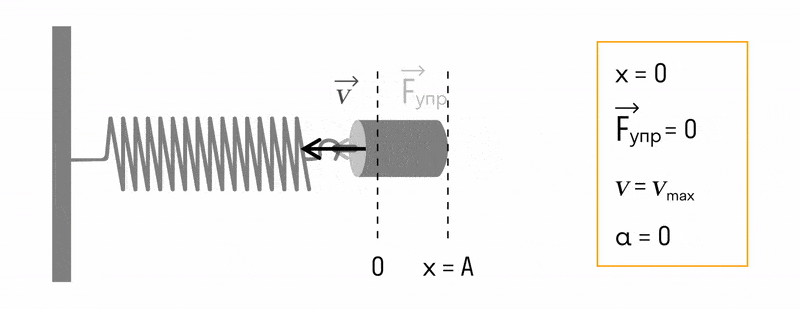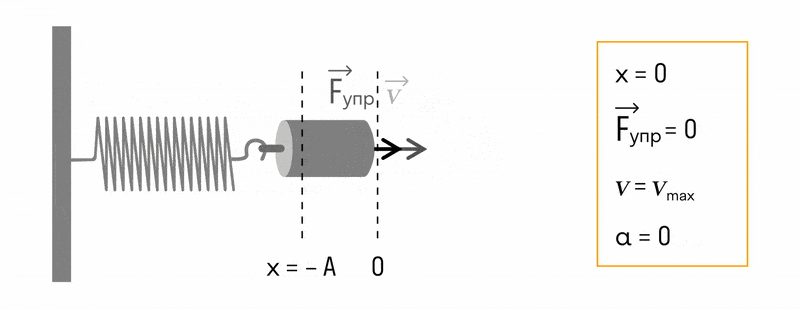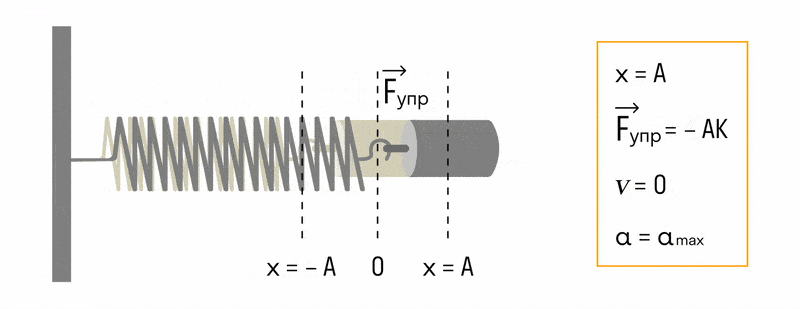
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

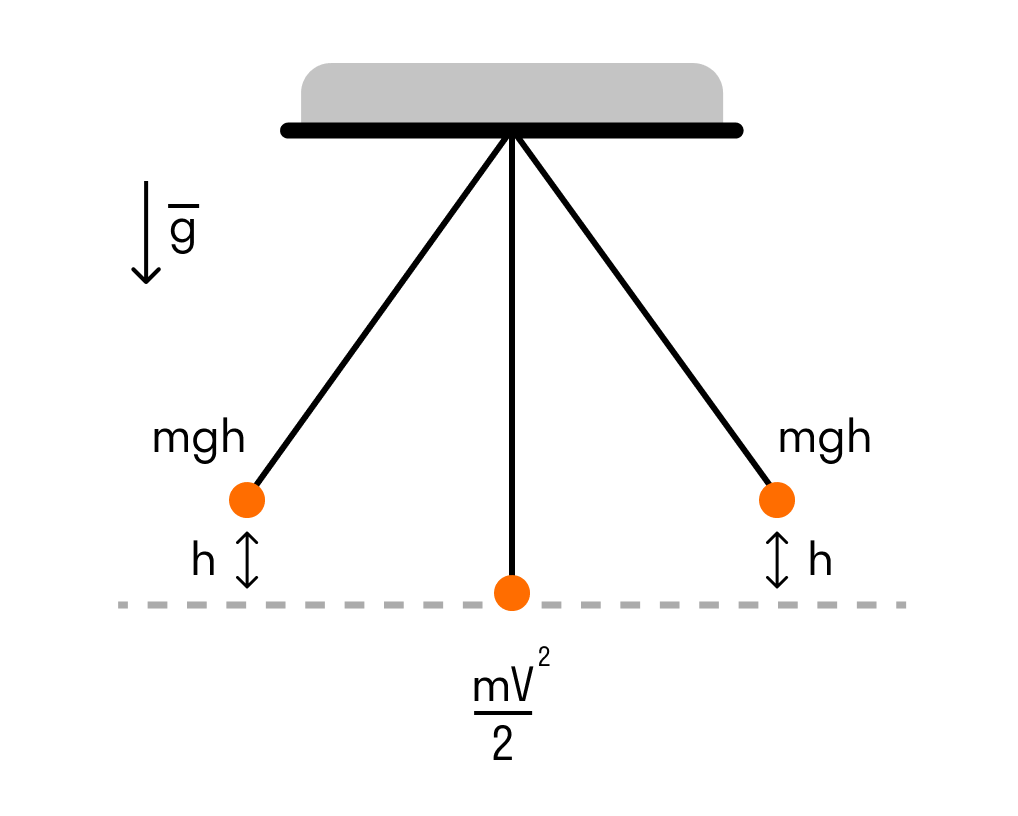
• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Гармонические колебания

теория по физике 🧲 колебания и волны

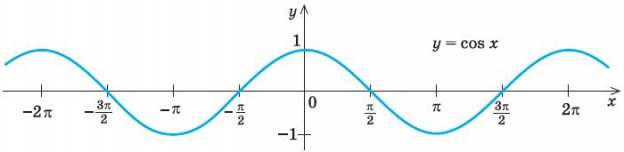
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.

Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.

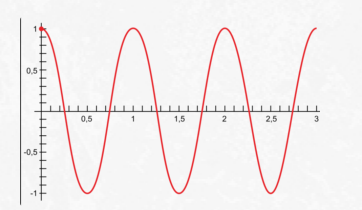
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.

Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.

Уравнение движения гармонических колебаний

Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:

Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x″ = − x m a x cos . t = − x

Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:

x = x m a x cos . √ k m . . t

Тогда первая производная примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x′ = − √ k m . . x m a x sin . √ k m . . t

Вторая производная примет вид:

x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x

Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:

x = x m a x sin . √ k m . . t

x = x m a x cos . √ k m . . t

Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω₀:

x = x m a x sin . ω 0 t

x = x m a x cos . ω 0 t

Само уравнение движения, описывающего свободные колебания, примет вид:

Период и частота гармонических колебаний

Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:

Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:

ω 0 = 2 π T . . = 2 π ν

Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.

Зависимость частоты и периода свободных колебаний от свойств системы

Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:

Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:

ω 0 = √ k m . . = 2 π T . . = 2 π ν

Отсюда период и частота колебаний соответственно равны:

T = 2 π ω 0 . . = 2 π √ m k . .

ν = 1 2 π . . √ k m . .

Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:

Отсюда период и частота колебаний математического маятника соответственно равны:

T = 2 π ω 0 . . = 2 π √ l g . .

ν = 1 2 π . . √ g l . .

Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.

Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.

Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.

Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?

Искомое число колебаний равно отношению времени к периоду колебаний:

Период колебаний для математического маятника определяется формулой:

N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68

Фаза колебаний

При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:

Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).

Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.

Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:

ϕ = ω 0 t = 2 π t T . .

t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:

Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. В этом случае графиком также будет являться косинусоида (или синусоида), но аргументом функции будет не время (период), а фаза, выражающаяся в радианах (см. рис.).

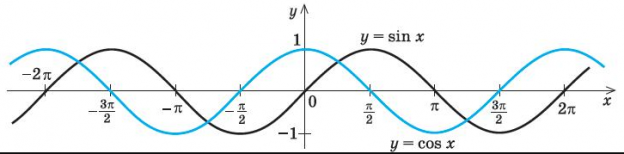
Синус от косинуса отличается только смещением аргумента на π 2 . . (см. рис. ниже). Поэтому для описания гармонических колебаний можно использовать как синусоидальный, так и косинусоидальный закон.

Выбор закона зависит от условий задачи. Если колебания начинаются с того, что тело выводят из положения равновесия и отпускают, удобнее пользоваться косинусоидальным законом, поскольку в начальный момент времени косинусоида показывает, что это тело отклонено максимально, а не находится в положении равновесия. Если для того чтобы начались колебания, совершают толчок, удобнее использовать синусоидальный закон, так как начальному моменту времени на синусоиде соответствует положение равновесия.

Колебания, совершаемые по закону синуса и косинуса, отличаются только фазой, которая смещена на значение, равное π 2 . . . Это значение называют сдвигом фаз, или их разностью. Поэтому косинусоидальная функция также может быть записана как:

x = x m a x cos . ω 0 t = x m a x sin . ( ω 0 t + π 2 . . )

Превращение энергии при гармонических колебаниях

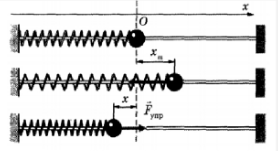
Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.

Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние x_max, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:

W p m a x = k x 2 m a x 2 . .

Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):

W k m a x = m v 2 m a x 2 . .

После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.

Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:

W = W p + W k = k x 2 x 2 . . + m v 2 x 2 . . = k x 2 m a x 2 . . = m v 2 m a x 2 . .

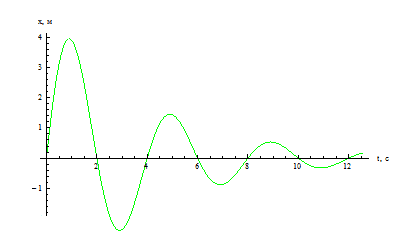
В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:

Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.

Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:

В это время потенциальная энергия груза будет равна:

W p = k x 2 2 . . = k ( x m a x 2 . . ) 2 2 . . = k x 2 m a x 8 . .

Согласно закону сохранения энергии, кинетическая энергия в это время равна:

Полная механическая энергия системы равна максимальной потенциальной энергии:

W = W p m a x = k x 2 m a x 2 . .

Тогда кинетическая энергия равна:

W k = k x 2 m a x 2 . . − k x 2 m a x 8 . .

Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:

W k W p . . = k x 2 m a x 2 . . − k x 2 m a x 8 . . k x 2 m a x 8 . . . . = k x 2 m a x 2 . . 8 k x 2 m a x . . − 1 = 4 − 1 = 3

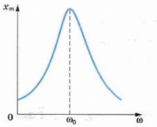
Резонанс

Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называют вынужденными.

Работы силы над такой системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.

Особый интерес вызывают вынужденные колебаний в системе, способной совершать свободные колебания. Примером такой системы служат качели. Их не получится отклонить на большой угол всего лишь одним толчком. Если их толкать то в одну, то в другую сторону, тоже ничего не получится. Но если подталкивать качели всякий раз, как они сравниваются с нами, можно раскачать их очень сильно. При этом не нужно прикладывать большую силу, но на это понадобится время. Причем после каждого такого толчка амплитуда колебаний качелей будет увеличиваться до тех пор, пока не достигнет своего максимального значения. Такое явление называется резонансом.

Резонанс — резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.

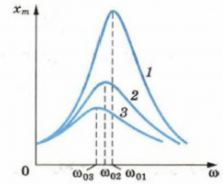
Графически явление резонанса можно изобразить как резкий скачок графика вверх (см. рис. выше). Причем высота «зубца», или амплитуда колебаний, будет зависеть от величины сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Это можно продемонстрировать графиками на рисунке ниже. Графику 1 соответствует минимальное трение, графику 3 — максимальное.

На явлении резонанса основан принцип работы частотомера — устройства, предназначенного для измерения частоты переменного тока. Он состоит из набора упругих пластин, которые закреплены на одной планке. Каждая пластина обладает определенной собственной частотой колебаний, которая зависит от упругих свойств, длины и массы. Собственные колебания пластин известны. Под действием электромагнита планка, а вместе с ней и пластины совершают вынужденные колебания. Но лишь та пластина, собственная частота которой совпадает с частотой колебаний планки, будет иметь большую амплитуду колебаний. Таким образом, определяется частота переменного тока.

Пример №3. Автомобиль движется по неровной дороге, на которой расстояние между буграми равно приблизительно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?

Колебания автомобиля в вертикальной плоскости будут заметны тогда, когда частота наезда на бугры сравняется с частотой свободных колебаний автомобиля на рессорах. Поскольку частота обратно пропорциональна периоду, можно сказать, что резонанс будет достигнут тогда, когда автомобиль будет наезжать на бугры каждые 1,5 секунды. Зная расстояние между буграми и время, можем вычислить скорость:

v = s t . . = 8 1 , 5 . . ≈ 5 , 33 ( м с . . ) ≈ 19 , 2 ( к м ч . . )

Смещение груза пружинного маятника меняется с течением времени по закону x = A cos . 2 π T . . t , где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника вернется к своему исходному значению?

Время, t (с)	0
Фаза, ϕ (рад)	0

Существует ли минимальный промежуток времени (квант времени)?