Как найти минимальный радиус окружности

Определить радиус и центр окружности минимального радиуса

Везде в дальнейшем будем обозначать через C(P,Z) окружность с центром в точке (P,O) и проходящую через точку Z=(Z x ,Z y ).

Очевидно, что на искомой окружности лежит по меньшей мере одна точка. Действительно, в противном случае мы можем, не меняя центра окружности, уменьшить ее радиус, а это противоречит предположению о том, что нами была построена окружность минимального радиуса.

Докажем следующее простое утверждение: Если на искомой окружности лежит единственная точка, то центр окружности есть проекция этой точки на ось абсцисс.

Предположим противное — на минимальной окружности лежит единственная точка Z(Z x ,Z y ), а центр ее не совпадает с (Z x ,0). Если мы начнем понемножку двигать центр окружности, проходящей через точку Z, в направлении (Z x ,0), то, так как все точки, кроме Z, лежат внутри окружности, до какого-то момента они и будут оставаться внутри нее. Таким образом мы можем хоть чуть-чуть, но сдвинуть центр, уменьшив при этом радиус окружности, содержащей все точки. Получаем противоречие с предположением о минимальности радиуса.

Следствие. Если на искомой окружности лежит только одна точка, то это точка с максимальной по модулю ординатой.

Отметим далее, что окружность с центром на оси абсцисс

единственным образом определяется двумя лежащими на ней точками (центр этой окружности — это точка пересечения оси абсцисс и срединного перпендикуляра к отрезку, соединяющего эти две точки).

Таким образом мы получаем следующий

Шаг 1. Ищем точку (x i ,y i ) с максимальной по модулю ординатой y i (если таких точек несколько, и у них разные абсциссы, то перейти на Шаг 2), и для окружности C(x i ,(x i ,y i )) проверяем, содержит ли она все N точек. Если да, то задача решена, если нет, то

Шаг 2. Среди окружностей, определяемых всевозможными парами точек (P i , P j ), находим те, которые содержат все точки, а затем выбираем из них окружность минимального радиуса.

Пар точек, которые могут определять окружности, всего N(N-1)/2, т.е. порядка N*N, следовательно, и возможных окружностей тоже порядка N*N. Для проверки принадлежности N точек каждой окружности требуется порядка N операций. Получаем, что сложность этого алгоритма порядка N 3 . (Когда мы говорим о сложности алгоритма, то мы рассматриваем только зависимость роста числа требуемых операций от числа N, игнорируя все константные множители и медленно растущие слагаемые).

Рассмотрим другой способ решения этой задачи, основанный

на более глубоком ее анализе.

Проверка по Шагу 1 ранее изложенного алгоритма остается без изменения. Пусть искомая окружность не найдена.

Для обоснования Шага 2 докажем следующее утверждение: Пусть окружность с центром (P ij ,0) определяется точками

P i (x i ,y i ) и P j (x j ,y j ). Она только тогда может быть содержащей все точки окружностью C минимального радиуса, когда (P ij ,0) лежит на ортогональной проекции отрезка [(x i ,y i ),(x j ,y j )] на ось абсцисс, т.е. должны выполняться неравенства x i ij j .

Окружность C с центром ( Pij0 ) должна проходить не менее чем через 2 точки заданного множества из N точек, и при этом из этих точек всегда можно выбрать две такие (обозначим их P i (x i ,y i ) и P j (x j ,y j )), что x i

ij j . Действительно, если бы абсциссы всех лежащих на окружности точек были, например, меньше P ij , то (P ij ,0) можно было бы сместить влево по оси абсцисс на некоторую величину с уменьшением радиуса охватывающей все точки окружности, что противоречит минимальности найденной ранее окружности.

Ни одна из точек, лежащих на окружности не может иметь абсциссы P ij вследствие невыполнения условия Шага 1.

Итак: всегда можно найти две лежащие на окружности точки P i и P j с абсциссами, соответственно, меньше и больше абсциссы центра окружности. Эти точки определяют центр окружности (P ij ,0) — точку пересечение серединного перпендикуляра к отрезку [P i ,P j ] с осью абсцисс. При этом точка (P ij ,0), естественно, будет лежать на проекции отрезка [P i ,P j ] на ось абсцисс.

Рассматривая все пары точек (P i ,P j ) таких, что точка пересечения (P ij ,0) серединного перпендикуляра к отрезку [P i ,P j ] с осью абсцисс лежит на проекции отрезка [P i ,P j ] на ось абсцисс, получаем, что центр искомой окружности минимального радиуса совпадает с одной из таким образом полученных точек. Каждая из рассматриваемых пар точек (P i ,P j ) определяет окружность минимального радиуса R ij , содержащую эти две точки.

Из всего вышесказанного получаем, что интересующая нас окружность минимального радиуса, содержащая N точек, должна

иметь максимальный из всех полученных радиусов R ij .

Всего пар точек (P i ,P j ) не более (N 2 -N)/2, и, следовательно, сложность алгоритма

O((N 2 -N)/2) = O(N 2 -N) = O(N 2 ).

Тут мы, как и обычно, избавляемся от констант и медленно растущих слагаемых.

Все вычисления на машине проводятся с ограниченной точностью, с определенным числом знаков после запятой. Поэтому нам бывает достаточно только указать, что интересующая нас точка лежит внутри отрезка заранее заданной длины epsilon. Epsilon задается пользователем. Например, если мы хотим найти координату точки с точностью 5 знаков после запятой, то epsilon = 10 -6 .

В отличие от варианта #2 мы не будем брать все перпендикуляры, попадающие на проекции отрезков и искать среди получаемых окружностей окружность с максимальным радиусом. Наоборот, описанным ниже способом будем выбирать точку на оси абсцисс и проверять, является ли она искомой или нет.

Из варианта решения #2 можно сделать вывод, что искомая точка лежит на отрезке [A 0 ,B 0 ]=[min,max]. Пусть C 0 =(A 0 +B 0 )/2 — середина этого отрезка, а L=B 0 -A 0 его длина.

D 1 (C 0 )=максимальное из расстояний от точки (C 0 ,0) до точек (x i ,y i ) с абсциссами x i 0 ;

D r (C 0 )=максимальное из расстояний от точки (C 0 ,0) до точек (x i ,y i ) с абсциссами x i >=C 0 .

i-ый итеративный (повторяющийся) шаг алгоритма, i=0, 1, 2, 3, . :

Если B i -A i i ,B i ] и желаемая точность достигнута. Стоп.

Вычисляем C i =(A i +B i )/2.

Находим D l (C i ) и D r (C i ).

Если D l (C i ) r (C i ), то искомая точка не может лежать на промежутке [A i ,C i ), так как радиус любой содержащей N точек окружности с центром на этом промежутке больше D r (C i ) (проверьте сами!), а окружность с центром C i имеет радиус D r (C i ). Поэтому центр искомой окружности лежит на [C i ,B i ], который мы обозначим [A i+1 ,B i+1 ],

иначе, если D r (C i ) l (C i ), то, аналогично, получаем, что центр искомой окружности лежит на [A i ,C i ], которой мы обозначим [A i+1 ,B i+1 ]

иначе, если D r (C i )=D l (C i ),

то C i — центр искомой окружности. Стоп.

Конец i-го итеративного шага. Выполнить шаг i+1.

Мы видим, что длина L начального отрезка на каждом шаге уменьшается вдвое. Алгоритм, вообще говоря, заканчивает работу при выполнении условия

L/(2 S ) 2 (L/epsilon)]+1 шагов, где log 2 — это логарифм по основанию 2.

Так как на каждом шаге (для вычисления D l и D r ) выполняется не более O(N) операций, то всего их потребуется порядка O(N log 2 (L/epsilon)).

Определить радиус и центр окружности минимального радиуса

Дано конечное множество точек на плоскости. Нужно найти окружность минимального радиуса такую, чтобы данные точки были внутри неё. Следующая функция находит такую окружность: Здесь data — это массив входных точек, а index — указатель на массив, в который будут записаны индексы точек по которым была построена окружность ( в том случае, если указатель не равен 0 ).

Описание алгоритма:
1. Если к-во входных точек равно 0, то возвращаем неопределённую окружность.
2. Если к-во входных точек равно 1, то возвращаем окружность с центром в этой точке и нулевым радиусом.
3. Если к-во входных точек равно 2, то возвращаем окружность с центром в середине между этими точками и соответсвующим радиусом.
4. Находим самую удалённую точку от первой. Если это расстояние будет равно 0, то возвращаем окружность с центром в первой точке и нулевым радиусом. Иначе считаем эти точки опорными и строим по ним окружность, как в пункте 3.
5. Начало цикла.
6. Находим самую удаленную точку от центра текущей окружности. Если это расстояние не больше, чем радиус текущей окружности или индекс самой удалённой точки равен одному из индексов опорных точек, то выходим из цикла. Иначе будем включать эту точку в число опорных, а пока назовём её новой.
7. Найдём среди опорных точек самую удаленную от новой точки и построим текущую окружность по двум точкам ( новой и найденной ).
8. Если к-во опорных точек текущей окружности было равным 3, то переходим к пункту 9. Иначе проверим выходит ли неиспользованная опорная точка за пределы текущей окружности. Если не выходит, то заменяем её на новую точку ( к-во опорных точек останется равным 2 ). Иначе добавляем новую точку в опорные и строим окружность по трём точкам. Переходим к пункту 10.
9. Находим из двух неиспользованных точек самую удаленную от центра текущей окружности. Если эта точка лежит вне круга, то она будет третьей опорной и тогда строим окружность по трём новым опорным точкам. Иначе опорных точек останется две.
10. Если радиус окружности не вырос за время цикла, то конец алгоритма, иначе идём на начало цикла.

Дано конечное множество окружностей на плоскости. Нужно найти окружность минимального радиуса такую, чтобы все данные окружности были внутри неё. Следующая функция находит такую окружность: Описание этого алгоритма аналогично описанию алгоритма для точек.

Дано конечное множество прямых на плоскости. Нужно найти окружность минимального радиуса такую, чтобы она пересекала все данные прямые. Следующая функция находит такую окружность:

Описание шаблонов классов CArrRef и DynArrRef находится здесь.
Описание шаблона классов Def находится здесь.
Описание класса Vector2d находится здесь.
Описание классов Line2d и Circle2d находится здесь.

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Конспект готов к прочтению.

Описание

Минимальная охватывающая окружность множества точек (smallest enclosing disc) — это задача, в которой необходимо по заданному набору точек найти окружность минимального радиуса, которая содержит все точки множества.

Алгоритм

Сперва приведем алгоритм, корректность которого позднее будет доказана.

Рассмотрим метод , который будет принимать на вход множество точек, а возвращать будет искомую охватывающую окружность. Идея метода в том, что он генерирует случайную перестановку из точек, которые поступили на вход и в получившимся порядке по одной добавляет их в текущую охватывающую окружность. Как будет доказано позднее, если на каком-то шаге алгоритма текущая точка оказалась вне текущей минимальной окружности, то утверждается, что она лежит на границе новой окружности, которая будет содержать в себе ее и все предыдущие точки. Опишем приведенный выше алгоритм псевдокодом:

MinDisc(S)
   Let P - random permutation of S
   Let D2 - be the smallest enclosing disc for {p1, p2}.
   for i = 3 to n {
       if pi  Di−1  then Di = Di−1 // point is inside. nothing to do here
                     else Di = MinDiscWithPoint ({p1,...,pi−1}, pi) // point is lying on the boundary of minimal circle
   }
   return Dn

Как вы заметили, мы использовали выше метод — это метод, который по множеству точек и еще одной точке возвращают искомую окружность. При этом выделенная точка (которая передается в качестве второго аргумента) обязательно лежит на окружности. Эта функция очень похожа на предыдущую, поэтому приведу лишь ее псевдокод:

MinDiscWithPoint(S, q)
   Let P - random permutation of S
   Let D1 - be the smallest enclosing disc for {p1, q}.
   for i = 2 to n {
       if pi  Di−1  then Di = Di−1 
                     else Di = MinDiscWith2Points ({p1,...,pi−1}, pi, q) 
   }
   return Dn

Как и в предыдущем случае мы использовали новый метод. аналогичен , но в нем уже передается две точки, которые будут лежать на построенной окружности. В этой функции шафлить инпут не требуется. Опишем его псевдоком:

MinDiscWith2Points(P, q1, q2)
   Let D0 - be the smallest enclosing disc for {q1, q2}.
   for i = 1 to n {
       if pi  Di−1  then Di = Di−1 
                     else Di = сircumcircle (прим. описанная окружность) of a triangle {pi, q1, q2} 
   }
   return Dn

Как мы видим больше подобных шагов делать не нужно, так как если известно, что три точки лежат на некоторой окружности, то они однозначно ее задают.

Корректность алгоритма

Попробуем разобраться почему этот алгоритм действительно находит искомую окружность.

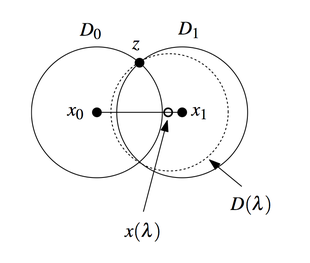
Докажем несколько вспомогательных лемм. Для удобства введем общие обозначения. Пусть и — два непересекающихся множества точек на плоскости, Пусть — некоторая точка из множества .

Лемма (лемма 1):

Окружность минимального радиуса, содержащая все точки внутри себя и все точки на границе, уникальна.

Доказательство:

Пусть это не так и существует две такие окружности и . Очевидно, что в таком случае все точки из должны лежать внутри . Пусть — точка пересечения окружностей (смотри рисунок). Рассмотрим некоторое семейство окружностей . При этом центры этих окружностей лежат на отрезке, соединяющем центры и , и перемещаются очевидным образом в зависимости от параметра . При этом радиус каждой из этих окружностей — расстояние от центра до точки , описанной выше. Рассмотрим окружность . Заметим, что лежит целиком внутри нее (по построению окружности ), а так как проходит через пересечение окружностей и , то она проходит через все точки (так все точки лежат на .). Из этого следует, что эта окружность явлется допустимой для нашей теоремы и при этом обладает меньшим радиусом, то наше предположение неверно и искомая окружность единственная. Далее будем называть искомую окружность .

Лемма (лемма 2):

Если , то

Доказательство:

Для множества справедливо, что для него минимальный диск по определению — это , но так как лежит внутри него, то он и является корректным диском для множества . Но если бы в существовал еще меньший диск, то он бы существовал бы и для . Значит эти диски равны(в силу единственности) и

Лемма (лемма 3):

Если , то

Доказательство:

Пусть и . Рассмотрим аналогичное семейство множеств как в лемме 1. Зададим это семейство с помощью окружностей и . Заметим, что , но . Значит найдется такое , что точка лежит на границе окружности . Но в таком случае так как эта окружность удовлетворяет условиям теоремы и к тому же обладает не большим радиусом, чем (которая в свою очередь является минимальной охватыающей окружностью), то . Это означает, что , то точка лежит на границе , то .

Эти три доказанные леммы полностью подтверждают корректность наших действий в приведенном выше алгоритме, ведь во всех трех методах в условном операторе мы используем леммы 2 и 3, корректность которых доказана. Другими словами, алгоритм действительно найдет искомую минимальную охватывающую окружность множества точек.

Память и время работы

Сначала разберемся с памятью. Тут все просто — никаких лишних затрат, кроме как на хранение точек нам требуется, то алгоритм требует памяти.

С временем работы дела обстоят интереснее. На самом деле приведенный алгоритм работает за линейное время. Докажем этот факт.

Рассмотрим некоторое множество и точку , которая лежит на границе построенной охватывающей окружности. Тогда попробуем удалить одну точку из набора . Искомая окружность может измениться только в том случае, когда эта удаленная точка лежала на границе, а вероятность этого (так как точек, которые образуют нашу окружность не более трех. при этом одна из этих трех точек — ).

То оценим время работы MinDiscWithPoint c помощью доказанного выше факта. На каждой итерации цикла будет происходить проверка, которая пройдет в «else» с вероятностью . А сложность работы каждого «else» — . То суммарное время работы MinDiscWithPoint вычисляется следующим образом:

.

Абсолютно аналогичным образом доказываем, что время работы есть . То есть рассматриваемый алгоритм имеет линейную сложность.

Источники

Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars-Computational Geometry Algorithms and Applications, p. 86

Given a positive integer K, a circle center at (0, 0) and coordinates of some points. The task is to find minimum radius of the circle so that at-least k points lie inside the circle. Output the square of the minimum radius. 

Examples:  

Input : (1, 1), (-1, -1), (1, -1), 
         k = 3
Output : 2
We need a circle of radius at least 2
to include 3 points.


Input : (1, 1), (0, 1), (1, -1), 
         k = 2
Output : 1
We need a circle of radius at least 1
to include 2 points. The circle around
(0, 0) of radius 1 would include (1, 1)
and (0, 1).

The idea is to find square of Euclidean Distance of each point from origin (0, 0). Now, sort these distance in increasing order. Now the k^th element of distance is the required minimum radius.
Below is the implementation of this approach: 

Time complexity: O(n + nlogn)
Auxiliary Space: O(n)ve.

Approach#2: Using binary search

This code uses binary search to find the minimum radius such that at least k points lie inside or on the circumference of the circle. It first finds the maximum distance between any two points, then performs binary search on the range [0, max_distance] to find the minimum radius.

Algorithm

1. Initialize left = 0 and right = maximum distance between any two points in the given set of points.
2. While left <= right, find mid = (left + right) / 2
3. Check if there exist k points inside or on the circumference of a circle with radius mid using a simple linear search. 4. If k or more points are inside or on the circumference of the circle, set right = mid – 1.
5. If less than k points are inside or on the circumference of the circle, set left = mid + 1.
6. After the binary search, the value of left will be the minimum radius required to include k points.

Time Complexity: O(n^2 * log(r)) where n is the number of points and r is the maximum distance between any two points.
Space complexity: O(1) as it uses only a constant amount of extra space irrespective of the size of the input.

This article is contributed by Anuj Chauhan. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed abo

Last Updated :
24 Apr, 2023

Like Article

Save Article