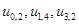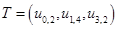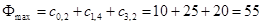Как найти минимальный разрез в сети
Решить задачу нахождения максимального потока в транспортной сети с помощью алгоритма Форда—Фалкерсона, и построить разрез сети S.
Исходные данные:
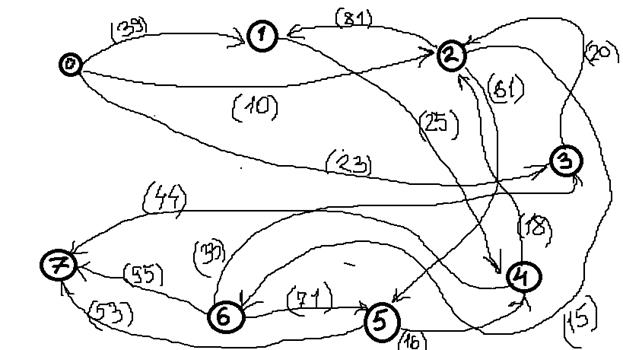
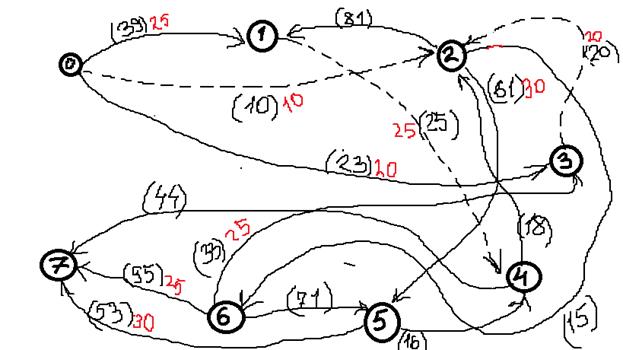
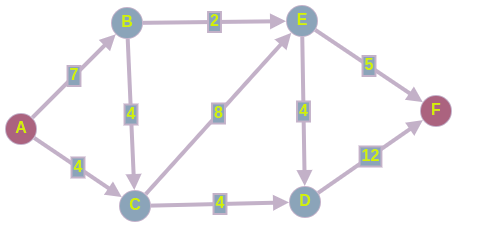
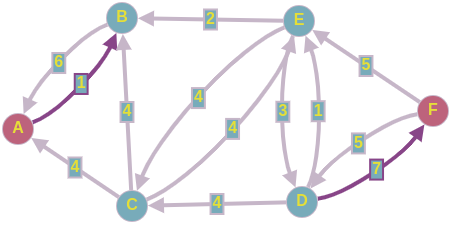
Дана сеть S(X,U) 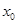
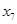
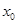
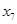
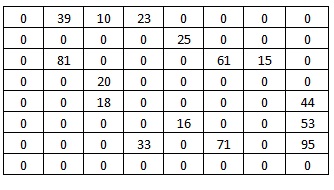
Значения пропускных способностей дуг 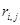
r[0,1] = 39; r[4,7] = 44; r[6,3] = 33; r[5,7] = 53; r[0,2] = 10;
r[4,2] = 18; r[6,7] = 95; r[5,4] = 16; r[0,3] = 23; r[2,5] = 61;
r[2,1] = 81; r[6,5] = 71; r[1,4] = 25; r[2,6] = 15; r[3,2] = 20
1. Зададим на сети нулевой поток (на всех дугах величина потока 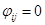
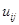
2. Выбираем на сети (произвольно) путь, ведущий из вершины x0 в вершину x7:
X0-X1-X4-X6-X7
3. Находим 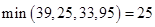
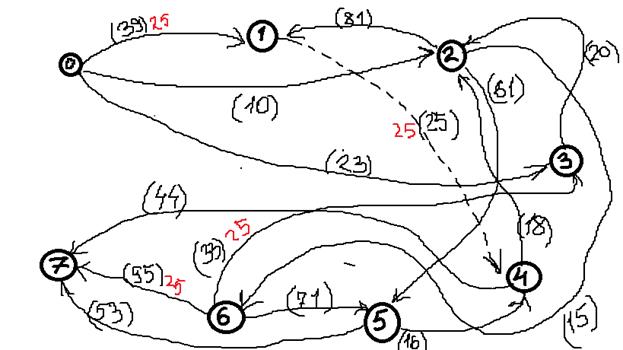
4. Выбираем еще один путь, например: Х0-Х2-Х5-Х7, находим 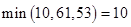
5. Выбираем еще один путь, например: Х0-Х3-Х2-Х5-Х7, находим 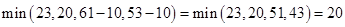
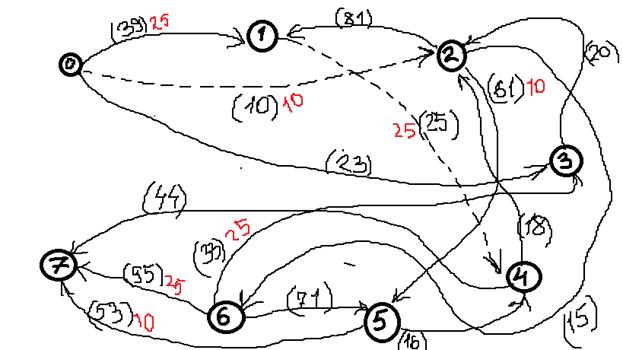
6. Более путей от Х0 до Х7 нет, суммируем увеличения потока: 25+10+20=55.
Вывод: максимальный поток равен 55.
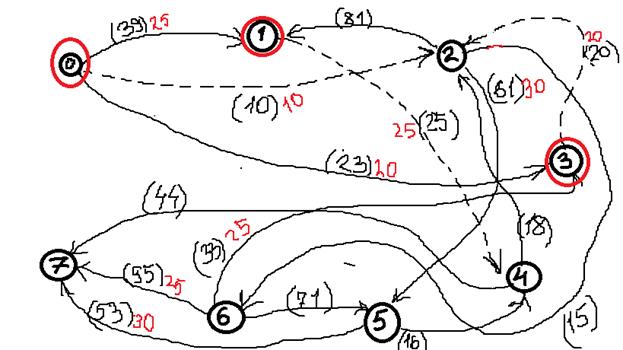
2) Построить разрез сети S.
Процедура «пометок вершин».
Начальное состояние: все вершины не имеют пометок.
Вершине Х0 приписывается пометка. Всем вершинам 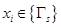
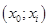
Определяем дуги минимального разреза: это дуги, начала которых находятся в помеченных вершинах, а концы — в непомеченных вершинах.
Это дуги:
Таким образом, минимальный разрез данной сети
Вычисление величины максимального потока
Алгоритм Форда-Фалкерсона
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток.
Исходный граф
Как работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
Отправлять определенное количество потока из текущей вершины в соседние.
Возвращать определенное количество потока из соседних вершин в текущую.
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
Допустим наш алгоритм нашел следующий путь из вершинывнашей остаточной сети, которая на момент начала, совпадает с исходным графом.
Сколько потока можем провести по этому пути.
— Больше 2 ед. мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в .
Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:
Пропускаем 3 ед . потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:
На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:
Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
На 4-ой итерации находим следующий путь в остаточной сети:
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
Итоговая остаточная сеть
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Максимальный поток и минимальный разрез
Теорема Форда-Фалкерсона 1 (о максимальном потоке и минимальном разрезе).
В любой сети существует максимальный поток. Величина максимального потока равна пропускной способности минимального разреза.
Теорема Форда-Фалкерсона 2.
Поток, вычисленный с помощью алгоритма Форда-Фалкерсона имеет максимальную величину, а разрез , где -множество вершин, помеченных при последнем помечивании, имеет минимальную пропускную способность.
Нахождение максимального потока и построение минимального разреза в сети с использованием алгоритма Форда-Фалкерсона
В данной задаче основным параметром на дугах сети является – пропускная способность. Пропускная способность показывает, сколько единиц потока может быть передано по дугам сети. Таким образом, потоком в сетиD = [N, M] называется неотрицательная вещественная функция, удовлетворяющая условиям:
1. ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги ;
2. сохранения: суммарный поток, заходящий в любую вершину сети (кроме истока и стока), равен суммарному потоку, выходящему из этой вершины.
Дуга сети называется насыщенной, если поток по этой дуге равен пропускной способности этой дуги, т. е. .
Разрезом сетиназывается множество дуг, удаление которых из сети приводит к тому, что исток и сток оказываются несвязанными.
Пропускной способностью разрезаназывается число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.
Отыскание минимального разреза – одна из основных задач анализа транспортных сетей. В силу конечности графа минимальный разрез может быть найден перебором всех разрезов, но этот путь, конечно, неприемлем для достаточно больших графов.
Минимальный разрез можно отыскать при помощи теоремы Форда – Фалкерсона: в любой транспортной сети величина любого максимального потокаравна пропускной способности любого минимального разреза.
Для нахождения максимального потока в сети разработан алгоритм Форда – Фалкерсона. Перед началом выполнения алгоритма все вершины сети нумеруются произвольным образом, кроме источника и стока (источник получает минимальный номер 1, сток – максимальный , где – число узлов).
Алгоритм состоит из следующих основных шагов:
1. Определить начальный поток в сети, сложив потоки по дугам, выходящим из источника.
2. Вершинам сети присвоить целочисленные метки, а дугам – знаки «+» и «–» по следующим правилам:
а) вершине-истоку присвоить метку ;
б) находим непомеченнуювершину , смежную помеченнойвершине . Если поток по соединяющей вершины дуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершина является образомпомеченной вершины , то происходит прямое помечивание (дуга в прямом направлении допустима): вершина получает метку, равную номеру вершины , соединяющая вершины дуга получает метку «+», переходим к рассмотрению следующей вершины. Если вершина не имеет ни одного помеченного прообраза, поток по дуге в прямом направлении больше 0, то происходит обратное помечивание (дуга допустима в обратном направлении): вершина получает метку, равную номеру вершины (являющейся в данном случае ее образом), соединяющая вершины дуга получает метку «–», происходит переход к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.
3. Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток – максимальный, переход к шагу 5. В противном случае перейти к пункту 4.
4. Рассмотреть последовательность вершин L, метка каждой из которых равна номеру следующей за ней вершины, и множество дуг МL, соединяющих соседние вершины из L.
Построение нового потока по схеме:
а) Если дуга принадлежит множеству МL (смотри выше) и имеет знак «+», то новый поток по этой дуге = старый поток по этой дуге + Δ (схему нахождения смотри далее).
б) Если дуга принадлежит множеству МL и имеет знак «–», то новый поток по этой дуге = старый поток по этой дуге – Δ.
в) Если дуга не принадлежит множеству МL, то поток по дуге оставляем без изменения.
I. , где для нахождения рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «+», и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге ( ). Затем из этих значений разностей выбирается минимальное значение и присваивается .
II. Для нахождения рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «–». Затем из этих дуг выбирается дуга с минимальным потоком ( ), и значение потока по этой дуге присваивается .
Перейти к шагу 2.
5. Определяем максимальный поток, складывая начальный поток и все полученные изменения потока.
В оптимальном решении, т. е. когда найден максимальный поток, минимальный разрез образуется насыщенными дугами.
Дата добавления: 2019-02-22 ; просмотров: 5017 ; Мы поможем в написании вашей работы!
Представим
себе нефтепровод. Возникает задача:
сколько нефти можно перекачать по нему
из пункта А в пункт В? Достаточна ли
пропускная способность труб, чтобы
перекачать запланированное количество
нефти, и если нет, то какую часть
нефтепровода надо расширить, чтобы
обеспечить запланированную поставку?
Такого
рода задачи возникают в транспортных
сетях, сетях связи, информационных сетях
и т.п. Бесчисленное количество такого
рода задач решаются с помощью математической
модели, которая называется «сеть».
Определение
6.9. Транспортной
сетью
называют связный взвешенный орграф без
петель
с выделенной парой вершин
и
.
Вершина– начало транспортной сети, из которой
ребра только выходят,– конец транспортной сети, в которую
ребра только входят.– множество весов ребер, вес каждого
ребра называютпропускной
способностью ребра.
Веса
ребер можно рассматривать как
функциональное соответствие между
множеством ребер
и набором весов
:
или
.
Рассмотрим случай,
когда все веса неотрицательны и
целочисленны.
Определение
6.10. Потоком
по транспортной сети
называют целочисленную функцию
,
заданную на множестве ребери обладающую следующими свойствами:
|
|
(6.7) |
|
|
(6.8) |
где
– внутренняя вершина графа, т.е
,
;
–множество
ребер, входящих в вершину
;
–множество
ребер, выходящих из вершины
.
Р
6.18 поясняет введенные термины. На рисунке
рядом с каждым ребром стоит дробь,
числитель которой – пропускная
способность ребра, знаменатель – поток
по ребру. Равенство (6.8) утверждает, что
поток, входящий в вершину равен потоку,
выходящему из нее, т.е. поток в вершинах
не скапливается.
Поскольку
вершина
– начало транспортной сети (источник),
из которой ребра только выходят, то
– поток, выходящий из источника.
Аналогично, так как– конец транспортной сети (сток),
в которую ребра только входят, то
– поток, входящий в сток. Поскольку
накопления потока ни в одной из вершин
не происходит, очевидно, что.
Пусть
разрез транспортной сети, разбивающий
вершины графа на два непересекающихся
подмножестваи
(
).
–мощность
разреза, т.е. максимально
возможный поток,
входящий в вершины множества
,
по ребрам, выходящим из вершин множества.
–поток,
который реально входит в вершины
множества
,
по ребрам, выходящим из вершин множества.
Очевидно, что.
П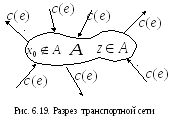
в вершины множествапоток не только входит, но и выходит из
него (рис. 6.19), то мощность разрезабольше потока, поступающего в сток сети
,
принадлежащий разрезу:
.
Основная
задача, возникающая при работе с сетями
– найти максимальный поток в сети,
другими словами, ответить на вопрос:
источник какой мощности может обслуживать
данная сеть?
При решении этой
задачи используется следующая теорема.
Теорема
Форда и Фалкерсона.
Максимальный поток по транспортной
сети равен мощности минимального разреза
сети, т.е.
|
|
(6.9) |
Доказательство
теоремы – это алгоритм определения
максимального потока по сети. Алгоритм
состоит из двух частей.
I.
Насыщение
потока.
Поток
называют насыщенным, если любой путь
от источника к стоку содержит ребро
,
реализующее свою пропускную способность,
т.е. для которой.
Задача первой части алгоритма состоит
в насыщении потока.
1.
Зададим произвольный начальный поток.
Например, нулевой на всех ребрах:
.
2.
Поиск пути из
в
.
Если путь найден, то переход к пункту
3. Если путь на найден, то переход к пункту
5.
3.
Увеличиваем поток по найденному пути,
так, чтобы одно из ребер было насыщенным.
4.
Условно разрываем насыщенное ребро и
переходим к пункту 2, на поиск пути из
в
.
5. Сеть насыщена и
«разорвана».
II.
Перераспределение
потока.
Пометим
следующим образом все возможные вершины
сети.
1.
Вершину
пометим -0.
2.
Пусть
– любая из уже помеченных вершин,
– произвольная непомеченная вершина,
смежная с.
Вершинупомечаем
,
если ввходит
ненасыщенное ребро из
,
().
Вершинупомечаем
,
если извыходит
непустое ребро в
,
().
После выполнения этого шага возможны
два случая: (1) стококазался помеченным, (2) сток
оказался непомеченным.
3.
Вершина
оказалась помеченной.
Это означает, что существует
последовательность помеченных вершин
от
к
.
В этой последовательности каждая
последующая вершина помечена номером
предыдущей. Определим новый поток,
увеличивая на единицу поток на ребрах,
ориентированных по направлению движения
отк
,
и уменьшая на ребрах, направленных
против этого движения. Поток можно
увеличивать на прямых ребрах и уменьшать
на обратных ребрах до тех пор, пока одно
их прямых ребер не станет насыщенным
или одно из обратных ребер – пустым.
Таким
образом, пометка вершины
позволяет увеличить поток через сеть
как минимум на единицу, а значит, алгоритм
конечен, т.е. наступит момент, когда
вершинаостанется непомеченной.
4.
Вершина
осталась непомеченной.
П
– множество всех непомеченных вершин,
куда попал и сток.
Все ребра, входящие в эти вершины из
множестваявляются насыщенными, а все выходящие
– пустыми. Поскольку все выходящие
ребра пусты, весь поток изскатывается в
,
он и определяет максимальную пропускную
способность сети. В то же времяи

Пример.
Найдем максимальный
поток в сети изображенной на рис. 6.18.
Насыщение потока
выполнено так, как показано на рисунке.
При это пройдены следующие пути:
,
все ребра этого пути насыщены;
,
два ребра
и
ненасыщенны.
В
перераспределение потока, для чего
пометим вершины, в которые входят
ненасыщенные ребра, метками со знаком
«+» и вершины, из которых выходят
непустые ребра, метками со знаком «-«.
В результате
получилась следующая последовательность
меток:
Сток
оказался помеченным, следовательно,
можно увеличить поток в сети, увеличивая
на единицу поток на ребрах ориентированных
по направлению ки уменьшая на ребрах, направленных от
:

В
результате получим новое распределение
потоков в ребрах, изображенное на рис.
Если
сейчас пометить
меткой «-0», а
— меткой «+0», то больше никакие
вершины пометить не возможно: вершинунельзя пометить метками «+0» и «+2»,
так как потокии
насыщены. Эту вершину нельзя пометить
и меткой «-2», поскольку потокпустой. Вершина
также не может быть помечена, так как
метка «+2» невозможна из-зи насыщенности
потока,
а метка «+1» – из-за того, что не
помечена вершина.
Таким
образом, максимальный поток в данной
сети равен 3. Ему соответствует минимальный
разрез
:
все ребра,
входящие внасыщены, а все ребра, выходящие из
пусты (ребро
).
Мощность минимального разреза – три
единицы.
131
Соседние файлы в папке учебник
- #
- #
- #
- #
- #
- #
- #
Транспортная сеть. Основные понятия и определения.
Транспортная сеть — ориентированный граф G = (V, E) , в котором каждое ребро (u,v) in E имеет неотрицательную пропускную способность c(u,v)>=0 и поток f(u,v).
Выделим теперь специальные типы вершин в сети.
Вершина y, из которой дуги только исходят, т.е. если , называется источником или входом сети S.
Вершина z, в которую дуги только входят, т.е. если , называется стоком или выходом сети S.
Потоком в транспортной сети Т называется неотрицательная вещественная функция, определенная на множестве дуг, удовлетворяющая условиям:
- ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги;
- сохранения: суммарный поток , заходящий в любую вершину сети ( кроме истока и стока ) равен суммарному потоку , выходящему из этой вершины.
Дуга сети называется насыщенной, если поток по этой дуге равен пропускной способности этой дуги.
Поток по пути называется полным, если хотя бы одна дуга пути насыщена.
Как упоминалось выше, поток в сети — это функция, определенная на множестве дуг. Величиной потока называется сумма значений этой функции по всем выходным дугам сети ( выходные дуги сети — это дуги, инцидентные стоку).Понятия потока и величины потока в сети часто путают, однако между ними существует различие: поток — это функция, а величина потока — число.
Разрезом сети называется множество, которому принадлежит исток, и не принадлежит сток. Т.е. разрез — это минимальное (в смысле отношения включения) множество дуг, удаление которых “ разрывает” все пути, соединяющие исток и сток.
Пропускной способностью разреза называется число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.
Теорема Форда – Фалкерсона.
В любой транспортной сети величина любого максимального потока равна пропускной способности любого минимального разреза.
Алгоритм Форда – Фалкерсона.
Алгоритм начинает свою работу с нулевого потока и на каждой своей итерации увеличивает поток в сети. На каждом шаге находится увеличивающая величину потока цепь. Поток увеличивается вдоль дуг этой цепи, пока она не станет насыщенной.
- Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.
- В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся.
- Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
- На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью Cmin.
- Для каждого ребра на найденном пути увеличиваем поток на Cmin, а в противоположном ему — уменьшаем на Cmin.
- Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
- Возвращаемся на шаг 2.
Или так
Для определения потока в сети используют алгоритм Форда-Фалкерсона:
а) ищем любую цепь из истока графа в сток;
б) каждой дуге приписываем возможный больший поток из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен);
в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе;
г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток;
д) поток в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).