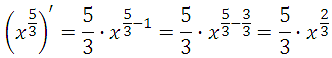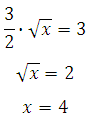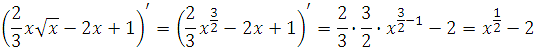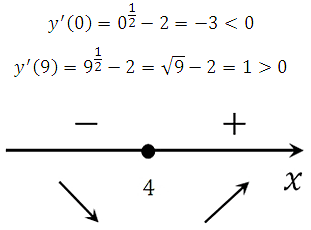Как найти минимум функции с дробями

СДАМ ГИА:

РЕШУ ЕГЭ

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

26 мая

Как за­ра­бо­тать +20–30 бал­лов на ЕГЭ бла­го­да­ря раз­бо­рам ЕГЭ с Даль­не­го Вос­то­ка

24 мая

Обновлённая панель инструментов

22 мая

Беседы Решу ЕГЭ по подготовке к ЕГЭ

11 мая

Решение досрочных ЕГЭ по всем предметам

5 мая

Обновленный поиск заданий по ключевым словам

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Каталог заданий.
Исследование частных

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

© Гущин Д. Д., 2011—2023

Анализ дробно-рациональной функции. Асимптоты, экстремум

Функция      $y=frac{k}{x}$ .     Гипербола.   Свойства.

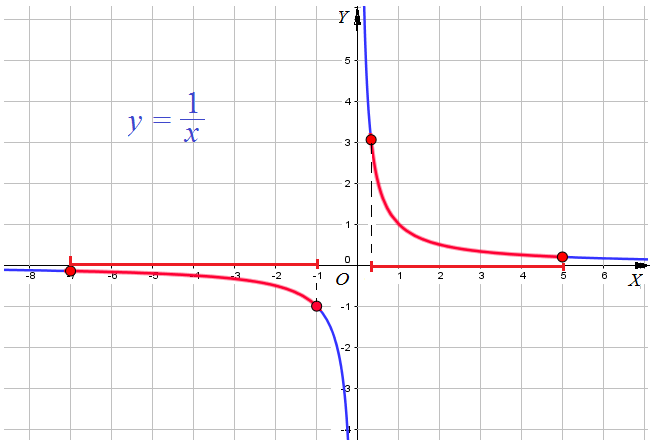
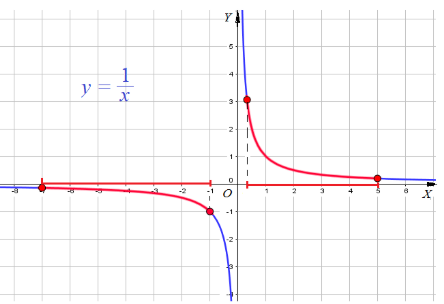
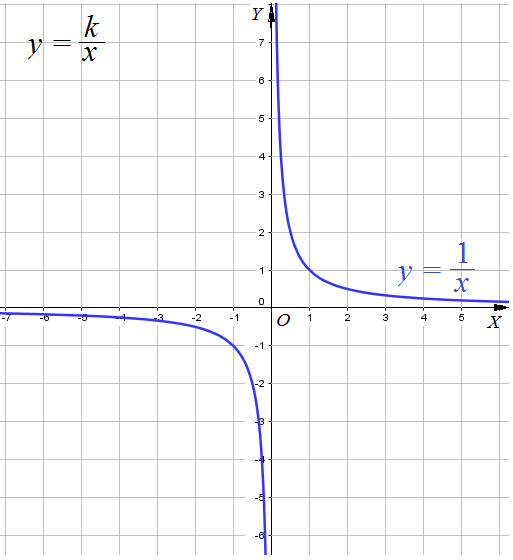
Пример 1:          Построить   график   для   функции    $y=frac{1}{x}$,      $fleft(xright)=frac{1}{x}$

• Вычислим значения функции   в   разнознаковых   точках   и   нанесем точки с вычисленными координатами в системе   $XOY$.
• $fleft(1right)=1$             $fleft(frac{1}{2}right)=2$                 $fleft(-1right)=-1$                $x=-frac{1}{2}$           $fleft(-frac{1}{2}right)=-2$       $fleft(2right)=frac{1}{2}$                   $fleft(frac{1}{4}right)=4$                          $fleft(-frac{1}{4}right)=-4$       $fleft(4right)=frac{1}{4}$                   $fleft(1right)=8$                $fleft(-4right)=-frac{1}{4}$                      $fleft(-frac{1}{8}right)=-8$        .
• Точки Графика $(1;1)$,   $(2;1/2)$,   $(4;1/4)$,   $(1/2;2)$,   $(1/4;4)$,   $(1/8;8)$,    $(-1;-1)$,   $(-2;-1/2)$,   Еще точки:   $(-4;-1/4)$,   $(-1/2;-2)$,     $(-1/4;-4)$,   $(-1/8;-8)$ . По всем   точкам построим   кривые   —   график функции   $y=frac{1}{x}$
• График имеет разрыв по вертикальной линии $x=0$.    Ветви графика прижимаются к горизонтальной линии $y=0$.

Графиком функции       $y=frac{k}{x}$       $kne0$      является   гипербола ,   ветви прижимаются к асимптотическим линиям.

• если коэффициент   $k > 0$ ,    в   I   и    III   координатных четвертях.   Точка   $(0;0)$   —   центр симметрии.
• если   $k < 0$ ,    то   во   II    и   IV   координатных четвертях. Точка   $(0;0)$   —   центр симметрии.
• Асимптоты:         Вертикальная асимптота,   линия   $x=0$,               Горизонтальная   асимптота,    линия    $y=0$               

Cвойства   функции      $y=frac{k}{x}$    при    $k > 0$        ( ветви   гиперболы   расположены   в   первом   и   третьем   координатных   углах) .

Свойство 1:     Область   Определения   Функции — вся   числовая   прямая , кроме    $x=0$.     Свойство 2:     $y > 0$   при   $x > 0$;      $y < 0$   при    $x < 0$.    Свойство 3:     Функция   убывает на    промежутках      $( — ∞ ; 0 )$      и     $( 0 ; + ∞)$       Свойство 4:     Функция   не   ограничена   ни   снизу,   ни   сверху. Свойство 5:     Ни   наименьшего,   ни   наибольшего   значений   $у$    у функций   нет.     Свойство 6:     Функция   непрерывна   на    $( — ∞ ; 0 )$    и    $( 0 ; + ∞)$. Свойство 7:     Область   значений функции   —    $( — ∞ ; 0 )$   U   $( 0 ; + ∞)$.    имеет   разрыв   в   точке     $x=0$.

Cвойства   функции      $y=frac{k}{x}$    при      $k < 0$        (ветви гиперболы расположены   во   втором   и   четвертом   координатных   углах).

Свойство 1:     Область   Определения   Функции   —   вся   числовая   прямая ,    кроме    $x=0$. Свойство 2:     $y > 0$    при    $x < 0$ ;        $y < 0$   при    $x > 0$. Свойство 3:     Функция   возрастает   на   промежутках     $( — ∞ ; 0 )$      и     $( 0 ; + ∞)$ Свойство 4:     Функция   не   ограничена   ни   снизу,   ни   сверху. Свойство 5:     Ни   наименьшего,   ни   наибольшего   значений    $у$    у функций   нет. Свойство 6:     Функция   непрерывна   на   $( — ∞ ; 0 )$ и $( 0 ; + ∞)$ Свойство 7:     Область   значений   функции   —   объединение     $( — ∞ ; 0 )$   U   $( 0 ; + ∞)$ .    имеет   разрыв   в   точке     $x=0$.

Метод Замены для построения Графика Функции.

Мысль: Умеем строить график функции попроще … используем его для построения функции при «сдвинутых» аргументах и значениях.

Как   построить   график   функции    $y=kcdot fleft(xright)$,    если   известен   график   функции     $y=fleft(xright)$.

• График   $y=5cdot fleft(xright)$:     Расстянуть вертикально вверх по оси   $OY$   5 раз все, что над $OX$ графика   $y=fleft(xright)$    ,    $k$ раза.
• График   $y=5cdot fleft(xright)$:     Расстянуть вертикально вниз по оси   $OY$   5 раз все, что под $OX$ графика   $y=fleft(xright)$    ,    $k$ раза.
• График   $y=frac{1}{3}cdot fleft(xright)$: Сжать по вертикали, оси   $OY$   график   $y=fleft(xright)$     3 раза.
• Еще способ: Перемасштабирование.     Для   $y=5cdot fleft(xright)$ … построить    $y=fleft(xright)$, изменить масштаб: «1» станет «5», «-2» станет «-10», и т.д.

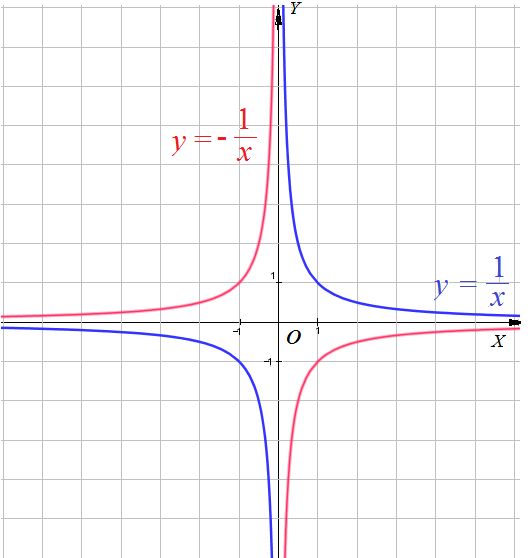
Как   построить   график   функции    $y=-fleft(xright)$,    если   известен   график   функции     $y=fleft(xright)$.

• Эти функции принимают ровно противоположные значения. Значит: график $y=fleft(xright)$   надо отразить по оси $OX$, «перевернуть».

Как   построить   график   функции    $y=fleft(x+lright)$,    если   известен   график   функции     $y=fleft(xright)$.

• Построить график   $y=fleft(x+lright)$,    где     $l > 0$?      Сдвинуть график   $y=fleft(xright)$    вдоль оси   $OX$    на   $l$   единиц масштаба влево.
• Построить график   $y=fleft(x-lright)$,    где     $l < 0$?     Сдвинуть график   $y=fleft(xright)$    вдоль оси   $OX$   на   $l$   единиц масштаба вправо.

Как построить график функции    $y=fleft(xright)+m$,    если известен график функции    $y=fleft(xright)$.

• Построить график   $y=fleft(xright)+m$,   где   $m > 0$?   Сдвинуть график   $y=fleft(xright)$ вдоль оси   $OY$ на   $m$   единиц масштаба вверх;
• Построить график   $y=fleft(xright)-m$,   где   $m > 0$?   Сдвинуть график   $y=fleft(xright)$   вдоль оси   $OY$   на   $m$   единиц масштаба вниз.

Как построить график функции   $y=fleft(x+lright)+m$,   если известен график функции    $y=fleft(xright)$.

• График функции    $y=fleft(x+lright)+m$   можно получить из графика    $y=fleft(xright)$ параллельными   сдвигами по осям    $OX$ и   $OY$.

График Дробной Функции.    

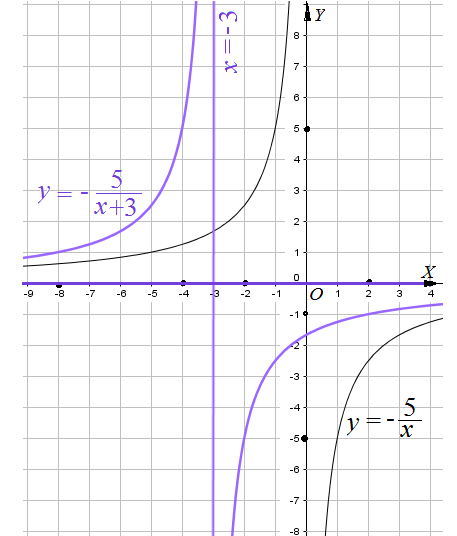
Пример 2:                Построить график функции     $y=-frac{5}{x+3}$ .

• сначала построим график функции       $y=-frac{5}{x}$ … от графика $y=frac{1}{x}$ … отразим от   $OX$ и растянем по вертикали 5 раз.
• сдвинем получившуюся гиперболу вдоль оси   $OX$    на   $3$   единицы влево, получится   требуемый   график.
• это   гипербола   с асимптотами $x=-3$;     $y=0$.     «почему   так?»   —   как   мы   строим графики?
• берем   несколько    $x$ — точек   и   находим   для   каждого   свои   $y$ — значения   в   соответствии «с   формулой функции».
• По точкам   проводим   график. Очевидно,   если, скажем,      $x=0,52$      функция   $y=-frac{5}{x+3}$       дает   какое-то   значение,
• … то,   конечно   для    $x=3,52$     другая   функция,      $y=-frac{5}{x}$    дает   ровно   такое же   значение.
• значит,   точки   графиков   будут различаться на   $3$   единицы    по   $x$ — координате   и совпадать по $y$ — координате.
• Ровно   так   и   для   всех   точек.   «Сравни две функции и вообрази их графики: каковы различия и что общего? «

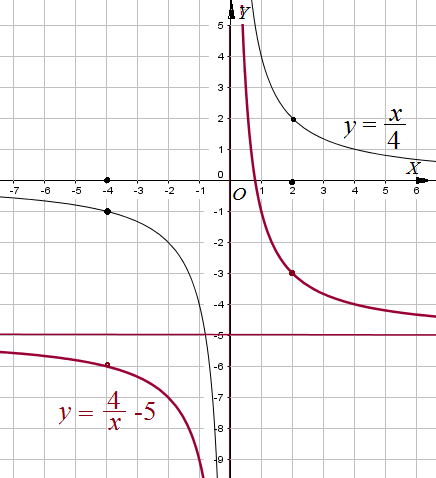
Пример 3:                Построить график функции     $y=frac{4}{x}-5$ .

• Сначала   надо   построить   график   функции       $y=frac{4}{x}$ .   Гиперболу   $y=frac{1}{x}$ «растянем» четыре раза.
• Сдвинуть   получившуюся   гиперболу   вдоль   оси     $OY$    на   $5$ клеточек   вниз.   Т.к. каждое значение должно отличаться на 5 единиц.
• получится   требуемый   график.    Это   гипербола   с   асимптотами     $x=0$;     $y=-5$.
• Важно знать где пересекается с нулем.   Решение, корень      $frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $left(0,8;0right)$.
• Исследование:     Найдем производное: $left(frac{4}{x}-5right)’=-frac{4}{x^2}$. Нигде не = 0, Экстремума нет!
• Производная для всех $x$   (кроме $0$) отрицательна — значит всюду убывает.
• Область Определения:    $D_f=left(-infty;0right)+left(0;+inftyright)$                          Область значений $E_f=left(-infty; -5right)+left(-5;+inftyright)$
• Знакопостоянство:    $+Z_f=left(-infty;0,8right)$ — функция   отрицательна,                $-Z_f=left(0,8;+inftyright)$   — функция   положительна.
• Монотонность:    $+M_f=left(-infty;-3right)+left(-3;0right)$ — возрастает         $-M_f=left(0;3right)+left(3;+inftyright)$   — функция убывает

Вертикальная асимптота ( $x=0$,) проходит в полюсе, точке разрыва функции.   Точка обнуления знаменателя.   Параллельно $OY$.

Горизонтальная асисмптота ( $y=-5$ ), линия, на которую «ложится» график при значениях $х$    около   $+-infty$. Параллельно $OX$.

Гипербола — график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы «зажаты — прижаты» к асимптотическим линиям .

Наклонная асимптота — линия типа $y=2x+3$, к которой    «прижимаются»   ветви графика   «на» или   «около»   + — бесконечнoсти.

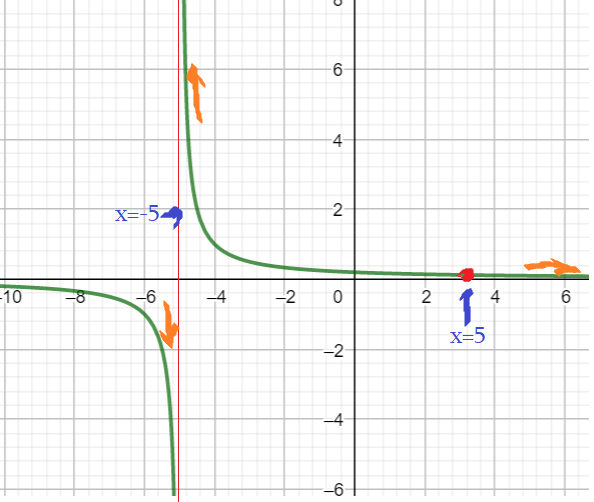
Пример 4:                Построить график функции     $y=frac{x-5}{x^2-25}$

• Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
• Тождественное преобразование, сокращение       $frac{x-5}{x^2-25}=frac{x-5}{(x+5)(x-5)}=frac{1}{x+5}$. Так, что график $y=frac{1}{x+5}$ ?
• Не спеши!   Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З — в исходной функции нет места $x=5$.
• Значит: можем строить гиперболу $y=frac{1}{x+5}$ взамен нашей $y=frac{x-5}{x^2-25}$, но «без точки $x=5$».
• Точка $x=5$ разрывает «гладкий» график гиперболы. Она называется «выколотая точка с координатами $left(5;0,1right)$».

Важно уметь исследовать функцию — график около точек разрыва.        + / — поблизости.    Куда тянется?

• Исследуем около   $x=-5$.        Возьмем «близкие» точки $-5,01$ и   $-4,99$.     Вычислим приближенные значения.
• Чуть левее … $fleft(-5,01right)=frac{-5,01-5}{(-5,01)^2-5^2}approx -100$.         Чуть правее … $fleft(-4,99right)=frac{-4,99-5}{(-4,99)^2-5^2}approx 100$.
• Прямая   $x=-5$ — вертикальная асимптота. Ветвь слева прижимается «вниз», к     $-infty$ . А справа поднимается вверх к     $+infty$.
• Около   $x=5$.    Чуть левее   $fleft(4,99right)=frac{4,99-5}{4,99^2-5^2}approx0,101$.   $fleft(5,01right)=frac{5,01-5}{5,01^2-5^2}approx0,099$.
• Значит, $x=5$ точка разрыва, на графике   выколотая точка    $left(5;0,1right)$.        Т.к. в ней   $y=frac{1}{5+5}=0,1$.
• «О нулях»:   при   $x=0$    $y=0,2$ .   Но функция нигде не обнуляется, $yne0$. Прямая   $y=0$ — горизонтальная асимптота.
• Анализ:    Найдем производное: $left(frac{x-5}{x^2-25}right)’=left(frac{1}{x+5}right)’=-frac{1}{left(x+5right)^2}$
• Производная не равна нулю нигде и всюду отрицательна. Экстремума нет, Всюду убывающая функция.
• Область Определения функции:    $D_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$   .
• Знакопостоянство:    $+Z_f=left(-5;5right)+left(5;+inftyright)$ — функция положительна.                $-Z_f=left(-infty;-5right)$   — функция отрицательна
• Монотонность:    $+M_f=varnothing $ — нет роста.         $-M_f=left(-infty;-5right)+left(-5;5right)+left(5;+inftyright)$   — функция убывает
• Область значений $E_f=left(-infty;0right)+left(0;0,8right)+left(0,8;inftyright)$

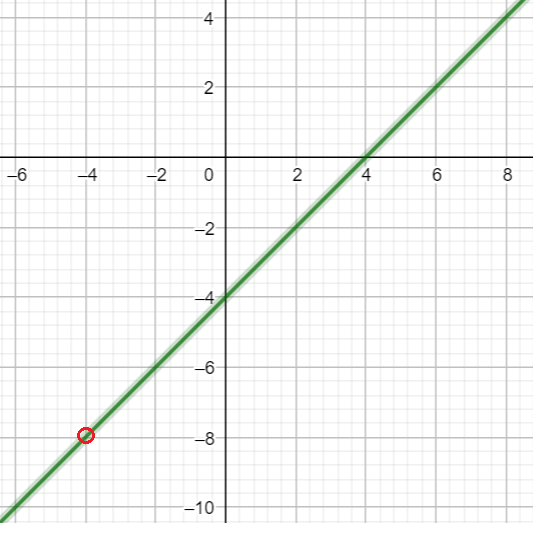
Пример 5:                Построить график функции     $y=frac{x^2-16}{x+4}$

• О.Д.З   функции    $xne-4$. Оговорив это, со спокойной совестью сократим   $y=frac{x^2-16}{x+4}=x-4$.
• График нашей функции     —     прямая линия       $y=x-4$       с выколотой точкой       $left(-4;-8right)$      при   $x=-4$.
• «Близко чуть левее»:    $x=-4,01$   значение      $fleft(-4,01right)=frac{(-4,01)^2-16}{-4,01+4}=-8,01$.         Ближе?    …     Предел    $approx-8$.
• «О нулях».      при   $x=0$    $y=-4$ .    Обнуление функции $y=0$    при    $x=4$ — пересечение с   $x$ — осью.
• Анализ: Найдем производное: $left(frac{x^2-16}{x+4}right)’=left(x-4right)’=1$
• Производное всюду равно 1. Постоянный рост. Кроме разрыва, конечно. Нет точки Экстремума.
• Область Определения:    $D_f=left(-infty;-4right)+left(4;+inftyright)$          Область значений $E_f=left(-infty;-8right)+left(-8;inftyright)$
• Знакопостоянство:    $+Z_f=left(4;+inftyright)$ — функция положительна.                $-Z_f=left(-infty;4right)$   — функция отрицательна
• Монотонность:    $+M_f=left(-infty;-4right)+left(-4;inftyright)$ — возрастает

График Дробно — Рациональной Функции.

Определение:     дробно-рациональной порядка     $left(n;mright)$     называется функция вида      $y=frac{acdot x^n+5x^3-x+c}{bcdot x^m-4x^2-7x+d}$   

Числитель — многочлен степени   $n$     , знаменатель — многочлен степени    $m$ .       Общий вид:   $y=frac{Pleft(xright)}{Qleft(xright)}$

Нули функции — корни числителя $Pleft(xright)=0$ , Асимптоты (полюсы) — корни знаменателя $Qleft(xright)=0$.

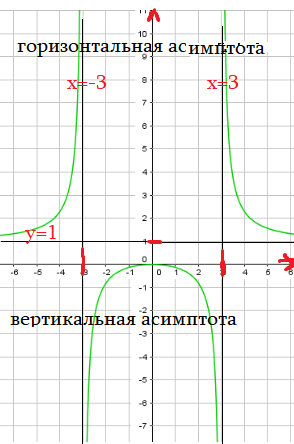
Пример 6:                  Построить график функции        $y=frac{x^2}{x^2-9}$.

• Функция    $fleft(xright)=frac{x^2}{x^2-9}$ — четная:    $fleft(xright)=fleft(xright)$      $fleft(8right)=fleft(-8right)$   — Слева и справа от $OY$ симметрично.
• Вычисления: $fleft(-4right)=frac{left(-4right)^2}{left(-4right)^2-9}=frac{16}{7}approx2,3$           $fleft(-10right)=frac{100}{91}approx 1,1$           $fleft(-5right)=frac{25}{16}approx 1,6$            $fleft(-3,5right)=frac{12.25}{3,25}approx 3,8$
• $fleft(-2right)=fleft(2right)=frac{4}{-5}approx -0,8$          $fleft(-1right)=fleft(1right)approx -0,1$             $fleft(3,5right)approx 3,8$ $fleft(4right)approx 2,3$          $fleft(5right)approx 1,6$          $fleft(10right)approx 1,1$
• Наша функция имеет нули в точке    $x=0$ , а вертикальные асимтоты — линии    $x=-3$   ,      $x=3$
• Асимптота — прямая линия, к которой «прижимается» график функции, «подходя» к ней бесконечно близко.
• Чему равно     $frac{x^2}{x^2-9}$      при очень больших   $x$ ?         $xapproxpm1000$ ? Конечно,    $yapprox1$                горизонтальная асимптота      $y=1$ .
• Анализ графика:      1)       Обнуляется   при   $x=0$ . 2) Значение       в нуле :     $y=frac{x^2}{x^2-9}$     в     $x=0$     равно      $y=0$.
• 3) Поведение в разрывах:    «чуть левее»    полюса      $xapprox-3-0,01$     значение     $y > 0$   — «большое    положительное».
• «чуть правее»    разрыва      $xapprox-3+0,01$     значение   функции    «большое отрицательное».
• Поведение около другого разрыва:   когда    $x$     «чуть левее» ,   например      $xapprox3-0,01$   ,     то        $y < 0$     ;
• когда    $x$      «чуть правее» ,    например       $xapprox3+0,01$     , то        $y > 0$.
• 4) Поведение на бесконечности: при        $xapproxpminfty$         значение    «ложится»    около       $yapprox1$.
• 5) Область определения функции — все точки оси     $x$ ,     кроме        $x=pm3$
• 6) Функция положительна      $y > 0$   на интервалах      $x < -3$    ,       $x > 3$.
• 7) Функция отрицательна      $y < 0$   на интервалах     $-3 < x < 0$     ,       $0 < x < 3$.

Исследование Функции:

• Найдем производное:   $left(frac{x^2}{x^2-9}right)’=frac{2xleft(x^2-9right)-x^2cdot2x}{left(x^2-9right)^2}=frac{-18x}{left(x^2-9right)^2}$
• Производное равно нулю дает точку Экстремума:    $x=0$.   Точка Максимума.
• Производная отрицательна — значит убывает   $x > 0$. Производная положительна, значит возрастает:   $x < 0$
• Область Определения:     $D_f=left(-infty;-3right)+left(-3;3right)+left(3;+infty8right)$   — область определения функции.
• Знакопостоянство:    $+Z_f=left(-infty;-3right)+left(3;+inftyright)$ — функция положительна.                $-Z_f=left(-3;3right)$   — функция отрицательна
• Монотонность:    $+M_f=left(-infty;-3right)+left(-3;0right)$ — возрастает         $-M_f=left(0;3right)+left(3;+inftyright)$   — функция убывает
• Область значений                   $E_f=left(-infty;0right)+left(1;inftyright)$

пробaп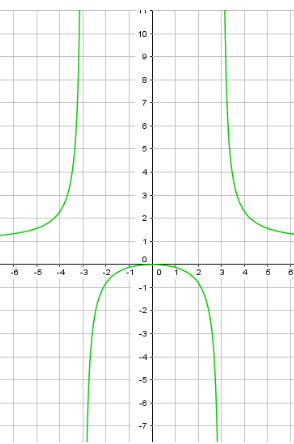                   

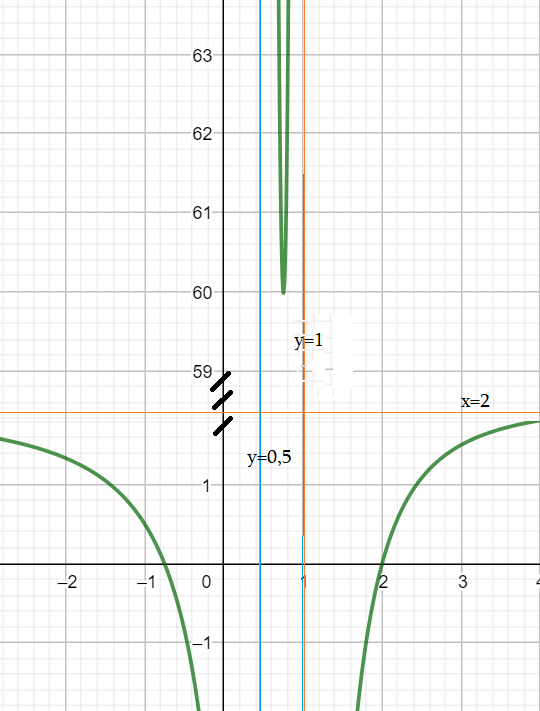
Пример 7:                  Анализ графика функции      $y=frac{4x^2-5x-6}{2x^2-3x+1}$

• нули — точки обнуления числителя         $4x^2-5x-6=0$         $x=2$         $x=-frac{3}{4}$
• Представление:     $frac{4x^2-5x-6}{2x^2-3x+1}=frac{2cdot left(2x^2-3x+1right)+x-8}{2x^2-3x+1}=2+frac{x-8}{2x^2-3x+1}=2+frac{x-8}{left(2x-1right)left(x-1right)}=2+frac{15}{2x-1}-frac{7}{x-1}$
• разрыв (полюс):             $2x^2-3x+1=0$        вертикальные асимптоты   —     $x=1$       и       $x=0,5$.
• при       $xapproxpm infty$      значение   «ложится»   около        $yapprox2$.        $-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}$        $x=0,75$     $x=15,24$
• Производное:        $left(2+frac{15}{2x-1}-frac{7}{x-1}right)’=-frac{30}{left(2x-1right)^2}+frac{7}{left(x-1right)^2}=frac{-2x^2+32x-23}{left(2x-1right)^2cdotleft(x-1right)^2}$
• Или так:   $left(frac{4x^2-5x-6}{2x^2-3x+1}right)’=frac{left(4x^2-5x-6right)’cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(2x^2-3x+1right)’}{left(2x^2-3x+1right)^2}=frac{left(8x-5right)cdotleft(2x^2-3x+1right)-left(4x^2-5x-6right)cdotleft(4x-3right)}{left(2x^2-3x+1right)^2}=frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}$
• Уравнение Экстремумов:          $frac{-2x^2+32x-23}{left(2x^2-3x+1right)^2}=0$.                 $-2x^2+32x-23=0$.                  $x=8pm0,5sqrt{210}$     
• Производная отрицательна на интервалах       $-M_f=left(-infty;0,5right)+left(0,5;8-0,5sqrt{210}right)+left(8+0,5sqrt{210};inftyright)$.    Убывает.
• Производная положительна на интервалах       $+M_f=left(8-0,5sqrt{210};1right)+left(1;8+0,5sqrt{210}right)$.         Возрастает.
• Точка Минимума:    $x=8-0,5sqrt{210}$       $xapprox0,75$ .                             Точка Максимума:        $x=8+0,5sqrt{210}$    $xapprox15,25$
• Область Определения:    $D_f=left(-infty;0,5right)+left(0,5;1right)+left(1;+inftyright)$   .
• Знакопостоянство:    $+Z_f=left(-infty;-0,75right)+left(0,5;1right)+left(2;+inftyright)$ — положительна.                $-Z_f=left(-0,75;0right)+left(1;2right)$   — отрицательна.
• Область значений (приближенно!)               $E_fapproxleft(-infty;2,001right)+left(60;inftyright)$

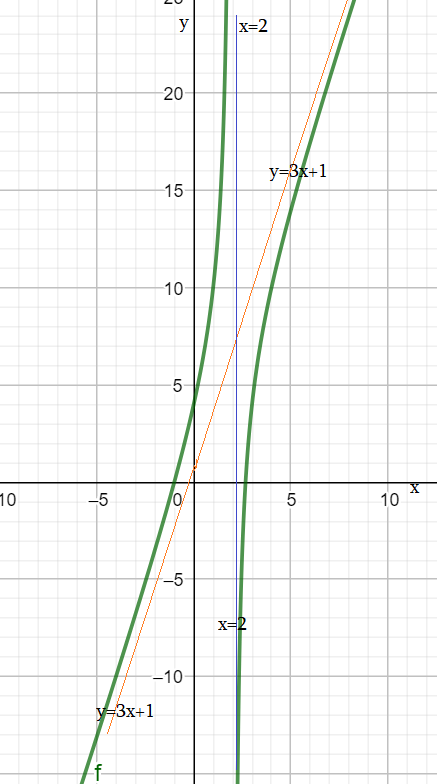
Пример 8:                  Анализ графика функции      $y=frac{3x^2-5x-8}{x-2}$

• нули — точки обнуления числителя         $3x^2-5x+8=0$         $x=-1$         $x=frac{8}{3}approx2,7$
• разрыв (полюс):             $x-2=0$        вертикальные асимптоты   —     $x=2$   .
• «чуть левее»:    $fleft(2-10^{-7}right)=frac{3cdotleft(2-10^{-7}right)^2-5left(2-10^{-7}right)-8}{2-10^{-7}-2}=frac{3cdot4-5cdot2-8-12cdot10^{-7}+5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{-10^{-7}}approx6cdot10^7$       Значит, уходит к $+infty$
• Чуть правее:    $fleft(2+10^{-7}right)=frac{3cdotleft(2+10^{-7}right)^2-5left(2+10^{-7}right)-8}{2+10^{-7}-2}=frac{3cdot4-5cdot2-8+12cdot10^{-7}-5cdot10^{-7}+3cdotleft(10^{-7}right)^2}{10^{-7}}approx-6cdot10^7$    …. бежит к   $-infty$
• Представим нашу функцию по-другому :       $frac{3x^2-5x-8}{x-2}=frac{3x^2-6x+x-2-6}{x-2}=3x+1-frac{6}{x-2}$
• Видно, что при больших   $x=2$     она     «почти совпадает» с линейной функцией   $3x+1$. «прижимается к ней».
• $y=3x+1$ — наклонная асимптота нашей функции.
• Найдем производное: $left(frac{3x^2-5x-8}{x-2}right)’=frac{left(6x-5right)left(x-2right)-1cdotleft(3x^2-5x-8right)}{(x-2)^2}=frac{3x^2-12x+18}{(x-2)^2}=frac{3left(x^2-4x+6right)}{(x-2)^2}$
• Производное нигде не равно нулю, нет Экстремума:    Производное   всюду положительно, значит, возрастает.
• Область Определения:    $D_f=left(-infty;2right)+left(2;+inftyright)$ .       Полюс в     $x=2$ .
• Знакопостоянство:     $+Z_f=left(-1;2right)+left(frac{8}{3};+inftyright)$ — функция положительна.                $-Z_f=left(-infty;-1right)+left(-1;frac{8}{3}right)$   — функция отрицательна
• Монотонность:                   $+M_f=left(-infty;2right)+left(2;inftyright)$    —   всюду возрастает
• Область значений                        $E_f=left(-infty;+inftyright)$

Графический способ решения уравнений

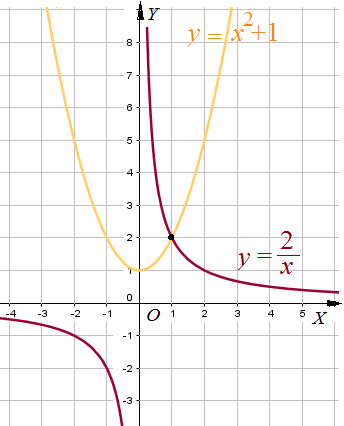
Пример 9:                Решить уравнение         $frac{2}{x}=x^2+1$       графическим   способом.

• Построим   гиперболу      $y=frac{2}{x}$      и   параболу      $y=x^2+1$ . Равенство означает пересечение.
• Левая функция   и   правая   функция приобретают   одинаковые значения    …    графики   этих   функций пересекаются.
• По чертежу   видно,   что   графики   пересекаются   в   точке    с   координатами    $left(1;2right)$.     ответ:      $x=1$.

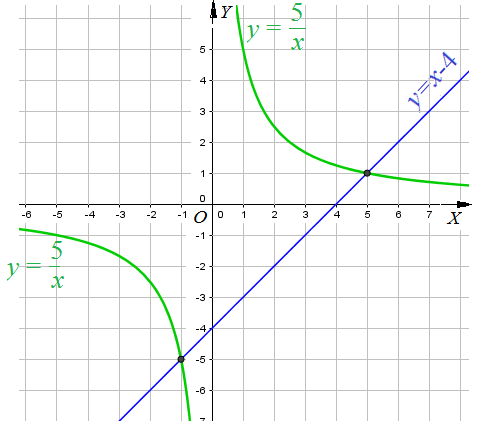
Пример 10:                Решить уравнение                            $frac{5}{x}=x-4$.

• Построим   их   графики:   гиперболу    $y=frac{5}{x}$    и   прямую   $y=x-4$.    пересекаются ?
• Гипербола   и   прямая   пересекаются    в   точках   $(-1;-5)$    и    $(5;1)$.    ответ:       $x_1=-1$;      $x_2=5$.

Пример 11:                  Найти наименьшее и наибольшее значения функции    $y=frac{1}{x}$     на отрезках   а)    $left[frac{1}{3};5right]$      и    б)   $left[-7;-1right]$.

• Построим график функции   $y=frac{1}{x}$ .
• Выделим   часть   графика,    соответствующую   значениям   переменной   $x$    на отрезке    $left[frac{1}{3};5right]$.
• Для   выделенной   части графика   находим:   наименьшее   значение   $y=frac{1}{5}$     при     $x=5$ ,     наибольшее      $y=3$    при     $x=frac{1}{3}$.
• Выделим   часть   графика,   соответствующую   значениям   переменной    $x$   на   отрезке    $left[-7;-1right]$.
• Для   выделенной части   графика   находим:   наименьшее   значение   $y=-frac{1}{7}$ при $x=-7$ наибольшее   $y=-1$    при    $x=-1$.     

Упражнения