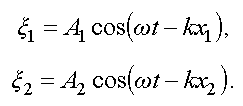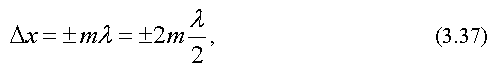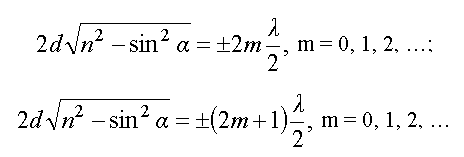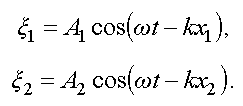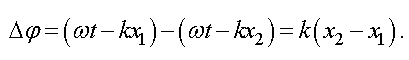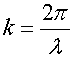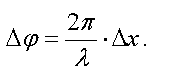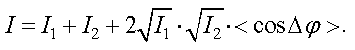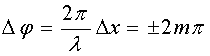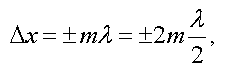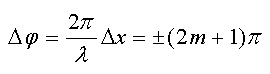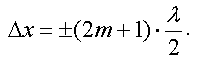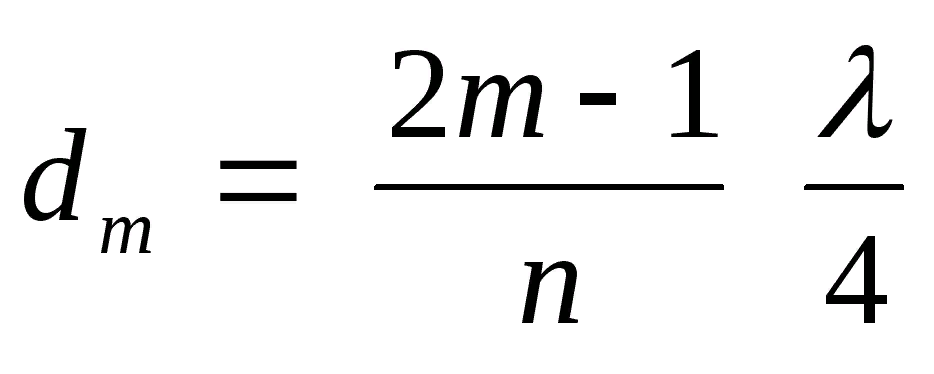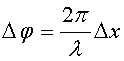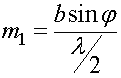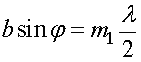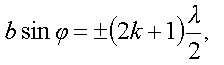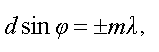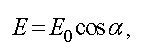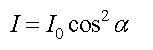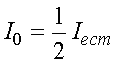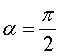Найдем
условия максимума и минимума интенсивности
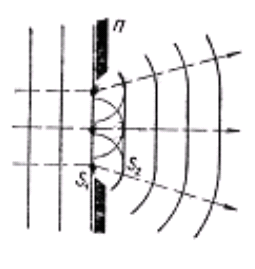
при интерференции. Пусть S1
и S2
— два когерентных источника, совершающих
колебания в одинаковой фазе. До точки
наблюдения М
волны проходят разное расстояние (рис.
3.8).
Рис.3.8
Запишем
для них уравнения волн (3.24)
Найдем разность
фаз складываемых волн
Обозначим
через Δx
— разность хода, т. е.
.
По формуле (3.22)
волновое число равно
,
тогда связь между разностью хода и
разностью фаз дается уравнением
Амплитуда
результирующего колебания в точке
наблюдения определяется уравнением
(3.16)
.
Так
как интенсивность пропорциональна
среднему значению квадрата амплитуды
(см. (3.34)):
,
то получим выражение для результирующей
интенсивности
Если
источники некогерентные, то
и
,
т. е. интерференция не наблюдается. Для
когерентных источников разность фаз
и
среднее значение косинуса равно косинусу
разности фаз
.
В
тех точках пространства, где
интенсивность
,
а там, где
интенсивность
.
Следовательно, при наложении двух
когерентных световых волн происходит
пространственное перераспределение
световой энергии, в результате чего в
одних местах возникают максимумы, а в
других — минимумы интенсивности, т. е.
появляется интерференционная картина.
Максимумы
интенсивности появляются там, где
,
т. е. при
,
где m
= 0, 1, 2, …
Следовательно,
.
Отсюда получим условие
максимума
интенсивности при интерференции
где
m
— порядок интерференционного максимума.
Условие максимума
интенсивности при интерференции читается
следующим образом.
Если разность хода равна целому числу длин волн или четному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.
Аналогично
найдем условие минимума. Если
,
то
,
где m
= 0, 1, 2, …
Тогда
и
Условие
минимума
интенсивности при интерференции читается
следующим образом.
Если разность хода равна нечетному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.
8, Интерференция в тонких пленках
Интерференцию в
тонких пленках часто можно наблюдать
в виде радужной окраски масляных пленок
на воде, на мыльных пузырях и т. д.
Рассмотрим,
как происходит интерференция в тонких
пленках. Пленка называется тонкой, если
ее размеры соизмеримы с длиной волны
λ.
Пусть на тонкую пленку толщиной d
падает параллельный пучок лучей
монохроматического света (рис. 3.10).
Рис.3.10
На верхней границе
раздела двух сред свет частично
отражается, частично преломляется. Тоже
происходит на нижней грани пленки.
Таким
образом, световой луч испытывает
многократное отражение и преломление.
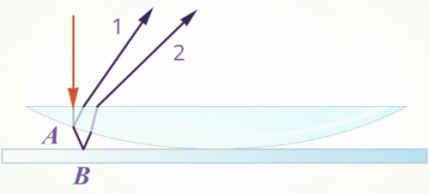
Отраженные лучи 1 и 2, а также преломленные
лучи 1/
и 2/,
когерентны между собой. Остальные лучи
не рассматриваются из-за малой
интенсивности.
Оптическую разность
хода находят из геометрических
представлений и законов геометрической
оптики.
Оптическая
разность хода лучей 1 и 2 в отраженном
свете, так же как и лучей 1/
и 2/
в проходящем свете, равна
,
где
i
— угол падения луча.
Кроме
оптической разности хода надо учесть
изменение фазы волны при отражении.
Теория и опыт показывают, что если свет
отражается от оптически более плотной
среды, фаза волны меняется на
противоположную, а если свет отражается
от оптически менее плотной среды, фаза
волны не меняется. Разность хода и
разность фаз связаны соотношением
(3.35)
.
Поэтому,
если фаза меняется на противоположную,
т. е.
,
то
.
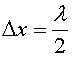
Следовательно, изменение
фазы на противоположную равносильно
изменению разности хода на половину
волны.
В
нашем случае (рис. 3.10) изменение фазы на
противоположную происходит при отражении
в точке А.
Условия
максимума и минимума интенсивности в
отраженном
свете
запишутся следующим образом.
Запишем
условие максимума и минимума интенсивности
в проходящем
свете
Эти формулы
используются при решении задач.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
Для всех волн характерны явления интерференции и дифракции. Если свет — это волна, то для него также должны быть присущи эти явления. Так рассуждали ученые, которые считали, что свет имеет волновую природу. Первым привел экспериментальные доказательства интерференции и дифракции света Томас Юнг в 1801 году.
Это интересно! Явление интерференции света было описано и объяснено в 1801 году, но само понятие «интерференция света» было введено немного позже — в 1803 году.
Интерференция механических волн
Чтобы лучше понять явление интерференции, сначала объясним его на примере механических волн, за которыми удобней наблюдать. Часто случается, что в среде одновременно распространяется несколько различных волн. К примеру, когда в комнате может одновременно находиться несколько источников звука. Что же происходит, когда волны пересекают друг друга? Объясним это на примере волн, образуемых на поверхности воды.
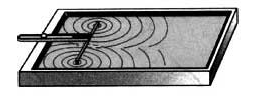
Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, мы увидим, что каждая волна проходит сквозь другую. Причем она ведет себя так, как будто другой волны не существовало. Точно так же любое количество звуковых волн может одновременно распространяться в воздухе. И они не будут друг другу мешать. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые улавливаются нами одновременно. При этом звуки не сливаются в шум: наши органы слуха способны легко отличить один звук от другого.
Теперь рассмотрим более подробно процесс, когда волны накладываются одна на другую. Для этого будем наблюдать волны на поверхности воды от двух брошенных в воду камней. При этом мы заметим, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если два гребня двух волн встречаются в одном месте, то в этом месте возмущение поверхности воды становится более сильным. Если же гребень одной волны встречается с впадиной другой, то поверхность воды в этом месте остается спокойной. Получается, что в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция — сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды.
Чтобы выяснить, при каких условиях наблюдается интерференция волн, одновременно возбудим две круговые волны в ванночке с помощью двух шариков, прикрепленных к стержням, колеблющимся по гармоническому закону.
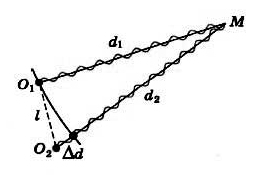
Теперь представим явление интерференции схематически. В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами от источников O1 и O2 (см. рисунок ниже). Амплитуды колебаний, вызванных в точке М обеими волнами, будут различаться, если волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей, то обе амплитуды можно считать приближенно одинаковыми.
Результат сложения волн, приходящих в точку М зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода, определяемую формулой:
Δd = d2 − d1
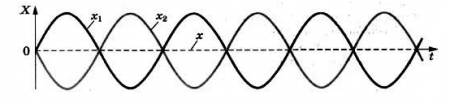
Когда разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период. Так как за период волна проходит путь, равный ее длине волны, то в точке встречи двух волн фазы совпадают. Если в этой точке волны имеют гребни, то совпадают гребни, если впадины — совпадают впадины.
Условие минимумов и максимумов
Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.
Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.
Δd=(2k+1)λ2
k = 0, 1, 2, … .
Если разность хода волн равна целому числу волн, то в точке наложения этих волн образуется интерференционный максимум. Амплитуда колебаний в данной точке максимальна.
Δd=kλ
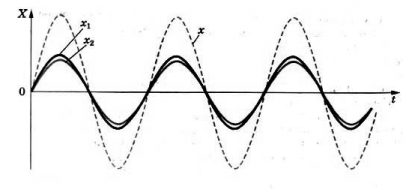
Если разность хода ∆d принимает промежуточное значение между λ и λ/2, амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важной примечательностью является то, что амплитуда колебаний в любой точке с течением времени не меняется. Поэтому на поверхности воды возникает определенное, постоянное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.
Для формирования устойчивой интерференционной картины важно, чтобы источники волн имели одинаковую частоту, и разность фаз их колебаний не менялась с течением времени. Такие источники волн называют когерентными.
Когерентные волны — это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Только когерентные волны при сложении формируют устойчивую интерференционную картину. Если же источники волн некогерентные, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет с течением времени изменяться. Поэтому амплитуда результирующих колебаний также будет непрерывно изменяться. В результате максимумы и минимумы в пространстве будут иметь неопределенное положение. Поэтому интерференционная картина получается размытой.
Распределение энергии при интерференции
Любая волна переносит энергию без переноса вещества. Но что же с этой энергией происходит при интерференции волн? Если волны встречаются друг с другом, энергия никуда не исчезает и не превращается в другие формы энергии. Она лишь перераспределяется таким образом, что в минимумах он не поступает совсем, поскольку концентрируется в максимумах.
Интерференция света
Ели свет — это поток волн, то должно наблюдаться явление интерференции. Однако получить интерференционную картину, при которой чередуются минимумы и максимумы с помощью двух независимых источников света (к примеру, двух ламп), невозможно. Включение второй лампы лишь увеличивает освещенность поверхности, но не создает картины из минимумов и максимумов. Это объясняется несогласованностью волн друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные, то есть когерентные световые волны. Они должны иметь одинаковые длины волн и постоянную во времени разность фаз в любой точке пространства.
Однако наблюдать интерференцию света все же можно. Вы ее наблюдали, когда пускали мыльные пузыри или рассматривали пленку нефти на поверхности воды.
Томас Юнг — первый из ученых, который предложил объяснить изменение цветов тонких пленок сложением волн. Согласно его предположению, одна волна отражается от наружной поверхности плёнки, а другая — от внутренней. При этом возникает явление, называемой интерференцией световых волн.
Усиление света происходит в том случае, если преломлённая волна запаздывает по сравнению с отражённой волной на целое число длин волн. Здесь действует условие максимумов, о котором мы говорили выше:
Δd=kλ
Если вторая волна запаздывает по сравнению с первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света. Здесь действует условие минимумов, о котором мы также уже говорили:
Δd=(2k+1)λ2
Четкая интерференционная картина получается потому, что волны, отраженные от внутренней и внешней оболочки тонкой пленки, являются когерентными. Когерентность этих волн объясняется тем, что они являются частями одного и того же светового луча.
Юнг сделал вывод, что многообразие цветов на мыльной пленке связано с разницей в длине волны. Если плёнка имеет неоднородную толщину, то при освещении её белым светом появляются различные цвета.
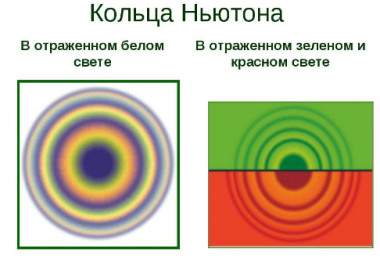
Простую интерференционную картину также можно получить, если положить на стеклянную поверхность плоско-выпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Интерференционная картина, полученная таким способом, носит название колец Ньютона.
Исаак Ньютон исследовал интерференционную картину, получаемую в тонкой прослойке воздуха между стеклом и линзой, не только в белом свете, но и при освещении линзы монохроматическими лучами. Так он установил, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному. Так, красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшаются с увеличением их радиусов.
Ньютону удалось получить кольца, но их появление он объяснить не смог. Но это удалось сделать Юнгу. Проведенный им опыт показал, что волна определённой длины падает на плосковыпуклую линзу почти перпендикулярно. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе сред стекло-воздух, а волна 2 — в результате отражения от пластины на границе сред воздуха- стекло.
Если вторая волна запаздывает по сравнению с первой на целое число длин волн, то при сложении волны усиливают друг друга. Если вторая волна запаздывает по сравнению с первой на нечётное число полуволн, то колебания в точке сложения будут совпадать в противоположных фазах. При этом волны погасят друг друга.
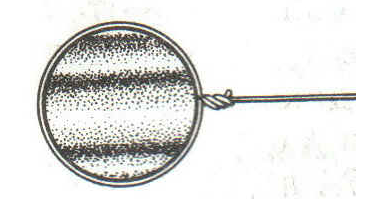
В результате проделанного эксперимента Юнг смог получить картину, которая состоит из чередующихся параллельных полос (темных и светлых)
Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующегося максимумом и минимумом интенсивности.
Это интересно! Измеряя радиусы колец Ньютона, можно вычислить длины волн. В ходе измерений было установлено, что для красного света λкр = 8∙10–7 м, а для фиолетового — λa = 4∙ 10–7 м.
Пример №1. Будет ли наблюдаться интерференционная картина при освещении мыльной пленки монохроматическим светом? Какой она будет?
Поскольку источник света один и тот же, то отраженные от обеих поверхностей мыльной пленки волны будут когерентными. Поэтому интерференционная картина наблюдаться будет. Она примет вид чередующихся цветных и темных полос. Цвет полос определяется цветом световой волны, который зависит от ее длины волны.
Задание EF17533
На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет
Ответ:
а) только зелёной
б) находиться ближе к красной области спектра
в) находиться ближе к синей области спектра
г) только полностью чёрной
Алгоритм решения
1.Описать наблюдаемое явление.
2.Записать условие наблюдения интерференционного максимума.
3.Выполнить решение в общем виде.
4.Установить, в какой цвет будет окрашена пленка.
Решение
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от передней и задней поверхностей плёнки. Условием интерференционного максимума для излучения с длиной волны λ является:
kλ=2dn+Δ
Δ — либо 0, либо λ2 (это зависит от соотношения показателей преломления на границе двуз сред). Тогда при малом изменении значения показателя преломления в меньшую сторону и сохранении порядка k (как в нашем случае и есть), длина волны света будет уменьшаться. Это значит, что из зеленой части спектра она сдвинется в синюю часть.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
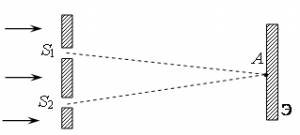
Задание EF17707
На две щели в экране слева падает плоская монохроматическая световая волна перпендикулярно экрану. Длина световой волны λ. Свет от щелей S1 и S2, которые можно считать когерентными синфазными источниками, достигает экрана Э. На нём наблюдается интерференционная картина. Тёмная полоса в точке А наблюдается, если
Ответ:
а) S2А – S1А = 2k⋅λ/2, где k– любое целое число
б) S2А – S1А = (2k + 1) ⋅λ/2, где k– любое целое число
в) S2А – S1А = λ/3k, где k– любое целое число
г) S2А – S1А = λ/(2k+1), где k– любое целое число
Алгоритм решения
1.Записать условие наблюдения интерференционного минимума.
2.Выбрать выражение, удовлетворяющее этому условию.
Решение
В точке А будет наблюдаться темное пятно, если волны, достигающие этой точки, будут гасить друг друга. Это возможно при соблюдении условия минимума:
Δd=(2k+1)λ2
Разность хода в данном случае равна:
Δd=S2A−S1A
Следовательно:
S2A−S1A=(2k+1)λ2
где k — целое число.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17972
Точечные источники света S1 и S2 находятся близко друг от друга и создают на удалённом экране Э устойчивую интерференционную картину (см. рисунок). Это возможно, если S1 и S2 – малые отверстия в непрозрачном экране, освещённые
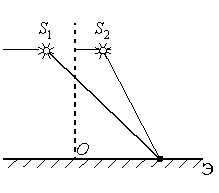
Ответ:
а) каждое своей лампочкой накаливания
б) каждое своей горящей свечой
в) одно зелёным лазером, другое красным
г) светом одной лампочки накаливания
Алгоритм решения
- Записать условие наблюдения интерференционной картины.
- Проанализировать источники и выбрать подходящий под условие.
Решение
Четкая интерференционная картина наблюдается только при освещении щелей когерентными лучами света, имеющими постоянную разность фаз. Когерентные — значит волнами одной частоты. Поэтому лазер зеленый и красный сразу не подходят — они имеют разные частоты.
Одна и та же частота и постоянная разность фаз будет только при условии, что щели освещаются одним источником света. В данном случае — одной и той же лампой накаливания.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.7k
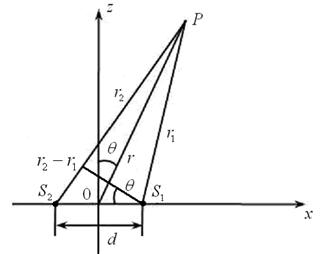
Рис.5.1
Согласно принципу суперпозиции волновое поле в точке наблюдения P имеет вид
(5.6)
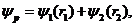
где
(5.7)
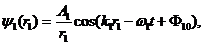
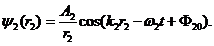
Приёмник измеряет интенсивность, пропорциональную средней величине квадрата полного волнового поля (5.6)
(5.8)
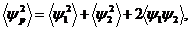
где время усреднения считается много больше периодов колебаний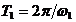 
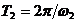
и 
. Нас интересуют условия, при которых наблюдается стационарная картина интерференции с максимальной видностью (контрастностью).
Рассмотрим частный случай, когда выполнены следующие условия:
1. ω1=ω2=ω, k1=k2=k=2π/λ; (5.9а)
2. A1=A2=A – источники одинаковой мощности, что обеспечивает максимальную видность интерференционной картины; (5.9б)
3. 
, что позволяет упростить выражение (5.8), где в знаменателе формул (5.7) можно положить 
; (5.9в)
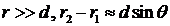
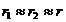
4. 
– не зависит от времени, что соответствует стабильным источникам. (5.9.г)
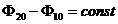
Выполняя в (5.8) усреднение по времени с учётом условий (5.9), можно получить следующее выражение
, (5.10)
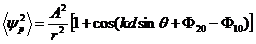
которому соответствует интенсивность
. (5.11)
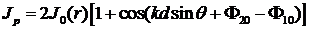
Здесь
(5.12)
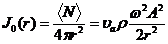
— интенсивность излучения одного источника в точке P и ‹N› — средняя мощность одного источника.
Для понимания пространственной структуры интерференционной картины необходимо найти экстремумы интенсивности 
.Главные максимумы интенсивности, определяющие главные «лепестки» диаграммы направленности, описываются формулами:
(5.13)
. (5.14)
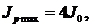
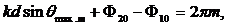
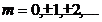
Здесь θmax.m — углы, в которых наблюдается максимальная интенсивность суммарного излучения.
Главные минимумы интенсивности направленности описываются формулами:
, (5.15)
. (5.16)
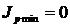
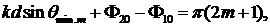
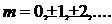
Два ближайших главных минимума по обе стороны от главного максимума определяют его угловую ширину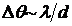 
.
В уравнениях (5.14) и (5.16) необходимо учитывать только те значения m, для которых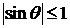 
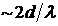
, поэтому число главных максимумов и минимумов всегда конечно. Для синфазных источников, когда Ф10= Ф20 ,максимальная разность фаз интерферирующих волн равна kd, поэтому полное число главных максимумов или минимумов 
и растет с увеличением этого отношения.
При определённых значениях 
и разности начальных фаз Ф20-Ф10 возможны так называемые побочные максимумы и минимумы, где интенсивность 0<Jp<4J. Положения всех главных и побочных экстремумов находятся с помощью уравнения
(5.17)
которое с учетом выражения (5.11) принимает вид
. (5.18)
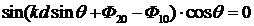
Уравнение (5.18) распадается на два независимых уравнения
, (5.19)
. (5.20)
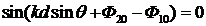
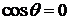
Здесь уравнение (5.19) определяет положения главных экстремумов интенсивности, описанных выше, а уравнение (5.20) – положения возможных побочных экстремумов.
Рассмотренная выше диаграмма двух источников направленности зависит от двух параметров и Ф20-Ф10, варьируя которые можно управлять числом и направлением главных максимумов. В современных излучателях радиоволн используются двумерные системы когерентных источников, распределённых в определённом порядке на поверхности большой площади. Такие системы могут излучать в очень малом телесном угле в заданном направлении, что достигается путём управления начальными фазами волн, излучаемых отдельными источниками системы.
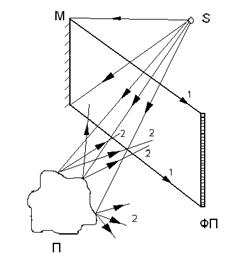
Интерференционную картину волновых полей, т. е. пространственное распределение интенсивности, зависящее от разности фаз этих полей, можно зафиксировать на материальном носителе. Так, с помощью специальной химической обработки фоточувствительного материала пространственное распределение интенсивности световой интерференционной картины преобразуется в подобное пространственное распределение показателя преломления этого материала. Зарегистрированная на фотопластинке интерференционная картина называется голограммой. Принципиальное отличие голограммы от фотографии заключается в том, что она содержит информацию о разности фаз интерферирующих волн. В случае фотографии фотопленка регистрирует пространственное распределение интенсивности света, отраженного от поверхности предметов.
Физические основы голографии были заложены Д. Габором в 1948г., который за открытие и развитие метода голографии в 1971г. получил Нобелевскую премию по физике. Голография – способ записи и восстановления волнового поля, основанный на регистрации интерференционной картины, которая образована предметной и опорной волнами. Предметной волной называется волна источника, отражённая от поверхности предмета. Опорной волной называется волна того же источника, идущая на фотопластинку непосредственно от источника. Предметная и опорная волны формируются одним источником, поэтому они являются когерентными и образуют в фотопластинке интерференционную картину.
Схема получения такой интерференционной картины показана на рис.5.2.
Явление интерференции света
Волны, как и колебания, могут складываться. Сложение волн может быть интерференционным и неинтерференционным. Интерференцией называется сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны, не изменяющееся с течением времени. Интерференция наблюдается только от когерентных источников. Когерентность — значит согласованность. Когерентными источниками называются такие источники, которые дают волны одинаковой частоты, и для фиксированной точки пространства разность фаз колебаний остается постоянной.
Независимые источники света не могут быть когерентными, так как в каждом из них свет испускается множеством атомов, излучающих несогласованно. Разность фаз колебаний, испускаемых совокупностью атомов таких источников, быстро и беспорядочно меняется во времени. Когерентность можно обеспечить, разделив волну от одного источника на две части и затем сведя их вместе. Две части одной волны когерентны между собой и при наложении будут интерферировать.
Существуют различные методы получения когерентных световых источников. Самый простой из них — метод Юнга, в котором световая волна делится на две части с помощью экрана с двумя узкими параллельными щелями.
Условия максимума и минимума интенсивности
при интерференции
Найдем условия максимума и минимума интенсивности при интерференции. Пусть S1 и S2 — два когерентных источника, совершающих колебания в одинаковой фазе. До точки наблюдения М волны проходят разное расстояние.
Запишем для них уравнения волн
Найдем разность фаз складываемых волн
Обозначим через Δx — разность хода. Волновое число равно
тогда связь между разностью хода и разностью фаз дается уравнением
Амплитуда результирующего колебания в точке наблюдения определяется уравнением
Так как интенсивность пропорциональна среднему значению квадрата амплитуды, то получим выражение для результирующей интенсивности
Если источники некогерентные, то
, т. е. интерференция не наблюдается. Для когерентных источников разность фаз и среднее значение косинуса равно косинусу разности фаз
При наложении двух когерентных световых волн происходит пространственное перераспределение световой энергии, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности, т. е. появляется интерференционная картина.
Максимумы интенсивности появляются там, где
т. е. при
где m = 0, 1, 2, … Следовательно,
Отсюда получим условие максимума интенсивности при интерференции
где m — порядок интерференционного максимума.
Условие максимума интенсивности при интерференции читается следующим образом.
Если разность хода равна целому числу длин волн или четному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.
Аналогично найдем условие минимума. Если
, то
, где m = 0, 1, 2, …
Тогда
и
Условие минимума интенсивности при интерференции читается следующим образом.
Если разность хода равна нечетному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.
Кольца Ньютона
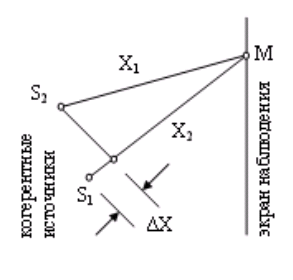
Установка для наблюдения колец Ньютона состоит из плоско-параллельной пластины и плосковыпуклой линзы большого радиуса кривизны. Свет на установку падает вертикально.
Тонкая пленка образуется между линзой и пластинкой. Это воздушная пленка или жидкая. Пленка имеет вид клина. Поэтому возникают полосы равной толщины. Из-за симметрии они имеют вид окружностей.
Рассмотрим ход одного из лучей. Поскольку угол клина мал, можно считать, что угол падения везде ноль. Когерентными являются лучи, отразившиеся в точках 1 и 2. В точке 1 они накладываются. Найдем радиус m-ого кольца rm.
Оптическая разность хода между лучами 1 и 2 равна:
В нашем случае α = 0, поэтому
Предположим, что кольцо темное, тогда
Отсюда выражаем толщину клина в точке m кольца dm:
Из рис. следует, что
Пренебрегая членом dm2, получаем:
Приравнивая оба выражения для dm, получаем:
Отсюда выражаем радиус m-ого темного кольца:
Для воздушной пленки (n = 1), это выражение принимает вид:
Найдем радиусы светлых колец. Оптическая разность хода в этом случае равна
Отсюда
Приравнивая с предыдущим выражением dm, получим:
Радиусы колец зависят от длины волны λ, поэтому, если свет немонохроматический, то кольца будут окрашены.
Явление дифракции. Принцип Гюйгенса — Френеля
Дифракцией называется огибание волнами препятствий. Дифракция наблюдается для волн различной природы (звуковых, световых, волн на воде и т. д.) Явление дифракции проявляется сильнее, если размеры препятствий соизмеримы с длиной волны.
Объяснить дифракционные явления можно с помощью принципа Гюйгенса — Френеля, согласно которому каждая точка фронта волны является источником вторичных волн, которые когерентны. Амплитуда и фаза волны в любой точке пространства — есть результат интерференции волн, излучаемых вторичными источниками.
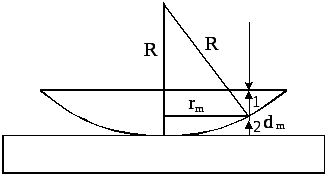
На рис. изображено препятствие П в форме щели шириной b, размеры которого соизмеримы с длиной волны λ. На щель падает плоская монохроматическая волна. Любая точка фронта волны S1 становится источником вторичных волн, которые являются сферическими и огибающая которых S2 дает положение фронта волны в следующий момент времени.
Проходя через щель, волны отклоняются от прямолинейного распространения (дифрагируют). Если на их пути поставить экран, то на нем будет наблюдаться дифракционная картина, причем интенсивность в любой точке экрана наблюдения будет определяться результатом интерференции вторичных волн, пришедших в точку наблюдения.
Зоны Френеля. Дифракция света на одной щели
Объяснить и рассчитать распределение интенсивности света в дифракционной картине можно, применив вспомогательный прием — метод зон Френеля. Зоны Френеля — это участки волновой поверхности, построенные таким образом, что расстояние от краев соседних зон до точки наблюдения различается на половину волны (на λ/2 ). Известно, что разность хода и разность фаз связаны соотношением
Следовательно, если Δx = λ/2 , то Δ φ = π, т. е. колебания, создаваемые соседними зонами Френеля находятся в противофазе и попарно гасят друг друга. Тогда, если отверстие щели открывает четное число зон Френеля, то в точке наблюдения находится минимум интенсивности, а, если нечетное, то — максимум.
Применим метод зон Френеля к рассмотрению дифракции света на одной щели.
Пусть на щель шириной b нормально падает плоская монохроматическая волна. Все точки волновой поверхности, открытые щелью, являются источниками вторичных волн, которые когерентны и распространяются по всем направлениям. Поставим между щелью и экраном наблюдения линзу, которая собирает параллельные лучи в одну точку. Дифракция в параллельных лучах называется дифракцией Фраунгофера. В результате интерференции вторичных волн на экране получится дифракционная картина. Распределение интенсивности вдоль экрана изображено в нижней части (кривая с максимумами и минимумами).
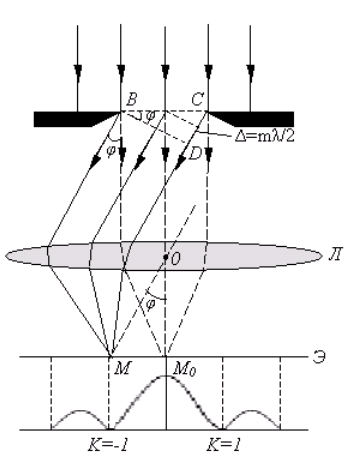
В центре дифракционной картины будет светлая полоса — центральный максимум, так как при φ = 0 все волны придут на экран в точку М0 в одинаковой фазе и усилят друг друга. Чтобы определить результат интерференции вторичных волн при φ ≠ 0, разобьем открытый участок волновой поверхности на ряд зон Френеля. В данном случае они будут представлять собой узкие полоски, параллельные краям щели. Чтобы найти число зон Френеля m1, нужно разность хода крайних лучей Δ = b sin φ поделить на λ/2
, тогда
При четном числе зон Френеля m1= 2k будет наблюдаться минимум интенсивности, при нечетном m1= 2k +1 — максимум. Условие дифракционного минимума для одной щели имеет вид
где k = 1, 2, 3, …
«Плюс-минус» показывает, что картина симметрична относительно центрального максимума.
Условие дифракционного максимума от щели имеет следующий вид
k называется порядком максимума или минимума, k = 1, 2, 3, …
Дифракция Фраунгофера на дифракционной решетке
Дифракционной решеткой называется совокупность большого числа одинаковых щелей, расположенных на одинаковом расстоянии друг от друга.
Величина d = a + b называется постоянной (или периодом) дифракционной решетки, где b — ширина щели, a — ширина непрозрачного промежутка.
Рассмотрим дифракцию плоской монохроматической волны, падающей нормально на дифракционную решетку. Для наблюдения дифракции Фраунгофера поставим между решеткой и экраном собирающую линзу.
Каждая из щелей посылает свет по всем направлениям, кроме тех, которые удовлетворяют условию дифракционного минимума. Следовательно, условие минимума для дифракции от одной щели является условием минимума для решетки. Распределение интенсивности за счет дифракции света на всех щелях будет подобно распределению, представленному на рисунке, но результирующая амплитуда будет в N раз, а интенсивность в N2 раз больше, чем от одной щели, где N — число щелей.
При определении характера дифракционной картины необходимо учесть не только дифракцию света на каждой из щелей, но и интерференцию лучей, приходящих в данную точку экрана от разных щелей.
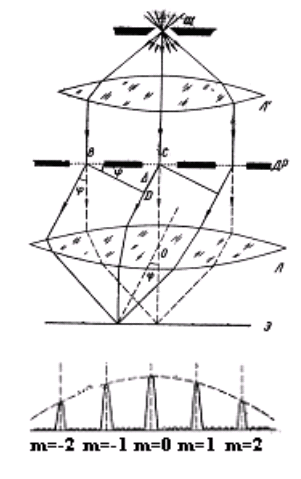
В нижней части рисунка изображено распределение интенсивности света вдоль экрана при дифракции на дифракционной решетке. Пунктирная кривая построена с учетом дифракции света на всех щелях, сплошная кривая учитывает также интерференцию волн от различных щелей. Разность хода лучей, идущих от двух соседних щелей под углом φ будет равна
Положение главных максимумов определяется условием:
где m = 1, 2, 3, … — порядок главного максимума, φ — угол дифракции.
Условие максимума при интерференции, согласно которому разность хода лучей, идущих от соседних щелей , должна быть равна четному числу полуволн. Из условия главных максимумов для дифракционной решетки следует, что, если освещать решетку белым светом, то все максимумы, кроме центрального, представляют собой спектры (так как при любом m ≠ 0 чем больше λ, тем больше φ ). Таким образом, дифракционная решетка разлагает сложный свет в спектр и поэтому применяется в спектральных приборах.
Поляризация света
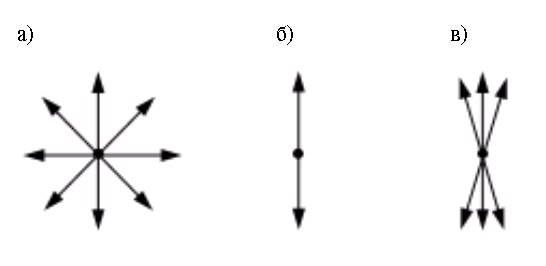
Согласно современным представлениям, свет представляет собой совокупность электромагнитных волн, которые излучаются отдельными атомами в виде порций (или квантов). Поскольку акты излучения отдельных атомов никак не связаны между собой, то свет от естественных источников представляет собой совокупность электромагнитных волн, световой вектор которых колеблется беспорядочно во всех направлениях перпендикулярно лучу, причем все направления равновероятны. Такой свет называется неполяризованным (или естественным).
Поляризованным светом называется свет, в котором колебания светового вектора каким-то образом упорядочены. Если колебания светового вектора происходят в одной плоскости, то такой свет называется плоскополяризованным. Плоскость, в которой колеблется вектор , называется плоскостью поляризации. Если имеется преимущественное (но не единственное) направление светового вектора , то такой свет называется частично поляризованным.
Возможные случаи колебаний вектора в плоскости, перпендикулярной лучу, представлены на рис.
а) естественный свет; б) плоскополяризованный свет;
в) частично поляризованный свет
Подчеркнем, что луч перпендикулярен чертежу.
Свет естественных источников может приобрести частичную или полную поляризацию при взаимодействии с веществом. Поляризация состоит в выделении из светового пучка колебаний определенного направления. Для этой цели используют специальные устройства, например, призму Николя, пластинку турмалина, поляроид и т. д. Устройства, создающие поляризованный свет, называются поляризаторами. Глаз человека не отличает поляризованный свет от ествественного. Для анализа поляризованного света используется такое же, как поляризатор, устройство, которое называется анализатором.
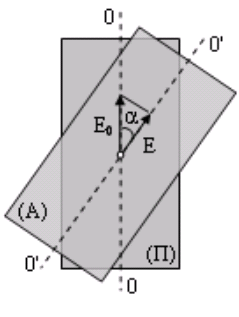
Если плоскополяризованный свет, прошедший через поляризатор (П), падает на анализатор (А) (луч перпендикулярен чертежу, то через него будет пропущена составляющая
где E0 — амплитуда света, прошедшего через поляризатор, E — амплитуда света, прошедшего через анализатор, α — угол между плоскостями пропускания колебаний поляризатора и анализатора.
Возведем в квадрат обе части уравнения. Так как интенсивность пропорциональна квадрату амплитуды, то получим:
Это уравнение представляет собой закон Малюса.
Интенсивность света, прошедшего поляризатор и анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла между плоскостями пропускания колебаний поляризатора и анализатора.
Если на поляризатор падает естественный свет, то интенсивность света уменьшается наполовину
При повороте анализатора вокруг луча можно найти его положение, при котором свет совсем не проходит. При
(«скрещенные» поляризатор и анализатор) — I = 0. Это надежный способ убедиться в том, что свет полностью поляризован.
Задачи:
- В установке для наблюдения колец Ньютона используется плосковыпуклая линза с радиусом кривизны 8,6 м. При освещении установки монохроматическим светом, падающим нормально на плоскую поверхность линзы, радиус четвертого темного кольца был равен 4,5 мм. Определить длину волны света, если наблюдение велось в отраженном свете.
- Почему при наблюдении на экране интерференционной картины от тонкой мыльной пленки, полученной на вертикально расположенном каркасе, в отраженном монохроматическом свете расстояние между интерференционными полосами в верхней части меньше, чем в нижней?
- Две когерентные световые волны приходят в некоторую точку пространства с разностью хода 2,25 мкм. Каков результат интерференции в этой точке, если свет: а) красный ( λ = 750 нм); б) зеленый ( λ = 500 нм)?
- Дифракционная решетка содержит 120 штрихов на 1 мм. Найти длину волны монохроматического света, падающего на решетку, если угол между двумя спектрами первого порядка равен 8°.
- Определить угол отклонения лучей зеленого света ( λ = 0,55 мкм) в спектре первого порядка, полученном с помощью дифракционной решетки, период которой равен 0,02 мм.
- Линия с длиной волны λ1 = 426 нм, полученная при помощи дифракционной решетки в спектре второго порядка, видна под углом φ1 = 4,9º. Найти, под каким углом φ2. видна линия с длиной волны λ2 = 713 нм в спектре первого порядка.
Задания и вопросы для самоконтроля
- Что называется интерференцией?
- Какие источники называются когерентными? В чем заключается общий принцип получения когерентных световых волн?
- Сформулируйте условия максимума и минимума интенсивности света при интерференции.
- В чем состоит явление дифракции? Сформулируйте принцип Гюйгенса — Френеля.
- Какой свет называется плоскополяризованным?
- Сформулируйте закон Малюса.