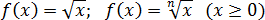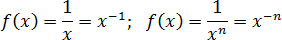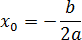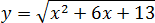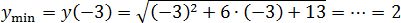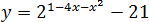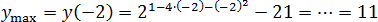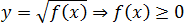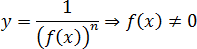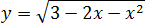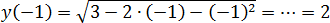Как найти минимум квадратного трехчлена

Как решать задачи B15 без производных

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Другими словами, для возрастающей функции Для убывающей функции все наоборот:

Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:

f ( x ) = log _a x ( a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только

f ( x ) = a x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы и найти ее вершину по формуле:
2. Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент

x ₀ = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.

Корень монотонно возрастает, значит точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,

x ₀ = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1

Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:

y _min = y (−1) = log ₂ ((−1) 2 + 2 · (−1) + 9) = . = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

В показателе стоит квадратичная функция Перепишем ее в нормальном виде:

Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

Аргумент логарифма должен быть положительным:

y = log _a f ( x ) ⇒ f ( x ) > 0

Арифметический квадратный корень существует только из неотрицательных чисел:

Знаменатель дроби не должен равняться нулю:

Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒

Теперь найдем вершину параболы:

Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:

Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x ₀ = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только

y _min = y (3) = log _0,5 (6 · 3 − 3 2 − 5) =

Минимум/максимум квадратичной функции

Минимум квадратного трехчлена

0.

0.1. Посмотрите картинки, например, здесь

0.2. Общее слово для «максимум» и «минимум» — «экстремум» (как «фрукт» для «яблоко» и «груша»).

0.3. БУДЬТЕ ВНИМАТЕЛЬНЫ! Возможны опечатки!

1.

1.1 f(x) = x 2 всегда неотрицательна и равна 0 только при x=0. Поэтому f(x) = x 2 имеет минимум при x=0 и этот минимум равен 0.

1.2. f(x) = 5x 2 и вообще f(x) = kx 2 при k >0 – аналогично.

1.3. f(x) = —kx 2 , где k > 0 – аналогично. Только при x=0 будет не максимум, а минимум.

1.4. f(x) = ax 2 + c (при любом знаке коэффициента a) – аналогично. То есть при х=0 функция имеет экстремум (минимум, если a>0; максимум, если a 2 – аналогично п. 1.1. Значения функции положительны, если x не равно p; f(x) = 0, если x=p. Функция имеет минимум при x=p; значение функции в точке минимума равно 0.

2.2. f(x) = 5(x-p) 2 и вообще f(x) = k(x-p) 2 при k >0 – аналогично.

2.3. f(x) = —k(x-p) 2 , где k > 0 – аналогично. Только при x=p будет не максимум, а минимум.

2.4. f(x) = a(x-p) 2 + c (при любом знаке коэффициента a) – аналогично. То есть при х=p функция имеет экстремум (минимум, если a>0; максимум, если a r1. Введем такие обозначения:

s = (r1+r2)/2; d = r2-s

Т.к. s – это среднее для r1 и r2, то

[Кто не уверен – проверьте: s-d = (r1+r2)/2 – (r2- (r1+r2)/2) = и т.д.]

Подставим в формулу s+d вместо r2 и s-d вместо r1. Получим:

(x – (s-d) ) * (x – (s+d) ) = (x-s + d) * (x-s — d) = ((x-s) +d) * ( (x-s) –d) =

[Напоминаю: (a+b)*(a-b) = a 2 – b 2 . Кто забыл – проверьте! ] Итак:

f(x) = (x-r1)*(x-r2) = (x-s) 2 – d 2

Здесь s = (r1+r2)/2; d = r2 – s = r2 — (r1+r2)/2 = (r2-r1)/2 [я пропускаю некоторые вычисления, кто не уверен — перепроверяйте].

Теперь понятно (см. п. 2.4), что наша функция имеет минимум при x = (r1+r2)/2. Значение функции в точке минимума равно – (r2-r1) 2 / 4 . К слову, это значение всегда отрицательное.

Еще кстати (для тех, кто забыл): r1, r2 – корни уравнения (x-r1)*(x-r2)=0.

3.2. f(x) = (x-r1)*(x-r2)+c. Эта функция имеет минимум в той же точке, что и уже знакомая нам функция f(x) = (x-r1)*(x-r2). Т.е. при x = (r1+r2)/2. А вот значение функции в точке минимума будет другое: с — (r2-r1) 2 / 4 .

3.3. f(x) = a*(x-r1)*(x-r2)+c. Умножение на a тоже не влияет на положение точки экстремума (если a>0, это будет минимум, если a 2 / 4

Советую самостоятельно вычислить значение функции в точке экстремума.

4. Общий случай.

4.1. f(x) = ax 2 +bx + c. Сводится к 2.4 с помощью выделения полного квадрата

Это означает вот что:

ax 2 +bx + c = a*(x+b/2a) 2 – (b 2 -4ac)/4a

Подробнее – см., например, здесь . Таким образом:

— наша функция имеет экстремум в точке x = -b/2a;

— экстремум будет минимум при a> 0 и максимумом при a 2 -4ac)/4a

Квадратичная функция.

Видео-уроки по теме «График квадратичной функции — парабола» расположены в конце страницы.

Квадратным трёхчленом называется многочлен 2-ой степени, то есть выражение вида ax 2 + bx + c, где a ≠ 0, b, c — (обычно заданные) действительные числа, называемые его коэффициентами, x — переменная величина.

Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax 2 + bx + c = 0·x 2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x 2 − 2x или x 2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x 2 − 2x = 3x 2 − 2x + 0 и x 2 + 5 = x 2 + 0x + 5.

Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax 2 + bx + c = 0, то имеем квадратное уравнение.

Если существуют действительные корни x₁ и x₂ некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax 2 + bx + c = a(x − x₁)(x − x₂)

Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.

Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax 2 + bx + c, то имеем дело с квадратичной функцией.

При этом корни квадратного уравнения являются нулями квадратичной функции.

Квадратный трёхчлен также можно представить в виде

Это представление удобно использовать при построении графика и изучении свойств квадратичной функции действительного переменного.

Квадратичной функцией называется функция, заданная формулой y = f(x), где f(x) — квадратный трёхчлен. Т.е. формулой вида

где a ≠ 0, b, c — любые действительные числа. Или преобразованной формулой вида

.

Графиком квадратичной функции является парабола, вершина которой находится в точке .

Обратите внимание: Здесь не написано, что график квадратичной функции назвали параболой. Здесь написано, что графиком функции является парабола. Это потому, что такую кривую математики открыли и назвали параболой раньше (от греч. παραβολή — сравнение, сопоставление, подобие), до этапа подробного изучения свойств и графика квадратичной функции.

Парабола — линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельной одной из образующих этого конуса.

Парабола обладает еще одним интересным свойством, которое также используется как её определение.

Парабола представляет собой множество точек плоскости, расстояние от которых до определенной точки плоскости, называемой фокусом параболы, равно расстоянию до определенной прямой, называемой директрисой параболы.

Построить эскиз графика квадратичной функции можно по характерным точкам.
Например, для функции y = x 2 берем точки

x	0	1	2	3
y	0	1	4	9

Соединяя их от руки, строим правую половинку параболы. Левую получаем симметричным отраженим относительно оси ординат.

Для построения эскиза графика квадратичной функции общего вида в качестве характерных точек удобно брать координаты её вершины, нули функции (корни уравнения), если они есть, точку пересечения с осью ординат (при x = 0, y = c) и симметричную ей относительно оси параболы точку (−b/a; c).

x	−b/2a	x1	x2	0	−b/a
y	−(b 2 − 4ac)/4a	0	0	с	с
при D ≥ 0

Но в любом случае по точкам можно построить только эскиз графика квадратичной функции, т.е. приблизительный график. Чтобы построить параболу точно, нужно использовать её свойства: фокус и директрису.
Вооружесь бумагой, линейкой, угольником, двумя кнопками и крепкой нитью. Прикрепите одну кнопку примерно в центре листа бумаги — в точке, которая будет фокусом параболы. Вторую кнопку прикрепите к вершине меньшего угла угольника. На основаниях кнопок закрепите нить так, чтобы её длина между кнопками равнялась большому катету угольника. Начертите прямую линию, непроходящую через фокус будущей параболы, — директрису параболы. Приложите линейку к директрисе, а угольник к линейке так, как показано на рисунке. Перемещайте угольник вдоль линейки, одновременно прижимая карандаш к бумаге и к угольнику. Следите за тем, чтобы нить была натянута.

Измерьте расстояние между фокусом и директрисой (напоминаю — расстояние между точкой и прямой определяется по перпендикуляру). Это фокальный параметр параболы p. В системе координат, представленной на правом рисунке, уравнение нашей параболы имеет вид: y = x 2 /2p. В масштабе моего рисунка получился график функции y = 0,15x 2 .

Замечание: чтобы построить заданную параболу в заданном масштабе, делать нужно всё то же самое, но в другом порядке. Начинать нужно с осей координат. Затем начертить директрису и определить положение фокуса параболы. И только потом конструировать инструмент из угольника и линейки. Например, чтобы на клетчатой бумаге построить параболу, уравнение которой у = x 2 , нужно расположить фокус на расстоянии 0,5 клеточки от директрисы.

Свойства функции у = x 2

1. Область определения функции — вся числовая прямая: D(f) = R = (−∞; ∞).
2. Область значений функции — положительная полупрямая: E(f) = [0; ∞).
3. Функция у = x 2 четная: f(−x) = (−x) 2 = x 2 = f(x) .
   Ось ординат является осью симметрии параболы.
4. На промежутке (−∞; 0) функция монотонно убывает.
   На промежутке (0; + ∞) функция монотонно возрастает.
5. В точке x = 0 достигает минимального значения.
   Точка с координатами (0;0) является вершиной параболы.
6. Функция непрерывна на всей области определения.
7. Асимптот не имеет.
8. Нули функции: y = 0 при x = 0.

Свойства квадратичной функции общего вида.

1. Область определения функции — вся числовая прямая: D(f) = R = (−∞; ∞).
2. Область значений функции зависит от знака коэффициента a.
   При a > 0 ветви параболы направлены вверх, функция имеет наименьшее (y_min), но не имеет наибольшего значения: E(f) = [ y_min; ∞) ;
   при aE(f) = (−∞; y_max ] .
3. В общем случае функция у = ax 2 + bx + c не является ни четной, ни нечетной.
   Осью симметрии параболы является прямая x = −b/2a .
   Функция будет четной только в случае, когда эта прямая совпадает с осью Oy, т.е. при b = 0.
4. При a > 0 функция монотонно убывает на промежутке (−∞; −b/2a) и монотонно возрастает на промежутке (−b/2a; ∞).
   При a 0 — минимум функции.

Оба значения определяются по формуле y = − b 2 − 4ac _______ . 4a

Точка с координатами является вершиной параболы.

Функция непрерывна на всей области определения.

Асимптот не имеет.

Парабола пересекает ось ординат в точке (0;c).
Если квадратный трёхчлен имеет дейтсивтельные корни x₁ ≠ x₂, то парабола пересекает ось абсцисс в точках (x₁;0) и (x₂;0).
При x₁ = x₂ парабола касается оси абсциcс в точке (x₁;0).

Производная квадратичной функции вычисляется по формуле (ax 2 + bx + c)’ = 2ax + b.

График квадратичной функции, заданной общей формулой, лучше всего строить и изучать пользуясь Правилами преобразования графиков функций.
Для этого нужно сначала перейти от формулы y = ax 2 + bx + c к виду, удобному для преобразований, y = m(kx + l) 2 + n, где k, l, m, n — числа, зависящие от a, b, c, т.е. к виду
.
Затем взять за основу параболу y = x 2 и применить к ней следующие преобразования:

• Параллельный перенос (сдвиг) исходной параболы на l = b/2a единиц влево (если l 2 − 4ac)/4a единиц вверх или вниз в зависимости от знака n (при n >0 вверх).

Формулы для такого перехода можно выучить наизусть, а можно научиться выделять полный квадрат из трёхчлена с заданными коэффициентами. Это умение весьма полезно также для решения некоторых уравнений и неравенств, для вычисления интегралов и т.д.

Рассмотрим пример:
Пусть y = 3x 2 − 5x + 2
1) Объединяем в скобки первые два слагаемых и выносим за скобки коэффициент при х 2 .
2) В скобках умножим и одновременно разделим на 2 коэффициент при x.
3) Сравним с формулой возведения двучлена в квадрат: имеем внутри скобок квадрат числа x, удвоенное произведение x на дробь 5/6. Чтобы применить эту формулу не хватает второго квадрата, поэтому добавим недостающее слагаемое 5 2 /6 2 и одновременно вычтем его, чтобы сохранилось исходное значение выражения.
4) Сворачиваем квадрат по формуле и раскрываем большую скобку.
5) Оставшиеся числовые дроби приводим к общему знаменателю и складываем.

Итак, чтобы построить график функции y = 3x 2 − 5x + 2 из графика y = x 2 нужно последний сдвинуть по оси Ox вправо на 5/6 ≈ 0,83 единицы. Затем растянуть вдоль оси Oy в 3 раза и, наконец, опустить по оси Oy на 1/12 ≈ 0,08 единицы.
Посмотрите, что получилось.

Если Вы являетесь моим учеником или подписчиком, то можете поработать с интерактивными версиями этих графиков.

Упражнение:
Постройте по характерным точкам эскиз графика функции y = x 2 .
Методом преобразования получите эскиз графика функции y = −x 2 + 4x + 6 .
Посмотрите в каких точках график этой функции пересекает ось Ox и сравните их координаты (абсциссы) с корнями уравнения −x 2 + 4x + 6 = 0 , вычисленными через дискриминант. Насколько точным оказалось ваше графическое решение уравнения?

Преобразуем выражение с выделением полного квадрата:

Строим график функции
.

Для этого применяем следующие шаги: сдвиг на 2 клетки вправо, разворот ветвей вниз (вершина — точка, относительно которой поворачиваем), поднимаем вершину и, соответственно, всю параболу вверх на 10 клеточек. Вот что должно получиться
.

Визуально определяем корни. Парабола пересекает ось Ox примерно на одну пятую часть клетки левее минус единицы и настолько же правее пятерки, т.е. x₁ ≈ −1,2 , x₂ ≈ 5,2 .

Решение по формулам нахождения корней квадратного уравнения дает ответы x₁ = 2 − √10 __ , x₂ = 2 + √10 __ .
С помощью калькулятора вычисляем x₁ = −1,162277660. , x₂ = 5,162277660.

Парабола — очень интересная кривая, квадратичная функция часто встречается при описании различных природных явлений, экономических процессов.

Видеоуроки с параболой.

Графики квадратичной функции и коэффициенты квадратного трёхчлена.

Положение и вид параболы в зависимости от знака и значения коэффициента а — коэффициента при х 2 .

Положение и вид параболы в зависимости от знака и значения коэффициента b — коэффициента при х.

Положение и вид параболы в зависимости от знака и значения параметра c.

Построение параболы по характерным точкам.

Быстрое построение параболы как графика квадратичной функции.

Другие случаи. Примеры построения.

Задачи на анализ графика квадратичной функции.

Задания вида «Установить соответствие между коэффициентами квадратного трёхчлена и приведенными графиками квадратичной функции» встречаются в ОГЭ по математике в 9-ом классе, а также необходимы сдающим ЕГЭ за 11 класс в качестве промежуточного действия.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

источники:

Минимум/максимум квадратичной функции

http://mathematichka.ru/school/functions/quadratic.html

Была ли эта статья полезной?

Минимум/максимум квадратичной функции

Минимум квадратного трехчлена

0.

0.1. Посмотрите картинки, например, здесь

0.2. Общее слово для «максимум» и «минимум» — «экстремум» (как «фрукт» для «яблоко» и «груша»).

0.3. БУДЬТЕ ВНИМАТЕЛЬНЫ! Возможны опечатки!

1.

1.1 f(x) = x² всегда неотрицательна  и равна 0 только при x=0. Поэтому f(x) = x²  имеет минимум при x=0 и этот минимум равен 0.

1.2.  f(x) = 5x²  и вообще f(x) = kx² при k >0 – аналогично.

1.3. f(x) = —kx², где  k > 0 – аналогично. Только при x=0 будет не максимум, а минимум.

1.4.  f(x) = ax² + c (при любом знаке коэффициента a) – аналогично. То есть при х=0 функция имеет экстремум (минимум, если a>0;  максимум, если a<0). Значение функции при x=0 равно c.

2.

2.1.  f(x) = (x-p)² – аналогично п. 1.1. Значения функции положительны, если x не равно p; f(x) = 0, если x=p. Функция имеет минимум при x=p; значение функции в точке минимума равно 0.

2.2.  f(x) = 5(x-p)²  и вообще f(x) = k(x-p)² при k >0 – аналогично.

2.3. f(x) = —k(x-p)², где  k > 0 – аналогично. Только при x=p будет не максимум, а минимум.

2.4.  f(x) = a(x-p)² + c (при любом знаке коэффициента a) – аналогично. То есть при х=p функция имеет экстремум (минимум, если a>0;  максимум, если a<0). Значение функции при x=0 равно c.

3.

3.1. f(x) = (x-r1)*(x-r2).  Например, f(x) = (x-3)*(x-5). Здесь r1 = 3; r2 = 5.

Это можно свести к случаю 2.4 (у нас для простоты a=1).

Опять таки для удобства считаем, что r2   > r1. Введем такие обозначения:

s = (r1+r2)/2;   d =  r2-s

Т.к. s – это среднее для r1 и r2, то

r1 = s-d

[Кто не уверен – проверьте: s-d = (r1+r2)/2 – (r2- (r1+r2)/2) = и т.д.]

Подставим в формулу s+d вместо r2 и s-d вместо r1.  Получим:

(x – (s-d) ) * (x – (s+d) ) = (x-s  + d) * (x-s  — d) = ((x-s) +d) * ( (x-s) –d) =

= (x-s)² – d² .

[Напоминаю: (a+b)*(a-b) = a² – b². Кто забыл – проверьте! ]  Итак:

f(x) = (x-r1)*(x-r2) = (x-s)² – d²

Здесь s = (r1+r2)/2; d = r2 – s = r2 — (r1+r2)/2 = (r2-r1)/2 [я пропускаю некоторые вычисления, кто не уверен — перепроверяйте].

Теперь понятно (см. п. 2.4), что наша функция имеет минимум при x = (r1+r2)/2. Значение функции в точке минимума равно – (r2-r1)² / 4 . К слову, это значение всегда отрицательное.

Еще кстати (для тех, кто забыл): r1, r2 – корни уравнения (x-r1)*(x-r2)=0.

3.2.  f(x) = (x-r1)*(x-r2)+c. Эта функция имеет минимум в той же точке, что и уже знакомая нам функция  f(x) = (x-r1)*(x-r2). Т.е. при x = (r1+r2)/2. А вот значение функции в точке минимума будет другое: с —  (r2-r1)² / 4 .

3.3.  f(x) = a*(x-r1)*(x-r2)+c. Умножение на a  тоже не влияет на положение точки экстремума (если a>0, это будет минимум, если  a<0 — максимум). Т.е. минимум будет достигаться при  при x = (r1+r2)/2.  Значение функции в точке  экстремума будет равно  с — a* (r2-r1)² / 4  

Советую самостоятельно вычислить значение функции в точке экстремума.

4. Общий случай.

4.1.  f(x) = ax² +bx + c. Сводится к 2.4 с помощью выделения полного квадрата

Это означает вот что:

ax² +bx + c = a*(x+b/2a)² – (b²-4ac)/4a

Подробнее – см., например, здесь . Таким образом:

— наша функция имеет экстремум в точке x = -b/2a;

— экстремум будет минимум при a> 0 и максимумом при a < 0;

            — значение функции в точке экстремума равно – (b²-4ac)/4a

Квадратный трёхчлен в функции. Год назад опубликовал статью, в которой были рассмотрены  функции в составе которых имеется квадратный трёхчлен. Задания на нахождение точек максимума (минимума) или на вычисление наибольшего (наименьшего) значения функции.

Недавно меня попросили рассказать и показать каким образом такие задания можно решить по стандартному алгоритму, то есть через производную. Сразу скажу, что такой подход к решению нерационален, требует больше времени и он «неудобен». Привожу его для вас (чтобы знали).

Рекомендую посмотреть статью «Исследование функций. Это нужно знать!», также помните, что производные элементарных функций нужно знать наизусть, в теме производной без этого никак нельзя. Также необходимо понимание того, что такое сложная функция, в указанной выше статье имеется видео.

Рассмотрим задачи:

Найдите точку максимума функции

Сначала определим, при каких х функция имеет смысл (найдём область определения функции). Так как подкоренное выражение есть число неотрицательное, то решаем неравенство:

13 + 6х – х² ≥ 0

*Как решается квадратное неравенство подробно можно посмотреть здесь.

Данные корни разбивают ось х на три интервала.

Проверим при каких значениях х неравенство будет верным. Подставим из каждого интервала любое значение х в неравенство:

Значит решением неравенства будут являться все значения х принадлежащие интервалу (включая границы):

*Приближенно полученные выражения равны:   

Область определения данной функции найдена.

Вычислим производную функции. Это сложная функция:

Найдем нули производной:

Дробь равна нулю тогда, когда её числитель равен нулю, значит:

6 – 2х  = 0

х = 3

Полученное  значение х входит в область определения и разбивает её на два отрезка. Определим знаки производной на каждом из них (подставим выборочно любые значения в выражение производной), например 2 и 4:

Получили, что в точке х = 3 производная функции меняет свой знак с положительного на отрицательный, а это означает, что данная точка есть точка максимума.

Ответ: 3

Комментарий: представленное решение – это полное, математически грамотное решение, то есть такое как должно быть. О чем я? Дело в том, что для составления «полной картины», в первую очередь необходимо найти область определения. Конечно, можно поспорить. Дело в том, можно сразу находить  производную, затем её «нули» и далее установить имеет ли функция значение при этом х. Затем определить знаки в «соседних» точках и станет понятно является ли эта точка точкой максимума (или минимума). Да, можно и так.

Кто проанализировал все типы таких примеров из единого банка заданий ЕГЭ по математике, тот справедливо может сказать, что достаточно вообще найти нули производной, полученное (целое) значение х и будет являться искомым. Согласен! Но понимать суть всего процесса решения «от и до»  необходимо.

Если в подобном задании на ЕГЭ будет стоять вопрос о вычислении наибольшего (наименьшего) значения, то оно будет в точке х, полученной при решении f′(х) = 0, то есть в «нуле функции».

Найдите точку максимума функции у =log₇(–2 – 12х – х²) + 10. 

Вычислим производную функции, используем формулу производной логарифма и производной сложной функции:

Найдем нули производной:

Дробь равна нулю тогда и только тогда, когда её числитель равен нулю:

– 2х –12 = 0

х = – 6

Данное значение обращает подлогарифмическое выражение в положительное:

–2 – 12∙(–6) – (–6)² = 34

то есть оно принадлежит области определения функции.

Определим знаки производной в «соседних» точках, например возьмем точки  –7 и –5:

Получили, что в точке х = – 6 производная функции меняет свой знак с положительного на отрицательный, а это означает, что данная точка есть точка максимума функции.

Ответ: –6

Комментарий: здесь мы не стали находить область определения. Сразу вычислили производную и нашли х, при котором производная обращается в нуль. Затем определили знаки производной на интервалах полученных разбиением числовой оси точкой х =  – 6 и сделали вывод.

Если в подобном задании (с логарифмом) будет стоять вопрос о вычислении наибольшего (наименьшего) значения функции, то также вычисляйте его в точке х, полученной при решении f′(х) = 0.

Найдите точку максимума функции 

Вычислим производную функции, используем формулу производной показательной и производной сложной функции:

Найдем нули производной. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другие при этом не теряют смысла. В данном случае нулю равен только один множитель:

–2х + 12 = 0

х = 6

Определим знаки производной на интервалах, которые получаются разбиением числовой оси точкой х=6, возьмём точки 0 и10:

Получили, что в точке х = 6 производная функции меняет свой знак с положительного на отрицательный, а это означает, что данная точка есть точка максимума функции.

Ответ: 6

Комментарий: в данном случае область определения не имеет ограничений, то есть при всех х функция имеет значение.

Если будет стоять вопрос о нахождении максимального  (минимального) значения функции на определённом интервале, то тут действуйте по стандартному алгоритму (посмотрите задания на сайте, их достаточно).

В любом случае, свойства производной для исследования функции, табличные значения производных и алгоритм нахождения точек максимума (минимума) нужно знать обязательно.

Как вы убедились, данный подход к решению таких заданий (через производную) требует больше времени, знания теории и умственного напряжения. Показал его для того, чтобы знали и понимали, каким образом ещё можно решить подобные задания. Конечно же, этот способ намного проще.

Успеха вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.