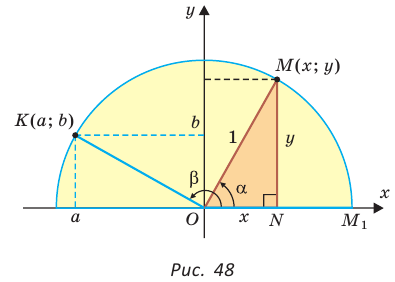
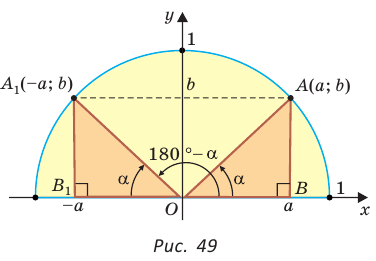
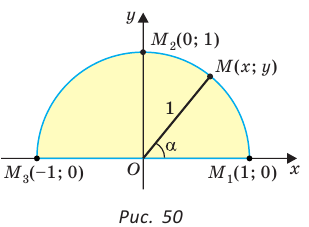
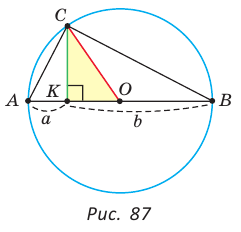
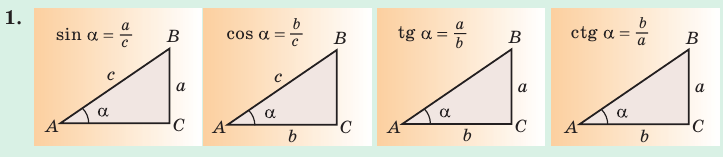
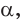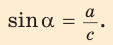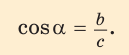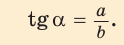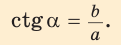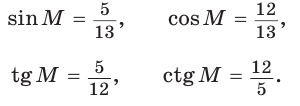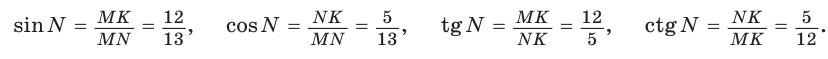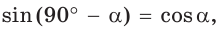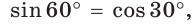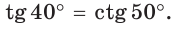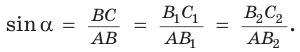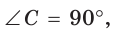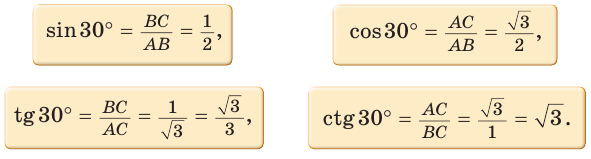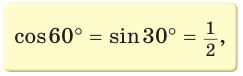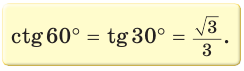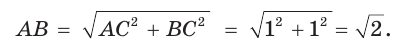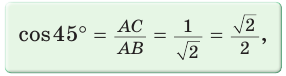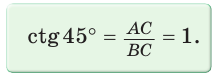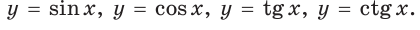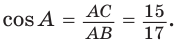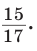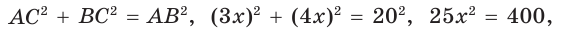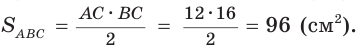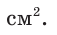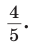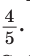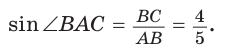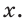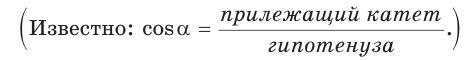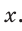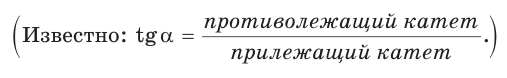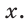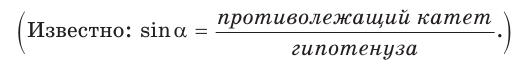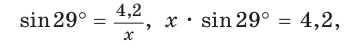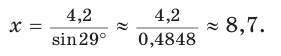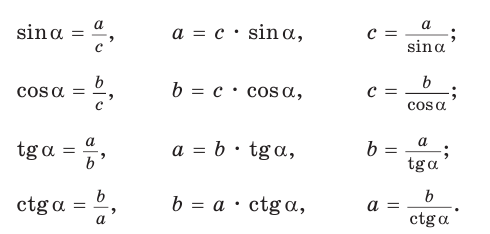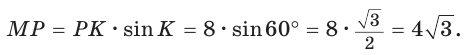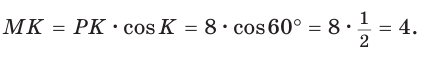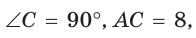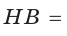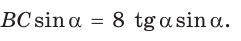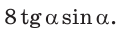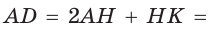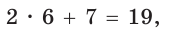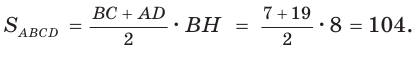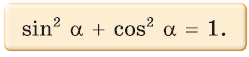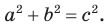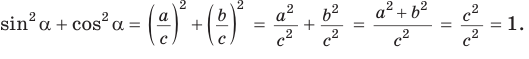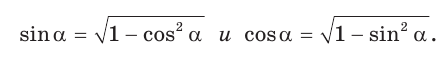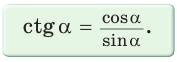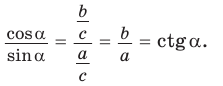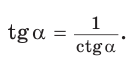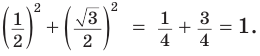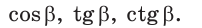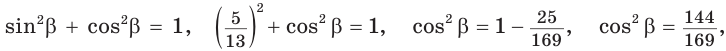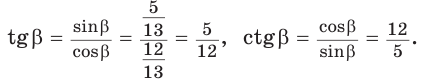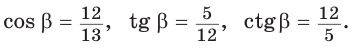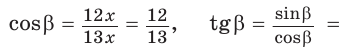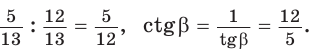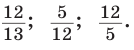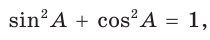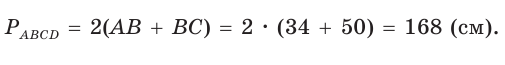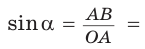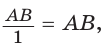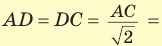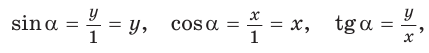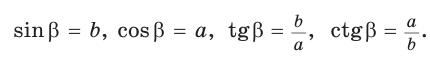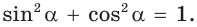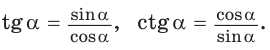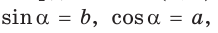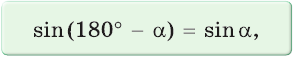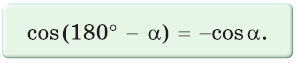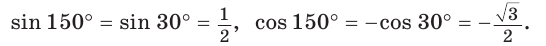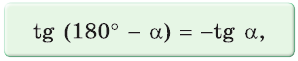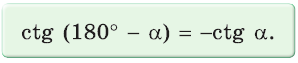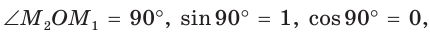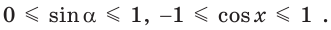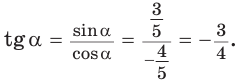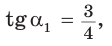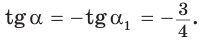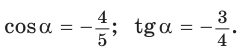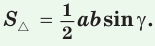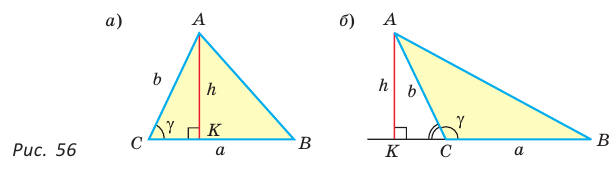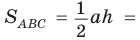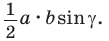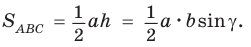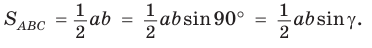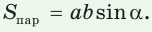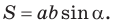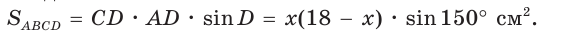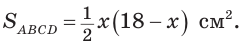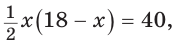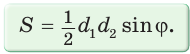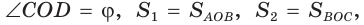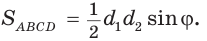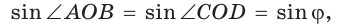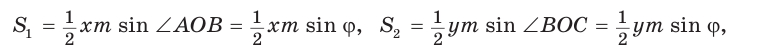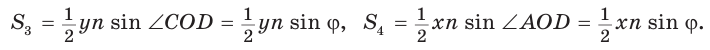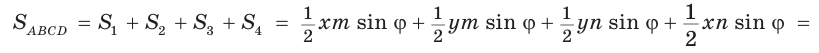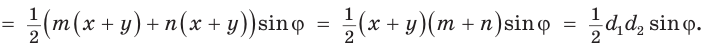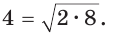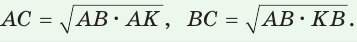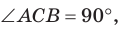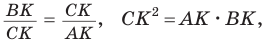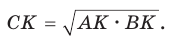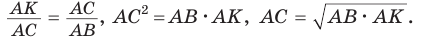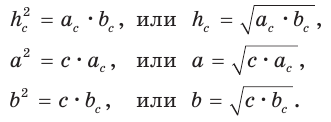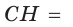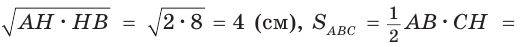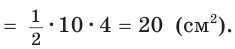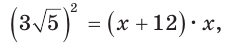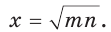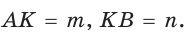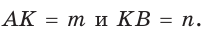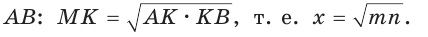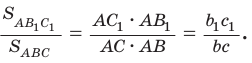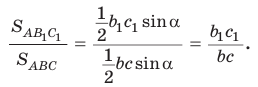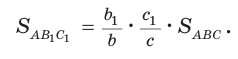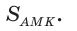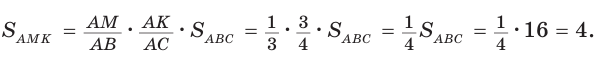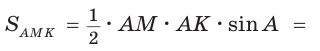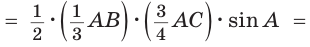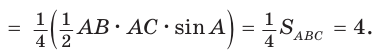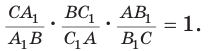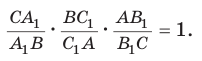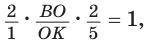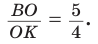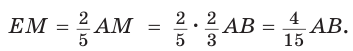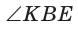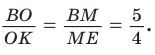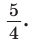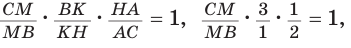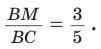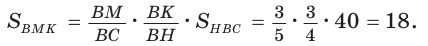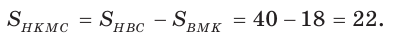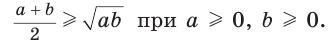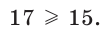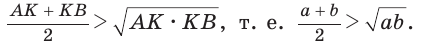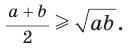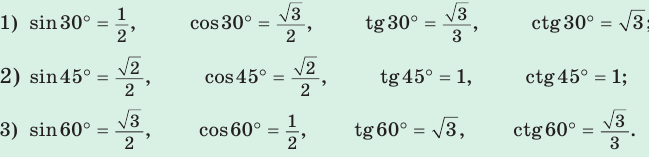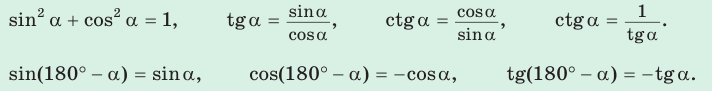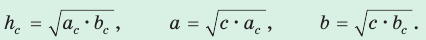sin(-a),cos(-a),tg(-a),ctg(-a). Минус в аргументе синуса, косинуса
И сразу два важных замечания.
Многие ученики думают, что если можно вынести минус из тригонометрической функции, то можно вынести и число, но это не так:
Квадрат меняет ситуацию. Всё дело в том, что (sin^2(-x)=(sin(-x) )^2=(-sin,x )^2=sin^2x), т.е. минус все равно выносится, но так как синуса два и они перемножаются, то в итоге получается плюс.
Примеры из ЕГЭ
Из рисунка видно, что и косинус, и синус положителен. Косинус из трех стандартных значений (frac<1><2>), (frac<sqrt<2>><2>), (frac<sqrt<3>><2>) принимает наименьшее т.е. (cos,frac<π><3>=frac<1><2>). Синус из трех стандартных значений будет равен среднему т.е. (sin,frac<π><4>=frac<sqrt<2>><2>). Получается:
Если вы не поняли почему (frac<π><3>) и (frac<π><4>) находятся на круге там, где мы из обозначили, то читайте статью « Как обозначать числа с пи на числовой окружности? ». А если не поняли, как мы нашли синус и косинус, то читайте статью « Как найти синус и косинус без тригонометрической таблицы ».
Пример (ЕГЭ). Найдите значение выражения (44sqrt<3>,tg,(-480^° )).
Решение. (44sqrt<3>,tg(-480^° )=-44sqrt<3>,tg(480^° )=-44sqrt<3>,tg(360^°+120^° )=-44sqrt<3>,tg(360^°+90^°+30^°)).
Находим (480^°) на окружности:
Соединяем точку, соответствующую (480^°) и центр окружности, и продляем до оси тангенсов:
Мы попадаем в самое маленькое (из стандартных) значение тангенса.
Значит, (tg(480^° )=-sqrt<3>).
В итоге имеем: (44sqrt <3>tg(-480^° )=-44sqrt<3>cdot(-sqrt<3>)=44cdot 3=132).
Ответ: (132).
Если вам не понятно, как мы нашли значение тангенса, то читайте статью « Как найти тангенс и котангенс без тригонометрической таблицы? ».
Доказательства формул с минусом в аргументе:
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
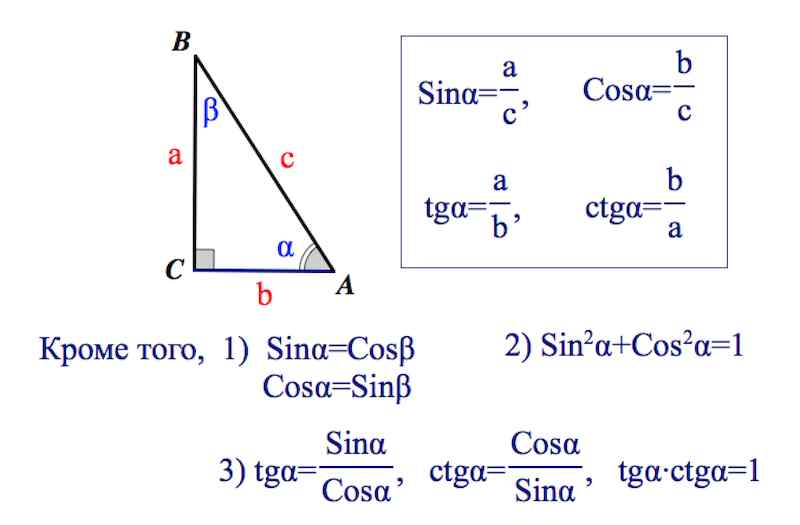
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
0 °
30 °
45 °
60 °
90 °
sin α
0
1 2
2 2
3 2
1
cos α
1
3 2
2 2
1 2
0
tg α
0
3 3
1
3
нет
ctg α
нет
3
1
3 3
0
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
http://matworld.ru/geometry/reshenie-treugolnikov.php
Содержание:
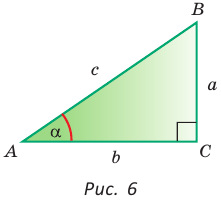
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен
Определения синуса, косинуса, тангенса и котангенса острого угла
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
Пример:
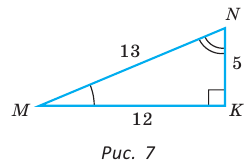
Угол К в 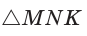
Тогда:
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 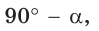
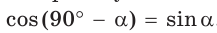
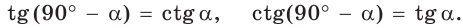
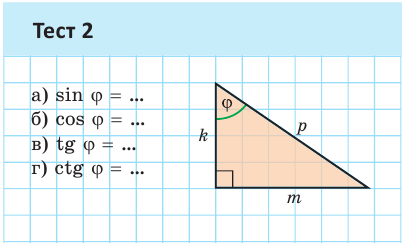
А теперь выполните Тест 1 и Тест 2.
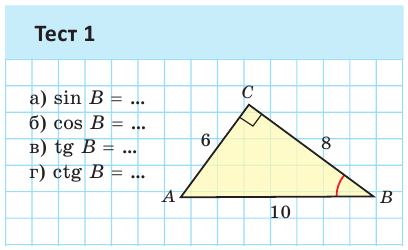
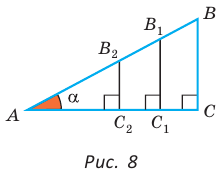
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в 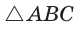

Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
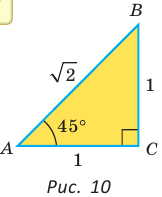
Рассмотрим прямоугольный треугольник АВС, у которого 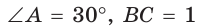
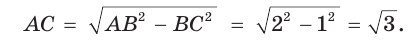
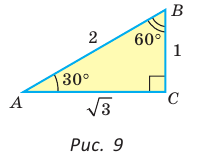
Так как 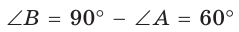

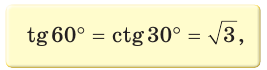
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 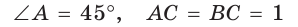
Тогда:
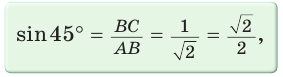
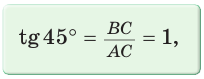
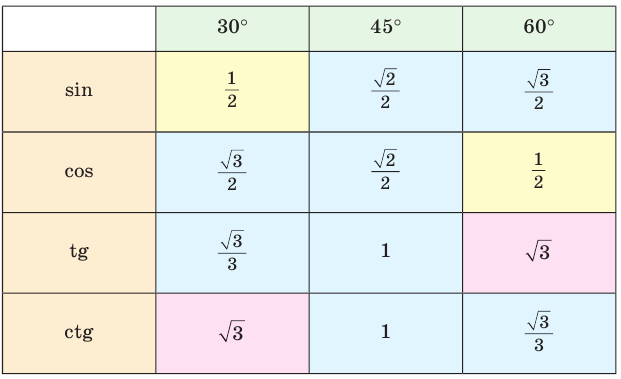
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 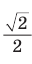
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно 
А теперь выполните Тест 3.
Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 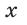
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 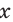
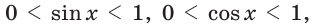
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
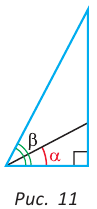
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 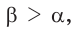
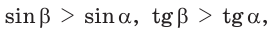
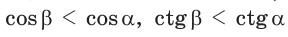
Пример №1
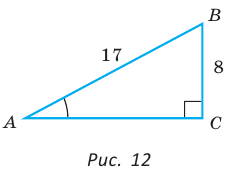
В прямоугольном треугольнике АВС, где 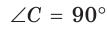
Решение:
По теореме Пифагора найдем катет 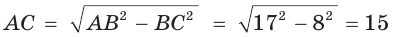
Ответ:
Пример №2
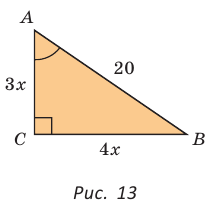
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 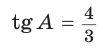
Решение:
Так как 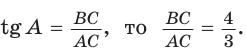
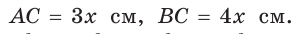
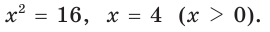
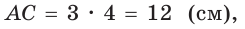
Ответ: 96
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен
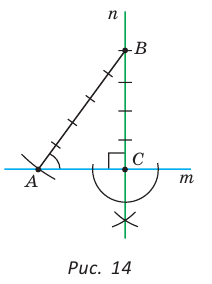
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую 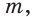
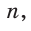
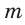
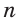
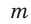
Угол ВАС — искомый.
Доказательство:
Из 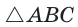
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
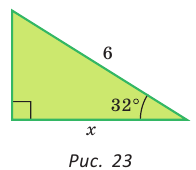
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
Решение:
Примем длину искомого катета за
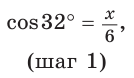

Ответ: 5,1.
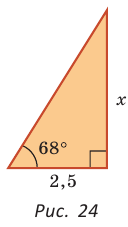
Пример №5
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за
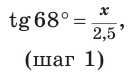
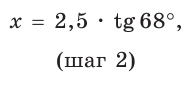
Ответ: 6,2.
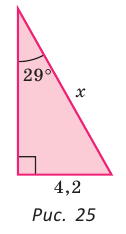
Пример №6
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за
Ответ: 8,7.
Правила решения прямоугольного треугольника
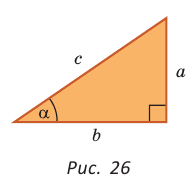
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
Удобно пользоваться следующими правилами:
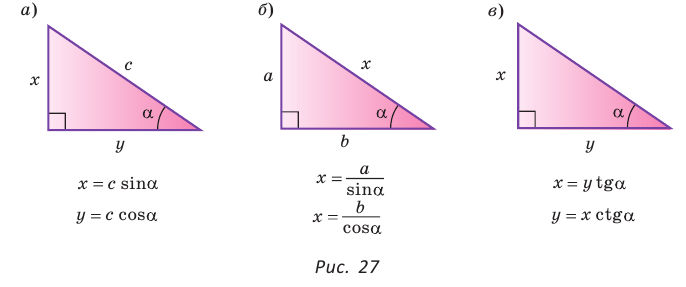
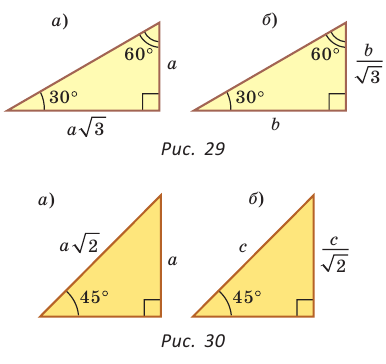
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 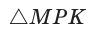
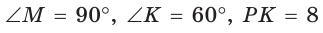
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 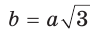
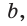
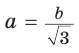
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 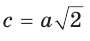
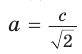
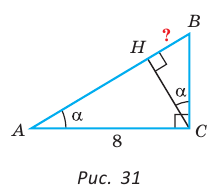
Пример №8
В прямоугольном треугольнике АВС известно: 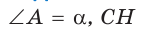
Решение:
Заметим, что 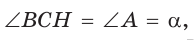
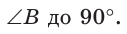
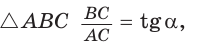
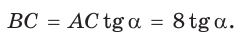
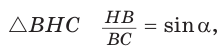
Ответ:
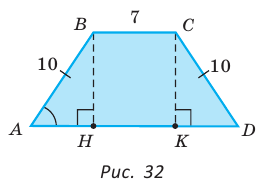
Пример №9
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 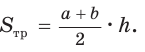
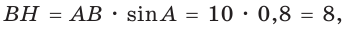
Ответ: 104.
Тригонометрические формулы
Используя формулы 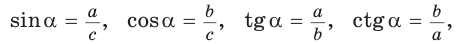
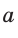
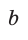
1. Основное тригонометрическое тождество
Доказательство:
По теореме Пифагора
Тогда
Следствие:
Так как синус и косинус острого угла а положительны, то
2. Выражение тангенса и котангенса через синус и косинус
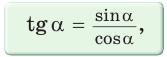
Доказательство:
a)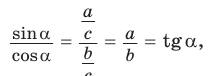
Следствие:
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 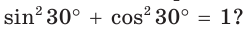
3. Основная задача
Дано: 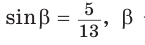
Найти:
Решение:
Способ 1. Используем основное тригонометрическое тождество: 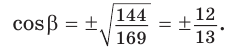
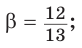
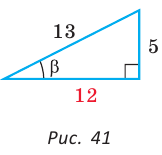
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 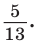
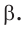
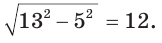
Способ 3. Пусть катет, противолежащий углу 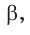
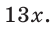
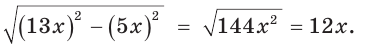
Ответ:
Пример №10
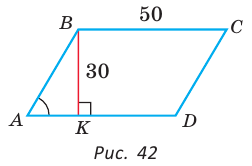
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 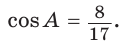
Решение:
Из треугольника АВК находим: 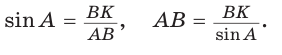
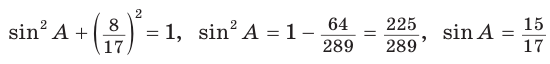
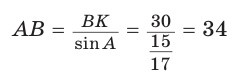
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
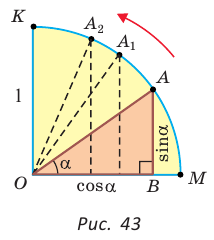
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 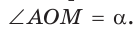
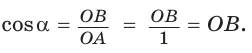
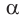
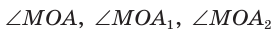
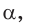
Из формулы 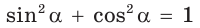
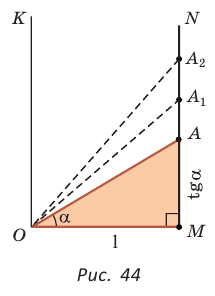
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 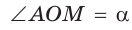
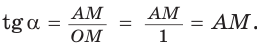
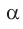
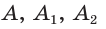
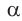
К такому же выводу можно прийти, рассматривая формулу 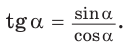
Пример №12
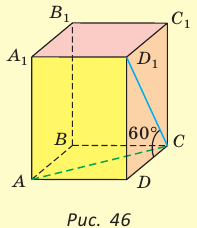
В основании прямоугольного параллелепипеда 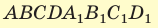
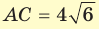
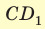
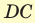

Решение:
Объем прямоугольного параллелепипеда находится по формуле 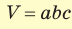
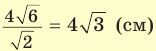
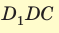
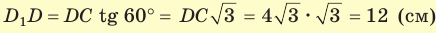
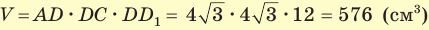
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 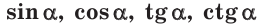
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси 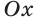
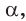
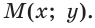
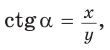
тангенс и котангенс острого угла а выражаются через координаты 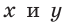
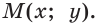
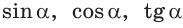
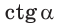
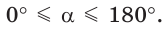
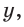
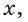
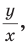
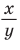
Например, для тупого 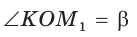
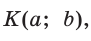
Для любого положения точки 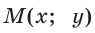
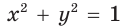
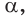

Также верны тождества:
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
Пусть 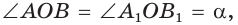
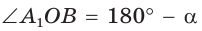
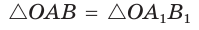
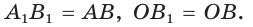
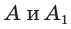
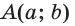
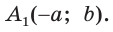
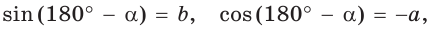
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1.
Разделив почленно равенство 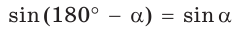
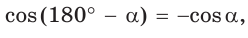
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2.
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
Если луч ОМ совпадет с лучом 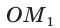
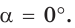
а) 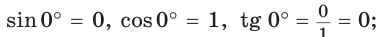
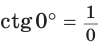
б) 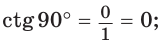
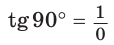
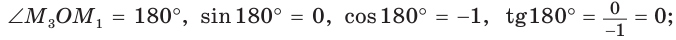
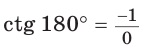
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 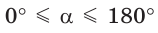
Пример №13
Найти 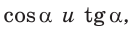
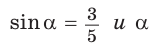
Решение:
Способ 1. Так как 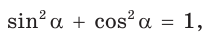
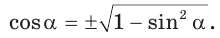
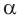
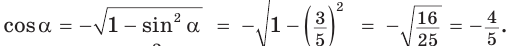
Способ 2. Синус острого угла 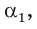
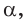
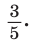
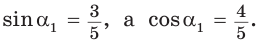
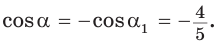
Ответ:
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е.
Доказательство:
Пусть в треугольнике 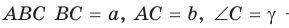
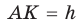
Из прямоугольного треугольника 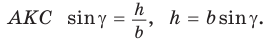
Если угол 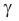
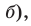
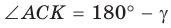
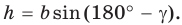
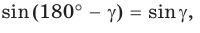
Если 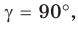
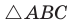
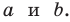

Теорема доказана.
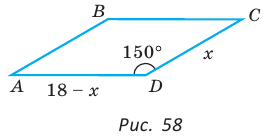
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е.
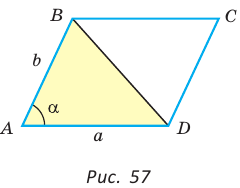
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 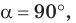
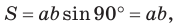

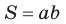
Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
Решение:
Полупериметр параллелограмма равен 18 см. Если 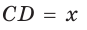
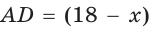
Тогда
Так как 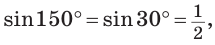
По условию 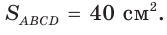
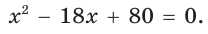
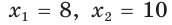
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
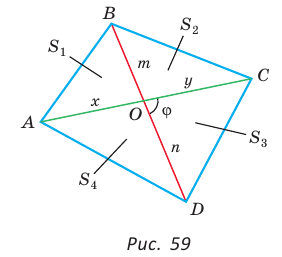
Пример №15
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е.
Доказательство:
Пусть диагонали 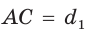
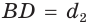
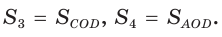
Обозначим 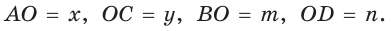
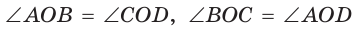
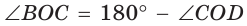
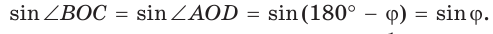
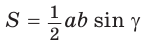
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 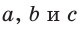
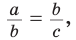
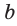
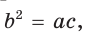
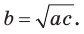
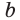
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 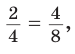
В прямоугольном треугольнике АВС, где 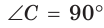
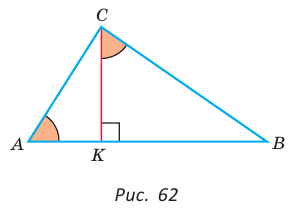
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 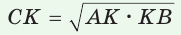
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е.
Доказательство:
а)3аметим, что если 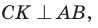
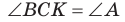
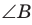
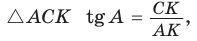
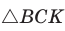
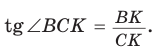
б) Из 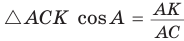
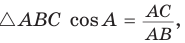
Аналогично доказывается, что 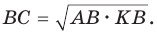
Обозначив катеты 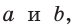
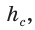
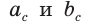
Пример №17
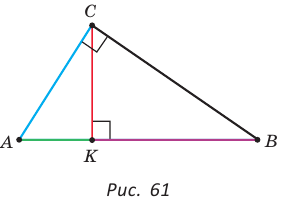
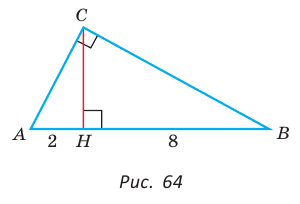
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
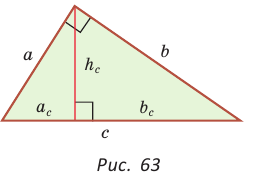
Пусть СН — высота прямоугольного треугольника АВС 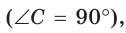
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то
Ответ: 20 см2.
Пример №18
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 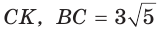
Решение:
Пусть 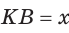
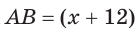
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 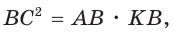
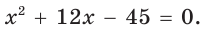
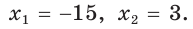
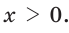
Ответ: 15 см.
Пример №19
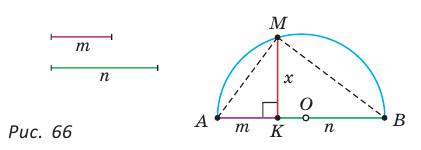
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок
Построение.
1) На произвольной прямой откладываем данные отрезки:
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 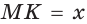
Доказательство:
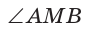
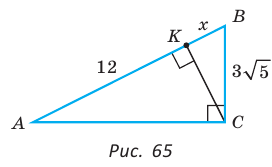
Повторение*
В 8-м классе мы доказали следующую теорему:
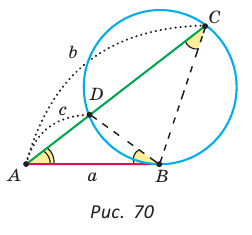
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 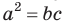
Как видим, отрезок 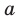
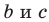
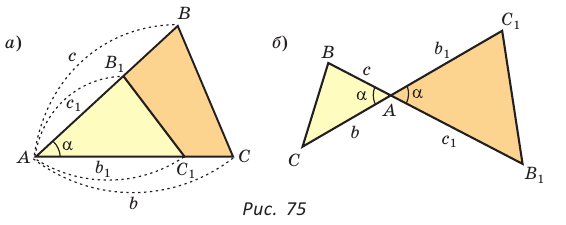
Теорема о площадях треугольников с общим (равным) углом
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е.
Доказательство:
Следствие: Верно:
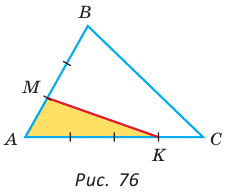
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
Способ 2.
Ответ: 4.
Теорема Менелая
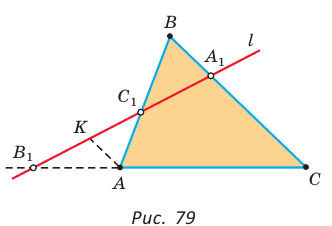
Если дан треугольник АВС и прямая 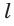
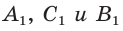
Доказательство:
Проведем отрезок 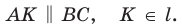
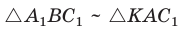

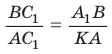
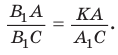
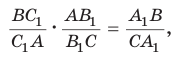
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой 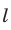
Пример №21
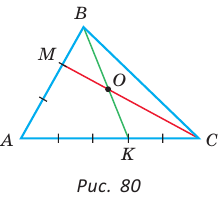
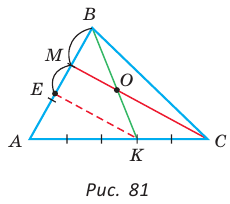
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
Решение:
Способ 1 (теорема Менелая). Рассмотрим 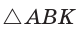
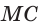
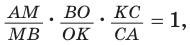
Способ 2 (теорема Фалеса обобщенная). Проведем 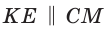
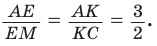
Но 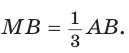
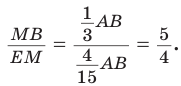
по теореме Фалеса
Ответ:
Пример №22
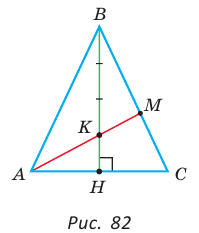
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) 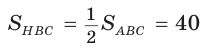
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке 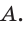
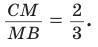
3)
4)
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
Например, 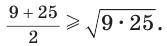
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 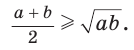
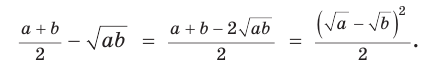
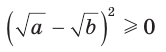
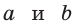
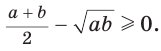
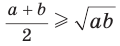
Неравенство 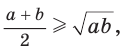
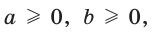
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 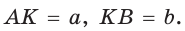

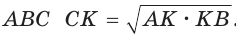
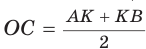
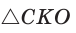
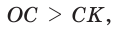
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 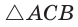
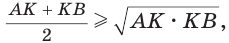
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
3. Тригонометрические формулы (тождества):
Примеры:
4. Формулы площади треугольника и параллелограмма:
5. Среднее пропорциональное в прямоугольном треугольнике:
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
22
Май 2013
Категория: ПланиметрияСправочные материалы
Синус, косинус, тангенс в прямоугольном треугольнике
2013-05-22
2021-07-18

Подробнее про прямоугольный треугольник здесь.
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
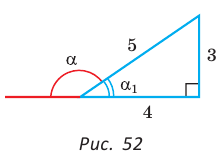
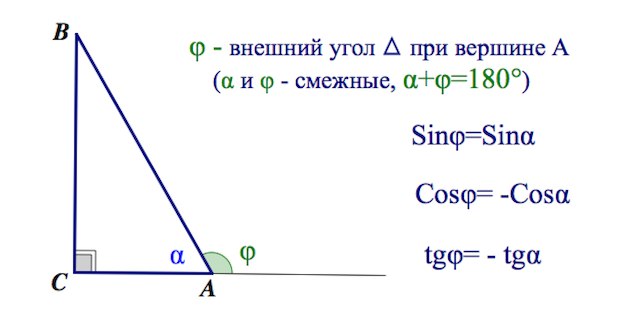
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Автор: egeMax |
комментариев 8
| Метки: шпаргалки-таблицы
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Enter any two known values for a right triangle below to calculate the edge lengths, altitude, angles, area, perimeter, inradius, and circumradius.
Right Triangle Properties:
| leg a: |
3 |
| leg b: |
4 |
| hypotenuse c: |
5 |
| angle α: |
36.87° | 0.6435 rad |
| angle β: |
53.13° | 0.9273 rad |
| height h: |
2.4 |
| area: |
6 |
| perimeter: |
12 |
| inradius: |
1 |
| circumradius: |
2.5 |
Type of Right Triangle:
scalene triangle
(3:4:5 Pythagorean triple)
Learn how we calculated this below
scroll down
On this page:
-
Calculator
-
What is a Right Triangle?
-
Types of Right Triangles
-
How to Find the Hypotenuse of a Right Triangle
-
How to Find a Missing Side
-
How to Find the Angle of a Right Triangle
-
How to Find the Area of a Right Triangle
-
Method One: Using Two Legs
-
Method Two: Using Hypotenuse and One Leg
-
Method Three: Using One Leg and One Angle
-
How to Find the Perimeter
-
Special Right Triangles
-
Formulas for 30 60 90 Right Triangles
-
Formulas for 45 45 90 Right Triangles
What is a Right Triangle?
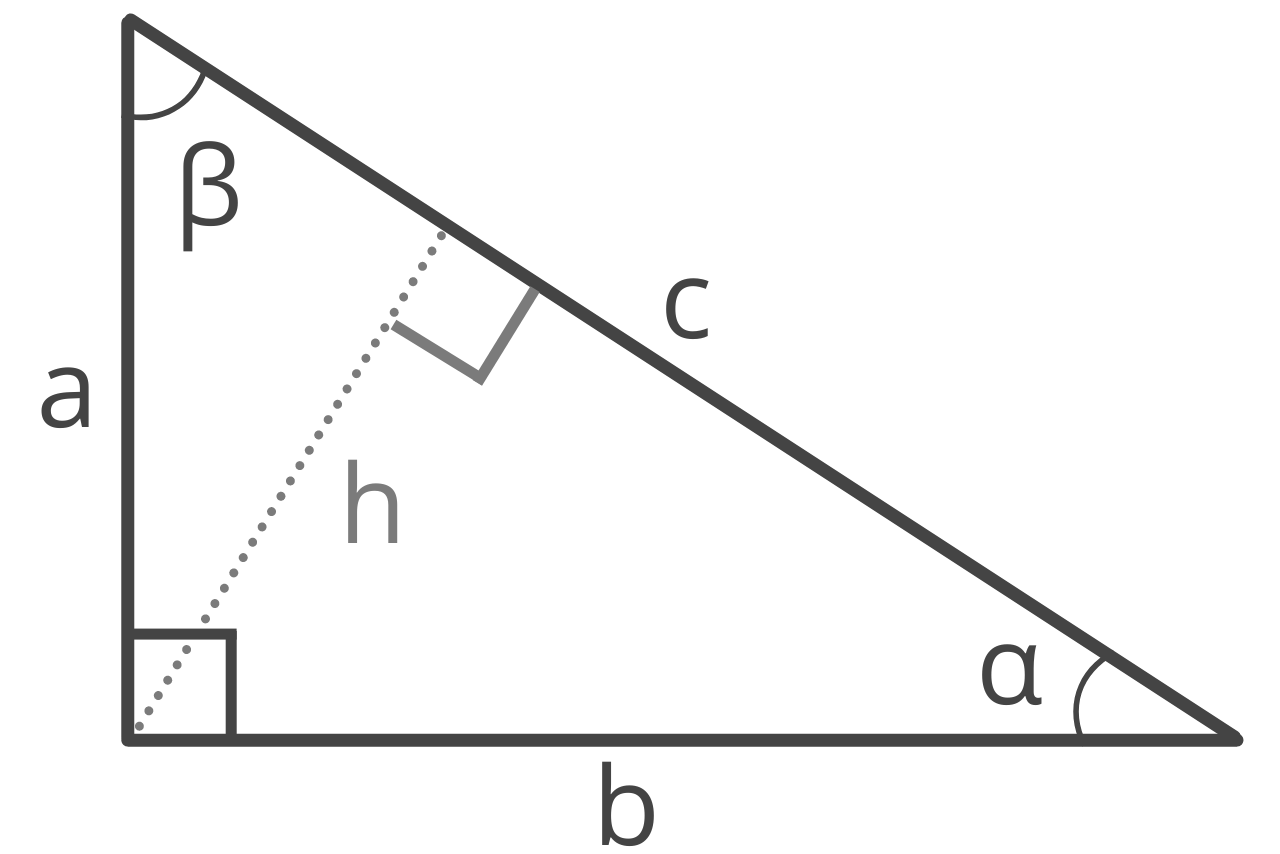
A right triangle, sometimes called a right-angled triangle, is a triangle that has one interior angle equal to exactly 90 degrees, forming what is called a right angle.
The sides adjacent to the right angle are referred to as legs a and b, and are also often referred to as the base and height. The calculator uses the term height to represent the altitude of a triangle.
The side opposite the right angle is called the hypotenuse c.

Types of Right Triangles
Right triangles can be broken into two categories: isosceles and scalene.
An isosceles right triangle is a special isosceles triangle that has two angles that are 45 degrees and legs a and b of equal length.
A scalene right triangle is one where all the angles are unequal, and all the sides are unequal in length.
How to Find the Hypotenuse of a Right Triangle
To calculate the length of the hypotenuse in a right triangle when you know the length of the two legs, you can use the Pythagorean theorem.
The Pythagorean theorem states that side a squared plus side b squared is equal to side c squared. Note, keep in mind that sides a and b specifically refer to the legs, and side c refers to the hypotenuse.
a² + b² = c²
To find the hypotenuse, take the square root of the sum of a squared and b squared.
c = a² + b²
So, the value of the hypotenuse is equal to the square root of leg a squared plus leg b squared.

For example, let’s find the hypotenuse c for a triangle with leg a = 3 and leg b = 4.
3² + 4² = c²
9 + 16 = c²
25 = c²
25 = c
5 = c
So, the hypotenuse c is equal to 5 for a right triangle with legs a = 3 and b = 4.
How to Find a Missing Side
To calculate the length of a missing side, you can use a known side and the hypotenuse and rearrange the Pythagorean theorem to solve the missing variable.
For instance, to find leg b, rearrange the Pythagorean theorem to solve for b by subtracting a² from both sides.
a² + b² = c²
a² + b² – a² = c² – a²
b² = c² – a²
Then take the square root of the right side of the equation to isolate the missing leg, which is b in this example.
b = c² – a²
So, the value of the missing leg b is equal to the square root of the hypotenuse c squared minus the length of the known leg a squared.
How to Find the Angle of a Right Triangle
If you know the lengths of two sides of a right triangle, then you can determine the interior angles using the trigonometric functions sine, cosine, and tangent. These are usually shortened to sin, cos, and tan.
To find the angle given two side lengths, you can use the following formulas:
sin(θ) = opposite ÷ hypotenuse
cos(θ) = adjacent ÷ hypotenuse
tan(θ) = opposite ÷ adjacent
In a right triangle, the adjacent side to θ is the side of the triangle that forms part of the angle θ but is not the hypotenuse. The opposite side to θ is the side that does not form part of the angle θ.
To find one of the angles, choose the formula that can be used given the two known side lengths, then substitute the known values in the formula and solve.
For example, let’s find the angle of a triangle if the adjacent side length is 7 and the hypotenuse is 15.
Start by choosing the equation using adjacent and hypotenuse:
cos(θ) = adjacent ÷ hypotenuse
cos(θ) = 7 ÷ 15
cos(θ) = 0.4667
θ = cos-1(0.4667)
θ = 62.18°
So, for a right triangle with angle θ, with an adjacent side length of 7 and hypotenuse of 15, the angle θ is 62.18°. Note, in the above example, the inverse of cosine was used in the second to last question to isolate θ.
You can find the remaining angle in a few ways. The first way is to repeat using the same method as before, but with a different formula to find the remaining angle.
You can also use the special rule of triangles where the sum of all angles must equal 180°. Subtract 90° (because this is a right triangle, we know one of the angles is 90°) and the angle you just found from 180 to find the missing angle.
You can use the mnemonic SOHCAHTOA to help remember the equations above.
If you split SOHCAHTOA into three parts, each part represents one of the formulas, where each letter is the first letter in the part of the equation.
SOH · CAH · TOA
SOH: sin(θ) = opposite ÷ hypotenuse
CAH: cos(θ) = adjacent ÷ hypotenuse
TOA: tan(θ) = opposite ÷ adjacent
How to Find the Area of a Right Triangle
There are a few methods to find the area of a right triangle.
Method One: Using Two Legs
If you know the length of the two legs in a right triangle, then you can find the area using the formula:
A = 1 / 2a × b
The area A of a right triangle is equal to one-half times leg a times leg b.
Method Two: Using Hypotenuse and One Leg
If you know the hypotenuse and one of the legs, then you can use a variation of the Pythagorean theorem to find the area:
A = a × 1 / 2c² – a²
The area A of a right triangle is equal to leg a times 1/2 times the square root of the hypotenuse c squared times minus leg a squared. Notice the √(c² – a²) portion of this formula is simply the Pythagorean theorem isolated for b.
Method Three: Using One Leg and One Angle
If you know the length of one leg and the value of an adjacent angle, then you can use the tangent function to find the area.
Given the value of leg a and angle β, find the area using the following formula:
A = a² × tan(β) / 2
Given the value of leg b and angle α, find the area using the following formula:
A = b² × tan(α) / 2
The area A of a right triangle is equal to leg a squared times one-half the tangent of angle β, or leg b squared times one-half the tangent of angle α.
Keep in mind that in the above formulas, angle β must be adjacent to leg a, and angle α must be adjacent to leg b.
How to Find the Perimeter
The formula to find the perimeter of a right triangle is:
perimeter = a + b + c
The perimeter is equal to leg a plus leg b plus hypotenuse c.
You can use the formulas above to find the lengths of the missing leg or hypotenuse if any are missing.
Special Right Triangles
There are a few types of special right triangles, which are triangles that have specific proportions. These special right triangles also have formulas to simplify solving them.
Formulas for 30 60 90 Right Triangles
A 30 60 90 triangle is a special right triangle with 30° and 60° interior angles adjacent to the right 90° angle.
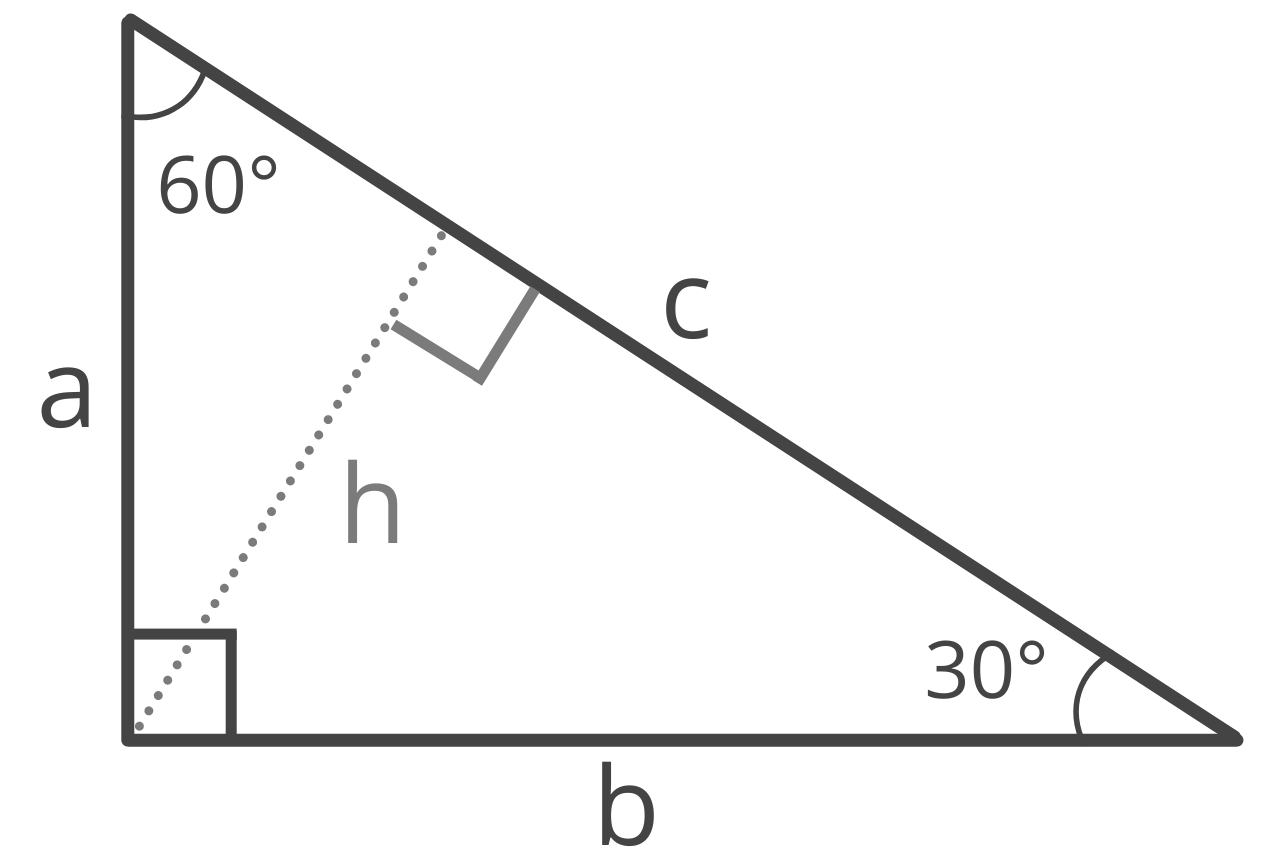
Leg a
Given the length of leg b (the side opposite the 60° angle), the formula to find the length of a is:
a = b × √3 / 3
The length of leg a is equal to b times the square root of 3, divided by 3.
Leg b
Given the length of leg a (the side opposite the 30° angle), the formula to find the length of b is:
b = a√3
The length of leg b is equal to a times the square root of 3.
Hypotenuse c
In the case of a 30 60 90 right triangle, the length of the hypotenuse is always equal to two times the length of the shortest leg. So, given the length of the short leg a, the formula to find the hypotenuse is:
c = 2a
The length of c is equal to 2 times a.
Formulas for 45 45 90 Right Triangles
A 45 45 90 triangle is a special right isosceles triangle with 45° interior angles adjacent to the 90° right angle.
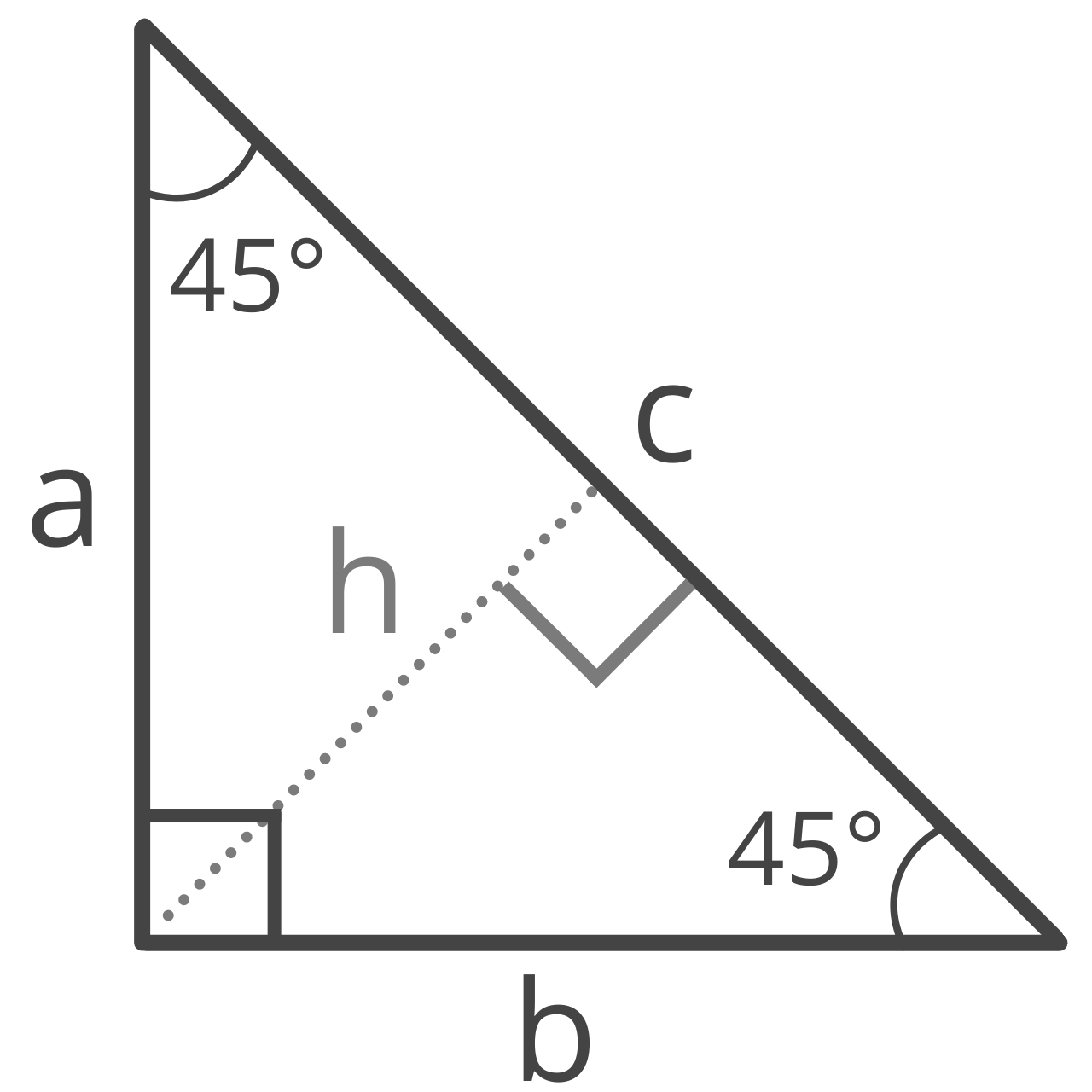
Legs a & b
Given the hypotenuse, you can find the length of the legs a and b in a 45 45 90 triangle using the formula:
a = b = c√2 / 2
The length of legs a and b are equal to hypotenuse c times the square root of 2, divided by 2.
Hypotenuse c
Since it is an isosceles triangle, both legs are the same length, so there is a special formula to find the length of the hypotenuse.
c = a√2
The length of side c is equal to the length of side a times the square root of 2.
Area
There is also a special formula to find the area of a 45 45 90 right triangle:
A = a² / 2
The area A of the right triangle is equal to the length of leg a squared, divided by 2.