Как найти мнимое число комплексного числа

8

Занятие 12.
Комплексные
числа.

12.1. Определение комплексных чисел в
алгебраической форме. Сравнение и
изображение комплексных чисел на
комплексной плоскости. Комплексное
сопряжение. Сложение, умножение, деление
комплексных чисел.

12.2. Модуль, аргумент комплексного числа.

12.3. Тригонометрическая и показательная
формы записи комплексного числа.

12.4. Возведение в целую степень и извлечение
корня из комплексного числа.

Определение комплексных чисел в
алгебраической форме. Сравнение и
изображение комплексных чисел на
комплексной плоскости. Комплексное
сопряжение. Сложение, умножение, деление
комплексных чисел.

Комплексным числом в алгебраической
форме называется число

,

(1)

где

называется мнимой единицей и

— действительные числа:

называется действительной (вещественной)
частью;

— мнимой частью комплексного числа
.
Комплексные числа вида

называются чисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой
.

По определению,

,

и т.д.

Множество всех действительных чисел

является частью множества

:
.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству
.
Например,

и
,
т.к.
.

Комплексные числа в алгебраической
форме естественным образом возникают
при решении квадратных уравнений с
отрицательным дискриминантом.

Пример 1. Решить уравнение
.

Решение.
,

т.к.
.

Следовательно, заданное квадратное
уравнение имеет комплексные корни

,

.

Пример 2. Найти действительную и
мнимую части комплексных чисел

,

,

.

Решение.

— соответственно вещественная и мнимая
части числа
,

.

.

.

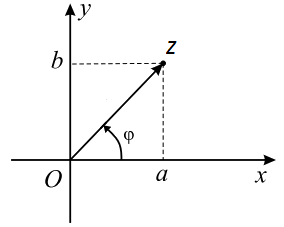
Любое комплексное число

изображается вектором на комплексной
плоскости
,
представляющей плоскость с декартовой
системой координат
.
Начало вектора лежит в точке
,
а конец — в точке с координатами
(рис
1.) Ось
называется
вещественной осью, а ось

— мнимой осью комплексной плоскости
.

Рис. 1.

Комплексные числа

сравниваются между собой только знаками
.

.
Если же хотя бы одно из равенств:

нарушено, то
.
Записи типа

не имеют смысла.

По определению, комплексное число

называется комплексно сопряженным
числу
.
В этом случае пишут
.
Очевидно, что
.
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.

Например,
.

Над комплексными числами можно выполнять
такие операции, как сложение (вычитание),
умножение, деление.

1. Сложение комплексных чисел

производится так:

.

Свойства операции сложения:

— свойство коммутативности;

— свойство ассоциативности.

Нетрудно видеть, что геометрически
сложение комплексных чисел

означает сложение отвечающих им на
плоскости

векторов по правилу параллелограмма.

Операция вычитание числа

из числа

производится так:

.

2. Умножение комплексных чисел

производится так:

.

Свойства операции умножения:

— свойство коммутативности;

— свойство ассоциативности;

— закон дистрибутивности.

3. Деление комплексных чисел

выполнимо только при

и производится так:

.

Пример 3. Найти
,
если
.

Решение.

1)
.(ош!)

2)
.(ош!)

3)
.(ош!)

4)
.

5)
.

Пример 4. Вычислить
,
если
.

Решение.

.

z, т.к.
.

.(ош!)

Нетрудно проверить (предлагается это
сделать самостоятельно) справедливость
следующих утверждений:

.

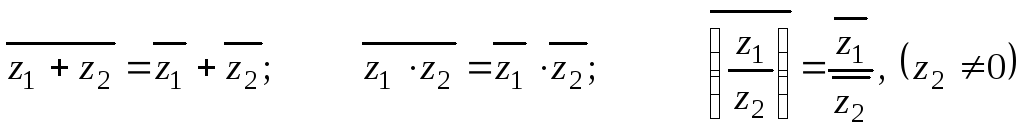
Модуль, аргумент комплексного числа.

Модуль комплексного числа

(модуль

обозначается
)
это — неотрицательное число
,
т.е.
.

Геометрический смысл

— длина вектора, представляющего число

на комплексной плоскости
.
Уравнение

определяет множество всех чисел

(векторов на
),
концы которых лежат на единичной
окружности
.

Аргумент комплексного числа

(аргумент

обозначается
)
это – угол

в радианах между вещественной осью

и числом

на комплексной плоскости
,
причем

положителен, если он отсчитывается от

до

против часовой стрелки, и

отрицателен, если

отсчитывается от оси

до

по часовой стрелке.

Таким образом, аргумент числа

определяется неоднозначно, с точностью
до слагаемого
,
где
.
Однозначно аргумент числа

определяется в пределах одного обхода
единичной окружности

на плоскости
.
Обычно требуется найти

в пределах интервала
,
такое значение называется главным
значением аргумента числа

и обозначается
.

и

числа

можно найти из уравнения
,
при этом обязательно нужно
учитывать, в какой четверти плоскости

лежит конец вектора

— точка
:

если

(1-я четверть плоскости
),
то
;

если

(2-я четверть плоскости
),
то;

если

(3-я четверть плоскости
),
то
;

если

(4-я четверть плоскости
),
то
.

Фактически, модуль и аргумент числа
,
это полярные координаты

точки

— конца вектора

на плоскости
.

Пример 5. Найти модуль и главное
значение аргумента чисел:

.

Решение.

1)
.

2)
.

3)

.

4)
.

5)

.

6)
.

7)

.

.

Аргументы чисел
,
лежащих осях
,
разделяющих четверти 1,2,3,4 комплексной
плоскости
,
находятся сразу же по графическим
изображениям этих чисел на плоскости
.

Тригонометрическая и показательная
формы записи комплексного числа.
Умножение и деление комплексных чисел
в тригонометрической и показательной
формах записи.

Тригонометрическая форма записи
комплексного числа

имеет вид:

,

(2)

где
—
модуль,
—
аргумент комплексного числа
.
Такое представление комплексных чисел
вытекает из равенств
.

Показательная (экспоненциальная)
форма записи комплексного числа

имеет вид:

,

(3)

где
—
модуль,
—
аргумент числа
.
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера:

.

(4)

Эта формула доказывается в курсе ТФКП
(Теория функций комплексного переменного).

Пример 6. Найти тригонометрическую
и экспоненциальную формы записи
комплексных чисел:

из примера 5.

Решение. Воспользуемся результатами
примера 5, в котором найдены модули и
аргументы всех указанных чисел.

1)

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма записи числа
.

2)

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма записи числа
.

3)

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма записи числа
.

4)

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма записи числа
.

5)

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма записи числа
.

6)

— тригонометрическая форма числа
,

— показательная (экспоненциальная)
форма числа
.

7)

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма числа
.

— тригонометрическая форма записи числа
,

— показательная (экспоненциальная)
форма записи числа
.

Показательная форма записи комплексных
чисел приводит к следующей геометрической
трактовке операций умножения и деления
комплексных чисел. Пусть

— показательные формы чисел
.

1.

При перемножении комплексных чисел
их модули перемножаются, а аргументы
складываются.

2.

При делении комплексного числа

на число

получается комплексное число
,
модуль

которого равен отношению модулей
,
а аргумент

— разности

аргументов чисел
.

Возведение в целую степень и извлечение
корня из комплексного числа.

По определению,

.

При возведении в целую степень
комплексного
числа
,
следует действовать так: сначала найти
модуль

и аргумент

этого числа; представить

в показательной форме
;
найти
,
выполнив следующую последовательность
действий

,
где
.
(5)

Замечание. Аргумент

числа

может не принадлежать интервалу
.
В этом случае следует по полученному
значению

найти главное значение

аргумента

числа
,
прибавляя (или вычитая) число

с таким значением
,
чтобы

принадлежало интервалу
.
После этого, нужно заменить в формулах
(5)

на
.

Пример 7. Найти

и
,
если
.

Решение.

1)
=
(см. число

из примера 6).

2)
,
где
.

.

.

Следовательно,

можно заменить на

и, значит,

,
где
.

3)
,
где
.

.

Заменим

на
.
Следовательно,

.

Извлечение корня
-й
степени

из комплексного числа

проводится по формуле Муавра-Лапласа

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

• Действительная и мнимая часть комплексного числа
• Мнимая единица
• Равные комплексные числа

Например. $z=3-7 i$

Действительная и мнимая часть комплексного числа

Например. Для комплексного числа
$z=3-7 i$ действительная часть
$a=operatorname{Re} z=3$, а мнимая —
$b=operatorname{Im} z=-7$ .

Если действительная часть комплексного числа $z=a+b i$
равна нулю ( $a=operatorname{Re} z=0$ ), то комплексное число
называется чисто мнимым.

Например. $z=-2 i$

Мнимая единица

Величина $i$ называется мнимой единицей и
удовлетворяет соотношению:

Равные комплексные числа

Два комплексных числа $z_{1}=a_{1}+b_{1} i$ и
$z_{2}=a_{2}+b_{2} i$ называются равными, если равны их
действительные и мнимые части соответственно:

$z_{1}=z_{2} Leftrightarrow a_{1}=a_{2} wedge b_{1}=b_{2}$

Число $overline{z}=a-b i$ называется
комплексно сопряженным числом к числу
$z=a+b i$ .

То есть комплексно сопряженные числа отличаются лишь знаком мнимой части.

Например. Для комплексного числа
$z_{1}=2+3 i$ комплексно сопряженным есть число
$overline{z}_{1}=2-3 i$ ; для
$z_{2}=i$ комплексно сопряженное
$overline{z}_{2}=-i$ и для
$z_{3}=-2$ имеем, что
$overline{z}_{3}=-2$ .

Комплексное число
 $-z=-a-b i$  называется противоположным к комплексному числу
$z=a+b i$ .

Например. Противоположным к числу
$z=2+i$ есть число:
$-z=-(2+i)=-2-i$ .

Читать дальше: геометрическая интерпретация комплексного числа.

Комплексные числа

В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ mathbb{C} $.

Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = sqrt{-1} $, числа $ a,b in mathbb{R} $ вещественные. 

Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ mathbb{R} subset mathbb{C} $. К слову говоря также возможно, что $ a = 0 $.

Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.

Введем понятие комплексно-сопряженных чисел. К каждому комплексному числу $ z = a+ib $ существует такое, что $ overline{z} = a-ib $, которое и называется сопряженным. Такие числа отличаются друг от друга только знаками между действительной и мнимой частью.

Формы

Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:

1. Алгебраическая $ z = a+ib $
2. Показательная $ z = |z|e^{ivarphi} $
3. Тригонометрическая $ z = |z|cdot(cos(varphi)+isin(varphi)) $

Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.

Изображение

Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:

Видим, что $ a,b in mathbb{R} $ расположены на соответствующих осях плоскости. 

Комплексное число $ z = a+ib $ представляется в виде вектора $ overline{z} $.

Аргумент обозначается $ varphi $.

Модуль $ |z| $ равняется длине вектора  $ overline{z} $ и находится по формуле $ |z| = sqrt{a^2+b^2} $

Аргумент комплексного числа $ varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.

Если:

1. $ a>0 $, то $ varphi = arctgfrac{b}{a} $
2. $ a<0, b>0 $, то $ varphi = pi + arctgfrac{b}{a} $
3. $ a<0, b<0 $, то $ varphi = -pi + arctgfrac{b}{a} $

Операции

Над комплексными числами можно проводить различные операции, а именно:

• Складывать и вычитать
• Умножать и делить
• Извлекать корни и возводить в степень
• Переводить из одной формы в другую 

Для нахождения суммы и разности складывается и вычитаются только соответствующие друг другу члены. Мнимая часть только с мнимой, а действительная только с действительной:

$$ z_1 + z_2 = (a_1+ib_1) + (a_2+ib_2) = (a_1 + a_2)+i(b_1 + b_2) $$

$$ z_1 — z_2 = (a_1+ib_1) — (a_2+ib_2) = (a_1 — a_2)+i(b_1 — b_2) $$

Умножение в алгебраической форме:

$$ z_1 cdot z_2 = (a_1+ib_1) cdot (a_2+ib_2) = (a_1 a_2 — b_1 b_2)+i(a_1 b_2 + a_2 b_1) $$

Умножение в показательной форме:

$$ z_1 cdot z_2 = |z_1|e^{ivarphi_1} cdot |z_2|e^{ivarphi_2} = |z_1|cdot|z_2|cdot e^{i(varphi_1 + varphi_2)} $$

Деление в алгебраической форме:

$$ frac{z_1}{z_2} = frac{a_1+ib_1}{a_2+ib_2} = frac{a_1 a_2 + b_1 b_2 }{a_2 ^2 + b_2 ^2} + i frac{a_2 b_1 — a_1 b_2}{a_2 ^2 + b_2 ^2} $$

Деление в показательной форме:

$$ frac{z_1}{z_2} = frac{|z_1|e^{ivarphi_1}}{|z_2|e^{ivarphi_2}} = frac{|z_1|}{|z_2|}e^{i(varphi_1 — varphi_2)} $$

Для возведения в степень необходимо умножить комплексное число само на себя необходимое количество раз, либо воспользоваться формулой Муавра:

$$ z^n = |z|^n(cos nvarphi+isin nvarphi) $$

Для извлечения корней необходимо также воспользоваться формулой Муавра:

$$ z^frac{1}{n} = |z|^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$

Так же теория комплексных чисел помогает находить корни многочленов. Например, в квадратном уравнении, если $ D<0 $, то вещественных корней нет, но есть комплексные. В последнем примере рассмотрен данный случай.

Рассмотрим на практике комплексные числа: примеры с решением.

Примеры с решением

Пример 1

Перевести из алгебраической в тригонометрическую и показательную форму:$$ z = 4-4i $$

Решение

Для начала приступим к нахождению модуля комплексного числа: $$ |z| = sqrt{4^2 + (-4)^2} = sqrt{16 + 16} = sqrt{32} = 4sqrt{2} $$ Осталось найти аргумент: $$ varphi = arctg frac{b}{a} = arctg frac{-4}{4} = arctg (-1) = -frac{pi}{4} $$ Теперь составляем тригонометрическую запись комплексного числа, указанного в условии примера: $$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ Тут же можно записать показательную форму: $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ z = 4sqrt{2}bigg(sin(-frac{pi}{4}) + isin(-frac{pi}{4}) bigg) $$ $$ z = 4sqrt{2} e^{-frac{pi}{4}i} $$

Пример 2

Вычислить сумму и разность заданных комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$

Решение

Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел: $$ z_1 + z_2 = (3+i) + (5-2i) = (3+5)+(i-2i) = 8 — i $$ Аналогично выполним вычитание чисел: $$ z_1 — z_2 = (3+i) — (5-2i) = (3-5)+(i+2i) = -2 + 3i $$

Ответ

$$ z_1 + z_2 = 8 — i; z_1 — z_2 = -2 + 3i $$

Пример 3

Выполнить умножение и деление комплексных чисел: $$ z_1 = 3+i, z_2 = 5-2i $$

Решение

$$ z_1 cdot z_2 = (3+i) cdot (5-2i) = $$ Просто на просто раскроем скобки и произведем приведение подобных слагаемых, так же учтем, что $ i^2 = -1 $: $$ = 15 — 6i + 5i -2i^2 = 15 — i — 2cdot(-1) = $$ $$ = 15 — i + 2 = 17 — i $$ Так, теперь разделим первое число на второе: $$ frac{z_1}{z_2} = frac{3+i}{5-2i} = $$ Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки: $$ = frac{(3+i)(5+2i)}{(5-2i)(5+2i)} = frac{15 + 6i + 5i + 2i^2}{25 + 10i — 10i -4i^2} = $$ $$ = frac{15 + 11i -2}{25 + 4} = frac{13 + 11i}{29} $$ Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы: $$ frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$

Ответ

$$ z_1 cdot z_2 = 17 — i; frac{z_1}{z_2} = frac{13}{29} + frac{11}{29}i $$

Пример 4

Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $

Решение

1) $ n = 2 $ Для возведения в квадрат достаточно умножить число само на себя: $$ z^2 = (3+3i)^2 = (3+3i)cdot (3+3i) = $$ Пользуемся формулой для умножения, раскрываем скобки и приводим подобные: $$ =9 + 9i + 3icdot 3 + 9i^2 = 9 + 18i — 9 = 18i $$ Получили ответ, что $$ z^2 = (3+i)^2 = 18i $$ 2) $ n = 7 $ В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую. Вычисляем значение модуля: $$ |z| = sqrt{3^2 + 3^2} = sqrt{9 + 9} = sqrt{18} = 3sqrt{2} $$ Найдем чем равен аргумент: $$ varphi = arctg frac{3}{3} = arctg(1) = frac{pi}{4} $$ Записываем в тригонометрическом виде: $$ z = 3sqrt{2}(cos frac{pi}{4} + isin frac{pi}{4}) $$ Возводим в степень $ n = 7 $: $$ z^7 = (3sqrt{2})^7 (cos frac{7pi}{4} + isin frac{7pi}{4}) = $$ Преобразуем в алгебраическую форму для наглядности: $$ =(3sqrt{2})^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^7 (frac{1}{sqrt{2}}-ifrac{1}{sqrt{2}}) = $$ $$ = 3^7 sqrt{2}^6 (1-i) = 3^7 cdot 8(1-i) = $$ $$ = 2187 cdot 8 (1-i) = 17496(1-i) $$

Ответ

$$ z^2 = (3+i)^2 = 18i $$ $$ z^7 = 17496(1-i) $$

Пример 5

Извлечь корень $ sqrt[3]{-1} $ над множеством $ mathbb{C} $

Решение

Представим число в тригонометрической форме. Найдем модуль и аргумент: $$ |z| = sqrt{(-1)^2 + 0^2} = sqrt{1+0} = sqrt{1}=1 $$ $$ varphi = arctg frac{0}{-1} +pi = arctg 0 + pi = pi $$ Получаем: $$ z = (cos pi + isin pi) $$ Используем знакомую формулу Муавра для вычисления корней любой степени: $$ z^frac{1}{n} = r^frac{1}{n}bigg(cos frac{varphi + 2pi k}{n}+isin frac{varphi + 2pi k}{n}bigg), k=0,1,…,n-1 $$ Так как степень $ n = 3 $, то по формуле $ k = 0,1,2 $: $$ z_0 = sqrt[3]{1} (cos frac{pi}{3}+isin frac{pi}{3}) = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = sqrt[3]{1} (cos frac{3pi}{3}+isin frac{3pi}{3}) = -1 $$ $$ z_2 = sqrt[3]{1} (cos frac{5pi}{3}+isin frac{5pi}{3}) = frac{1}{2} — ifrac{sqrt{3}}{2} $$

Ответ

$$ z_0 = frac{1}{2}+ifrac{sqrt{3}}{2} $$ $$ z_1 = -1 $$ $$ z_2 = frac{1}{2} — ifrac{sqrt{3}}{2} $$

Пример 6

Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ mathbb{C} $

Решение

Решать будем по общей формуле, которую все выучили в 8 классе. Находим дискриминант $$ D = b^2 — 4ac = 2^2 — 4cdot 1 cdot 2 = 4-8 = -4 $$ Получили, что $ D=-4<0 $ и казалось бы, что решение можно заканчивать. Но нет! В нашем задании требуется решить уравнение над комплексным множеством, а то что дискриминант отрицательный означает только лишь отсутствие вещественных корней. А комплексные корни есть! Найдем их продолжив решение: $$ x_{1,2} = frac{-bpm sqrt{D}}{2a} = frac{-2pm sqrt{-4}}{2} = $$ Заметим, что $ sqrt{-4} = 2sqrt{-1} = 2i $ и продолжим вычисление: $$ = frac{-2 pm 2i}{2} = -1 pm i $$ Получили комплексно-сопряженные корни: $$ x_1 = -1 — i; x_2 = -1 — i $$ Как видите любой многочлен можно решить благодаря комплексным числам.

Ответ

$$ x_1 = -1 — i; x_2 = -1 — i $$

В статье «Комплексные числа: примеры с решением» было дано определение, основные понятия, формы записи, алгебраические операции и решение практических примеров.

Содержание:

1. Комплексные числа
2. Алгебраическая форма комплексного числа
3. Действия над комплексными числами в алгебраической форме
4. Геометрическая интерпретация комплексного числа
5. Тригонометрическая форма комплексного числа
6. Действия над комплексными числами в тригонометрической форме
7. Показательная форма комплексного числа
8. Что такое комплексное число
9. Понятие о комплексном числе
10. Арифметические операции над комплексными числами
11. Отыскание комплексных корней уравнений

Комплексные числа

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i² = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.

Алгебраическая форма комплексного числа

На множестве действительных чисел ряд алгебраических задач, в частности нахождение корней квадратных уравнений с отрицательным дискриминантом, не имеет решения. Введём некоторое навое число, которое будем считать решением уравнения х² + 1 = 0. Корень уравнения  х² + 1 = 0 или  х² = -1 называется мнимой единицей и обозначается буквой i. Таким образом i² = -1.

В некоторых технических дисциплинах мнимую единицу обозначают буквой j. В дальнейшем будем использовать оба обозначения.

Мнимая единица позволяет ввести числа нового вида, которые называют комплексными.

Комплексным числом называют выражение вида , где  — действительные числа, i — мнимая единица.

Число  называют действительной, а число  — мнимой частями комплексного числа. Комплексное число, как правило, обозначают буквой . Два комплексных числа  называют равными тогда и только тогда, когда , то есть когда равны их действительные части и коэффициенты при мнимой части. 

Понятия «больше» и «меньше» для комплексных чисел не определено. Комплексное число  называется нулём и обозначается 0; комплексное число  отождествляется с действительным числом ; комплексное число  называют чисто мнимым и обозначают . Число 0 является единым числом, которое одновременно и является действительным, и чисто мнимое.

Комплексные числа  называются сопряжёнными и обозначаются  и. Например, в числе , сопряжённым к нему будет число , а для числа  сопряжённым будет число .

Множество комплексных чисел принято обозначать буквой С. Запись комплексного числа в виде  называется алгебраической формой комплексного числа.

Действия над комплексными числами в алгебраической форме

Сложение, вычитание, умножение комплексных чисел в алгебраической форме по правилам соответствующих действий над многочленами.

Пример 1. Найти сумму и произведение комплексных чисел 

Решение: Сумму находим формальным сложением двучленов 

произведение находим перемножив двучлены  с последующей заменой .

Ответ: 

Легко увидеть, что слагаемое двух сопряжённых чисел является действительным числом:

Воспользуемся этим свойством для введения действия деления двух комплексных чисел.

При делении комплексных чисел , где  достаточно умножить числитель и знаменатель дроби  на число сопряжённое к знаменателю, то есть на 

Пример 2. Даны комплексные числа   и  Найдите разность  и частное 

Решение:

Находим разность вычитанием двучленов 

Чтобы найти частное  умножим числитель и знаменатель на число, сопряжённое к знаменателю:

Ответ: 

Действия над комплексными числами имеют следующие интересные свойства:

Доказательство выходит из определения сопряжённых чисел. Действительно, 

Аналогично доказываются и другие приведённые свойства.

Возведение комплексного числа в степень выполняется по формулам возведения двучлена в степень. При этом следует учитывать, что

Например:

Пример 3. Найти комплексное число  

Решение: 

Выполнив в знаменателе возведение в степень, получим:

Умножив числитель и знаменатель на число, сопряжённое к знаменателю, то есть на -5-12i, получим:

Ответ: z = i.

Геометрическая интерпретация комплексного числа

Каждому комплексному числу  можно поставить в соответствие упорядоченную пару действительных чисел  и наоборот. Такая упорядоченная пара действительных чисел определяет точку или вектор на плоскости.

Следовательно, комплексное число вида  изображается на координатной плоскости точкой  или вектором, начало которого совпадает с началом координат, а конец с т. М.

Сама координата плоскости называется при этом комплексной плоскости, ось абсцисс — действительной осью, ось ординат — мнимой осью.

Например, изобразим числа 

Представление комплексного числа как вектора на плоскости позволяет ввести понятие модуля и аргумента комплексного числа.

Модулем комплексного числа называют длину вектора, которая соответствует данному числу (обозначают r либо p).

Аргументом комплексного числа  называют величину угла  между положительным направлением действительной оси и вектора, который соответствует данному комплексному числу.

Рассмотрим рисунок:

На основе теоремы Пифагора получаем 

Например, комплексное число  имеет модуль равный 10, так как 

Аргумент комплексного числа , в отличии от модуля, вычисляется неоднозначно. Так аргументом числа 5 являются следующие углы  Среди бесконечного множества значений аргумента только одно принадлежит промежутку . Эти значения аргумента мы и будем вычислять.

Аргумент легко вычислить, если комплексное число расположено в I четверти. Действительно, согласно тригонометрическим соотношениям в прямоугольном треугольнике (рис. 2) имеем:

Если комплексные числа размещены в других четвертях, то необходимо провести дополнительные рассуждения. Рассмотрим рис. 3. Видим, что для

Таким образом, алгоритм нахождения аргумента комплексного числа следующий:

1.Определить коэффициент  заданного комплексного числа.

2. Найти  

3. Установить, в какой четверти расположено комплексное число.

4. Вычислить аргумент  согласно приведённым формулам.

Возможны и другие способы нахождения аргумента комплексного числа, например:

Пример 4. Найти аргумент комплексного числа 

Тригонометрическая форма комплексного числа

Рассмотрим рис. 2. Согласно тригонометрическим соотношениям в прямоугольном треугольнике числа  можно выразить через r и  таким образом:

Тогда комплексное число запишется в виде:

Запись комплексного числа в таком виде называется тригонометрической формой комплексного числа.

Следовательно, для того, чтобы перейти от алгебраической формы записи комплексного  числа  к тригонометрической, достаточно найти его модуль и аргумент.

Пример 5. Записать число  в тригонометрической форме.

Решение:

Найдём модуль 

Найдём острый угол 

Вектор, который соответствует данному комплексному числу принадлежит третьей четверти, поэтому аргумент равен  следовательно 

Ответ:

Для того, чтобы перейти от тригонометрической формы записи комплексного числа  к алгебраической, достаточно найти действительные числа  из формул 

Пример 6. Записать число  в алгебраической форме.

Найдём  и 

Ответ:

Действия над комплексными числами в тригонометрической форме

В тригонометрической форме записи комплексного числа выполняют действия умножения, деления, возведения в степень, извлечения корня n-й степени. Выведение формул, по которым выполняются действия, относительно просты и основываются на основных формулах тригонометрии.

Следовательно, при умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножают, а аргументы складывают; при делении — модули делят, а аргументы вычитают.

Правило умножения комплексных чисел автоматически распространяется на произвольное число множителей. Если взять равные множители 

Полученную формулу называют формулой Муавра.

Для извлечении корня n-й степени из комплексного числа  используют формулу:

где  арифметический корень, 

Пример 8. Вычислить  Ответ записать в алгебраической форме.

Решение: Находим:

Ответ: 

Пример 9. Вычислить

Решение: Запишем число в тригонометрической форме:

Пример 10. Вычислите . Ответ запишите в алгебраической и тригонометрической формах.

Решение: Запишем число -81 в тригонометрической форме:

Тогда:

Показательная форма комплексного числа

Рассматривая функцию  для комплексной переменной, известный математик Л. Эйлер установил соотношение 

Из заданной формулы следует, что каждое комплексное число  можно записать в виде  которое называется показательной формой записи.

Над комплексными числами в показательной форме выполняют те же действия что и в тригонометрической форме. Выведение формул, по которым выполняют действия основывается на основных свойствах степени.

Пусть , тогда:  

Пример 11. Представить число  в алгебраической форме.

Решение: Согласно условию задачи , поэтому

значит

Ответ:

Пример 12. Выполнить действия, результат записать в тригонометрической и показательной формах: 

Решение: Сначала выполним действия:

Теперь полученное число запишем в тригонометрической и показательной формах. Для этого найдём модуль и аргумент:

Тогда

Ответ: 

Что такое комплексное число

Комплексные числа — это числа вида , где  — вещественные числа, — мнимая единица, то есть число, для которого выполняется равенство: 

Понятие о комплексном числе

Процесс расширения понятия числа от натуральных к действительным был связан как с потребностями практики, так и с нуждами самой математики. Сначала для счета предметов использовались натуральные числа. Необходимость выполнения деления привела к понятию обыкновенной (и десятичной) дроби, необходимость выполнения вычитания — к понятиям нуля и отрицательного числа, необходимость извлечения корней из положительных чисел — к понятию иррационального числа.

Все перечисленные операции выполнимы на множестве действительных чисел. Однако остались и невыполнимые на этом множестве операции, например извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел, отличных от действительных.

Геометрически действительные числа изображаются точками на координатной прямой: каждому действительному числу соответствует одна точка прямой («образ» действительного числа) и, обратно, каждая точка координатной прямой соответствует одному действительному числу. Координатная прямая сплошь заполнена образами действительных чисел, т. е., выражаясь фигурально, «на ней нет места для новых чисел». Возникает предположение о том, что геометрические образы новых чисел надо искать уже не на прямой, а на плоскости. Однако каждую точку М координатной плоскости ху можно отождествить с координатами этой точки. Поэтому естественно в качестве новых чисел ввести упорядоченные пары действительных чисел (упорядоченные в том смысле, что — разные точки, а значит, и разные числа).

Комплексным числом называют всякую упорядоченную пару действительных чисел

Два комплексных числа называют равными тогда и только тогда, когда

Арифметические операции над комплексными числами

Суммой комплексных чисел называют комплексное число

Например,

Комплексным нулем считают пару (0; 0). Числом, противоположным числу считают число обозначают его

Разностью комплексных чисел называют, как обычно, такое число Разность всегда существует и единственна. В самом деле, пусть Тогда  Это значит, что откуда находим

Таким образом, получаем следующее правило вычитания комплексных чисел:

Например, (9; 10) — (8; 12) = (9 — 8; 10 — 12) = (1;-2).

Произведением комплексных чисел  называют комплексное число

Например, если то

Арифметические операции над комплексными числами обладают теми же свойствами, что арифметические операции над действительными числами (см. п. 29).

Пусть Существует, и только одно, комплексное число такое, что Это число и называют, как обычно, частным от деления z на w.

Имеем Так как то должны выполняться равенства

Из этой системы двух уравнений с двумя переменными находим (см. п. 164)  Итак,

Получили следующее правило деления комплексных чисел: если то

Например,

Алгебраическая форма комплексного числа

Используя введенные в п. 45 определения сложения и умножения комплексных чисел, легко получить следующие равенства:

Условились вместо писать просто , а комплексное число (0; 1) обозначать буквой и называть мнимой единицей. Тогда равенство (1) принимает вид т. е.

а равенство (2) — вид

Запись называют алгебраической формой комплексного числа при этом число называют действительной частью комплексного числа z, a bi — его мнимой частью.

Например,

Если мнимая часть комплексного числа отлична от нуля, то число называют мнимым, если при этом = 0, т. е. число имеет вид bi, то его называют чисто мнимым, наконец, если у комплексного числа мнимая часть равна нулю, то получается действительное число .

Алгебраическая форма существенно облегчает выполнение арифметических операций над комплексными числами.

Сложение. Известно (см. п. 45), что

Выполнив сложение тех же чисел в алгебраической форме, считая и с + di обычными двучленами, находим

Сравнивая равенства (7) и (8), замечаем, что получился верный результат.

Вычитание. Известно (см. п. 45), что

Выполнив вычитание тех же чисел в алгебраической форме, считая и с + di обычными двучленами, находим

Сравнивая равенства (9) и (10), замечаем, что получился верный результат.

Умножение. Известно (см. п. 45), что

Выполнив умножение тех же чисел в алгебраической форме, считая  и с + di обычными двучленами, находим

Воспользуемся тем, что (см. равенство (5)); тогда В результате получаем

Сравнивая равенства (11) и (12), замечаем, что получился верный результат.

Деление. Известно (см. п. 45), что если  то

Выполним деление тех же чисел в алгебраической форме, считая и с + di обычными двучленами, a — обычной дробью. Умножив числитель и знаменатель этой дроби на с — di (предполагая, что значение дроби от этого не изменится), находим

Итак,

Сравнивая равенства (13) и (14), замечаем, что получился верный результат.

Подводя итоги, приходим к следующему важному практическому выводу: над комплексными числами, записанными в алгебраической форме, можно осуществлять все арифметические операции как над обычными двучленами, учитывая лишь, что  Чтобы преобразовать в комплексное число дробь вида  нужно числитель и знаменатель дроби умножить на число с — di; числа с + di и с — di называют комплексно-сопряженными.

Пример 1.

Вычислить

Решение: 

Применив формулу , получим

Пример 2.

Вычислить

Решение: 

Пример 3.

Найти действительные числа х и у такие, что выполняется равенство

Решение: 

Имеем  Тогда заданное равенство можно переписать в виде

Комплексные числа  равны тогда и только тогда, когда равны их действительные части ( = с) и коэффициенты при мнимых частях (Ь = d). Значит, приходим к системе уравнений

из которой находим (см. п. 164)

Пример 4.

Найти комплексные числа z, удовлетворяющие равенству

Решение: 

Будем искать комплексное число z в виде х + yi. Имеем

Из последнего равенства следует, что

Эта система имеет два решения (см. п. 164): (2; 3) и (-2; -3). Значит,

Пример 5.

Вычислить

Решение: 

Имеем (см. п. 58)        

Значит,  

Далее, имеем 

Значит,

Отыскание комплексных корней уравнений

Пусть > 0. Так как  Тем самым мы получаем возможность извлекать квадратные корни из отрицательных действительных чисел. Это позволяет находить не только действительные, но и мнимые корни уравнений.

Пример 1.

Решить уравнение

Решение.

Имеем (см. п. 137)  Итак,

Пример 2.

Решить уравнение

Решение.

Имеем Значит, либо х — 2 = 0, откуда находим  либо откуда находим  Итак,  

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

• Математика решение заданий и задач

Смотрите также дополнительные лекции по предмету «Математика»:

Напомним необходимые сведения о комплексных числах.

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i² = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.

Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i² = –1). Число  = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·  = a² + b² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

.

(Например, .)

У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z₁ · z₂ = |z₁| · |z₂| · (cos(Arg z₁ + Arg z₂) + i sin(Arg z₁ + Arg z₂)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра: zⁿ = |z|ⁿ · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wⁿ = z. Видно, что , а , где k может принимать любое значение из множества {0, 1, …, n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).

Далее: Фрактальные размерности