План урока:
Многочлен, вычисление значений многочлена
Стандартный вид многочлена
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Многочлен, вычисление значений многочлена
В предыдущем уроке мы познакомились с понятием одночлена. При записи одночленов не используется операция сложения. Если же возникает необходимость сложить несколько одночленов, то в результате получается многочлен.
В качестве примера многочленов можно привести следующие выражения:
Стоит обратить внимание, что в записи многочлена может использоваться и знак минус, при этом его всё равно можно считать суммой одночленов, а не разностью. Дело в том, что можно условно считать, что знак минус относится к коэффициенту одночлена, например:
Для некоторых видов многочленов существуют особые названия. Если многочлен состоит из двух одночленов, то его называют двучленом. Многочлен, состоящий из 3 одночленов, называют трехчленом.
Иногда в литературе используются такие термины, как «моном» (синоним «одночлена»), «бином» (синоним «двучлена»), «полином» (синоним «многочлена»).
Если известно значение переменных, входящих в полином, то возможно вычисление значения многочлена.
Пример. Найдем значение полинома x3+2x2+5y+1 при значении x=2 и y = 3.
Решение.
Пример. Вычислим значение полинома v4– d4при значении переменных v = 4 и d = 3.
Решение.
Стандартный вид многочлена
Иногда некоторые мономы, входящие в состав полинома, имеют одинаковую буквенную часть. Например, в выражении
первый и третий мономы отличаются лишь своими коэффициентами. Такие слагаемые называются подобными.
У подобных слагаемых одинаковый набор переменных, и при этом они возведены в одинаковые степени. Так, подобными являются мономы:
- 7a2s3 и 2a2s3, так как совпадает буквенная часть a2s3;
- 5v9m7t5 и – 4v9m7t5, так как у них одинаковая буквенная часть – 4v9m7t5;
- a2 и 1000a2, так как есть одинаковая буквенная часть a2.
Также подобными слагаемыми можно считать и числа без буквенной части, например 8 и 2.
В качестве примеров неподобных слагаемых можно привести:
- 7a2s3и 2a2s4 – у переменной s разные степени (3 и 4) в этих мономах;
- 4x2yи 5x2– в буквенной части первого монома есть переменная y, а у второго его нет.
У подобных слагаемых может быть изменен порядок множителей. Так, подобными являются мономы 5p2u4и 9u4p2, так как у одних и тех же переменных стоят одинаковые показатели.
Подобные слагаемые можно складывать друг с другом. В этом случае буквенная часть останется неизменной, а коэффициенты сложатся друг с другом. Например:
Такое действие называется приведением подобных слагаемых.
Пример. Приведите подобные слагаемые полинома:
Решение. В данном полиноме есть три пары подобных слагаемых:
Сгруппируем подобные слагаемые друг с другом, после чего сложим их:
Если в полиноме нет подобных слагаемых, а все входящие в него мономы записаны в стандартном виде, то его называют многочленом стандартного вида.
Что такое одночлен стандартного вида, можно узнать из ранее изученного урока. Примерами полиномов стандартного вида являются:
Далее рассмотрим понятие степени многочлена. Каждый из входящих в полином мономов имеет свой показатель степени(см. урок 3). Степенью полинома стандартного вида называется наибольшая из всех степеней одночленов, входящих в его состав.
Рассмотрим пример. Дан трехчлен 2y2 + x3y + 5y2x, требуется найти его степень.
Решение. Рассматриваемый трехчлен находится в стандартном виде. Он состоит из трех мономов:
Найдем степень каждого из них:
- 2y2 – степень равна 2;
- x3y – степень равна 4 = (3+1);
- 5y2x – степень равна 3 = (2+1).
Получается, что максимальную степень, равную 4, имеет моном x3y. Соответственно, и степень трехчлена также равна 4.
Ответ: 4.
Если же рассматривается полином, не находящийся в стандартном виде, то для вычисления его степени сначала надо привести полином к этому виду.
Пример. Найдите степень полинома с6 + ac2 + 9 – с6.
Решение. На первый взгляд может показаться, что она равна 6, так как один из его мономов, с6, имеет показатель, равный 6. Но это не так. Приведем полином к стандартному виду:
Оказалось, что подобные мономы c6 и – с6 сократились. Получившийся полином состоит из двух мономов, ac2 и 9, чьи степени равны 3 и 0 соответственно. Значит, и степень всего двучлена равна трём.
Ответ: 3.
Определение степени полинома потребуется для решения уравнений в старших классах. Если в одной части уравнения стоит полином, например, третьей степени, в другой части – ноль, то его называют уравнением третьей степени:
Аналогично выделяют уравнения первой, второй, четвертой и любой другой степени.
В зависимости от степени уравнения используются различные методы их решения. Ранее (ссылка на урок уравнения) мы уже научились решать линейные уравнения, которые являются уравнениями 1-ой степени. Обычно чем выше степень уравнения, тем сложнее его решать. Также существует интересная зависимость – количество корней уравнения не превышает его степень (за исключением одного частного случая, при котором есть бесконечное множество решений).
Особое значение в алгебре имеют те полиномы, в которых содержится только одна переменная, например:
- m2 + 4m4 + 5m3 +9(здесь переменная m);
- c6 + 1(единственная переменная – с);
- 3x + 10(запись содержит только x);
- – y4 + 89y10– 2,56y100(используется только y).
Их называют полиномами с одной переменной. Обычно их принято записывать по мере убывания степеней одночленов. То есть впереди пишется моном с максимальной степенью, а в самом конце – число без буквенной части:
То число, которое стоит перед одночленом в наибольшей степени, называют старшим коэффициентом, а число, не имеющее буквенной части – свободным членом (реже свободным коэффициентом):
Для некоторых полиномов с одной переменной есть особое название. Так, многочлен второй степени называют квадратным трехчленом. Дело в том, вторую степень в математике часто называют квадратом, а состоит квадратный трехчлен из трех монов. В качестве примера можно привести:
Конечно, квадратный многочлен может содержать и меньше трех одночленов:
В этом случае иногда бывает удобно добавить «недостающее» слагаемое, поставив перед ним коэффициент, равный нулю:
В общем случае квадратным трехчленом называют выражение вида
где x – произвольная переменная, а, b и c являются произвольными действительными числами. При этом a не должно равняться нулю, иначе получится полином уже только 1-ой степени.
Квадратные трехчлены будут изучены подробнее в старших классах при изучении темы «Квадратные уравнения».
Сложение и вычитание многочленов
Полиномы можно складывать друг с другом, а также вычитать. При этом, возможно, придется приводить подобные слагаемые.
Пример. Произведите сложение многочленов 8z2 + 3z +12 и 2z4 + 9z.
Решение. Запишем интересующую нас сумму:
Если перед скобками стоит знак «+», то можно просто опустить скобки:
Осталось привести полином к стандартному виду. Здесь есть лишь одна пара подобных одночленов, 3z и 9z:
При вычитании многочленов надо учитывать следующее правило:
Пример. Вычтите из полинома x5 + 3x3– 7y3 + 9x2 + 17 трехчлен 2y4 + 0,4y3– 25.
Решение:
Запишем разность полиномов:
Первые скобки можно опустить, так как перед ними нет никакого знака. Перед вторыми скобками стоит минус, а потому для раскрытия скобок знаки слагаемых в них надо поменять на противоположные. Вместо 2y4 надо написать – 2y4, вместо 0,4y3 поставим – 0,4y3, а – 25 заменим на + 25:
Осталось привести подобные слагаемые:
Стоит заметить, что при сложении и вычитании полиномов их степени не могут увеличиться. Так, если складываются два полинома 5-ой и 4-ой степени, то в результате получится многочлен, чья степень будет не больше 5.
Рассмотрим более сложный пример с вложенными (внутренними) скобками. Необходимо упростить выражение
Решение. Раскроем первые скобки. Перед ними стоит минус, поэтому знаки слагаемых должны поменяться на противоположные. Однако обратите внимание, что здесь есть вложенные скобки (2a2b – ab) и (ab2 + 2a2b). Менять следует только знак перед ними, а знаки внутри вложенных скобок не меняются! Они рассматриваются как единые, неизменяемые слагаемые:
Теперь раскроем оставшиеся две скобки:
Приведем подобные слагаемые. Для наглядности пары подобных мономов подчеркнуты. Одной чертой подчеркнуты мономы с буквенной частью ab2, двумя чертами – мономы с a2b, а штриховой линией выделены мономы с буквенной частью ab:
Умножение одночлена на многочлен
Напомним распределительный закон умножения:
Используя этот закон, можно производить умножение одночлена на многочлен.
Пример. Перемножьте выражения 5v2 и 9v3 + 2t4.
Решение: Запишем произведение выражений:
Такое раскрытие скобок можно объяснить с помощью «метода фонтанчика»:
От множителя 5v2 строят линии (синего цвета к) КАЖДОМУ слагаемому в скобке. Каждой такой линии соответствует отдельное произведение в получаемом полиноме.
После раскрытия скобок получили два произведения одночлена на одночлен, которые считаем по отдельности (см. урок 3):
Можно сформулировать следующее правило умножения многочлена на одночлен:
Ещё один пример. Перемножьте полином 2x2y + 4xy2 – 1 и моном – 3ху.
Решение:
Здесь метод «фонтанчика» будет выглядеть так:
Можно заметить, что после умножения монома на полином получится столько одночленов, сколько их было в исходном полиноме. Это правило можно использовать для самоконтроля.
Умножение многочлена на многочлен
Пусть нам надо перемножить два полинома, a+bи c+d. Запишем их произведение:
Заменим выражение a + b переменной k:
Теперь исходное произведение можно выразить как произведение монома и полинома:
Проведем обратное преобразование, заменив k на a + b:
Наконец, раскроем скобки в этом выражении:
Эту формулу можно проиллюстрировать геометрически. Рассмотрим прямоугольник со сторонами a + b и c + d:
Площадь этого прямоугольника, как и любого другого, равна произведению его сторон, то есть(a + b)(c + d).С другой стороны, она состоит из 4 прямоугольников, чьи площади также вычисляются как произведения их сторон, и составляют ac, bc, ad и bd. Поэтому можно записать равенство
Получается, что для умножения многочлена на многочлен нужно перемножать попарно все мономы, входящие в их состав, после чего сложить их.
Если в одном полиноме содержится m слагаемых, а в другом n, то результатом их перемножения окажется новый полином, содержащий m•n мономов (до приведения подобных слагаемых). Для перемножения многочленов также используется метод «фонтанчика».
Пример. Найдем произведение выражений 3a2 – 4ab + b2и 2a– b.
Решение: В первом полиноме содержится 3 монома, а во втором – 2, поэтому после их перемножения мы получим сумму 3•2 = 6 одночленов:
Раскрытие скобок «фонтанчиком» будет выглядеть так:
В результате действительно получилась сумма 6 мономов. Осталось вычислить каждый из них, после чего привести подобные слагаемые:
Заметим, что при перемножении полиномов происходит сложение степеней многочленов. Действительно, в рассмотренном выше примере мы умножили полином второй степени 3a2 – 4ab + b2 на полином первой степени 2a– b, и получили в результате многочлен 3-ей (2+1) степени.
Также возможно умножение многочленов в столбик. Особенно это удобно делать в случае с полиномами с одной переменной.
Пример. Найдите произведение выражений 2x3 + 3x2 +5x + 9 и x2 + 4x + 7.
Решение: Запишем полиномы в столбик, один под другим:
Далее умножим самый правый моном второго многочлена, то есть число 7, на первый полином, и запишем его ниже:
Далее умножим следующий моном, 4х, на первый полином, и запишем результат ещё ниже, причем сместим запись чуть влево, чтобы подобные члены оказались друг под другом:
Также умножим последний одночлен, x2, на первый полином:
Осталось сложить подобные слагаемые (то есть переменные х с одинаковыми степенями), которые записаны друг под другом:
Ещё раз цветом выделим подобные слагаемые и результаты их суммирования:
Ответ: 2х5 + 11х4 + 31х3 + 50х2 + 71х +63.
Содержание
Полином одной переменной
§
Полиномы нескольких переменных рассматриваются
☞
ЗДЕСЬ.
Будем обозначать через $ mathbb A_{} $ какое-либо из множеств $ mathbb Z,mathbb Q, mathbb R_{} $ или
$ mathbb C_{} $.
Общая информация
Функция вида
$$
f(x)=a_0x^n+a_1x^{n-1}+dots+a_n = sum_{j=0}^n a_jx^{n-j}
$$
при $ n_{} in {0,1,dots } $ и $ {a_{0},dots,a_n}subset mathbb A $ относительно переменной $ x_{} $ называется
полиномом1)
или многочленом от указанной переменной над множеством $ mathbb A_{} $. Число $ a_{j} $
называется коэффициентом2) полинома (при $ (n-j)_{} $-й степени переменной),
выражение $ a_{j}x^{n-j} $ — членом (одночленом) полинома,
$ a_{n} $ — свободным членом, $ x_{}^{n-j} $ — мономом.
П
Пример. Выражения
$$ x^{2}+2,x-679, x^{2}+sqrt{2}x-pi , {mathbf i} , x^{3}- 2,x +sqrt{3} $$
являются полиномами; а
$$ x^{-2}+3, x +x^{2} , x^{x}, sum_{j=0}^{infty} x^{j}/j_{} $$
полиномами не являются.
Если $ a_{0}ne 0 $, то член $ a_0x^{n} $ называется ведущим членом, а
$ a_{0} $ — старшим коэффициентом полинома. При этом
число $ n_{} $ называется степенью полинома и обозначается3) $ deg f_{}(x) $.
Полином первой степени называется линейным полиномом.
Полином, все коэффициенты которого, кроме, возможно, $ a_{n} $, равны нулю,
называется константой4); будем обозначать его const.
Очевидно, что степень константы равна нулю; исключительным для этого
утверждения является случай когда константа является нулем.
Если все коэффициенты полинома равны нулю,
то такой полином называется (тождественно) нулевым. В этом
случае его степень не определяется.
На переменную $ x_{} $ мы пока не накладываем ни какого ограничения: она может
принимать значения из любого указанного выше множества — не обязательно
из того, которому принадлежат коэффициенты полинома. Обозначим область
определения полинома через $ mathbb B_{} $.
Значением полинома при (или в точке) $ cin mathbb B_{} $ называется число
$$
f(c) = a_0c^n+a_1c^{n-1}+dots+a_n .
$$
Два полинома
$$ f(x)=a_0x^n+dots+a_n u g(x)=b_0x^m+dots+b_m $$
с коэффициентами из $ mathbb A $ называются (тождественно) равными:
$$ f(x)equiv g(x) $$
если совпадают множества их членов; или, что то же, равны их степени
и равны коэффициенты при одинаковых степенях переменной.
Это определение отличается от привычного определения равенства двух функций:
две функции $ F_{}(x) $ и $ G(x)_{} $ называются равными на множестве $ mathbb B_{} $ если
совпадают их значения при любом $ x in mathbb B_{} $.
На самом деле, для случая полиномов эти два определения — алгебраическое и функциональное — эквивалентны.
Т
Теорема. $ f_{}(x)equiv g(x) $ тогда и только тогда, когда
$ f(c)=g(c)_{} $ для $ forall cin mathbb B_{} $.
Одним из следствий теоремы является тот факт, что для полинома совершенно
не важен порядок следования его членов; в частности, наряду с записью
полинома по убывающим степеням переменной, мы имеем право
записывать его и по возрастающим: $ f_{}(x)= sum_{j=0}^n a_{n-j}x^{j} $.
Форма полинома, в которой его разложение записывается
по убывающим степеням переменной, называется его канонической формой.
Кроме того, теорема дает нам право на операцию, называемую
приведением подобных членов:
$$ ax^{j}+bx^j equiv (a+b)x^j, quad ax^jcdot bx^k=ab x^{j+k} .$$
Имея в виду этот факт, определим теперь две основные операции для полиномов:
сложение и умножение.
Суммой двух полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином, составленный как сумма всех одночленов, входящих в состав
$ f_{}(x) $ и $ g_{}(x) $:
$$ f(x) + g(x) = (a_n+b_m) + (a_{n-1}+b_{m-1})x+dots +
left{begin{array}{ll}
(a_0+b_0)x^n & npu m=n, \
a_0x^n & npu m<n, \
b_0x^m & npu m>n.
end{array} right.
$$
Т
Теорема. $ deg (f+g_{})le max (deg f, deg g) $.
Произведением двух полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином, составленный как сумма всевозможных попарных произведений членов первого полинома на члены второго:
$$
begin{matrix}
f(x)g(x) &=& a_0b_0x^{n+m}+(a_1b_0+a_0b_1)x^{n+m-1}
+(a_2b_0+a_1b_1+a_0b_2)x^{n+m-2}+ \
& &+dots + (a_0b_k+a_1b_{k-1}+dots+a_kb_0)x^{n+m-k}+ dots + a_nb_m .
end{matrix}
$$
(В записи коэффициента при $ x^{n+m-k} $ мы полагаем $ a_{j}= 0 $ при $ j>n_{} $ и
$ b_{ell} = 0 $ при $ ell>m_{} $).
Т
Теорема. Если $ f_{}(x) notequiv 0 $ и $ g_{}(x) notequiv 0 $,
то $ deg (fcdot g_{})= deg f + deg g_{} $.
Фактическое выполнение операции перемножения полиномов возможно по схеме,
напоминающей алгоритм умножения целых чисел «столбиком»: это позволяет
сэкономить время на выписывание степеней переменной.
П
Пример. Перемножить полиномы
$$ x^{5}+x^3-2,x^2+3 quad mbox{ и } quad 2, x^{4}-3,x^3 +4,x^2-1 , . $$
Решение. Представим полиномы наборами их коэффициентов, расположив
один из них горизонтально, а второй — вертикально. Умножение полинома
$ f_{}(x) $ на $ b_{j}x^{n-j} $ сводится к умножению набора $ (a_{0},dots,a_n) $
на $ b_{j} $; результат следующего умножения — на $ b_{j+1}x^{n-j-1} $ —
получается аналогичным образом, но записывается со сдвигом на одну позицию
вправо. Получившиеся ряды суммируются по столбцам.
$$
begin{array}{r|rrrrrrrrrr}
&1 & 0 & 1 & -2& 0 & 3 \
hline
2 & 2 & 0 & 2 & -4 & 0 & 6 \
-3& & -3 & 0 & -3 & 6 & 0 & -9 \
4 & & & 4 & 0 & 4 & -8 & 0 & 12 \
0 & & & \
-1 &&&&& -1 & 0 & -1 & 2 & 0 & -3 \
hline& 2 & -3 & 6 & -7 & 9 & -2 & -10 & 14 & 0 & -3
end{array}
$$
(В отличие от перемножения чисел здесь результаты сложения в столбиках не
переносятся в следующий разряд.)
Ответ. $ 2,x^{9}-3,x^8+6,x^7-7,x^6+9,x^5-2,x^4-10,x^3+14,x^2 — 3 $.
Множество всех полиномов от переменной $ x_{} $ с коэффициентами из $ mathbb A_{} $
будем обозначать $ mathbb A_{} [x] $.
§
Способы более эффективного умножения полиномов излагаются
☞
ЗДЕСЬ
Схема Хорнера
Задача. Вычислить значение полинома в точке $ c $.
Схема вычисления, заложенная в самом определении, «стóит» $ 3n_{}-1 $ операции:
$$ begin{array}{rrrrr}
& &c^2=ctimes c, & dots, & c^n=c^{n-1}times c , \
&a_{n-1} times c, & a_{n-2} times c^2, & dots, & a_0 times c^n ,\
a_n & +a_{n-1} times c & + a_{n-2} times c^2 & + dots & + a_0 times c^n,
end{array}
$$
т.е. $ 2n_{}-1 $ операции умножения и $ n_{} $ операций сложения. Организуем теперь
вычисления по-другому:
$$
begin{matrix}
f(c)&=&a_n+a_{n-1}c+a_{n-2}c^2+dots +a_1c^{n-1}+a_0c^n = \
&=&a_n+cleft(a_{n-1}+a_{n-2}c+ dots + a_0c^{n-1} right) = \
&= &a_n+cleft(a_{n-1}+cleft(a_{n-2}+dots + a_0c^{n-2} right) right) = \
&=& dots = \
&=&a_n+cleft(a_{n-1}+cleft(a_{n-2}+dots + c(a_1+ a_0c)dots right) right) .
end{matrix}
$$
Начинаем вычислять с самой внутренней скобки:
$${mathfrak b}_1= a_1+ a_0c, {mathfrak b}_2= a_2+ {mathfrak b}_1 c,dots,
{mathfrak b}_{n-1} = a_{n-1} +{mathfrak b}_{n-2}c,, {mathfrak b}_{n} = a_{n} +{mathfrak b}_{n-1}c=f(c)
$$
Вычисление каждой величины $ {mathfrak b}_{k} $ «стоит» $ 2_{} $ операции — одного
сложения и одного умножения (при условии, что предварительно вычислено $ {mathfrak b}_{k-1}^{} $).
Приведем компактную запись алгоритма:
$$
{mathfrak b}_k = a_k + {mathfrak b}_{k-1}c quad npu quad {mathfrak b}_0 = a_0 quad u quad
kin {1,dots,n }
.
$$
«Стоимость» вычисления значения $ f_{}(c) $ по этой схеме Хорнера составляет
$ 2n_{} $ операций. Налицо экономия по сравнению с прямым способом вычисления $ f_{}(c) $.
Вычисления удобно производить с помощью таблицы, стартовое состояние которой следующее:
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0
end{array}
$$
Будем отсчитывать строки сверху вниз, начиная от горизонтальной черты, т.е.
нулевой строкой будем считать строку из коэффициентов полинома.
Вычисление значения $ {mathfrak b}_{1} $ в первой строке производится по схеме: предыдущее число умножается на $ c_{} $ и складывается с верхним, т.е.
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0 & underbrace{a_1+ca_0}_{{mathfrak b}_1}
end{array}
$$
Далее вычисления идут по тому же правилу:
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0 &{mathfrak b}_1&underbrace{a_2+c{mathfrak b}_1}_{{mathfrak b}_2}
end{array}
$$
и т.д. Величина, получившаяся в последнем столбце, и будет искомым значением $ f_{}(c) $:
$$
begin{array}{c|ccccccc}
& a_0 & a_1 & a_2 & dots & a_{n-2} & a_{n-1} & a_n \
hline
c & a_0 &{mathfrak b}_1&{mathfrak b}_2&dots &{mathfrak b}_{n-2} & {mathfrak b}_{n-1}&
underbrace{a_n+c{mathfrak b}_{n-1}}_{{mathfrak b}_n=f(c)}
end{array}
$$
П
Пример. Вычислить значение полинома $ x^{5}-3, x +1 $ в точке $ 2+ mathbf i_{} $.
Решение.
$$
begin{array}{c|cccccc}
& 1 & 0 & 0 & 0 & -3 & 1 \
hline
2+ mathbf i & 1& 2+mathbf i &3+4 mathbf i &2+11 mathbf i & -10+24mathbf i& -43+38mathbf i
end{array}
$$
Ответ. $ -43+38mathbf i_{} $.
Выясним теперь смысл коэффициентов $ {mathfrak b}_{1},dots, {mathfrak b}_{n-1} $
первой строки схемы Хорнера.
Т
Теорема. Пусть $ cin mathbb B_{} $ и $ mathbb Bsubset mathbb A_{} $. Полином
$ f_{}(x)in mathbb A[x] $ допускает единственное представление в виде:
$$
f(x)equiv (x-c)q(x)+r npu r=constin mathbb A, q(x)in mathbb A[x],
deg q = deg f — 1 .
$$
Доказательство. Будем искать константу $ r_{} $ и полином $ q_{}(x) $ методом неопределенных
коэффициентов:
$ q(x)= q_{0}x^{n-1}+q_1x^{n-2}+ dots + q_{n-1} $. Подставим его в правую часть доказываемого
тождества, приведем подобные и приравняем коэффициенты
полученного полинома коэффициентам полинома $ f_{}(x) $. Получим линейные уравнения,
из которых последовательно определяем $ q_{0},q_1, dots, q_{n-1} $ :
$$
begin{array}{l|lll}
x^n& a_0&=q_0, & \
x^{n-1}& a_1&=q_1-q_0c &Rightarrow q_1=a_1+q_0c, \
x^{n-2}& a_2&=q_2-q_1c &Rightarrow q_2=a_2+q_1c, \
vdots & & dots & \
x & a_{n-1}&=q_{n-1}-q_{n-2}c &Rightarrow q_{n-1}=a_{n-1}+q_{n-2}c,\
1 & a_n&=qquad -q_{n-1}c+r & Rightarrow r=a_n+q_{n-1}c.
end{array}
$$
Видим, что формулы, определяющие коэффициенты $ q_{k} $, полностью совпадают
с формулами, определяющими элементы первой строки
схемы Хорнера, т.е. $ q_0={mathfrak b}_{0},dots,q_{n-1}={mathfrak b}_{n-1} $.
Но тогда $ r=a_n+q_{n-1}c=a_{n}+{mathfrak b}_{n-1}c={mathfrak b}_{n}=f(c) $.
♦
Итак, имеем:
$$q(x)={mathfrak b}_0x^{n-1}+dots+{mathfrak b}_{n-1}, r={mathfrak b}_{n} , $$
при этом все коэффициенты вычисляются по схеме Хорнера, а старший коэффициент
полинома $ q_{}(x) $ совпадает со старшим коэффициентом $ f_{}(x) $. Так, для полинома приведенного выше примера имеет место тождество:
$$x^5-3, x +1 equiv
$$
$$
equiv (x-2-mathbf i)left(x^4+ (2+mathbf i)x^3+(3+4,mathbf i)x^2+ (2+11,mathbf i)x
-10+24,mathbf i right) -43+38 mathbf i .
$$
Фактически результат предыдущей теоремы говорит о возможности деления полинома $ f_{}(x) $ на линейный полином $ (x-c)_{} $ с остатком. Строгое определение операции деления полиномов дается
☟
НИЖЕ.
Алгоритм схемы Хорнера можно развить и до вычисления значений производных от полинома $ f(x_{}) $ в точке $ c_{} $. См.
☞
ЗДЕСЬ.
Корни
Если значение полинома $ f_{}(x) $ при $ x=cin mathbb B_{} $ равно нулю, то число $ c_{} $ называется корнем полинома $ f_{}(x) $.
Иными словами, корень полинома $ f_{}(x) $ — это решение уравнения $ f_{}(x)=0 $, принадлежащее множеству
$ mathbb B_{} $.
«Корень»
как название неизвестной величины, которую требуется определить («извлечь») из уравнения,
является переводом арабского слова
ریشه
«джизр, джазир» — буквально означающего
«корень растения». В свою очередь, арабский вариант, по-видимому, является переводом санскритского слова «мула», применявшегося индийскими
учеными для обозначения квадратного корня.
Уравнение $ f_{}=0 $, в левой части которого стоит полином одной или
нескольких переменных, называется алгебраическим.
Задача. Выяснить количество корней полинома $ f_{}(x)in mathbb A[x] $,
принадлежащих множеству $ mathbb B_{} $, и вычислить их.
Решить алгебраическое уравнение $ f_{}(x)=0 $ над множеством
$ mathbb B $ означает найти все корни $ f_{}(x) $, принадлежащие $ mathbb B_{} $.
На основании теоремы из предыдущего пункта имеет место следующая
Т
Теорема [Безу]. Пусть $ mathbb B subset mathbb A_{} $ и $ cin mathbb B_{} $ — корень полинома $ f_{}(x), deg fge 1 $. Тогда полином $ f_{}(x)in mathbb A [x] $ допускает представление в виде произведения:
$$
f(x)equiv (x-c)f_1(x) ,
$$
где полином $ f_{1}(x)in mathbb A [x], deg f_1 = deg f — 1 $ определяется единственным образом.
Итак, теорема Безу утверждает, что в случае существования корня полинома,
возможно разложение этого полинома в произведение двух полиномов — одного
первой степени и одного полинома степени, на единицу меньшей исходного.
Тем самым, задача о нахождении корней полинома $ f_{}(x) $ сведется к аналогичной
задаче для полинома $ f_{1}(x) $; вторая задача может оказаться более простой
за счет понижения степени.
Фактическое нахождение полинома $ f_{1}(x) $ возможно произвести с помощью схемы Хорнера.
П
Пример. Решить уравнение
$$ x^{3}+3 mathbf i, x^2-3(1+2 mathbf i)x+10-5 mathbf i =0 $$
над множеством $ mathbb C_{} $, если известно, что число $ (-1-2 mathbf i)_{} $ — одно из его решений.
Решение. Строим схему Хорнера:
$$
begin{array}{c|cccc}
& 1& 3mathbf i & -3(1+2 mathbf i) & 10-5 mathbf i \
hline
-1-2 mathbf i & 1& -1+ mathbf i & -5 mathbf i & 0
end{array}
$$
Видим, что число $ (-1-2 mathbf i)_{} $ действительно является корнем полинома, и, следовательно, последний раскладывается в произведение двух полиномов: линейного и квадратичного. Коэффициенты квадратичного полинома выбираются из той же схемы:
$$ (x+1+2 mathbf i )(x^2 + (-1+ mathbf i )x- 5 mathbf i) . $$
Квадратное уравнение над $ mathbb C_{} $ можно решить (см.
☞
ЗДЕСЬ ), его корни:
$ (-1-2 mathbf i)_{} $ и $ 2+mathbf i_{} $.
Ответ. $ (-1-2 mathbf i), 2+ mathbf i_{} $.
Если полином $ f_{}(x) $ раскладывается в произведение $ f_{}(x)equiv (x-c)f_1(x) $, то полином $ (x-c) $ называется линейным множителем для $ f_{}(x) $ над множеством $ mathbb B_{} $.
=>
Для того, чтобы $ (x-c)_{} $ был линейным множителем для $ f_{}(x) $ необходимо и достаточно чтобы число $ c_{} $ было корнем $ f_{}(x) $.
Начиная с этого места, корни полинома будем обозначать греческими буквами: $ lambda, mu_{} $ и т.д.
Примеры показывают, что не для всякого полинома и множества $ mathbb B_{} $
корни существуют. Очевидно не имеет корней полином нулевой степени
(константа, отличная от нуля); любой полином первой степени над $ mathbb A_{} $
имеет единственный корень, принадлежащий $ mathbb A_{} $.
Квадратный полином $ x^{2}+1 $ не имеет вещественных корней,
но имеет мнимые.
Основная теорема высшей алгебры
Т
Теорема. Любой полином с комплексными коэффициентами, степень которого больше нуля, имеет хотя бы один корень, в общем случае, комплексный.
Эта теорема гарантирует существование корня $ lambda_{1}in mathbb C $.
На основании теоремы Безу, можно утверждать, что $ f_{}(x) $ допускает представление
$$ f(x)equiv (x-lambda_1)f_1(x) quad npu quad f_1(x)in mathbb C [x], deg f_1(x)=deg f(x) -1 .$$
Если $ deg f_{1}(x) ge 1 $, то, по той же теореме, полином $ f_{1}(x) $
также должен обладать корнем, который мы обозначим5) $ lambda_{2} $; теорема Безу гарантирует тогда представление
$$
f(x)equiv (x-lambda_1)(x-lambda_2)f_2(x) quad npu quad f_2(x)in mathbb C [x], deg f_2(x)=deg f(x) -2
.$$
Продолжая процесс далее, мы за $ n_{} $ шагов придем к представлению
$$
f(x)equiv (x-lambda_1)(x-lambda_2)times dots times (x-lambda_n)f_n(x) quad npu quad f_n(x)in mathbb C[x], deg f_n(x)=0
,$$
т.е. полином $ f_{n}(x)^{} $ представляет собой константу. На основании условия
тождественного равенства полиномов утверждаем, что $ f_{n}(x) equiv a_0 $.
Таким образом приходим к следующей альтернативной версии основной теоремы высшей алгебры.
Т
Теорема. Для произвольного полинома $ f_{}(x) $ степени $ n_{}ge 1 $
существует его представление в виде произведения линейных множителей
$$
f(x)equiv a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_n) ;
$$
это представление единственно с точностью до перестановки сомножителей.
Как уже отмечалось в доказательстве теоремы, в этом представлении
могут встречаться одинаковые линейные сомножители. Собрав их вместе, получим
иной вид этого представления
$$
f(x)equiv a_0(x-lambda_1)^{{mathfrak m}_{1}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}}} , npu
{mathfrak m}_{1}+{mathfrak m}_{2}+dots+{mathfrak m}_{mathfrak r}=n
$$
и все числа $ lambda_{1},dots,lambda_{mathfrak r} $ теперь различны. Эта
формула называется формулой разложения полинома $ f_{}(x) $ на линейные сомножители или линейным представлением полинома $ f_{}(x) $; при этом число
$ {mathfrak m}_{j}^{}in mathbb N $ называется кратностью линейного сомножителя
$ x-lambda_{j} $ или кратностью корня $ lambda_{j} $ в полиноме $ f_{}(x) $.
Корень $ lambda_{j} $ называется простым, если $ {mathfrak m}_{j}=1_{} $ и
кратным кратности $ {mathfrak m}_{j}^{} $ если $ {mathfrak m}_{j}>1_{} $ (двойным или двукратным, если $ {mathfrak m}_{j}=2_{} $, тройным или трехкратным если $ {mathfrak m}_{j}=3_{} $ и т.д.)
Здесь имеет место неоднозначность математической терминологии:
простой корень — не обязательно простое число!
П
Пример. Найти линейное представление полинома
$$ f(x)=x^{6}-2, x^3+1 , .$$
Решение. Линейное представление легко получить если сначала заметить, что $ f(x)equiv (x^3-1)^{2} $, а затем использовать
выражения для корней кубических из единицы:
$$f(x)equiv (x-1)^2 left(x- frac{-1+ mathbf i sqrt{3}}{2} right)^2
left(x- frac{-1 — mathbf i sqrt{3}}{2} right)^2
.
$$
Все корни полинома имеют вторую кратность.
♦
§
Выведение условия наличия кратного корня (в терминах коэффициентов полинома)
☞
ЗДЕСЬ. При известном корне, нахождение его кратности
☞
ЗДЕСЬ.
Т
Теорема. Два полинома, степени которых
не превосходят $ n_{} $, равны тождественно если они имеют равные значения более
чем при $ n_{} $ различных значениях переменной.
Доказательство необходимости очевидно. Если полиномы $ f_{}(x) $ и $ g_{}(x) $ удовлетворяют условию теоремы, то полином $ f(x)-g_{}(x) $ должен иметь более,
чем $ n_{} $ корней, что, ввиду основной теоремы высшей алгебры, возможно лишь если он тождественно
нулевой.
♦
Теорема утверждает, что полином $ f_{}(x) $ степени,
$ le n_{} $, однозначно определяется своими значениями при более чем $ n_{} $
различных значениях переменной. Можно ли эти значения задавать произвольно?
Оказывается задание $ (n+1)_{} $-й пары $ (x_{1},y_1),dots,(x_{n+1},y_{n+1}) $
при всех различных $ x_{1},dots,x_{n+1} $ позволяет однозначно определить
полином $ f_{}(x) $ такой, что $ f(x_{1})=y_1,dots,f(x_{n+1})=y_{n+1} $ и
$ deg f_{} le n $. Практические способы решения этой задачи обсуждаются в разделе
☟
Интерполяция
Раздел находится
☞
ЗДЕСЬ.
Корни и коэффициенты полинома
Симметрические функции корней
Разложение полинома $ f_{}(x) $ на линейные множители дает интересные
соотношения между корнями полинома и его коэффициентами. Сначала выведем их
для малых степеней. Для $ n_{}=2 $:
$$a_0x^2+a_1x+a_2equiv a_0(x-lambda_1)(x-lambda_2)equiv
a_0x^2-a_0(lambda_1+lambda_2)x+a_0lambda_1lambda_2
Rightarrow
$$
$$
Rightarrow
left{ begin{array}{ccr}
lambda_1+lambda_2&=&-a_1/a_0, \
lambda_1lambda_2&=&a_2/a_0,
end{array}
right.
$$
т.е. получили формулы известные из школьного курса алгебры. Далее, для $ n_{}=3 $:
$$a_0x^3+a_1x^2+a_2x+a_3equiv a_0(x-lambda_1)(x-lambda_2)(x-lambda_3)equiv $$
$$equiv
a_0x^3-a_0(lambda_1+lambda_2+lambda_3)x^2+a_0(lambda_1lambda_2
+ lambda_1lambda_3+lambda_2lambda_3)x-a_0lambda_1lambda_2lambda_3
Rightarrow
$$
$$
Rightarrow
left{ begin{array}{ccr}
lambda_1+lambda_2+lambda_3&=&-a_1/a_0, \
lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3&=&a_2/a_0,\
lambda_1lambda_2lambda_3&=&-a_3/a_0.
end{array}
right.
$$
Т
Теорема. Для корней $ lambda_{1},dots,lambda_n $ полинома
$$ f(x)=a_{0}x^n+a_1x^{n-1}+dots+a_n,, a_0ne 0 $$
справедливы формулы Виета
$$
sum_{1 le jle n} lambda_j = lambda_1+ dots+ lambda_n= -frac{a_1}{a_0},
$$
$$
sum_{1le j_1<j_2le n} lambda_{j_1} lambda_{j_2}= lambda_1 lambda_2 +
lambda_1 lambda_3 +dots + lambda_2 lambda_3
+ dots+ lambda_{n-1}lambda_n= frac{a_2}{a_0},
$$
$$
sum_{1le j_1<j_2<j_3le n} lambda_{j_1} lambda_{j_2} lambda_{j_3}=
lambda_1 lambda_2 lambda_3+ lambda_1 lambda_2 lambda_4 + dots+
lambda_{n-2} lambda_{n-1} lambda_n = -frac{a_3}{a_0},
$$
$$
dots
$$
$$
lambda_{1} lambda_{2}times dots timeslambda_{n-1}
+ lambda_{1} lambda_{2} times dots times lambda_{n-2} lambda_n
+ dots + lambda_{2} lambda_{3}times dots times lambda_n
= (-1)^{n-1} frac{a_{n-1}}{a_0},
$$
$$ lambda_{1} lambda_{2}times dots times lambda_{n}= (-1)^{n} frac{a_{n}}{a_0} .$$
Здесь в левой части $ k_{} $-й формулы стоит сумма всевозможных
произведений из $ k_{} $ чисел, выбранных из $ lambda_{1},dots,lambda_n $ (корни учитываются в
соответствии с их кратностями); в правой части формулы стоит $ (-1)^ka_{k}/a_0 $.
Доказательство
☞
ЗДЕСЬ.
И
Биографические заметки о Виете
☞
ЗДЕСЬ
П
Пример. Найти все корни полинома $ 3,x^3-16,x^2+23,x-6 $,
если известно, что произведение двух из них равно $ 1_{} $.
Решение. Имеем:
$$
left{ begin{array}{ccl}
lambda_1+lambda_2+lambda_3&=&16/3, \
lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3
&=&23/3,\
lambda_1lambda_2lambda_3&=&6/3=2.
end{array}
right.
$$
Вдобавок к этим уравнениям, мы должны записать дополнительное условие:
$$lambda_1 lambda_2=1 .$$
Из третьего уравнения системы получаем тогда $ lambda_3=2 $. Подставив его
в два оставшихся, придем к двум идентичным:
$$lambda_1 + lambda_2=10/3 .$$
Теперь для нахождения неизвестных $ lambda_{1} $ и $ lambda_{2} $ можем воспользоваться
формулами Виета «в обратном порядке», составив квадратный полином,
имеющий их корнями:
$$t^2-10/3,t+1 .$$
Ответ. $ 2,,3,, 1/3 $.
?
Можно ли использовать формулы Виета для решения уравнения ?
Ответ
☞
ЗДЕСЬ.
Обдумаем еще раз результаты основной теоремы высшей алгебры и формул Виета. С одной
стороны, задав коэффициенты $ a_{0},a_1,dots,a_n $ мы однозначно определяем
набор из $ n_{} $ комплексных чисел $ lambda_{1},dots,lambda_n $ — корней этого
полинома. С другой стороны, задав произвольным образом набор корней
$ lambda_{1},dots,lambda_n $, по формулам Виета однозначно определим
величины $ a_1/a_0,dots,a_n/a_0 $. Для простоты, рассмотрим подмножество
полиномов степени $ n_{} $, имеющих старший коэффициент равным $ 1_{} $. Получаем
тогда взаимно-однозначное соответствие:
$$ (a_1,dots,a_n) leftrightarrow (lambda_1,dots,lambda_n) . $$
Итак, каждый корень $ lambda_{j} $ полинома является какой-то функцией его
коэффициентов $ a_1,dots,a_{n} $, т.е. формально говоря, функцией от многих
переменных. Относительно этой функции мы пока ничего сказать не можем; более того, как мы узнаем НИЖЕ, для степеней полинома бóльших $ 4_{} $ не существует
«хороших» общих формул, выражающих корни полинома через его
коэффициенты. Несмотря на это, формулы Виета подтверждают, что
некоторые комбинации этих неизвестных нам функций оказываются равными
коэффициентам полинома. Какова основная отличительная особенность этих
комбинаций?
Функция $ Phi(x_1,dots,x_n) $ называется симметрической функцией своих переменных, если ее значение не меняется ни при какой перестановке этих переменных:
$$Phi(x_1,dots,x_n) equiv Phi(x_{j_1},dots,x_{j_n}) $$
при всех различных $ j_1,dots, j_n in {1,dots,n} $.
П
Пример. Функции
$$ sqrt{1+x_1x_2x_3} , frac{x_1x_2}{x_3}+frac{x_1x_3}{x_2}+frac{x_2x_3}{x_1} $$
являются симметрическими функциями переменных $ x_1,x_2,x_3 $, а функция
$$ x_1^2x_2x_3+x_1x_2^2x_3 $$
симметрической функцией не является, поскольку ее значения меняются при перестанове $ (x_1,x_2,x_3) leftrightarrow (x_3,x_2,x_1) $.
В левых частях формул Виета как раз и стоят симметрические полиномы
относительно $ lambda_{1},dots,lambda_n $. Оказывается результат теоремы
допускает следующее обобщение.
Т
Теорема [Гаусс]. Значение любого симметрического полинома
$ Phi(x_1,dots,x_n) $ на корнях $ lambda_1,dots,lambda_n $ полинома
$ x^n+a_1x^{n-1}+ dots+a_n $ является полиномиальной функцией от $ a_{1},dots,a_n $:
$$
Phi(lambda_1,dots,lambda_n) equiv {mathfrak F}(a_1,dots,a_n) .
$$
П
Пример. Пусть $ lambda_{1} $ и $ lambda_{2} $
означают корни полинома $ x^2+a_1x+a_2 $.
Выразить
$$lambda_1^2+lambda_2^2-3,lambda_1^2lambda_2-3,lambda_1lambda_2^2$$
через коэффициенты полинома.
Решение. Поскольку выражения для корней квадратного уравнения нам известны:
$$
lambda_1= frac{-a_1+sqrt{a_1^2-4,a_2}}{2} quad u quad
lambda_2= frac{-a_1-sqrt{a_1^2-4,a_2}}{2} ,
$$
то непосредственной подстановкой их в заданный полином, получаем
$$ a_1^2-2,a_2+3,a_1a_2 . $$
♦
П
Пример. Пусть $ lambda_1,, lambda_2,, lambda_3 $
означают корни полинома $ x^3+a_1x^2+a_2x+a_3 $.
Выразить
$$lambda_1^2lambda_2+lambda_1^2lambda_3+lambda_1lambda_2^2+
lambda_1lambda_3^2+lambda_2^2lambda_3+lambda_2lambda_3^2
-lambda_1^2-lambda_2^2-lambda_3^2
$$
через коэффициенты полинома.
Решение. Выделим в требуемом выражении комбинации
корней, стоящие в левых частях формул Виета.
Первые $ 6_{} $ слагаемых можно представить в виде
$$(lambda_1lambda_2+lambda_1lambda_3+lambda_2lambda_3)
(lambda_1+lambda_2+lambda_3)-3lambda_1lambda_2lambda_3 , $$
а
$$lambda_1^2+lambda_2^2+lambda_3^2=
left(lambda_1+lambda_2+lambda_3 right)^2-2, (lambda_1lambda_2+
lambda_1lambda_3+lambda_2lambda_3) .$$
Далее применяем формулы Виета.
Ответ. $ 3,a_3-a_1a_2-a_1^2+2, a_2 $.
Существуют общие алгоритмы нахождения полинома $ {mathfrak F} $ по заданному полиному $ Phi $: см.
[3], [4]. Однако в своей практике я встречал необходимость в подобном представлении лишь для некоторых классов полиномов $ Phi_{} $; сейчас их и рассмотрим.
Суммы Ньютона
Для полинома $ f(x)=a_{0}x^n+a_1x^{n-1}+dots+a_n, (a_0ne 0) $ его $ k_{} $-й суммой Ньютона называется сумма $ k_{} $-х степеней его корней:
$$
s_k=lambda_1^k + dots + lambda_n^k .
$$
При этом обычно считают $ k_{} in {mathbb N} $ (хотя формально можно определить суммы Ньютона и для отрицательных индексов $ k_{} $ при условии $ a_{n} ne 0 $). Для однообразия полагают также $ s_{0}=n $.
T
Теорема. Суммы Ньютона выражаются рационально через коэффициенты полинома $ f_{}(x) $ посредством следующих рекуррентных формул Ньютона:
$$s_0=n, s_1=-a_1/a_0, $$
$$
s_k=left{begin{array}{lr}
-(a_1s_{k-1}+a_2s_{k-2}+dots+a_{k-1}s_1+a_kk)/a_0,
&npu kle n ;\
-(a_1s_{k-1}+a_2s_{k-2}+dots+a_ns_{k-n})/a_0
& npu k > n.
end{array}
right.
$$
П
Пример.
$$
s_2=(a_1^2-2, a_0a_2) big/ a_0^2 ,
$$
$$
s_3=-(a_1s_2+a_2s_1+3,a_3)big/ a_0=
$$
$$
=-left(a_1 (a_1^2-2, a_0a_2) big/ a_0^2 +a_2 (-a_1 big/ a_0)+3,a_3 right)
big/ a_0=
$$
$$
=left(-a_1^3+3,a_0a_1a_2-3,a_0^2a_3 right) big/ a_0^3 .
$$
♦
§
Подробнее о суммах Ньютона
☞
ЗДЕСЬ.
Результант и дискриминант
Пусть $ g(x)=b_0x^m+dots + b_{m} $ — произвольный полином из $ mathbb A_{} [x] $. Тогда выражение
$$ g(lambda_1) times dots times g(lambda_n) $$
является симметрическим полиномом от корней $ lambda_{1},dots,lambda_n $ полинома $ f_{}(x) $.
По теореме Гаусса, оно должно рационально выражаться через коэффициенты $ a_{0},dots,a_n $. С другой стороны, очевидно, это выражение обращается в нуль тогда и только тогда, когда хотя бы один сомножитель обратится в нуль, т.е. будет существовать общий корень полиномов $ f_{}(x) $ и $ g_{}(x) $. Выражение
$$ a_0^m prod_{j=1}^n g(lambda_j) $$
называется результантом полиномов $ f_{}(x) $ и $ g_{}(x) $.
§
Способы вычисления результанта, его свойства и применения
☞
ЗДЕСЬ.
В частном случае, когда $ g_{}(x) $ совпадает с производной полинома $ f_{}(x) $ результант переходит в дискриминант — выражение отличающееся от
$$ a_0^{n-1} prod_{j=1}^n f^{prime}(lambda_j) $$
только сомножителем $ (-1)^{n(n-1)/2}/a_0 $ и
обращающееся в нуль тогда и только тогда, когда $ f^{prime}(x) $ имеет общий корень с $ f_{}(x) $.
Как мы увидим НИЖЕ, последнее условие оказывается необходимым и достаточным наличия у полинома $ f_{}(x) $ кратного корня.
П
Пример. Для $ f(x)=a_{0}x^2+a_1x+a_2 $ указанное произведение оказывается равным
$$ (2a_0lambda_1 +a_1)(2a_0lambda_2 +a_1)=(4a_0^2lambda_1 lambda_2+2a_0a_1(lambda_1 +lambda_2)+a_1^2)=
$$
$$
=left(4a_0^2 frac{a_2}{a_0}-2a_0a_1frac{a_1}{a_0}+a_1^2right)=4a_0a_2-a_1^2,
$$
т.е. привычному «школьному» понятию.
§
Способы вычисления дискриминанта, его свойства и применения
☞
ЗДЕСЬ.
Преобразования корней
Если $ lambda_{1},dots,lambda_n $ — корни полинома $ f(x)=a_0x^n+a_1x^{n-1}+dots+a_{n} $, то
1.
корнями полинома
$$ f(-x)=(-1)^nleft(a_0x^n-a_1x^{n-1}+dots+(-1)^na_nright) = $$
$$ =(-1)^n sum_{j=0}^n (-1)^ja_jx^{n-j} $$
являются $ -lambda_1, dots, -lambda_n $;
2.
корнями полинома
$$f(x- {color{Red} alpha })=a_0(x-{color{Red} alpha } )^n+a_1(x-{color{Red} alpha })^{n-1}+dots+a_n=
$$
$$
= sum_{j=0}^n a_j(x-{color{Red} alpha })^{n-j}
$$
являются $ {color{Red} alpha }+lambda_1, dots, {color{Red} alpha }+lambda_n $;
3.
при дополнительном условии, что $ a_{n} ne 0 $, корнями полинома
$$f^{ast}(x)= x^nfleft(1/x right) equiv a_0+a_1x+dots+a_nx^n =
$$
$$
=sum_{j=0}^n a_jx^{j}
$$
являются $ 1/{lambda_1}, dots, 1/{lambda_n} $.
Преобразования
1-3
часто используются как при выводе теоретических результатов так и в практике вычислений.
Поясним идею этих применений. Корни исходного и корни преобразованного полинома остаются неизвестными. Допустим, мы получили какой-то результат, касающийся оценки положительных корней полинома $ f_{}(x) in mathbb R[x] $, и хотим распространить эту оценку и на отрицательные корни (см., к примеру,
☟
НИЖЕ ). Производится замена переменной $ x rightarrow — x $, которая меняет знаки всех корней: отрицательные становятся положительными, и к новому полиному применяется полученный результат. В приложениях возникают и более сложные преобразования корней: когда, к примеру, все их надо «загнать» в ограниченную область комплексной плоскости — скажем, в круг $ |x|le 1 $ (см.
☟
НИЖЕ ).
П
Пример. Построить полином $ F_{}(x) $, корни которого равны квадратам корней полинома $ f_{}(x) $.
Решение. Составим выражение
$$
f(sqrt{x})f(-sqrt{x}) .
$$
С одной стороны, используя линейное представление полинома $ f_{}(x) $ получим
$$
f(sqrt{x})f(-sqrt{x})=(-1)^n a_0^2(x-lambda_1^2)times dots times (x-lambda_n^2) ,
$$
т.е. полином с требуемыми корнями. С другой стороны, мы можем найти выражения для коэффициентов этого полинома:
$$
begin{matrix}
f(sqrt{x})&equiv & a_n+a_{n-1} sqrt{x} +a_{n-2} x + a_{n-3} x sqrt{x}+dots equiv \
& equiv & (a_n+a_{n-2} x +a_{n-4} x^2 +dots ) + sqrt{x} (a_{n-1}+ a_{n-3} x + a_{n-5} x^2+ dots ) ;\
f(-sqrt{x})&equiv & (a_n+a_{n-2} x +a_{n-4} x^2 +dots ) — sqrt{x} (a_{n-1}+ a_{n-3} x + a_{n-5} x^2+ dots ) .
end{matrix}
$$
В результате, искомый полином представляется в виде
$$
F(x)=(a_n+a_{n-2} x +a_{n-4} x^2 +dots )^2-x(a_{n-1}+ a_{n-3} x + a_{n-5} x^2+ dots )^2 .
$$
Это преобразование иногда называется квадрированием корней полинома $ f_{}(x) $; оно применяется в методе Греффе-Лобачевского вычисления корней полинома.
♦
Общий метод построения полинома $ F_{}(x) $ , корни которого связаны с корнями $ f_{}(x) $ соотношением вида $ Lambda_j = g(lambda_j) $ при $ g_{}(x) $ — произвольном полиноме
☞
ЗДЕСЬ.
Непрерывность корней
Т
Теорема [5]. Корни полинома
$$ f(x)=x^n+a_1x^{n-1}+dots+a_n in mathbb C[x],quad nge 1 $$
являются непрерывными функциями его коэффициентов. Строго говоря,
если $ lambda_1,dots,lambda_{n} $ — корни этого полинома,
а $ {tilde lambda_1},dots,{tilde lambda_n} $ — корни полинома
$${tilde f}(x)=x^n+{tilde a}_1x^{n-1}+dots+{tilde a}_n in mathbb C[x]
,
$$
то эти корни можно перенумеровать таким образом, чтобы
$$ |lambda_j-{tilde lambda}_j| < 2n varepsilon quad npu quad jin{1,dots,n} . $$
Здесь
$$varepsilon= sqrt[n]{sum_{k=1}^n|a_k-{tilde a}_k| gamma^{n-k} } quad
npu quad gamma = max_{jin {1,dots,n}}
left( sqrt[j]{|a_j|} ,
sqrt[j]{|{tilde a}_j|} right) . $$
П
Пример. Для полинома
$$ f(x)=192,x^5+[(259-173{mathbf i}){color{Red} alpha }+211-413{mathbf i}]x^4 +
$$
$$
+[(80-320{mathbf i}){color{Red} alpha }-304-704{mathbf i}]x^3
+384{mathbf i},x^2-192-192,{mathbf i}
$$
исследовать динамику корней при изменении значений параметра $ {color{Red} alpha }_{} $ от $ -2_{} $ до $ 3_{} $.
Решение. На рисунке

показаны следы, «заметаемые» корнями на комплексной плоскости. Направления движений указаны стрелками.
Сначала посмотрим на начало процесса. При $ {color{Red} alpha }=-2 $ полином имеет следующие
корни:
$$ lambda_1approx-1.0726-0.5122 {mathbf i}, lambda_{2}approx -0.7337+0.1972{mathbf i},
lambda_{3}approx 0.3557+0.9054 {mathbf i},
$$
$$
lambda_4 approx 0.5028-0.3812 {mathbf i}, lambda_5 approx 2.5467+0.1398 {mathbf i} .
$$
Эти стартовые точки отмечены отрезками
|
|
|
|
|
. При увеличении значений $ {color{Red} alpha }_{} $ от $ -2 $ до $ -1_{} $ происходит «дрейф» корней — плавный, но разный по скорости. К примеру, синий и фиолетовый корни меняются очень медленно, а вот зеленый и малиновый быстро сближаются пока не столкнутся при значении $ {color{Red} alpha }=-1 $:
$$ lambda_1approx -1.5096-0.4133 {mathbf i}, lambda_2 approx -0.6768+0.1479 {mathbf i},
lambda_3 approx 0.4364-0.4845 {mathbf i}, lambda_4 = 1+ {mathbf i},
$$
$$
lambda_5 =1+ {mathbf i} .
$$
Что происходит при дальнейшем увеличении $ {color{Red} alpha }_{} $? Число корней должно остаться инвариантным — по основной теореме высшей алгебры оно продолжает совпадать со степенью полинома, т.е. корни не
аннигилируют. Поэтому столкнувшиеся корни порождают два новых — голубой и коричневый — которые начинают расходиться. При $ {color{Red} alpha }=1 $ ситуация следующая:
$$
lambda_1 approx -2.3350+0.4836 {mathbf i}, lambda_2 approx -0.5794+0.1185{mathbf i}, lambda_3 approx 0.2721-0.4926 {mathbf i},
$$
$$
lambda_4 approx -0.3888+2.5945 {mathbf i},
lambda_5 approx 0.5832+0.3480 {mathbf i} .
$$
Имея перед глазами полную картину истории, понимаем, что корни, обозначенные $ lambda_{1} $ (красный) и $ lambda_{4} $ (голубой), стремятся к столкновению — и оно действительно происходит при $ {color{Red} alpha }=2 $:
$$ lambda_1 = -2+2{mathbf i}, lambda_2 approx -0.5458+0.1142 {mathbf i}, lambda_3 approx 0.2296-0.4712 {mathbf i}, lambda_4 = -2+2{mathbf i},
$$
$$
lambda_5 approx 0.5193+0.3101 {mathbf i} .
$$
Дальнейшую динамику можем предсказать «по прецеденту» — столкнувшиеся корни должны разойтись. При $ {color{Red} alpha }=3_{} $:
$$
lambda_1 approx -4.0682+3.6140 {mathbf i}, lambda_2 approx -0.5184+0.1116 {mathbf i},
lambda_3 approx 0.2007-0.4506{mathbf i},
$$
$$
lambda_4 approx -1.2359+1.2927{mathbf i},
lambda_5 approx 0.4759+0.2864{mathbf i} .
$$
♦
?
К какому числу стремится желтый корень при $ {color{Red} alpha } to +infty $ ?
Последний пример наводит на еще одну гипотезу: мы видим, что графики корней получились гладкими, за исключением, возможно, некоторых специфических точек.
Т
Теорема. Корни полинома
$$ f(x)=x^n+a_1x^{n-1}+dots+a_n in mathbb C[x] $$
являются непрерывно дифференцируемыми функциями коэффициентов за исключением тех наборов значений коэффициентов, которые определяют кратные корни.
Доказательство
☞
ЗДЕСЬ.
§
Условие наличия кратного корня у полинома $ f_{}(x) $ может быть получено в виде явного условия на его коэффициенты. См.
☞
ДИСКРИМИНАНТ.
Теоремы настоящего пункта имеют теоретический, качественный характер. Для оценки реального влияния изменений коэффициентов полинома на динамику его корней приходится проводить отдельные — и весьма кропотливые — исследования: см.
☞
ЧУВСТВИТЕЛЬНОСТЬ КОРНЕЙ.
Поиск корней алгебраических уравнений: решение в радикалах
Можно ли выразить корни полинома $ f(x)in mathbb C[x] $ в виде «хороших» функций от его коэффициентов? Вспомним, что для квадратного уравнения
существует общая формула вычисления корней:
$$x^2+ax+b=0 Rightarrow lambda_{1,2}=frac{-apm sqrt{a^2-4b}}{2}
.
$$
Эта формула включает в себя элементарные алгебраические операции
$ +,- ,times, div $ и операцию извлечения квадратного корня. По аналогии
можно сформулировать и общую задачу.
Задача. Найти выражения корней полинома степени $ n_{}>2 $ в виде функций его коэффициентов; при этом функции должны представлять конечную комбинацию элементарных алгебраических
операций и операций извлечения корней произвольных (целых) степеней.
Поставленная задача называется задачей о разрешимости уравнения в радикалах6).
Оказывается, что любое уравнение третьей или четвертой степени разрешимо в радикалах. Перед тем, как изложить способы их решения, сделаем два упрощения. Первое из них заключается в том, что уравнение $ f_{}(x)=0 $ делится на старший коэффициент полинома $ f_{}(x) $.
Полином называется нормализованным7), если его старший коэффициент равен $ 1_{} $. Операция деления полинома на его старший коэффициент называется нормализацией полинома.
Очевидно, что нормализованный полином имеет те же корни, и в тех же кратностях, что и
исходный. Для простоты обозначений, будем считать, что полином уже
нормализован:
$$ f(x)=x^n+a_1x^{n-1}+dots+a_n .$$
Второе упрощение заключается в замене переменной (подстановке): $ x=y+{color{Red} alpha } $.
Ее результатом будет новый полином той же степени, что и исходный, относительно
переменной $ y_{} $:
$$ F(y)equiv f(y+{color{Red} alpha }) , . $$
Корни нового полинома связаны (cм. преобразование
2
☞
ЗДЕСЬ ) с корнями старого
по формуле $ lambda_j = Lambda_j+{color{Red} alpha } $; так что, найдя корни одного полинома,
легко установим и корни другого. Подберем теперь параметр $ {color{Red} alpha } $ так,
чтобы обратить в нуль коэффициент при $ y^{n-1} $ в полиноме $ F_{}(y) $.
Используя формулу бинома Ньютона, получаем
$$
begin{matrix}
f(x)&=&x^n+a_1x^{n-1}+a_2x^{n-2}+dots+a_n= \
&=&(y+{color{Red} alpha })^n +a_1(y+{color{Red} alpha })^{n-1}+a_2(y+{color{Red} alpha })^{n-2}+dots+a_n = \
&=&y^n + C_n^1 {color{Red} alpha } y^{n-1} +C_n^2 {color{Red} alpha }^2 y^{n-2}+dots+
{color{Red} alpha }^n + \
& & qquad + a_1y^{n-1}+a_1 C_{n-1}^1 {color{Red} alpha } y^{n-2}+dots
+a_1{color{Red} alpha }^{n-1} + \
& & quad qquad qquad +a_2y^{n-2} + dots + a_n.
end{matrix}
$$
Понятно, что если положить $ {color{Red} alpha }= — a_1/n $, то коэффициент при $ y^{n-1} $
исчезнет. Для простоты обозначений, будем считать, что полином уже
предварительно подвергнут такому преобразованию:
$$ f(x)=x^n qquad +a_2x^{n-2}+dots+a_n .$$
Уравнение третьей степени
Рассмотрим уравнение третьей степени:
$$
x^3+p,x+q=0
$$
Сделаем в этом уравнении замену переменной: $ x=u+v $, введя две неизвестные
$ u_{} $ и $ v_{} $; получим:
$$
u^3+v^3+3,uv(u+v)+p(u+v)+q=0 .
$$
Сгруппируем:
$$
u^3+v^3+(3,uv+p)(u+v)+q=0 .
$$
Подчиним теперь неизвестные $ u_{} $ и $ v_{} $ условию
$$
3,uv+p=0 iff uv=-frac{p}{3} .
$$
Тогда предыдущее уравнение приведется к виду
$$u^3+v^3=-q . $$
Итак, для определения неизвестных величин $ u_{} $ и $ v_{} $ мы получили систему
уравнений
$$
u^3+v^3=-q,
uv=-frac{p}{3} .
$$
Возведя последнее уравнение в куб, получим
$$
u^3v^3=-frac{p^3}{27} .
$$
Два полученных равенства, связывающие $ u^3 $ и $ v^3 $,
позволяет утверждать, что эти величины являются решениями квадратного
уравнения:
$$t^2+q,t- frac{p^3}{27}=0 .$$
Выражение
$$
Delta = frac{q^2}{4}+frac{p^3}{27}
$$
называется дискриминантом кубического уравнения.
Решив квадратное уравнение, получим:
$$
u^3=-frac{q}{2}+ sqrt{Delta}, v^3=-frac{q}{2}- sqrt{Delta} .
$$
В итоге имеем формулу для решений уравнения:
$$
x=u+v=sqrt[3]{-frac{q}{2}+sqrt{frac{q^2}{4}+frac{p^3}{27}}}+
sqrt[3]{-frac{q}{2}-sqrt{frac{q^2}{4}+frac{p^3}{27}}} ;
$$
она называется формулой Кардано.
Формула Кардано не очень удобна для практических вычислений.
Вспомним, что корень кубический из комплексного числа может принимать три различных значения.
Решение же, представленное формулой Кардано, имеет в правой части
комбинацию из двух кубических корней. Таким образом, получаем
9 всевозможных комбинаций из значений корней кубических. С другой стороны, основная теорема высшей алгебры утверждает, что кубическое уравнение должно иметь только
три решения. Для того, чтобы установить соответствие между значениями $ u_{} $
и $ v_{} $, обратимся к условию $ uv=-p/3 $ . Согласно этому условию, задание
значений для $ u_{} $ позволит однозначно восстановить $ v_{} $. Пусть
$$
u_1=sqrt[3]{-frac{q}{2}+sqrt{frac{q^2}{4}+frac{p^3}{27}}}
$$
какое-то одно из трех возможных значений корня кубического. Два оставшихся значения корня кубического получаются домножением $ u_1 $ на корни кубические из единицы:
$$u_2=u_1varepsilon_1, u_3=u_1varepsilon_2 $$
при
$$varepsilon_1=cos frac{2pi}{3} + {mathbf i} sin frac{2pi}{3}=
frac{-1}{2}+
{mathbf i} frac{sqrt{3}}{2} u
varepsilon_2=cos frac{4pi}{3} + {mathbf i} sin frac{4pi}{3}=
frac{-1}{2}-
{mathbf i} frac{ sqrt{3}}{ 2}
.
$$
Если теперь взять
$$
v_1=-frac{p}{3u_1} ,
$$
то решения кубического уравнения можно выразить в виде комбинаций
$ u_1 $ и $ v_1 $:
$$
begin{array}{ccl}
lambda_1&=&u_1+v_1, \
lambda_2&=&u_2+v_2=u_2-frac{displaystyle p}{displaystyle 3u_2}=u_1varepsilon_1-frac{displaystyle p}{displaystyle 3u_1varepsilon_1}
=u_1varepsilon_1-frac{displaystyle pvarepsilon_2}{displaystyle 3u_1}=u_1varepsilon_1+v_1varepsilon_2,\
lambda_3&=&u_3+v_3=u_1varepsilon_2+v_1varepsilon_1 .
end{array}
$$
Окончательно получаем формулы для вычисления корней:
$$
left{
begin{array}{lcl}
lambda_1&=&u_1+v_1, \
lambda_2&=&-frac{scriptstyle 1}{scriptstyle 2}(u_1+v_1)
+{mathbf i} frac{scriptstyle sqrt{3}}{scriptstyle 2} (u_1-v_1),\
lambda_3&=&-frac{scriptstyle 1}{scriptstyle 2}(u_1+v_1)
-{mathbf i} frac{scriptstyle sqrt{3}}{scriptstyle 2} (u_1-v_1),
end{array} right.
$$
где $ u_1 $ — одно из значений корня кубического, а $ v_1 $ связано с ним
соотношением $ v_1=-p/(3u_1) $.
П
Пример [2]. Решить уравнение $ x^3-6{mathbf i},x^2-10,x+8 {mathbf i}=0 $.
Решение. Подстановка $ x=y+2 {mathbf i} $ приводит уравнение к виду
$$y^3+2,y+4{mathbf i} =0 , $$
т.е. $ p=2,,q=4 {mathbf i} $. Далее
$$Delta=-frac{100}{27} Rightarrow sqrt{Delta} = pm frac{10 {mathbf i}}{3sqrt{3}}
Rightarrow u_1=sqrt[3]{left(-2 + frac{10}{3sqrt{3}} right){mathbf i}}
.
$$
Одно из значений последнего корня:
$$u_1=-{mathbf i}, sqrt[3]{-2 + frac{10}{3sqrt{3}}} , $$
это выражение можно упростить, если повезет заметить, что подкоренное выражение
равно $ left(-1+1/{sqrt{3}}right)^3 $:
$$u_1={mathbf i}left(1-frac{1}{sqrt{3}}right) Rightarrow
v_1=-frac{p}{3u_1}= {mathbf i} left(1+frac{1}{sqrt{3}}right) .
$$
Получаем:
$$mu_1=2, {mathbf i} , mu_2=1- {mathbf i}, mu_3=-1- {mathbf i} .$$
Значения корней исходного уравнения получатся «сдвигом» на
$ 2 {mathbf i} $.
Ответ. $ 4{mathbf i},, 1 + {mathbf i},, -1+ {mathbf i} $.
§
Дальнейший анализ формулы Кардано
☞
ЗДЕСЬ
Уравнение четвертой степени
$$ x^4+a_1x^3+a_2x^2+a_3x+a_4 = 0 $$
также может быть решено в радикалах. Идея решения заключается в сведении задачи к решению некоторого кубического уравнения. Ее реализация
☞
ЗДЕСЬ.
Уравнения высших степеней
Успех в решении уравнений третьей и четвертой степени побудил
исследователей искать подобные формулы для уравнений высших степеней.
Методология подхода была очевидна: свести решение уравнения $ n $-й
степени к решению уравнения $ (n-1) $-й степени. Однако, несмотря на почти трехвековые усилия лучших математиков, решить уравнение пятой степени не удавалось. Наконец, в начале
XIX века был получен отрицательный результат.
Т
Теорема [Руффини, Абель]. Уравнение степени выше четвертой в общем
случае неразрешимо в радикалах.
П
Пример. Уравнение $ x^5-4, x -2=0 $ не разрешимо в радикалах.
Установить разрешимо или нет данное конкретное уравнение в радикалах возможно с помощью теории, развитой французским математиком Галуа.
П
Пример. Уравнение $ x^5+x+1=0 $ разрешимо в радикалах, поскольку
$$ x ^5+x+1equiv (x^2+x+1)(x^3-x^2+1) , .$$
Отрицательный характер результата теоремы Руффини-Абеля не должен слишком уж
разочаровывать. Он означает только лишь то, что корни полинома нельзя представить в виде
формулы, состоящей из конечного набора сравнительно простых функций. Тем не
менее, если расширить класс допустимых в формуле функций (или допустить бесконечность числа операций), представление для корня можно найти (см., к примеру,
☞
ЗДЕСЬ ). Наконец, для практических задач часто более важна не столько «красивая»
аналитическая формула для корня, сколько приближенное его значение с требуемой точностью.
Поиск корней алгебраических уравнений: возможность упрощений
Для некоторых классов уравнений удается упростить задачу: свести решение исходного уравнения к решению уравнения меньшей степени 
Возвратное уравнение
Так называется уравнение вида
$ a_0z^n+a_1z^{n-1}+dots+a_{n-1}z+a_n=0, a_0ne 0 $, у которого набор коэффициентов
$ (a_0,a_1,dots, a_{n-1},a_n) $ симметричен относительно
середины:
$$ a_0=a_{n},a_1=a_{n-1},dots, a_{j}=a_{n-j} dots $$
П
Пример. Уравнения
$$ z^2-3,z+1=0,quad -sqrt{2}z^5+2,z^4+mathbf i z^3+2,z-sqrt{2},quad z^n+1=0 , $$ $$ z^n+z^{n-1}+z^{n-2}+dots + z^2 +z+1=0 $$
являются возвратными.
§
Методы упрощения подобных уравнений
☞
ЗДЕСЬ.
Делимость полиномов
Здесь $ mathbb A_{} $ означает какое-то из множеств $ mathbb Q, mathbb R $ или $ mathbb C_{} $.
Т
Теорема. Для полиномов $ f_{}(x) $ и $ g(x)not equiv 0 $ из $ mathbb A[x] $
существует единственная пара полиномов $ q_{}(x) $ и $ r_{}(x) $ из
$ mathbb A[x] $ таких, что
$$
f(x) equiv g(x) q(x) + r(x) quad mbox{ и } quad
deg r < deg g .
$$
Доказательство
☞
ЗДЕСЬ.
В этом представлении полином $ f_{}(x) $ называется делимым, $ g_{}(x) $ — делителем,
$ r_{}(x) $ — остатком от деления $ f_{}(x) $ на $ g_{}(x) $, а $ q_{}(x) $ —
частным9).
При $ r(x) equiv 0 $, говорят, что полином $ f_{}(x) $ делится (нацело)
на $ g_{}(x) $, а полином $ g_{}(x) $ называется делителем $ f_{}(x) $. Тривиальными делителями полинома $ f_{}(x) $ называют сам полином $ f_{}(x) $ и полином тождественно равный $ 1_{} $ (оба — с точностью до домножения на ненулевую константу). Любой другой делитель полинома (если существует) называется нетривиальным.
П
Пример [1]. Найти частное и остаток от деления
$$f(x)=2, x^5 +x^4 -x^2 +2, x +1 quad mbox{ на } quad
g(x)=x^3+2, x^2 — x -1 .$$
Решение.
$$
begin{array}{rrrrrrr|l}
2,x^5&+ x^4 &+0x^3 &-x^2 &+2x &+1 && x^3+2,x^2-x-1\
2,x^{5}&+4 x^4&-2,x^3&-2x^2&& && overline{ 2,x^2 -3, x +8 quad } \
hline
&-3,x^4&+2,x^3&+x^2&+2,x& \
&-3,x^{4}&-6,x^3&+3,x^2&+3,x& \
hline
&&8,x^{3}&-2,x^2&-x&+1 \
&&8,x^{3}&+16,x^2&-8,x&-8 \
hline
&&& -18x^{2}&+7,x&+9
end{array}
$$
Ответ. $ q(x)=2, x^2 -3, x + 8, r(x)=-18, x^2 + 7, x +9 $.
Фактическое выполнение операции деления полиномов можно производить, действуя лишь над наборами их коэффициентов — подобно тому, как мы производили их умножение.
П
Пример. Найти частное и остаток от деления
$$f(x)=x^8+x^7+3,x^4-1 quad mbox{ на } quad g(x)=x^4-3, x^3 +4, x +1 .$$
Решение.
$$
begin{array}{rrrrrrrrrr|l}
1& 1 &0&0&3&0 &0 & 0&-1 &&1 -3 0 4 1\
1&-3 &0&4&1& & & & && overline{ 1 4 12 32 82} \
hline
&4 & 0 &-4 & 2 & 0 & {} \
&4 &-12& 0 & 16 & 4& {} \
hline
&& 12& -4 &-14 & -4 & 0 & {} \
&& 12& -36 & 0 & 48 & 12 & {} \
hline
&&& 32 & -14& -52&-12 & 0 & {} \
&&& 32 & -96& 0 & 128& 32 & {} \
hline
&&&&82&-52&-140&-32&-1 \
&&&&82&-246&0&328&82 \
hline
&&&&&194&-140&-360&-83
end{array}
$$
Ответ. $ q(x)=x^4+4,x^3+12,x^2+32, x+82,, r(x)=194, x^3-140, x^2-360, x -83 $.
Свойства.
1.
Если $ m le n $ при $ a_0ne 0, b_0 ne 0 $, то $ deg q(x) =n-m $ и ведущий член $ q_{}(x) $ равен $ {a_0}/{b_0}, x^{n-m} $.
2.
Если $ g(x)equiv x-c $, то коэффициенты частного $ q_{}(x) $ найдутся из схемы Хорнера.
Наибольший общий делитель
Рассмотрим множество всех общих делителей полиномов $ f_{}(x) $ и $ g_{}(x) $:
$$
mathbb D={d_1(x) in mathbb A[x] , | f(x) mbox{ делится на } d_1(x), g(x) mbox{ делится на } d_1(x) } .
$$
Наибольшим общим делителем полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином $ d_{}(x) $, который является делителем как $ f_{}(x) $, так и $ g_{}(x) $ и, вместе с тем, сам делится на любой другой общий делитель этих полиномов:
$$ operatorname{HOD} (f(x),g(x)) = d(x) iff d(x) in mathbb D
, d(x) mbox{ делится на } forall d_1(x) in mathbb D
.
$$
Рассмотрим множество всех полиномов, которые делятся и на $ f_{}(x) $ и на $ g_{}(x) $:
$$
mathbb K={k_1(x) in mathbb A[x] , | k_1(x) mbox{ делится на } f(x), k_1(x) mbox{ делится на } g(x) } .
$$
Наименьшим общим кратным полиномов $ f_{}(x) $ и $ g_{}(x) $ называется полином $ k_{}(x) $, который делится как на $ f_{}(x) $, так и на $ g_{}(x) $ и, вместе с тем, сам является делителем любого другого полинома, который делится на $ f_{}(x) $ и $ g_{}(x) $:
$$ operatorname{HOK} (f(x),g(x)) = k(x) iff k(x) in mathbb K
, forall k_1(x) in mathbb K
mbox{ делится на } k(x) .
$$
Пока открытым является вопрос существования $ operatorname{HOD} (f,g)_{} $ и $ operatorname{HOK} (f,g)_{} $. Для первого случая этот вопрос решается
конструктивно — построением $ operatorname{HOD} (f,g)_{} $ с помощью алгоритма, позаимствованного из
☞
ТЕОРИИ ЧИСЕЛ.
Алгоритм Евклида.
Пусть $ f(x) not equiv 0 $ и $ g(x) not equiv 0 $ — полиномы из $ mathbb A_{}[x] $ . Поделим $ f_{}(x) $ на $ g_{}(x) $:
$ f(x)=g(x)q_{1}(x)+r_1(x) $, пусть остаток $ r_{1}(x) not equiv 0 $, тогда
$ 0 le deg r_{1}(x)< deg g(x) $. Поделим делитель на
этот остаток: $ g(x)=r_{1}(x)q_2(x)+r_2(x) $, предположим, что остаток
$ r_{2}(x) not equiv 0 $, тогда $ 0 le deg r_{2}(x)< deg r_1(x) $.
Снова разделим делитель на остаток и продолжим процесс далее
до тех пор, пока на каком-то шаге не произойдет деление нацело, т.е.
остаток будет тождественно равен нулю (это обязательно случится за конечное число
шагов, т.к. степени полиномов $ r_{j}(x) $ уменьшаются). Запишем процедуру в виде схемы:
$$
begin{array}{lcl}
f(x)&=&g(x)q_1(x)+r_1(x) , quad 0 le deg r_1(x)< deg g(x) , \
g(x)&=&r_1(x)q_2(x)+r_2(x) , quad 0 le deg r_2(x)< deg r_1(x), \
r_1(x)&=&r_2(x)q_3(x)+r_3(x) , quad 0 le deg r_3(x)< deg r_2(x), \
dots && dots \
r_{j-2}(x)&=&r_{j-1}(x)q_{j}(x)+r_{j}(x) , quad
0 le deg r_j(x)< deg r_{j-1}(x) , \
dots && dots \
r_{k-2}(x)&=&r_{k-1}(x)q_{k}(x)+r_{k}(x) , quad 0 le deg r_k(x)< deg r_{k-1}(x) , \
r_{k-1}(x)&=&r_{k}(x)q_{k+1}(x) .
end{array}
$$
Т
Теорема. Последний не равный нулю остаток в алгоритме Евклида совпадает с $ operatorname{HOD}(f(x),g_{}(x)) $.
Доказательство полностью аналогично доказательству соответствующего результата из теории целых чисел.
♦
П
Пример. Вычислить
$$ operatorname{HOD} left( x^4+3, x^3 -x^2 -4, x -3, ,
3, x^3 +10, x^2 +2, x -3 right) , . $$
Решение.
$$
begin{array}{rrrrrr|l}
x^4 &+3,x^3 &-x^2 &-4,x &-3 && 3,x^3+10,x^2+2,x-3\
x^4&+10/3, x^3&+2/3, x^2&-, x &
&& overline{ 1/3 x -1/9 quad } \
hline
&-1/3,x^3&-
5/3,x^2&-3,x&-3 \
&-1/3,x^3&-10/9,x^2&
-2/9,x&{}
+1/3 \
hline
&&-5/9,,x^2&
-25/9,x&-10/3
end{array}
$$
В обозначениях алгоритма Евклида, имеем:
$$ q_{1}(x)=1/3, x -1/9, r_{1}(x)=-5/9, x^2 -25/9, x-10/3 . $$
Поскольку $ r_{1}(x) notequiv 0 $, делим $ g_{}(x) $ на этот остаток:
$$
begin{array}{rrrrr|l}
3,x^3 &+10,x^2 &+2,x &-3 && -5/9,,x^2
-25/9,x-10/3 \
3, x^3&+15, x^2&+18, x & &&,
overline{-27/5, x +9 quad } \
hline
&-5,x^2&-16,x&-3 \
&-5,x^2&-25,x&-30 \
hline
&&9,x&+27
end{array}
$$
Здесь $ q_{2}(x)=-27/5, x +9, r_2(x)=9x+27 notequiv 0 $ и алгоритм деления продолжается:
$$
begin{array}{rrrr|l}
-5/9,,x^2&
-25/9,x&
-10/3 && 9,x+27 \
-5/9,,x^2&
-5/3,x& && ,
overline{ -5/81, x
— 10/81 quad } \
hline
&-10/9,x&
-10/3 \
&-10/9,x&-10/3 \
hline
& & 0
end{array}
$$
Здесь остаток получился равным нулю, следовательно $ r_{2}(x)=operatorname{HOD}(f(x),g(x)) $.
Ответ. $ 9(x+3)_{} $.
Легко видеть, что если $ d_{}(x) = operatorname{HOD} (f(x),g(x)) $, то и $ Ccdot d(x)_{} $
также будет $ operatorname{HOD} (f(x),g(x)) $ при любой константе $ C ne 0 $. Так, в только
что решенном примере мы имели право записать ответ в виде $ operatorname{HOD}(f,g)=x+3 $
или $ operatorname{HOD} (f,g)=mathbf{i} x+3, mathbf{i} $ и т.д.
Обычно, получив какое-то представление $ d_{}(x) $ для $ operatorname{HOD} (f(x),g(x)) $,
подбирают константу $ C_{} $ так, что либо — в случае $ d(x)in mathbb{Q}[x] $ —
полином $ C_{}d(x) $ имел коэффициенты целыми:
$$ Cd(x) in mathbb{Z}[x] $$
(например, положив $ C_{} $ равным наименьшему общему кратному знаменателей коэффициентов $ d_{}(x) $ ;
либо же так, чтобы $ C_{}d(x) $ был нормализован (имел старший коэффициент равным $ 1_{} $):
$$C=1/(mbox{старший коэффициент } d(x)) .$$
Еще один способ нахождения $ operatorname{HOD} $ для полиномов из $ mathbb{C}[x] $ вытекает из основной теоремы высшей алгебры.
Т
Теорема. Пусть множество $ { (x-lambda_1),dots,(x-lambda_{mathfrak r}) } $ представляет собой объединение множеств линейных сомножителей полиномов $ f_1(x),dots,f_k(x) $. Выпишем «универсальное» разложение каждого $ f_j $ на линейные сомножители:
$$ f_j(x)equiv a_{0j} (x-lambda_1)^{{mathfrak m}_{1j}}(x-lambda_2)^{{mathfrak m}_{2j}}times
dots times
(x-lambda_{mathfrak r})^{{mathfrak m}_{{mathfrak r}j}}
$$
(здесь возможно, что некоторые из кратностей $ {mathfrak m}_{ij} $ равны 0). Тогда
$$ operatorname{HOD} left(f_1(x),dots,f_k(x) right)=
(x-lambda_1)^{{mathfrak m}_1}(x-lambda_2)^{{mathfrak m}_2}times cdots times (x-lambda_{mathfrak r})^{{mathfrak m}_{mathfrak r}} ,
$$
$$
operatorname{HOK} left(f_1(x),dots,f_k(x) right)=
(x-lambda_1)^{{mathfrak M}_1}(x-lambda_2)^{{mathfrak M}_2}times cdots times (x-lambda_{mathfrak r})^{{mathfrak M}_{mathfrak r}}
$$
где $ displaystyle {mathfrak m}_{ell} = min_{jin{1,dots, k}} {mathfrak m}_{ell j}, displaystyle {mathfrak M}_{ell} = max_{jin{1,dots, k}} {mathfrak m}_{ell j} $.
П
Пример. Вычислить $ operatorname{HOD} left(x^2-1,, x^3+1 right) $ .
Решение. Выписываем разложения полиномов на линейные сомножители:
$$x^2-1equiv (x-1)(x+1), quad x^3+1 equiv(x+1)
left(x-left( 1/2 — sqrt{3}/2 mathbf{i} right) right)
left(x- left( 1/2 + sqrt{3}/2 mathbf{i} right) right) .$$
Ответ. $ x+1 $.
Разумеется, этот способ нахождения $ operatorname{HOD} $ имеет
лишь теоретическое значение, поскольку, как было указано
☞
ЗДЕСЬ, получить выражение корней полинома в радикалах, как правило, не удается.
Т
Теорема. Существуют полиномы $ u(x)_{} $ и $ v(x)_{} $ из
$ mathbb A[x] $, удовлетворяющие уравнению линейного представления $ operatorname{HOD} $:
$$
v(x)f(x)+u(x)g(x)equiv operatorname{HOD}(f,g) .
$$
Доказательство этого результата и практический способ построения полиномов $ u(x)_{} $ и $ v(x)_{} $ можно скопировать из соответствующего раздела теории чисел.
§
Явное представление $ operatorname{HOD} (f(x),g(x)) $ через коэффициенты полиномов с помощью аппарата определителей приведено
☞
ЗДЕСЬ.
Алгоритм Евклида имеет приложение и к задаче локализации корней полинома $ f(x) $ с вещественными коэффициентами, т.е. к нахождению числа всех вещественных корней и точного количества их на произвольном интервале вещественной оси. Подробне
☟
ЗДЕСЬ.
Взаимно простые полиномы
— это полиномы, у которых
нормализованный $ operatorname{HOD} $ равен $ 1_{} $ (тождественно). Подробное рассмотрение этого случая
☞
ЗДЕСЬ.
Производные от полинома
Для случая произвольной функции
$ F(x): mathbb R mapsto mathbb R $ это определение строится на предельном переходе:
$$ frac{d, F}{d, x} bigg|_{_{x=c}}
= F^{prime}(c) = lim_{hto 0} frac{F(c+h)-F(c)}{h} .$$
Пусть $ F(x)equiv x^k $ при $ kin mathbb N_{} $. Тогда, с помощью формулы бинома Ньютона
получаем:
$$(c+h)^k-c^k=kc^{k-1}h+C_k^2c^{k-2}h^2+dots+h^k $$
и
$$frac{F(c+h)-F(c)}{h} to kc^{k-1} quad npu hto 0 . $$
Отсюда следует, что функция $ x^{k} $ дифференцируема в любой точке $ xinmathbb R_{} $
и ее производная равна $ kx^{k-1} $. Обобщим это определение и на комплексную
плоскость $ mathbb C^{} $ . Всюду в предыдущих рассуждениях допустим, что и точка
$ c_{} $ и приращение $ h_{} $ могут быть комплексными. Окончательный вывод не изменится:
формула
$$(x^k)^{prime}= kx^{k-1} $$
остается справедливой и для $ xin mathbb C_{} $. С помощью этой формулы, а также с
помощью основных правил дифференцирования функций:
$$
left(F_1pm F_2 right)^{prime}=F_1^{prime}pm F_2^{prime},
left(cFright)^{prime}=cF^{prime},
left(F_1F_2 right)^{prime}=F_1^{prime}F_2+F_1F_2^{prime}
$$
получаем
$$ f^{prime}(x)=(a_0x^n+a_1x^{n-1}+dots+a_{n-1}x+a_n)^{prime}
= na_0x^{n-1}+(n-1)a_1x^{n-2}+dots +a_{n-1} . $$
Таким образом, $ f^{prime}(x) $ также будет полиномом над $ mathbb A_{} $ и
$ deg f^{prime} = deg f — 1 $. Кроме того, обобщая по индукции
формулу дифференцирования произведения, выводим:
$$
left(f_1f_2times dots times f_k right)^{prime}=
f_1^{prime}f_2times dots times f_k+f_1f_2^{prime}times dots times f_k+
dots+ f_1f_2times dots times f_k^{prime} .
$$
Если применить ее к формуле разложения полинома на линейные
множители, то получим формулу
$$
begin{matrix}
f^{prime}(x)&=&a_0(x-lambda_2)(x-lambda_3)times dots times (x-lambda_n)+
\
&+&a_0(x-lambda_1)(x-lambda_3)times dots times (x-lambda_n)+ \
&+ & dots + \
&+& a_0(x-lambda_1)(x-lambda_2)times dots times (x-lambda_{n-1}).
end{matrix}
$$
Из нее, в частности, следует, что
$$
f^{prime}(lambda_j)=a_0(lambda_j-lambda_1)times dots times
(lambda_j-lambda_{j-1})(lambda_j-lambda_{j+1})
times dots times (lambda_j-lambda_{n})=
$$
$$
=a_0
prod_{1le k le n atop
scriptstyle kne j} (lambda_j — lambda_k) .
$$
Последняя формула, впрочем, может быть получена и напрямую из определения производной:
$$
f^{prime}(lambda_j)=lim_{xto lambda_j} frac{f(x)-f(lambda_j)}{x-lambda_j}
=lim_{xto lambda_j} frac{a_0(x-lambda_1)timesdotstimes (x-lambda_n)}{x-lambda_j} .
$$
Производные высших порядков вводятся определением
$$F^{(k)}(x)= left(F^{(k-1)}(x) right)^{prime} npu k>1 ; $$
для однотипности обозначений считают также нулевой производной сам полином:
$$F^{(0)}(x)= F(x) .$$
В дальнейшем нам пригодится следующая формула Лейбница:
$$left(F_1 F_2 right)^{(k)}=sum_{j=0}^k C_k^j F_1^{(k-j)}F_2^{(j)}=$$
$$
=F_1^{(k)}F_2+ C_k^1F_1^{(k-1)}F_2^{prime}
+ C_k^2F_1^{(k-2)}F_2^{prime prime }+ dots +F_1F_2^{(k)} ,
$$
где $ C_k^{j} $ означает биномиальный коэффициент.
Для полинома $ f(x)_{} $ степени $ n_{} $ имеем:
$$f^{(k)}(x)=n(n-1)times dots times (n-k+1)a_0x^{n-k}+dots+k!a_{n-k}
npu kle n $$
и $ deg f^{(k)} = deg f — k $. Очевидно $ f^{(k)}(x)equiv 0 $ при $ k> n_{} $.
Т
Теорема. Простой корень полинома не является корнем его производной. Кратный корень полинома кратности $ mathfrak m $ является корнем его производной кратности $ ({mathfrak m}-1) $.
Доказательство. Если $ x=lambda_{} in mathbb C $ — простой корень для $ f_{}(x) $, то
$ f(x)equiv (x-lambda)tilde{f}(x) $ при $ tilde{f}(lambda) ne 0 $.
Дифференцируя и подставляя $ x=lambda $, получаем
$$
f^{prime}(x)equiv tilde{f}(x) +(x-lambda)tilde{f}^{prime}(x)
Rightarrow f^{prime}(lambda)=tilde{f}(lambda)ne 0
$$
по предположению.
Если $ x=lambda_{} $ — кратный корень кратности $ mathfrak m $ для $ f_{}(x) $, то
$ f(x)equiv (x-lambda)^{mathfrak m}widehat{f}(x) $ при $ widehat{f}(lambda) ne 0 $. Снова дифференцируем:
$$
f^{prime}(x)={mathfrak m}(x-lambda)^{{mathfrak m}-1} widehat{f}(x)+
(x-lambda)^{{mathfrak m}}widehat{f}^{prime}(x)=
$$
$$
=(x-lambda)^{{mathfrak m}-1}
underbrace{left({mathfrak m}widehat{f}(x)
+(x-lambda)widehat{f}^{prime}(x)
right)}_{= H(x)} .
$$
Из этого представления следует, что $ x=lambda_{} $ является корнем $ f^{prime}(x) $
кратности, не меньшей $ ({mathfrak m}-1) $. Если бы кратность была
больше этого значения, то необходимо $ H(lambda)=0 $. Однако, этого не
может быть, т.к. $ widehat{f}(lambda) ne 0 $.
♦
=>
Полином $ f(x)_{} $ имеет кратный корень тогда и только
тогда, когда он имеет нетривиальный наибольший общий делитель со своей производной
$$ operatorname{HOD} (f(x),f^{prime}(x)) notequiv const . $$
П
Пример. При каком условии на коэффициенты $ p_{} $ и $ q_{} $ полином
$$ x^3+p,x+q $$
имеет кратный корень?
Решение. На основании теоремы на этом корне $ x=lambda_{} $
должно быть выполнено
$$lambda^3+p,lambda+q=0 , quad 3, lambda^2 + p=0 .$$
Из второго равенства выражаем $ lambda^2 $ и подставляем в первое:
$$lambda^2=-frac{p}{3} Rightarrow lambda left(-frac{p}{3} right)
+p,lambda+q=0 Rightarrow lambda=-frac{3,q}{2,p} $$
при $ pne 0 $.
Подставляя это значение в любое из исходных равенств, получаем:
$$
frac{27,q^2+4,p^3}{4, p^2} =0 Rightarrow
left(frac{q}{2} right)^2 + left(frac{p}{3} right)^3 =0 .
$$
Это условие уже встречалось нам ВЫШЕ при анализе формулы решения уравнения третьей степени.
При $ p=0 $ кратный корень может встретиться лишь при $ q=0 $, т.е. опять же
при обращении в нуль дискриминанта кубического уравнения.
Ответ. $ left( p/3 right)^3 + left( q/2 right)^2=0 $.
Предыдущий пример позволяет выявить общую закономерность:
наличие у полинома $ f_{}(x) $ кратного корня является ситуацией исключительной,
наблюдаемой только тогда, когда коэффициенты полинома связаны некоторым
условием типа равенства. Общий способ получения этого условия
☞
ЗДЕСЬ
?
При каком условии на коэффициенты $ p_{} $ и $ q_{} $ полином
а) $ x^4+p,x+q $ ; б) $ x^5+p,x+q $
имеет кратный корень?
П
Пример. Найти все значения параметра $ {color{Red} alpha } $, при которых полином
$$ x^4-5,x^2+{color{Red} alpha },x+28 $$
имеет кратный корень.
Решение. На основании следствия к теореме для выполнения
условия необходимо и достаточно, чтобы был нетривиален
$ operatorname{HOD} (f(x),f^{prime}(x)) $. Ищем его по алгоритму Евклида, делим $ f(x) $ на $ f^{prime}(x) $:
$$
f(x)equiv frac{1}{4} , x, f^{prime}(x) +
overbrace{left(-frac{5}{2}, x^2
+frac{3}{4}, {color{Red} alpha }, x +28 right)}^{r_1(x)}
,
$$
затем $ f^{prime}(x) $ на полученный остаток $ r_{1}(x) $:
$$
f^{prime}(x) equiv left(-frac{8}{5},x-
frac{12}{25}, {color{Red} alpha } right) r_1(x) +
overbrace{left(frac{3}{25},(3, {color{Red} alpha }^2 + 290),x+
frac{361}{25}, {color{Red} alpha } right)}^{r_2(x)}
,
$$
и, при дополнительном предположении $ 3, {color{Red} alpha }^2 + 290ne 0 $, делим $ r_{1}(x) $ на $ r_{2}(x) $:
$$
r_1(x) equiv frac{25}{36left(3, {color{Red} alpha }^2 +290 right)^2}
left[-30,left(3, {color{Red} alpha }^2 +290 right) x +
alpha, (27, {color{Red} alpha }^2 + 6220) right] r_2(x) +
$$
$$
+ frac{25, left(-27, {color{Red} alpha }^4 -19660, {color{Red} alpha }^2 + 3390912right)
}{36, left(3, {color{Red} alpha }^2 +290 right)^2} .
$$
$ operatorname{HOD} (f(x),f^{prime}(x)) $ может быть нетривиальным (равным $ r_{2}(x) $)
только при условии
$$-27, {color{Red} alpha }^4 -19660, {color{Red} alpha }^2 + 3390912=0 . $$
Решить последнее уравнение легко если заменить
переменную $ A = {color{Red} alpha }^2 $:
$$( A-144)(27, A +23548)=0 .$$
При $ 3, {color{Red} alpha }^2 + 290= 0 $ будет
$ operatorname{HOD} (f(x),f^{prime}(x))= r_2(x)not equiv 0 $, так что
при этих значениях параметра кратных корней у $ f(x)_{} $ быть не может.
Ответ. $ {color{Red} alpha } in { pm 12, pm {scriptstyle 58}/{scriptstyle 3} sqrt{{scriptstyle 7}/{scriptstyle 3}}, mathbf i } $.
=>
Число $ lambda_{} $ является корнем кратности $ mathfrak m_{} $ для $ f(x)_{} $ тогда и
только тогда, когда выполнены условия:
$$
underbrace{f^{(0)}(lambda)=0,dots, f^{({mathfrak m}-1)}(lambda)=0}_{mathfrak m},,
f^{({mathfrak m})}(lambda)ne 0 .
$$
Доказательство необходимости следует из теоремы. Достаточность вытекает из результатов следующего пункта (формализация способа проверки приводится
☞
ЗДЕСЬ).
Формула Тейлора
Представление полинома $ f(x)_{}in mathbb A[x] $ в канонической форме $ a_{0}x^n+a_1x^{n-1}+dots + a_n $ не является единственно возможным способом задания полинома. В конце концов,
полином можно представить и с помощью разложения на линейные сомножители — разумеется, если известен набор его корней. Саму
эту каноническую форму можно описать как разложение полинома по
степеням переменной $ x_{} $. Пусть теперь $ cin mathbb A_{} $ — произвольная константа.
Любую степень $ x^{k} $ можно «переразложить» по степеням линейного полинома
$ x-c_{} $ с помощью формулы бинома Ньютона:
$$ x^kequiv left[c+(x-c) right]^kequiv c^k +kc^{k-1}(x-c)+
frac{k(k-1)}{2}c^{k-2}(x-c)^2+dots+ (x-c)^k .$$
Если это сделать для каждого монома полинома $ f(x)_{} $, то
получим разложение $ f(x)_{} $ по степеням $ x-c_{} $ в виде
$$
f(x)equiv A_0+A_1(x-c)+A_2(x-c)^2+dots+A_n(x-c)^n .
$$
Задача. Найти коэффициенты $ A_{0},dots,A_n $ в этом разложении.
Для решения этой задачи продифференцируем несколько раз последнее тождество:
$$
begin{matrix}
f^{prime}(x)&=&A_1+2,A_2(x-c)+3,A_3(x-c)^2+dots+nA_n(x-c)^{n-1} , ,\
f^{prime prime}(x)&=&2,A_2+3cdot 2,A_3(x-c)+dots +n(n-1)A_n(x-c)^{n-2}, ,\
f^{prime prime prime}(x)&=&3cdot 2,A_3+dots +n(n-1)(n-2)A_n(x-c)^{n-3}, ,\
dots & & dots
end{matrix}
$$
Подстановка в эти формулы $ x=c_{} $ дает:
$$f^{prime}(c)=A_1, f^{prime prime}(c)=2,A_2, f^{prime prime prime}(c)=
3cdot 2,A_3,dots $$
Т
Теорема. Разложение полинома $ f_{}(x) $ по степеням $ x-c_{} $ имеет вид
$$
f(x) equiv f(c)+
frac{f^{prime}(c)}{1!} (x-c) + frac{f^{prime prime }(c)}{2!} (x-c)^2+
dots + frac{f^{(n)}(c)}{n!} (x-c)^{n} =
$$
$$
=sum_{j=0}^n frac{f^{(j)}(c)}{j!} (x-c)^{j} ;
$$
это тождество называется формулой Тейлора для полинома $ f_{}(x) $ в точке $ x=c $.
Доказательство и алгоритм эффективного вычисления коэффициентов формулы Тейлора (схема Хорнера)
☞
ЗДЕСЬ.
Формула Тейлора имеет гораздо большее значение,
чем просто переразложение полинома $ f_{}(x) $ по степеням заданного линейного полинома.
Она связана с задачей о приближении, аппроксимации функций.
Пусть функция $ F_{}(x) $ неизвестной заранее структуры описывает поведение
какого-то природного процесса. Мы имеем возможность провести серию (конечное
число) экспериментов (наблюдений), чтобы на их основе найти приближенное значение функции в произвольной точке $ x_{} $. Экспериментальные серии могут различаться по своему типу. Это могут быть серии экспериментов
-
однотипных, когда, например, удается узнать (засечь) положение спутника в разные моменты времени $ x_1,x_{2},dots $ на неизвестной орбите;
-
разнотипных, когда для того же спутника мы имеем возможность измерения большого количества различных параметров движения (положения, скорости, ускорения, ускорения ускорения, и пр.), но только в один фиксированный момент времени $ x=c_{} $.
На основании этих серий мы должны предсказать величину $ F(x)_{} $.
Самой простой функцией, решающей задачи в таких постановках, является
полином. Если этот полином $ f(x)_{} $ удается построить, то именно его
мы и будем считать приближением неизвестной нам функции $ F(x)_{} $.
Задача построения такого полинома для серии экспериментов первого типа обсуждается
☞
ЗДЕСЬ. А формула Тейлора позволяет найти полином $ f(x)_{} $ для серии
экспериментов второго типа. Геометрически: неизвестный нам заранее график функции $ y=F(x)_{} $ (красный) приближается (аппроксимируется) либо прямой (зеленый), либо параболой (серый), либо кубикой (фиолетовый) — и все кривые приближения строятся только на основании информации о функции $ F(x)_{} $ в одной-единственной точке $ c_{} $.
П
Пример. Найти приближенное значение $ F(1)_{} $, если известно, что
$$F(-1)=F^{prime}(-1)=F^{prime prime}(-1)=F^{prime prime prime}(-1)=0.367
.$$
Решение. По формуле Тейлора получаем полином
$$f(x)=0.367+0.367(x+1) + frac{0.367}{2} (x+1)^2+frac{0.367}{6} (x+1)^3 $$
и $ f(1)=2.324(3) $.
Ответ. $ F(1)approx 2.324 $.
Полиномы с вещественными коэффициентами
Рассмотрим теперь случай полинома с вещественными коэффициентами
$ f(x)=a_0x^n+a_1x^{n-1}+ dots + a_n in mathbb R [x] $.
Т
Теорема. Значения полинома $ f(x) in mathbb R [x] $ от комплексно-сопряженных значений переменной будут также комплексно-сопряженными:
$$ mbox{если} f(c)=A+mathbf i B mbox{при} {A,B} subset mathbb R, mbox{то} f(overline{c})=A-mathbf i B , . $$
Доказательство. Действительно, поскольку $ a_jin mathbb R $,
то $ overline{a_j}=a_j $ для $ forall jin {0,1,dots,n} $, и тогда
$$
begin{matrix}
fleft(overline{c} right)&=&a_0 overline{c}^n + a_1 overline{c}^{n-1} +
dots + a_n = overline{a_0} overline{c^n} +
overline{a_1} overline{c^{n-1}}+ dots +
overline{a_n}= \
&=&overline{a_0c^n+a_1c^{n-1}+ dots + a_n}=A-mathbf i B .
end{matrix}
$$
=>
Если мнимое число
$ c=alpha + mathbf i beta , beta ne 0 $ является корнем $ f_{}(x) $, то и
ему комплексно-сопряженное $ overline c = alpha — mathbf i beta $ также
является корнем $ f_{}(x) $.
Иными словами, мнимые корни полинома $ f_{}(x) $ с вещественными коэффициентами «ходят пáрами»:
$ alpha pm mathbf i beta $. Геометрический смысл: на комплексной плоскости точки,
изображающие корни $ f_{}(x) $, расположены симметрично относительно вещественной
оси.

Как следствие предыдущей теоремы и основной теоремы высшей алгебры, получим
Т
Теорема. Любой полином $ f_{}(x)in mathbb R [x] $ может быть представлен в виде произведения вещественных полиномов степеней не выше второй:
$$
begin{array}{rl}
f(x) & equiv a_0 (x- lambda_1)^{{mathfrak m}_1} times dots times
(x- lambda_r)^{{mathfrak m}_r} times \
& times (x^2 +p_1x+ q_1)^{{mathfrak M}_1} times dots times
(x^2 +p_{ell}x+ q_{ell})^{{mathfrak M}_{ell}} .
end{array}
$$
Здесь $ lambda_1 , dots , lambda_r $ — различные вещественные числа,
а квадратные трехчлены
$$ {x^2 +p_1x+ q_1, dots , x^2 +p_{ell}x+ q_{ell}} subset mathbb R [x] $$
— различные с отрицательными дискриминантами
$ mathcal D_j=p_j^2-4q_j<0 $. Это представление единственно с точностью до перестановки множителей.
П
Пример. Разложить полином
$$
x^7-sqrt{3}x^6+(-3+2sqrt{3})x^5+(2+sqrt{3})x^4+(3-6sqrt{3})x^3+(-12+11sqrt{3})x^2+
$$
$$
+(10-8sqrt{3})x+4sqrt{3}-6
$$
на вещественные множители.
Ответ. $ (x+sqrt{3})(x+(1-sqrt{3}))^2(x^2-x+1)^2 $.
=>
Полином $ f_{}(x) $ с вещественными коэффициентами нечетной степени имеет хотя бы один вещественный корень, а, в общем случае, нечетное число вещественных корней (с учетом их кратностей ).
Геометрия
Полиномы с вещественными коэффициентами удобны тем, что теоретические результаты, полученные в предыдущих пунктах, получают геометрическую интерпретацию. Прежде всего, следует отметить, что полином является частным случаем непрерывной функции и на него распространяются все результаты математического анализа, разработанные для подобных функций. Итак, полином $ f_{}(x) $ — непрерывная функция при любых $ x in mathbb R $. Более того, поскольку производные полинома снова оказываются полиномами, то свойство непрерывности наследуется при дифференцировании: полином является непрерывно-дифференцируемой функцией. Из этого следует, что на плоскости $ (x_{},y) $ график полинома $ y=f_{}(x) $ представляет из себя непрерывную и гладкую кривую (ни разрывов, ни углов!) — касательная к графику существует в любой его точке.
Далее, вещественному корню $ x=lambda_{} $ полинома $ f_{}(x) $ на плоскости
$ (x_{},y) $ соответствует точка пересечения графика $ y=f_{}(x) $ с осью абсцисс.

По основной теореме высшей алгебры, таких точек может быть только конечное число: их — не более степени полинома $ deg f (x) $. Далее, между каждой парой $ lambda_j, lambda_k $ вещественных корней полинома $ f_{}(x) $, его график обязан иметь «впадину» или «горб». Обращаясь к языку математического анализа, можно сказать (и доказать), что между двумя вещественными корнями полинома находится точка его локального минимума или локального максимума. В этой точке касательная к графику функции параллельна оси абсцисс и, следовательно, тангенс угла наклона касательной должен быть равен нулю. Иными словами, точки $ mu_1,mu_2,dots $, в которых полином имеет локальный минимум или максимум, должны быть корнями его производной. См. следующий ПУНКТ.
К сожалению, не имеется наглядной интерпретации мнимых корней полинома .
§
Дальнейшие геометрические свойства полинома с вещественными коэффициентами см.
☞
ЗДЕСЬ.
Экстремумы
Говорят, что полином $ f(x)in mathbb R[x] $ имеет в точке
$ c_{} $ (локальный) минимум если существует некоторое $ delta>0 $, что при всех значениях аргументов из $ delta_{} $-окрестности точки $ c_{} $, т.е. при всех $ x_{} $, удовлетворяющих неравенству $ |x-c|<delta $
будет выполнено $ f(x)> f(c) $.
Если последнее неравенство изменить на противоположное, то получим
определение (локального) максимума. Говорят, что полином
имеет в точке $ c_{} $ (локальный) экстремум10) если он имеет в этой точке либо максимум либо минимум.
Т
Теорема [Ферма для полиномов]. Если полином $ f_{}(x) $ имеет в точке
$ c_{} $ экстремум, то в этой точке его производная обращается в нуль:
$$
f'(c)=0 .
$$
Геометрический смысл этого результата пояснен в предыдущем пункте. Обращение производной полинома в нуль в точке $ c_{} $ является условием необходимым для существования в ней экстремума. Для выяснения будет ли в этой точке минимум, максимум или же экстремум отсутствует, следует обратиться к формуле Тейлора. Рассмотрим эту формулу в точке $ c_{} $ «подозрительной на экстремум», т.е. в такой, где $ f'(c)=0 $:
$$
f(x)-f(c)=frac{1}{2}f»(c)(x-c)^2+frac{1}{6}f»'(c)(x-c)^3+dots+frac{1}{n!}f^{(n)}(c)(x-c)^n
.
$$
Если $ f»(c)ne 0 $, то можем переписать эту разность в виде
$$
f(x)-f(c)=(x-c)^2underbrace{left[frac{1}{2}f»(c)+frac{1}{6}f»'(c)(x-c)+dots+frac{1}{n!}f^{(n)}(c)(x-c)^{n-2}right]}_{P(x)} .
$$
Полином $ P(x) $ в точке $ c_{} $ имеет значение $ frac{1}{2}f»(c) $, и его знак в некоторой окрестности точки $ c_{} $ полностью определяется знаком этого числа. Таким образом, в той же окрестности имеем:
$$ operatorname{sign} (f(x)-f(c)) = operatorname{sign} (f»(c)) . $$
=>
Если в точке $ c_{} $ выполнены условия $ f'(c)=0, f»(c)> 0 $ то в этой точке полином имеет локальный минимум; если же в ней выполнены условия $ f'(c)=0, f»(c)< 0 $, то в этой точке полином имеет локальный максимум.
Остался нерассмотренным случай $ f'(c)=0, f»(c)= 0 $ — крайне исключительный. Эта исключительность будет понятной если обратиться к результатам пункта о производных полинома: вероятность того, чтобы случайным образом выбранный полином $ f_{}(x) $ обладал такой точкой $ c_{} $ — нулевая. Тем не менее, надо довести исследование до конца и в этом случае. Если $ f»'(c) ne 0 $, то из той же формулы Тейлора имеем формулу:
$$
f(x)-f(c)=(x-c)^3underbrace{left[frac{1}{6}f»'(c)+dots+frac{1}{n!}f^{(n)}(c)(x-c)^{n-3}right]}_{Q(x)} .
$$
Вне зависимости от знака $ f»'(c) $ эта разность принимает значения разных знаков в произвольной окрестности точки $ c_{} $:
$$ operatorname{sign} (f(x)-f(c)) = left{ begin{array}{r}
operatorname{sign} f»'(c) quad npu x > c \
— operatorname{sign} f»'(c) quad npu x < c
end{array}
right.
$$
В точке $ c_{} $ полином не имеет ни минимума, ни максимума. По аналогии рассматривается и общий случай.
Т
Теорема. Для того, чтобы в точке $ c_{} $ полином $ f_{}(x) $ имел экстремум необходимо и достаточно, чтобы в этой точке были выполнены условия
$$ f'(c)=0,f»(c)=0,dots, f^{(k)}(c)=0,f^{(k+1)}(c)ne 0 $$
при произвольном нечетном $ k_{} $. При этом в точке $ c_{} $ полином будет иметь локальный минимум при $ f^{(k+1)}(c)>0 $ и локальный максимум при $ f^{(k+1)}(c)<0 $.
При известной точке $ c_{} $ условия теоремы удобно проверять с помощью схемы Хорнера.
Еще одним аспектом проблемы является вычисление собственно экстремальных значений полинома, т.е. величин $ f(c) $. В самом деле, поставим, например, задачу нахождения абсолютного (глобального) максимума полинома на всем множестве вещественных чисел. Такая постановка задачи имеет смысл при дополнительном условии, что полином $ f_{}(x) $ имеет четную степень и отрицательный старший коэффициент (только при этом условии при $ x to + infty $ и при $ x to -infty $ значения полинома не будут неограниченно возрастать). В соответствии с теоремой Ферма, нам нужно найти все вещественные корни производной полинома, т.е. решить уравнение $ f'(x)=0 $, подставить найденные величины в сам полином и ранжировать полученные значения по возрастанию. Вспомним, однако, что для корней полинома, как правило, не получить точных формул (см.
☞
ЗДЕСЬ ), поэтому оценить корни полинома $ f'(x) $ мы можем, разве что, приближенно. После их нахождения, приближенные значения подставляются в полином $ f_{}(x) $ и ошибка вычислений накапливается… Можно ли избежать этого накопления? — Частично, да. Для полинома $ f_{}(x) $ (четной) степени $ n_{} $ можно построить новый полином степени $ n-1 $ по новой переменной $ z_{} $:
$$ mathcal F(z) = (z-f(mu_1))times dots times(z-f(mu_{n-1})) , $$
где $ mu_1,dots,mu_{n-1} $ — корни $ f'(x) $. При этом коэффициенты нового полинома $ mathcal F(z) $ будут рационально выражаться через коэффициенты полинома $ f'(x) $ на основании теоремы Гаусса о симметрических полиномах. Подробности конструктивного построения см.
☞
ЗДЕСЬ. Как правило, максимальный вещественный корень полинома $ mathcal F(z) $ и будет давать значение $ max f(x) $.
П
Пример. Найти
$$ max_{xin mathbb R} (-x^6+12,x^2+12,x+2) , . $$
Решение. Если идти по традиционной схеме математического анализа, то мы должны сначала найти корни производной полинома $ f(x)=-x^6+12,x^2+12,x+2 $, т.е. решить уравнение
$ x^5-4,x-2=0 $. В радикалах это уравнение не решается, так что приходится применять приближенные методы поиска вещественных корней: $ mu_1approx -1.24359, mu_2 approx — 0.50849, mu_3 approx 1.51851 $. Наконец, требуется сравнить по величине $ f(mu_1), f(mu_2), f(mu_3) $.
В альтернативу этому подходу, можно избежать нахождения корней производной и построить (хоть и кропотливо, но зато безошибочно) полином
$$ mathcal F(z)= -z^5+10,z^4+472,z^3+16208,z^2-16272,z-32800 , $$
найти один его (максимальный вещественный) корень $ approx 35.6321 $ — он и будет искомым максимумом.
Проверка: $ max f = f(mu_3) approx 35.6321 $.
Подчеркнем, что указанная возможность гарантирована только полиномиальностью рассматриваемой экстремальной задачи и на произвольные (неполиномиальные) функции предлагаемый метод не распространяется.
Приводимость
Полином $ Phi(x) in mathbb A[x] $, отличный от константы, называется неприводимым в (или неприводимым над) $ mathbb A_{} $ если у $ Phi(x) $ нет нетривиального делителя в $ mathbb A[x] $. В противном случае $ Phi(x) $ называется приводимым в (или приводимым над) $ mathbb A_{} $. Полином $ Phi(x) in mathbb A[x] $ неприводим над $ mathbb A_{} $ тогда и только тогда, когда $ operatorname{HOD} (Phi(x),g(x)) equiv const in mathbb A_{} $ для любого полинома $ g(x)in mathbb A_{}[x], deg g(x) < deg Phi (x) $.
Понятие неприводимости полинома является аналогом понятия простоты числа в теории (целых) чисел.
Т
Теорема. Любой полином $ f(x) in mathbb A [x] $ можно представить в виде
$$
begin{array}{rl}
f(x) & equiv a_0 (x- lambda_1)^{{mathfrak m}_1} times dots times
(x- lambda_r)^{{mathfrak m}_r} times \
& times (x^2 +p_1x+ q_1)^{{mathfrak M}_1} times dots times
(x^2 +p_{ell}x+ q_{ell})^{{mathfrak M}_{ell}} .
end{array}
$$
где $ Phi_1(x),dots , Phi_K(x) $ — различные нормализованные и неприводимые в $ mathbb A_{} $ полиномы, а $ { {mathfrak m}_1,dots,{mathfrak m}_K } subset mathbb N $.
Последнее тождество называется каноническим разложением $ f(x)_{} $ над $ mathbb A_{} $.
П
Пример. Полином $ x^{2}-2 $ неприводим в $ mathbb Q_{} $, но приводим в $ mathbb R_{} $:
$$ x^2-2 equiv left(x-sqrt{2} right) left(x + sqrt{2} right) , .$$
Полином $ x^{2}+2 $ неприводим в $ mathbb Q_{} $, но приводим в $ mathbb C_{} $:
$$ x^2+2 equiv left(x+mathbf i sqrt{2} right) left(x — mathbf i sqrt{2} right) , .$$
Полином $ x^{4}+4 $ не имеет вещественных корней, но, тем не менее, приводим в $ mathbb Q_{} $, т.к.
$$ x^4+4equiv (x^2+2, x +2)(x^2-2, x +2) , . $$
Т
Теорема. Любой полином $ f(x)in mathbb C [x] $ степени большей $ 1_{} $ приводим в $ mathbb C_{} $.
Доказательство следует из основной теоремы высшей алгебры.
♦
Т
Теорема. Любой полином $ f(x)in mathbb R [x] $ степени большей $ 2_{} $ приводим в $ mathbb R_{} $. Неприводимыми в $ mathbb R_{} $ являются полиномы вида
$$ x+a quad mbox{и} quad x^2+p, x +q_{} quad mbox{при} quad {a,p,q } subset mathbb R, p^2 — 4q <0 , .$$
Каноническое разложение в $ mathbb R_{} $ произвольного полинома $ f(x)in mathbb R [x] $
имеет вид
$$
f(x)equiv a_0 (x- lambda_1)^{{mathfrak m}_1} times dots times
(x- lambda_r)^{{mathfrak m}_r} times
$$
$$
times (x^2 +p_1x+ q_1)^{{mathfrak M}_1} times dots times
(x^2 +p_{ell}x+ q_{ell})^{{mathfrak M}_{ell}} ,
$$
где $ lambda_{1} , dots , lambda_r $ — различные вещественные числа, а квадратные трехчлены $ {x^2 +p_1x+ q_1, dots , x^2 +p_{ell}x+ q_{ell}} subset mathbb R [x] $ — различные с отрицательными дискриминантами $ mathcal D_j=p_j^2-4q_j<0 $.
Фактически, эта теорема является переформулировкой результата, приведенного
☞
ЗДЕСЬ.
Рассмотрим теперь полином с рациональными коэффициентами:
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_n in mathbb Q [x] , a_0 ne 0 . $$
Если полином $ f_{}(x) $ приводим в $ mathbb Q_{} $, то будет приводимым и
полином $ Ccdot f_{}(x) $ при $ forall C in mathbb Q, C ne 0 $; верно и обратное.
Представив коэффициенты $ a_{0},dots, a_n $ в виде несократимых дробей,
возьмем
$$ C=operatorname{HOK}(mbox{ знаменатель } a_{0},dots, mbox{ знаменатель } a_n ) , $$
тогда приводимость (или неприводимость) полинома $ f_{}(x) $ в $ mathbb Q_{} $
эквивалентна приводимости (соответственно, неприводимости)
в $ mathbb Q_{} $ полинома $ Ccdot f(x) $ с целыми коэффициентами. Поэтому в дальнейшем
будем сразу предполагать
$ f(x)in mathbb Z[x] $. Можно ли пойти дальше и утверждать, что приводимость
такого полинома в $ mathbb Q_{} $ эквивалентна приводимости его в $ mathbb Z_{} $, т.е.
полином раскладывается на произведение полиномов меньших степеней с рациональными коэффициентами тогда и
только тогда, когда он раскладывается на произведение полиномов меньших степеней с целыми коэффициентами?
Т
Теорема. Полином $ f(x)in mathbb Z[x] $ неприводимый в $ mathbb Z_{} $ будет неприводимым и в $ mathbb Q_{} $.
Приводимость полинома с целыми коэффициентами $ f(x)in mathbb Z[x] $ в $ mathbb Z_{} $ означает, что он раскладывается на два множителя с целыми коэффициентами:
$$
a_0x^n+a_1x^{n-1}+ dots + a_n equiv (b_0x^k+b_1x^{k-1} + dots + b_k)
(c_0x^{ell}+c_1x^{ell-1} + dots + c_{ell})
$$
при $ k<n, ell < n, k+ell = n $. Для практического решения вопроса о существовании такого разложения, сначала установим условия его существования для случая, когда один из
сомножителей — линейный полином.
Т
Теорема. Если полином
$$f(x)=a_0x^n+a_1x^{n-1} + dots + a_n in mathbb Z[x] , a_0 ne 0,a_n ne 0 $$
имеет рациональный корень, представленный в виде несократимой дроби $ lambda=mathfrak p/mathfrak q,, {{mathfrak p}, {mathfrak q}}subset mathbb Z $, то ее числитель $ {mathfrak p} $ является делителем свободного члена $ a_{n} $, а знаменатель $ {mathfrak q}_{} $ — делителем старшего коэффициента $ a_{0} $.
Доказательство
☞
ЗДЕСЬ
.
♦
Итак, для поиска рациональных корней полинома $ f_{}(x) $ надо выписать множество всех натуральных делителей $ {{mathfrak p}_1=1,dots,{mathfrak p}_{s}} $ числа $ |a_n| $, и множество всех натуральных делителей $ {{mathfrak q}_1=1,dots,{mathfrak q}_{t}} $ числа $ |a_0| $, и после этого организовать вычисление $ fleft(pm {mathfrak p}_j/{mathfrak q}_i right) $
при всех возможных значениях индексов $ jin {1,dots,s }, i in {1,dots, t } $. Если ни одно из полученных чисел не равно нулю, то рациональных корней полином не имеет.
=>
Если нормализованный полином $ f(x) in mathbb Z[x] $ имеет рациональные корни, то они — только целые и находятся среди делителей свободного члена.
П
Пример. Найти рациональные корни полинома
$$f(x)=6,x^6-55, x^5+331, x^3-86,x^4+289,x^2-25,x+350 . $$
Решение. Выписываем множества делителей
для $ 350 : quad {1,, 2 ,, 5 ,, 7,, 10,, 14,, 25
,, 35,, 50,, 70,, 175 } $ и для $ 6 : {1,, 2,, 3,, 6 } $.
Составляем всевозможные несократимые дроби:
$$ left{
begin{array}{ccccccccccc}
1,& 2 ,& 5 ,& 7,& 10,& 14,& 25 ,& 35,& 50,& 70,& 175, \
{scriptstyle 1}/{scriptstyle 2},& &
{scriptstyle 5}/{scriptstyle 2} ,& {scriptstyle 7}/{scriptstyle 2}, &
& & {scriptstyle 25}/{scriptstyle 2}
& {scriptstyle 35}/{scriptstyle 2}, & & &
{scriptstyle 175}/{scriptstyle 2}, \
{scriptstyle 1}/{scriptstyle 3},& {scriptstyle 2}/{scriptstyle 3},&
{scriptstyle 5}/{scriptstyle 3},& {scriptstyle 7}/{scriptstyle 3},&
{scriptstyle 10}/{scriptstyle 3},&
{scriptstyle 14}/{scriptstyle 3},& {scriptstyle 25}/{scriptstyle 3},&
{scriptstyle 35}/{scriptstyle 3},& {scriptstyle 50}/{scriptstyle 3},&
{scriptstyle 70}/{scriptstyle 3},& {scriptstyle 175}/{scriptstyle 3}, \
{scriptstyle 1}/{scriptstyle 6},& &
{scriptstyle 5}/{scriptstyle 6}, & {scriptstyle 7}/{scriptstyle 6}, &
& &
{scriptstyle 25}/{scriptstyle 6},& {scriptstyle 35}/{scriptstyle 6},& &
& {scriptstyle 175}/{scriptstyle 6}
end{array}
right}
$$
Подставляем все эти значения со знаками $ +_{} $ и $ — $ в $ f(x)_{} $ и проверяем (например, с использованием схемы Хорнера ) на равенство нулю.
Ответ. $ 10,, {scriptstyle 5}/{scriptstyle 2},, -{scriptstyle 7}/{scriptstyle 3} $.
Из того факта, что полином $ f(x) in mathbb Z[x] $ не имеет рациональных корней не
следует, что он неприводим в $ mathbb Z_{} $: в разложении $ f(x)equiv f_{1}(x)f_2(x) $ сомножители
могут оказаться и нелинейными — например, как указанный выше полином $ x^{2}+4 $. Как найти эти сомножители?
§
Подробнее о приводимости и неприводимости полиномов в $ mathbb Z_{} $
☞
ЗДЕСЬ.
Локализация корней
Границы расположения корней
Т
Теорема [Маклорен].11) Все корни полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_n in mathbb C [x], a_0 ne 0$$
удовлетворяют неравенству
$$
|lambda_j|<1+ A,quad npu quad A=
max_{kin{1,dots,n}} left| frac{a_k}{a_0} right| .
$$
Оценка Маклорена довольно грубая и для корней полиномов с вещественными коэффициентами
чаще применяется другой критерий.
Т
Теорема [Лагранж]. Все вещественные корни полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_n in mathbb R [x], a_0>0$$
удовлетворяют неравенству
$$
lambda_j<1+ sqrt[r]{A},quad npu quad
A=max_{kin {1,dots,n}} left| frac{a_k}{a_0} right| ,
$$
где $ r $ — номер первого отрицательного коэффициента.
Оценка Лагранжа, являясь оценкой вещественных корней сверху, фактически ограничивает возможные положительные корни.
?
А как получить нижнюю оценку возможных отрицательных корней?
Это можно сделать с помощью преобразования
1
полинома, рассмотренного
☞
ЗДЕСЬ.
В самом деле, отрицательные корни полинома $ f(x) $ являются положительными
корнями полинома $ f(-x) $. Найдя верхнюю границу последних с помощью любого
из приведенных выше критериев, мы меняем у нее знак и в результате получаем
нижнюю оценку отрицательных корней $ f(x) $.
Преобразование
3
,
рассмотренное в том же пункте, позволяет получить отдельные
интервалы для возможных положительных и отрицательных корней.
П
Пример. Найти оценки положительных и отрицательных корней полинома
$$
f(x)=x^8+2, x^7-2, x^6 +6, x^5 -80, x^4 + 100, x^3 -400, x^2 + 15, x +30
.
$$
Решение. Сначала ограничим положительные корни сверху. В теореме
Лагранжа имеем $ r=2,, A=400 $, следовательно $ lambda_j<21 $.
Теперь ограничим отрицательные корни снизу.
$$
f(-x)=x^8-2, x^7-2, x^6 -6, x^5 -80, x^4 — 100, x^3 -400, x^2 — 15, x +30
,
$$
и теперь $ r=1,, A=400 $, следовательно $ -lambda_j<401 Rightarrow
lambda_j > -401 $. Формируем полином
$$
f^{ast}(x) = x^8f(1/x)=
1+2, x-2, x^2 +6, x^3 -80, x^4 + 100, x^5 -400, x^6 + 15, x^7 +30,x^8
$$
для оценки нижней границы положительных корней:
$$1/lambda_j < 1 + sqrt{400/30}
Rightarrow lambda_j > frac{1}{1 +sqrt{40/3}}
.
$$
Наконец, оценка Лагранжа для полинома $ f^{ast}(-x) $:
$$-1/lambda_j < 1+ 40/3
Rightarrow lambda_j < — frac{1}{1 +40/3}
$$
позволяет ограничить сверху отрицательные корни полинома $ f(x) $.
Ответ. Положительные корни находятся в интервале $ ]0.214, ,21[ $,
а отрицательные — в интервале $ ]-401,-0.06[ $.
Проверка. Вещественные корни полинома:
$$-4.324358112, -0.2473416673, 0.3027275675, 2.716544138 .$$
Правило знаков Декарта
Для полиномов с вещественными коэффициентами следующий полезный результат очень прост в проверке.
Будем использовать сокращение $ operatorname{nrr} $ для числа вещественных корней12).
Т
Теорема [Декарт]. Число положительных корней полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_{n-1}x+a_n in mathbb R[x], quad (a_0> 0,a_n ne 0)$$
с учетом их кратностей равно или меньше на четное число числа знакоперемен в ряду его коэффициентов:
$$
operatorname{nrr} { f(x)=0 mid x>0 } = {mathcal V}(a_0,a_1,dots,a_n)-2 k , quad
kin {0,1,2, dots } .
$$
Доказательство
☞
ЗДЕСЬ.
С помощью преобразования корней полинома (см. пункт
1
☞
ЗДЕСЬ ) можно доказать следствие:
=>
Число отрицательных корней полинома
$$f(x)=a_0x^n+a_1x^{n-1}+dots+a_{n-1}x+a_n, quad (a_0> 0,a_n ne 0)$$
с учетом их кратностей можно оценить по формуле
$$
operatorname{nrr} { f(x)=0 mid x<0 } = {mathcal V}(a_0,-a_1,a_2,dots,(-1)^na_n)-2 k’
,
$$
а если среди коэффициентов $ a_{j} $ нет нулевых, то — по формуле
$$
operatorname{nrr} { f(x)=0 mid x<0 } = {mathcal P}(a_0,a_1,a_2,dots,a_n)-2 k’ ,
$$
где $ k’in {0,1,2, dots } $ и $ {mathcal P} $ обозначает число знакопостоянств.
П
Пример. Оценить число положительных и число отрицательных корней
полинома
$$ f(x)=x^5-2, x^4-8,x^3-x^2-9, x+1 , .$$
Решение. $ {mathcal V}(1,-2,-8,-1,-9,1)=2 $.
$$ operatorname{nrr} { f(x)=0 mid x>0 } =2-2k ge 0
,$$
следовательно $ f_{}(x) $ имеет либо два, либо ни одного положительного
корня. Далее, по следствию:
$$
operatorname{nrr} { f(x)=0 mid x<0 } = {mathcal P}(1,-2,-8,-1,-9,1)=3-2k’ge 0
,
$$
следовательно $ f_{}(x) $ имеет либо три, либо один отрицательный корень.
Проверка. Вещественные корни полинома: $ -2.23233, 0.10863, 4.12369 $.
=>
Если каким-то образом заранее известно, что все корни полинома вещественны, то число положительных из них определяется по правилу знаков Декарта однозначно:
$$ operatorname{nrr} { f(x)=0 mid x>0 } = {mathcal V}(a_0,a_1,dots,a_n) . $$
П
Пример. Характеристический полином вещественной симметричной матрицы удовлетворяет условию следствия. См.
☞
ЗДЕСЬ.
Не смотря на кажущуюся грубость (приблизительность) оценки, правило знаков Декарта позволяет иногда делать достаточно глубокие выводы относительно корней полинома. В частности, из него следует, что чем больше коэффициентов полинома $ f_{}(x) $ обращается в нуль13), тем меньше у него потенциальных возможностей иметь вещественные корни!
Корни полинома в областях комплексной плоскости
Задача. Для полинома14) $ f(z) $ получить точную информацию о числе его корней в заданной области $ mathbb S $ комплексной плоскости $ mathbb C $.
Оказывается, для достаточно широкого класса областей $ mathbb S $ эту информацию можно получить без
применения численных, т.е. приближенных методов. Существуют алгоритмы,
позволяющие за конечное число элементарных алгебраических операций
($ +,-,times, div $) над коэффициентами $ f(z) $ установить количество корней
этого полинома в таких областях, как, к примеру,
$$
begin{array}{ccl}
mathbb S&=&{ zin mathbb R big| a<z<b } npu {a,b} subset mathbb R , \
&& \
mathbb S&=&{ zin mathbb C big| Re e (z) <0 } , \
&& \
mathbb S&=&{ zin mathbb C big| |z| <1 } .
end{array}
$$
Интервал вещественной оси
Задача. Для полинома $ f(x)_{}in mathbb R[x] $ установить точное число его
корней на заданном интервале $ ]a,b[ $:
$$ operatorname{nrr} {f(x)=0 | a<x<b } .$$
Система полиномов Штурма
Для полинома $ f_{}(x) $ система полиномов
$$
f_0(x)equiv f(x), f_1(x),dots, f_K(x)
$$
называется системой полиномов Штурма15) на заданном интервале $ ]a,b[ $ если на этом
интервале
1.
cоседние полиномы $ f_j(x) $ и $ f_{j+1}(x) $ не имеют общих корней;
2.
$ f_K(x)ne 0 $;
3.
если $ f_j(x_0)=0 $ при $ x_0 in ]a,b[ $ и $ jin {1,dots,k-1} $, то
числа $ f_{j-1}(x_0) $ и $ f_{j+1}(x_0) $ имеют разные знаки:
$ f_{j-1}(x_0)f_{j+1}(x_0)<0 $;
4.
произведение $ f_{0}(x)f_{1}(x) $ меняет знак с отрицательного на положительный когда $ x_{} $, возрастая, проходит корень $ lambdain ]a,b[ $ полинома $ f_0(x)equiv f(x) $.
Число знакоперемен
$$
{mathcal V}_x= {mathcal V}(f_0(x), f_1(x),dots, f_K(x))
$$
при $ x_{} $ возрастающем от $ a_{} $ к $ b_{} $, будет меняться когда $ x_{} $ проходит через
корень какого-либо полинома системы. Доказывается, что это число может
разве лишь уменьшаться, и уменьшается на единицу тогда и только тогда,
когда $ x_{} $ проходит через корень начального полинома системы, т.е. через корень $ f(x)_{} $.
Т
Теорема [Штурм]. Если $ f(a)ne 0, f(b)ne 0 $, и система $ f_0(x), f_1(x),dots, f_K(x) $
является системой полиномов Штурма для $ f(x_{}) $, то
$$
operatorname{nrr} {f(x)=0 mid a<x<b }= {mathcal V}_a — {mathcal V}_b=
$$
$$
={mathcal V}(f_0(a), f_1(a),dots, f_K(a))-
{mathcal V}(f_0(b), f_1(b),dots, f_K(b)) .
$$
Самый распространенный способ построение системы полиномов Штурма основан на алгоритме Евклида нахождения наибольшего общего делителя полинома $ f_{}(x) $ и его производной $ f{‘}(x) $.
Предположим, что $ f_{}(x) $ не имеет кратных корней. Это равносильно
тому, что $ operatorname{HOD} (f(x),f'(x))= const ne 0 $ (см.
☞
ЗДЕСЬ ). Установить этот факт можно по алгоритму Евклида нахождения $ operatorname{HOD} $. Оказывается, что в качестве полиномов системы Штурма можно взять последовательность остатков из алгоритма Евклида, если только домножить некоторые из них на $ -1_{} $. Именно, возьмем
$$f_1(x) equiv f'(x) .$$
Поделим $ f_{0}(x) equiv f(x) $ на $ f_{1}(x) $ и обозначим через $ f_{2}(x) $ остаток,
домноженный на $ -1_{} $:
$$f_0(x)equiv q_1(x) f_1(x)-f_2(x), quad deg f_2 < n-1 .$$
Поделим $ f_{1}(x) $ на $ f_{2}(x) $ и обозначим через $ f_{3}(x) $ остаток,
домноженный на $ -1_{} $:
$$f_1(x)equiv q_2(x) f_2(x)-f_3(x), quad deg f_3 < deg f_2 .$$
Продолжаем алгоритм далее, в конце концов дойдем до последнего ненулевого
остатка $ f_{K}(x) $, который совпадает с $ operatorname{HOD} (f(x),f'(x)) $. По предположению, этот последний $ f_{K}(x)equiv const ne 0 $.
§
Если на интервале $ ]a,b[ $ полином $ f_{}(x) $ имеет корень четной кратности, то построение системы полиномов Штурма невозможно.
П
Пример. Отделить корни полинома $ f (x)=x^{4}-x-1 $.
Решение. $ f_1=f'(x)=4, x^{3}-1 $.
$$
begin{array}{rrrrrr|l}
x^4+ &{}0x^3 +&{}0x^2 &-x &-1 &&,4, x^3-1\
x^{4}+& & &
— frac{scriptstyle 1}{scriptstyle 4} x & &&,
overline{quad frac{scriptstyle 1}{scriptstyle 4}, x quad } \
hline
& & &- frac{scriptstyle 3}{scriptstyle 4} , x &-1 \
end{array}
$$
Полагаем $ f_2(x)= frac{scriptstyle 3}{scriptstyle 4} , x+1 $.
$$
begin{array}{rrrrr|l}
4x^3 +&{}0x^2 &+0x &-{}1 &&frac{scriptstyle 3}{scriptstyle 4}, x+1\
4x^3 +&frac{scriptstyle 16}{scriptstyle 3}, x^2 & & &
& overline{ frac{scriptstyle 16}{scriptstyle 3},x^{2}-frac{scriptstyle 64}{scriptstyle 9}, x+
frac{scriptstyle 256}{scriptstyle 27}} \
hline
&-frac{scriptstyle 16}{scriptstyle 3}, x^{2} & &{}-1 \
&-frac{scriptstyle 16}{scriptstyle 3}, x^2 &-frac{scriptstyle 64}{scriptstyle 9}, x & \
hline
& & frac{scriptstyle 64}{scriptstyle 9}, x & -1 \
& & frac{scriptstyle 64}{scriptstyle 9}, x & +frac{scriptstyle 256}{scriptstyle 27} \
hline
& & & — frac{scriptstyle 283}{scriptstyle 27}
end{array}
$$
Полагаем $ f_3(x)=frac{scriptstyle 283}{scriptstyle 27} $.
| $ x_{} $ | $ f_{}(x) $ | $ f_{1}(x) $ | $ f_{2}(x) $ | $ f_{3}(x) $ | $ {mathcal V}_x $ | Комментарии |
|---|---|---|---|---|---|---|
| $ -infty $ | $ +_{} $ | — | — | $ +_{} $ | $ 2_{} $ | сначала устанавливаем |
| $ +infty $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ 0_{} $ | число вещественных корней, |
| $ 0_{} $ | — | — | $ +_{} $ | $ +_{} $ | $ 1_{} $ | затем положительных и отрицательных, |
| $ -1 $ | $ +_{} $ | — | $ +_{} $ | $ +_{} $ | $ 2_{} $ | затем просто дробим |
| $ 1_{} $ | — | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ 1_{} $ | промежутки, отыскивая такие, |
| $ 2_{} $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ +_{} $ | $ 0_{} $ | чтобы на каждом $ {mathcal V}_{a}-{mathcal V}_{b}=1 $ |
Ответ. Полином $ f_{}(x) $ имеет два различных вещественных корня, один на
интервале $ ]-1,0_{}[ $, другой — на $ ]1,2_{}[ $.
§
Более подробный анализ алгоритма, а также альтернативный способ локализации корней полинома, основанный на ганкелевых матрицах
☞
ЗДЕСЬ
Левая полуплоскость: устойчивость
Полином $ f(z) $ с комплексными коэффициентами называется устойчивым, если все его корни удовлетворяют условию $ {mathfrak Re}(z)<0 $.
Понятие устойчивого полинома важно в теории оптимального управления.
Т
Теорема [Раус, Гурвиц]. Для устойчивости
полинома $ f(z)=a_0z^n+a_1z^{n-1}+dots+a_n $ с вещественными коэффициентами и $ a_0 > 0 $ необходимо и достаточно, чтобы были выполнены неравенства
$$
a_1>0, left| begin{array}{ll} a_1 & a_3 \
a_0 & a_2
end{array}
right|>0,
left| begin{array}{lll} a_1 & a_3 & a_5\
a_0 & a_2 & a_4 \
0 & a_1 & a_3
end{array}
right|>0,dots,
left| begin{array}{lllcl} a_1 & a_3 & a_5 & dots & 0\
a_0 & a_2 & a_4 & dots & 0 \
0 & a_1 & a_3 & dots & 0 \
0 & a_0 & a_2 & dots & 0 \
dots & & & ddots & dots \
dots & & & dots & a_n
end{array}
right|>0 .
$$
Условия теоремы Рауса-Гурвица являются избыточными: примерно от половины неравенств можно избавиться. См.
☞
Теорема Льенара-Шипара ).
Единичный круг
Единичным кругом на комплексной плоскости назовем круг $ |z|le 1 $.
Задача. Найти необходимые и достаточные условия на коэффициенты
полинома $ f(z)=a_0z^n+dots+ a_n $, при которых все его корни $ lambda_1,dots, lambda_n $
находятся внутри единичного круга, т.е. удовлетворяют условию $ |z|<1 $.
По аналогии с предыдущим случаем, иногда такой полином называют дискретно устойчивым; также употребляется и название устойчивый по Шуру.
Решить эту задачу можно сведением ее к задаче установления критерия
устойчивости некоторого вспомогательного полинома.
Т
Теорема. Замена переменной
$$ z = frac{w+1}{w-1} $$
производит взаимно-однозначное отображение внутренности единичного круга
плоскости $ z $ в левую полуплоскость плоскости $ w $.

Т
Теорема. Полином $ f(z)=a_0z^n+dots+a_n $ имеет все свои корни
лежащими внутри единичного круга тогда и только тогда, когда полином
$$
F(w) = (w-1)^n fleft( frac{w+1}{w-1} right) =
a_0(w+1)^n+a_1(w+1)^{n-1}(w-1)+dots+a_n(w-1)^n
$$
будет устойчив.
П
Пример. Определить все вещественные значения параметра
$ {color{Red} alpha } $, при которых полином
$$f(z)=3,z^3+{color{Red} alpha } , z^2+z+2 $$
будет иметь все корни лежащими внутри единичного круга.
Решение. Строим полином из теоремы
$$
F(w)=underbrace{(6+{color{Red} alpha })}_{A_0}w^3+underbrace{(2+{color{Red} alpha })}_{A_1}w^2
+underbrace{(14-{color{Red} alpha })}_{A_2}w+underbrace{2-{color{Red} alpha }}_{A_3} .
$$
Теорема Льенара-Шипара дает условия устойчивости $ F(w) $
в виде
$$A_0>0, A_1>0, A_2>0, A_3>0, A_1A_2-A_0A_3>0 ; $$
и
$$A_0<0, A_1<0, A_2<0, A_3<0, A_1A_2-A_0A_3>0 .$$
Подставляя сюда выражения для коэффициентов, получим, что первая система ограничений
имеет решение $ -1< {color{Red} alpha } < 2 $, вторая же — несовместна.
Косвенной проверкой истинности полученного интервала могут служить его границы:
$$
f(z)equiv
left{ begin{array}{rl}
(3z+2)(z^2-z+1)
& npu {color{Red} alpha }=-1 ; \
(z+1)(3,z^2-z+2)
& npu {color{Red} alpha }=2 .
end{array}
right.
$$
В обоих случаях имеются корни, удовлетворяющие условию $ |z|=1 $: в первом
случае это будет комплексно-сопряженная пара
$ 1/2 pm {mathbf i} sqrt{3}/2 $,
во втором — корень $ (-1) $.
Ответ. $ -1< {color{Red} alpha } < 2 $.
Известен еще один результат, позволяющий решить поставленную задачу.
Т
Теорема [Шур, Кон]. Полином $ f(z)=a_0z^n+dots+a_n $ с вещественными коэффициентами имеет все свои корни лежащими внутри единичного круга тогда и только тогда, когда
$$
|mbox{ старший коэффициент } f(z) |>|mbox{ свободный член } f(z)| ,
$$
т.е. $ |a_0| > |a_n| $, и полином
$$
f_1(z) = frac{a_0f(z)-a_nf^{*}(z)}{z} quad npu quad f^{*}(z) = z^nf(1/z) equiv a_0+a_1z+dots+a_nz^n
$$
имеет все свои корни лежащими внутри единичного круга.
На первый взгляд, конструктивность этого результата не очень очевидна:
исходная задача для полинома $ f(z) $ сводится к аналогичной задаче для
полинома $ f_1(z) $. Обратим, однако, внимание на то, что полином
$$
begin{matrix}
f_1(z)&=& left[a_0(a_0z^n+dots+a_n)-a_n (a_0+a_1z+dots+a_nz^n) right] big/ z = \
&=& left[(a_0^2-a_n^2)z^n+(a_0a_1-a_{n-1}a_n)z^{n-1} + dots +
(a_0a_{n-1}-a_{1}a_n)z right] big/ z = \
&=& (a_0^2-a_n^2)z^{n-1}+(a_0a_1-a_{n-1}a_n)z^{n-2} + dots +
(a_0a_{n-1}-a_{1}a_n)
end{matrix}
$$
имеет степень меньшую, чем $ deg f $. Таким образом, алгоритм конструктивен
в том смысле, что он сводит исходную задачу к более простой. Применяя
к полиному $ f_1(z) $ снова критерий Шура-Кона, получим следующее необходимое
условие
$$
|mbox{ старший коэффициент } f_1(z) | > | mbox{ свободный член }
f_1(z)|
iff quad |a_0^2-a_n^2| > |a_0a_{n-1}-a_{1}a_n| ,
$$
при выполнении которого дальнейшему исследованию подлежит полином
$$
f_2(z) = frac{(a_0^2-a_n^2)f_1(z)-(a_0a_{n-1}-a_{1}a_n)f^{*}_1(z)}{z} .
$$
Продолжая процедуру, за конечное число шагов мы дойдем до полинома первой
степени. Окончательно, необходимые и достаточные условия нахождения
всех корней полинома $ f(z) $ степени $ n_{} $ внутри единичного круга получаются
объединением $ n_{} $ условий
$$
|mbox{ старший коэффициент } f(z) |>|mbox{ свободный член } f(z)|
,
$$
$$
|mbox{ старший коэффициент } f_1(z) | > |mbox{ свободный член } f_1(z)|
,
$$
$$
vdots qquad qquad qquad vdots
$$
$$
|mbox{ старший коэффициент } f_{n-1}(z) |>|mbox{ свободный член }
f_{n-1}(z)| .
$$
§
Пример на применение этой теоремы
☞
ЗДЕСЬ.
Численные методы поиска корней полинома
Как упоминалось
☝
ВЫШЕ, корни полинома $ f_{}(z) $, как правило,
не выражаются в радикалах уже при $ deg f=5 $ . Но даже в тех случаях, когда
выражаются, как, например,
$$lambda=frac{sqrt{5}-1 + sqrt{10- sqrt{20}}}{2} quad mbox{ для }
f(x)=x^4+2x^3-6x^2-2x+1 ,
$$
толку от такого представления мало: на каком интервале вещественной оси лежит $ lambda $?
Поэтому наряду с поиском аналитических формул для корней полиномов
практический интерес представляет нахождение их приближенных значений.
Эту задачу будем решать, в основном, для полиномов над $ mathbb R_{} $ (т.е. полиномов с вещественными коэффициентами), с которыми чаще всего и приходится иметь дело на практике.
Задачу поиска мнимых корней таких полиномов можно свести к поиску вещественных решений системы алгебраических уравнений от двух переменных и специальными приемами свести к поиску вещественных корней одного уравнения от одной переменной. Подробнее см.
☞
ЗДЕСЬ. Имеются и другие способы поиска мнимых корней, (например, метод Греффе-Лобачевского), но я о них еще нескоро напишу.
Нас, прежде всего, будут интересовать именно вещественные корни полиномов. В дальнейшем переменную этих полиномов будем обозначать через $ x_{} $ и считать ее вещественной. Для поиска вещественных корней полинома, как правило, требуется их предварительно отделить, т.е. найти интервалы
$ ]a,b_{}[ $, каждый из которых содержит только один корень $ f_{}(x) $. Поиск такого интервала
можно производить разными способами, самый общий из которых изложен
☝
ВЫШЕ. Однако, для предварительного понимания изложенных ниже методов, достаточно будет ориентироваться на теорему Больцано: полином имеет корень на $ ]a,b_{}[ $, если на концах интервала он принимает значения разных знаков.
Этот корень будет единственным, если дополнительно предположить, что функция $ f_{}(x) $ монотонна на $ ]a,b_{}[ $.
Последнее условие будет очевидно выполнено, если производная $ f^{prime}(x) $ не меняет знака на $ ]a,b_{}[ $, т.е. полином $ f^{prime}(x) $
не имеет корней на рассматриваемом интервале. Действительно, если
предположить существование двух корней у $ f_{}(x) $ на $ ]a,b_{}[ $, то, по соображениям, упомянутым
☞
ЗДЕСЬ16), должна существовать точка этого интервала, в которой $ f^{prime}(x) $ обращается в нуль. Анализ знака $ f^{prime}(x) $ на $ ]a,b_{}[ $ часто удается произвести элементарными рассуждениями.
Метод Руффини-Хорнера
Метод Лагранжа (непрерывных дробей)
Метод Ньютона
Универсальный метод: подходит не только для полиномов.
Рассматривается
☞
ЗДЕСЬ.
Метод Бернулли и его развитие
Подходит для полиномов в том числе и с комплексными коэффициентами (и мнимые корни тоже ищет). Не предполагает предварительного отделения корней. Рассматривается
☞
ЗДЕСЬ.
Характеристический полином матрицы
рассматривается
☞
ЗДЕСЬ
Полином нескольких переменных
рассматривается
☞
ЗДЕСЬ
Задачи
Источники
Схема Горнера
11 июля 2022
Схема Горнера — это алгоритм для быстрого (счёт идёт на секунды) вычисления значения многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
в точке $x=a$. Также схема Горнера позволяет быстро (быстрее, чем столбиком) делить многочлен $Pleft( x right)$ на линейные двучлены вида $x-a$, искать остатки от деления и многое другое.
Содержание
- Описание Схемы Горнера
- Вычисление значения многочлена
- Деление многочлена с остатком
- Перебор корней уравнения
- Разложение на множители
- Разложение по степеням
- Как всё это работает
1. Описание схемы Горнера
Итак, рассмотрим многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
Для наглядности коэффициенты выделены синим цветом. Распишем схему Горнера для многочлена $Pleft( x right)$ в точке $x=color{red}{a}$. Для этого заполним таблицу
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {} & {} & {} & {} & {} & {} \ end{array}]
В первой строке мы видим коэффициенты многочлена $Pleft( x right)$ в порядке убывания степеней. Таких коэффициентов всегда на один больше, чем степень многочлена: для квадратного многочлена всего 3 коэффициента, для кубического — уже 4, и т.д.
Во второй строке таблицы мы вписываем лишь число $color{red}{a}$ в самой левой клетке. Остальные клетки заполняются последовательно по следующему алгоритму.
В первую свободную клетку мы переносим элемент из верхней строки без изменений. Назовём этот элемент ${{b}_{n-1}}$ — дальше вы поймёте, зачем нужна такая нумерация:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}}={{a}_{n}} & {} & {} & {} & {} & {} \ end{array}]
Вторая клетка — элемент ${{b}_{n-2}}$ — считается по формуле ${{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}}$. Другими словами, берём элемент слева, умножаем на число $a$ и добавляем элемент сверху:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}} & {} & {} & {} & {} \ end{array}]
Далее находим элемент ${{b}_{n-3}}$ по аналогичной формуле: ${{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}}$. Заносим результат в третью клетку:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}a & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}} & {} & {} & {} \ end{array}]
Аналогично находим элементы ${{b}_{n-4}}$, ${{b}_{n-5}}$ и далее. Берём элемент слева, умножаем на исходное число $color{red}{a}$, добавляем элемент сверху, результат записываем в клетку:
[{{b}_{k-1}}={{b}_{k}}cdotcolor{red}{a}+color{blue}{{a}_{k}}]
В какой-то момент мы доберёмся до элемента ${{b}_{0}}$, который находится в клетке под коэффициентом $color{blue}{{a}_{1}}$:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}}={{b}_{1}}cdot color{red}{a}+color{blue}{{a}_{1}} & {} \ end{array}]
Элемент в последней клетке считается по той же схеме: ${{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}}$. Обозначим его буквой $r$:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r={{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}} \ end{array}]
Итак, мы заполнили все клетки и получили таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Схема заполнения этой таблицы как раз и называется схемой Горнера. Найденные элементы ${{b}_{n-1}}$, …, ${{b}_{0}}$ и $r$ позволяют переписать исходный многочлен $Pleft( x right)$ в виде
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
Такая запись оказывается грозным оружием для решения задач с многочленами, если знать её свойства. И сегодня мы изучим все эти свойства, но сначала немного практики.
Пример 1. Простой многочлен
Заполните таблицу по схеме Горнера для многочлена
[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]
в точке $x=3$.
Решение. Для начала аккуратно запишем коэффициенты исходного многочлена. Для наглядности они вновь помечены синим:
[Pleft( x right)= color{blue}{2}cdot {{x}^{4}}+left( color{blue}{-7} right)cdot {{x}^{3}}+color{blue}{1}cdot {{x}^{2}}+color{blue}{2} cdot x+left( color{blue}{-3} right)]
Составим таблицу. Поскольку степень многочлена $deg Pleft( x right)=4$, в таблице будет пять основных столбцов и один дополнительный столбец слева, в котором мы запишем число $x=color{red}{3}$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & {} & {} & {} & {} & {} \ end{array}]
Заполняем пустые клетки во второй строке. В первую клетку переносим без изменений элемент сверху:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & {} & {} & {} & {} \ end{array}]
Элемент во второй клетке считается по формуле $2cdot color{red}{3}+left( color{blue}{-7} right)=-1$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & {} & {} & {} \ end{array}]
Третью и четвёртую клетку заполняем аналогично: сначала $-1cdot color{red}{3}+color{blue}{1}=-2$, затем $-2cdot color{red}{3}+color{blue}{2}=-4$:
[begin{array}{c|c|r|r|r|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & {} \ end{array}]
Наконец, последняя клетка: $-4cdot color{red}{3}+left( color{blue}{-3} right)=-15$:
[begin{array}{c|c|r|r|r|r} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & -15 \ end{array}]
Готово! Мы заполнили таблицу по схеме Горнера.
Пример 2. Пропущенные коэффициенты
Заполните таблицу по схеме Горнера для многочлена
[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-4]
в точке $x=1$.
Решение. Обратите внимание: в записи многочлена отсутствуют одночлены ${{x}^{2}}$ и $x$. Другими словами, коэффициенты в этих двух одночленах равны нулю:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+color{blue}{0}cdot {{x}^{2}}+color{blue}{0} cdot x+left( color{blue}{-4} right)]
Для наглядности мы вновь отметили коэффициенты синим цветом — всего их снова пять, т.е. на один больше степени многочлена. И все они переносятся в таблицу. Пропуск нулевых коэффициентов будет грубой ошибкой:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & {} & {} & {} & {} & {} \ end{array}]
Заполняем таблицу по схеме Горнера. Первый элемент переносим сверху:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & {} & {} & {} & {} \ end{array}]
Второй, третий и четвёртый элемент считаем по формуле: $1cdot color{red}{1}+color{blue}{3}=4$; $4cdot color{red}{1}+color{blue}{0}=4$; $4cdot color{red}{1}+color{blue}{0}=4$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & {} \ end{array}]
Наконец, последний элемент таблицы: $4cdot color{red}{1}+left( color{blue}{-4} right)=0$:
[begin{array}{c|c|c|c|c|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & 0 \ end{array}]
Готово! Таблица заполнена, последний элемент оказался равен нулю. И это не случайно. Скоро узнаем почему.:)
2. Вычисление значения многочлена
Чтобы понять, зачем нужна схема Горнера, давайте вкратце повторим всю цепочку рассуждений. Берём произвольный многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
и произвольную точку $x=color{red}{a}$. Составляем таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Найденные коэффициенты ${{b}_{n-1}}$, …, ${{b}_{0}}$, $r$ позволяют переписать многочлен $Pleft( x right)$ в новом виде:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
Но чем так примечательна эта запись? В ближайших четырёх пунктах мы детально разберём все её свойства. И начнём с самого простого. Подставим в эту новую запись число $x=color{red}{a}$, т.е. вычислим $Pleft( color{red}{a} right)$:
[Pleft( color{red}{a} right)=left( {{b}_{n-1}}{color{red}{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]
Итак, последнее число $r$ в таблице — это значение многочлена $Pleft( x right)$ в точке $x=color{red}{a}$:
[Pleft( color{red}{a} right)=r]
А это значит, что благодаря схеме Горнера можно считать значения многочленов быстро (нет операции возведения в степень) и надёжно (в сложении мы ошибаемся реже, чем в умножении).
Так, из Примера 1 следует, что значение многочлена
[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]
в точке $x=3$ равно
[Pleft( 3 right)=r=-15]
Сравните это с прямой подстановкой $x=3$ в многочлен:
[begin{align} Pleft( 3 right) &=2cdot {{3}^{4}}-7cdot {{3}^{3}}+{{3}^{2}}+2cdot 3-3= \ &=2cdot 81-7cdot 27+left( 9+6-3 right)= \ &=162-189+12= \ &=-15 end{align}]
Результат один и тот же, но объём вычислений вырос на порядок.
Пример 3. «Некрасивые» значения
С помощью схемы Горнера найдите значение многочлена
[Pleft( x right)=8{{x}^{4}}-12{{x}^{3}}-24{{x}^{2}}+11x+7]
в точке $x=2,5$.
Решение. Выделим коэффициенты многочлена
[Pleft( x right)= color{blue}{8}cdot {{x}^{4}}+left( color{blue}{-12} right)cdot {{x}^{3}}+left( color{blue}{-24} right)cdot {{x}^{2}}+color{blue}{11} cdot x+color{blue}{7}]
и заполним таблицу для $x=color{red}{2,5}$:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{8} & color{blue}{-12} & color{blue}{-24} & color{blue}{11} & color{blue}{7} \ hlinecolor{red}{2,5} & 8 & 8 & -4 & 1 & 9,5 \ end{array}]
Итого значение многочлена $Pleft( color{red}{2,5} right)=9,5$. Точно такое же значение можно получить прямой подстановкой, но вычисления будут настолько громоздкими, что мы не будем приводить их.
3. Деление многочлена с остатком
Напомню, что разделить многочлен $color{blue}{Pleft( x right)}$ на многочлен $color{red}{Aleft( x right)}$ с остатком — значит найти многочлены $Qleft( x right)$ и $Rleft( x right)$ такие, что
[color{blue}{Pleft( x right)}=Qleft( x right)cdot color{red}{Aleft( x right)}+Rleft( x right)]
причём степень многочлена $Rleft( x right)$ строго меньше степени делителя $color{red}{Aleft( x right)}$:
[deg Rleft( x right) lt deg color{red}{Aleft( x right)}]
Многочлен $Qleft( x right)$ называют неполным частным, $Rleft( x right)$ — остатком от деления. Можно показать, что $Qleft( x right)$ и $Rleft( x right)$ определены однозначно для исходных многочленов $color{blue}{Pleft( x right)}$ и $color{red}{Aleft( x right)}$.
3.1. Случай линейного делителя
Пусть $Aleft( x right)=x- color{red}{a}$ — линейный двучлен. Очевидно, его степень $deg Aleft( x right)=1$.
Рассмотрим произвольный многочлен
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
и составим таблицу для $x=color{red}{a}$ по схеме Горнера:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Получим новую запись многочлена $Pleft( x right)$:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
где $r$ — обычное число, т.е. $deg r=0 lt deg Aleft( x right)$. Но тогда многочлен
[Qleft( x right)={{b}_{n-1}}{{x}^{n-1}}+{{b}_{n-2}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}}]
является неполным частным при делении $Pleft( x right)$ на двучлен $x-color{red}{a}$, а число $r$ — остаток этого деления:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
Итак, схема Горнера позволяет быстро находить неполное частное и остаток от деления произвольного многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$.
Пример 4. Деление с остатком
Найдите частное и остаток при делении многочлена
[{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-6x+10]
На многочлен $x-1$.
Решение. Выделим синим цветом коэффициенты исходного многочлена:
[color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-2} right)cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+left( color{blue}{-6} right)cdot x+color{blue}{10}]
Заполним таблицу по схеме Горнера для $x=color{red}{1}$:
[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & 1 & -1 & 3 & -3 & 7 \ end{array}]
Первые четыре числа — это коэффициенты многочлена-частного. Отметим их зелёным цветом:
[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & color{#green}{1} & color{#green}{-1} & color{#green}{3} & color{#green}{-3} & 7 \ end{array}]
Остаток от деления равен $r=7$. Составим многочлен-частное:
[Qleft( x right)= color{#green}{1}cdot {{x}^{3}}+left( color{#green}{-1} right)cdot {{x}^{2}}+color{#green}{3}cdot x+left( color{#green}{-3} right)]
Очевидно, при делении на линейный двучлен степень частного должна быть на единицу меньше степени исходного многочлена. Так и получилось:
[deg Qleft( x right)=4-1=3]
Пример 5. Проверка делимости
Убедитесь, что многочлен
[{{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28]
делится на двучлен ${{left( x-2 right)}^{2}}$.
Решение. Многочлен делится без остатка на ${{left( x-2 right)}^{2}}$, если сначала он делится на двучлен $x-2$, а затем частное вновь делится на $x-2$. Следовательно, решение состоит из двух шагов.
Первый шаг: выделим коэффициенты исходного многочлена
[color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right)]
[begin{align}color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right) \ end{align}]
Составим таблицу для $x=color{red}{2}$. В ней будет 6 основных столбцов:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & {} & {} & {} & {} & {} & {} \ end{array}]
Заполним все пустые клетки по схеме Горнера:
[begin{array}{c|c|c|c|r|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & color{green}{1} & color{green}{-4} & color{green}{8} & color{green}{-17} & color{green}{18} & 0 \ end{array}]
Получили остаток $r=0$, поэтому исходный многочлен действительно делится на $x-color{red}{2}$, а частное равно
[Qleft( x right)= color{green}{1}cdot {{x}^{4}}+left( color{green}{-4} right)cdot {{x}^{3}}+color{green}{8}cdot {{x}^{2}}+left( color{green}{-17} right) cdot x+color{green}{18}]
Следовательно, исходный многочлен можно представить так:
[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{4}}-4{{x}^{3}}+8{{x}^{2}}-17x+18 right)cdot left( x-color{red}{2} right) \ end{align}]
Второй шаг: выделяем коэффициенты и заполняем ту же самую таблицу, но уже для многочлена $Qleft( x right)$.
[Qleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-4} right)cdot {{x}^{3}}+color{blue}{8}cdot {{x}^{2}}+left( color{blue}{-17} right) cdot x+color{blue}{18}]
Но все коэффициенты в нужном количестве уже присутствуют в таблице, которую мы получили на предыдущем шаге. А потому достаточно приписать к этой таблице ещё одну строку и вновь заполнить её для $x=color{red}{2}$:
[begin{array}{c|c|c|c|r|c|c} {} & 1 & -6 & 16 & -33 & 52 & -36 \ hlinecolor{red}{2} & color{blue}{1} & color{blue}{-4} & color{blue}{8} & color{blue}{-17} & color{blue}{18} & 0 \ hlinecolor{red}{2} & color{green}{1} & color{green}{-2} & color{green}{4} & color{green}{-9} & 0 & {} \ end{array}]
Остаток от деления равен нулю, поэтому многочлен $Qleft( x right)$ делится на $x-color{red}{2}$, и его можно переписать так:
[Qleft( x right)=left( color{green}{1}cdot {{x}^{3}}+left( color{green}{-2} right){{x}^{2}}+color{green}{4} cdot x+left( color{green}{-9} right) right)cdot left( x-color{red}{2} right)]
Возвращаясь к исходному многочлену, получим
[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{3}}-2{{x}^{2}}+4x-9 right)cdot {{left( x-color{red}{2} right)}^{2}} \ end{align}]
Такая запись, как и приведённая выше таблица, доказывает, что исходный многочлен делится на ${{left( x-color{red}{2} right)}^{2}}$.
Обратите внимание: на каждом следующем шаге количество коэффициентов уменьшается на единицу:
- В первой строке мы выписали все 6 коэффициентов исходного многочлена.
- Во второй строке осталось лишь 5 коэффициентов, а последнее число — остаток.
- Третья срока — 4 коэффициента и вновь остаток.
Всё это пригодится нам в следующем пункте.
4. Перебор корней уравнения
До сих пор мы применяли схему Горнера для некоторой точки $x=color{red}{a}$, которая была прямо указана в условии задачи. Но что если найти такую точку — как раз и есть условие задачи?
Рассмотрим уравнение
[color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}=0]
Число $x=color{red}{a}$ будет корнем этого уравнения, если $Pleft( color{red}{a} right)=0$. Это значит, что последний элемент в схеме Горнера должен быть равен нулю:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & color{green}{0} \ end{array}]
Следовательно, мы можем быстро проверить, является ли число $x=color{red}{a}$ корнем уравнения. Достаточно просто подставить его в таблицу и найти последний элемент.
Кроме того, мы знаем, что последний элемент — это остаток $r$. При $r=color{green}{0}$ исходное уравнение примет вид
[left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)=0]
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Откуда либо $x-color{red}{a}=0$ (этот случай мы уже разобрали), либо
[color{blue}{{b}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{b}_{1}}x+color{blue}{{b}_{0}}=0]
Получили новое уравнение — меньшей степени, чем исходное. Коэффициенты этого уравнения уже занесены в таблицу, и к нему вновь применима схема Горнера для перебора кандидатов в корни.
Более того: этот перебор можно ускорить. Но об этом чуть позже. Сначала рассмотрим пару простых примеров.
Пример 6. Уравнение третьей степени
Решите уравнение:
[{{x}^{3}}+9{{x}^{2}}+23x+15=0]
Решение. Заметим, что все коэффициенты многочлена положительны, поэтому уравнение не имеет положительных корней. Иначе, если $x gt 0$, левая часть равенства представляет собой сумму положительных чисел, которая никогда не равна нулю.
Рассмотрим отрицательные числа. Начнём с $x=color{red}{-1}$:
[begin{array}{c|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ end{array}]
Получили $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ — корень, и всё уравнение можно переписать так:
[left( {{x}^{2}}+8x+15 right)left( x+1 right)=0]
Далее уравнение разделяется на линейное $x+1=0$, которое мы уже решили, и квадратное
[{{x}^{2}}+x+15=0]
Такое уравнение можно решить через дискриминант или по теореме Виета. Получим корни $x=-3$ и $x=-5$.
Окончательный ответ: $x=-1$, $x=-3$, $x=-5$.
Впрочем, с тем же успехом мы могли продолжить решение по схеме Горнера:
[begin{array}{r|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ hlinecolor{red}{-3} & 1 & 5 & color{green}{0} & {} \ hlinecolor{red}{-5} & 1 & color{green}{0} & {} & {} \ end{array}]
При этом уравнение примет вид
[left( x+3 right)left( x+5 right)left( x+1 right)=0]
По сути, мы получили разложение на множители. И чуть ниже об этом будет отдельный пункт.
Пример 7. Ещё одно уравнение
Решите уравнение:
[2{{x}^{3}}-{{x}^{2}}-5x-2=0]
Решение. В этот раз мы видим, что корни вполне могут быть положительными. Начнём с $x=color{red}{1}$:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ end{array}]
Получили $r=color{red}{-6}ne 0$. Следовательно, $x=color{red}{1}$ не является корнем. Проверим $x=color{red}{2}$:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]
Обратите внимание: при заполнении третьей строки таблицы мы игнорируем вторую строку, где нас постигла неудача. И если бы мы могли стирать строки, то схема Горнера выглядела бы так:
[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]
В любом случае мы получили $r=color{green}{0}$, поэтому $x=color{red}{2}$ — корень, и уравнение примет вид
[left( 2{{x}^{2}}+3x+1 right)left( x-2 right)=0]
Далее можно решить квадратное уравнение через дискриминант, а можно продолжить заполнять таблицу. Например, для $x=color{red}{-1}$:
[begin{array}{r|c|r|r|r} {} & 2 & -1 & -5 & -2 \ hline1 & 2 & 1 & -4 & -6 \ hline2 & color{blue}{2} & color{blue}{3} & color{blue}{1} & color{green}{0} \ hline-1 & 2 & 1 & color{green}{0} & {} \ end{array}]
Вновь получили ноль в последней клетке, поэтому $x=color{red}{-1}$ — тоже корень, а уравнение примет вид
[left( 2x+1 right)left( x+1 right)left( x-2 right)=0]
Теперь ответ очевиден: $x=2$, $x=-1$, $x=-0,5$.
Помните: «неудачные» строки — это нормально. Их бывает много. Главное при переборе корней — игнорировать такие строки и заполнять таблицу так, будто этих строк не существует.
4.1. Теорема Безу
Теорема Безу и следствия из неё позволяет значительно сузить круг потенциальных корней.
Теорема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x-a$ равен $Pleft( a right)$.
Несложно заметить, что схема Горнера и следующая из неё запись многочлена
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]
является прямым доказательством этой теоремы. Действительно, если подставить в эту запись значение $x=color{red}{a}$, мы получим
[Pleft( color{red}{a} right)=left( {{b}_{n-1}}color{red}{{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]
У теоремы Безу огромное количество полезных приложений — см. урок «Теорема Безу». Сейчас же нас интересует не сама теорема, а следствие из неё, связанное с корнями многочлена.
Пусть $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. Распишем многочлен по схеме Горнера для $x=color{red}{a}$:
[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)]
Поскольку $x=color{red}{a}$ — корень, остаток $r=0$, и мы получили разложение многочлена $Pleft( x right)$ на множители. А теперь выполним обратную операцию — раскроем скобки и приведём подобные слагаемые:
[Pleft( x right)={{b}_{n-1}}{{x}^{n}}+ldots -color{red}{a}cdot {{b}_{0}}]
Получается, что корень $x=color{red}{a}$ является делителем свободного члена $Pleft( x right)$. Более того, можно показать, что в многочлене
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
с целыми коэффициентами $color{blue}{{a}_{n}}$, …, $color{blue}{{a}_{0}}$ все рациональные корни имеют вид
[x=frac{m}{n}]
где $min mathbb{Z}$ — делитель свободного члена $color{blue}{{a}_{0}}$, а $nin mathbb{N}$ — делитель старшего коэффициента $color{blue}{{a}_{n}}$.
И хоть при первом взгляде на все эти рассуждения они могут показаться сложными, на практике теорема Безу значительно упрощает поиск корней. Взгляните на примеры.:)
Пример 8. Сплошной перебор
Решите уравнение:
[{{x}^{5}}+8{{x}^{4}}+24{{x}^{3}}+35{{x}^{2}}+28x+12=0]
Решение. Слева от знака равенства стоит многочлен пятой степени. Старший коэффициент многочлена ${{a}_{5}}=color{blue}{1}$, свободный член ${{a}_{0}}=color{blue}{12}$. Если такой многочлен имеет рациональные корни вида
[x=frac{m}{n}]
то $n=1$ — это единственный натуральный делитель для ${{a}_{5}}=color{blue}{1}$. А вот число $m$ будем искать среди делителей числа ${{a}_{0}}=color{blue}{12}$:
[m=pm 1, pm 2, pm 3, pm 4, pm 6, pm 12.]
Итого 12 вариантов. Далее заметим, что все коэффициенты исходного многочлена положительны, поэтому достаточно проверить лишь отрицательные корни. Начнём с $x=color{red}{-1}$, затем $x=color{red}{-2}$, $x=color{red}{-3}$ и т.д.:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-1} & 1 & 7 & 17 & 18 & 10 & color{red}{2} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ end{array}]
Как видим, вариант $x=color{red}{-1}$ не подошёл, поэму строку с проверкой этого числа можно вычеркнуть. Зато $x=color{red}{-2}$ и $x=color{red}{-3}$ — корни. Более того: можно повторно проверить $x=color{red}{-2}$. Получим интересный результат:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ hline color{red}{-2} & 1 & 1 & 1 & color{green}{0} & {} & {} \ end{array}]
Другими словами, исходное уравнение можно переписать так:
[left( {{x}^{2}}+x+1 right){{left( x+2 right)}^{2}}left( x+1 right)=0]
Число $x=color{red}{-2}$ оказалось корнем второй кратности, а квадратное уравнение
[{{x}^{2}}+x+1=0]
не имеет корней. Поэтому окончательный ответ: $x=-2$, $x=-3$.
Пример 9. Дробные корни
Решите уравнение:
[3{{x}^{4}}+5{{x}^{3}}-{{x}^{2}}-5x-2=0]
Решение. По теореме Безу получаем, что рациональные корни вида
[x=frac{m}{n}]
должны быть составлены из чисел $min left{ pm 1, pm 2 right}$ и $nin left{ 1,3 right}$. Всего существует восемь таких комбинаций:
[xin left{ pm 1; pm 2; pm frac{1}{3}; pm frac{2}{3} right}]
Рассмотрим самые простые корни: $x=color{red}{1}$ и $x=color{red}{-1}$. Причём на каждом шаге будем проверять возможную кратность:
[begin{array}{r|c|c|c|c|c} {} & color{blue}{3} & color{blue}{5} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hline color{red}{1} & 3 & 8 & 7 & 2 & color{green}{0} \ hline color{red}{1} & 3 & 11 & 18 & color{red}{20} & {} \ hline color{red}{-1} & 3 & 5 & 2 & color{green}{0} & {} \ hline color{red}{-1} & 3 & 2 & color{green}{0} & {} & {} \ end{array}]
Получили корень $x=color{red}{1}$ (первой кратности) и $x=color{red}{-1}$ (как минимум второй кратности), а само уравнение можно переписать так:
[left( 3x+2 right){{left( x+1 right)}^{2}}left( x-1 right)=0]
Теперь очевидно, что всего уравнение имеет три корня: $x=1$, $x=-1$ и $x=-{2}/{3};$.
4.2. Учёт кратности корней
Как видим, схема Горнера позволяет не просто перебирать корни, но и определять их кратность. Это особенно важно при решении неравенств и задач с параметрами.
Чтобы определить кратность корня $x=color{red}{a}$, достаточно подставлять его в таблицу до тех пор, пока не появится остаток, отличный от нуля. Либо пока исходный многочлен не будет полностью разложен на множители.
Пример 10. Корень четвёртой кратности
Решите уравнение и определите кратность корней:
[{{x}^{5}}-10{{x}^{3}}-20{{x}^{2}}-15x-4=0]
Решение. Слева стоит многочлен с целыми коэффициентами. Выпишем потенциальные корни по теореме Безу:
[xin left{ pm 1; pm 2; pm 4 right}]
Начнём с самых простых чисел: $x=color{red}{1}$ и $x=color{red}{-1}$. Проверим их по схеме Горнера:
[begin{array}{r|c|r|r|r|r|r} {} & color{blue}{1} & color{blue}{0} & color{blue}{-10} & color{blue}{-20} & color{blue}{-15} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 1 & -9 & -29 & -44 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -1 & -9 & -11 & -4 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -2 & -7 & -4 & color{green}{0} & {} \ hlinecolor{red}{-1} & 1 & -3 & -4 & color{green}{0} & {} & {} \ hlinecolor{red}{-1} & 1 & -4 & color{green}{0} & {} & {} & {} \ end{array}]
Перепишем исходное уравнение:
[{{left( x+1 right)}^{4}}left( x-1 right)left( x-4 right)=0]
Итого уравнение имеет три различных корня: $x=-1$ (четвёртой кратности), $x=1$ (первой кратности) и $x=4$ (тоже первой кратности).
Ключевая мысль: с помощью схемы Горнера можно решать даже уравнения высших степеней. Поэтому если при решении текстовой задачи (и особенно задачи с параметром) возникло уравнение 3-й степени и выше, это вовсе не означает, что вы где-то ошиблись. Вполне возможно, что составители задачи хотят проверить, умеете ли вы решать уравнения высших степеней.
5. Разложение на множители
Схему Горнера часто применяют для разложения многочлена на множители. Мы знаем, что для всякого $x=color{red}{a}$ такого, что последний элемент таблицы $r=color{green}{0}$, можно переписать исходный многочлен $Pleft( x right)$ в виде
[Pleft( x right)=left( x-color{red}{a} right)cdot Qleft( x right)]
Коэффициенты многочлена $Qleft( x right)$ будут также даны в таблице, и к нему тоже применима схема Горнера.
Пример 11. Простой многочлен
Разложите на множители многочлен
[{{x}^{4}}+2{{x}^{3}}+4{{x}^{2}}+3x-10]
Решение. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+color{blue}{3}cdot x+left( color{blue}{-10} right)]
Будем выделять из него двучлены вида $left( x-color{red}{a} right)$, где $x=color{red}{a}$ — корни многочлена $Pleft( x right)$. Рассмотрим в качестве таких корней делители свободного члена ${{a}_{0}}=color{blue}{-10}$. Начнём с $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|c|c|c|c|c} {} & color{blue}{1} & color{blue}{2} & color{blue}{4} & color{blue}{3} & color{blue}{-10} \ hlinecolor{red}{1} & 1 & 3 & 7 & 10 & color{green}{0} \ hlinecolor{red}{-1} & 1 & 2 & 5 & color{red}{5} & {} \ hlinecolor{red}{-2} & 1 & 1 & 5 & color{green}{0} & {} \ end{array}]
Итого одна неудачная попытка и две удачных. Получили разложение многочлена
[Pleft( x right)=left( x-1 right)left( x+2 right)left( {{x}^{2}}+x+5 right)]
Квадратный трёхчлен в третьей скобке всегда положителен:
[{{x}^{2}}+x+5 gt 0]
Его нельзя разложить на множители, поэтому указанное разложение $Pleft( x right)$ — окончательное.
Пример 12. Сложный многочлен
Разложите на множители многочлен
[{{x}^{5}}-6{{x}^{4}}+2{{x}^{3}}+36{{x}^{2}}-27x-54]
Решение. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right)cdot x+left( color{blue}{-54} right)]
[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+ \ &+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right) cdot x+left( color{blue}{-54} right) \ end{align}]
Проверим делители свободного члена ${{a}_{0}}=color{blue}{-54}$. Таких делителей очень много, поэтому начнём с самых простых: $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{2} & color{blue}{36} & color{blue}{-27} & color{blue}{-54} \ hlinecolor{red}{1} & 1 & -5 & -3 & 33 & 6 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -7 & 9 & 27 & -54 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -8 & 17 & 10 & color{red}{-64} & {} \ hlinecolor{red}{2} & 1 & -5 & -1 & 25 & color{red}{-4} & {} \ hlinecolor{red}{-2} & 1 & -9 & 27 & -27 & color{green}{0} & {} \ hlinecolor{red}{3} & 1 & -6 & 9 & color{green}{0} & {} & {} \ hlinecolor{red}{3} & 1 & -3 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{3} & 1 & color{green}{0} & {} & {} & {} & {} \ end{array}]
Получили три неудачных попытки и пять удачных. В целом многочлен привет вид
[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]
Это и есть искомое разложение на множители.
Обратите внимание: после проверки корня $x=color{red}{-2}$ в таблице возникла формула сокращённого умножения — куб разности:
[{{x}^{3}}-9{{x}^{2}}+27x-27={{left( x-3 right)}^{3}}]
С этим замечанием дальше можно было вообще не заполнять таблицу, поскольку многочлен сразу примет вид
[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]
6. Разложение по степеням
Наконец, ещё одно применение схемы Горнера — это разложение многочлена по степеням двучлена $left( x-color{red}{a} right)$. Для этого достаточно составлять таблицу с указанным $x=color{red}{a}$ до тех пор, пока не закончатся столбцы с коэффициентами.
Полученные остатки будут коэффициентами искомого разложения. Взгляните на примеры.
Пример 13. Разложение многочлена
Разложите по степеням $left( x-1 right)$ многочлен
[{{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-17x-5]
Решение. Выделим коэффициенты многочлена:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-17} right)cdot x+left( color{blue}{-5} right)]
[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{4}} &+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-17} right) cdot x+left( color{blue}{-5} right) \ end{align}]
Занесём эти коэффициенты в таблицу и будем заполнять её по схеме Горнера для $x=color{red}{1}$ до тех пор, пока не вычеркнем все столбцы:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-17} & color{blue}{-5} \ hlinecolor{red}{1} & 1 & -5 & 11 & -6 & color{green}{-11} \ hlinecolor{red}{1} & 1 & -4 & 7 & color{green}{1} & {} \ hlinecolor{red}{1} & 1 & -3 & color{green}{4} & {} & {} \ hlinecolor{red}{1} & 1 & color{green}{-2} & {} & {} & {} \ hlinecolor{red}{1} & color{green}{1} & {} & {} & {} & {} \ end{array}]
Числа, выделенные зелёным — это остатки от деления в каждой новой строке. Они и будут коэффициентами разложения в порядке возрастания степеней. Внизу таблицы находится старший коэффициент, а в первой строке — свободный член:
[Pleft( x right)= color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right)]
[begin{align}Pleft( x right) &=color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+ \ &+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right) \ end{align}]
Представим эту запись более компактно:
[Pleft( x right)={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+4{{left( x-1 right)}^{2}}+left( x-1 right)-11]
[begin{align}Pleft( x right) &={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+ \ &+4{{left( x-1 right)}^{2}}+left( x-1 right)-11 \ end{align}]
Это и есть искомое разложение.
Пример 14. Финал
Разложите по степеням $left( x-2 right)$ многочлен
[{{x}^{4}}-8{{x}^{3}}+24{{x}^{2}}-50x+48]
Решение. В раз не будем переписывать многочлен с выделением коэффициентов, а сразу составим таблицу:
[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-8} & color{blue}{24} & color{blue}{-50} & color{blue}{48} \ hlinecolor{red}{2} & 1 & -6 & 12 & -26 & color{green}{-4} \ hlinecolor{red}{2} & 1 & -4 & 4 & color{green}{-18} & {} \ hlinecolor{red}{2} & 1 & -2 & color{green}{0} & {} & {} \ hlinecolor{red}{2} & 1 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{2} & color{green}{1} & {} & {} & {} & {} \ end{array}]
Запишем найденное разложение в порядке убывания степеней:
[color{green}{1}cdot {{left( x-2 right)}^{4}}+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right)]
[begin{align}color{green}{1}cdot {{left( x-2 right)}^{4}}&+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+ \ &+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right) \ end{align}]
То же самое разложение, но более компактно:
[{{left( x-2 right)}^{4}}-18left( x-2 right)-4]
Это окончательный ответ.
7. Как работает Схема Горнера
Очень просто. Вернёмся к исходному многочлену:
[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]
Вынесем за скобки множитель $x$ из всех слагаемых, кроме последнего:
[Pleft( x right)=left( color{blue}{{a}_{n}}{{x}^{n-1}}+color{blue}{{a}_{n-1}}{{x}^{n-2}}+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]
В скобках стоит новый многочлен. Вновь вынесем за скобки $x$. Сделаем так много раз и в какой-то момент получим запись вида
[Pleft( x right)=left( ldots left( left( color{blue}{{a}_{n}} right)cdot x+color{blue}{{a}_{n-1}} right)cdot x+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]
Мы видим множество скобок. Обозначим элемент в самой внутренней скобке через ${{b}_{n-1}}$:
[{{b}_{n-1}}=color{blue}{{a}_{n}}]
Элемент в предыдущей скобке обозначим ${{b}_{n-2}}$:
[{{b}_{n-2}}={{b}_{n-1}} cdot x+color{blue}{{a}_{k}}]
И так далее по уже известной формуле
[{{b}_{k-1}}={{b}_{k}} cdot x+color{blue}{{a}_{k}}]
В какой-то момент мы находим ${{b}_{0}}$ и $r$:
[begin{align} {{b}_{0}} &={{b}_{1}}cdot x+color{blue}{{a}_{1}} \ r &={{b}_{0}}cdot x+color{blue}{{a}_{0}} end{align}]
Собираем все найденные значения в таблицу:
[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hline x & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]
Легко показать, что $r=Pleft( x right)$. Кроме того, согласно теореме Безу, при подстановке $x=color{red}{a}$ найденное число $r=Pleft( color{red}{a} right)$ есть остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
В частности, при $r=0$ деление выполнено без остатка, поэтому многочлен $Pleft( x right)$ раскладывается на множители:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Далее по индукции или прямым вычислением можно показать, что коэффициенты $Qleft( x right)$ — это те самые числа ${{b}_{n-1}}$, …, ${{b}_{0}}$ из таблицы. Поскольку $deg Qleft( x right)=n-1$, на каждом шаге степень этого многочлена будет уменьшаться.
В какой-то момент окажется, что $Qleft( x right)= color{blue}{{a}_{n}}$ — константа, и дальнейшее заполнение таблицы по схеме Горнера невозможно. Вот и всё.:)
Смотрите также:
- Бином Ньютона
- Теорема Безу и корни многочленов
- Решение задач B12: №448—455
- Задача B3 — работа с графиками
- Пример решения задачи 15
- Задача B15: частный случай при работе с квадратичной функцией
Вычисление значений многочленов.
Очень
часто в качестве аппроксимирующей
функции
берут многочлен. Это связано с тем, что
множество многочленов всюду плотно во
множестве непрерывных функций. То есть
имеет место следующая теорема.
Теорема
4.1. (Теорема Вейерштрасса.)
Если
,
то для любогосуществует многочлен
такой, что
при всех
.
Кроме того, и это
немаловажно, значения многочлена легко
вычисляются. Рассмотрим алгебраический
многочлен
,
где
,
,
…,– числовые коэффициенты,n
– степень многочлена. Если проводить
вычисления в «лоб», то есть находить
значения каждого члена и суммировать
их, то при больших n
потребуется выполнить большое число
операций:
умножений иn
сложений. Кроме того, это может привести
к потере точности за счет погрешности
округлений.
Запишем многочлен
в следующем виде:
.
Согласно
этой формуле вычисление значения
сводится к последовательному нахождению
следующих величин:
;
;
;
…
;
.
Способ
нахождения значения многочлена по
вышеописанным формулам называется
схемой Горнера. Для реализации этой
схемы требуется n
умножений и n
сложений, то есть всего 2n
арифметических действий. Схема Горнера
является в общем случае самым оптимальным
способом вычисления значения многочлена.
Использование этой схемы не только
экономит машинное время, но и повышает
точность вычислений за счет уменьшения
погрешности округления. Схема Горнера
удобна также для реализации на ЭВМ
благодаря цикличности вычислений и
необходимости сохранять кроме
коэффициентов многочлена и значения
аргумента только одно значение
промежуточной величины, а именно
при текущем
.
Интерполирование функции многочленом.
Теорема
Вейерштрасса не дает способа построения
аппроксимирующего многочлена, она
устанавливает лишь принципиальную
возможность этого построения. Для
построения приближающих многочленов
разработано много способов. Один из них
– интерполирование, который заключается
в следующем.
Пусть имеется
таблица значений
-
x
x0
x1
x2
…
xn
y
y0
y1
y2
…
yn
Таблица 4.1.
некоторой
функции
,
причем если,
то.
Задача состоит в том, чтобы найти такой
многочлен степени не вышеn,
который в заданных точках
принимает те же значения
,
что и функция.
Таким образом, близость интерполяционного
многочлена для заданной функции состоит
в том, что их значения совпадают на
заданной системе точек (сетке).
Различают
интерполяцию глобальную и локальную
(или кусочную). Если один многочлен
используется для интерполяции функции
на всем рассматриваемом интервале
изменения аргументаx,
то говорят о глобальной интерполяции.
В этом случае максимальная степень
интерполяционного многочлена равна n,
то есть на единицу меньше количества
узлов интерполирования.
С
геометрической точки зрения задача
глобальной интерполяции заключается
в построении такого многочлена степени
не выше n,
график которого проходит через данные
точки
,
,
…,
кривой
.
Если
интерполяционный многочлен строится
отдельно для разных частей рассматриваемого
интервала изменения x,
то имеет место локальная интерполяция.
Например, можно по трем лежащим рядом
точкам построить кусочки парабол.
Теорема
4.2. Глобальный
интерполяционный многочлен существует
и единственен.
Доказательство.
Пусть
– глобальная интерполяция функции
по системе узлов
.
Учитывая,
что
(
),
можем записать
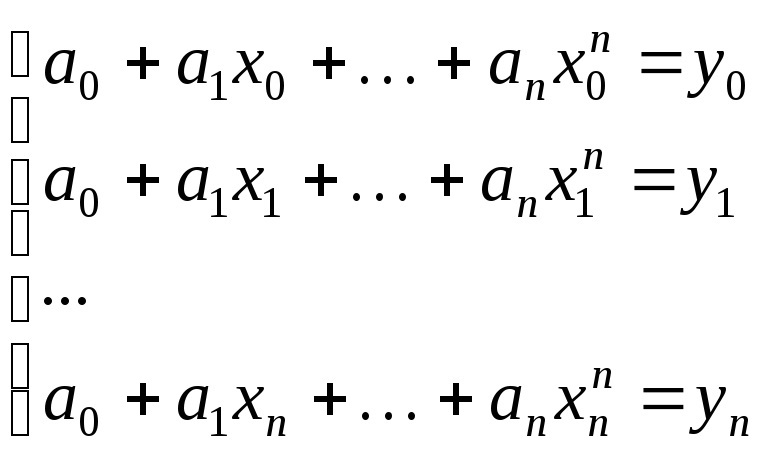
Это
система для определения коэффициентов
интерполяционного многочлена
,
,
…,.
Как известно, многочлен однозначно
задается системой своих коэффициентов.
Определитель
системы (4.1) является определителем
Вандермонда.
Этот
определитель не равен 0, если среди чисел
,
,
…,нет равных. Так как при постановке задачи
интерполирования мы потребовали, чтобы
узлы были различны, то.
Тогда
система (4.1) имеет единственное решение.
Таким образом, для данной системы узлов
существует единственный глобальный
интерполяционный многочлен.
Из приведенных
рассуждений следует способ построения
интерполяционного многочлена: нужно
составить и решить систему (4.1).
Пример.
-
x
0
1
2
y
0
1
4
,


.
Однако для
практического применения этот способ
является не удобным. Существуют способы,
позволяющие построить интерполяционный
многочлен более экономичными методами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Схема Горнера
Схема Горнера – способ деления многочлена
$$P_n(x)=sumlimits_{i=0}^{n}a_{i}x^{n-i}=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+ldots+a_{n-1}x+a_n$$
на бином $x-a$. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена (они выделены для наглядности синим цветом). Первым элементом второй строки будет число $a$, взятое из бинома $x-a$:
$$
P_n(x)=normblue{a_{0}}x^{n}+normblue{a_{1}}x^{n-1}+normblue{a_{2}}x^{n-2}+ldots+normblue{a_{n-1}}x+normblue{a_n}\
$$
$$
begin{array} {c|c|c|c|c|c|c|c}
& normblue{a_0} & normblue{a_1} & normblue{a_2} & normblue{a_3} & ldots & normblue{a_{n-1}} & normblue{a_n} \
hline a & & & & & & &
end{array}
$$
Вторая строка таблицы заполняется постепенно. Второй элемент этой строки (обозначим его $b_0$) равен $a_0$, т.е., по сути, мы просто переносим вниз число $a_0$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0=a_0 & & & & & &
end{array}
$$
Следующий элемент второй строки, который мы обозначим как $b_1$, получается по такой формуле: $b_1=acdot{b_0}+a_1$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1=acdot{b_0}+a_1 & & & & &
end{array}
$$
Далее находим элемент $b_2$ по формуле $b_2=acdot{b_1}+a_2$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1 & b_2=acdot{b_1}+a_2 & & & &
end{array}
$$
Аналогично вычисляем и элемент $b_3=acdot{b_2}+a_3$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1 & b_2 & b_3=acdot{b_2}+a_3 & & &
end{array}
$$
Далее находим $b_4$, $b_5$ и так далее. В целом, общая формула для вычисления $b_i$, где $ige{1}$, будет такой:
$$
b_i = acdot{b_{i-1}}+a_i
$$
В конечном итоге, мы вычислим последний элемент $b_n = acdot{b_{n-1}}+a_n$, и на этом работа будет закончена. Заполненная таблица будет иметь такой вид:
$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1 & b_2 & b_3 & ldots & b_{n-1} & b_n
end{array}
$$
После деления исходного многочлена n-ой степени $P_n(x)$ на бином $x-a$, получим многочлен, степень которого на единицу меньше исходного, т.е. равна $n-1$. Последнее число второй строки, т.е. $b_n$, есть остаток от деления $P_n(x)$ на $x-a$:
$$
a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+ldots+a_{n-1}x+a_n
=(x-a)cdotleft(b_{0}x^{n-1}+b_{1}x^{n-2}+ldots+b_{n-1}right)+b_n
$$
Если вспомнить теорему Безу, то можно сформулировать и так: число $b_n$ равно значению многочлена $P_n(x)$ при $x=a$, т.е. $b_n = P_n (a)$.
Если $b_n=0$, то исходный многочлен делится на бином $x-a$ нацело, т.е. число $a$ является корнем этого многочлена. Непосредственное применение схемы Горнера проще всего показать на примерах.
Пример №1
Разделить $5x^4+5x^3+x^2-11$ на $x-1$, используя схему Горнера.
Решение
Для сокращения записи обозначим заданный многочлен как $P(x)$, т.е. $P(x)=5x^4+5x^3+x^2-11$. Для начала составим таблицу из двух строк. В первой строке запишем коэффициенты многочлена $P(x)$, расположенные по убыванию степеней переменной $x$. Заметьте, что данный многочлен не содержит $x$ в первой степени, т.е. коэффициент перед $x$ в первой степени равен 0:
$$
normblue{5}cdot{x^4}+normblue{5}cdot{x^3}+normblue{1}cdot{x^2}+normblue{0}cdot{x}+normblue{(-11)}\
$$
Так как мы делим на $x-normred{1}$, то в первой ячейке второй строки запишем число $normred{1}$. Таблица, с которой мы будем работать, имеет такой вид:
$$
begin{array} {c|c|c|c|c|c}
& normblue{5} & normblue{5} & normblue{1} & normblue{0} & normblue{-11} \
hline normred{1} & & & & &
end{array}
$$
Начнём заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число $5$, просто перенеся его вниз из второй ячейки первой строки:
$$
begin{array} {c|c|c|c|c|c}
& normgreen{5} & 5 & 1 & 0 & -11 \
hline 1 & normgreen{5} & & & &
end{array}
$$
Следующую ячейку заполним по такому принципу: $normred{1}cdotnormgreen{5}+normpurple{5}=normblue{10}$:
$$
begin{array} {c|c|c|c|c|c}
& 5 & normpurple{5} & 1 & 0 & -11 \
hline normred{1} & normgreen{5} & normblue{10} & & &
end{array}
$$
Аналогично заполним и четвертую ячейку второй строки: $normred{1}cdotnormgreen{10}+normpurple{1}=normblue{11}$:
$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & normpurple{1} & 0 & -11 \
hline normred{1} & 5 & normgreen{10} & normblue{11} & &
end{array}
$$
Для пятой ячейки получим: $normred{1}cdotnormgreen{11}+normpurple{0}=normblue{11}$:
$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & 1 & normpurple{0} & -11 \
hline normred{1} & 5 & 10 & normgreen{11} & normblue{11} &
end{array}
$$
И, наконец, для последней, шестой ячейки, имеем: $normred{1}cdotnormgreen{11}+normpurple{(-11)}=normblue{0}$:
$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & 1 & 0 & normpurple{-11} \
hline normred{1} & 5 & 10 & 11 & normgreen{11} &normblue{0}
end{array}
$$
Числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления $P(x)$ на $x-1$. Последнее число во второй строке (ноль) равно остатку от деления многочлена $P(x)$ на $x-1$. Остаток равен нулю, т.е. многочлен $P(x)$ делится на $x-1$ нацело. Для наглядности я запишу полученный результат, выделив коэффициенты разными цветами:
$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & 1 & 0 & -11 \
hline normred{1} & normblue{5} & normblue{10} & normblue{11} & normblue{11} &normgreen{0}
end{array}
$$
$$
P(x)
=(x-normred{1})cdotleft(normblue{5}cdot{x^4}+normblue{10}cdot{x^3}+normblue{11}cdot{x^2}+normblue{11}cdot{x}right)+normgreen{0}
=(x-1)left(5x^3+10x^2+11x+11right)
$$
Естественно, что так как степень исходного многочлена $P(x)$ равнялась четырём, то степень многочлена $5x^3+10x^2+11x+11$ на единицу меньше, т.е. равна трём.
Полученный нами результат можно ещё охарактеризовать так: значение многочлена $P(x)$ при $x=1$ равно нулю. Так как значение многочлена $P(x)$ при $x=1$ равно нулю, то единица является корнем многочлена $P(x)$.
Ответ: $5x^4+5x^3+x^2-11 = (x-1)left(5x^3+10x^2+11x+11right)$.
Пример №2
Разделить многочлен $x^4+3x^3+4x^2-5x-47$ на $x+3$ по схеме Горнера.
Решение
Для сокращения записи обозначим заданный многочлен как $P(x)$, т.е. $P(x)=x^4+3x^3+4x^2-5x-47$. Сразу оговорим, что выражение $x+3$ нужно представить в форме $x-(-3)$. В схеме Горнера будет учавствовать именно $-3$. Выполняем преобразования, аналогичные сделанным в примере №1:
$$
begin{array} {c|c|c|c|c|c}
& 1 & 3 & 4 & -5 & -47 \
hline -3 & 1 & 0 & 4 & -17 & 4
end{array}
$$
Так как степень исходного многочлена $P(x)$ равна четырём, то в результате деления получим многочлен третьей степени.
$$P(x)=(x+3)left(x^3+0cdot x^2 +4x-17right)+4=(x+3)left(x^3+4x-17right)+4$$
Полученный результат означает, что многочлен $P(x)$ делится на бином $x+3$ не нацело. Остаток от деления $P(x)$ на $x+3$ равен $4$. Этот же результат означает, что значение многочлена $P(x)$ при $x=-3$ равно $4$, т.е. $P(-3)=4$. Кстати, это несложно перепроверить непосредственной подстановкой $x=-3$ в заданный многочлен:
$$
x^4+3x^3+4x^2-5x-47=(-3)^4+3 cdot (-3)^3-5 cdot (-3)-47=4.
$$
Т.е. схему Горнера можно также использовать, если необходимо найти значение многочлена при заданном значении переменной.
Ответ: $x^4+3x^3+4x^2-5x-47=(x+3)left(x^3+4x-17right)+4$.
Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.
Пример №3
Найти все целочисленные корни многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$, используя схему Горнера.
Решение
Для сокращения записи обозначим заданный многочлен как $P(x)$, т.е.
$$P(x)=x^6+2x^5-21x^4-20x^3+71x^2+114x+45$$
Коэффициенты рассматриваемого многочлена есть целые числа, а коэффициент перед старшей степенью переменной (т.е. перед $x^6$) равен единице. В этом случае целочисленные корни многочлена нужно искать среди делителей свободного члена, т.е. среди делителей числа 45. Для заданного многочлена такими корнями могут быть числа $45; ; 15; ; 9; ; 5; ; 3; ; 1$ и $-45; ; -15; ; -9; ; -5; ; -3; ; -1$. Проверим, к примеру, число $1$:
Табл. №1
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline 1 & 1 & 3 & -18 & -38 & 33 & 147 & 192
end{array}
$$
Как видите, значение многочлена $P(x)$ при $x=1$ равно $192$ (последнее число в второй строке), а не $0$, посему единица не является корнем данного многочлена. Так как проверка для единицы окончилась неудачей, проверим значение $x=-1$. Новую таблицу составлять не будем, а продолжим использование табл. №1, дописав в нее новую (третью) строку. Вторую строку, в которой проверялось значение $1$, выделим красным цветом и в дальнейших рассуждениях использовать её не будем.
Можно, конечно, просто переписать таблицу заново, но при заполнении вручную это займет немало времени. Тем более, что чисел, проверка которых окончится неудачей, может быть несколько, и каждый раз записывать новую таблицу затруднительно. При вычислении «на бумаге» красные строки можно просто вычёркивать.
Табл. №2
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0
end{array}
$$
Итак, значение многочлена $P(x)$ при $x=-1$ равно нулю, т.е. $P(-1)=0$. Это значит, что число $-1$ есть корень многочлена $P(x)$. После деления многочлена $P(x)$ на бином $x-(-1)=x+1$ получим многочлен $x^5+x^4-22x^3+2x^2+69x+45$, коэффициенты которого взяты из третьей строки табл. №2. Результат вычислений можно также представить в такой форме:
$$
begin{equation}
P(x)=(x+1)left(x^5+x^4-22x^3+2x^2+69x+45right)
end{equation}
$$
Продолжим поиск целочисленных корней. Теперь уже нужно искать корни многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Опять-таки, целочисленные корни этого многочлена ищут среди делителей его свободного члена, – числа $45$. Попробуем ещё раз проверить число $-1$. Новую таблицу составлять не будем, а продолжим использование предыдущей табл. №2, т.е. допишем в нее еще одну строку:
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 &
end{array}
$$
Итак, число $-1$ является корнем многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Этот результат можно записать так:
$$
begin{equation}
x^5+x^4-22x^3+2x^2+69x+45=(x+1)left(x^4-22x^2+24x+45right)
end{equation}
$$
Учитывая равенство (2), равенство (1) можно переписать в такой форме:
$$
begin{equation}
P(x)=(x+1)left(x^5+x^4-22x^2+2x^2+69x+45right)=\
=(x+1)(x+1)left(x^4-22x^2+24x+45right)
=(x+1)^2left(x^4-22x^2+24x+45right)
end{equation}
$$
Теперь уже нужно искать корни многочлена $x^4-22x^2+24x+45$, – естественно, среди делителей его свободного члена (числа $45$). Проверим еще раз число $-1$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 & \
hline -1 & 1 & -1 & -21 & 45 & 0 & &
end{array}
$$
Число $-1$ является корнем многочлена $x^4-22x^2+24x+45$. Этот результат можно записать так:
$$
begin{equation}
x^4-22x^2+24x+45=(x+1)left(x^3-x^2-21x+45right)
end{equation}
$$
С учетом равенства (4), равенство (3) перепишем в такой форме:
$$
begin{equation}
P(x)=(x+1)^2left(x^4-22x^3+24x+45right)=\
=(x+1)^2(x+1)left(x^3-x^2-21x+45right)
=(x+1)^3left(x^3-x^2-21x+45right)
end{equation}
$$
Теперь ищем корни многочлена $x^3-x^2-21x+45$. Проверим еще раз число $-1$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 & \
hline -1 & 1 & -1 & -21 & 45 & 0 & & \
hline -1 & 1 & -2 & -19 & 64 & & &
end{array}
$$
Проверка окончилась неудачей. Выделим шестую строку красным цветом и попробуем проверить иное число, например, число $3$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 & \
hline -1 & 1 & -1 & -21 & 45 & 0 & & \
hline normred{-1} & normred{1} & normred{-2} & normred{-19} & normred{64} & & & \
hline 3 & 1 & 2 & -15 & 0 & & &
end{array}
$$
В остатке ноль, посему число $3$ – корень рассматриваемого многочлена. Итак,
$$x^3-x^2-21x+45=(x-3)left(x^2+2x-15right)$$
Теперь равенство (5) можно переписать так:
$$
begin{equation}
P(x)=(x+1)^3left(x^3-x^2-21x+45right)
=(x+1)^3(x-3)left(x^2+2x-15right)
end{equation}
$$
Проверим ещё раз число $3$:
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 & \
hline -1 & 1 & -1 & -21 & 45 & 0 & & \
hline normred{-1} & normred{1} & normred{-2} & normred{-19} & normred{64} & & & \
hline 3 & 1 & 2 & -15 & 0 & & & \
hline 3 & 1 & 5 & 0 & & & &
end{array}
$$
Полученный результат можно записать так (это продолжение равенства (6)):
$$
begin{equation}
P(x)=(x+1)^3(x-3)left(x^2+2x-15right)
=(x+1)^3(x-3)(x-3)(x+5)
=(x+1)^3(x-3)^2(x+5)
end{equation}
$$
Из последней скобки видно, что число $-5$ также является корнем данного многочлена. Можно, конечно, формально продолжить схему Горнера, проверив значение $x=-5$, но необходимости в этом нет. Итак,
$$ P(x)=(x+1)^3(x-3)left(x^2+2x-15right)=(x+1)^3(x-3)^2(x+5)$$
Числа $-1$, $3$, $-5$ – корни данного многочлена. Причем, так как скобка $(x+1)$ в третьей степени, то $-1$ – корень третьего порядка; так как скобка $(x-3)$ во второй степени, то $3$ – корень второго порядка; так как скобка $(x+5)$ в первой степени, то $x=-5$ – корень первого порядка (простой корень).
Вообще, обычно оформление таких примеров состоит из таблицы, в которой перебираются возможные варианты корней, и ответа:
$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 & \
hline -1 & 1 & -1 & -21 & 45 & 0 & & \
hline normred{-1} & normred{1} & normred{-2} & normred{-19} & normred{64} & & & \
hline 3 & 1 & 2 & -15 & 0 & & & \
hline 3 & 1 & 5 & 0 & & & &
end{array}
$$
Из таблицы следует вывод, полученный нами ранее с подробным решением:
$$ P(x)=(x+1)^3(x-3)left(x^2+2x-15right)=(x+1)^3(x-3)^2(x+5)$$
Ответ: $-1$, $3$, $-5$.
Пример №4
Убедиться, что числа $2$ и $-5$ являются корнями многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$. Разделить заданный многочлен на биномы $x-2$ и $x+5$.
Решение
Как и ранее, для сокращения записи обозначим заданный многочлен как $P(x)$, т.е.
$$P(x)=3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$$
Степень многочлена $P(x)$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.
$$
begin{array} {c|c|c|c|c|c|c|c}
& 3 & 9 & -28 & 6 & -30 & -30 & 100 \
hline normblue{2} & 3 & 15 & 2 & 10 & -10 & -50 & 0 \
hline normpurple{-5} & normgreen{3} & normgreen{0} & normgreen{2} & normgreen{0} & normgreen{-10} & 0 &
end{array}
$$
$$
P(x)=(x-normblue{2})cdot(x-(normpurple{-5}))cdotleft(normgreen{3}cdot{x^4}+normgreen{0}cdot{x^3}+normgreen{2}cdot{x^2} + normgreen{0}cdot{x} + (normgreen{-10})right)
=(x-2)(x+5)left(3x^4+2x^2-10right)
$$
Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.






























































