1. Постановка задачи
Задача
приближения (аппроксимации) функций
заключается в том, чтобы для данной
функции построить другую, отличную от
нее функцию, значения которой достаточно
близки к значениям данной функции. Такая
задача возникает на практике достаточно
часто. Укажем наиболее типичные случаи.
1.
Функция задана таблицей в конечном
множестве точек, а вычисления нужно
произвести в других точках.
2.
Функция задана аналитически, но ее
вычисление по формуле затруднительно.
При
решении задачи поиска приближенной
функции возникают следующие проблемы.
1.
Необходимо выбрать вид приближенной
функции. Для приближения широко
используются многочлены, тригонометрические
функции, показательные функции и т. д.
2.
Необходимо выбрать критерий близости
исходной и приближенной функции. Это
может быть требование совпадения обеих
функций в узловых точках (задача
интерполяции), минимизация
среднеквадратического уклонения (метод
наименьших квадратов) и др.
3.
Необходимо указать правило (алгоритм),
позволяющее с заданной точностью найти
приближение функции.
2. Приближение функции многочленами Тейлора
Пусть
функция y
= f(x)
определена
в окрестности точки a
и имеет в этой окрестности n
+ 1
производную. Тогда в этой окрестности
справедлива формула Тейлора:
f(x)
=
c0
+ c1(x
— a)
+ c2(x
— a)2
+ … +
cn(x
— a )n
+ Rn(x)
= Tn(x)
+ Rn(x),
где
ck
=
Tn(x)
— многочлен Тейлора:
Tn(x)=
c0
+ c1(x
— a)
+ c2(x
— a)2
+ … +
cn(x
— a )n,
(4.1)
Rn(x)
— остаточный
член формулы Тейлора. Его можно записать
различными способами, например, в форме
Лагранжа:
Rn(x)=
, a x.
Многочлен
Тейлора (4.1) обладает свойством, что в
точке x
=
a все
его производные до порядка n
включительно совпадают с соответствующими
производными функции f,
т. е.
T(a)=
f(k)(a),
k = 0,
1, …, n.
В
этом легко убедиться, дифференцируя
Tn(x).
Благодаря этому свойству многочлен
Тейлора хорошо приближает функцию f
в
окрестности точки a.
Погрешность приближения составляет
|f(x)
— Tn(x)|
= |Rn(x)|,
т.
е. задавая некоторую точность >
0,
можно определить окрестность точки a
и
значение n
из условия:
|Rn(x)|
= <
.
(4.2)
Пример
4.1.
Найдем
приближение функции y
= sinx
многочленом Тейлора в окрестности точки
a
= 0.
Воспользуемся известным выражением
для k-ой
производной функции sinx:
(sinx)(k)
= sin
x
+ k
(4.3)
Применяя
последовательно формулу (4.3), получим:
f(0)
= sin0
= 0;
f
(0)
= cos(0)
= 1;
f»(0)
= —sin0
= 0;
f(2k-1)(0)
= sin
(2k
— 1) = (-1)k
— 1
;
f(2k)(0)
= 0;
f(2k+1)()
= (-1)kcos.
Следовательно,
многочлен Тейлора для функции y
= sinx
для n
= 2k
имеет
вид:
sinx
= x — + … + (-1)k
— 1
+
R2k(x),
R2k(x)
= (-1)k
.
Зададим
=
10
-4
и отрезок [-,].
Определим n
=2k
из
неравенства:
|R2k(x)|
= < < < =
10-4.
Таким
образом, на отрезке —,
функция y
= sinx с
точностью до =
10-4
равна многочлену 5-ой степени:
sinx
=
x
— + =
x
— 0.1667x3
+ 0.0083x5.
Пример
4.2.
Найдем
приближение функции y
= ex
многочленом Тейлора на отрезке [0, 1] с
точностью =
10
-5.
Выберем
a
= ?, т. е в середине отрезка. При этом
величина погрешности в левой части
(4.2) принимает минимальное значение. Из
математического анализа известно, что
для k-ой
производной от ex
справедливо равенство:
(ex)(k)
= ex.
Поэтому
(ea)(k)
=
ea
= e1/2,
Следовательно,
многочлен Тейлора для функции y
= ex
имеет
вид:
ex
= e1/2
+ e1/2(x
— ?)
+ (x
— ?)2
+ … + (x
— ?)n+
Rn(x),
При
этом, учитывая, что x
[0,
1], получим оценку погрешности:
|Rn(x)|
< .
(4.4)
Составим
таблицу погрешностей, вычисленных по
формуле (4.4):
|
n |
2 |
3 |
4 |
5 |
6 |
|
|
Rn |
0.057 |
0.0071 |
0.00071 |
0.000059 |
0.0000043 |
|
Таким
образом, следует взять n
=
6.
Соседние файлы в папке ВМ 2012, заочники
- #
- #
- #
- #
- #
- #
- #
Аннотация: Лекция посвящена вопросам
приближения числовых функций полиномами. Рассмотрены вопросы
построения полиномов Лагранжа и Ньютона.
Цель лекции: Рассмотреть основные методы аппроксимации
числовых функций полиномами. Описать методы полиномиальной
интерполяции функций.
Довольно часто возникает задача восстановление значений функции,
которая задана лишь в некоторых точках. Совершенно очевидно, что
если мы знаем значения функции лишь в некоторых фиксированных
точках, то значения функции в промежуточных значениях аргумента
могут быть любыми. Однако часто имеется некоторая априорная
информация о свойствах функции, с помощью которой удается найти
приемлемое значение функции.
Пусть на отрезке ![[a,b]](https://intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)

![[a,b]](https://intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
точек 
Точки 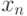
на ряду с разбиением отрезка нам дан набор чисел 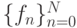
точках 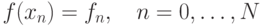
Задача интерполяции состоит в том, чтобы найти значение
функции 
![xin[a,b]](https://intuit.ru/sites/default/files/tex_cache/c7c42309c359c25dfe77f397d5261997.png)
возникает задача экстраполяции состоящей в том, чтобы найти
значение функции 
![xnotin[a,b]](https://intuit.ru/sites/default/files/tex_cache/88b6f307d5be729ea91741e247bb2b7c.png)
рассматривать задачу интерполяции.
Решение задачи интерполяции может быть представлено в виде функции
(алгоритма)
Однако чаще под решением задачи интерполяции понимают построение
такой функции 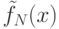
![[a,b]](https://intuit.ru/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
Классическим методом построения интерполяционной функции является
построение многочлена степени
такого, что
Очевидно, что для определения этого многочлена необходимо и
достаточно найти значения 
Покажем, что такой многочлен всегда можно построить. Точнее мы
предъявим формулу, которая даст нам этот интерполяционный
многочлен.
Введем функции:
Видно, что эти функции сами являются многочленами порядка 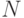
Непосредственно из этой формулы мы имеем следующие соотношения
и
Тогда искомый интерполяционный многочлен может быть найден по
формуле
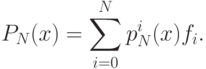 |
( 14.1) |
Можно убедиться также в том, что этот многочлен единственный.
Действительно, для любого другого многочлена, для которого
мы имеем, что 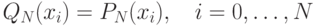
Тогда многочлен 
чем 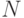
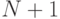
этот многочлен 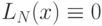
Многочлен, заданный по формуле 14.1 называется
интерполяционным многочленом в форме Лагранжа.
Лагранжева форма интерполяционного многочлена является не
единственной формой интерполяционного многочлена. Более удобной
для практических расчетов является интерполяционный многочлен в
форме Ньютона. Для заданного разбиения отрезка и значений функции
в этих узлах введем понятие раздельной разности. Раздельной
разностью первого порядка называется число
Раздельная разность 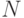
рекуррентной формуле
Теперь мы можем определить интерполяционный многочлен в форме
Ньютона по формуле
Разумеется, интерполяционный многочлен в форме Ньютона совпадает с
интерполяционным многочленом в форме Лагранжа.
Хотя формулы для построения интерполяционных многочленов выглядят
просто, метод интерполяции функций многочленами имеет серьезные
недостатки для больших значений 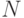
многочленами большой степени, как правило, сопряжено с
вычислительной неустойчивостью. Во-вторых, как было показано
К.Рунге в своей знаменитой работе 1901 года, существует такая
бесконечно гладкая функция, для которой интерполяционный
многочлен, построенный на равномерной сетке может иметь бесконечно
большое отклонение с увеличением количества узловых точек.
Рассмотрим этот пример. Пусть функция
заданная на ![[-1,1]](https://intuit.ru/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png)
«хорошими» свойствами. Для каждого 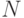
формуле
Через 
формуле 14.1. К.Рунге было показано, что для этого
случая имеет место
Ключевые термины
Разбиение отрезка — конечное множество точек,
принадлежащих заданному отрезку.
Узловые точки — элементы из множества разбиения отрезка.
Интерполяция — процедура приближенного вычисления значений
функции по заданным значениям функции в узловых точках.
Экстраполяция — процедура вычисления значений функции вне
отрезка, на котором задана функция.
Интерполяционная функция — функция, которая реализует
интерполяцию.
Краткие итоги: Рассмотрены методы интерполяции функции на
основе приближения полиномами. Приведены методы построения
интерполяционных полиномов в форме Лагранжа и в форме Ньютона.
Приближение многочленом с условием прохождения через точки
Время на прочтение
6 мин
Количество просмотров 7.5K
При моделировании данных методом наименьших квадратов, кривая обычно не проходит через точки измерений (рис. 1).
Что, если нужно, чтобы эта кривая точно проходила через одну или несколько особо выделенных точек (рис. 2 — показаны зелёными кружочками)?
Тогда читаем дальше.
1. Мотивация
Рассмотрим обычную задачу приближения многочленом и посмотрим, чего нам в ней не хватает.
Дано N точек на плоскости (xi,yi) — значения неизвестной функции f(x). Требуется найти многочлен p(x) степени M (M<N), наилучшим образом приближающий эту функцию.
Часто полагают, что «наилучшим» является многочлен, сумма квадратов отклонений которого от заданных точек минимальна:
В таком виде задача решается широко известным методом наименьших квадратов (МНК).
При M<N-1 многочлен p(x), вообще говоря, не проходит через все заданные точки (xi, yi) (рис. 1). Более того, часто оказывается, что он не проходит ни через одну из них.
Само по себе это не плохо. Обычно данные, по которым строится приближение, содержат погрешности измерений. Даже лучше, что многочлен не проходит через все точки, так как при этом ошибки измерений сглаживаются.
Однако бывает, что о моделируемой зависимости имеются дополнительные сведения. Например, моделируется отклик датчика на некую величину. И из физических соображений ясно, что этот отклик строго равен нулю при равенстве нулю величины. При моделировании характеристики такого датчика может оказаться, что аппроксимирующий многочлен не пройдет через нуль. В результате модель даст большую погрешность в районе нуля.
В такой ситуации хотелось бы найти многочлен со следующими свойствами:
-
Точно проходит через нуль
-
Имеет наименьшую сумму квадратов отклонений от остальных измеренных значений
В статье описывается метод, позволяющий найти такой многочлен. Более того, можно потребовать точного прохождения многочлена не через одну, а несколько выделенных точек.
2. Решение
2.1. Взвешенный метод наименьших квадратов
Как ингредиент нам потребуется взвешенный метод наименьших квадратов, который минимизирует сумму квадратов отклонений с весовыми коэффициентами в каждой точке:
Где wi — весовые коэффициенты. Обычно взвешенный МНК используется для учета погрешностей измерений в каждой точке, поэтому в литературе часто используют не понятие веса, а обратную дисперсию σ2 погрешностей:
Взвешенный МНК хорошо описан в книге [1], гл. 15.1, 15.4.
2.2. Точное прохождение через нуль
Начнём с простого случая: потребуем точного прохождения многочлена p(x) через нуль.
Для этого найдём многочлен q(x) степени M-1 по модифицированным точкам (xi, yi/xi) с помощью взвешеннго МНК, выбрав в качестве весов wi=xi2; и умножим его на x. Тогда:
Он будет иметь степень M и точно проходить через нуль.
Рассмотрим сумму квадратов его отклонений от остальных точек (xi, yi):
Но именно эта величина и минимизируется взвешенным МНК по модифицированным точкам. Поэтому многочлен p(x) будет соответствовать и второму условию задачи — иметь наименьшую сумму квадратов отклонений от (xi, yi).
2.3. Точное прохождение через одну произвольную точку
Усложним задачу и потребуем точного прохождения многочлена p(x) через одну произвольно заданную точку (ξ,η).
Путём замены переменных u=x-ξ, v=y-η, задача сводится к рассмотренной выше. Находим коэффициенты многочлена p0(u), проходящего через нуль и имеющего наименьшую сумму квадратов отклонений p0(ui)-vi. Далее переходим к исходным переменным:
Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с коэффициентами p0(x-ξ), но есть и более простой на практике способ. Поскольку у нас в программе уже имеется реализация обычного МНК, то можно просто вычислить значения p(x) по формуле (1) в каких-нибудь M+1 или более точках, и применить к этим значениям обычный МНК, задав степень многочлена M. Тем самым и будут найдены коэффициенты p(x).
2.4. Точное прохождение через несколько точек
И, наконец, самый общий случай — потребуем точного прохождения многочлена p(x) через K заданных точек (ξi, ηi). Следует выбирать K ≤ M, в противном случае задача вырождается в интерполяцию.
Переходя к решению, введем многочлен z(x) степени K:
Он имеет нули в точках ξ1, ξ2, … ξK.
Также введем интерполяционный многочлен Лагранжа L(x) степени K-1, проходящий через точки (ξi, ηi) [1], гл. 3.1.
Используем взвешенный МНК для нахождения многочлена q(x) степени M-K по модифицированным точкам: (xi, (yi-L(xi))/z(xi)) с весовыми коэффициентами wi=z(xi)2. Получим коэффициенты {aj} для q(x), которые минимизируют сумму:
Теперь составим многочлен p(x) как:
Докажем, что p(x) является решением задачи.
-
Прохождение через точки (ξi, ηi) обеспечивается тем, что z(ξi)=0, обращая в нуль первое слагаемое. Второе слагаемое в этих же точках, L(x), проходит через (ξi, ηi) по построению.
-
Степень p(x) равна M, так как степень произведения многочленов q(x) и z(x) равна сумме степеней множителей. В данном случае M-K+K=M. Сумма же многочленов имеет степень старшего из слагаемых. Степень L(x) равна K-1, что по условию меньше M.
-
Запишем сумму квадратов отклонений в точках (xi, yi):
Но это совпадает с величиной (2), которая минимизировалась при нахождении коэффициентов q(x). Следовательно, p(xi) имеет наименьшую сумму квадратов отклонений от yi. Что и требовалось доказать.
Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с q(x), z(x) и L(x), но это еще сложнее, чем в разделе 2.3. выше. Так что здесь тоже рекомендуется вычислить значения p(x) в M+1 или более точках по формуле (3) и применить к ним обычный МНК.
3. Цена вопроса и рекомендации к применению
За всё в этой жизни приходится платить. Наложение условия точного прохождения через точки (ξi, ηi) на многочлен p(x) приводит к тому, что сумма квадратов его отклонений от остальных точек (xi, yi) оказывается, вообще говоря, выше, чем без наложения условий.
Фактически, мы решили задачу условной оптимизации суммы квадратов отклонений p(xi)-yi. Как и в других задачах условной оптимизации, достигаемое значение целевой функции получается хуже, чем при оптимизации безусловной. В противном случае и безусловная оптимизация дала бы тот же результат.
Когда же следует применять описанный метод? Тогда, когда о моделируемой зависимости имеются «железобетонные» сведения, что она должна проходить через точки (ξi, ηi) независимо от экспериментальных данных (xi, yi).
В моей практике был один такой случай. Моделировалась нелинейная характеристика датчика. Истинный вид функциональной зависимости был неизвестен. Оставалось только использовать многочлены в попытке хоть как-то компенсировать нелинейность. Но многочлены плохо описывали характеристику около нуля. Полученные обычным МНК, они стремились не проходить через нуль. Тем не менее, из физических соображений было ясно, что характеристика датчика должна проходить через нуль. Вот тогда наложение условия и пригодилось. Его применение позволило улучшить компенсацию нелинейности в окрестностях нуля и уменьшить относительную погрешность прибора в целом.
4. Пример с конкретными числами
Этот пример был использован для построения графиков, приведенных на рис. 1 и рис. 2.
В качестве «истинной зависимости» был взят следующий многочлен:
Где T3(x) — многочлен Чебышева третьего порядка. Модификации применены к нему для того, чтобы отобразить интересный участок графика в диапазон x,y ∈ [0; 1]. p1(x) проходит через точки (0,0) и (1,1). Разложение его по степеням x выглядит так:
В качестве данных для метода наименьших квадратов (обычного и условного) взяты значения p1(x) в 11 равноотстоящих точках между 0 и 1 с шагом в 0,1. К значениям многочлена была добавлена нормально распределенная «ошибка измерений» δi с дисперсией σ2=0,04. В точках x1=0 и x11=1 ошибка не добавлялась. По случайным числам карты легли следующим образом:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
δi |
0 |
-0,1617 |
0,0162 |
0,0294 |
-0,0458 |
0,3358 |
0,2476 |
-0,1325 |
-0,3986 |
-0,4477 |
0 |
Приближение обычным МНК по заданным точкам при M=3 дало следующие коэффициенты:
График p2(x) изображен на рис. 1. Достигнутая сумма квадратов отклонений p2(x)-yi составила 0,4019.
Для испытания описываемого в разд. 2.4. метода было поставлено условие точного прохождения многочлена через точки (0,0) и (1,1), а в остальных точках — минимизация суммы квадратов отклонений. В результате был получен следующий многочлен:
Его график изображен на рис. 2. Достигнутая сумма квадратов отклонений p3(x)-yi составила 0,5046.
Из приведенного примера можно сделать вывод, что теоретические выкладки подтвердились. Был найден многочлен p3(x), приближающий «экспериментальные данные» и проходящий через точки (0,0) и (1,1). Как предсказывалось в разд. 3, сумма квадратов его отклонений от точек (xi, yi) оказалась больше, чем у многочлена p2(x), найденного обычным МНК. Тем не менее, эта жертва может быть оправданной, если прохождение p3(x) через точки (0,0) и (1,1) важнее.
Что касается совпадения коэффициентов многочленов p2(x) и p3(x) с коэффициентами «истинного» многочлена p1(x) — то на паре-тройке наборов тестовых данных особой закономерности не выявилось. Наверное, есть смысл провести тест Монте-Карло и сравнить распределения коэффициентов p2(x) и p3(x) на большой выборке.
Заключение
В статье был получено обобщение метода наименьших квадратов, позволяющее налагать на многочлен условие прохождения через заданные точки.
Задачу удалось свести к применению взвешенного метода наименьших квадратов и интерполяции многочленом Лагранжа. Поскольку обе операции сводятся к решению системы линейных уравнений, то и описанный в статье метод сохраняет эту (невысокую) вычислительную сложность. Точное решение можно получить за конечное число действий и (при должной усидчивости или использовании систем компьютерной алгебры) выразить аналитически.
Возможны обобщения метода для задач приближения не только многочленами, а и другими функциями. Но эта тема обширна и может быть рассмотрена только в отдельных публикациях.
Литература
[1] William H. Press и др. «Numerical Recipes in C++: The Art of Scientific Computing», Second Edition. Cambridge University Press, ISBN 0-521-75033-4


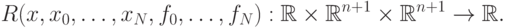
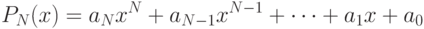
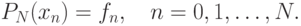
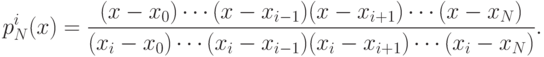
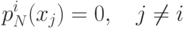







![limlimits_{Ntoinfty}maxlimits_{xin[-1,1]}|f(x)-P_N(x)|=infty.](https://intuit.ru/sites/default/files/tex_cache/296d0647d3dc5bcbd4126503c0ea99be.png)
