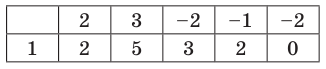
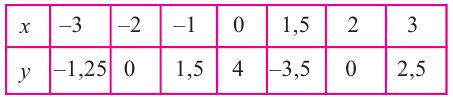
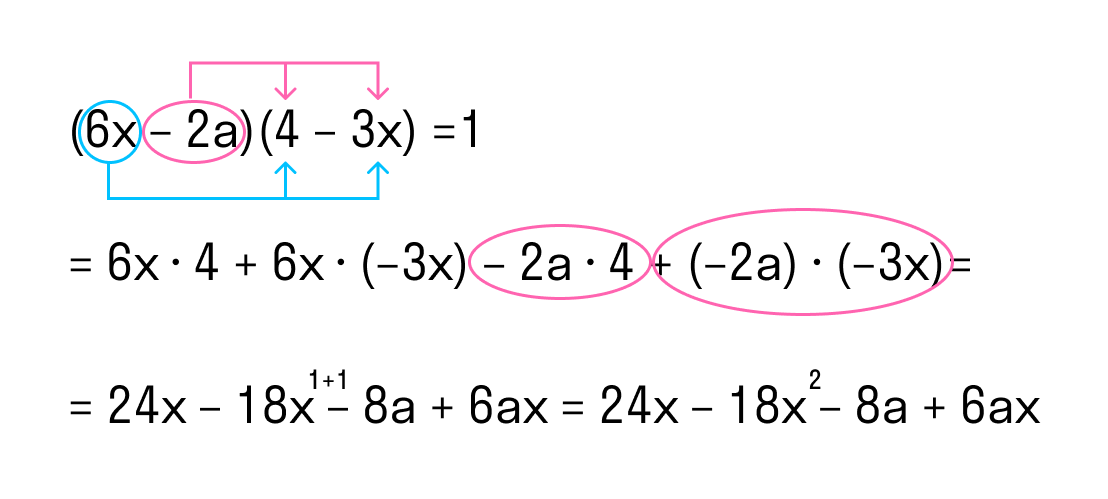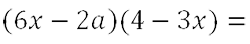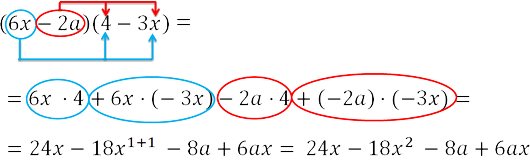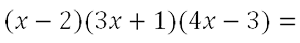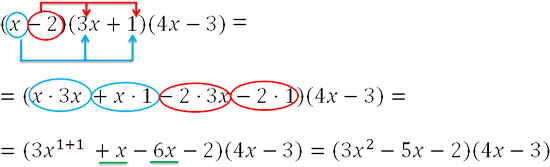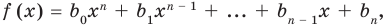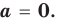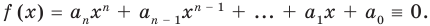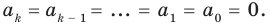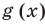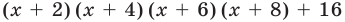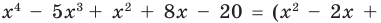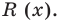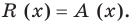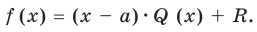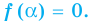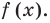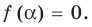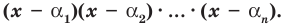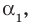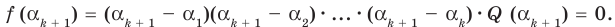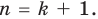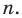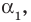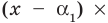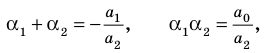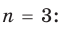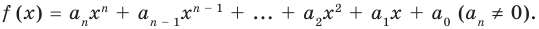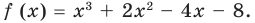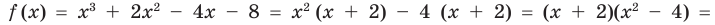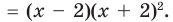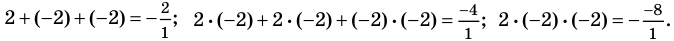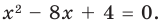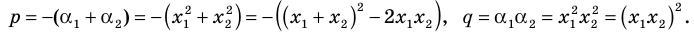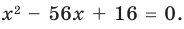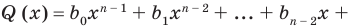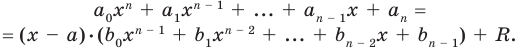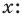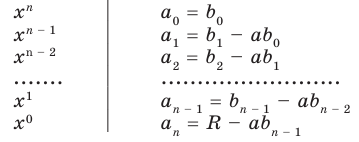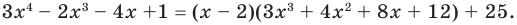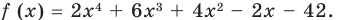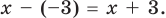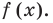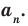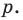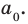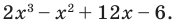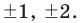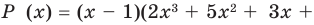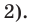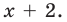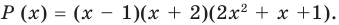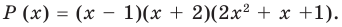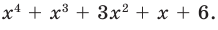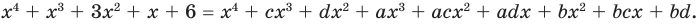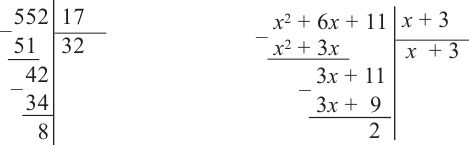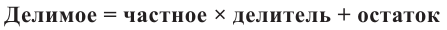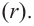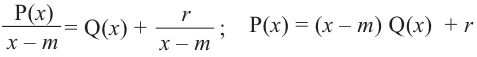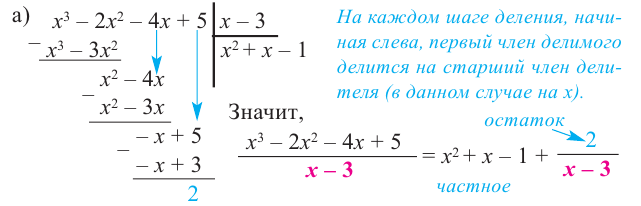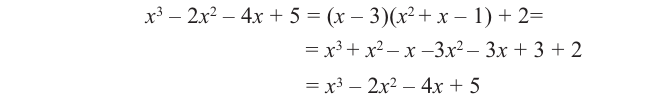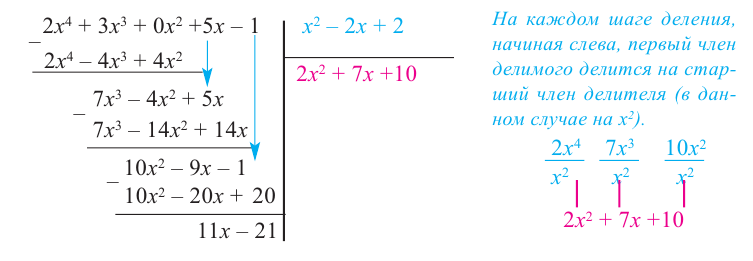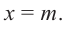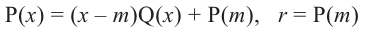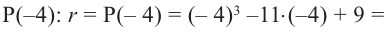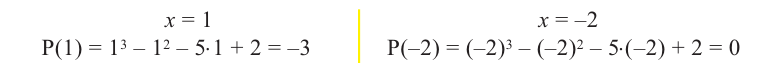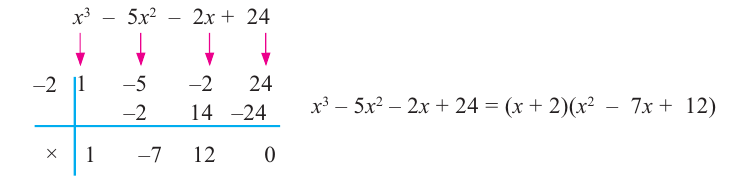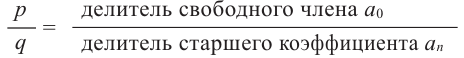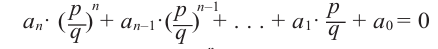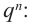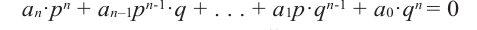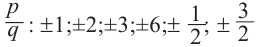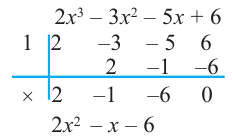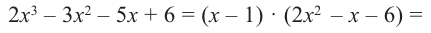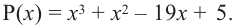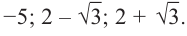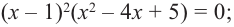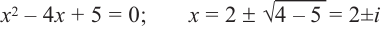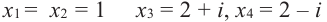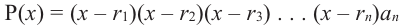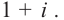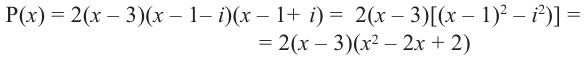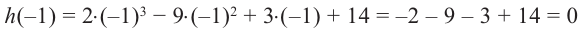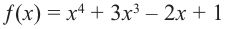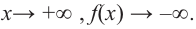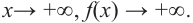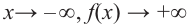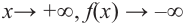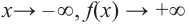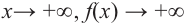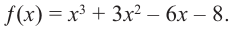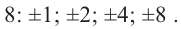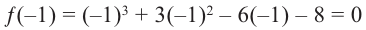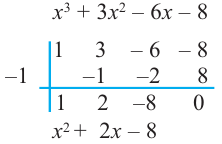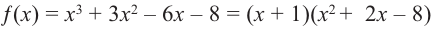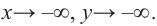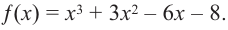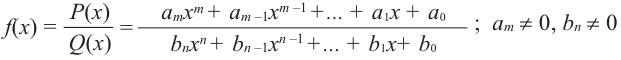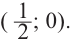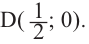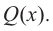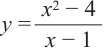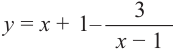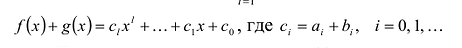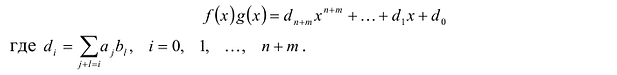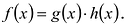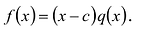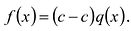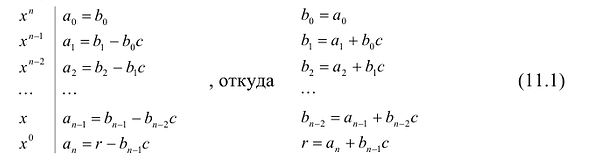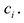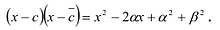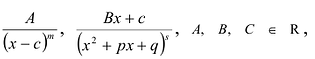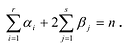Определение многочлена
Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.
Одночлен — это произведение чисел, переменных и степеней.
Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.
Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.
Как привести многочлен к стандартному виду:
- Привести к стандартному виду все одночлены, которые входят в многочлен.
- Привести подобные члены.
Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:
- Правило умножения двучленов:
(a + b) * (c + d) = ac + ad + bc + bd.
- Правило умножения двучлена на трехчлен:
(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.
- Правило перемножения трехчленов:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc.
Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Правило умножения многочлена на многочлен
Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:
- Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
- Сначала составим их произведение: (a + b)(c + d).
- Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
- Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
- Проведем обратную замену x на (c + d):
a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd. -
Как изменилось произведение исходных многочленов:
(a + b)(c + d) = ac + ad + bc + bd.
Как раз так и выглядит формула умножения многочлена на многочлен.
Запоминаем!
Результат умножения многочлена на многочлен — всегда многочлен.
Правило умножения многочлена на многочлен
Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.
Алгоритм умножения многочлена на многочлен:
- Первый член первого многочлена умножить на каждый член второго многочлена.
Второй член первого многочлена умножить на каждый член второго многочлена.
И так далее. - Сложить полученные произведения.
- Преобразовать полученную сумму в многочлен стандартного вида.
Запоминаем!
Умножение трех, четырех и большего количества многочленов нужно свести к последовательному умножению двух многочленов. То есть, сначала умножаем первые два многочлена, затем результат умножаем на третий многочлен, и этот результат умножаем на четвертый многочлен и так далее.
Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).
Как решаем:
- Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
- Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.
Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x2 – 8a + 6ax.
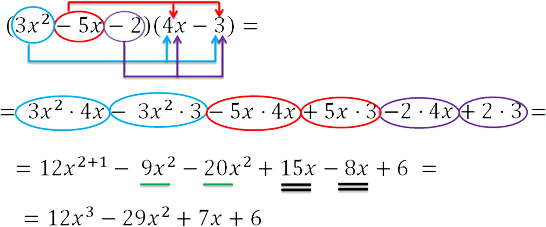
Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).
Как решаем:
Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x3 – 29x2 + 7x + 6.
Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Примеры умножения многочлена на многочлен
Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.
Пример 1. Выполнить умножение многочленов:
2 − 3x и x2 − 7x + 1.
Как решаем:
Запишем произведение: (2 − 3x)(x2 − 7x + 1).
Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x2, 2(−7x) и 2*1.
Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx2, −3x(−7x) и −3x*1.
Из полученных выражений составим сумму: 2x2 + 2(−7x) + 2*1 − 3xx2 − 3x(−7x) − 3x*1.
Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.
Осталось полученную сумму преобразовать в многочлен стандартного вида:
2x2 + 2(−7x) + 2*1 − 3xx2 − 3x(−7x) − 3x*1 = 2x2 − 14 x + 2 − 3x3 + 21x2 − 3x = (2x2 + 21x2) + (−14x − 3x) + 2 − 3x3 = 23x2 − 17x + 2 − 3x3.
Получается, что (2 − 3x)(x2 − 7x + 1) = 23x2 − 17x + 2 − 3x3.
Ответ: (2 − 3x)(x2 − 7x + 1) = 23x2 − 17x + 2 − 3x3.
Пример 2. Найти произведение трех многочленов:
x2 + xy − 1, x + y и 2y − 3.
Как решаем:
Запишем их произведение: (x2 + xy − 1)(x + y)(2y − 3).
Умножим первые два многочлена:
(x2 + xy − 1)(x + y) = x2x + x2y + xyx + xyy − 1x − 1y = x3 + 2x2y + xy2 − x − y.
Таким образом: (x2+ xy − 1)(x + y)(2y − 3) = (x3 + 2x2y + xy2 − x − y)(2y − 3).
Снова выполним умножение двух многочленов:
(x3 + 2x2y + xy2 − x − y)(2y − 3) = x32y + x3(−3) + 2x2y2y + 2x2y(−3) + xy22y + xy2(−3) − x2y − x(−3) − y2y − y(−3) = 2x3y − 3x3 + 4x2y2 − 6x2y + 2xy3 − 3xy2 − 2xy + 3x − 2y2 + 3y.
Ответ: (x2 + xy − 1)(x + y)(2y − 3) = 2x3y − 3x3 + 4x2y2 − 6x2y + 2xy3 − 3xy2 − 2xy + 3x − 2y2 + 3y.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Умножение многочлена на многочлен
Поддержать сайт
Запомните!
Чтобы умножить многочлен на многочлен, нужно:
- каждый
одночлен первого многочлена умножить на каждый одночлен второго многочлена; - полученные произведения сложить (то есть записать друг за другом с учетом знаков полученных при умножении).
Рассмотрим пример умножения многочлена на многочлен.
Умножим последовательно первый одночлен «6x» из первой скобки на оба одночлена второй скобки.
Затем умножим второй одночлен «−2a» первой скобки на оба одночлена второй скобки.
Умножать одночлены будем по правилам
умножения одночленов.
Важно!
Не забывайте при умножении одночленов использовать
правило знаков.
Результат умножения многочлена на многочлен будет всегда многочленом.
Примеры умножения многочлена на многочлен
-
(a − b)(−a − 2) = a · (−a) − 2a + ab + 2b =
−a2 − 2a + ab + 2b -
(a2 + ab + b2)(a − b) =
= a2 · a − a2 · b + ab · a − ab · b + b2 ·
a − b2 · b =
=
a2 + 1 − a2b + a1 + 1b − ab1 + 1 + b2a
− b2 + 1 =
= a3 −
a2b +
a2b
− ab2 +
ab2
− b3 =
a3 − b3
Как умножить 3 многочлена
Запомните!
Чтобы умножить 3 или более многочленов нужно:
- перемножить первые два многочлена между собой и записать результат в скобки;
- умножить полученный новый многочлен из пункта 1 на следующий многочлен.
Другими словами, умножать несколько многочленов нужно последовательно.
Рассмотрим пример умножения трёх многочленов.
Сначала умножим первый многочлен на второй, и их результат запишем в скобках.
Теперь перемножим получившийся многочлен и третий многочлен. Не забудем после умножения
привести подобные одночлены.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 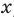
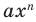
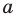
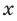
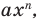
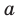
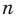
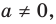
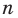
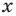
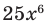
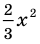
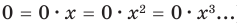
По определению многочлен от одной переменной 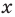
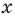
многочленом от одной переменной 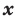
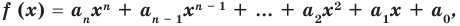
где коэффициенты 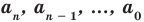
Если 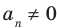
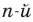
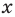
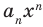
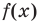
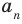
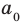
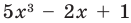
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 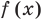
где 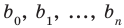
Теорема 1. Одночлены 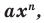
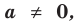
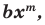
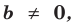
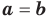
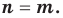
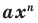
Поскольку равенство одночленов
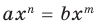
выполняется при всех значениях 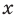
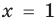
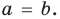
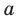
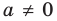
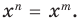
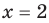
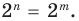
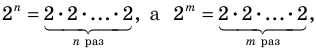
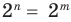
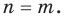
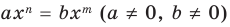
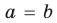
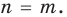
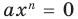
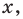
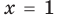
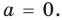
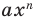
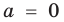
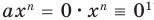
Далее любой одночлен вида 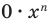
Теорема 2. Если многочлен 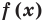
Для доказательства используем метод математической индукции. Пусть
При 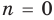
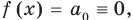
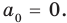
Предположим, что при 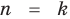
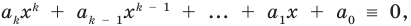
Докажем, что данное утверждение выполняется и при 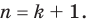
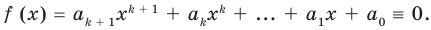
Поскольку равенство (3) выполняется при всех значениях 
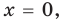
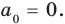
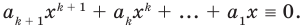

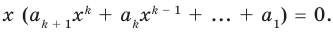
Равенство (4) должно выполняться при всех значениях 
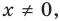
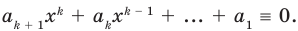
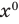
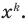
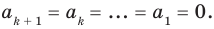
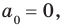
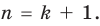
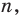
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 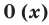
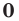
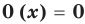
Теорема 3. Если два многочлена 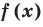
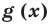
Пусть многочлен 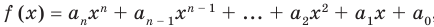
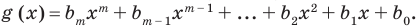
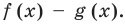
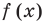
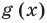
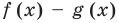
Но 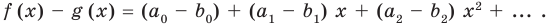
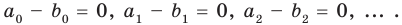
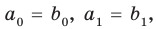
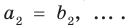
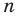
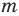
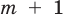
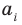
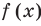
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
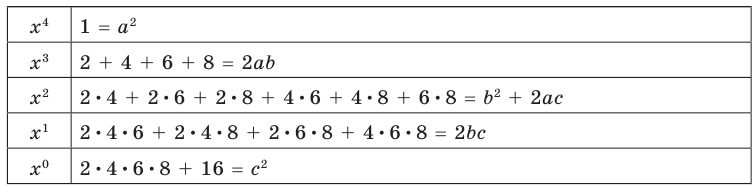
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 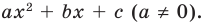
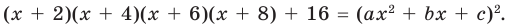
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 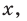
Из первого равенства получаем 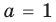
При 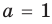
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 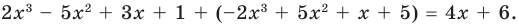
Например, 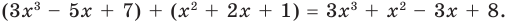
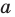
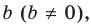
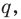
Определение: Многочлен 
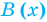
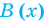

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 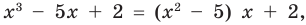
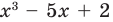
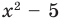
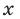
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 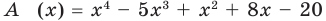
Решение:
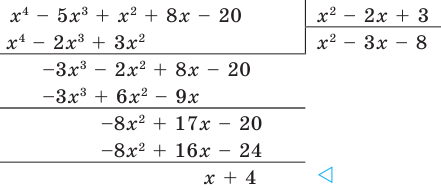
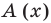
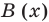
Если обозначить результат выполнения первого шага алгоритма через 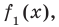
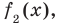
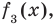
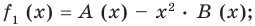
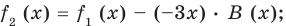
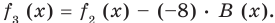
Сложим почленно равенства (1), (2), (3) и получим
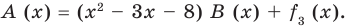
Учитывая, что степень многочлена 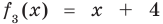
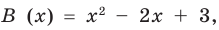
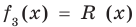
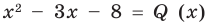
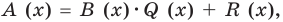
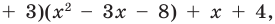
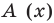
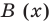
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 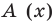
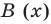
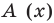
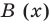
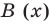
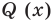
Отметим, что в случае, когда степень делимого 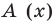
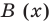
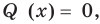
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 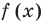
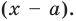
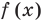
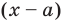
Это равенство выполняется тождественно, то есть при любом значении 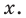
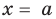
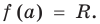
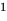
Теорема 1 (теорема Безу). Остаток от деления многочлена 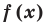
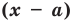
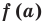
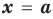
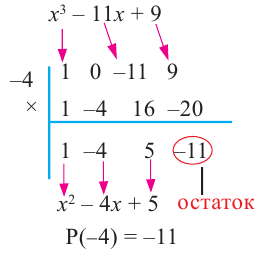
Пример №2
Докажите, что 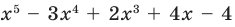
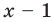
Решение:
► Подставив в 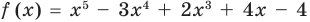
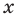
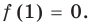
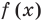

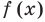

Определение: Число 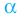
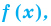
Если многочлен 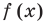

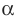
Действительно, если 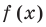
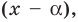

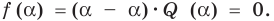
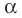
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 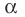
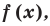
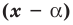
По теореме Безу остаток от деления 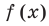

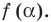
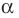
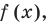
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 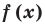
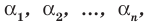
Для доказательства используем метод математической индукции.
При 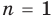
Допустим, что утверждение справедливо при 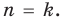
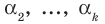
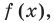
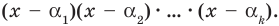
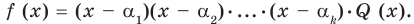
Докажем, что утверждение теоремы справедливо и при 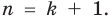
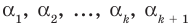
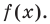
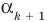
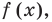
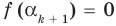
По условию все корни 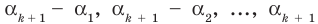
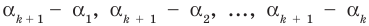
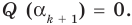
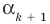
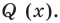
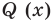
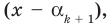
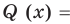
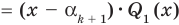
Это означает, что 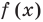
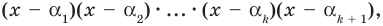
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 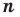
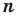
Допустим, что многочлен 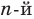
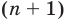
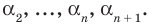
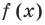
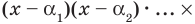
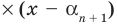
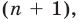
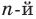
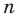
Пусть теперь многочлен 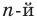
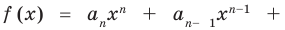
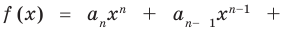
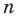
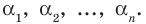
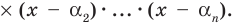
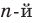
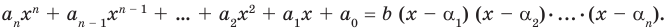
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 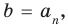
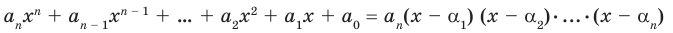
Сравнивая коэффициенты при одинаковых степенях 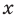
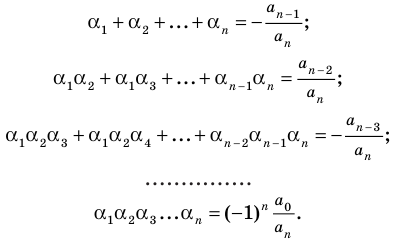
Например, при 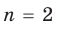
а при
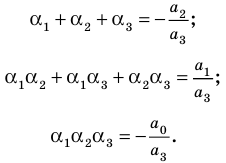
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 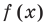
Если многочлен 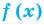
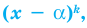
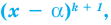


Например, если произведение 
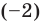
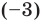
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
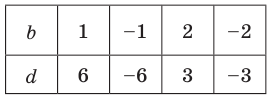
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 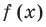
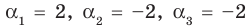
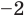
Проверим справедливость формулы (5). В нашем случае: 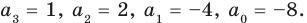
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 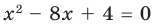
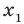
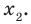
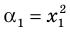
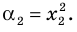
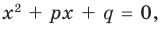
По формулам Виета имеем 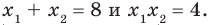
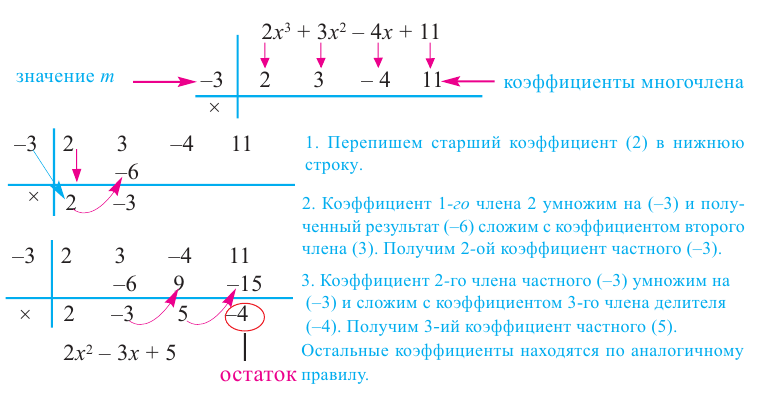
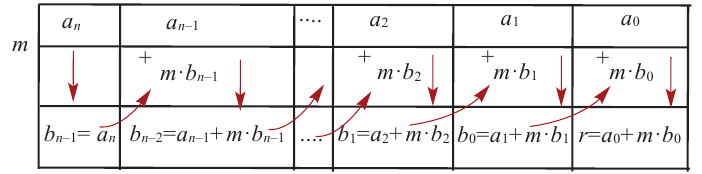
Схема Горнера
Делить многочлен 
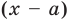
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 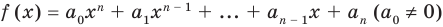
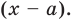
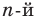
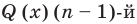
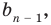
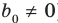
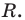
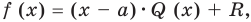
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 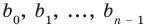
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 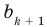
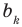
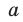
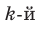
Пример №5
Разделите по схеме Горнера многочлен 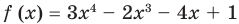
Решение:
► Запишем сначала все коэффициенты многочлена 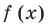
Таким образом,
Пример №6
Проверьте, является ли 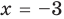
Решение:
► По теореме Безу остаток от деления многочлена 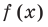
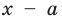
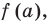
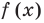
Поскольку 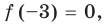
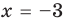
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 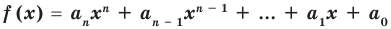
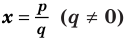
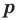
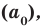
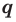
Если 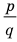
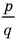
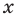
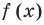
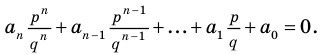
Умножим обе части равенства (1) на 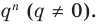
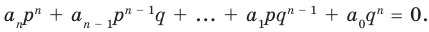
В равенстве (2) все слагаемые, кроме последнего, делятся на 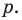
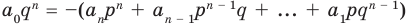
Но когда мы записываем рациональное число в виде 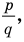
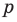
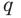
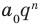
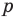
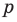
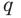
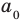
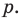
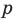
Аналогично все слагаемые равенства (2), кроме первого, делятся на 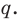
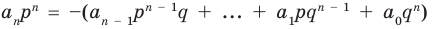
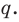
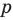
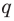
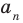
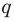
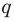
Отметим два следствия из этой теоремы. Если взять 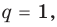
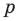
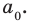
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 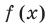
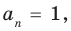
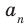
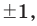
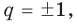
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
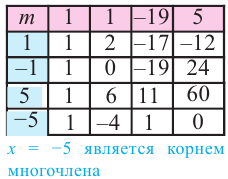
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 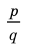
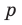
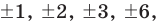
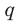
Таким образом, рациональные корни многочлена необходимо искать среди чисел 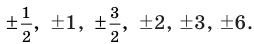
При 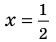
Кроме того, по схеме Горнера можно записать, что
Многочлен 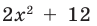
Пример №8
Разложите многочлен 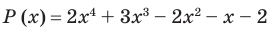
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 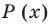

Тогда
Ищем целые корни кубического многочлена 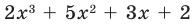
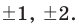
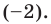
Имеем
Квадратный трехчлен 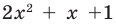
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 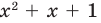
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
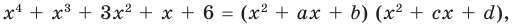
где 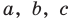
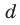
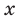
Получаем систему
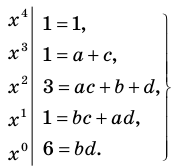
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 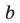
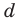
Коэффициенты 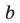
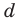
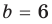
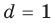
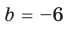
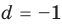
Для каждой пары значений 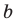
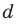
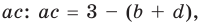
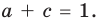
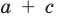
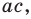
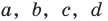
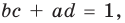
Как видим, системе (4) удовлетворяет набор целых чисел 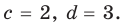
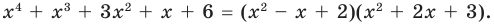
Поскольку квадратные трехчлены 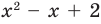
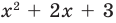
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 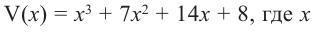
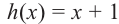
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 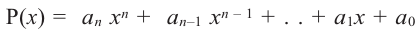
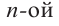
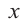
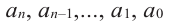
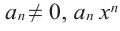
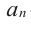
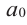
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 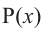
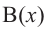
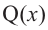
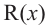
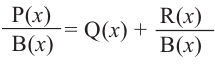
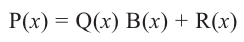
Здесь, степень многочлена 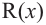
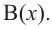
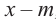
В этом случае:
Пример №10
а) Разделите многочлен 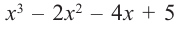
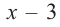
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 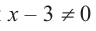
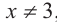
c) Должно выполняться тождество
Пример №11
Разделите 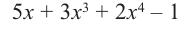
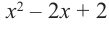
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 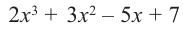
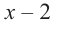
2) На каждом шаге деления делимое делится на старший член делителя, на 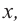
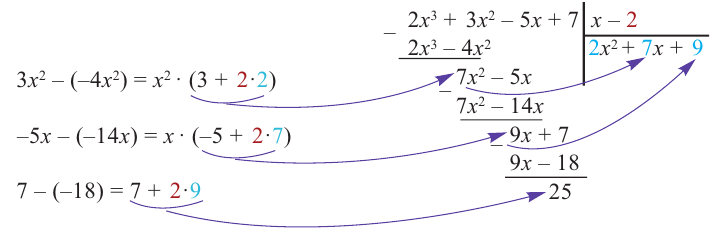
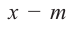
При делении многочлена на двучлен вида 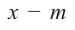
Пример №13
Разделите многочлен 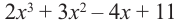
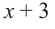
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 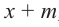
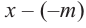
Запишем двучлен 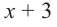
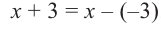
Таким образом, для делимого 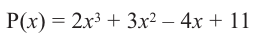
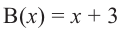
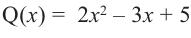
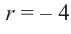
Деление можно записать в виде: 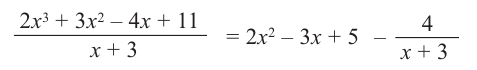
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 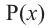
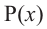
Доказательство: В равенстве 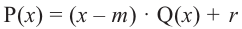
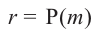
Пример №14
Найдите остаток от деления многочлена 
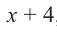
Решение: запишем делитель в виде 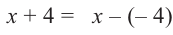
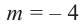
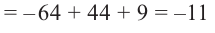
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 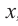
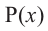
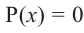
Теорема. Если число 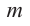
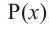
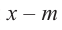
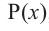
Действительно, если 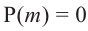
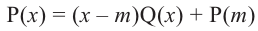
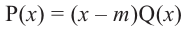
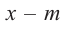
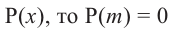
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 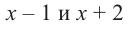
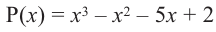
Решение: вычислим значение многочлена 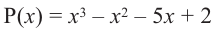
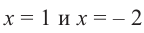
Значит, 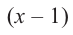
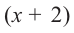
Пример №16
Зная, что 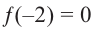
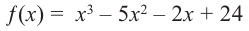
Решение: так как 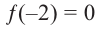
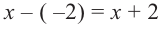
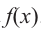
Учитывая, что 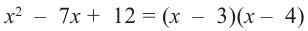
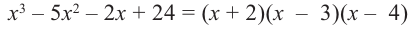
Отсюда получаем, что 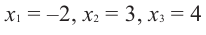
Примечание: Если многочлен задан в виде 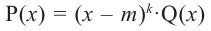
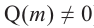
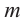
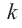
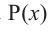
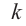
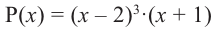
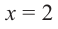
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 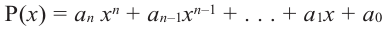
Доказательство. Пусть несократимая дробь 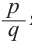
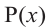
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 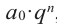
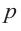
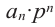
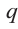
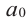
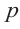
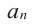
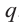
Пример №17
Найдите рациональные корни многочлена 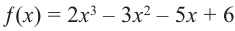
Решение: свободный член 6, старший коэффициент 2.
Для 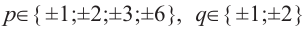
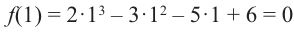
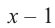
Так как, 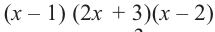
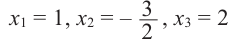
Следствие 1. Если старший коэффициент 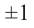
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 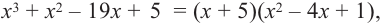
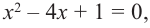
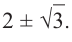
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 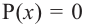
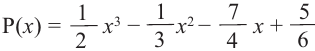
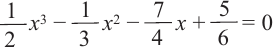
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 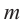
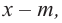
3. Для данного многочлена при помощи синтетического деления на двучлен 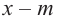
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 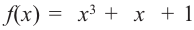
Проверим: 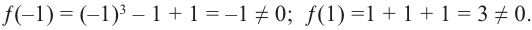
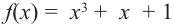
Основная теорема алгебры
Покажем на примере, что многочлен 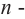
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 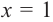
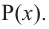
В выражении 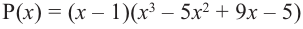
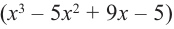
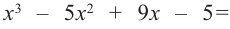
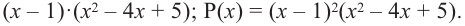
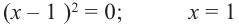
Корни:
Во всех рассмотренных нами примерах уравнение 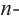
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 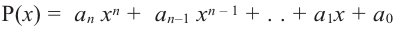
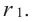
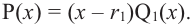
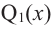
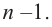
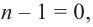
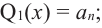
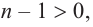
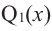
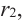
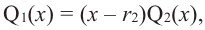
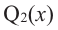
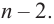
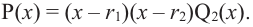
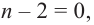
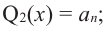
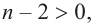
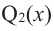
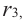
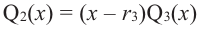
Продолжая процесс 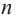
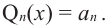
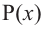
здесь числа 
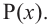
Следствие. Многочлен 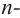
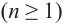
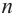
Отметим, что если комплексное число 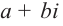
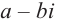
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 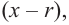
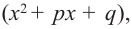
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 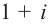
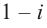
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 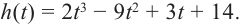
Решение: во всех случаях, кроме значений 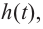
1. Проверим, является ли число 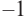
2. Число 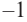
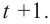
Учитывая, что 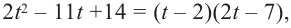
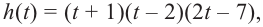
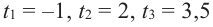
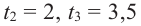
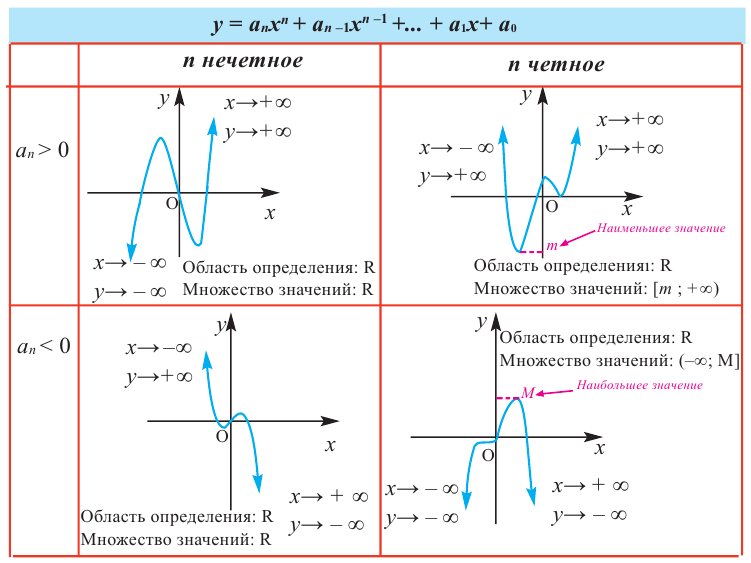
Функция-многочлен
График функции-многочлен
В стандартном виде функция — многочлен записывается как 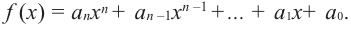
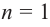
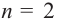
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 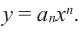
Пример №22
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 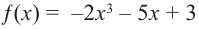
Решение: а) степень многочлена 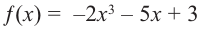
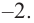
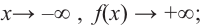
b) степень многочлена 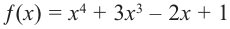
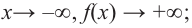
Пример №23
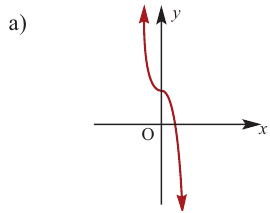
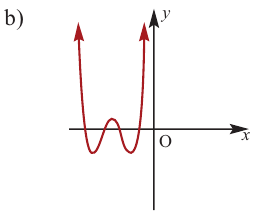
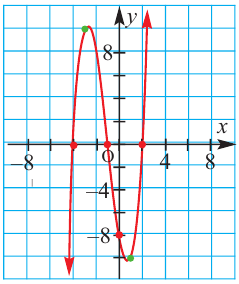
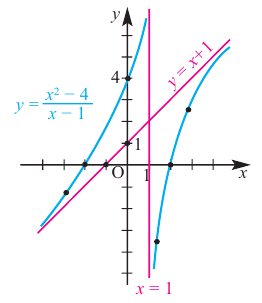
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 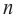
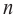
Алгоритм построения эскиза графика функции — многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 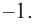
Значит, двучлен 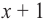
Зная, что 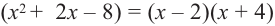
Отсюда находим нули 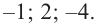
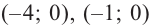
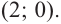
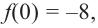
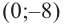
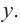
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 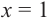
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 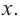
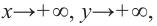
4. Соединим отмеченные точки и получим схематический график функции
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
Самым простым примером рациональной функции является функция
График функции 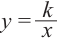
При стремлении значений 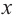
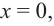
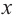
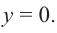
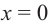
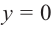
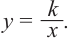
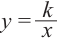
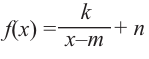
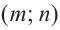
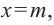
Пример №25
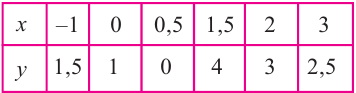
Постройте график функции
Решение: точки пересечения с осью 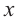
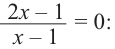
При 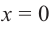
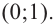
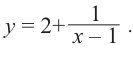
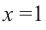
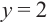
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 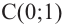
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 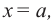
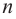
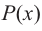
Для 
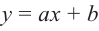
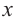
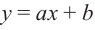
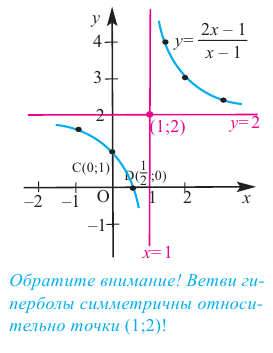
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 
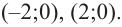
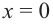
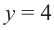
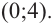
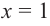
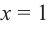
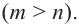
Для больших, но модулю, значений 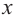
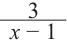
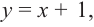
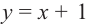
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
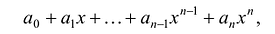
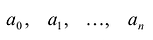
Если коэффициент 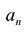
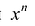
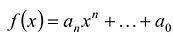
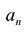
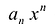
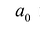
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 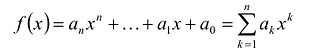
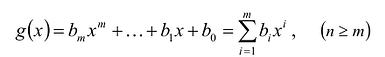
Произведением многочленов 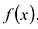
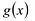
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 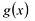
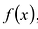
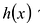
Теорема о делении с остатком
Для любых многочленов 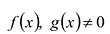
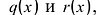
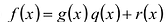
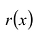
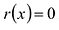
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
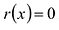
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с — корень многочлена 


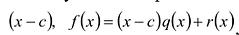
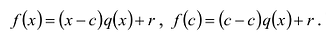

Обратно, пусть (х-с) делит 
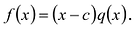
Следствие. Остаток от деления многочлена 
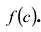
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 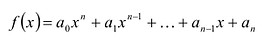
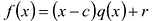
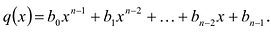
Число с-называется корнем кратности к многочлена 
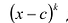

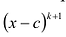

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 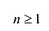
где 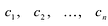

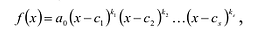
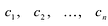

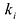
Если многочлен 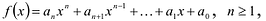
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 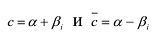


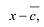
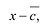

Утверждение 2. Многочлен с действительными коэффициентами степени 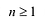
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где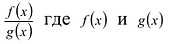
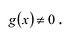

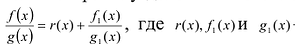
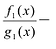
Лемма 1, Если 
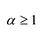
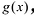
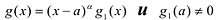
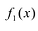
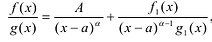
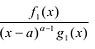
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
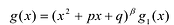
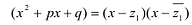
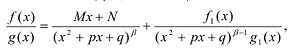
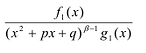
Рациональные дроби вида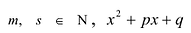
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 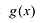
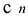
Число неизвестных 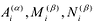
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
План урока:
Многочлен, вычисление значений многочлена
Стандартный вид многочлена
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Многочлен, вычисление значений многочлена
В предыдущем уроке мы познакомились с понятием одночлена. При записи одночленов не используется операция сложения. Если же возникает необходимость сложить несколько одночленов, то в результате получается многочлен.
В качестве примера многочленов можно привести следующие выражения:
Стоит обратить внимание, что в записи многочлена может использоваться и знак минус, при этом его всё равно можно считать суммой одночленов, а не разностью. Дело в том, что можно условно считать, что знак минус относится к коэффициенту одночлена, например:
Для некоторых видов многочленов существуют особые названия. Если многочлен состоит из двух одночленов, то его называют двучленом. Многочлен, состоящий из 3 одночленов, называют трехчленом.
Иногда в литературе используются такие термины, как «моном» (синоним «одночлена»), «бином» (синоним «двучлена»), «полином» (синоним «многочлена»).
Если известно значение переменных, входящих в полином, то возможно вычисление значения многочлена.
Пример. Найдем значение полинома x3+2x2+5y+1 при значении x=2 и y = 3.
Решение.
Пример. Вычислим значение полинома v4– d4при значении переменных v = 4 и d = 3.
Решение.
Стандартный вид многочлена
Иногда некоторые мономы, входящие в состав полинома, имеют одинаковую буквенную часть. Например, в выражении
первый и третий мономы отличаются лишь своими коэффициентами. Такие слагаемые называются подобными.
У подобных слагаемых одинаковый набор переменных, и при этом они возведены в одинаковые степени. Так, подобными являются мономы:
- 7a2s3 и 2a2s3, так как совпадает буквенная часть a2s3;
- 5v9m7t5 и – 4v9m7t5, так как у них одинаковая буквенная часть – 4v9m7t5;
- a2 и 1000a2, так как есть одинаковая буквенная часть a2.
Также подобными слагаемыми можно считать и числа без буквенной части, например 8 и 2.
В качестве примеров неподобных слагаемых можно привести:
- 7a2s3и 2a2s4 – у переменной s разные степени (3 и 4) в этих мономах;
- 4x2yи 5x2– в буквенной части первого монома есть переменная y, а у второго его нет.
У подобных слагаемых может быть изменен порядок множителей. Так, подобными являются мономы 5p2u4и 9u4p2, так как у одних и тех же переменных стоят одинаковые показатели.
Подобные слагаемые можно складывать друг с другом. В этом случае буквенная часть останется неизменной, а коэффициенты сложатся друг с другом. Например:
Такое действие называется приведением подобных слагаемых.
Пример. Приведите подобные слагаемые полинома:
Решение. В данном полиноме есть три пары подобных слагаемых:
Сгруппируем подобные слагаемые друг с другом, после чего сложим их:
Если в полиноме нет подобных слагаемых, а все входящие в него мономы записаны в стандартном виде, то его называют многочленом стандартного вида.
Что такое одночлен стандартного вида, можно узнать из ранее изученного урока. Примерами полиномов стандартного вида являются:
Далее рассмотрим понятие степени многочлена. Каждый из входящих в полином мономов имеет свой показатель степени(см. урок 3). Степенью полинома стандартного вида называется наибольшая из всех степеней одночленов, входящих в его состав.
Рассмотрим пример. Дан трехчлен 2y2 + x3y + 5y2x, требуется найти его степень.
Решение. Рассматриваемый трехчлен находится в стандартном виде. Он состоит из трех мономов:
Найдем степень каждого из них:
- 2y2 – степень равна 2;
- x3y – степень равна 4 = (3+1);
- 5y2x – степень равна 3 = (2+1).
Получается, что максимальную степень, равную 4, имеет моном x3y. Соответственно, и степень трехчлена также равна 4.
Ответ: 4.
Если же рассматривается полином, не находящийся в стандартном виде, то для вычисления его степени сначала надо привести полином к этому виду.
Пример. Найдите степень полинома с6 + ac2 + 9 – с6.
Решение. На первый взгляд может показаться, что она равна 6, так как один из его мономов, с6, имеет показатель, равный 6. Но это не так. Приведем полином к стандартному виду:
Оказалось, что подобные мономы c6 и – с6 сократились. Получившийся полином состоит из двух мономов, ac2 и 9, чьи степени равны 3 и 0 соответственно. Значит, и степень всего двучлена равна трём.
Ответ: 3.
Определение степени полинома потребуется для решения уравнений в старших классах. Если в одной части уравнения стоит полином, например, третьей степени, в другой части – ноль, то его называют уравнением третьей степени:
Аналогично выделяют уравнения первой, второй, четвертой и любой другой степени.
В зависимости от степени уравнения используются различные методы их решения. Ранее (ссылка на урок уравнения) мы уже научились решать линейные уравнения, которые являются уравнениями 1-ой степени. Обычно чем выше степень уравнения, тем сложнее его решать. Также существует интересная зависимость – количество корней уравнения не превышает его степень (за исключением одного частного случая, при котором есть бесконечное множество решений).
Особое значение в алгебре имеют те полиномы, в которых содержится только одна переменная, например:
- m2 + 4m4 + 5m3 +9(здесь переменная m);
- c6 + 1(единственная переменная – с);
- 3x + 10(запись содержит только x);
- – y4 + 89y10– 2,56y100(используется только y).
Их называют полиномами с одной переменной. Обычно их принято записывать по мере убывания степеней одночленов. То есть впереди пишется моном с максимальной степенью, а в самом конце – число без буквенной части:
То число, которое стоит перед одночленом в наибольшей степени, называют старшим коэффициентом, а число, не имеющее буквенной части – свободным членом (реже свободным коэффициентом):
Для некоторых полиномов с одной переменной есть особое название. Так, многочлен второй степени называют квадратным трехчленом. Дело в том, вторую степень в математике часто называют квадратом, а состоит квадратный трехчлен из трех монов. В качестве примера можно привести:
Конечно, квадратный многочлен может содержать и меньше трех одночленов:
В этом случае иногда бывает удобно добавить «недостающее» слагаемое, поставив перед ним коэффициент, равный нулю:
В общем случае квадратным трехчленом называют выражение вида
где x – произвольная переменная, а, b и c являются произвольными действительными числами. При этом a не должно равняться нулю, иначе получится полином уже только 1-ой степени.
Квадратные трехчлены будут изучены подробнее в старших классах при изучении темы «Квадратные уравнения».
Сложение и вычитание многочленов
Полиномы можно складывать друг с другом, а также вычитать. При этом, возможно, придется приводить подобные слагаемые.
Пример. Произведите сложение многочленов 8z2 + 3z +12 и 2z4 + 9z.
Решение. Запишем интересующую нас сумму:
Если перед скобками стоит знак «+», то можно просто опустить скобки:
Осталось привести полином к стандартному виду. Здесь есть лишь одна пара подобных одночленов, 3z и 9z:
При вычитании многочленов надо учитывать следующее правило:
Пример. Вычтите из полинома x5 + 3x3– 7y3 + 9x2 + 17 трехчлен 2y4 + 0,4y3– 25.
Решение:
Запишем разность полиномов:
Первые скобки можно опустить, так как перед ними нет никакого знака. Перед вторыми скобками стоит минус, а потому для раскрытия скобок знаки слагаемых в них надо поменять на противоположные. Вместо 2y4 надо написать – 2y4, вместо 0,4y3 поставим – 0,4y3, а – 25 заменим на + 25:
Осталось привести подобные слагаемые:
Стоит заметить, что при сложении и вычитании полиномов их степени не могут увеличиться. Так, если складываются два полинома 5-ой и 4-ой степени, то в результате получится многочлен, чья степень будет не больше 5.
Рассмотрим более сложный пример с вложенными (внутренними) скобками. Необходимо упростить выражение
Решение. Раскроем первые скобки. Перед ними стоит минус, поэтому знаки слагаемых должны поменяться на противоположные. Однако обратите внимание, что здесь есть вложенные скобки (2a2b – ab) и (ab2 + 2a2b). Менять следует только знак перед ними, а знаки внутри вложенных скобок не меняются! Они рассматриваются как единые, неизменяемые слагаемые:
Теперь раскроем оставшиеся две скобки:
Приведем подобные слагаемые. Для наглядности пары подобных мономов подчеркнуты. Одной чертой подчеркнуты мономы с буквенной частью ab2, двумя чертами – мономы с a2b, а штриховой линией выделены мономы с буквенной частью ab:
Умножение одночлена на многочлен
Напомним распределительный закон умножения:
Используя этот закон, можно производить умножение одночлена на многочлен.
Пример. Перемножьте выражения 5v2 и 9v3 + 2t4.
Решение: Запишем произведение выражений:
Такое раскрытие скобок можно объяснить с помощью «метода фонтанчика»:
От множителя 5v2 строят линии (синего цвета к) КАЖДОМУ слагаемому в скобке. Каждой такой линии соответствует отдельное произведение в получаемом полиноме.
После раскрытия скобок получили два произведения одночлена на одночлен, которые считаем по отдельности (см. урок 3):
Можно сформулировать следующее правило умножения многочлена на одночлен:
Ещё один пример. Перемножьте полином 2x2y + 4xy2 – 1 и моном – 3ху.
Решение:
Здесь метод «фонтанчика» будет выглядеть так:
Можно заметить, что после умножения монома на полином получится столько одночленов, сколько их было в исходном полиноме. Это правило можно использовать для самоконтроля.
Умножение многочлена на многочлен
Пусть нам надо перемножить два полинома, a+bи c+d. Запишем их произведение:
Заменим выражение a + b переменной k:
Теперь исходное произведение можно выразить как произведение монома и полинома:
Проведем обратное преобразование, заменив k на a + b:
Наконец, раскроем скобки в этом выражении:
Эту формулу можно проиллюстрировать геометрически. Рассмотрим прямоугольник со сторонами a + b и c + d:
Площадь этого прямоугольника, как и любого другого, равна произведению его сторон, то есть(a + b)(c + d).С другой стороны, она состоит из 4 прямоугольников, чьи площади также вычисляются как произведения их сторон, и составляют ac, bc, ad и bd. Поэтому можно записать равенство
Получается, что для умножения многочлена на многочлен нужно перемножать попарно все мономы, входящие в их состав, после чего сложить их.
Если в одном полиноме содержится m слагаемых, а в другом n, то результатом их перемножения окажется новый полином, содержащий m•n мономов (до приведения подобных слагаемых). Для перемножения многочленов также используется метод «фонтанчика».
Пример. Найдем произведение выражений 3a2 – 4ab + b2и 2a– b.
Решение: В первом полиноме содержится 3 монома, а во втором – 2, поэтому после их перемножения мы получим сумму 3•2 = 6 одночленов:
Раскрытие скобок «фонтанчиком» будет выглядеть так:
В результате действительно получилась сумма 6 мономов. Осталось вычислить каждый из них, после чего привести подобные слагаемые:
Заметим, что при перемножении полиномов происходит сложение степеней многочленов. Действительно, в рассмотренном выше примере мы умножили полином второй степени 3a2 – 4ab + b2 на полином первой степени 2a– b, и получили в результате многочлен 3-ей (2+1) степени.
Также возможно умножение многочленов в столбик. Особенно это удобно делать в случае с полиномами с одной переменной.
Пример. Найдите произведение выражений 2x3 + 3x2 +5x + 9 и x2 + 4x + 7.
Решение: Запишем полиномы в столбик, один под другим:
Далее умножим самый правый моном второго многочлена, то есть число 7, на первый полином, и запишем его ниже:
Далее умножим следующий моном, 4х, на первый полином, и запишем результат ещё ниже, причем сместим запись чуть влево, чтобы подобные члены оказались друг под другом:
Также умножим последний одночлен, x2, на первый полином:
Осталось сложить подобные слагаемые (то есть переменные х с одинаковыми степенями), которые записаны друг под другом:
Ещё раз цветом выделим подобные слагаемые и результаты их суммирования:
Ответ: 2х5 + 11х4 + 31х3 + 50х2 + 71х +63.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.
При умножении одночлена на многочлен используется распределительное свойство умножения:
a(b + c) = ab + ac,
правило умножения степеней с одинаковыми основаниями:
ax · ay = ax + y
и правило знаков при умножении.
Произведением одночлена и многочлена будет многочлен.
Пример 1. Умножить одночлен -5a на многочлен 3a + 4b2.
Решение: Составим произведение одночлена и многочлена и с помощью распределительного свойства умножения раскроем скобки:
Теперь осталось выполнить умножение одночленов друг на друга:
-5a · 3a + (-5a) · 4b2 = -15a2 — 20ab2.
Так как в получившемся результате нет подобных членов, то многочлен -15a2 — 20ab2 — это окончательный результат умножения одночлена -5a на многочлен 3a + 4b2.
Пример 2. Выполните умножение многочлена x — xy + 2 на одночлен 2y.
Решение: Составим произведение многочлена и одночлена:
(x — xy + 2)2y.
Для удобства можно записать одночлен перед многочленом, используя переместительное свойство умножения. После этого раскроем скобки:
Теперь надо перемножить одночлены:
2y · x — 2y · xy + 2y · 2 = 2xy — 2xy2 + 4y.
Решение данного примера можно записать короче, не выписывая промежуточные результаты:
(x — xy + 2)2y = 2xy — 2xy2 + 4y.
Пример 3. Упростите выражение:
3x2 — x(4x — 6y).
Решение: Раскроем скобки, выполнив умножение —x на 4x — 6y, и затем сделаем приведение подобных членов (если они будут):
3x2 — x(4x — 6y) = 3x2 — 4x2 + 6xy = -1x2 + 6xy.
Так как получившийся в результате многочлен является алгебраической суммой, то его можно записать так:
6xy — 1x2.