Описание презентации по отдельным слайдам:
-
1 слайд
Урок математики
2 класс
Тема: Множество чисел
Пересечение множествОШ им.С.Т.Ельгизекова
учитель начальных классов
Трусова С.Ю. -
2 слайд
МОТИВАЦИЯ
— Что такое МНОЖЕСТВО?МНОЖЕСТВО– это группа предметов или явлений, у которых есть что – то общее: признак, свойство, качество, действие или еще что –то.
— Любое множество состоит из отдельных элементов.
-
3 слайд
МНОЖЕСТВА
6
79
5
А н тЖ о м
К я е
папа мама
каша молоко
хлеб ложка
ЧИСЕЛ
БУКВ
ГЕОМЕТРИЧЕСКИХ ФИГУР
СЛОВ -
4 слайд
Мотивация
Казахстан объединил под своим шаныраком людей разных национальностей, с разной культурой. Мы живем в стране, которую люди разных народов считают своей Родиной. А их язык, культура, обычаи составляют неповторимое лицо нашей страны, ее богатство. Н.А. Назарбаев -
5 слайд
30, 27, 24, …, …
НАЙДИ ЗАКОНОМЕРНОСТЬ
И ПРОДОЛЖИ РЯД -
6 слайд
РАБОТА С УЧЕБНИКОМ
стр.54 № 1 -
7 слайд
РАБОТА С УЧЕБНИКОМ
стр.54 №1 -
8 слайд
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
-
-
10 слайд
ДАЙТЕ НАЗВАНИЕ ПЕРЕСЕЧЕНИЮ МНОЖЕСТВ
-
11 слайд
РАБОТА С УЧЕБНИКОМ
стр.55 № 2 -
12 слайд
РАБОТА С УЧЕБНИКОМ
стр.55 № 3
САМОСТОЯТЕЛЬНАЯ РАБОТА -
-
14 слайд
ПОВТОРЕНИЕ РАНЕЕ ИЗУЧЕННОГО
УЧЕБНИК стр.55 № 4 (б)
вычисли -
15 слайд
ДОМАШНЕЕ ЗАДАНИЕ
стр.55 № 5 -
16 слайд
РЕФЛЕКСИЯ
На сегодняшнем уроке
— я понял,
— я узнал,
— я разобрался…;
«Я похвалил бы себя за …»;
«Особенно мне понравилось …»;
«Сегодня мне удалось…» -
Цели:
- Ввести понятие «множество».
- Ввести понятие «элементы множества».
- Научить определять принадлежность элемента множеству.
Предварительная подготовка:
- Принести мяч.
- Принести картинки, на которых изображены предметы с общим названием (можно использовать карточки детского лото).
Ход урока
— Ребята, сегодня на уроке мы с вами узнаем, что такое «множество» и что называют «элементами множества»!
— У меня на доске нарисован мешок. Пока он пуст. Давайте соберем в него зверей, которых вы знаете.
Игра:
Учитель ходит с мячом по классу и кидает ученику мяч, а ученик должен быстро назвать какого-либо зверя.
-А теперь давайте всех названных зверей соберем в наш мешок.
Дети вспоминают, а учитель выписывает на доске всех названных в игре зверей (или использует карточки с магнитом).
— Много в мешке получилось зверей?
— Много.
— В математике такую группу предметов (или живых существ) с общим названием и собранных вместе называют «множеством». «Множество» от слова МНОГО. (Слайд 3,4)
— Попробуйте дать название множеству.
«Назови множество»:
Учитель показывает картинки с однородными предметами. Дети должны дать название этому множеству, например – рыбы, птицы, растения, книги.
— Это множество рыб. (Слайд 5)
— Это множество птиц. (Слайд 6)
— Давайте выполним задание №1 в тетради.
Задание №1. (Слайд 7)
Ученики должны назвать и подписать название предлагаемых множеств.
Множество: посуды, животных, обуви, игрушек, банных принадлежностей, предметов для рисования.
— Теперь давайте поиграем.
Игра «Назови множество» (Слайды 8,9,10)
Учитель перечисляет ряд предметов, а ученики придумывают название этому множеству.
— платье, брюки, шуба, юбка, кофта, куртка… — одежда.
(- шкаф, стул, стол, диван, тумбочка… — мебель.)
— береза, сосна, ель, тополь, дуб, ива… — деревья.
(- Москва, Одесса, Лондон, Париж, Санкт-Петербург… — города.)
— стрекоза, кузнечик, бабочка, муха, пчела… — насекомые.
После игры на доске появляется еще один мешок, в котором перечислены названия предметов, но нет общего названия. Его дети должны придумать сами. Например, сапоги, валенки, кроссовки, ботинки, тапочки.
— Это множество обуви.
— Все предметы из этого множества называют элементами этого множества. (Слайд 11,12)
— Выполним задание №2.
Задание №2.(Слайд 13)
При выполнении задания для каждой картинки следует проверить каждое предлагаемое слово.
— Можно сказать, что на лугу пасется стая коров?
— Нет
— А рой коров?
— Нет
— А букет коров?
-Нет
-Значит, для коров, пасущихся на лугу, подходит только слово «стадо».
Аналогично для остальных картинок перебираются возможные варианты, и выбирается подходящее слово.
— Итак, для некоторых групп предметов есть определенные слова, называющие эти группы, например, «стадо коров». Но сказать «рой коров» уже нельзя. Но зато любую группу предметов, собранных вместе, можно назвать «множеством»: множество коров, множество рыб, множество цветов.
— Сейчас снова будем играть. Для игры нам понадобятся ваши ладошки.
Игра «Найди лишнего» (Слайды 14,15,16)
Учитель называет какое-либо множество и начинает перечислять его элементы. Ученики должны хлопнуть в ладоши, если какой-либо названный предмет не является элементом заданного множества.
— Мы идем по парку и видим деревья: березу, дуб, розу (хлопок), тополь, сосну, ромашку (хлопок), ель, сирень (хлопок)…
— Мы заходим в магазин и покупаем овощи: помидоры, картошку, апельсины (хлопок), морковь, колбасу (хлопок), огурцы, свекла, яблоки (хлопок)…
— В спортивном зале мы видим спортивные принадлежности: мяч, лыжи, гантели, кресло (хлопок), теннисные ракетки, расческу (хлопок), коньки, стул (хлопок)…
— Выполняем задания в тетради.
Задание №3. (Слайд 17)
Ученики должны определить предмет, который мешает назвать множество остальных предметов.
— В клетке находится множество птиц, а кролик среди них является лишним.
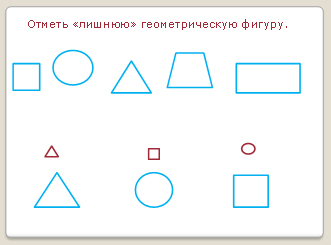
Задание №4. (Слайд 18)
Аналогично предыдущему.
— Почему Незнайка вычеркнул круг?
— Потому что все остальные предметы с углами.
— А если оставить круг в начальном множестве, то какая другая фигура может быть лишней и почему?
— Лишним может быть прямоугольник, как серая фигура.
Задание №5. (Слайд 19)
Из заданного множества дети должны выделить элементы названных множеств: овощей и фруктов. Исследуется каждый предмет: если это овощ – подчеркивать одной чертой, если фрукт – двумя чертами. Предмет, не входящий ни в одно из названных множеств, подчеркивать не надо.
После этого следует перечислить все полученные множества вслух.
— Множество овощей: картошка, свекла, морковь, огурец, помидор, тыква.
— Множество фруктов: груша, яблоко, апельсин, лимон, ананас.
— Не подчеркнуты: масло, хлеб, колбаса, сыр, мяч.
Задание №6. (Слайд 20)
Главное в задании, чтобы ученик мог назвать выделенное им множество и перечислить его элементы.
— Множество музыкальных инструментов: труба, скрипка, гитара, гармошка, барабан.
— Множество спортивных принадлежностей: гантели, мяч, коньки, ракетка.
— Множество строительных инструментов: пила, пассатижи, отвертка.
— И снова играем. Здесь понадобятся ваши знания.
Игра «Продолжи ряд»:
Учитель перечисляет ряд предметов, а ученики, догадываясь о названии множества по перечисленным предметам, продолжают его своими элементами.
Обязательно в конце каждого этапа подвести итог: что же было перечислено, т.е. дать название множеству.
- сыроежка, мухомор, опенок…(подберезовик, подосиновик, лисичка) – это…множество грибов
- лиса, медведь, слон, бегемот…(волк, заяц, тигр, носорог) – это…множество зверей
- стрекоза, бабочка, кузнечик…(жук, комар, пчела, муха) – это…множество насекомых
- беретка, шляпа, панамка…(платок, кепка, шапка) – это…множество головных уборов
- щука, окунь, сом, плотва…(акула, карась, лещ) – это…множество рыб
Задание №7. (Слайд 21)
Дети выполняют самостоятельно. Можно 1-2 учеников попросить озвучить свои ответы.
— Дорисовал тюльпан, т.к. это множество цветов.
— Ребята, назовите известные вам города (дети перечисляют названия городов).
— Можно городом назвать «Волгу»?
— Нет, это река.
— Можно ли назвать городом Россию?
— Нет, это страна.
Задание №8. (Слайд 22)
Выполняется самостоятельно.
Задание №9. (Слайд 23)
Ученики должны дать название каждому столбцу с тремя предметами (одежда, рыбы, деревья). После чего дуб должен быть вписан в столбец под названием «деревья», т.к. он является деревом.
Аналогично исследуются остальные предметы: окунь, лещ – «рыбы», юбка – «одежда».
|
ОДЕЖДА |
РЫБЫ |
ДЕРЕВЬЯ |
|
Шуба |
Щука |
Береза |
|
Брюки |
Акула |
Ель |
|
Рубашка |
Карась |
Сосна |
|
Юбка |
Окунь |
Дуб |
|
Лещ |
Итог урока:
— Итак, сегодня на уроке мы с вами познакомились с такими понятиями, как «множество» и «элементы множества». Научились определять множество, а также принадлежность элемента заданному множеству.
Карточки с заданиями (Слайды 24-30)
Учащимся раздаются карточки с заданиями в виде тестов на два варианта. Проверяется степень усвоения нового материала.
1 вариант:
2 вариант:
Домашнее задание: (Слайд 31)
№10.
Дети должны нарисовать любое множество предметов с общим названием и подписать название под картинкой.
Литература:
- Методические рекомендации для учителя, 2 класс, А.В.Горячев, К.И.Горина, Н.И.Суворова.
- Информатика в играх и задачах, 2 класс, часть 2. А.В.Горячев, К.И.Горина, Н.И.Суворова.
- Информатика тесты, 2 класс, О.Н.Крылова.
Напиши два множества чисел. В одно множество должны войти числа, которые больше 24 и меньше 32, а в другое − числа, которые больше 28 и меньше 34. Сколько чисел в каждом множестве? Какие числа вошли в оба множества?
reshalka.com
ГДЗ учебник по математике 2 класс Дорофеев. Часть 2. Страница 78. Номер №5
Решение
Получай решения и ответы с помощью нашего бота
Посмотреть калькулятор Вычисления в столбик
Первое множество:
25, 26, 27, 28, 29, 30, 31.
Второе множество:
29, 30, 31, 32, 33.
В первом множестве 7 чисел, а во втором 5 чисел.
В оба множества вошли числа:
29, 30, 31.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
-
А = {а, в, с, у} – А состоит из четырех элементов.
-
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
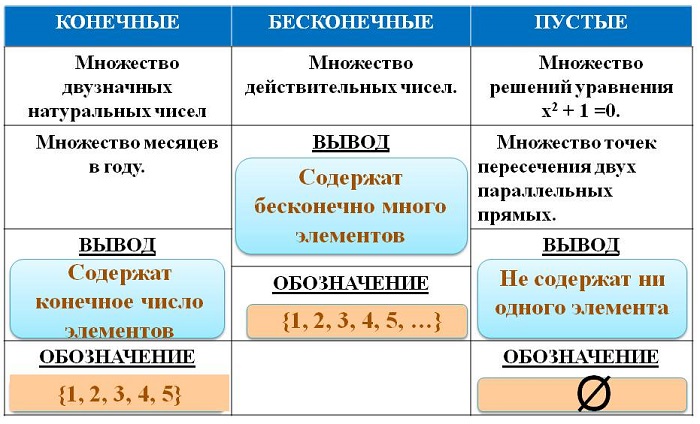
Выделяют три вида множеств:
-
конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
-
бесконечные — не являющиеся конечными (например, числовые);
-
пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
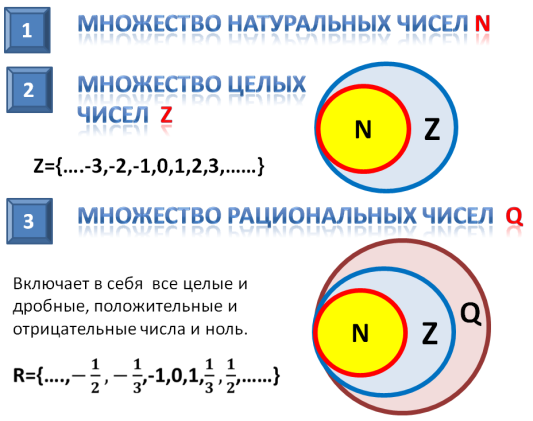
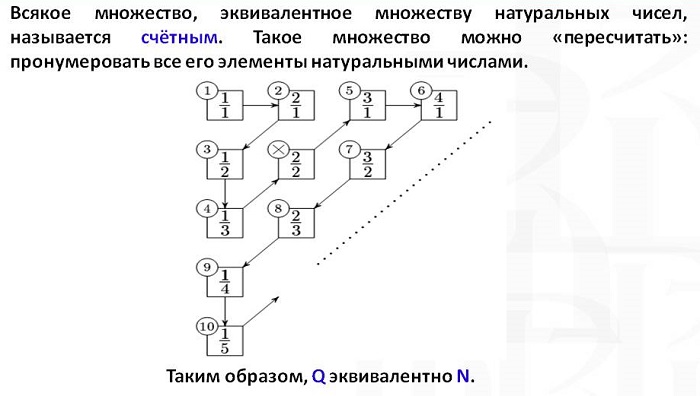
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.
Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.
N = {9, 11, 13, 15……}.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Z = {-112, -60, -25, 0, 36, 58, 256}.
Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Q={-½; 0; ½, 5; 10}.
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
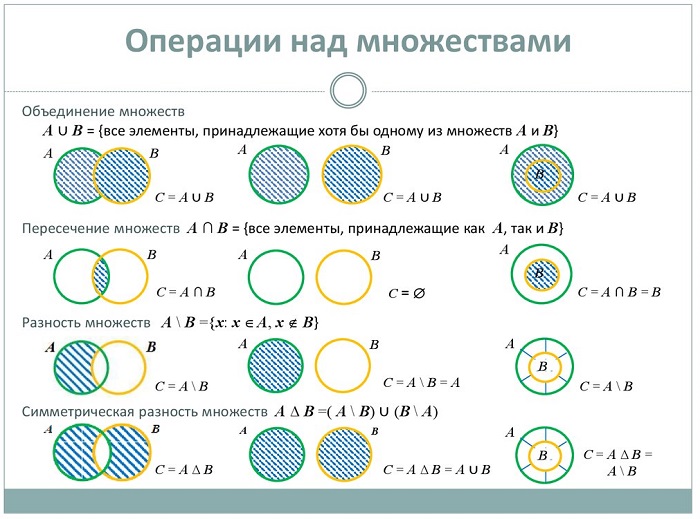
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
-
умножения S ∩ D = D ∩ S;
-
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
-
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
-
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
-
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
-
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
-
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
Транзитивность — законы включения:
-
если S ⊆ Fи F ⊆ J, то S ⊆ J;
-
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
-
S ∩ S = S;
-
S ∪ S = S.
О других свойствах операций можно узнать из картинки:
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.
Множества чисел бывают конечными или бесконечными и их принято обозначать большими буквами A, B, …, а их элементы – маленькими буквами, например, x, y, z,….
Что такое множество чисел
Термин множества чисел можно описать, как совокупность, объединение, набор некоторых объектов произвольной природы – элементы множества. Например, множество книг в библиотеке, множество студентов факультета, множество парных чисел, множество точек заданного отрезка и т. п.
Если элемент принадлежит множеству
, тогда пишут
, если же элемент
не принадлежит множеству
, тогда пишут, что
или
.
Множества, в которых нет ни одного элемента, называется пустым множеством и обозначается .
Рассмотрим несколько важных операций:
1. Два множества и
называются равными (обозначают
), если они состоят из одинаковых элементов.
2. Множество называется подмножным множеством
, если каждый элемент множества
есть элементом множества
.
Это обозначается так: и читается
содержится в
или в
находится
. Очевидно, что пустое множество входит в любое множество
.
Например, если множество состоит из элементов
обозначают:
= {
}), а в
= {
} тогда
.
3. Множества элементов , которые принадлежат множеству
или множеству
, или
и
, называется объединением этих множеств и обозначается
.
4. Множества элементов , которые принадлежат двум множествам
и
называется пересечением множеств
и
и обозначается
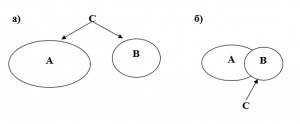
Если, например, и
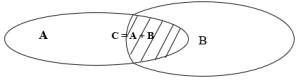
– это множества точек, что принадлежат двум фигурам соответственно, тогда схематически на рис. 1 изображены их объединения в случаях а) и б). На рис. 2 изображено пересечение множеств
и
.
Рис. 1
Рис. 2
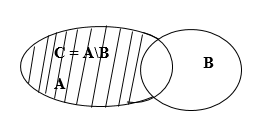
5. Разницей множеств A и называется множество
, что содержит те элементы
, которые не есть элементами множества
(см. рис. 3).
Рис. 3
Виды чисел
Существует 7 видов чисел:
1. Натуральные – ;
2. натуральные числа, в которые включается нуль – ;
3. целые числа – ;
а) целые положительные числа – ;
б) целые отрицательные числа – ;
4. рациональные числа – ;
5. иррациональные числа
6. Действительные числа – ;
7. Комплексные числа – .
Рассмотрим каждый вид числа более подробно:
1. Натуральные числа всегда используются при естественном счёте или перечислении предметов, вернее при их нумерации, то есть “первый”, “второй”, “третий”. Описывается множество натуральных чисел так:
= {1, 2, 3, …, }.
2. Натуральные числа, в которые включён нуль используются для обозначения количества предметов:
= {0, 1, 2, 3, …}
3. Целые числа – это числа, в которые входят натуральные числа с положительным и отрицательным знаками:
а) целые положительные числа (обозначаются ) и пишутся:
{1, 2, 3, …};
б) целые отрицательные числа (обозначаются ) и пишутся:
{…, -3, -2, -1};
= {…, -3, -2, -1, 0, 1, 2, 3, …}.
4. Рациональные числа – числа, которые представляются в виде обыкновенной дроби , где
и
– целые числа, а
. Рациональные числа обозначаются латинской большой буквой
:
= {
}. Если переводить в десятичную дробь, тогда рациональное число может представляться конечной и бесконечной дробью.
5. Иррациональные числа – вещественное число, которое не рациональное и не может представляться в виде десятичной дроби.
6 Действительные числа или вещественные – это числа, в которых объединяются рациональные и иррациональные числа ().
7. Комплексные числа – это числа, в которых содержится – мнимая единица:
= {
и
}.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Примеры решения задач
Задача
Записать множество , если
, причём
= {2, 4, 6, 8, 10, 12},
= {3, 6, 9, 12}.
Решение
есть не что иное, как объединение множеств
и
, то есть, множество
будет состоять из элементов, принадлежащих как множеству
, так и множеству
:
= {2, 3, 4, 6, 8, 9, 10, 12}.
Ответ
Множество состоит из элементов, которые принадлежат двум множествам
и
.
Задача
Все студенты курса изучают разные иностранные языки. Значит, из них, 91 студент изучает английский язык, ещё 96 студентов изучают немецкий язык, 94 студента изучают исключительно французский язык, 36 студентов изучают не только английский, но и немецкий языки, ещё 32 студента изучают английский и французский языки, а 10 студентов занимаются изучением всех языков без исключения.
Вопрос: сколько студентов занимаются изучением немецкого и французского языков, если всего на курсе по списку 189 студентов?
Решение
Итак, для начала введём обозначения:
– множество всех студентов, которые находятся на данном курсе;
– множество студентов, которые изучают только английский язык;
– множество студентов, которые занимаются изучением немецкого языка;
– множество студентов, изучающих исключительно французский язык;
– множество студентов, которые изучают, как английский, так и немецкий язык;
– множество студентов, изучающие английский и французский языки;
– множество студентов, которіе изучают немецкий и французский язіки;
– множество студентов, которые изучают абсолютно все языки;
– количество элементов множества
.
По условию задачи:
Найдём – количество студентов, которые изучают немецкий и французский языки. Согласно вышеописанному обозначению, у нас получается:
,
,
,
.
Из методов включения и исключения следует, что
.
Ответ
студента занимаются изучением немецкого и французского языков.