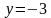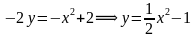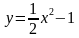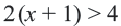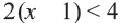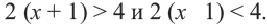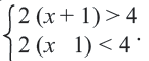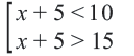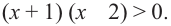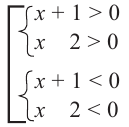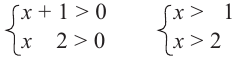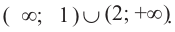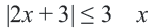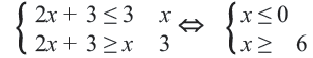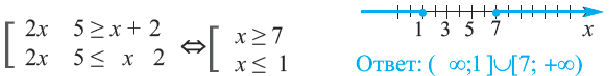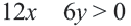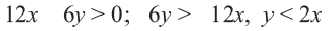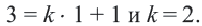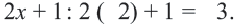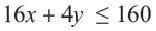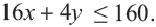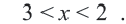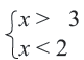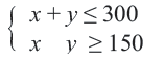В данной статье я отвечаю на очередной вопрос от моих подписчиков. Вопросы приходят разные. Не все из них корректно сформулированы. А некоторые из них сформулированы так, что не сразу получается понять, о чём хочет спросить автор. Поэтому среди огромного множества присылаемых вопросов приходится отбирать действительно интересные, такие «жемчужины», отвечать на которые не просто увлекательно, но ещё и полезно, как мне кажется, для других моих читателей. И сегодня я отвечаю на один из таких вопросов. Как изобразить множество решений системы неравенств?
Это действительно хороший вопрос. Потому что метод графического решения задач в математике — это очень мощный метод. Человек так устроен, что ему удобнее воспринимать информацию с помощью различных наглядных материалов. Поэтому если вы овладеете этим методом, то поверьте, он для вас окажется незаменимым как при решении заданий из ЕГЭ, особенно из второй части, других экзаменов, так и при решении задач оптимизации и так далее, и так далее.
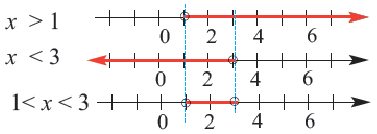
Так вот. Как же нам ответить на этот вопрос. Давайте начнём с простого. Пусть в системе неравенств содержится только одна переменная .
Упростим эту систему. Для этого прибавим к обеим частям первого неравенства 7 и поделим обе части на 2, не меняя при этом знак неравенства, так как 2 — положительное число. К обеим частям второго неравенства прибавим 4. В результате получим следующую систему неравенств:
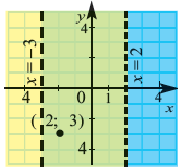
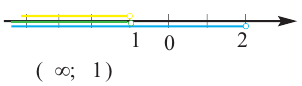
Обычно такую задачу называют одномерной. Почему? Да потому что для того, чтобы изобразить множество её решений, достаточно прямой. Числовой прямой, если быть точным. Отметим точки 6 и 8 на этой числовой прямой. Понятно, что точка 8 будет находиться правее, чем точка 6, потому что на числовой прямой большие числа находятся правее меньших. Кроме того, точка 8 будет закрашенной, так как согласно записи первого неравенства она входит в его решение. Наоборот, точка 6 будет незакрашенной, так как она не входит в решение второго неравенства:
Отметим теперь стрелочной сверху значения , которые меньше или равны 8, как того требует первое неравенство системы, а стрелочкой снизу — значения
, которые больше 6, как того требует второе неравенство системы:
Осталось ответить на вопрос, где на числовой прямой находятся решения системы неравенств. Запомните раз и навсегда. Знак системы — фигурная скобка — в математике заменяет союз «И». То есть, переводя язык формул на человеческий язык, можно сказать, что от нас требуется указать значения , которые больше 6 И меньше или равны 8. То есть искомый промежуток лежит на пересечении отмеченных промежутков:
Вот мы и изобразили множество решений системы неравенств на числовой прямой в случае, если в системе неравенств содержится только одна переменная. В этот заштрихованный промежуток входят все значения , при которых все неравенства, записанные в системе, выполняются.
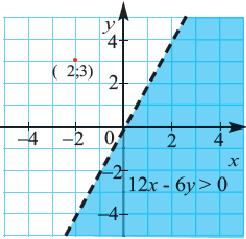
Рассмотрим теперь более сложный случай. Пусть в нашей системе содержатся неравенства с двумя переменными и
. В этом случае обойтись только прямой для изображения решений такой системы не получится. Мы выходим за рамки одномерного мира и добавляем к нему ещё одно измерение. Здесь нам понадобится уже целая плоскость. Рассмотрим ситуацию на конкретном примере.
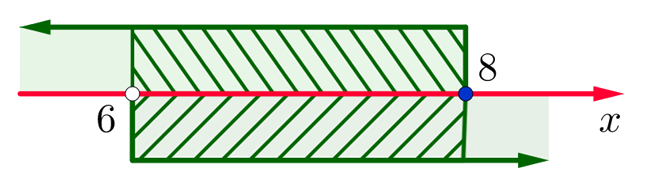
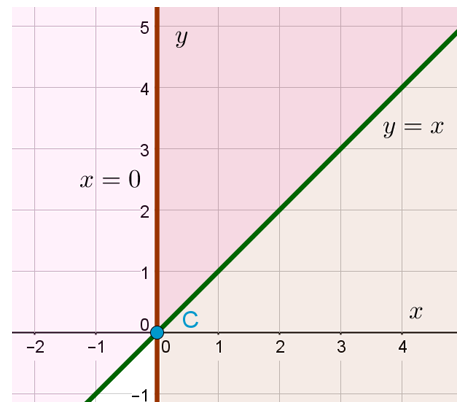
Итак, как же можно изобразить множество решений данной системы неравенств с двумя переменными в прямоугольной системе координат на плоскости? Начнём с самого простого. Зададимся вопросом, какую область этой плоскости задаёт неравенство . Уравнение
задаёт прямую, проходящую перпендикулярно оси OX через точку (0;0). То есть фактически это прямая совпадает с осью OY. Ну а раз нас интересуют значения
, которые больше или равны 0, то подойдёт вся полуплоскость, лежащая справа от прямой
:
Причём все точки, которые лежат на оси OY, нам тоже подходят, потому что неравенство — нестрогое.
Чтобы понять, какую область на координатной плоскости задаёт третье неравенство, нужно построить график функции . Это прямая, проходящая через начало координат и, например, точку (1;1). То есть фактически это прямая, содержащая биссектрису угла, образующего первую координатную четверть.
А теперь посмотрим на третье неравенство в системе и подумаем. Какую область нам нужно найти? Смотрим: . Знак «больше или равно». То есть ситуация аналогична той, что была в предыдущем примере. Только здесь «больше» означает не «правее», а «выше». Потому что OY — это у нас вертикальная ось. То есть область, задаваемая на плоскости третьим неравенством, — это множество точек, находящихся выше прямой
или на ней:
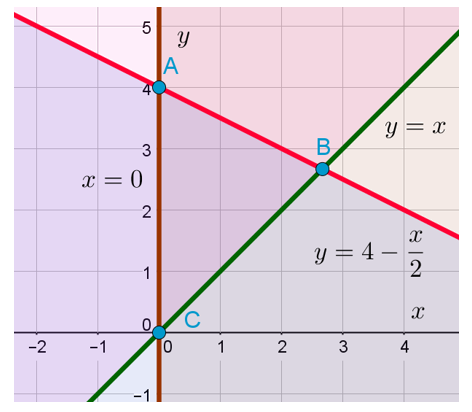
С первым неравенством системы чуть менее удобно. Но после того, как мы смогли определить область, задаваемую третьим неравенством, я думаю, что уже понятно, как нужно действовать.
Нужно представить это неравенство в таком виде, чтобы слева находилась только переменная , а справа — только переменная
. Для этого вычтем из обеих частей неравенства
и поделим обе части на 2, не меняя при этом знак неравенства, потому что 2 — это положительное число. В результате получаем следующее неравенство:
Осталось только изобразить на координатной плоскости прямую , которая пересекает ось OY в точке A(0;4) и прямую
в точке
. Последнее я узнал, приравняв правые части уравнений прямых и получив уравнение
. Из этого уравнения находится координата
точки пересечения, а координата
, я думаю вы догадались, равна координате
. Для тех, кто всё-таки не догадался, это потому что у нас уравнение одной из пересекающихся прямых:
.
Как только мы нарисовали эту прямую, сразу можно отметить искомую область. Знак неравенства у нас здесь «меньше или равно». Значит, искомая область находится ниже или непосредственно на изображённой прямой:
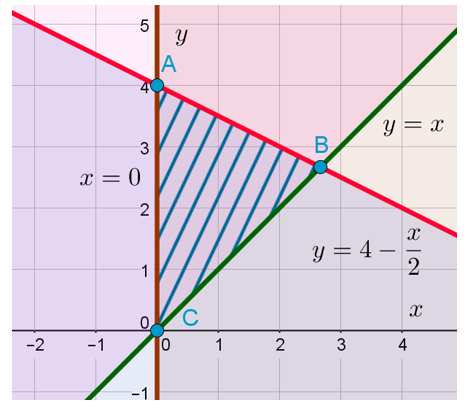
Ну и последний вопрос. Где же всё-таки находится искомая область, удовлетворяющая всем трём неравенствами системы? Очевидно, что она находится на пересечении всех трёх отмеченных областей. Опять пересечение! Запомните: знак системы в математике означает пересечение. Вот она, эта область:
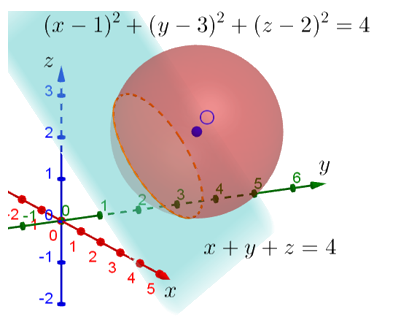
Ну и последний пример. Ещё более общий. Предположим теперь что у нас не одна переменная в системе и ни две, а аж целых три!
Поскольку переменных целых три, то для изображения множества решений такой системы неравенств нам потребуется третье измерение в добавок к двум, с которыми мы работали в предыдущем примере. То есть мы вылезаем из плоскости в пространство и изображаем уже пространственную систему координат с тремя измерениями: X, Y и Z. Что соответствует длине, ширине и высоте.
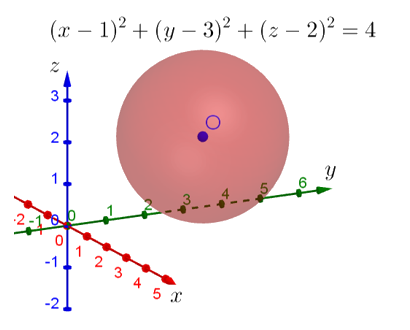
Начнём с того, что изобразим в этой системе координат поверхность, задаваемую уравнением . По форме оно очень напоминает уравнение окружности на плоскости, только добавляется ещё одно слагаемое с переменной
. Несложно догадаться, что это уравнение сферы с центром в точке (1;3;2), квадрат радиуса которой равен 4. То есть сам радиус равен 2.
Тогда вопрос. А что тогда задаёт само неравенство? Для тех, кого этот вопрос ставит в тупик, предлагаю рассудить следующим образом. Переводя язык формул на человеческий, можно сказать, что требуется указать все сферы с центром в точке (1;3;2), радиусы которых меньше или равны 2. Но тогда все эти сферы будут находиться внутри изображённой сферы! То есть фактически данным неравенством задаётся вся внутренняя область изображённой сферы. Если хотите, задаётся шар, ограниченный изображённой сферой:
Поверхность, которую задаёт уравнение x+y+z=4 — это плоскость, которая пересекает оси координат в точках (0;0;4), (0;4;0) и (4;0;0). Ну и понятно, что чем больше будет число справа от знака равенства, тем дальше от центра координат будут находиться точки пересечения этой плоскости с осями координат. То есть второе неравенство задаёт полупространство, находящееся «выше» данной плоскости. Используя условный термин «выше», я имею ввиду дальше в сторону увеличения значений координат по осям.
Данная плоскость пересекает изображённую сферу. При этом сечение пересечения — это окружность. Можно даже посчитать, на каком расстоянии от центра системы координат находится центр этой окружности. Кстати, кто догадается, как это сделать, пишите свои решения и ответы в комментариях. Таким образом исходная система неравенств задаёт область пространства, которая находится дальше от этой плоскости в сторону увеличения координат, но заключённая в изображённую сферу:
Вот таким образом изображают множество решений системы неравенств. В случае, если переменных в системе больше, чем 3 (например, 4), наглядно изобразить множество решений уже не получится. Потому что для этого потребовалась бы 4-х мерная система координат. Но нормальный человек не способен представить себе, как могли бы располагаться 4 взаимно перпендикулярные оси координат. Хотя у меня есть знакомый, который утверждает, что может сделать это, причём с лёгкостью. Не знаю, правду ли он говорит, может быть и правду. Но всё-таки нормальное человеческое воображение этого сделать не позволяет.
Надеюсь, сегодняшний урок оказался для вас полезным. Чтобы проверить, насколько хорошо вы его усвоили, выполните записанное ниже домашнее задание.
Изобразите множество решений системы неравенств:
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными

Примеры изображения на координатной плоскости множества решений уравнений, неравенств и систем неравенств с двумя переменными
Просмотр содержимого документа
«Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными»
Изображение на координатной плоскости множества решений уравнений и неравенств
с двумя переменными.
1. Изображение множества решений уравнений с двумя переменными.
Определение. Уравнение вида 
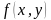
Решить уравнение – значит найти множество всех его корней.
Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.
Для того, чтобы решить уравнение с двумя переменными нужно построить его график.
Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Задача 1. Изобразить на координатной плоскости множество решений уравнений
Построим график уравнения
Так как произведение равно нулю, то каждый из множителей также равен нулю.
Решим каждое из полученных уравнений:
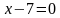
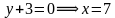
Решением является множество точек двух прямых: 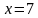
Задача 2. Изобразить на координатной плоскости множество решений уравнений
Построим график уравнения 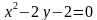
Для этого выразим переменную 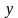
Уравнение задает параболу с вершиной в точке
То есть решением уравнения является множество точек параболы
Задача 3. Изобразить на координатной плоскости множество решений уравнений
Построим график уравнения
Уравнение задает окружность с центром в точке 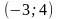
То есть решением уравнения является множество точек построенной окружности
2. Изображение множества решений неравенств с двумя переменными.
Определение. Выражение вида 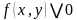
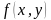
Решить неравенство – значит найти множество всех его решений.
Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.
Алгоритм решения неравенства
1. Построить график уравнения 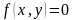
Если неравенство «строгое», тогда график изображаем пунктирной линией;
Если неравенство «нестрогое», тогда график изображаем сплошной линией.
2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.
Задача 1. Изобразить на координатной плоскости множество решений неравенства
Построим график заданного неравенства . Для этого выразим переменную 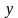
Уравнение задает линейную функцию, проходящую через точки:
Поскольку неравенство имеет знак «больше либо равно», значит выделяем часть координатной плоскости, которая лежит выше построенной прямой . Выделенная часть является решением заданного неравенства.
Задача 2. Изобразить на координатной плоскости множество решений неравенства
Построим график заданного неравенства.
Уравнение задает параболу с вершиной в точке
Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы.
Задача 3. Изобразить на координатной плоскости множество решений неравенства .
Графиком уравнения является гипербола .
Данная гипербола разбивает координатную плоскость на три области А, В и С.
Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.
Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства.
Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства.
Возьмем из области С точку с координатами Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область С входит в решение заданного неравенства.
3. Изображение множества решений системы неравенств с двумя переменными.
Решить систему неравенств – значит найти множество всех решений системы.
Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы
Задача 4. Изобразить на координатной плоскости множество решений системы неравенств
На координатной плоскости множество всех решений неравенства
изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой (смотри задачу 1).
Аналогично строим график неравенства .
То есть строим на координатной плоскости прямую
Множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше прямой и на этой прямой.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.
Задача 5. Изобразить на координатной плоскости множество решений системы неравенств
На координатной плоскости множество всех решений неравенства
изображается в виде множества точек полуплоскости, лежащих ниже параболы и на этой параболе.
Аналогично, множество решений неравенства изображается в виде множества точек полуплоскости, лежащих выше параболы и на этой параболе.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы.
Фигуры в координатной плоскости (6 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Фигуры в координатной плоскости
(1; 7), (0; 10), (-1; 11), (-2; 10), (0; 7), (-2; 5), (-7; 3), (-8; 0), (-9; 1), (-9; 0), (-7; -2), (-2; -2), (-3; -1), (-4; -1), (-1; 3), (0; -2), (1; -2), (0; 0), (0; 3), (1; 4), (2; 4), (3; 5), (2; 6), (1; 9),
(1; 8), (2; 9), (4; 9) глаз (2,5; 9,5)
(-2,5; -5,5), (-3; -3) и (5; -2), (5; -5), (4; -6), (5,5; -6) глаз (-7; 5)
(3; 12), (2; 12), (2; 11), (3,5; 12,5), (4; 12,5)
(10; 5), (10; 4), (11; 3), (12; 3), (12; 2), (11; 2) (9; 4), (10; 2), (10; 1), (9; 1), (9; 2), (6; 7),
(5,5; 7,5), (6; 9), (3; 14), (4; 14), (6; 12), (7; 9)
(9; 6), (10; 6), (10; 7), (11; 6), (12; 7), (12; 5),
глаза (10,5; 5,5) и (11,5; 5,5)
(9; 4), (8; 9), (8; 11), (9; 12), (9; 14), (8; 15)
(7; 15), (5; 13), (5; 12), (4; 11), (2; 10), (4; 9)
(4; 1), (3; 1), (3; 0), (5; 0), 95; 2), (7; 2), (7; 1)
(9; 4), (11; 4), (11; 9) глаз (5; 11)
глаза и нос (7; -3) и (9; -3) и (8; -4)
(5; 4), (7; 4), (9; 5), (9; 7), (8; 7), (7; 6), (5; 6), (3; 3), (-2; 1), (-4; 4), (-5; 4), (-5; 5), (-10; 2), (-9; 2), (-10; 1), (-6; 1), (-6; -1), (-5; -2),
№ 17 Морской котик
(6; 4), (7; 3), (7; 2), (5; 1), (3; 1), (2; 2), (3; 2), (4;3), (2; 3), (1; 2), (0;, 4), (-1; 5), (-2; 5),
(0; -2), (1; -4), (7; -4), (8; -2), (10; -2), (9; 0), (10; 1), (12; 1), (12; 4), (10; 3), (10; 5), (8; 2), (1; 2), (-0,5; 3), (-0,5; 4), (1,5; 7), (1,5; 11), (0; 12), (-1; 11), (-4; 9), (0; 9), (0; 7), (-2; 4), (-2; 0), (0; -2) и (2,5; -4), (2; -5), (3; -5),
(2,5; -4) и (4,5; -4), (4; -4), (5; -4), (4,5; -4) глаз (-1; 10)
(-7; 0), (9; 0) и (0; 2), (5; 6), (7; 6), (4; 2)
(1; 3), (-1; 3), (-2; 1), (-2; -8), (-1; -9), (1; -9), (2; -8), (2; 1), (1; 3), (5; 0), (7; 0), (3; 9),
(1; -3), (2; -2), (34 -2), (2; -1) и (3; 2), (4; 2), (4; 3), (3; 3), (3; 2), и (0; 4), (1; 4), (1; 5),
(0; 
(0; 12) и (0; 1), (-1; -10), (0; -8), (0; 1) и
№ 26 Собака Дружок
(7,5; -8), (8; -6), (9; -5), (9; -3), (8; -1), (9; 0), (8; 1), (7,5; 0), (5,5; 0), (4; -1), (0; 0), (-1; 1), (1; 7), (0; 10), (-1; 10,5), (-2; 10,5), (-3; 10),
(-2; -9), (-1; -13), (-3; -15), (-2; -16), (0; -14), (0; -7) и (-1; 10), (-1,5; 8), (0; 
(4; -3), (6; 0), (1; 12), (5; 12), (1; 14), (0; 12), (3; 1), (-6; 4), (-7; 3), (-9; 4), (-9; 1), (-10; 0), (-8; -3), (4; -3) глаз (2; 13)
(-7; -15), (-4; 15), (-3; -14), (-2; -12), (0; -5), (1; 0), (2; 3), (3; 2), (4; -3), (6; 0), (8; -4),
(8; -8), (10; -4), (11; 1), (11; 5), (9; 8), (5; 11), (6; 13) и (5; 11), (-1; 12), (-8; 9), (-9; 7),
(0; -6), (1; 0), (3; 12), (13; 25) и (1; 0),
(6; 9), (7; 6), (5,5; 7), (5; 5), (4,5; 7), (3; 6), (4; 9), (5; 10) и (6; 16), (7; 16), (8; 15),
(9; 14), (9; 13), (10; 11), (8,5; 12), (8; 10),
(7,5; 12), (6; 11), (7; 13), (7; 14), (8; 15) и (10; 21), (11; 20), (12; 19), (13; 16),
(10; 19), (11; 20) и (13; 25), (13,; 24),
(14; 23), (14,5; 21), (13,5; 22), (13; 20),
(12,5; 22), (11,5; 21), (12; 23), (13; 24)
(3; 0), (2; -1), (2; -3), (4; -5), (3; -7) (5; -7), (6; -6), (5; -5), (5; 1), (6; 6), (5; 7), (4; 7),
(-7; 2), (-5; 3), (-1; 2). Глаза (-6; 4) и (-4; 4)
(-1; -3), (-1; -5), (-2; -5), (-3; -4), (-4; -4) и (1; -2), (0; -2), (-1; -3), (-1; -5), (0; -5), (1; -4), (2; -4). Глаза (-2; 3) и (0; 3)
(4; 13), (8; 13), (9; 10), (7; 11), (9; 8), (7; 8),
( 9; 6), (8; 6), (3; -1), (3; -4), (4; -5), (1; -5) и (-4; 11), (-2; 11) и (0; 1), (0; 3), (1; 4), (2; 4), (4; 1), (0; 1) глаз (-4; 10)
(-14; -4), (-15; -6), (-15; -3), (-14; 2), (-11; 4), (-10; 8), (-8; 9), (-6; 8), (-5; 5), (-3; 8), (-1; 9), (0; 8), (0,5; 6), (0,5; 4), (3; 2,5), (4; 3), (5; 4), (6; 6), (8; 7), (9,5; 7), (10; 6), (11,5; 5,5),
(3; 5), (2; 3), (1; 5), (2; 6), (3; 5), (6; 5), (6; 4), (8; 4), (8; 2), (6; 1), (3; -1), (4; -6), (6; -7),
(1,5;.0,5), (3; 0), (3,5; 0), (8; 0,5), (7,5; 4,5), (9; 3), (12; 1,5), (18; 1,5), (12,5; 3), (11; 3,5), (9,5; 7), (8; 10), (6; 11), (4; 12,5), (3; 14),
(2; 16), (2,5; 17,5), (2; 18), (1; 16,5), (0,5; 18), (0; 16), (-0,5; 15,5), (-2; 14,5), (-1,5; 14),
(6,5; 4), (6,5; 1), (1,5; 0,5) глаз (0; 15,5)
(4; 3), ( 5; 4), (5; 2), (6; 3), (6; 1), (7; 2), (7; 0)
(12; -15), (11; -12), (8; -11), (7; -9), (10; 0), (7; 3), (9; 4), (11; 7), (10; 10), (7; 13)
(4; 8), (5; 7), (12; 6), (14; 8), (14; 10), (15; 11)
(16; 0), (15; 0), (14; 1), (13; 3), (5; 3), (3; 2), (3; 1), (4; 1), (4; 0) и (14; 10), (15; 8), (15; 11) глаз ( 16; 10)
(8; 2), (13; 7), (13; 15), (8; 10), (7; 10), (6; 9), (10; 17), (10; 22), (8; 24), (6; 24), (3; 21),
(4; 20), (1; 17), (2; 17), (4; 19), (5; 19), (7; 21)
(12; 0), (16; 8), (16; 11), (14; 9), (13; 10) и
(4; 19), (5; 20) глаз (4,5; 20,5)
Курс повышения квалификации
Охрана труда
- Сейчас обучается 140 человек из 48 регионов
Курс профессиональной переподготовки
Пожарная безопасность
- Сейчас обучается 131 человек из 45 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 251 человек из 56 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 840 974 материала в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 01.11.2020
- 1033
- 99
- 20.10.2020
- 336
- 8
- 04.10.2020
- 193
- 1
- 08.08.2020
- 5774
- 273
- 10.07.2020
- 75
- 0
- 06.07.2020
- 105
- 0
- 26.06.2020
- 321
- 5
- 25.06.2020
- 81
- 0
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 28.04.2020 7507
- DOCX 3.3 мбайт
- 572 скачивания
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Пономарева Татьяна Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 3 месяца
- Подписчики: 0
- Всего просмотров: 34284
- Всего материалов: 217
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте
Время чтения: 1 минута
Онлайн-конференция о профессиональном имидже педагога
Время чтения: 2 минуты
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
В Брянской области часть школ переводят на дистанционное обучение
Время чтения: 0 минут
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Урок на тему «Метод областей». 11-й класс
Класс: 11
Презентация к уроку
«Считай несчастным тот день и тот час,
вк оторый ты не усвоил ничего нового и ничего
не прибавил к своему образованию».
Я.А Коменский
Тип урока: урок-обобщения и систематизации знаний учащихся.
Цели урока:
- создать условия для систематизации, обобщения знаний и умений обучающихся по применению различных методов решения неравенств;
- воспитание нравственных качеств личности, таких как ответственность, аккуратность, дисциплинированность;
- воспитание культуры общения.
- развитие у учащихся умений выделять главное, существенное в изучаемом материале, обобщать изучаемые факты, логически излагать свои мысли;
- развитие психических процессов, таких как память, внимание, мышление, а также наблюдательности, активности, самостоятельности.
Задачи:
- формировать умение классифицировать неравенства по методам решения;
- закрепить навыки решения неравенств различными методами;
- отрабатывать навыки самоконтроля с целью подготовки к итоговой аттестации;
- воспитывать чувство коллективизма, ответственности.
Оборудование:
- Компьютер
- Мультимедийный проектор, звуковые колонки
- Программа «MicrosoftPowerPoint 2003»
Методы обучения:
- частично-поисковый метод,
- репродуктивный,
- обобщающий.
План урока.
План урока рассчитан на 2 учебных часа (90 мин)
- Организационный момент.
- Вступительное слово учителя.
- Повторение теории.
- Решение неравенств различными методами (варианты ЕГЭ)
- Самостоятельная работа с самопроверкой.
- Итог урока.
- Рефлексия.
Ход урока
I. Организационный момент
«То, что мы знаем, — ограничено, а то чего
мы не знаем, — бесконечно».
Приветствие учащихся.Ученики под руководством учителя проверяют наличие дневника, рабочей тетради, инструментов, отмечаются отсутствующие, проверяется готовность класса к уроку, учитель психологически настраивает детей на работу на уроке.Формулируется тема и цели урока. Знакомство с этапами урока.
II. Вступительное слово учителя
Для успешного исследования многих задач повышенной сложности полезно уметь строить не только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.
Метод областей особенно полезен при решении уравнений или неравенств с параметром. Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.
III. Повторение теории
Метод интервалов на координатной прямой и метод областей на координатной плоскости.
Точка х=а разбивает числовую прямую на два множества, задаваемые неравенствами x a
Всякая действительная кривая на координатной плоскости, заданная уравнением F(x;y)=0 разбивает координатную плоскость на конечное число областей, в каждой из которых для всех точек области выполняется только одно из неравенств: F(x;y)>0 или F(x;y) kx+p или y c
Решением системы неравенств с двумя переменными являются координаты точек пересечения множеств, удовлетворяющих одному из неравенств системы
Уравнение y= k(x-x0) + y0 задает множество прямых, проходящих через точку с координатами (x0,y0).
При изменении значений параметра прямые y= k(x-x0) + y0 «поворачиваются» вокруг данной точки. При увеличении параметра прямая поворачивается «против часовой стрелки», при уменьшении – «по часовой стрелке».
Уравнение y=kx+p при фиксированном значении параметра k = k0 задает семейство прямых, параллельных прямой y=kx+p проходящей через начало координат
Если точка с координатами 
Задача
Пусть M – множество точек плоскости с координатами (x; y) таких, что числа x, y, 6-2x являются сторонами некоторого треугольника. Найдите его площадь.
Если три числа являются сторонами некоторого треугольника, то это числа положительные и каждое из них меньше суммы двух других чисел. Поэтому, координаты точек, удовлетворяющих условию задачи, будут задаваться системой линейных неравенств с двумя переменными:
Геометрическое место точек на плоскости
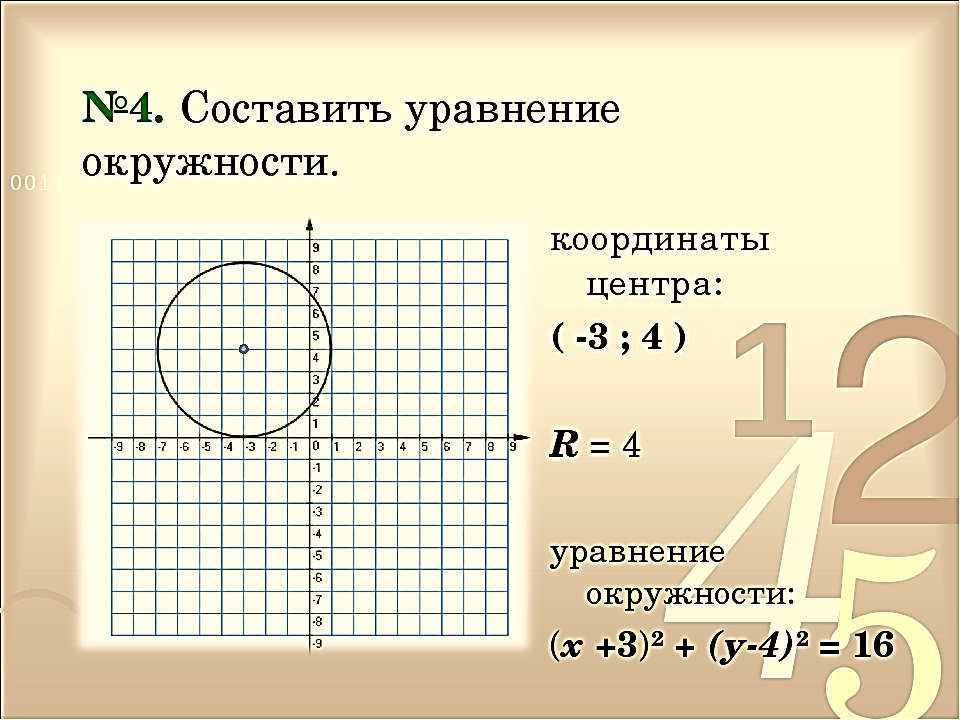
Множество точек плоскости, равноудаленных от данной точки на расстояние, равное положительной величине R, называется окружностью.
Уравнением окружности называется уравнение вида
Множество точек, удаленных от данной точки на положительное расстояние, меньшее R, называется кругом. Круг задается неравенством
Множество точек, лежащих вне круга, задается неравенством
Геометрическое место точек на плоскости
Квадратным трехчленом относительно переменной, называется выражение
Графиком квадратного трехчлена является кривая, называемая параболой.
Расположение параболы зависит от знака старшего коэффициента и знака дискриминанта квадратного трехчлена
Парабола разбивает плоскость на часть, лежащую «над» параболой и лежащую «под» параболой. Первая задается неравенством
, а вторая –
Метод областей при решении задач с параметрами
1. Свойства функций
2. Графический прием
Параметр – «равноправная» переменная Þ отведем ему координатную ось, т.е. задачу с параметром будем рассматривать как функцию f(x ;a) >0
Общие признаки задач подходящих под рассматриваемый метод:
- В задаче дан один параметр а и одна переменная х
- Они образуют некоторые аналитические выражения F(x;a), G(x;a)
- Графики уравнений F(x;a)=0,G(x;a)=0 строятся несложно
- Строим графический образ
- Пересекаем полученный график прямыми, перпендикулярными параметрической оси
- «Считываем» нужную информацию
Обобщенный метод областей («переход» метода интервалов с прямой на плоскость)
Неравенства с одной переменной
Неравенства с двумя переменной
- ОДЗ
- Граничные линии
- Координатная плоскость
- Знаки в областях
- Ответ по рисунку
IV. Решение неравенств
Пример №1
Найти все значения параметра p, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства
Применим обобщенный метод областей.
1. Построим граничные линии
2. Определяем знаки в полученных областях и получаем решение 1 неравенства
3. Из полученного множества исключим решение
Пример № 2
При каких значениях параметра а система неравенств не имеет решений.
1. Рассмотрим 1 неравенство и получаем
2. Рассмотрим 2 неравенство и получаем
3. Заметим, что исходная система неравенств равносильна системе:
4. Изобразим систему неравенств в виде плоской фигуры на координатной плоскости. Для этого введём параметрическую плоскость Oax
5. Мы получили плоскую фигуру, множество точек которой является решением системы.
Таким образом, отвечая на вопрос задачи, решений системы нет при
Пример №3
При каких положительных значениях параметраа система уравнений имеет ровно 4 решения.
1. Запишем систему в следующем виде:
2. Построим график 1 уравнения.
3. Построим график 2 уравнения – семейство окружностей с центром в точке (2; 0) и радиусом а.
Ответ: при
V. Самостоятельная работа с самопроверкой
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
1. ОДЗ: 
2. Строим граничные линии:
3. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение.
Ответ: заштрихованная область на рисунке
На координатной плоскости изобразите множество точек, координаты которых удовлетворяют неравенству
- На координатной плоскости нарисуем линии определённые равенствами x-y=0 и xy-1=0, которые разбивают плоскость на несколько областей.
- Определяем знаки в областях.
Ответ: заштрихованная область на рисунке
VI. Итог урока
(подвожу итог, комментирую работу учащихся, сообщаю оценки за урок.)
VII. Рефлексия.
Ребята. На этом урок окончен. Спасибо за урок!
Литература.
- П. И. Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. 3-е издание, дополненное и переработанное. — М.: Илскса, Харьков: Гимназия, 2005,- 328 с.
- Черкасов О. Ю., Якушев А. Г. Математика: интенсивный курс подготовки к экзамену.
- Экзаменационные материалы для подготовки к ЕГЭ-2007. Математика. М.: ООО «РУСТЕСТ», 2006. — 108с. Сост. — Клово А.Г.
- Задачи с параметром и другие сложные задачи. Козко А.И., Чирский В.Г. М.: МЦНМО, 2007. — 296с.
- ЕГЭ 2011. Математика. Задача С5. Козко А.И., Панферов В.С., Сергеев И.Н., Чирский В.Г.
http://infourok.ru/figury-v-koordinatnoj-ploskosti-6-klass-4903759.html
http://urok.1sept.ru/articles/664756
Системы неравенств с двумя переменными
- Алгоритм графического решения системы неравенств с двумя переменными
- Примеры
п.1. Алгоритм графического решения системы неравенств с двумя переменными
На входе система: (left{ begin{array}{ l } mathrm{F(x,y) lt 0} & \ mathrm{G(x,y gt 0)} & end{array}right. )
Шаг 1. Построить на координатной плоскости кривую F(x, y) = 0. Заштриховать область F(x, y) < 0.
Шаг 2. Построить на координатной плоскости кривую G(x, y) = 0. Заштриховать область G(x, y) > 0.
Шаг 3. Множество решений данной системы – это пересечение двух заштрихованных областей.
Системы с другими знаками сравнения (≤, ≥ и т.д.), а также системы с любым количеством неравенств решаются аналогично.
Например:
 |
Найти на координатной плоскости множество решений системы неравенств: $$ left{ begin{array}{ l } mathrm{x^2+y^2leq 9} & \ mathrm{x+ygt 3} & end{array}right. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит. |
п.2. Примеры
Пример 1. Найдите на координатной плоскости множество решений системы неравенств.
a) ( left{ begin{array}{ l } mathrm{x+ygeq 4} & \ mathrm{2x-yleq 2} & end{array}right. )
Выразим y(x) в явном виде
( left{ begin{array}{ l } mathrm{ygeq -x+4} & \ mathrm{ygeq 2x-2} & end{array}right. )
Строим прямые, заштриховываем области над ними, находим пересечение.
б) ( left{ begin{array}{ l } mathrm{y+x^2-6leq 0} & \ mathrm{2y-x^2geq 0} & end{array}right. )
Выразим y(x) в явном виде
( left{ begin{array}{ l } mathrm{yleq -x^2+6} & \ mathrm{ygeq frac{x^2}{2}} & end{array}right. )
Строим параболы.
Заштриховываем область под первой параболой и над второй параболой.
Находим пересечение.
в) ( left{ begin{array}{ l } mathrm{y-frac{6}{x}leq 0} & \ mathrm{3x-2ylt 0} & end{array}right. )
Выразим y(x) в явном виде
( left{ begin{array}{ l } mathrm{yleq frac{6}{x}} & \ mathrm{ygt 1,5x} & end{array}right. )
Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.
Находим пересечение.
г) ( left{ begin{array}{ l } mathrm{x^2+y^2gt 4} & \ mathrm{x^2+y^2leq 9} & end{array}right. )
Строим окружности.
Заштриховываем области вне первой окружности и внутри второй.
Находим пересечение – кольцо.
Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:
AB
begin{gather*} mathrm{ frac{x-x_A}{x_B-x_A}=frac{y-y_A}{y_B-y_A}Rightarrowfrac{x-2}{4-2}=frac{y-3}{4-3}Rightarrow x-2=2(y-3) }\ mathrm{ x-2y+4=0} end{gather*}
BC
begin{gather*} mathrm{ frac{x-x_B}{x_C-x_B}=frac{y-y_B}{y_C-y_B}Rightarrowfrac{x-4}{3-4}=frac{y-4}{0-4}Rightarrow -4(x-4)=-(y-4) }\ mathrm{ 4x-y-12=0} end{gather*}
AC
begin{gather*} mathrm{ frac{x-x_A}{x_C-x_A}=frac{y-y_A}{y_C-y_A}Rightarrowfrac{x-2}{3-2}=frac{y-3}{0-3}Rightarrow -2(x-2)=y-3 }\ mathrm{ 3x+y-9=0} end{gather*}
Чтобы расставить знаки ≤, ≥, выбираем произвольную точку внутри треугольника, например D(3; 2), подставляем в полученные уравнения и получаем необходимые знаки:
3 – 2 · 2 + 4 = 3 > 0, 4 · 3 – 2 – 12 = –2 < 0, 3 · 3 + 2 – 9 = 2 > 0
Искомая система неравенств: ( left{ begin{array}{ l } mathrm{x-2y+4geq 0} & \ mathrm{4x-y-12leq 0} & \ mathrm{3x+y-9geq 0} & end{array}right. )
Рейтинг пользователей
Изображение на координатной плоскости множества решений уравнений и неравенств
с двумя переменными.
1. Изображение множества решений уравнений с двумя переменными.
Определение. Уравнение вида 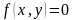
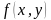
Решить уравнение – значит найти множество всех его корней.
Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.
Для того, чтобы решить уравнение с двумя переменными нужно построить его график.
Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Примеры
Задача 1. Изобразить на координатной плоскости множество решений уравнений 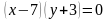
Решение
|
Построим график уравнения Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
Решением является множество точек двух прямых: |
|
Задача 2. Изобразить на координатной плоскости множество решений уравнений 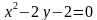
Решение
|
Построим график уравнения Для этого выразим переменную
Уравнение задает параболу с вершиной в точке То есть решением уравнения является множество точек параболы |
|
Задача 3. Изобразить на координатной плоскости множество решений уравнений 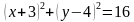
Решение
|
Построим график уравнения Уравнение задает окружность с центром в точке То есть решением уравнения является множество точек построенной окружности |
|
2. Изображение множества решений неравенств с двумя переменными.
Определение. Выражение вида 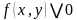
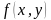
Решить неравенство – значит найти множество всех его решений.
Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.
Алгоритм решения неравенства 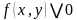
1. Построить график уравнения 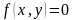
Если неравенство «строгое», тогда график изображаем пунктирной линией;
Если неравенство «нестрогое», тогда график изображаем сплошной линией.
2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.
Примеры
Задача 1. Изобразить на координатной плоскости множество решений неравенства
Решение.
Построим график заданного неравенства . Для этого выразим переменную
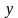
Получим: .
|
Уравнение
Поскольку неравенство |
Задача 2. Изобразить на координатной плоскости множество решений неравенства
Решение.
|
Построим график заданного неравенства. Уравнение Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы. |
Задача 3. Изобразить на координатной плоскости множество решений неравенства .
Решение
Графиком уравнения является гипербола
.
Данная гипербола разбивает координатную плоскость на три области А, В и С.
Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.
|
Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства. Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства. Возьмем из области С точку с координатами |
3. Изображение множества решений системы неравенств с двумя переменными.
Решить систему неравенств – значит найти множество всех решений системы.
Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы
Задача 4. Изобразить на координатной плоскости множество решений системы неравенств
Решение
|
На координатной плоскости множество всех решений неравенства
|
|
|
Аналогично строим график неравенства То есть строим на координатной плоскости прямую Множество решений неравенства |
|
|
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы. |
Задача 5. Изобразить на координатной плоскости множество решений системы неравенств
Решение
|
На координатной плоскости множество всех решений неравенства Аналогично, множество решений неравенства Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы. |
Содержание:
Системы неравенств и совокупность неравенств
Исследование. Если альпинисты увеличат скорость на 1км/ч, то путь 4 км до вершины они преодолеют быстрее чем за 2 часа. Если же они уменьшат скорость на 1 км/ч, то не смогут добраться до вершины за 2 часа. С какой скоростью движутся альпинисты? Решение: Примем за
Если скорость увеличится на 1 км/ч, то длина пройденного пути будет больше 4-х км и соответствующее неравенство примет вид:
Если скорость уменьшится на 1 км/ч, то длина пройденного пути будет меньше 4-х км и соответствующее неравенство примет вид:
По условию задачи нужно найти такое значение 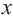
Неравенства, объединенные союзом 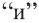
В данной задаче нужно решить систему неравенств
Если каждое неравенство системы заменить на равносильное неравенство, то получим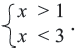
Для того, чтобы решить систему неравенств нужно найти множество решений каждого неравенства и найти пересечение этих множеств, то есть, общую часть.
Ответ: Решение системы промежуток 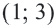
Совокупность неравенств
Задача. Наргиз и Эльшан играют в игру, построенную на числах. Каждый берег карточку с числом и прибавляет к нему 5. Если ответ будет меньше 10-ти или же больше 15-ти, то владелец карточки зарабатывает очко. Выразите с помощью неравенства ситуацию, когда Эльшан взяв одну карточку заработал очко.
Решение: Пусть число на карге будет 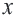
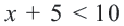
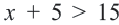
Решением данной совокупности неравенств будет множество: 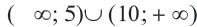
Пример.
Решите неравенство:
Решение: Для того, чтобы произведение двух множителей было положительным, нужно чтобы множители были одинакового знака. То есть, множители 

Данное неравенство сводится к решению совокупности:
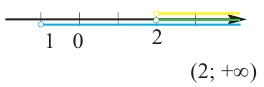
Решение 1-ой системы совокупности:
Геометрическое изображение:
Геометрическое изображение:
Неравенства, содержащие переменную под знаком модуля
Система неравенств, совокупность неравенств
Пример 2.
Решение:
Пример 3.
Решение:
Линейные неравенства с двумя переменными
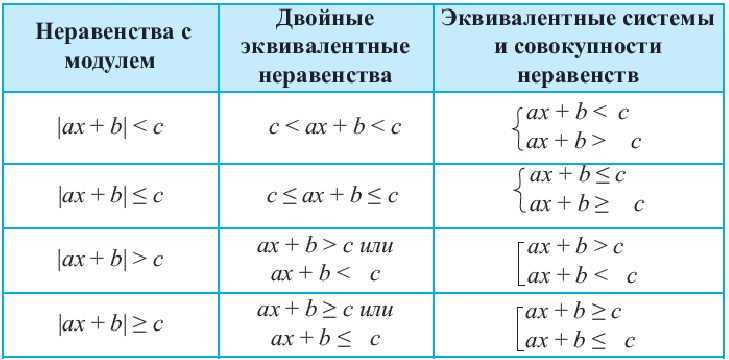
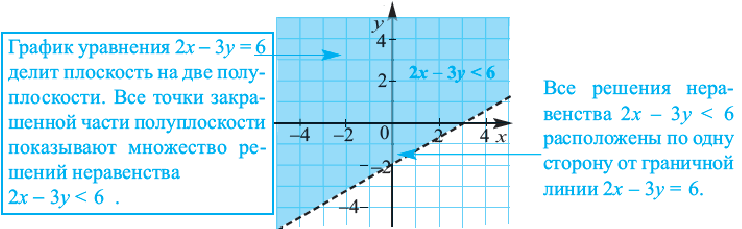
Неравенства вида 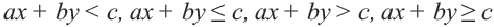
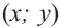
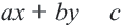
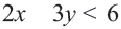
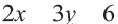
• Чтобы убедиться в правильности выбора полуплоскости, соответствующей решению неравенства, выбираются пробные точки в каждой из полуплоскостей. Закрашивается та полуплоскость, в которой расположена точка, удовлетворяющая данному неравенству.
• Если неравенство выражается знаками 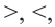
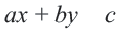
• Если неравенство выражается знаками 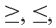
Пример 1.
1. Решим неравенство относительно переменной 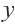
2. Нарисуем график уравнения 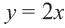
3. Проверим неравенство в точке 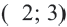
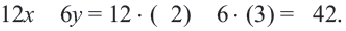
Пример 2. Напишите неравенство, соответствующее графику.
1. Определим уравнение 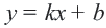
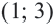
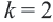
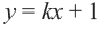
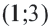
Уравнение линии границы: 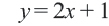
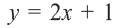
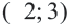
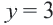
Левая часть 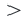
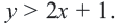
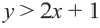
- Заказать решение задач по высшей математике
Прикладные задания.
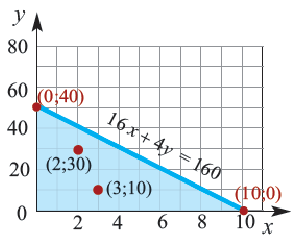
Пример 1. Билет в театр для взрослых стоит 16 манат, а детский — 4 манат. Деньги, вырученные от продажи билетов в кассе, составляют не более 160 манат. Определите различные варианты количества проданных билетов. Числовые информации и переменные, соответствующие условию задачи:
Математическая запись:
1. Чтобы решить неравенство, выразим 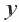
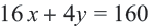
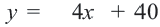
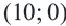
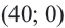
2. Закрасим фигуру, заданную графиком и осями координат.
3. Любые целые значения 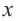
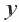
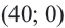
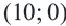
Системы линейных неравенств с двумя переменными
Решением системы линейных неравенств с двумя переменными называется множество пар чисел 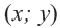
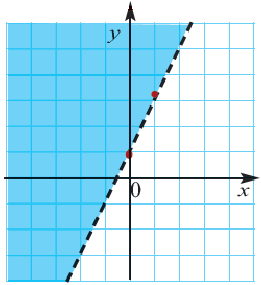
Пример 1.
1. С помощью граничной прямой 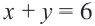
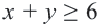
2. С помощью уравнения 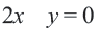
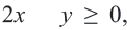
3. Множеством решений данной системы неравенств будет часть плоскости, закрашенная обоими цветами.
4. Выберем отсюда одну точку, например 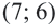
Каждая пара 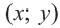
Пример 2. Изобразите графически на координатой плоскости неравенство
1. Запишем двойное неравенство 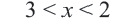
2. Изобразим неравенство 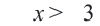

3. Изобразим неравенство 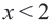
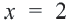
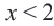
4. Часть плоскости, соответствующая неравенствам 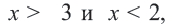
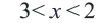
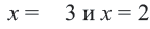
5. Проверка: проверим в точке
График системы линейных неравенств, соответствующий реальным жизненным ситуациям, в большинстве случаев строится в первой четверти координатной плоскости.
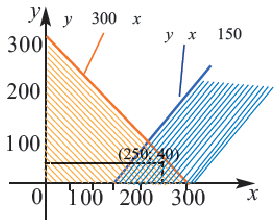
Пример 3. На одном из двух конвейеров производят кастрюли из нержавеющей стали, а на другом медные кастрюли. Если каждый из конвейеров работает на полную мощность, то ежедневно производится не более 300 кастрюль. Так как потребность в кастрюлях из нержавеющей стали больше, их ежедневно производят больше чем медных, но не меньше 150 штук. Напишите систему неравенств, показывающую ежедневное количество производимых кастрюль, и изобразите графически.
Решение: 1) Примем за 
2) Решение неравенства 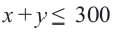
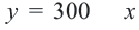
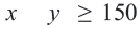
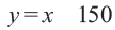
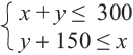
3. С помощью пробной точки 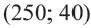
Решение системы неравенств найдено верно.
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
- Тригонометрические функции произвольного угла
- Теоремы синусов и косинусов
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Решение уравнений высших степеней

![Rendered by QuickLaTeX.com [ begin{cases} 2x-7leqslant 9 \ x-4>2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c2d2fbf06d37908176f7855348bd1ee1_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} xleqslant 8 \ x>6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e354e782b309f49f3d2a32ba3ecfdfa7_l3.png)


![Rendered by QuickLaTeX.com [ begin{cases} x+2yleqslant 8 \ xgeqslant 0 \ ygeqslant x. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2d9632160c48b2777a035f3d176edea6_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (x-1)^2+(y-3)^2+(z-2)^2leqslant 4 \ x+y+zgeqslant 4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-410af121e91222c804c36bc597b5c082_l3.png)
![Rendered by QuickLaTeX.com [ 1. begin{cases} y-x>-2 \ xgeqslant 0 \ 2x+3y<7 end{cases} 2. begin{cases} x^2+y^2leqslant 9 \ y-2xgeqslant 4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-93c8b684ed39e31068e1d3ae7d10d55a_l3.png)
![Rendered by QuickLaTeX.com [ 3. begin{cases} x^2+y^2leqslant 16 \ (x-5)^2+y^2geqslant 4 . end{cases} 4. begin{cases} x^2+y^2+z^2leqslant 16 \ x>0. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-702028826923aa849704d859954b2811_l3.png)