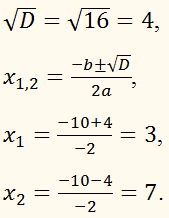Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax2+bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.
В зависимости от значения a ветви графика направлены вверх или вниз:
- если a>0, то ветви параболы направлены вверх;
- если a<0, то ветви параболы направлены вниз;
- точки пересечения параболы с осью x, называются нулями функции и являются корнями квадратного уравнения: ax2+bx+c=0
Квадратные неравенства имеют вид.
ax2+bx+c>0
ax2+bx+c<0
ax2+bx+c≥0
ax2+bx+c≤0
Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?
Как решать квадратные неравенства?
Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).
Пример:
3x2+2x+20>0
Приравняем к 0
3x2+2x+20=0
D=22—4•3•20=—236
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x2+2x+20>0.
3•12+2•1+20>0
25>0
Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.
Ответ: x∈(-∞; +∞)
Пример:
Рассмотрим этот же пример со знаком неравенства меньше 0
3x2+2x+20<0
Приравняем к 0
3x2+2x+20=0
D=22—4•3•20=—236
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.
А знак уравнения меньше <0. Так как ниже оси x у нас нет параболы, следовательно нет решения у данного неравенства.
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x2+2x+20<0.
3•12+2•1+20<0
25<0
Получили неверное неравенство 25<0, следовательно у неравенства нет решения или пустое множество ø.
Ответ: x∈ ø
Пример:
Рассмотрим следующий пример.
x2+x-2<0
Приравняем к 0
x2+x-2=0
D=12—4•1•(—2)=9
x1=(-1+3)⁚2=1
x2=(-1-3)⁚2=-2
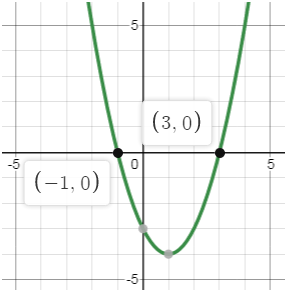
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения меньше <0. Нам в ответ необходимо записать часть параболы, которая находится ниже оси x. Визуально графически можно оценить по картинке, нам подходит интервал (-2;1).
Также можно решить методом интервалов. Ось x делится на три участка. Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x2+x-2<0 вместо переменой x.
(-3)2+(-3)-2<0
4<0
Получили неверное неравенство 4<0, следовательно у неравенства нет решения на участке (-∞; 2).
Второй участок (-2; 1). На этом участке можно взять число 0.
(0)2+(0)-2<0
-2<0
Получили верное неравенство -2<0, следовательно этот участок (-2; 1) подходит нам для ответа.
Третий участок (1; +∞). На этом участке можно взять число 2.
(2)2+(2)-2<0
4<0
Получили неверное неравенство 4<0, следовательно у неравенства нет решения на участке (1; +∞).
Ответ: x∈(-2; 1)
Пример:
Рассмотрим этот же пример с другим знаком неравенства.
x2+x-2>0
x2+x-2=0
D=12—4•1•(—2)=9
x1=(-1+3)⁚2=1
x2=(-1-3)⁚2=-2
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x2+x-2<0 вместо переменой x.
(-3)2+(-3)-2>0
4>0
Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.
Второй участок (-2; 1). На этом участке можно взять число 0.
(0)2+(0)-2>0
-2>0
Получили неверное неравенство -2>0, следовательно этот интервал (-2; 1) не подходит.
Третий участок (1; +∞). На этом участке возьмем число 2.
(2)2+(2)-2>0
4>0
Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.
Ответ: x∈(-∞; 2)⋃(1; +∞)
Квадратные неравенства — коротко о главном
Квадратичная функция–это функция вида: ( displaystyle fleft( x right)=a{{x}^{2}}+bx+c=0), ( displaystyle ane 0)
График квадратичной функции – парабола. Её ветви направлены вверх, если ( displaystyle a>0), и вниз, если ( displaystyle a<0):
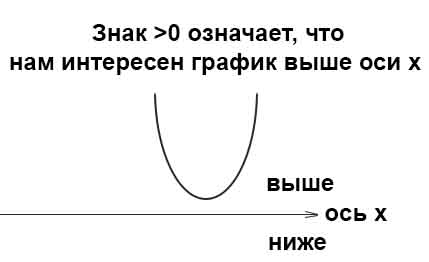
Если требуется найти числовой промежуток, на котором квадратный трёхчлен больше нуля, то это числовой промежуток, где парабола лежит выше оси ( Ox).
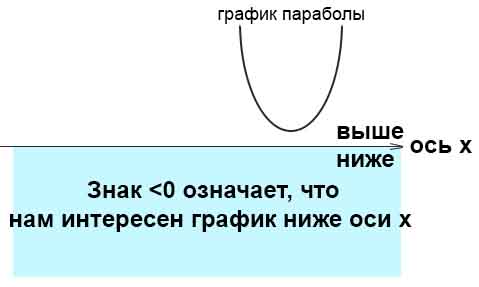
Если требуется найти числовой промежуток, на котором квадратный трёхчлен меньше нуля, то это числовой промежуток, где парабола лежит ниже оси ( Ox).
Виды квадратных неравенств
Все квадратные неравенства сводятся к следующим четырём видам:
( displaystyle left. begin{array}{l}a{{x}^{2}}+bx+c ge 0\a{{x}^{2}}+bx+c>0\a{{x}^{2}}+bx+cle 0\a{{x}^{2}}+bx+c<0end{array} rightrangle ane 0)
Алгоритм решения квадратных неравенств:
1) Запишем соответствующее неравенству квадратное уравнение (просто меняем знак неравенства ( >,text{ }<,text{ }ge ,text{ }le ) на знак равенства «( displaystyle=)»).
Пример:
( 2{{x}^{2}}+x-3ge 0)
( 2{{x}^{2}}+x-3=0)
2) Найдём корни этого уравнения:
( {{x}_{1}}=-frac{3}{2};text{ }{{x}_{2}}=1)
3) Отметим корни на оси ( Ox) и схематично покажем ориентацию ветвей параболы («вверх» или «вниз»)
4) Расставим на оси знаки, соответствующие знаку квадратичной функции: там где парабола выше оси, ставим «( +)», а там где ниже – «( —)».
5) Выписываем интервал(ы), соответствующий(ие) «( +)» или «( —)», в зависимости от знака неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое — не входят.
( xin left( -infty ;-frac{3}{2} right]cup left[ 1;+infty right))
А теперь еще раз тоже самое но более сжато (то есть на языке математики)
Прежде чем говорить о теме «квадратные неравенства», вспомним что такое квадратичная функция и что из себя представляет её график.
Квадратичная функция – это функция вида ( fleft( x right)=a{{x}^{2}}+bx+c=0), ( ane 0)
Другими словами, это многочлен второй степени.
График квадратичной функции – парабола (помнишь, что это такое?)
- если ( a>0), то ветви параболы направлены вверх;
- если ( a<0), то ветви параболы направлены вниз.
Если парабола не пересекает ось Х и ее ветви направлены вверх, функция при всех значениях Х принимает лишь положительные значения.
Если парабола не пересекает ось Х и ее ветви направлены вниз – лишь отрицательные.
В случае, когда у уравнения (( 1)) ровно один корень (например, если дискриминант равен нулю), это значит, что график касается оси ( Ox):
Тогда, аналогично предыдущему случаю, при ( a>0) функция неотрицательна ( left( f(x) ge 0 right)) при всех ( x), а при ( a<0) – неположительна ( left( f(x) le 0 right)).
Так вот, мы ведь недавно уже научились определять, где квадратичная функция больше нуля, а где – меньше:
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое — не входят.
Если корень только один, – ничего страшного, будет везде один и тот же знак. Если корней нет, всё зависит только от коэффициента ( a): если ( a>0), то всё выражение больше 0, и наоборот.
Ну что, уловил? Тогда давай смотреть примеры!
ВИДЕО УРОК
Графическое решение линейных
неравенств.
ПРИМЕР:
Решите неравенство с помощью графика:
(х – 6)2 – (5 – х)2 < 3.
РЕШЕНИЕ:
Сначала проведём простейшие преобразования – раскроем
скобки полных квадратов и приведём подобные слагаемые:
(х – 6)2 – (5 – х)2 < 3,
(х2 – 12х + 36) – (25 – 10х + х2) < 3,
х2 – 12х + 36 – 25 + 10х – х2 < 3,
– 2х + 11 < 3,
– 2х < 3 – 11,
– 2х < –8,
Дальше делим обе части неравенства на отрицательное
число (–2), при этом надо поменять знак неравенства на
противоположный.
х ˃ 8/2,
х ˃ 4.
Неравенство нестрогое, поэтому 4 не включается в промежуток, и решением будут
являться все точки, которые находятся правее
4, так как
5
больше 4, 6 больше
4 и так
далее.
ОТВЕТ:
х ∈
(4; + ∞)
Графическое решение квадратных
неравенств.
Графиком
квадратичной функции
y = ах2 + bx + c
является парабола с
ветвями, направленными вверх, если а ˃ 0,
и вниз, если а < 0. При этом возможны три случая:
1) парабола пересекает ось х (то есть уравнение
ах2 + bx + c = 0
имеет два различных
корня);
2) парабола имеет вершину на оси х (то есть уравнение
ах2 + bx + c = 0
имеет один корень);
3) парабола не пересекает ось х (то есть уравнение
ах2 + bx + c = 0
не имеет корней).
Итого возможны
шесть положений параболы, служащей графиком функции
у = ах2 + bx
+ c
относительно оси х, – они представлены на рисунку.
Опираясь на эти графические иллюстрации, можно
решать квадратные неравенства.
Квадратным неравенством называют неравенства вида
ax2
+ bx
+ c
˃ 0,
где вместо знака
˃ может быть любой другой знак неравенства.
Для решения
квадратного неравенства с помощью графика нужно:
– определить направление ветвей параболы по знаку
старшего коэффициента квадратичной функции;
– найти корни соответствующего квадратного уравнения
или установить, что их нет;
– построить эскиз графика квадратичной функции,
учитывая точки пересечения (или касания) с осью Ох, если они есть;
– по графику определить промежутки, на которых
функция принимает нужные значения.
ПРИМЕР:
Решите неравенство графическим способом:
–х2 + 10х –21 < 0.
РЕШЕНИЕ:
Сначала решаем квадратное уравнение:
–х2 + 10х –21 = 0
D = b2 – 4ac,
D = 100 – 4 × (–1) × (–21)
= 100 – 84 = 16,
Затем схематично рисуем
параболу, не высчитывая, где у нё находится вершина, ведь по сути это не нужно,
у нас есть основное – точки пересечения параболы с осью Ох.
Возвращаемся к неравенству
–х2 + 10х –2 < 0.
и отмечаем нужные нам промежутки:
Запишем теперь ответ.
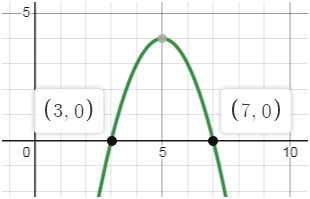
ОТВЕТ:
х ∈
(–∞; 3) ∪ (7; +∞)
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 ˃ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Решить неравенство
х2 – 2х – 3 ˃ 0
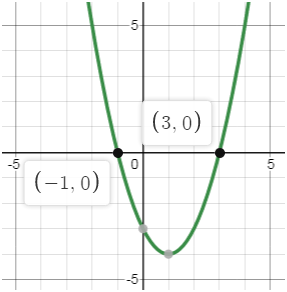
это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны.
Замечаем, что у ˃ 0, то есть график функции расположен выше оси х,
при х
< –1 и при х
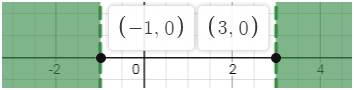
˃ 3. Значит, решениями неравенства служат все точки
интервалов
(–∞; –1) ∪ (3; +∞).
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 < 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Неравенство
х2 – 2х – 3 < 0
или у < 0, где
у = х2 – 2х – 3,
также можно решить с помощью графика. График расположен
ниже оси х,
если
–1 < х < 3.
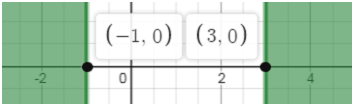
Поэтому решением данного неравенства служат все точки
интервала
(–1; 3).
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 ≥ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Неравенство
х2 – 2х – 3 ≥ 0
отличается от неравенства
х2 – 2х – 3 ˃ 0
тем, что в ответ надо включить и корни уравнения
х2 – 2х – 3 = 0
то есть точки
х1 = –1 и х2 = 3.
Таким образом, решениями данного нестрогого неравенства
являются все точки интервалов
(–∞; –1] ∪ [3; +∞)
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 ≤ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Неравенство
х2 – 2х – 3 ≤ 0
Отличается от неравенства
х2 – 2х – 3 < 0
тем, что в ответ надо включить и корни уравнения
х2 – 2х – 3 = 0,
то есть х1 = –1 и х2 = 3,
Следовательно, решениями данного нестрогого неравенства
служат все точки отрезка
[–1; 3].
ПРИМЕР:
Решите неравенство графическим способом:
х2 – х – 2 ≥ 0.
РЕШЕНИЕ:
Представим такое неравенство в виде
х2 ≥ х + 2.
В одной и той же системе координат построим графики
функций
у1 = х2 (парабола) и
у2 = х + 2 (прямая
линия).
Найдём абсциссы точек пересечения этих графиков. Приравняем
правые части функций и получим уравнение:
х2 = х + 2
или
х2 – х – 2 = 0.
Корни этого квадратного уравнения
х1 = –1 и х2 = 2.
Поэтому такие графики пересекаются в двух точках А и В,
абсциссы которых, соответственно, равны
х1 = –1 и х2 = 2.
Неравенству
х2 ≥ х + 2
или
у1 ≥ у2
удовлетворяют те значения х,
при которых значения первой функции больше или равны значениям второй функции,
то есть при которых график первой функции расположен выше или на уровне второй
функции. Из рисунка видно, что такими значениями являются все числа из
промежутков
х1 ≤ –1 и х2 ≥ 2.
Этот способ оказывается более полезным при решении
сложных неравенств (кубических неравенств, неравенств с модулем
и так далее).
ПРИМЕР:
Решите неравенство графическим способом:
–х2 + 2х – 1 ≥ 0.
РЕШЕНИЕ:
Запишем неравенство в виде
–(х – 1)2 ≥ 0
и построим эскиз графика функции
у = –(х – 1)2.
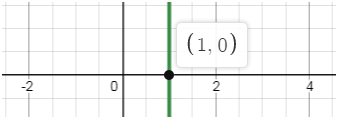
Ветви этой параболы направлены вниз. Уравнение
–(х – 1)2 = 0
имеет один корень х = 1.
Поэтому парабола касается оси Ох в точке
(1; 0). Для решения неравенства
–(х – 1)2 ≥ 0
надо определить, при каких значениях х функции
у неотрицательны.
Из рисунка видно, что функция положительных значений не
имеет. Значение у = 0 получается
только при х = 0. Поэтому
данное неравенство
–х2 + 2х – 1 ≥ 0
имеет единственное решение х = 1.
ПРИМЕР:
Решите неравенство графическим способом:
2х2 + 5х + 2 ˃ 0.
РЕШЕНИЕ:
Уравнение
2х2 + 5х + 2 = 0
имеет два корня:
х1 = –2, х2 = –1/2.
Парабола, служащая графиком функции
у = 2х2 + 5х + 2,
имеет вид, изображённый на рисунке.
Неравенство
2х2 + 5х + 2 ˃ 0
выполняется при тех значениях х,
при которых точки параболы лежат выше оси
х.
Это будет при
х < х1 или при х ˃ х2,
то есть при х < –2 или при
х ˃ –1/2.
Значит решения неравенства таковы:
х < –2, х ˃
–1/2.
ОТВЕТ:
х < –2, х ˃
–1/2
ПРИМЕР:
Решите неравенство графическим способом:
3х2 – 7х – 10 ≤ 0.
РЕШЕНИЕ:
Уравнение
3х2 – 7х – 10 = 0
имеет два корня:
х1 = –1, х2 = 10/3.
Парабола, служащая графиком функции
у = 3х2 – 7х – 10,
имеет вид, изображённый на рисунке.
Неравенство
3х2 – 7х – 10 ≤ 0
выполняется при тех значениях х,
при которых точки параболы лежат на оси х или ниже её. Это
будет при х из промежутка
[х1; х2]
Значит множество решений неравенства есть отрезок
[–1; 10/3].
ОТВЕТ: [–1; 10/3]
ПРИМЕР:
Решите неравенство графическим способом:
–х2 + 4х – 4 ˃ 0.
РЕШЕНИЕ:
Уравнение
–х2 + 4х – 4 = 0
имеет один корень:
х = 2.
Парабола, служащая графиком функции
у = –х2 + 4х – 4,
имеет вид, изображённый на рисунке.
Неравенство
–х2 + 4х – 4 ˃ 0
выполняется при тех значениях х,
при которых точки параболы лежат выше оси
х. Таких
точек нет. Значит, неравенство не имеет решений.
ОТВЕТ: решений
нет
ПРИМЕР:
Решите неравенство графическим способом:
–3х2 + х – 5 < 0.
РЕШЕНИЕ:
Уравнение
–3х2 + х – 5 = 0
не имеет действительных корней.
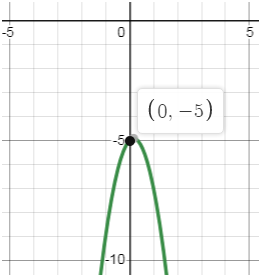
Парабола, служащая графиком функции
у = –3х2 + х – 5,
имеет вид, изображённый на рисунке.
Неравенство
–3х2 + х – 5 < 0
выполняется при тех значениях х,
при которых точки параболы лежат ниже оси
х. Так
как вся парабола лежит ниже оси х, то неравенство
выполняется при любых значениях х.
ОТВЕТ: –∞ < х < +∞
Графическое решение нелинейных
неравенств.
ПРИМЕР:
Решите неравенство графическим
способом:
√͞͞͞͞͞x
< 6 – х.
РЕШЕНИЕ:
Будуємо
графіки функцій
у = √͞͞͞͞͞x и у = 6 – х.
Графіки
перетинаються у точці (4; 2). Значення функції
у
= 6 – х
більші
від значень функції
у = √͞͞͞͞͞x,
якщо х ∈ (0; 4)
Покажем, как с помощью графика функции y = ax2 + bx + c решать квадратные неравенства.
Квадратичная функция, или парабола, — это функция вида
Вспомним свойства этой функции:
Координаты вершины параболы:
Если , ветви вверх
Если , ветви вниз
Точки пересечения с осью X: и
где и
— корни квадратного уравнения
Точка пересечения с осью Y: М (0; с).
Вспомним также, как выражение раскладывается на множители.
где и
— корни квадратного уравнения
1. Часто на тестировании мы предлагаем решить неравенство
x2 < 400
Справляются далеко не все. Очень часто, не задумываясь, выдают «ответ»: x < ± 20.
Однако сама эта запись — абсурдна! Представьте, что вы слышите прогноз погоды: «Температура будет меньше плюс-минус двадцати градусов». Что, спрашивается, надеть — рубашку или шубу? 
Давайте решим это неравенство с помощью графика. Изобразим схематично график функции y = x2 и отметим все значения x, для которых y < 400.
Теперь мы видим правильный ответ: x ∈ (−20; 20).
Запомним: извлекать корень из неравенства нельзя. Такого действия просто нет.
2. Следующее неравенство:
Переносим всё в левую часть неравенства. Раскладываем левую часть на множители.
Рисуем ось X. Рисуем параболу с ветвями вверх.
Эта парабола пересекает ось X в точках — 4 и 4. Отмечаем знаки выражения в левой части на каждом интервале.
Записываем ответ:
3. Решим неравенство: x2 − 3x − 10 ≥ 0.
Графиком функции y = x2 − 3x − 10 служит парабола, ветви которой направлены вверх. Решая квадратное уравнение x2 − 3x − 10 = 0, находим x1 = −2 и x2 = 5 — в этих точках парабола пересекает ось X. Нарисуем схематично нашу параболу:
Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит ниже оси X). В точках −2 и 5 функция обращается в нуль, а при x < −2 и x > 5 значения функции положительны. Следовательно, наше неравенство выполняется при .
Обратите внимание, что для решения неравенства нам достаточно было схематично изобразить параболу. Ось Y вообще не понадобилась!
4. Ещё одно неравенство: x2 + 2x + 4 > 0.
Ветви параболы y = x2 + 2x + 4 направлены вверх. Дискриминант отрицателен, т. е. уравнение x2 + 2x + 4 = 0 не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.
Раз ветви параболы направлены вверх и она не пересекает ось X — значит, парабола расположена над осью X.
Получается, что значения функции положительны при всех возможных x. Иными словами, решения нашего неравенства — это все действительные числа.
Ответ: .
Квадратные неравенства являются неотъемлемой частью ЕГЭ. Разберём типичные примеры из банка заданий ЕГЭ.
5. Следующее квадратичное неравенство:
Разложим его левую часть на множители.
Получим:
И больше ничего не пишем. Рисуем ось X. Рисуем параболу с ветвями вверх.
Эта парабола пересекает ось X в точках 1 и 5. Отмечаем знаки выражения в левой части на каждом интервале.
Записываем ответ:
6. Еще неравенство:
Квадратное уравнение не имеет решений — его дискриминант отрицателен. Это значит, что парабола
нигде не пересекает ось X. Ветви этой параболы направлены вверх. Все значения функции
положительны. Неравенство
выполняется для всех действительных X.
Соберем в одну таблицу примеры решения различных квадратичных неравенств.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Квадратичные неравенства» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Вопросы
занятия:
·
повторить, какие неравенства называются квадратичными;
·
подробно рассмотреть такой способ решения квадратных неравенств как
графический;
·
вспомнить алгоритм решения таких неравенств.
Материал
урока
Напомним,
что квадратным неравенством называется неравенство вида:
Для
решения такого рода неравенств как правило используют два основных метода
решения: графический и аналитический метод или по-другому, метод
интервалов. В любом случае, чтобы решить квадратное неравенство сначала
надо решить соответствующее квадратное уравнение.
Сегодня
мы с вами повторим графический метод решения квадратных неравенств.
Для
того, чтобы применить этот способ, давайте вспомним, что графиком квадратичной
функции является парабола.
Мы
знаем, что если рассматривать не неравенство, а квадратное уравнение, то, в
зависимости от знака дискриминанта у уравнения может не быть корней, быть один
или два корня.
Графически
решениями уравнения будут абсциссы точек пересечения параболы и оси Ох.
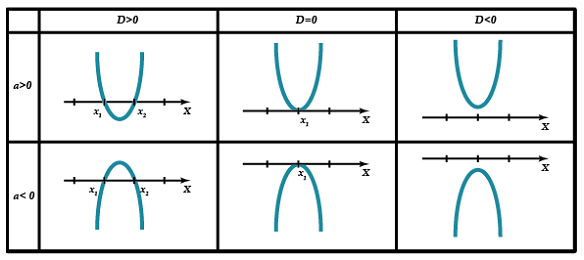
То
есть можно составить таблицу, в которой графически будут изображены все случаи,
пересечения параболы и оси Ох.
Найдя
корни соответствующего квадратного уравнения, решить квадратное неравенство
нетрудно.
Рассмотрим несколько примеров.
Пример.
Для
того, чтобы не заучивать таблицу, которую мы заполняли выше, давайте вспомним алгоритм
решения квадратного неравенства.
1.
Определить направление ветвей параболы.
2.
Найти корни соответствующего квадратного уравнения или установить, что это
уравнение не имеет корней.
3.
Схематично изобразить график квадратичной функции, отмечая абсциссы точек
пересечения графика с осью Ох.
4.
По графику определить промежутки, которые будут решениями неравенства.
Рассмотрим
пример.
Пример.
Рассмотрим
ещё один пример.
Пример.
Рассмотрим
ещё один пример.
Пример.
Итоги
урока
Сегодня
на уроке мы вспомнили какие неравенства называются квадратными, подробнее
рассмотрели такой способ решения квадратных неравенств как графический.
Вспомнили алгоритм решения таких неравенств.