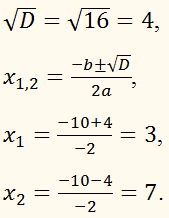ВИДЕО УРОК
Графическое решение линейных
неравенств.
ПРИМЕР:
Решите неравенство с помощью графика:
(х – 6)2 – (5 – х)2 < 3.
РЕШЕНИЕ:
Сначала проведём простейшие преобразования – раскроем
скобки полных квадратов и приведём подобные слагаемые:
(х – 6)2 – (5 – х)2 < 3,
(х2 – 12х + 36) – (25 – 10х + х2) < 3,
х2 – 12х + 36 – 25 + 10х – х2 < 3,
– 2х + 11 < 3,
– 2х < 3 – 11,
– 2х < –8,
Дальше делим обе части неравенства на отрицательное
число (–2), при этом надо поменять знак неравенства на
противоположный.
х ˃ 8/2,
х ˃ 4.
Неравенство нестрогое, поэтому 4 не включается в промежуток, и решением будут
являться все точки, которые находятся правее
4, так как
5
больше 4, 6 больше
4 и так
далее.
ОТВЕТ:
х ∈
(4; + ∞)
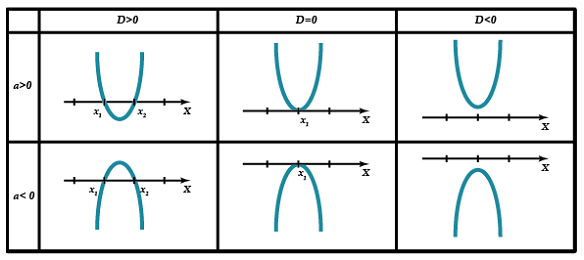
Графическое решение квадратных
неравенств.
Графиком
квадратичной функции
y = ах2 + bx + c
является парабола с
ветвями, направленными вверх, если а ˃ 0,
и вниз, если а < 0. При этом возможны три случая:
1) парабола пересекает ось х (то есть уравнение
ах2 + bx + c = 0
имеет два различных
корня);
2) парабола имеет вершину на оси х (то есть уравнение
ах2 + bx + c = 0
имеет один корень);
3) парабола не пересекает ось х (то есть уравнение
ах2 + bx + c = 0
не имеет корней).
Итого возможны
шесть положений параболы, служащей графиком функции
у = ах2 + bx
+ c
относительно оси х, – они представлены на рисунку.
Опираясь на эти графические иллюстрации, можно
решать квадратные неравенства.
Квадратным неравенством называют неравенства вида
ax2
+ bx
+ c
˃ 0,
где вместо знака
˃ может быть любой другой знак неравенства.
Для решения
квадратного неравенства с помощью графика нужно:
– определить направление ветвей параболы по знаку
старшего коэффициента квадратичной функции;
– найти корни соответствующего квадратного уравнения
или установить, что их нет;
– построить эскиз графика квадратичной функции,
учитывая точки пересечения (или касания) с осью Ох, если они есть;
– по графику определить промежутки, на которых
функция принимает нужные значения.
ПРИМЕР:
Решите неравенство графическим способом:
–х2 + 10х –21 < 0.
РЕШЕНИЕ:
Сначала решаем квадратное уравнение:
–х2 + 10х –21 = 0
D = b2 – 4ac,
D = 100 – 4 × (–1) × (–21)
= 100 – 84 = 16,
Затем схематично рисуем
параболу, не высчитывая, где у нё находится вершина, ведь по сути это не нужно,
у нас есть основное – точки пересечения параболы с осью Ох.
Возвращаемся к неравенству
–х2 + 10х –2 < 0.
и отмечаем нужные нам промежутки:
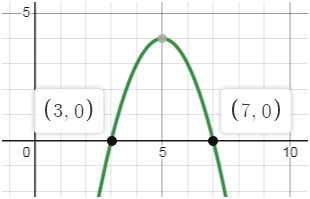
Запишем теперь ответ.
ОТВЕТ:
х ∈
(–∞; 3) ∪ (7; +∞)
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 ˃ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Решить неравенство
х2 – 2х – 3 ˃ 0
это значит ответить на вопрос, при каких значениях х ординаты точек параболы положительны.
Замечаем, что у ˃ 0, то есть график функции расположен выше оси х,
при х
< –1 и при х
˃ 3. Значит, решениями неравенства служат все точки
интервалов
(–∞; –1) ∪ (3; +∞).
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 < 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Неравенство
х2 – 2х – 3 < 0
или у < 0, где
у = х2 – 2х – 3,
также можно решить с помощью графика. График расположен
ниже оси х,
если
–1 < х < 3.
Поэтому решением данного неравенства служат все точки
интервала
(–1; 3).
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 ≥ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Неравенство
х2 – 2х – 3 ≥ 0
отличается от неравенства
х2 – 2х – 3 ˃ 0
тем, что в ответ надо включить и корни уравнения
х2 – 2х – 3 = 0
то есть точки
х1 = –1 и х2 = 3.
Таким образом, решениями данного нестрогого неравенства
являются все точки интервалов
(–∞; –1] ∪ [3; +∞)
ПРИМЕР:
Решите неравенство графическим способом:
х2 – 2х – 3 ≤ 0.
РЕШЕНИЕ:
Рассмотрим параболу
у = х2
– 2х – 3.
Неравенство
х2 – 2х – 3 ≤ 0
Отличается от неравенства
х2 – 2х – 3 < 0
тем, что в ответ надо включить и корни уравнения
х2 – 2х – 3 = 0,
то есть х1 = –1 и х2 = 3,
Следовательно, решениями данного нестрогого неравенства
служат все точки отрезка
[–1; 3].
ПРИМЕР:
Решите неравенство графическим способом:
х2 – х – 2 ≥ 0.
РЕШЕНИЕ:
Представим такое неравенство в виде
х2 ≥ х + 2.
В одной и той же системе координат построим графики
функций
у1 = х2 (парабола) и
у2 = х + 2 (прямая
линия).
Найдём абсциссы точек пересечения этих графиков. Приравняем
правые части функций и получим уравнение:
х2 = х + 2
или
х2 – х – 2 = 0.
Корни этого квадратного уравнения
х1 = –1 и х2 = 2.
Поэтому такие графики пересекаются в двух точках А и В,
абсциссы которых, соответственно, равны
х1 = –1 и х2 = 2.
Неравенству
х2 ≥ х + 2
или
у1 ≥ у2
удовлетворяют те значения х,
при которых значения первой функции больше или равны значениям второй функции,
то есть при которых график первой функции расположен выше или на уровне второй
функции. Из рисунка видно, что такими значениями являются все числа из
промежутков
х1 ≤ –1 и х2 ≥ 2.
Этот способ оказывается более полезным при решении
сложных неравенств (кубических неравенств, неравенств с модулем
и так далее).
ПРИМЕР:
Решите неравенство графическим способом:
–х2 + 2х – 1 ≥ 0.
РЕШЕНИЕ:
Запишем неравенство в виде
–(х – 1)2 ≥ 0
и построим эскиз графика функции
у = –(х – 1)2.
Ветви этой параболы направлены вниз. Уравнение
–(х – 1)2 = 0
имеет один корень х = 1.
Поэтому парабола касается оси Ох в точке
(1; 0). Для решения неравенства
–(х – 1)2 ≥ 0
надо определить, при каких значениях х функции
у неотрицательны.
Из рисунка видно, что функция положительных значений не
имеет. Значение у = 0 получается
только при х = 0. Поэтому
данное неравенство
–х2 + 2х – 1 ≥ 0
имеет единственное решение х = 1.
ПРИМЕР:
Решите неравенство графическим способом:
2х2 + 5х + 2 ˃ 0.
РЕШЕНИЕ:
Уравнение
2х2 + 5х + 2 = 0
имеет два корня:
х1 = –2, х2 = –1/2.
Парабола, служащая графиком функции
у = 2х2 + 5х + 2,
имеет вид, изображённый на рисунке.
Неравенство
2х2 + 5х + 2 ˃ 0
выполняется при тех значениях х,
при которых точки параболы лежат выше оси
х.
Это будет при
х < х1 или при х ˃ х2,
то есть при х < –2 или при
х ˃ –1/2.
Значит решения неравенства таковы:
х < –2, х ˃
–1/2.
ОТВЕТ:
х < –2, х ˃
–1/2
ПРИМЕР:
Решите неравенство графическим способом:
3х2 – 7х – 10 ≤ 0.
РЕШЕНИЕ:
Уравнение
3х2 – 7х – 10 = 0
имеет два корня:
х1 = –1, х2 = 10/3.
Парабола, служащая графиком функции
у = 3х2 – 7х – 10,
имеет вид, изображённый на рисунке.
Неравенство
3х2 – 7х – 10 ≤ 0
выполняется при тех значениях х,
при которых точки параболы лежат на оси х или ниже её. Это
будет при х из промежутка
[х1; х2]
Значит множество решений неравенства есть отрезок
[–1; 10/3].
ОТВЕТ: [–1; 10/3]
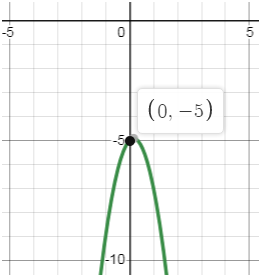
ПРИМЕР:
Решите неравенство графическим способом:
–х2 + 4х – 4 ˃ 0.
РЕШЕНИЕ:
Уравнение
–х2 + 4х – 4 = 0
имеет один корень:
х = 2.
Парабола, служащая графиком функции
у = –х2 + 4х – 4,
имеет вид, изображённый на рисунке.
Неравенство
–х2 + 4х – 4 ˃ 0
выполняется при тех значениях х,
при которых точки параболы лежат выше оси
х. Таких
точек нет. Значит, неравенство не имеет решений.
ОТВЕТ: решений
нет
ПРИМЕР:
Решите неравенство графическим способом:
–3х2 + х – 5 < 0.
РЕШЕНИЕ:
Уравнение
–3х2 + х – 5 = 0
не имеет действительных корней.
Парабола, служащая графиком функции
у = –3х2 + х – 5,
имеет вид, изображённый на рисунке.
Неравенство
–3х2 + х – 5 < 0
выполняется при тех значениях х,
при которых точки параболы лежат ниже оси
х. Так
как вся парабола лежит ниже оси х, то неравенство
выполняется при любых значениях х.
ОТВЕТ: –∞ < х < +∞
Графическое решение нелинейных
неравенств.
ПРИМЕР:
Решите неравенство графическим
способом:
√͞͞͞͞͞x
< 6 – х.
РЕШЕНИЕ:
Будуємо
графіки функцій
у = √͞͞͞͞͞x и у = 6 – х.
Графіки
перетинаються у точці (4; 2). Значення функції
у
= 6 – х
більші
від значень функції
у = √͞͞͞͞͞x,
якщо х ∈ (0; 4)
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
Решение уравнений с помощью графиков
Решение линейных уравнений
Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.
Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.
Сейчас же я покажу тебе, как это сделать графическим способом.
Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)
Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:
( displaystyle 2x=2+10)
( displaystyle 2x=12)
Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.
Иными словами, у нас будет:
( displaystyle {{y}_{1}}=2x)
( displaystyle {{y}_{2}}=12)
А теперь строим. Что у тебя получилось?
Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:
Наш ответ: ( displaystyle x=6)
Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!
Вариант 1. Напрямую
Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)
Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:
( displaystyle x=-frac{b}{2a})
( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})
Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.
Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!
Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:
( displaystyle x=frac{-2}{2}=-1)
( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:
Возвращаемся к нашей параболе.
Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?
Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).
При ( displaystyle x=0):
( displaystyle y={{0}^{2}}+0-8=-8)
При ( displaystyle x=2):
( displaystyle y={{2}^{2}}+2cdot 2-8=0)
Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:
Как ты думаешь, что является решением уравнения?
Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).
И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).
Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!
Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.
Что у тебя получилось? То же самое?
Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!
Решение смешанных неравенств
Теперь перейдем к более сложным неравенствам!
Как тебе такое:
( displaystyle 4x<{{x}^{3}})?
Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!
Первое, с чего мы начнем, – это с построения двух графиков:
( displaystyle {{y}_{1}}=4x)
( displaystyle {{y}_{2}}={{x}^{3}})
Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).
Расписал? Теперь строй два графика.
Сравним наши рисунки?
У тебя так же? Отлично!
Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).
Смотри, что получилось в итоге:
А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!
На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).
Это и есть ответ!
Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!
Загрузить PDF
Загрузить PDF
График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения). Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости. С помощью математических операций и знака неравенства можно определить множество решений неравенства.
-
1
Решите неравенство. Для этого изолируйте переменную при помощи тех же алгебраических приемов, которыми пользуетесь при решении любого уравнения.[1]
Помните, что при умножении или делении неравенства на отрицательное число (или член), поменяйте знак неравенства на противоположный. -
2
Нарисуйте числовую прямую. На числовой прямой отметьте найденное значение (переменная может быть меньше, больше или равна этому значению). Числовую прямую рисуйте соответствующей длины (длинную или короткую).
- Например, если вы вычислили, что
, на числовой прямой отметьте значение 1.
- Например, если вы вычислили, что
-
3
-
4
На числовой прямой заштрихуйте область, определяющую множество решений. Если переменная больше найденного значения, заштрихуйте область справа от него, потому что множество решений включает все значения, которые больше найденного. Если переменная меньше найденного значения, заштрихуйте область слева от него, потому что множество решений включает все значения, которые меньше найденного.[3]
- Например, если дано неравенство
, на числовой прямой заштрихуйте область справа от 1, потому что множество решений включает все значения больше 1.
Реклама
- Например, если дано неравенство
-
1
Решите неравенство (найдите значение
). Чтобы получить линейное уравнение, изолируйте переменную на левой стороне при помощи известных алгебраических методов.[4]
В правой части должна остаться переменнаяи, возможно, некоторая постоянная.
-
2
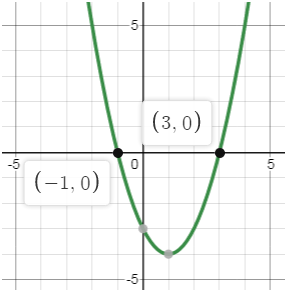
На координатной плоскости постройте график линейного уравнения. Для этого преобразуйте неравенство в уравнение и постройте график, как строите график любого линейного уравнения.[5]
Нанесите точку пересечения с осью Y, а затем при помощи углового коэффициента нанесите другие точки. -
3
-
4
Реклама
-
1
-
2
На координатной плоскости постройте график. Для этого преобразуйте неравенство в уравнение и постройте график, как строите график любого квадратного уравнения. Помните, что график квадратного уравнения является параболой.[9]
-
3
-
4
Выберите несколько контрольных точек. Чтобы определить, какую область заштриховать, выберите точки внутри и снаружи параболы.
-
5
Заштрихуйте соответствующую область. Чтобы определить, какую область заштриховать, в исходное неравенство подставьте значения
и
контрольных точек. Если при подстановке координат некоторой точки неравенство выполняется, заштрихуйте область, в которой лежит эта точка.[11]
Реклама
Советы
- Всегда упрощайте неравенство, прежде чем строить его график.
- Если вы не можете решить задачу, введите неравенство в графический калькулятор и попытайтесь справиться с задачей, действуя в обратном направлении.
Реклама
Об этой статье
Эту страницу просматривали 55 098 раз.
Была ли эта статья полезной?
Видеоурок 1: Графический способ решения неравенств
Видеоурок 2: Графики неравенств
Лекция: Использование свойств и графиков функций при решении неравенств
Для решения неравенств можно пользоваться аналитическим и графическим способами. Но, несмотря на способ, который Вы выберете, необходимо учитывать свойства функций и вид их графиков.

1. Парность/ непарность
Если функция на графике является симметричной относительно оси ОУ, то данная функция будет называться парной. Для такой функции значение функции будет одинаковым, как для положительных «х», так и для отрицательных.
f(-x) = f(x).
можно назвать квадратичную функцию, графиком которой является парабола с вершиной в начале координат. Так же график выражения в модуле будет являться парной функцией. Среди тригонометрических функций существует единственная функция, которую можно назвать парной — косинус без сдвига фаз.
Если функция симметрична относительно начала координат, то её называют
непарной
.
f(-x) = — f(x).
К таким функциям можно отнести любую функцию, старший член которой будет иметь нечетную степень или же, например, функция синуса.
Множество остальных функций нельзя отнести ни к парным, ни к непарным.
2. Периодичность
Если некоторая функция повторяется через некоторый период. Такие функцию будут повторяться до бесконечности. К периодичным функциям относятся все тригонометрические функции, не ограниченные на некотором промежутке.
3. Нули функции и промежутки знакопостоянства
Нуль функций — это такое значение ординаты, при которой функция обращается в нуль.
Когда мы находим решение уравнений, мы, как раз, находим нули функций. Иными словами нулем называется точка, в которой график функции пересекает ось ОХ.
Промежутки знакопостоянства — это диапазон, в котором функция имеет одинаковый знак, то есть принимает только положительные, или только отрицательные значения.
Нули функции разбивает всю числовую прямую на интервалы. Именно относительно нулей происходит решение неравенств высоких степеней. Чередование знаков на промежутках происходит именно относительно нулей функции.
Судя по указанному графику, если нам необходимо найти решение неравенств, где функция будет больше нуля, нам подходят диапазоны (-10; -8), (-4; 5).
4. Убывание/ возрастание функции
Если на некотором промежутке [а,б] функция f(x1) < f(x2) для любых x1 < x2, то такую функцию называют монотонно возрастающей.
Если на некотором промежутке [а,б] функция f(x1) > f(x2) для любых x1 < x2, то такую функцию называют монотонно убывающей.
5. Минимум/ максимум/ экстремум
Если для некоторого участка функции в точке выполняется неравенство f(x1) < f(x0)(f(x1) > f(x0)), то точка x0 является максимумом (минимумом) функции.
То есть точкой, в которой функция будет принимать максимальное (минимальное) значение.
Точки, в которых функция принимает максимальное или минимальное значения, называются экстремумами функции.
В данном случае xmax, xmin — точки экстремума, а функция в данной точке называется экстремумом функции.
Точки, в которых производная функции равная нулю или не существует вовсе, называются критическими точками.
Если производная некоторой функции в точке равна нулю, а вторая производная отлична от нуля, то данная точка будет точкой максимума, если вторая производная меньше нуля, и минимума, если она больше нуля.
6. ОДЗ
Это одно из наиболее важных свойств функций, используемых в неравенствах, поскольку ОДЗ позволяет моментально, на первых этапах избавиться от возможных решений системы.