Как найти множество степень

Онлайн калькулятор для вычисления булеана (степень множества, показательное множество, множество частей) — множество всех подмножеств некоего множества A называют булеаном или степенью множества A. Обозначается булеан как P(A) или 2A .

В математике для данного множества , степень множества, множество подмножеств или булеан , записывается как , или — это множество всех подмножеств множества . В аксиоматической теории множеств, существование булеана произвольного множества постулируется аксиомой булеана.

Любое подмножество из называется семейством множеств под .

Например, если — это множество , то полный список подмножеств имеет вид:

и, следовательно, булеан множества равен

Если — конечное множество из элементов, то его булеан состоит из элементов. (Можно – и компьютеры иногда так делают – представить элементы как —битовые числа; -й бит отвечает за присутствие или отсутствие -го элемента из в соответствующем подмножестве. Существует таких -битовых чисел.)

Диагональ Кантора показывает, что булеан множества (бесконечного или нет) всегда имеет строго большую мощность, чем само множество (проще говоря, булеан должен быть ‘больше’, чем исходное множество). Булеан множества натуральных чисел, например, можно поставить во взаимно-однозначное соответствие с множеством вещественных чисел (см. мощность континуума).

Булеан множества вместе с операциями объединения, пересечения и дополнения можно рассматривать как типичный пример булевой алгебры. Действительно, можно показать, что любая конечная булева алгебра изоморфна булевой алгебре булеана конечного множества. Для бесконечных булевых алгебр это не остается верным, но каждая булева алгебра является подалгеброй булевой алгебры (хотя это не всегда особенно упоминаемое представление бесконечной Булевой алгебры).

Булеан множества образует абелеву группу, когда рассматривается вместе с операцией симметрической разности (с пустым множеством в качестве единицы и каждым множеством, обратным самому себе) и коммутативной полугруппой, когда рассматривается вместе с операцией пересечения. Можно, следовательно, показать (используя дистрибутивные законы), что булеан, рассматриваемый вместе с двумя этими операциями образует коммутативное кольцо.

Обозначения и

В теории множеств — это множество всех функций из в . Поскольку можно определить как , то (т.е., ) — это множество всех функций из в . Сопоставляя функции из соответствующий прообраз из 1, мы увидим, что существует биекция между и , где каждая функция – это индикаторная функция того подмножества из , которому она сопоставлена. Следовательно, и могут рассматриваться идентичными в в теоретико-множественном смысле.

См. также

• Булеан множества событий

Рассмотрим
декартово произведение

,
в котором декартовы сомножители
совпадают:

.
Обозначим каждое из этих множеств через

.
Тогда декартово произведение

представляет собой декартову


степень множества

:

.

Декартова
степень множества

с показателем степени

представляет собой множество упорядоченных

.
Высказывательная форма множества

имеет вид:

.

Пример 2.9

Рассмотрим
множество

.
Найдём для него вторую декартову степень:

.

Аналогично
можно задать множество, представляющее
слбой третью декартову степень множества

:

.

Если
число элементов множества

обозначить как

,
то

.

2.8. Сечение и проекция

Сначала
разберём понятие проекции. Рассмотрим
некоторое множество

и

.
В соответствии с определением элемент

представляет собой упорядоченную пару

,
первый элемент которой принадлежит
множеству

,
а второй – множеству

:

,

.
Элемент

является проекцией множества

на множество

и обозначается

,
а

проекцией множества

на множество

и обозначается

.

Рассмотрим
множество Е, которое представляет
собой подмножество множества

:

.

Можно
говорить о проекции подмножества E
на множества

и

.

Проекцией
множества

на множество

называется множество тех элементов,
которые являются проекциями всех
элементов множества

на множество

.
Высказывательная форма проекций
множества

на множества

и

записывается в виде:

,

.

Пример 2.10

Рассмотрим
множества

и

.
Множество

зададим таблицей 2.1.

Зададим
множество

методом перечисления его элементов:

.

Тогда
если

,
то

,

,

,

.

Таблица 2.1

Декартово произведение

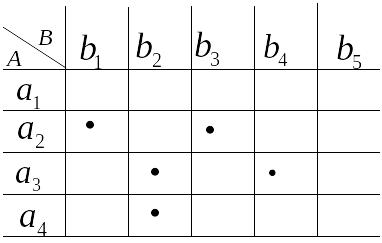
Пример 2.11

Декартово
произведение

.
Если

и

представляют собой множества действительных
чисел, то геометрической интерпретацией
множества

является множество точек плоскости

(рис 2.10.).

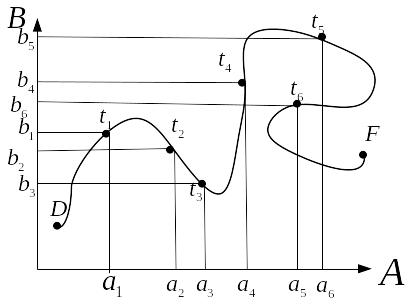
Рис. 2.10. Множество

для примера 1

Рассмотрим
подмножество

,
представляющее собой некоторую кривую

и множество

,
в свою очередь являющееся подмножеством

,

.
Проекциями множества

на множества

и

являются следующие множества:

,

.

Множество

может представлять собой декартово
произведение множеств, число которых
больше двух:

.

Если
рассмотреть некоторое подмножество
этого множества

,
то можно говорить о проекции этого
множества на множество

:

.

Разберём
понятие сечения. Рассмотрим некоторый
элемент

из множества

.
Тогда сечение множества

элементом

называется множество элементов из

,
которые составляют упорядоченную пару
из множества

:

.

Аналогично
можно рассматривать сечение множества

элементом

:

.

Пример 2.12

Рассмотрим
множества

,

и множество

,
заданное таблицей 2.1. Тогда сечением
множества

элементом

является множество

,
а сечением множества

элементом

является множество

.

Рассмотрим
понятие сечения, когда множество

является подмножеством множества

.

Тогда
сечение множества

элементом

представляет собой множество, задаваемое
высказывательной формой:

.

Можно
говорить о сечении множества

более сложным элементом, представляющим
собой упорядоченное множество

:

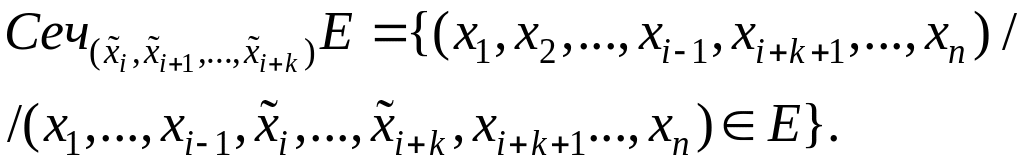
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.

Прямое произведение в теории множеств

Произведение двух множеств

в	в	в	в	в	в	в	в
и	и	и	и	и	и	и	и
к	к	к	к	к	к	к	к
Произведение множества {в, и, к} на множество цветов радуги

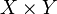
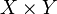
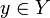
Пусть дано два множества X и Y. Прямое произведение множества X и множества Y есть такое множество , элементами которого являются упорядоченные пары (x,y) для всевозможных и .

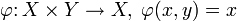
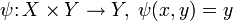
Отображения произведения множеств в его множители ( и ) называют координатными функциями.

Аналогично строятся произведения нескольких множеств.

Декартова степень

000	001	002	010	011	012	020	021	022
100	101	102	110	111	112	120	121	122
200	201	202	210	211	212	220	221	222
{0, 1, 2}3, 33 = 27 элементов

n-я Декартова степень множества X определяется для целых неотрицательных n, как n-кратное Декартово произведение X на себя:

При положительных n Декартова степень Xⁿ состоит из всех упорядоченных наборов (кортежей) элементов из X длины n.

При n = 0, Декартова степень X⁰ по определению содержит единственный элемент — пустой кортеж.

Прямое произведение семейства множеств

Дальнейшее обобщение понятия прямого произведения приводит к произведениям по индексному множеству I (возможно, бесконечному): X = ΠX_i, элементы которого сопоставляют каждому индексу i из I элемент множества X_i.

Прямое произведение отображений

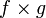
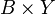
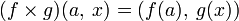
Пусть f — отображение из A в B, а g — отображение из X в Y. Их прямым произведением называется отображение из в : .

Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.

Воздействие на математические структуры

Прямое произведение групп

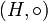
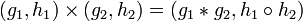
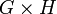
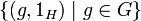
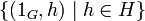
Прямое (декартово) произведение двух групп (G, * ) и  — это группа из всех пар элементов (g,h) с операцией поэлементного умножения: . Эта группа обозначается как . Сомножители G и H изоморфны двум нормальным подгруппам своего произведения, и соответственно. Пересечение этих подгрупп состоит из одного элемента (1_G,1_H), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.

Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.

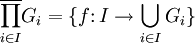
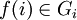
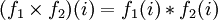
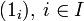
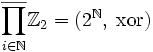
Однако, для бесконечного числа перемножаемых групп понятия декартового и прямого произведения принято различать. В общем случае, , где и . (Операция в правой части — это операция группы G_i.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: . Например, для счётного числа групп: , где в правой части стоит множество всех бесконечных двоичных последовательностей.

Подгруппа на множестве всех f, носитель которых (то есть множество 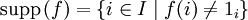) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать как двоичные представления натуральных чисел.

Прямое произведение других алгебраических структур

Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1_i (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.

Прямое произведение топологических пространств

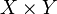
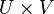
Пусть X и Y — два топологических пространства. Топология произведения задаётся базой, состоящей из всевозможных произведений , где U — открытое подмножество X и V — открытое подмножество Y.

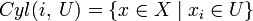
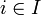
Определение легко обобщается на случай произведения нескольких пространств. Для бесконечного произведения X = ΠX_i определение усложняется. Определим открытый цилиндр , где и U — открытое подмножество X_i.

Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).

Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).

Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).

Прямое произведение графов

	—	
	—	
		
	—	

Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:

Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.

Вариации и обобщения

Дальнейшее развитие идея прямого произведения получила в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов A и B — это наиболее общий объект в данной категории, для которого существуют проекции на A и B. Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные объекты.

См. также

• Дизъюнктное объединение
• Полупрямое произведение
• Прямая сумма
• Тензорное произведение
• Декартовы координаты
• Операции над множествами
• Комбинаторика

Prerequisite – Introduction of Set theory, Set Operations (Set theory) 
For a given set S, Power set P(S) or 2^S represents the set containing all possible subsets of S as its elements. For example, 
S = {1, 2, 3} 
P(S) = {ɸ, {1}, {2}, {3} {1,2}, {1,3}, {2,3}, {1,2,3}} 

Number of Elements in Power Set – 
For a given set S with n elements, number of elements in P(S) is 2^n. As each element has two possibilities (present or absent}, possible subsets are 2×2×2.. n times = 2^n. Therefore, power set contains 2^n elements. 

Note – 

• Power set of a finite set is finite.
• Set S is an element of power set of S which can be written as S ɛ P(S).
• Empty Set ɸ is an element of power set of S which can be written as ɸ ɛ P(S).
• Empty set ɸ is subset of power set of S which can be written as ɸ ⊂ P(S).

Let us discuss the questions based on power set. 

Q1. The cardinality of the power set of {0, 1, 2 . . ., 10} is _________. 
(A) 1024 
(B) 1023 
(C) 2048 
(D) 2043 

Solution: The cardinality of a set is the number of elements contained. For a set S with n elements, its power set contains 2^n elements. For n = 11, size of power set is 2^11 = 2048. 

Q2. For a set A, the power set of A is denoted by 2^A. If A = {5, {6}, {7}}, which of the following options are True. 

I.Φ ϵ 2 A         II.  Φ⊆ 2 A       III. {5,{6}} ϵ 2 A       IV. {5,{6}} ⊆ 2 A 

(A) I and III only 
(B) II and III only 
(C) I, II and III only 
(D) I, II and IV only 

Explanation: The set A has 5, {6}, {7} has its elements. Therefore, the power set of A is: 

2^S = {ɸ, {5}, {{6}}, {{7}}, {5,{6}}, {5,{7}}, {{6},{7}}, {5,{6},{7}} } 

Statement I is true as we can see ɸ is an element of 2^S. 
Statement II is true as empty set ɸ is subset of every set. 
Statement III is true as {5,{6}} is an element of 2^S. 
However, statement IV is not true as {5,{6}} is an element of 2^S and not a subset. 
Therefore, correct option is (C). 

Q3. Let P(S) denotes the power set of set S. Which of the following is always true? 
 

(a) P(P(S))=P(S)          (b) P(S) ∩ P(P(S)) = { Φ }
(c) P(S) ∩ S = P(S)       (d) S ∉ P(S)

(A) a 
(B) b 
(C) c 
(D) d 

Solution: Let us assume set S ={1, 2}. Therefore P(S) = { ɸ, {1}, {2}, {1,2}} 
Option (a) is false as P(S) has 2^2 = 4 elements and P(P(S)) has 2^4 = 16 elements and they are not equivalent. 
Option (b) is true as intersection of P(P(S) )and P(S) is empty set. 
Option (c) is false as intersection of S and P(S) is empty set. 
Option (d) is false as S is an element of P(S). 

Countable set and its power set – 
A set is called countable when its element can be counted. A countable set can be finite or infinite. 
For example, set S1 = {a, e, i, o, u} representing vowels is a countably finite set. However, S2 = {1, 2, 3……} representing set of natural numbers is a countably infinite set. 

Note – 

• Power set of countably finite set is finite and hence countable. 
  For example, set S1 representing vowels has 5 elements and its power set contains 2^5 = 32 elements. Therefore, it is finite and hence countable.
• Power set of countably infinite set is uncountable. 
  For example, set S2 representing set of natural numbers is countably infinite. However, its power set is uncountable.

Uncountable set and its power set – 
A set is called uncountable when its element can’t be counted. An uncountable set can be always infinite. 
For example, set S3 containing all real numbers between 1 and 10 is uncountable. 

Note – 

• Power set of uncountable set is always uncountable. 
  For example, set S3 representing all real numbers between 1 and 10 is uncountable. Therefore, power set of uncountable set is also uncountable. 
   

Let us discuss gate questions on this. 

Q4. Let ∑ be a finite non-empty alphabet and let 2^∑* be the power set of ∑*. Which of the following is true? 
 

(A). Both 2^∑*  and ∑* are countable  
(B). 2^∑*  is countable and ∑* is uncountable
(C). 2^∑*  is uncountable and ∑* is countable  
(D). Both 2^∑* and ∑* are uncountable

Solution: Let ∑ = {a, b} 
then ∑* = { ε, a, b, aa, ba, bb, ……………….}. 
As we can see, ∑* is countably infinite and hence countable. But power set of countably infinite set is uncountable. 
Therefore, 2^∑* is uncountable. So, the correct option is (C). 

Last Updated :
23 Feb, 2022

Like Article

Save Article