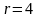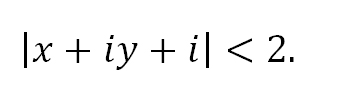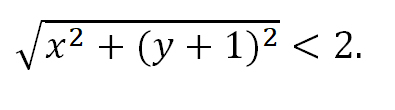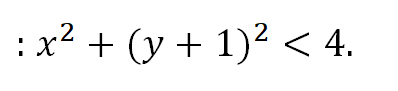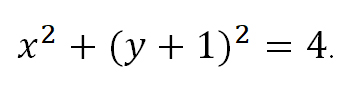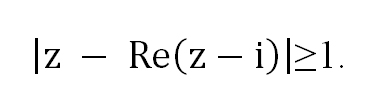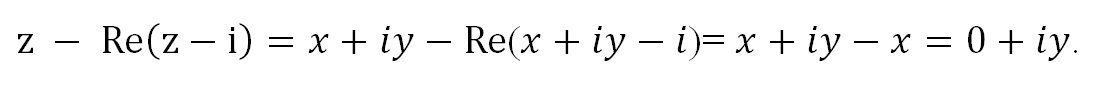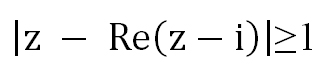В данной статье я отвечаю на очередной вопрос от моих подписчиков. Вопросы приходят разные. Не все из них корректно сформулированы. А некоторые из них сформулированы так, что не сразу получается понять, о чём хочет спросить автор. Поэтому среди огромного множества присылаемых вопросов приходится отбирать действительно интересные, такие «жемчужины», отвечать на которые не просто увлекательно, но ещё и полезно, как мне кажется, для других моих читателей. И сегодня я отвечаю на один из таких вопросов. Как изобразить множество решений системы неравенств?
Это действительно хороший вопрос. Потому что метод графического решения задач в математике — это очень мощный метод. Человек так устроен, что ему удобнее воспринимать информацию с помощью различных наглядных материалов. Поэтому если вы овладеете этим методом, то поверьте, он для вас окажется незаменимым как при решении заданий из ЕГЭ, особенно из второй части, других экзаменов, так и при решении задач оптимизации и так далее, и так далее.
Так вот. Как же нам ответить на этот вопрос. Давайте начнём с простого. Пусть в системе неравенств содержится только одна переменная .
Упростим эту систему. Для этого прибавим к обеим частям первого неравенства 7 и поделим обе части на 2, не меняя при этом знак неравенства, так как 2 — положительное число. К обеим частям второго неравенства прибавим 4. В результате получим следующую систему неравенств:
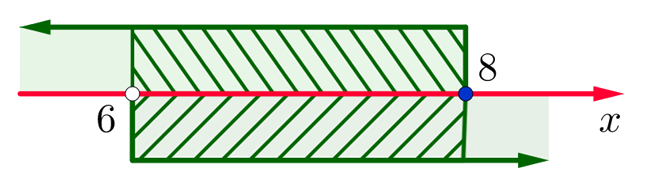
Обычно такую задачу называют одномерной. Почему? Да потому что для того, чтобы изобразить множество её решений, достаточно прямой. Числовой прямой, если быть точным. Отметим точки 6 и 8 на этой числовой прямой. Понятно, что точка 8 будет находиться правее, чем точка 6, потому что на числовой прямой большие числа находятся правее меньших. Кроме того, точка 8 будет закрашенной, так как согласно записи первого неравенства она входит в его решение. Наоборот, точка 6 будет незакрашенной, так как она не входит в решение второго неравенства:
Отметим теперь стрелочной сверху значения , которые меньше или равны 8, как того требует первое неравенство системы, а стрелочкой снизу — значения
, которые больше 6, как того требует второе неравенство системы:
Осталось ответить на вопрос, где на числовой прямой находятся решения системы неравенств. Запомните раз и навсегда. Знак системы — фигурная скобка — в математике заменяет союз «И». То есть, переводя язык формул на человеческий язык, можно сказать, что от нас требуется указать значения , которые больше 6 И меньше или равны 8. То есть искомый промежуток лежит на пересечении отмеченных промежутков:
Вот мы и изобразили множество решений системы неравенств на числовой прямой в случае, если в системе неравенств содержится только одна переменная. В этот заштрихованный промежуток входят все значения , при которых все неравенства, записанные в системе, выполняются.
Рассмотрим теперь более сложный случай. Пусть в нашей системе содержатся неравенства с двумя переменными и
. В этом случае обойтись только прямой для изображения решений такой системы не получится. Мы выходим за рамки одномерного мира и добавляем к нему ещё одно измерение. Здесь нам понадобится уже целая плоскость. Рассмотрим ситуацию на конкретном примере.
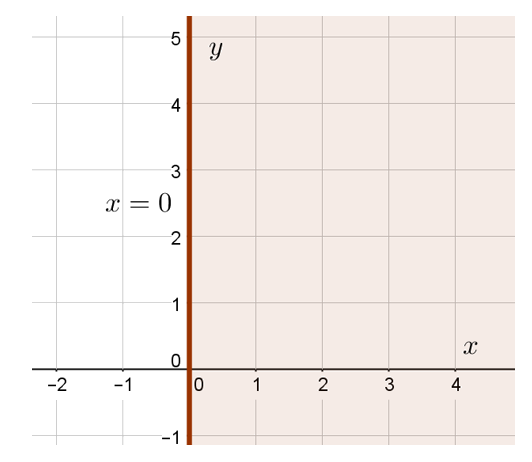
Итак, как же можно изобразить множество решений данной системы неравенств с двумя переменными в прямоугольной системе координат на плоскости? Начнём с самого простого. Зададимся вопросом, какую область этой плоскости задаёт неравенство . Уравнение
задаёт прямую, проходящую перпендикулярно оси OX через точку (0;0). То есть фактически это прямая совпадает с осью OY. Ну а раз нас интересуют значения
, которые больше или равны 0, то подойдёт вся полуплоскость, лежащая справа от прямой
:
Причём все точки, которые лежат на оси OY, нам тоже подходят, потому что неравенство — нестрогое.
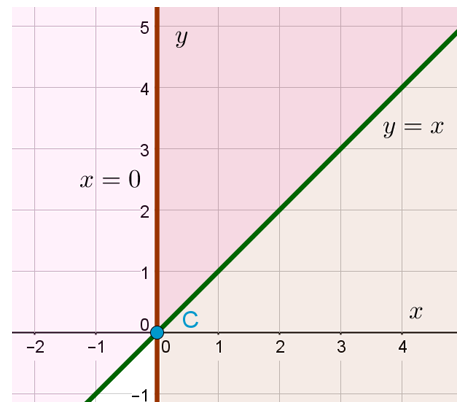
Чтобы понять, какую область на координатной плоскости задаёт третье неравенство, нужно построить график функции . Это прямая, проходящая через начало координат и, например, точку (1;1). То есть фактически это прямая, содержащая биссектрису угла, образующего первую координатную четверть.
А теперь посмотрим на третье неравенство в системе и подумаем. Какую область нам нужно найти? Смотрим: . Знак «больше или равно». То есть ситуация аналогична той, что была в предыдущем примере. Только здесь «больше» означает не «правее», а «выше». Потому что OY — это у нас вертикальная ось. То есть область, задаваемая на плоскости третьим неравенством, — это множество точек, находящихся выше прямой
или на ней:
С первым неравенством системы чуть менее удобно. Но после того, как мы смогли определить область, задаваемую третьим неравенством, я думаю, что уже понятно, как нужно действовать.
Нужно представить это неравенство в таком виде, чтобы слева находилась только переменная , а справа — только переменная
. Для этого вычтем из обеих частей неравенства
и поделим обе части на 2, не меняя при этом знак неравенства, потому что 2 — это положительное число. В результате получаем следующее неравенство:
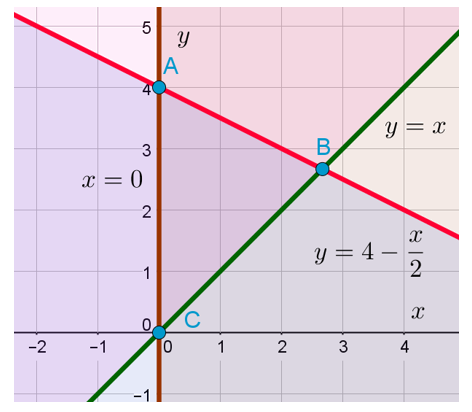
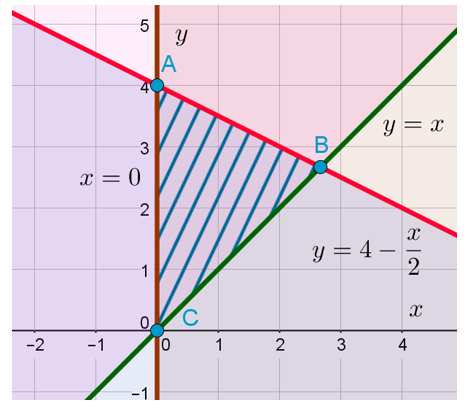
Осталось только изобразить на координатной плоскости прямую , которая пересекает ось OY в точке A(0;4) и прямую
в точке
. Последнее я узнал, приравняв правые части уравнений прямых и получив уравнение
. Из этого уравнения находится координата
точки пересечения, а координата
, я думаю вы догадались, равна координате
. Для тех, кто всё-таки не догадался, это потому что у нас уравнение одной из пересекающихся прямых:
.
Как только мы нарисовали эту прямую, сразу можно отметить искомую область. Знак неравенства у нас здесь «меньше или равно». Значит, искомая область находится ниже или непосредственно на изображённой прямой:
Ну и последний вопрос. Где же всё-таки находится искомая область, удовлетворяющая всем трём неравенствами системы? Очевидно, что она находится на пересечении всех трёх отмеченных областей. Опять пересечение! Запомните: знак системы в математике означает пересечение. Вот она, эта область:
Ну и последний пример. Ещё более общий. Предположим теперь что у нас не одна переменная в системе и ни две, а аж целых три!
Поскольку переменных целых три, то для изображения множества решений такой системы неравенств нам потребуется третье измерение в добавок к двум, с которыми мы работали в предыдущем примере. То есть мы вылезаем из плоскости в пространство и изображаем уже пространственную систему координат с тремя измерениями: X, Y и Z. Что соответствует длине, ширине и высоте.
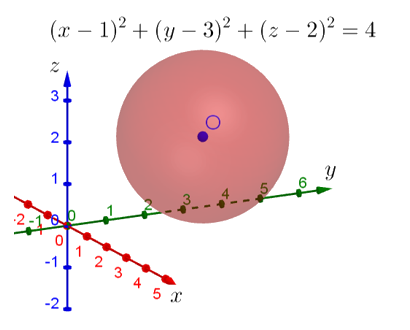
Начнём с того, что изобразим в этой системе координат поверхность, задаваемую уравнением . По форме оно очень напоминает уравнение окружности на плоскости, только добавляется ещё одно слагаемое с переменной
. Несложно догадаться, что это уравнение сферы с центром в точке (1;3;2), квадрат радиуса которой равен 4. То есть сам радиус равен 2.
Тогда вопрос. А что тогда задаёт само неравенство? Для тех, кого этот вопрос ставит в тупик, предлагаю рассудить следующим образом. Переводя язык формул на человеческий, можно сказать, что требуется указать все сферы с центром в точке (1;3;2), радиусы которых меньше или равны 2. Но тогда все эти сферы будут находиться внутри изображённой сферы! То есть фактически данным неравенством задаётся вся внутренняя область изображённой сферы. Если хотите, задаётся шар, ограниченный изображённой сферой:
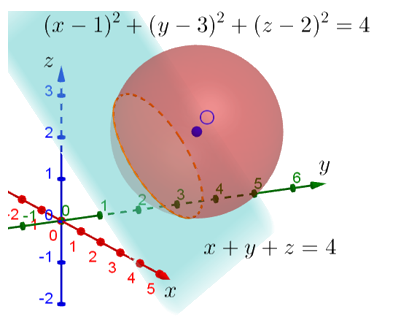
Поверхность, которую задаёт уравнение x+y+z=4 — это плоскость, которая пересекает оси координат в точках (0;0;4), (0;4;0) и (4;0;0). Ну и понятно, что чем больше будет число справа от знака равенства, тем дальше от центра координат будут находиться точки пересечения этой плоскости с осями координат. То есть второе неравенство задаёт полупространство, находящееся «выше» данной плоскости. Используя условный термин «выше», я имею ввиду дальше в сторону увеличения значений координат по осям.
Данная плоскость пересекает изображённую сферу. При этом сечение пересечения — это окружность. Можно даже посчитать, на каком расстоянии от центра системы координат находится центр этой окружности. Кстати, кто догадается, как это сделать, пишите свои решения и ответы в комментариях. Таким образом исходная система неравенств задаёт область пространства, которая находится дальше от этой плоскости в сторону увеличения координат, но заключённая в изображённую сферу:
Вот таким образом изображают множество решений системы неравенств. В случае, если переменных в системе больше, чем 3 (например, 4), наглядно изобразить множество решений уже не получится. Потому что для этого потребовалась бы 4-х мерная система координат. Но нормальный человек не способен представить себе, как могли бы располагаться 4 взаимно перпендикулярные оси координат. Хотя у меня есть знакомый, который утверждает, что может сделать это, причём с лёгкостью. Не знаю, правду ли он говорит, может быть и правду. Но всё-таки нормальное человеческое воображение этого сделать не позволяет.
Надеюсь, сегодняшний урок оказался для вас полезным. Чтобы проверить, насколько хорошо вы его усвоили, выполните записанное ниже домашнее задание.
Изобразите множество решений системы неравенств:
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
и неравенствами
с двумя переменными
Пусть на плоскости
выбрана система координат. Тогда любое
уравнение с двумя переменными F(x;y) = 0 задает множество
точек на плоскости, а именно множество
точекM(x;y), координатыкоторых
удовлетворяют этому уравнению.
Например, точка
M(– 3; 4) принадлежит
множеству, заданному уравнениемx2+y2= 25, а точкаN(1; 6) не принадлежит
этому множеству, так как (–3)2+ 42= 25, а 12+ 62≠ 25. В этом легко
убедиться, если построить график данного
уравнения в декартовой системе координат
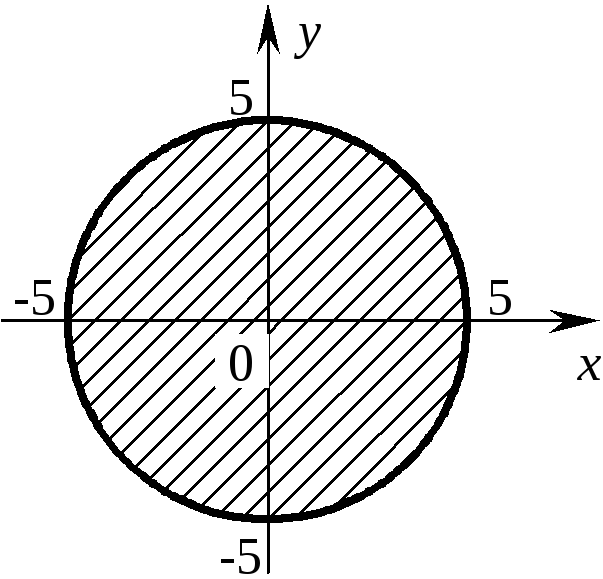
(рис. 7.1). Геометрическим местом всех
точек, принадлежащих этому множеству,
является окружностьR= 5 с центром в начале координат.
Рис. 7.1
Если мы рассмотрим
множество, заданное в виде неравенства
x2+y2< 25, то множеством будут являться все
точки, находящиеся внутри этой окружности
(рис.7.2). Сама окружность изображена
пунктиром, чтобы показать, что точки,
принадлежащие самой окружности (границе
области) в данном случае на нее не
попадают и точкаM(–
3; 4)множествуx2+y2< 25 (области),
в чем легко убедится, а точкаN(1;
2){x2+y2< 25}.
Рис.
7.2
Если же x2+y2≤ 25, то здесь
уже войдет и граница (сама окружность).
Изобразим ее жирной линией (рис. 7.3).
Рис.
7.3
То же касается
систем линейных неравенств.
Пример.Построить область допустимых решений
системы линейных неравенств.
Решение.Нумеруем ограничения задачи
В прямоугольной
декартовой системе координат (рис. 7.4)
строим прямую 2x
– y = 2,
соответствующую ограничению (1).
Рис.
7.4
Находим, какая
из двух полуплоскостей, на которые эта
прямая делит всю координатную плоскость,
является областью решения неравенства
(1). Для этого достаточно координаты
какой-либо точки, не лежащей на прямой,
подставить в неравенство. Так как прямая
(1) не проходит через начало координат,
подставляем координаты точки О (0,
0) в первое ограничение: 2·0 – 0 < 2.
Получаем строгое неравенство 0 < 2.
Следовательно, точкаОлежит в
полуплоскости решений. Таким образом,
стрелки на концах прямой (1) должны быть
направлены в полуплоскость, содержащую
точкуО.
Аналогично
строим прямые x+y= 3 и –x+ 2y= 4 и области решений ограничений (2) и
(3).
Находим общую
часть полуплоскостей решений. Полученную
область допустимых решений отмечаем
на рис. 7.4 штриховкой. В этой области
находятся все точки M(x;y), в которых выполняются
все три неравенства системы. ◄
Задание 3
Решить неравенство
(а) и систему неравенств (б).
|
3.1.а) б) |
3.2.а) б) |
|
3.3.а) б) |
3.4.а) б) |
|
3.5.а) б) |
3.6.а) б) |
|
3.7.а) б) |
3.8.а) б) |
|
3.9.а) б) |
3.10.а) б) |
|
3.11.а) б) |
3.12.а) б) |
|
3.13.а) б) |
3.14.а) б) |
|
3.15.а) б) |
3.16.а) б) |
|
3.17.а) б) |
3.18.а) б) |
|
3.19.а) б) |
3.20.а) б) |
|
3.21.а) б) |
3.22.а) б) |
|
3.23.а) б) |
3.24.а) б) |
|
3.25.а) б) |
3.26.а) б) |
|
3.27.а) б) |
3.28.а) б) |
|
3.29.а) б) |
3.30.а) б) |
Изображение на координатной плоскости множества решений уравнений и неравенств
с двумя переменными.
1. Изображение множества решений уравнений с двумя переменными.
Определение. Уравнение вида 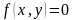
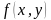
Решить уравнение – значит найти множество всех его корней.
Решением уравнения с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное уравнение в верное числовое равенство.
Для того, чтобы решить уравнение с двумя переменными нужно построить его график.
Графиком уравнения с двумя переменными является множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Примеры
Задача 1. Изобразить на координатной плоскости множество решений уравнений 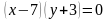
Решение
|
Построим график уравнения Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
Решением является множество точек двух прямых: |
|
Задача 2. Изобразить на координатной плоскости множество решений уравнений 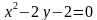
Решение
|
Построим график уравнения Для этого выразим переменную
Уравнение задает параболу с вершиной в точке То есть решением уравнения является множество точек параболы |
|
Задача 3. Изобразить на координатной плоскости множество решений уравнений 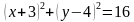
Решение
|
Построим график уравнения Уравнение задает окружность с центром в точке То есть решением уравнения является множество точек построенной окружности |
|
2. Изображение множества решений неравенств с двумя переменными.
Определение. Выражение вида 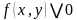
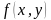
Решить неравенство – значит найти множество всех его решений.
Решением неравенства с двумя переменными называется любая упорядоченная пара (х; у), которая обращает заданное неравенство с переменными в верное числовое неравенство.
Алгоритм решения неравенства 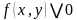
1. Построить график уравнения 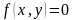
Если неравенство «строгое», тогда график изображаем пунктирной линией;
Если неравенство «нестрогое», тогда график изображаем сплошной линией.
2. Выделить штриховой часть координатной плоскости, соответствующей знаку неравенства.
Примеры
Задача 1. Изобразить на координатной плоскости множество решений неравенства
Решение.
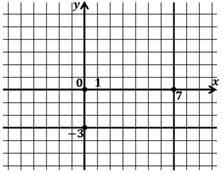
Построим график заданного неравенства . Для этого выразим переменную
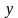
Получим: .
|
Уравнение
Поскольку неравенство |
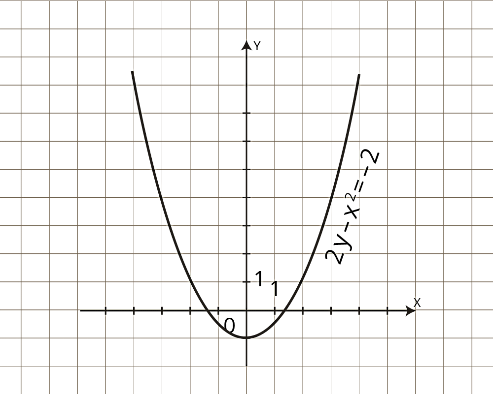
Задача 2. Изобразить на координатной плоскости множество решений неравенства
Решение.
|
Построим график заданного неравенства. Уравнение Поскольку заданное неравенство имеет знак «больше либо равно», значит решением неравенства является множество всех точек, расположенных выше (внутри) параболы. |
Задача 3. Изобразить на координатной плоскости множество решений неравенства .
Решение
Графиком уравнения является гипербола
.
Данная гипербола разбивает координатную плоскость на три области А, В и С.
Для определения необходимой области нужно выбрать контрольные точки, по одной из каждой области.
|
Возьмем из области А точку с координатами (5;4). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили верное неравенство. Значит область А входит в решение заданного неравенства. Возьмем из области В точку с координатами (1;2). Подставим координаты в заданное неравенство и проверим его истинность. Имеем: получили неверное неравенство. Значит область В не входит в решение заданного неравенства. Возьмем из области С точку с координатами |
3. Изображение множества решений системы неравенств с двумя переменными.
Решить систему неравенств – значит найти множество всех решений системы.
Решением системы неравенств с двумя переменными называется любая упорядоченная пара (х; у), которая обращает все неравенства заданной системы в верные числовые неравенства.
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы
Задача 4. Изобразить на координатной плоскости множество решений системы неравенств
Решение
|
На координатной плоскости множество всех решений неравенства
|
|
|
Аналогично строим график неравенства То есть строим на координатной плоскости прямую Множество решений неравенства |
|
|
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы. |
Задача 5. Изобразить на координатной плоскости множество решений системы неравенств
Решение
|
На координатной плоскости множество всех решений неравенства Аналогично, множество решений неравенства Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, задаваемых каждым из неравенств системы. |
Рассмотрим задачи на нахождение областей в комплексной плоскости, заданных неравенствами. Чтобы решить данные неравенства с комплексными числами, вначале необходимо перейти к декартовым координатам, т.е. перейти к действительному представлению.
Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z действительными переменными x и y, а именно z = x + iy, где
x = Re(z), y = Im(z).
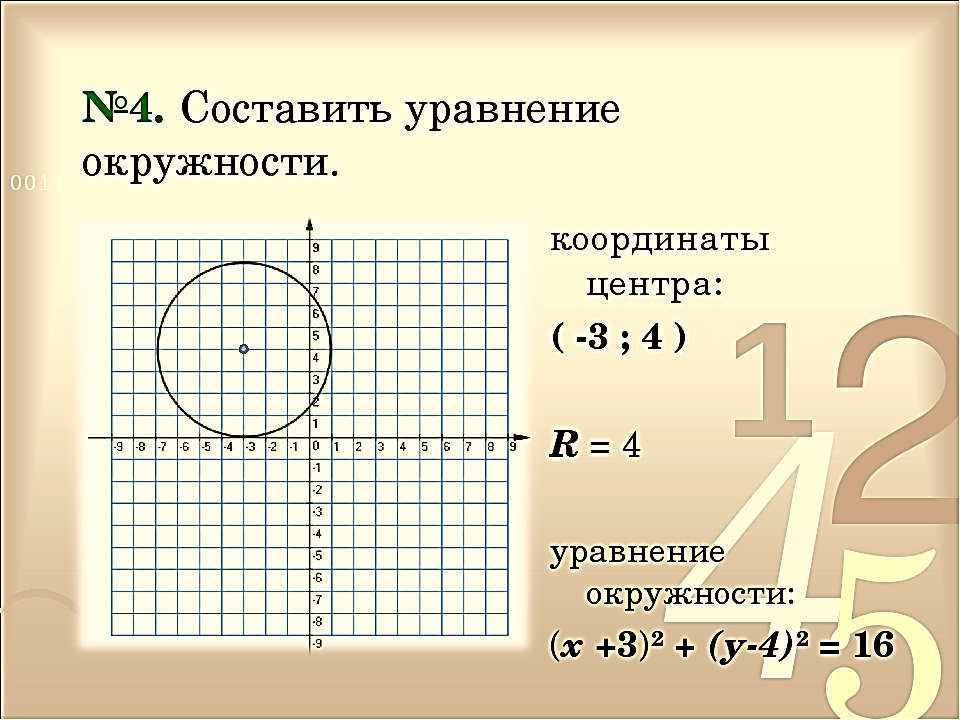
Пример 1. Найти на комплексной плоскости множество точек, удовлетворяющих неравенству
|z + i| < 2.
Решение неравенства с комплексными числами начинается с представления числа в действительной форме. Неравенство примет вид:
или
Для того, чтобы избавиться от ограждающего знака модуля, используют стандартную замену:
или
Как мы знаем из начальных уроков, |z| это модуль комплексного числа, х — действительная часть комплексного числа, y — это мнимая часть комплексного числа, которая находится в связке с мнимой единицей. Итоговый ответ, область решения — это часть плоскости, расположенная внутри круга
Пример 2. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству
Заменяем переменную z представлением в действительной форме z = x + iy, приводим подобные члены, берем действительную часть от получившегося комплексного числа и
приводим к стандартному виду получившееся комплексное число:
Областью решения неравенства
является плоскость, расположенная выше прямой у = 1. Рисунок не прикрепляю, все просто — чертим прямую у = 1 и штрихуем область выше этой прямой.
Чтобы изобразить область, заданную несколькими неравенствами, нужно изобразить области, задаваемые отдельными неравенствами, а затем найти их общую часть.
Пример 3. Построить область, заданную неравенствами
Вначале, заменяем z=x+iy, затем группируем подобные члены, чтобы сформировать действительное представление комплексного числа.
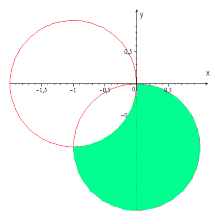
Первое неравенство задает внешнюю часть окружности радиуса 1 с центром в точке (-1; 0) с границей (белый круг). Второе неравенство задает внутреннюю часть окружности радиуса 1 с центром в точке (0; -1) без границы.
Сделаем рисунок в качестве графического доказательства. Область окружности, закрашенная зеленым цветом, является графическим ответом к решению заданного неравенства с комплексными числами:
Скачать материал

Скачать материал




- Сейчас обучается 622 человека из 78 регионов


- Сейчас обучается 140 человек из 50 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Неравенства и системы неравенств
с двумя переменными -
2 слайд
Неравенства с двумя переменными
Выражения, составленные с помощью чисел, двух переменных, знаков действий и знаков сравнения : больше (больше или равно), меньше (меньше или равно), называются неравенствами с двумя переменными. -
3 слайд
Устно:
Найти отличия:x + 5 > 10, у-9 < 2у + 11,
х + 4 < y + 12, 2х + 3y > 16,
x + 2 > y, 6y > 21y + 3.
-
4 слайд
Решением неравенства с двумя переменными
называется
пара значений переменных, обращающая данное неравенство в верное числовое неравенство. -
5 слайд
Задание 1. Изобразить на координатной плоскости XOY фигуру M, состоя-
щую из точек, координаты которых удовлетворяют неравенству
2x + 3y > 6 . -
6 слайд
План выполнения задания
3. Построить график полученного
уравнения;y = – 2/3х + 2
2. Выразить переменную у через переменную х;
2x + 3y = 6
1. Заменить знак неравенства на равно;
-
-
8 слайд
4. Выделить часть плоскости, соответствующую знаку неравенства
2x + 3y > 6 .
y > – 2/3х + 2 -
9 слайд
Задание 2. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству
Выполняем задание по плану. -
10 слайд
План
выполнения задания:
1. Заменить знак неравенства на равно;
2. Выразить переменную у через переменную х;
3. Построить график полученного
уравнения;
4. Выделить часть плоскости, соответствующую знаку неравенства -
-
-
13 слайд
Задание 3. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству
х2 + y2 < 4 -
14 слайд
План выполнения задания
х2 + y2 = 4 – уравнение окружности, с центром в начале координат, R = 2.
2. Определить, какая фигура задаётся таким уравнением:х2 + y2 = 4
1. Заменить знак неравенства на равно;
-
15 слайд
3. Построить данную фигуру в системе координат и выделить область, соответствующую знаку неравенства.
-
16 слайд
Системы неравенств с двумя переменными
-
17 слайд
Изображение на координатной плоскости множества
решений системы неравенств
Первое неравенство задает
открытую полуплоскость,
расположенную выше прямой
Второе неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у =2x – 3
у =-0,5x+2
Пересечением этих множеств
является угол
– множество решений данной
системы неравенств -
18 слайд
Изображение на координатной плоскости множества
решений системы неравенств
Первое неравенство задает
открытую полуплоскость,
расположенную выше прямой
Второе неравенство задает
открытую полуплоскость,
расположенную ниже прямой
у =3x – 4
у = 3x+3,5
Пересечением этих множеств
является полоса, ограниченная
этими прямыми, – множество
решений данной системы неравенств
Запишем систему
неравенств в виде: -
19 слайд
Изображение на координатной плоскости множества
решений системы неравенств
Первое неравенство задает
открытую полуплоскость,
расположенную ниже прямой
Второе неравенство задает
открытую полуплоскость,
расположенную выше прямой
у =3x – 4
у = 3x+3,5
Множество точек, заданное
данной системой неравенств –
пустое множество.
Запишем систему
неравенств в виде: -
20 слайд
Изображение на координатной
плоскости множества
решений системы неравенств
Изобразим множества точек
решений каждого неравенства:
у = 3x – 6
у = 0,25x+4
Пересечением этих множеств
является треугольник,
образованный прямыми,
– множество решений данной
системы неравенств.
у = — x-4
Запишем систему
неравенств в виде: -
21 слайд
Изображение на координатной
плоскости множества
решений системы неравенств
Запишем систему
неравенств в виде:
Изобразим множества точек
решений каждого неравенства:
Данная система неравенств задает ту из образовавшихся областей, которая расположена выше параболы и ниже прямой. -
22 слайд
Данная система задает
две области, образовавшиеся
при пересечении множеств
решений ее неравенств.
Изображение на координатной
плоскости множества
решений системы неравенств
Изобразим множества точек
решений каждого неравенства: -
23 слайд
Домашнее задание:
Глава 2 Параграф 5 – пункт 5 «Неравенства и системы неравенств с двумя переменными» — читать.
№5.22 – (а,б)
№5.39
+тест ОГЭ
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 046 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра», Мордкович А.Г., Николаев Н.П.
Тема
§ 10. Основные понятия, связанные с системами уравнений и неравенств с двумя переменными
Больше материалов по этой теме
Другие материалы
- 07.11.2020
- 152
- 2








Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
-
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Методы и инструменты современного моделирования»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
-
Курс повышения квалификации «Международные валютно-кредитные отношения»
-
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»

![Rendered by QuickLaTeX.com [ begin{cases} 2x-7leqslant 9 \ x-4>2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c2d2fbf06d37908176f7855348bd1ee1_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} xleqslant 8 \ x>6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e354e782b309f49f3d2a32ba3ecfdfa7_l3.png)


![Rendered by QuickLaTeX.com [ begin{cases} x+2yleqslant 8 \ xgeqslant 0 \ ygeqslant x. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2d9632160c48b2777a035f3d176edea6_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (x-1)^2+(y-3)^2+(z-2)^2leqslant 4 \ x+y+zgeqslant 4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-410af121e91222c804c36bc597b5c082_l3.png)
![Rendered by QuickLaTeX.com [ 1. begin{cases} y-x>-2 \ xgeqslant 0 \ 2x+3y<7 end{cases} 2. begin{cases} x^2+y^2leqslant 9 \ y-2xgeqslant 4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-93c8b684ed39e31068e1d3ae7d10d55a_l3.png)
![Rendered by QuickLaTeX.com [ 3. begin{cases} x^2+y^2leqslant 16 \ (x-5)^2+y^2geqslant 4 . end{cases} 4. begin{cases} x^2+y^2+z^2leqslant 16 \ x>0. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-702028826923aa849704d859954b2811_l3.png)



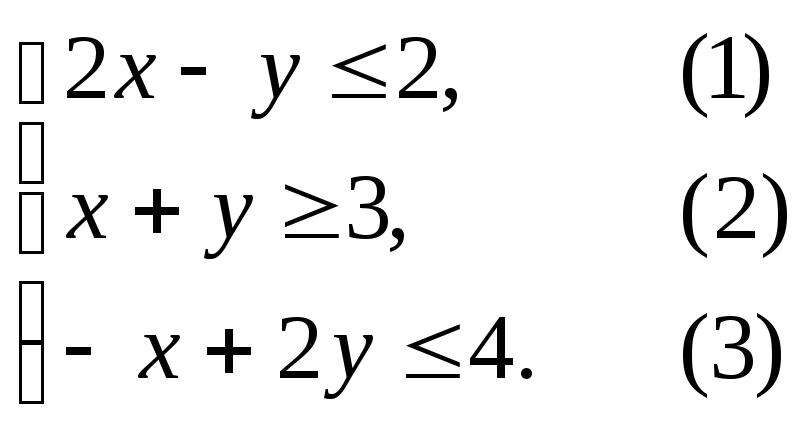












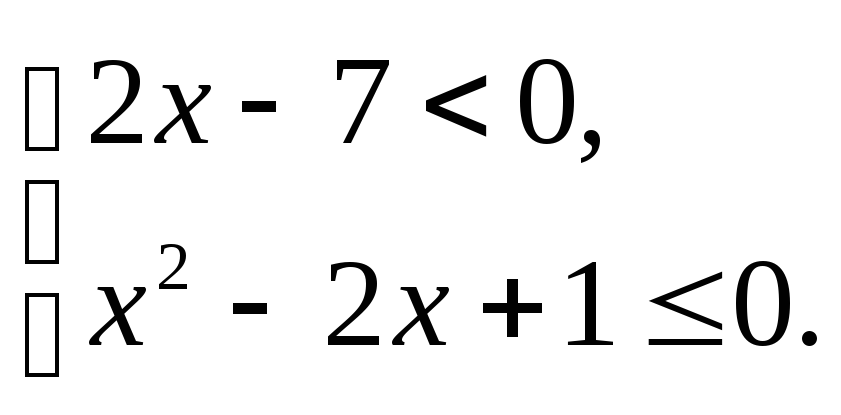
















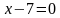 или
или 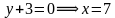
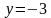
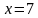 ,
, 
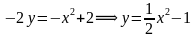
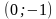
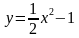
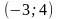 , радиусом
, радиусом