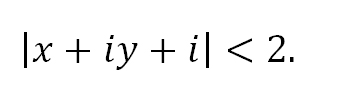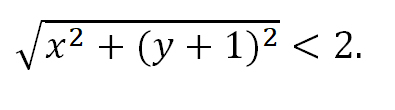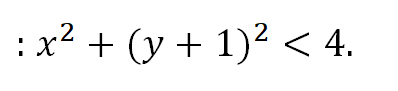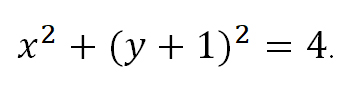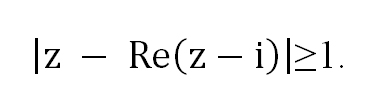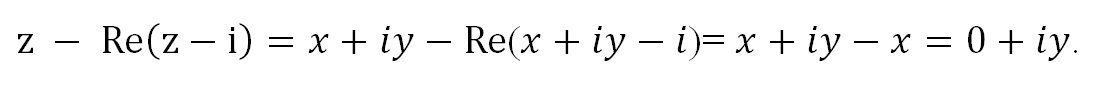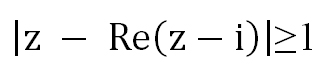Как найти множество точек удовлетворяющих неравенству - Исправление недочетов и поиск решений вместе с Examum.ru

ВИДЕО УРОК

Каждое неравенство с двумя переменными х и у
определяет множество пар (х; у)
значений переменных, которые являются его
решениями, то есть задаёт некоторое отношение между значениями переменной х и
значениями переменной у.

Решением
неравенства с двумя переменными называется пара значений переменных, обращающая
его в истинное неравенство.

ПРИМЕР:

Неравенство

у > –0,5х + 4

содержит две переменные х и у. Чтобы найти какое-либо решение этого неравенства,
выберем произвольное значение х, например

х
= 2,

и вычислим соответствующее
значение выражения

–0,5х + 4.

Получим:

–0,5×2 + 4 = 3.

Любая пара, в которой значение х равно 2,
а значение у больше 3,
например

(2; 4), (2; 5,2), (2; 100)

и так далее, является решением
рассматриваемого неравенства:

у > –0,5х + 4.

Вообще, выбрав значение х произвольно и взяв значение у,
большее соответствующего значения выражения

–0,5х + 4,

мы получим некоторое решение
неравенства

у > –0,5х + 4.

Очевидно, что множество решений
этого неравенства бесконечно.

Графическое решение неравенств с двумя переменными.

Известно, что пара
действительных чисел (х; у)
однозначно определяет точку координатной плоскости. Это даёт возможность
изобразить решения неравенства с двумя переменными геометрически, в виде
некоторого множества точек координатной плоскости.

График
отношения, заданного неравенства с двумя переменными, есть множество точек плоскости, координаты
которых являются решениями этого неравенства.

Для краткости график отношения, заданного неравенством с двумя переменными,
будем называть графиком
неравенства.

ПРИМЕР:

Найти множество точек
координатной плоскости, удовлетворяющих неравенству:

2х + 3 < 0.

РЕШЕНИЕ:

Неравенство 2х + 3 < 0
равносильно неравенству х < –³/₂, которому удовлетворяют точки, лежащие слева от прямой х = –³/₂.

В общем случае прямая

Ах + Ву + С
= 0

разделяет плоскость на две полуплоскости, в одной из которых выполняется
неравенство

Ах + Ву + С
< 0,

а в другой – неравенство

Ах + Ву + С
˃ 0.

Чтобы решить эти неравенства, достаточно взять какую-нибудь точку М₁(х₁; у₁), не
лежащую на прямой

Ах + Ву + С
= 0,

и определить знак числа

Ах₁ + Ву₁+ С.

ПРИМЕР:

Найти множество точек
координатной плоскости, удовлетворяющих неравенству:

2у – 3х – 6 < 0.

РЕШЕНИЕ:

Уравнение

2у – 3х – 6 = 0

является уравнением прямой,
проходящей через точки

(–2; 0) и
(0; 3).

Пусть М₁(х₁; у₁) – точка, лежащая ниже прямой l (в заштрихованной на рисунке
полуплоскости), а М₂ –
точка с абсциссой х₁ и ординатой у₂,
лежащая на прямой l. Тогда

2у₂
– 3х₁ – 6 = 0, а

2у₁
– 3х₁ – 6 < 0,

так как у₁
< у₂.

Таким образом, в любой
точке М(х; у),
лежащей ниже прямой l, выполняется неравенство

2у₁
– 3х₁ – 6 < 0.

Аналогично, в любой точке М(х; у),
лежащей выше прямой l, выполняется неравенство

2у₁
– 3х₁ – 6 ˃ 0.

Точно так же можно решить неравенство общего вида:

Ах + Ву + С
< 0,

где по крайней мере одно из чисел А и
В не равно нулю.

Если
В ˃ 0, то неравенство

Ах + Ву + С
< 0

выполняется во всех точках лежащих ниже прямой, заданной уравнением

Ах + Ву + С
= 0.

Если
В < 0, то неравенство

Ах + Ву + С
< 0

справедливо в точках, лежащих выше этой прямой.

Если
В = 0, то неравенство

Ах + Ву + С
< 0

примет вид

Ах + С < 0

Это неравенство равносильно неравенству

х
< –^С/_А при
А ˃ 0

и неравенству

х ˃ –^С/_А при А < 0.

ПРИМЕР:

Найти множество точек
координатной плоскости, удовлетворяющих неравенству:

3х – 4у – 12 < 0.

РЕШЕНИЕ:

Неравенство

3х – 4у – 12 < 0

верно в полуплоскости,
расположенной выше прямой

3х – 4у – 12 = 0,

так как при х
= у = 0 выражение

3х – 4у – 12

отрицательно. Эта прямая
проходит через точки

(4; 0) и (0; –3)

ПРИМЕР:

Изобразить на координатной
плоскости множество решений неравенства

х + у – 1 ˃ 0.

РЕШЕНИЕ:

Преобразуем данное неравенство
к виду

у ˃ –х + 1.

Построим на координатной
плоскости прямую

у = –х + 1.

Так как ордината любой точки,
лежащей выше прямой

у = –х + 1,

больше, чем ордината точки, имеющей такую же
абсциссу, но лежащей на прямой, то множество точек плоскости, расположенных
выше этой прямой, и будет геометрическим изображением решений заданного
неравенства.

ПРИМЕР:

Найти множество точек координатной
плоскости, удовлетворяющих неравенству:

у ˃ –0,5х + 4.

РЕШЕНИЕ:

Выясним, что представляет собой
график неравенства

у > –0,5х
+ 4.

Известно, что множество точек,
координаты которых являются решениями уравнения

у = –0,5х + 4,

есть прямая.

Выберем на этой прямой
какую-либо точку А и проведём через
точку А
прямую l,
параллельную оси у. Координаты точки
А удовлетворяют уравнению

у = –0,5х + 4.

У любой точки В,
расположенной на прямой l выше точки А,

абсцисса та же, а ордината больше, чем ордината точки А.
Значит, её координаты удовлетворяют неравенству

у > –0,5х + 4.

Координаты точки А и точек прямой l,
расположенных ниже точки А, этому неравенству не удовлетворяют. Вообще неравенству

у > –0,5х + 4

удовлетворяют координаты тех и
только тех точек плоскости, которые расположены выше прямой

у = –0,5х + 4,

то есть выше соответствующей
точки этой прямой, лежащей на той же вертикали.

График неравенства

у > –0,5х + 4

есть открытая полуплоскость,
расположенная выше прямой

у = –0,5х + 4.

На рисунке эта полуплоскость
показана штриховкой. Для того чтобы подчеркнуть, что прямая

у = –0,5х + 4

не принадлежит графику
отношения, заданного неравенством

у > –0,5х + 4,

её изобразили штриховой линией.

Рассуждая аналогично, можно
показать, что график неравенства

у < –0,5х + 4

есть открытая полуплоскость,
расположенная ниже прямой

у = –0,5х + 4.

Вообще прямая

у = kх +
b,

где k и b – некоторые
числа, разбивает множество точек плоскости, не принадлежащих этой прямой, на
две открытые полуплоскости, одна из которых задаётся неравенством

у > kх +
b,

а другая – неравенством

у < kх +
b.

ПРИМЕР:

Решить неравенство:

2х + 5у ˃ 7.

РЕШЕНИЕ:

Для начала выразим у через х:

Построим
прямую

Множество всех решений неравенства
расположено, либо выше, либо ниже данной прямой.

Можно подставить любую пару
чисел и проверить, выполнилось неравенство или нет. Если неравенство
выполнилось, то мы выбираем в качестве решения ту область, которой принадлежит
эта пара чисел, если не выполнилось, то выбираем противоположную область.

Выберем пару

(1; 2)

и подставим значения х = 1 и у = 2 в неравенство

Так как 2 больше 1, то неравенство верное.

Значит, надо выбрать область выше прямой.
Область, в которой выполняется наше неравенство обычно принято изображать
штриховкой или другим цветом.

ПРИМЕР:

Изобразите в координатной
плоскости множества решений неравенства:

2х + 3у < 6.

РЕШЕНИЕ:

Начертим график уравнения

2х + 3у = 6.

Пара (0;0) является решением неравенства

2х + 3у < 6,

и принадлежит нижней
полуплоскости, значит графиком неравенства

2х + 3у < 6

является нижняя полуплоскость.

ПРИМЕР:

Парабола

у = ¹/₄х²

Разбивает множество не
принадлежащих ей точек плоскости на два подмножества. Множество точек,
расположенных выше параболы, задаётся неравенством

у > ¹/₄х²,

а множество точек,
расположенных ниже параболы, – неравенством

у < ¹/₄х².

На рисунке изображён график неравенства

у ≥ ¹/₄х²

(объединение множества точек параболы

у = ¹/₄х²

и множества точек плоскости,
расположенных выше параболы).

ПРИМЕР:

Изобразить на координатной
плоскости множество решений неравенства

х(х – 2) ≤ у – 3.

РЕШЕНИЕ:

Преобразуем неравенство к виду

у ≥ х² – 2х + 3.

Построим на координатной
плоскости параболу – график функции

у = х² – 2х + 3.

Так как ордината любой точки,
лежащей выше параболы

у = х² – 2х + 3,

больше, чем ордината точки,
имеющей ту же абсциссу, но лежащей на параболе, и так как неравенство

у ≥ х² – 2х + 3

нестрогое, то геометрическим
изображением решений заданного неравенства будет множество точек плоскости,
лежащих на параболе

у = х² – 2х + 3

и выше неё.

ПРИМЕР:

Решить неравенство:

ху
<
3.

РЕШЕНИЕ:

Рассмотрим три возможных случая:

1) х
= 0, то получаем верное неравенство 0
< 3. Что значит, неравенство выполняется для любых у,
если х
= 0.

2) х ˃ 0. Перейдём к неравенству у
< ³/_х.
В правой полуплоскости данному неравенству удовлетворяют множество всех точек,
расположенных ниже прямой у = ³/_х.

3) х < 0. Перейдём к
неравенству у ˃ ³/_х.
В левой полуплоскости данному неравенству удовлетворяют множество всех точек,
расположенных выше прямой у = ³/_х.

Построим график и отметим множество всех
решений.

ПРИМЕР:

График уравнения

х² + у² = 36

есть окружность с центром в
начале координат и радиусом, равным 6 единицам. Точки,
лежащие внутри круга, ограниченного этой окружностью, и только эти точки удалены
от начала координат менее чем на 6 единиц, и,
следовательно, их координаты удовлетворяют неравенству

х² + у² < 36.

Координаты точек, лежащих вне
круга, удовлетворяют неравенству

х² + у² > 36.

На рисунке

изображён график неравенства

х² + у² ≤ 36.

Он определяет собой круг с центром в начале
координат и радиусом, равным 6.

ПРИМЕР:

На координатной плоскости
изобразить множество точек, координаты которых удовлетворяют неравенству:

|3х – 2у| ≤ 4.

РЕШЕНИЕ:

Используя свойство модуля,
запишем данное неравенство в виде двойного неравенства:

–4 ≤ 3х – 2у ≤ 4

и выразим из него у.

Получаем:

–4 – 3х ≤ –2у ≤ 4 – 3х,

откуда

Сначала построим две
граничные линии:

Они представляют собой
две параллельные прямые.

Эти прямые разбивают точки
координатной плоскости на область, расположенную между ними, и область, расположенную
за ними. Проверка показывает, что данному неравенству удовлетворяют точки,
расположенные между этими прямыми (эти точки заштрихованы). Например, для начала координат (контрольная точка х
= 0, у = 0) получаем, что данное неравенство

|3х – 2у| ≤ 4

выполняется

|3 ∙ 0 – 2
∙ 0| ≤ 4.

Задания к уроку 13

Задание 1
Задание 2
Задание 3

Урок 1. Числовые неравенства
Урок 2. Свойства числовых неравенств
Урок 3. Сложение и умножение числовых неравенств
Урок 4. Числовые промежутки
Урок 5. Линейные неравенства
Урок 6. Системы линейных неравенств
Урок 7. Нелинейные неравенства
Урок 8. Системы нелинейных неравенств
Урок 9. Дробно-рациональные неравенства
Урок 10. Решение неравенств с помощью графиков
Урок 11. Неравенства с модулем
Урок 12. Иррациональные неравенства
Урок 14. Системы неравенств с двумя переменными
Урок 15. Приближённые вычисления
Урок 16. Абсолютная и относительная погрешность

Источник

Решением уравнения с двумя переменными (p(x;y)=0) является пара чисел ((x;y)), при которых данное уравнение является верным числовым равенством.

Уравнение с двумя переменными часто имеет бесконечно много решений.

Пример:

решением уравнения

x2+y2=9

является любая пара ((x;y)), такая, что точка (M(x;y)) лежит на окружности радиусом (3) с центром в начале координат.

Диофантово уравнение — это уравнение с несколькими переменными и с целыми коэффициентами, для которого нужно найти целые решения.

Пример:

решить уравнение в целых числах

3x+4y=19

Выразим (x) из данного уравнения:

x=19−4y3

При делимости числа (y) на (3) могут быть три возможности:

1) (y = 3k),

2) (y = 3k+1),

3) (y = 3k+2).

Если (y = 3k), то получим

19−4y=19−4⋅3k=19−12k

. Это число на (3) не делится, т. к. (12k) делится на (3), а (19) не делится на (3).

Если (y = 3k+1), то получим

19−4y=19−4⋅3k+1=19−12k−4=15−12k=3⋅5−4k

Это число на (3) делится.

Если (y = 3k+2), то получим

19−4y=19−4⋅3k+2=19−12k−8=11−12k

. Это число на (3) не делится.

Значит, единственная возможность целочисленного решения уравнения есть пара чисел ((5-4k); (3k+1)), где (k) — любое целое число.

Решением неравенства (p(x;y)>0) называют всякую пару чисел ((x;y)), которая удовлетворяет этому неравенству, т. е. обращает его в верное числовое неравенство.

Пример:

решить неравенство (2x+3y>0).

Построим график уравнения (2x+3y=0) — прямую.

Решением неравенства являются точки полуплоскости выше или ниже построенной прямой.

Для правильного определения нужной полуплоскости выберем любую точку из неё, координаты которой подставим в данное неравенство.

Если неравенство будет верным, то полуплоскость выбрана верно.

Выбрав контрольную точку ((1;1)) из верхней полуплоскости, получим верное числовое неравенство:

2⋅1+3⋅1>0

Значит, решением данного неравенства является верхняя полуплоскость.

Аналогично можно рассуждать при решении системы неравенств с двумя переменными.

Решить систему неравенств с двумя переменными — найти на координатной плоскости множество всех точек, координаты которых удовлетворяют каждому неравенству системы.

Источник

Алгебра и начала математического анализа, 11 класс

Урок №42. Линейные уравнения и неравенства с двумя переменными

Перечень вопросов, рассматриваемых в теме:

Решение уравнений, неравенств, систем уравнений и систем неравенств с двумя переменными;
Изображение в координатной плоскости множества решений уравнений, неравенств, систем уравнений, систем неравенств;
Нахождение площади получившейся фигуры.

Глоссарий по теме

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными, где a, b и c — некоторые числа (a ≠ 0 , b ≠0), а, х и у — переменные.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Историческая справка

Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.

В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек». Не обозначали степень надстрочными индексами. И т.д. Их уравнения записаны в виде текстовых задач. Также, как и решения, не похожи на современные, а скорее напоминают цепочку логических рассуждений.

Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим: . И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.

Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».

Актуализация знаний

1.Найдите уравнения, которые являются линейными.

4х + 5у = 10; ; у = 7х +4

Ответ: 4х + 5у = 10; у = 7х +4

Сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.

Линейные уравнения с двумя переменными.

Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.

Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.

Если одновременно а и b, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.

Пример

Построить график уравнения 2х+у =1

у = -2х + 1

Если х=0, то у=1;

Если х=2, то у=-3.

На координатной плоскости отметим точки с координатами (0;1) и (2;-3). Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.

Линейные неравенства с двумя переменными.

Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с < 0 или ах + bу + с > 0, где х и у – переменные, а, b, c – некоторые числа.

Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.

Является ли пара (2;1) решением неравенства 5х + 2у > 4 . Является, тк при подстановке в него вместо х числа 2, а вместо у числа 1 получается верное равенство 10 + 2 > 4.

Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.

Пример

Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.

Уравнение 3х – 2у +6 = 0 является уравнением прямой, проходящей через точки(- 2; 0) и (0; 3).
Пусть точка М₁(х_1,у₁) лежит в заштрихованной полуплоскости (ниже прямой 3х – 2у +6 = 0, аМ₂(х_1,у₂)лежит на прямой 3х – 2у +6 = 0_. Тогда 2у₂ – 3х₁ – 6 = 0, а 2у₁ – 3х₁ – 6 < 0, т.к. у₁< у₂

Изобразим множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0 штриховкой (рис. 1)

Рисунок 1 – решение неравенства 3х – 2у +6 > 0

Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что и . Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с < 0, а другая – графиком неравенства ах + bу + с > 0

Чтобы решить неравенство ах + bу + c < 0 или aх + bу + c > 0, достаточно взять какую-нибудь точку М₁(х₁; у₁), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх₁ + bу₁ + c.

Пример

Изобразите в координатной плоскости множества решений неравенства 2х + 3у < 6

Начертим график уравнения 2х + 3у = 6.

Пара (0;0) является решением неравенства 2х + 3у < 6, и принадлежит нижней полуплоскости, значит графиком неравенства 2х + 3у < 6 является нижняя полуплоскость (рис. 2).

Рисунок 2 – решение неравенства 2х + 3у < 6

Система линейных уравнений с двумя переменными.

Система вида , где а,b,с,d,e,f – некоторые числа, называется линейной системой с двумя переменными х и у.

Пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство называют решением системы.

Решить систему – значит найти множество ее решений.

Пример

Решите систему:

Каждое решение уравнения с двумя переменными представляет координаты некоторой его точки его графика. Каждое решение системы есть координаты общих точек графиков уравнений системы. Построим графики этих уравнений и найдем координаты точки пересечения (рис.3).

Рисунок 3 – решение системы

Система имеет единственное решение: x = 4 , y = 4 .

Система линейных неравенств с двумя переменными.

Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Рассмотрим систему линейных неравенств с двумя переменными на примере:

Построим прямые х – у = 2 и х + 3у = 6
Пара (4;1) является решением как первого, так и второго неравенства, те является общим решением неравенств системы. Такую пару чисел называют решением системы неравенств с двумя переменными. Множество общих решений неравенств есть множество решений системы (пересечение множеств решений неравенств, составляющих систему).

Множество решение системы изображается двойной штриховкой. (плоской угол) (рис. 4).

Рисунок 4 – решение системы

Примеры и разбор решения заданий тренировочного модуля

Пример 1

Изобразите в координатной плоскости множества решений неравенства 3х – 2у + 6 0.

Начертим график уравнения 3х – 2у + 6 = 0
Отметим в какой-нибудь полуплоскости, например, точку (1;2).

Пара (1;2) не является решением неравенства и принадлежит нижней полуплоскости, значит графиком неравенства является верхняя полуплоскость вместе с прямой 3х – 2у + 6 = 0. 9 (рис. 5)

Рисунок 5 – решение неравенства

Пример 2

Изобразим на координатной плоскости множество решений системы

Построим прямые х + у = 3 и 4х – 5у = 20.

Множество решений первого неравенства показано горизонтальной штриховкой, а множество решений второго неравенства – вертикальной штриховкой. Двойная штриховка – множество решений системы. Система задает плоский угол (рис. 6)

Рисунок 6 – решение системы

Если к системе добавить еще одно неравенство

, то получится система трех неравенств с двумя переменными

Этой системой задается треугольник (рис. 7)

Рисунок 7 – решение системы

Точка О принадлежит , левая часть неравенства положительна, и поэтому множество его решений – объединение множеств .

Источник

В данной статье я отвечаю на очередной вопрос от моих подписчиков. Вопросы приходят разные. Не все из них корректно сформулированы. А некоторые из них сформулированы так, что не сразу получается понять, о чём хочет спросить автор. Поэтому среди огромного множества присылаемых вопросов приходится отбирать действительно интересные, такие «жемчужины», отвечать на которые не просто увлекательно, но ещё и полезно, как мне кажется, для других моих читателей. И сегодня я отвечаю на один из таких вопросов. Как изобразить множество решений системы неравенств?

Это действительно хороший вопрос. Потому что метод графического решения задач в математике — это очень мощный метод. Человек так устроен, что ему удобнее воспринимать информацию с помощью различных наглядных материалов. Поэтому если вы овладеете этим методом, то поверьте, он для вас окажется незаменимым как при решении заданий из ЕГЭ, особенно из второй части, других экзаменов, так и при решении задач оптимизации и так далее, и так далее.

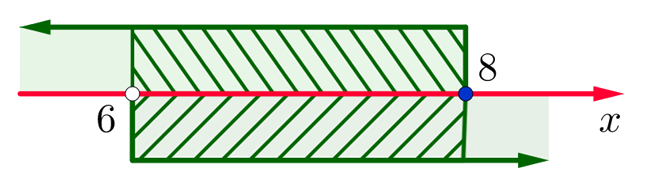
Так вот. Как же нам ответить на этот вопрос. Давайте начнём с простого. Пусть в системе неравенств содержится только одна переменная .

Пример 1. Изобразите множество решений системы неравенств:

$[ begin{cases} 2x-7leqslant 9 \ x-4>2. end{cases} ]$

Упростим эту систему. Для этого прибавим к обеим частям первого неравенства 7 и поделим обе части на 2, не меняя при этом знак неравенства, так как 2 — положительное число. К обеим частям второго неравенства прибавим 4. В результате получим следующую систему неравенств:

$[ begin{cases} xleqslant 8 \ x>6. end{cases} ]$

Обычно такую задачу называют одномерной. Почему? Да потому что для того, чтобы изобразить множество её решений, достаточно прямой. Числовой прямой, если быть точным. Отметим точки 6 и 8 на этой числовой прямой. Понятно, что точка 8 будет находиться правее, чем точка 6, потому что на числовой прямой большие числа находятся правее меньших. Кроме того, точка 8 будет закрашенной, так как согласно записи первого неравенства она входит в его решение. Наоборот, точка 6 будет незакрашенной, так как она не входит в решение второго неравенства:

Отметим теперь стрелочной сверху значения , которые меньше или равны 8, как того требует первое неравенство системы, а стрелочкой снизу — значения , которые больше 6, как того требует второе неравенство системы:

Осталось ответить на вопрос, где на числовой прямой находятся решения системы неравенств. Запомните раз и навсегда. Знак системы — фигурная скобка — в математике заменяет союз «И». То есть, переводя язык формул на человеческий язык, можно сказать, что от нас требуется указать значения , которые больше 6 И меньше или равны 8. То есть искомый промежуток лежит на пересечении отмеченных промежутков:

Вот мы и изобразили множество решений системы неравенств на числовой прямой в случае, если в системе неравенств содержится только одна переменная. В этот заштрихованный промежуток входят все значения , при которых все неравенства, записанные в системе, выполняются.

Рассмотрим теперь более сложный случай. Пусть в нашей системе содержатся неравенства с двумя переменными и . В этом случае обойтись только прямой для изображения решений такой системы не получится. Мы выходим за рамки одномерного мира и добавляем к нему ещё одно измерение. Здесь нам понадобится уже целая плоскость. Рассмотрим ситуацию на конкретном примере.

Пример 2. Изобразите на координатной плоскости множество решений системы неравенств:

$[ begin{cases} x+2yleqslant 8 \ xgeqslant 0 \ ygeqslant x. end{cases} ]$

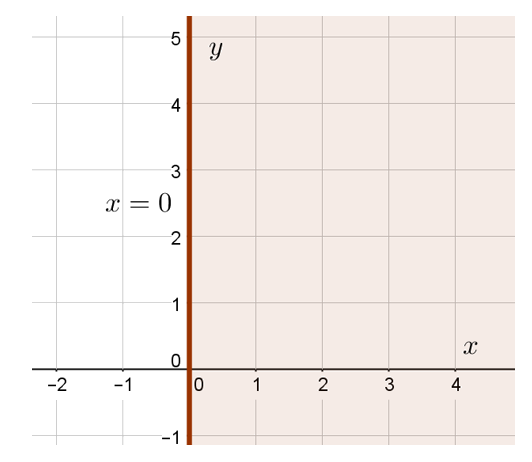
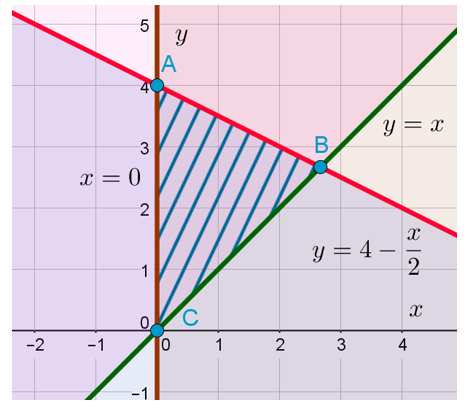
Итак, как же можно изобразить множество решений данной системы неравенств с двумя переменными в прямоугольной системе координат на плоскости? Начнём с самого простого. Зададимся вопросом, какую область этой плоскости задаёт неравенство . Уравнение задаёт прямую, проходящую перпендикулярно оси OX через точку (0;0). То есть фактически это прямая совпадает с осью OY. Ну а раз нас интересуют значения , которые больше или равны 0, то подойдёт вся полуплоскость, лежащая справа от прямой :

Причём все точки, которые лежат на оси OY, нам тоже подходят, потому что неравенство — нестрогое.

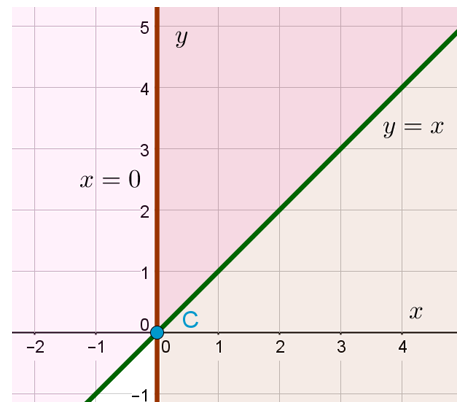
Чтобы понять, какую область на координатной плоскости задаёт третье неравенство, нужно построить график функции . Это прямая, проходящая через начало координат и, например, точку (1;1). То есть фактически это прямая, содержащая биссектрису угла, образующего первую координатную четверть.

А теперь посмотрим на третье неравенство в системе и подумаем. Какую область нам нужно найти? Смотрим: . Знак «больше или равно». То есть ситуация аналогична той, что была в предыдущем примере. Только здесь «больше» означает не «правее», а «выше». Потому что OY — это у нас вертикальная ось. То есть область, задаваемая на плоскости третьим неравенством, — это множество точек, находящихся выше прямой или на ней:

С первым неравенством системы чуть менее удобно. Но после того, как мы смогли определить область, задаваемую третьим неравенством, я думаю, что уже понятно, как нужно действовать.

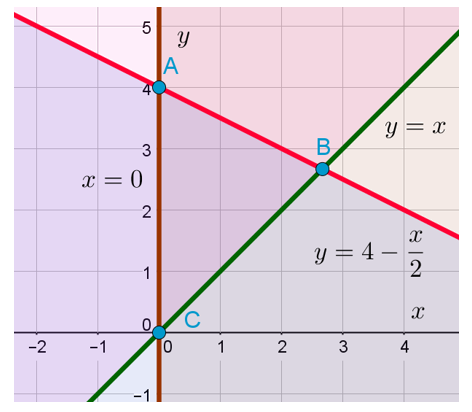
Нужно представить это неравенство в таком виде, чтобы слева находилась только переменная , а справа — только переменная . Для этого вычтем из обеих частей неравенства и поделим обе части на 2, не меняя при этом знак неравенства, потому что 2 — это положительное число. В результате получаем следующее неравенство: $yleqslant 4-frac{x}{2}.$

Осталось только изобразить на координатной плоскости прямую $y=4-frac{x}{2}$ , которая пересекает ось OY в точке A(0;4) и прямую в точке $Bleft(frac{8}{3};frac{8}{3}right)$ . Последнее я узнал, приравняв правые части уравнений прямых и получив уравнение $x=4-frac{x}{2}$ . Из этого уравнения находится координата точки пересечения, а координата , я думаю вы догадались, равна координате . Для тех, кто всё-таки не догадался, это потому что у нас уравнение одной из пересекающихся прямых: .

Как только мы нарисовали эту прямую, сразу можно отметить искомую область. Знак неравенства у нас здесь «меньше или равно». Значит, искомая область находится ниже или непосредственно на изображённой прямой:

Ну и последний вопрос. Где же всё-таки находится искомая область, удовлетворяющая всем трём неравенствами системы? Очевидно, что она находится на пересечении всех трёх отмеченных областей. Опять пересечение! Запомните: знак системы в математике означает пересечение. Вот она, эта область:

Ну и последний пример. Ещё более общий. Предположим теперь что у нас не одна переменная в системе и ни две, а аж целых три!

Пример 3. Изобразите множество решений следующей системы неравенств:

$[ begin{cases} (x-1)^2+(y-3)^2+(z-2)^2leqslant 4 \ x+y+zgeqslant 4 end{cases} ]$

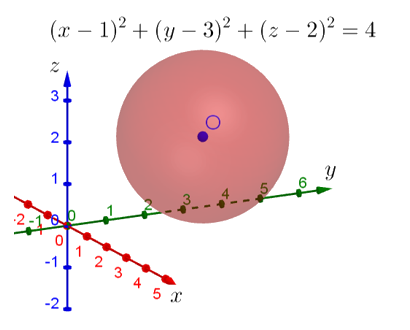
Поскольку переменных целых три, то для изображения множества решений такой системы неравенств нам потребуется третье измерение в добавок к двум, с которыми мы работали в предыдущем примере. То есть мы вылезаем из плоскости в пространство и изображаем уже пространственную систему координат с тремя измерениями: X, Y и Z. Что соответствует длине, ширине и высоте.

Начнём с того, что изобразим в этой системе координат поверхность, задаваемую уравнением . По форме оно очень напоминает уравнение окружности на плоскости, только добавляется ещё одно слагаемое с переменной . Несложно догадаться, что это уравнение сферы с центром в точке (1;3;2), квадрат радиуса которой равен 4. То есть сам радиус равен 2.

Тогда вопрос. А что тогда задаёт само неравенство? Для тех, кого этот вопрос ставит в тупик, предлагаю рассудить следующим образом. Переводя язык формул на человеческий, можно сказать, что требуется указать все сферы с центром в точке (1;3;2), радиусы которых меньше или равны 2. Но тогда все эти сферы будут находиться внутри изображённой сферы! То есть фактически данным неравенством задаётся вся внутренняя область изображённой сферы. Если хотите, задаётся шар, ограниченный изображённой сферой:

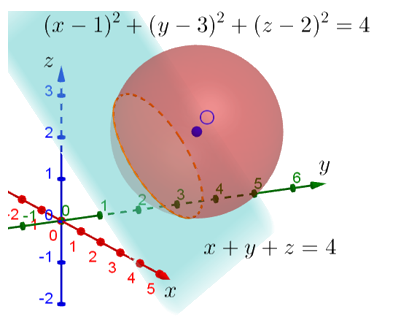
Поверхность, которую задаёт уравнение x+y+z=4 — это плоскость, которая пересекает оси координат в точках (0;0;4), (0;4;0) и (4;0;0). Ну и понятно, что чем больше будет число справа от знака равенства, тем дальше от центра координат будут находиться точки пересечения этой плоскости с осями координат. То есть второе неравенство задаёт полупространство, находящееся «выше» данной плоскости. Используя условный термин «выше», я имею ввиду дальше в сторону увеличения значений координат по осям.

Данная плоскость пересекает изображённую сферу. При этом сечение пересечения — это окружность. Можно даже посчитать, на каком расстоянии от центра системы координат находится центр этой окружности. Кстати, кто догадается, как это сделать, пишите свои решения и ответы в комментариях. Таким образом исходная система неравенств задаёт область пространства, которая находится дальше от этой плоскости в сторону увеличения координат, но заключённая в изображённую сферу:

Вот таким образом изображают множество решений системы неравенств. В случае, если переменных в системе больше, чем 3 (например, 4), наглядно изобразить множество решений уже не получится. Потому что для этого потребовалась бы 4-х мерная система координат. Но нормальный человек не способен представить себе, как могли бы располагаться 4 взаимно перпендикулярные оси координат. Хотя у меня есть знакомый, который утверждает, что может сделать это, причём с лёгкостью. Не знаю, правду ли он говорит, может быть и правду. Но всё-таки нормальное человеческое воображение этого сделать не позволяет.

Надеюсь, сегодняшний урок оказался для вас полезным. Чтобы проверить, насколько хорошо вы его усвоили, выполните записанное ниже домашнее задание.

Изобразите множество решений системы неравенств:

$[ 1. begin{cases} y-x>-2 \ xgeqslant 0 \ 2x+3y<7 end{cases} 2. begin{cases} x^2+y^2leqslant 9 \ y-2xgeqslant 4 end{cases} ]$

$[ 3. begin{cases} x^2+y^2leqslant 16 \ (x-5)^2+y^2geqslant 4 . end{cases} 4. begin{cases} x^2+y^2+z^2leqslant 16 \ x>0. end{cases} ]$

Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич

Источник

Рассмотрим задачи на нахождение областей в комплексной плоскости, заданных неравенствами. Чтобы решить данные неравенства с комплексными числами, вначале необходимо перейти к декартовым координатам, т.е. перейти к действительному представлению.

Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z действительными переменными x и y, а именно z = x + iy, где
x = Re(z), y = Im(z).

Пример 1. Найти на комплексной плоскости множество точек, удовлетворяющих неравенству

|z + i| < 2.

Решение неравенства с комплексными числами начинается с представления числа в действительной форме. Неравенство примет вид:

или

Для того, чтобы избавиться от ограждающего знака модуля, используют стандартную замену:

или

Как мы знаем из начальных уроков, |z| это модуль комплексного числа, х — действительная часть комплексного числа, y — это мнимая часть комплексного числа, которая находится в связке с мнимой единицей. Итоговый ответ, область решения — это часть плоскости, расположенная внутри круга

Пример 2. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству

Заменяем переменную z представлением в действительной форме z = x + iy, приводим подобные члены, берем действительную часть от получившегося комплексного числа и
приводим к стандартному виду получившееся комплексное число:

Областью решения неравенства

является плоскость, расположенная выше прямой у = 1. Рисунок не прикрепляю, все просто — чертим прямую у = 1 и штрихуем область выше этой прямой.

Чтобы изобразить область, заданную несколькими неравенствами, нужно изобразить области, задаваемые отдельными неравенствами, а затем найти их общую часть.

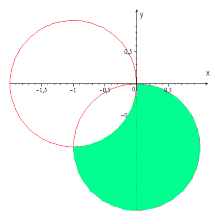
Пример 3. Построить область, заданную неравенствами

Вначале, заменяем z=x+iy, затем группируем подобные члены, чтобы сформировать действительное представление комплексного числа.

Первое неравенство задает внешнюю часть окружности радиуса 1 с центром в точке (-1; 0) с границей (белый круг). Второе неравенство задает внутреннюю часть окружности радиуса 1 с центром в точке (0; -1) без границы.

Сделаем рисунок в качестве графического доказательства. Область окружности, закрашенная зеленым цветом, является графическим ответом к решению заданного неравенства с комплексными числами:

Источник