Как найти множество значений функции тригонометрической функции

Каждому действительному числу

x

 соответствует единственная точка единичной окружности

A

, получаемая поворотом точки ((1;0)) на угол

x

 рад.

Значит, каждому действительному числу

x

 соответствует число, равное

sinx

, и каждому действительному числу

x

 соответствует число, равное

cosx

. Так заданы функции

y=sinx

и

y=cosx

 на множестве

ℝ

.

Алгебра и начала математического анализа, 11 класс

Урок №1. Область определения и множество значений тригонометрических функций.

Перечень вопросов, рассматриваемых в теме

• Овладение понятиями «область определения», «область определения тригонометрических функций», «множество значений функции», «множество значений тригонометрических функций»;
• Нахождение области определения и множества значений тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.;
• Объяснение зависимости области определения и множества значений функции вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.

Глоссарий по теме

Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.

Множеством значений функции y = sin x и y = cos x  является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.

Областью определения функции y = tg x  является множество чисел x ≠ π/2 + πk, kЄ Z.

Областью определения функции y = сtg x  является множество чисел x ≠ πk, kЄ Z.

Множеством значений функции y = tg x и y =сtg x  является множество R всех действительных чисел, т.к. уравнения tg x = a  и сtg x = a  имеют корни при любом действительном значении a. Функции неограниченные.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Актуализация знаний

Вопросы:

1. Что такое функция?
2. Что такое область определения функции? Чем является область определения функции геометрически?
3. Что такое множество значений функции? Чем является множество значений функции геометрически?

Ответы на вопросы:

1. Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают y=f(x).
2. Областью определения функции называют множество всех допустимых значений переменной x. Геометрически – это проекция графика функции на ось Ох.

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.

Найдите область определения функции и множество значений функции:

1) ; 2) ; 3) .

Ответы:

D(f): 1) ; 2) ; 3)

E(f): 1); 2) ; 3) .

Объяснение нового материала

С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций.

Заполните таблицу:

Функция	Область определения	Множество значений

Ответ:

Функция	Область определения	Множество значений

Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.

 Множеством значений функции y = sin x и y = cos x  является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.

Областью определения функции y = tg x  является множество чисел x ≠ π/2 + πk, kЄ Z.

Областью определения функции y = сtg x  является множество чисел x ≠ πk, kЄ Z.

Множеством значений функции y = tg x и y =сtg x  является множество R всех действительных чисел, т.к. уравнения tg x = a  и сtg x = a  имеют корни при любом действительном значении a. Функции неограниченные.

Примеры и разборы решения заданий тренировочного модуля:

Пример 1. Найти область определения функции .

;

;

;

Ответ: −.

Пример 2. Найти все решения уравнения

;

;

Ответ:

.

ВИДЕО УРОК

Области определения
тригонометрических функций.

Всякая функция имеет свою
собственную совокупность значений аргумента, при которых она определена, то
есть существует. Эта совокупность всех допустимых значений аргумента, при
которых функция определена, называется областью определения или областью существования функции.

Функции  sin α  и  соs α  определены при любом значении  α. В самом деле, любая точка  М, лежащая на единичной окружности, имеет вполне
определённые координаты  х  и  у, первая из которых
есть косинус угла  α, составленного с
осью  Ох  подвижным радиусом  ОМ, а вторая – синус угла  α.

Функция  tg α  определена
при всех значениях  α, за исключением
случая, когда подвижной радиус перпендикулярен к оси  Ох, то есть кроме значений  α, равных

± ^π/₂, ± ^3π/₂, ± ^5π/₂,
…

И вообще кроме значений  α, равных

 ^π/₂ + kπ,

где  k – любое целое
число.

В самом деле, при этих (и
только при этих) значениях  α  подвижной радиус лежит на оси  Оу, абсцисса  х  конца подвижного радиуса равна нулю  (х = 0)  и поэтому
делить  у  на  х  нельзя.

Функция  сtg α  определена
при всех значениях  α, за исключением
следующих:

0, ±π,
±2π, ±3π,
…

И вообще – за исключением
значений  α, равных  kπ, где  k – любое целое
число, так как при этих (и только при этих) значениях α  подвижной радиус лежит на оси  Ох, ордината  у  его конца равна нулю  (у = 0)  и поэтому
делить  х  на  у  нельзя.

ПРИМЕР:

Найдите область определения функции

f(x) = tg 2x.

РЕШЕНИЕ:

В область определения не войдут следующие точки:

2х ≠ ^π/₂ + kπ.

или

В
результате получим:

х ≠ ^π/₄ + ^πk/₂, k ∈ Z.

Отразим графически.

ОТВЕТ:

Область определения функции  tg 2x  все
действительные числа за исключением

х ≠ ^π/₄ + ^πk/₂, k ∈ Z.

Области значения
тригонометрических функций.

Функции  sin α  и  соs α  принимают все значения между  –1  и  +1, включая и эти числа. В самом деле, синус угла  α, составленного с осью  Ох  подвижным
радиусом  ОМ  единичной окружности, есть ордината  у  точки  М  единичной
окружности, которая, как легко видеть, принимает все значения между  –1  и  +1, включая и эти числа.

Задача нахождения угла  α, имеющего данный синус  у, при условии, что число  у  заключено в
пределах от  –1  до  +1, имеет бесконечное множество решений.

И действительно,
построим на оси  Оу  точку  Р,

ордината
которой равна  у, и через эту точку
проведём прямую параллельную оси  Ох. Пусть  М₁  и  М₂ – точки, в которых эта прямая пересекает единичную
окружность. Если обозначим через  α  любой угол, составленный с осью  Ох  любым из
подвижных радиусов  ОМ₁  и  ОМ₂, то  sin α =
у.
На чертеже

отмечено несколько углов,
составленных с осью  Ох  одним из подвижных радиусов  ОМ₁  и  ОМ₂.

Аналогично убеждаемся в том,
что  соs α  принимает
все значения  от  –1  до  +1, включая и эти числа.

В самом деле, косинус
угла  α, составленного с осью  Ох  подвижным
радиусом  ОМ  единичной окружности, есть абсцисса  х  конца  М  подвижного
радиуса  ОМ, а абсцисса  х  точки
единичной окружности, принимает все значения от 
–1  до  +1, включая и эти числа.

Так же как и для функции  sin α, для заданного числового значения косинуса

соs α = х,

при условии, что число  х  по
абсолютной величине не больше единицы,

–1 ≤ х ≤  +1,

существует бесконечное
множество углов, косинус которых равен  х.

И действительно, построим на
оси  Ох  точку  Q, абсцисса которой
равна  х, и проведя через эту точку
прямую, параллельную оси  Оу. Пусть  М₁  и  М₂ – точки, в которых эта прямая пересекает единичную
окружность. Если через  α  мы обозначим любой угол, составленный с
осью  Ох  любым из подвижных радиусов  ОМ₁  или  ОМ₂, то  соs α = х.

На чертеже

отмечено несколько углов,
составленных с осью  Ох  одним из подвижных радиусов  ОМ₁  или  ОМ₂.

На чертеже

мы взяли  0 < у
< 1.

На чертеже

мы берём

–1 < х
< 0.

Функция  tg α  принимает
все действительные значения. В самом деле, пусть  р – любое действительное число. Докажем, что
существует и притом бесконечное множество углов, тангенсы которых равны  р.

Построим на оси
тангенсов точку  Р,

ордината которой равна  р. Соединим точку 
Р  с началом
координат и продолжим  РО  за центр до пересечения с единичной
окружностью. Пусть  М₁  и 
М₂ – точки, в которых прямая  РО  пересекает
окружность. Тогда, если  α – угол, составленный
с осью  Ох  любым из подвижных радиусов  ОМ₁  или  ОМ₂, то

tg α = р.

На чертеже

мы считали, что  р ˃ 0. На этом же чертеже отмечено несколько углов,
составленных с осью  Ох  радиусами 
ОМ₁  или  ОМ₂. Тангенсы всех этих углов равны  р.

Наконец, функция  сtg α, как и  tg α, принимает все действительные значения.

В самом деле, пусть  q – любое число. Построим на оси котангенсов
точку  Q, абсцисса которой
равна  q, соединим эту точку  Q  с началом
координат и продолжим  QО  за центр до
пересечения с единичной окружностью.

Обозначим через  М₁  и  М₂  точки пересечения прямой  QО  с единичной окружностью. Тогда котангенс
любого из углов, составленных с осью  Ох  радиусом 
ОМ₁  или  ОМ₂, будет равен  q.

ПРИМЕР:

Найти область значений функции:

у = 5 – 4 sin х.

РЕШЕНИЕ:

Из определения синуса следует,

–1 ≤ sin х ≤ 1.

Далее воспользуемся свойствами числовых неравенств.

Умножим все три части двойного неравенства на  –4.

–4 ≤ –4 sin х ≤ 4.

Прибавим к трём частям двойного неравенства  5.

1 ≤ 5 – 4 sin х ≤ 9.

Так как данная функция непрерывна на всей области определения, то
множество её значений заключено между наименьшим и наибольшим её значением на
всей области определения, если таковые существуют. В данном случае множество
значений функции

у = 5 – 4 sin х

есть множество  [1; 9].

ОТВЕТ:  [1; 9]

ПРИМЕР:

Найти область определения и область значений функции:

y = tg x.

РЕШЕНИЕ:

Функция  y = tg x  определяется формулой

Эта функция определена при значениях х, для которых  соs х ≠ 0.

Известно, что  соs х = 0  при

х = ^π/₂ + πn, n ∈ Z.

Следовательно, областью определения функции  y = tg x  является множество чисел кроме

х = ^π/₂ + πn, n ∈ Z.

Так как уравнение  tg x = а  имеет корни при любом
действительном значении  а, то множеством значений функции  y = tg x  является множество  R  всех действительных чисел.

ПРИМЕР:

Найти область определения функции:

y = sin 3х + tg 2x.

РЕШЕНИЕ:

Нужно выяснить, при каких значениях 
х  выражение

y = sin х + tg 2x

имеет смысл. Выражение  sin 3х  имеет
смысл при любом значении  х, а выражение  tg 2x – при всех значениях 
х  кроме

2х = ^π/₂ + πn, n ∈ Z  или

х = ^π/₄ + ^πn/₂, n ∈ Z.

Следовательно, областью определения данной функции является множество
действительных чисел, кроме

х = ^π/₄ + ^πn/₂, n ∈ Z.

ПРИМЕР:

Найти
область значения тригонометрической функции:

у = 3 соs х – 2.

РЕШЕНИЕ:

Для нахождения
области значения функции

у = 3 соs х – 2

используем
тот факт, что функция  у = соs х  изменяет своё значение от  –1  до  1, то есть имеет место двойное неравенство:

–1 ≤ соs х ≤ 1.

Умножим
все части этого неравенства на  3:

–3 ≤ 3 соs х ≤ 3.

Вычтем
из всех частей полученного неравенства  2, получим:

–3 – 2 ≤ 3 соs х – 2 ≤ 3 – 2,

–5 ≤ 3 соs х – 2 ≤ 1.

Таким
образом, область значений функции будет промежуток

[–5; 1].

ОТВЕТ:  [–5; 1]

ПРИМЕР:

Найти
область значения тригонометрической функции:

у = 3 соs х – 4 sin х.

РЕШЕНИЕ:

Для нахождения
области значения функции

у = 3 соs х – 4 sin х

воспользуемся следующей формулой:

В нашем случае 
а = 3, b = –4, то есть:

Следовательно,
областью значений является промежуток:

[–5; 5].

ОТВЕТ:  [–5; 5]

Сегодня на уроке мы с вами вспомним, как устанавливается
соответствие между действительными точками и точками окружности с помощью
поворота точки окружности, а также вспомним, что называют синусом, косинусом и
тангенсом произвольного угла. Скажем, какие функции называются
тригонометрическими функциями. Выясним, что является областью определения и
множеством значений тригонометрических функций.

Прежде чем приступить к рассмотрению новой темы, давайте возьмём окружность
единичного радиуса с центром в начале координат и отметим на ней точку .

Тогда при повороте точки  на угол  радиан мы получим точку . При этом помним, что ордината точки  – это синус угла , а абсцисса этой точки – это косинус угла .

Далее считаем, что все углы измерены в радианной мере, и поэтому
обозначение «радиан», как правило, опускается. Договорившись считать единицу
измерения углов (1 радиан) фиксированной, определяем, например, синус числа x как синус угла в x радиан; косинус числа x как косинус угла в x радиан и так далее.

Так, каждому действительному числу x поставлены в соответствие
числа синус x и косинус x, то есть на множестве действительных чисел определены функции  и .

Получается, что областью определения функций игрек  и  является множество  всех действительных чисел.

Давайте найдём множество значений функции . Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для
каких значений y существуют такие значения x, при которых  равен y.

Мы знаем, что уравнение  имеет корни, если . И уравнение не имеет корней, если . Из этого следует, что множеством значений функции  является отрезок .

Найдём множество значений функции . Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для
каких значений y существуют такие значения x, при которых  равен y.

Знаем, что уравнение  имеет корни, если . И уравнение не имеет корней, если .

А значит, множеством значений функции  является отрезок .

Таким образом, можно сказать, что функции  и  являются ограниченными.

Теперь поговорим про функцию . Она определяется формулой .

 не должен обращаться в нуль, так как делить на нуль нельзя.

Функция  определена при тех значениях x, для которых .

Мы знаем, что решением уравнения  является .

Тогда областью определения функции  является множество  всех действительных чисел, кроме .

Известно, что уравнение  имеет корни при любом действительном значении . Следовательно, множеством значений функции  является множество  всех действительных чисел.

Осталось выяснить, что является областью определения и множеством
значений функции . Запишем: . Здесь  не должен обращаться в нуль, так как делить на нуль нельзя. А
значит, функция  определена при тех значениях x, для которых .

Корнем уравнения  является . Тогда областью определения функции  является множество  всех действительных чисел, кроме , .

Уравнение  имеет корни при любом действительном значении a, а значит, множеством
значений функции  является множество  всех действительных чисел.

Таким образом, мы с вами выяснили, что является областью
определения и множеством значений функций , ,  и . Эти функции называются тригонометрическими функциями.

А сейчас давайте выполним несколько заданий.

Задание первое. Найдите область определения
функций:

а) ; б) ; в) .

Решение.

Задание второе. Найдите множество
значений функций:

а) ; б) .

Решение.

Задание третье. Найдите наибольшее и
наименьшее значения функции

.

Решение.

План изучения темы

1. Область определения и множество значений тригонометрических функций.
2. Чётность, нечётность, периодичность тригонометрических функций.
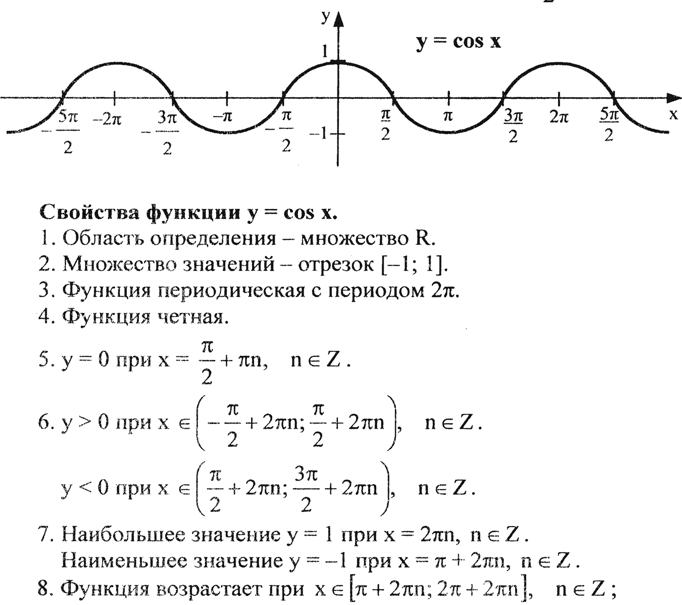
3. Свойства функции y=cosx и её график.
4. Свойства функции y=sinx и её график.
5. Свойства функции y=tgx и её график.
6. Свойства функции y=ctgx и её график.
7. Решение задач на применение свойств функций.

Область определения и множество значений тригонометрических функций

Разберемся, какая область определения у тригонометрических функций. Каждому действительному числу Х соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол Х радиан. Таким образом каждому действительному числу Х поставлены в соответствие числа sinx и cosx, т.е. на множестве R всех действительных чисел определены функции y=sinx и y=cosx.

Областью определения функций y=sinx и y=cosx является множество R всех действительных чисел.

Областью определения функции y=tgx является множество чисел

Так как функции y=sinx и y=cosx принимают значения в рамках единичной окружности, то множество их значений ею ограничено.

Множеством значений функций y=sinx и y=cosx является отрезок [-1;1].

Функции y=sinx и y=cosx являются ограниченными.

Множеством значений функции y=tgx является множество R всех действительных чисел, так как уравнение tgx=a имеет корни при любом действительном значении a.

Пример 1

Найти область определения функции

Решение: сами функции y=sinx и y=cosx имеют в области определения все действительные числа. Но тут они стоят в сумме, в знаменателе. А мы знаем, что если знаменатель будет равным нулю, то выражение потеряет смысл. Значит, для нахождения области определения необходимо приравнять знаменатель к нулю и решить получившееся уравнение.

Значит, областью определения являются все значения, кроме найденных выше:

Пример 2

Найдите множество значений функции

Решение: видим, что в правой части есть возможность применить тригонометрическую формулу двойного угла для синуса. Сделаем это:

Областью значений функции y=sinx является отрезок [-1;1]. Здесь есть функция синуса, просто она умножена на одну вторую и ещё прибавлено 3. Учтём всё сказанное и получим новое множество значений:

То есть на первом шаге мы умножили концы отрезка на одну вторую, а затем прибавили к ним 3. В итоге мы получили множество значений данной функции. Никакой роли тут не играет двойной угол, так как он влияет на сужение/растяжение графика вдоль оси ОХ.

Ответ: [2,5;3,5]

Чётность, нечётность, периодичность тригонометрических функций

Чётная функция — функция y=f(x), область определения которой симметрична относительно нуля и для каждого Х из области определения имеет место равенство: 

График чётной функции симметричен относительно оси ординат. Примером может служить парабола.

Нечетная функция — функция y=f(x), область определения которой симметрична относительно нуля и для каждого Х из области определения имеет место равенство: 

График нечётной функции симметричен относительно начала координат. Примером может служить кубическая парабола.

значит, это нечётная функция.

значит, это чётная функция.

значит, это нечётная функция.

значит, это нечётная функция.

Пример 3

Выяснить, является ли функция чётной или нечётной:

Решение:

После применения формулы приведения, мы получаем функцию в виде

Воспользуемся правилом определения чётности/нечётности и проверим, что у нас получится:

То есть, мы видим, что данная функция является чётной, из-за появившегося квадрата в показателе степени. 

Ответ: чётная

Мы с вами знаем, что при полном обороте по единичной окружности мы попадаем в точку с такими же координатами, то есть верны равенства:

Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на два пи. Такие функции называются периодическими с периодом:

Аналогично, выполняются ещё два равенства:

Значит, тангенс и котангенс — это периодические функции, с периодом:

Пример 4

Найдём несколько периодов функций на конкретных примерах. 

Решение:

Задание 1. Смотрим, чем отличается функция от стандартного вида. Видим 3 перед аргументом. Значит, нужно взять основной период для синуса:

и просто поделить его на 3. Значит период для первой функции будет равен:

Задание 2. Перед аргументом у тангенса мы видим дробь 3/2. Значит, основной период тангенса нужно просто разделить на эту дробь. Получаем:

Задание 3. Перед аргументом стоит дробь 1/2 и прибавлено ещё пи на 6. Это прибавление не играет никакой роли, просто график будет двигаться налево вдоль оси, поэтому ищем период как обычно. Берём основной период косинуса и делим на дробь:

Задание 4. Видим у косинуса аргумент умножен на 4, значит просто на него делим основной период:

Задание 5. Перед аргументом у синуса дробь 1/5, просто делим на неё. Не обращаем на 4 впереди, это просто растяжение графика вдоль оси ОХ.

Задание 6. Перед аргументом синуса стоит 2, делим на неё:

Задание 7. У тангенса перед аргументом стоит 5. Берём основной период и делим на 5:

Задание 8. Аналогично тангенс, просто дробь впереди 1/2:

Задание 9. Тут уже нужно найти период для каждого слагаемого. Для синуса:

Для косинуса:

А общим периодом будет наименьшее общее кратное наших двух, которые мы нашли. То есть тот, который делится на каждый из найденных.

Свойства функции y=cosx и её график

 

Свойства функции y=sinx и её график

Свойства функции y=tgx и её график

Свойства функции y=ctgx и её график

Решение задач на применение свойств функций