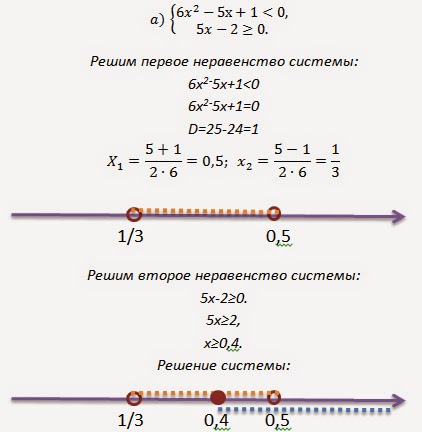
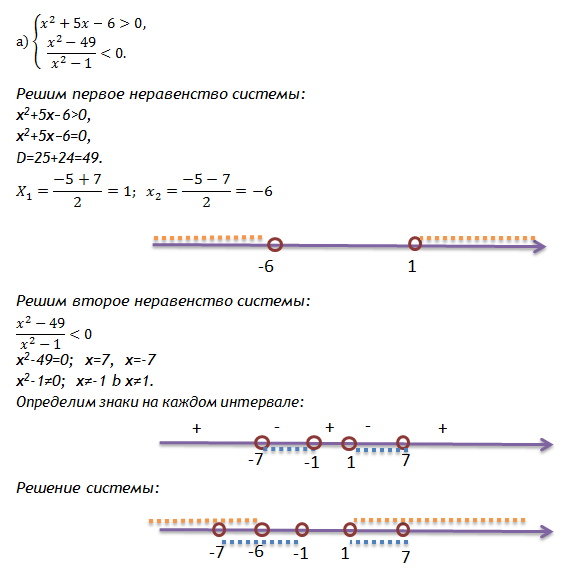
Понятие системы неравенств с одной переменной и его решения
Несколько неравенств с одной переменной образуют систему, если нужно найти такое множество значений переменной, которое будет решением каждого из неравенств.
Решением системы неравенств с одной переменной является такое множество значений этой переменной, которое превращает каждое из неравенств в верное числовое неравенство.
Следствие: общим решением системы неравенств с одной переменной является пересечение частных решений каждого из неравенств системы.
Например: ${left{ begin{array}{c} x+7 ge 2 \ x-4 lt 1 end{array} right.} iff {left{ begin{array}{c} x ge -5 \ x lt 5 end{array} right.} iff -5 le x lt 5 или x in Bbb[-5;5)$ — полуинтервал
О пересечении числовых промежутков подробней см. §17 данного справочника
Алгоритм решения системы неравенств с одной переменной
Подробно о числовой прямой и видах числовых промежутков на ней рассказано в §16 данного справочника. Здесь мы изобразим числовые промежутки как решения неравенств на более простых примерах.
Шаг 1. Найти множество частных решений для каждого из неравенств системы. Если хотя бы одно из частных решений является пустым множеством, вся система неравенств не имеет решений; перейти к шагу 4.
Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать .
Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их пересечение – это и будет общим решением системы .
Шаг 4. Работа завершена.
Например: ${left{ begin{array}{c} x-2 lt 1 \ x+5 ge 6 end{array} right.} iff {left{ begin{array}{c} x lt 3 \ x ge 1 end{array} right.} iff 1 le x lt 3 или x in Bbb[1;3)$ — полуинтервал
Внимание!
Если в системе неравенств есть несколько неравенств со знаком «больше», то из них останется одно неравенство по принципу «больше большего».
Аналогично:
Если в системе неравенств есть несколько неравенств со знаком «меньше», то из них останется одно неравенство по принципу «меньше меньшего» .
Например:
1) В системе $ {left{ begin{array}{c} x gt 5 \ x gt 2 \ x gt 3 end{array} right.} $ наибольшее число (условие) справа 5.
По принципу «больше большего» останется: $ {left{ begin{array}{c} x gt 5 \ x gt 2 \ x gt 3 end{array} right.} iff x gt 5 $
2) В системе $ {left{ begin{array}{c} x lt 5 \ x lt 2 \ x lt 3 end{array} right.} $ наименьшее число (условие) справа 2.
По принципу «меньше меньшего» останется: $ {left{ begin{array}{c} x lt 5 \ x lt 2 \ x lt 3 end{array} right.} iff x lt 2 $
Примеры
Пример 1. Решите системы уравнений:
$а) {left{ begin{array}{c} 2(x-8) ge x-16 \ 3(x+1) le 11 end{array} right.} iff {left{ begin{array}{c} 2x-x ge -16+16 \ 2x le 11-3 end{array} right.} iff {left{ begin{array}{c} x ge 0 \ 2x le 8 end{array} right.} iff {left{ begin{array}{c} x ge 0 \ x le 4 end{array} right.} iff 0 le x le 4$
$x in [0;4]$ — интервал
$б) {left{ begin{array}{c} 5(x-6) gt x-10 \ 4(x-1) lt x+5 end{array} right.} iff {left{ begin{array}{c} 5x-x gt 30-10 \ 4x-x lt 5+4 end{array} right.} iff {left{ begin{array}{c} 4x gt 20 \ 3x lt 9 end{array} right.} iff {left{ begin{array}{c} x gt 5 \ x lt 3 end{array} right.} iff x in varnothing$
$x in varnothing$ — решений нет
$в) {left{ begin{array}{c} -5 lt 3x+1 le 4 \ 3 lt 2x+5 lt 9 end{array} right.} iff {left{ begin{array}{c} -5-1 lt 3x le 4-1 \ 3-5 lt 2x lt 9-5 end{array} right.} iff {left{ begin{array}{c} -6 lt 3x le 3 \ -2 lt 2x lt 4 end{array} right.} iff {left{ begin{array}{c} -2 lt x le 1 \ -1 lt x lt 2 end{array} right.} iff$
$$iff -1 lt x le 1$$
$x in (-1;1] $ — полуинтервал
Пример 2. При каких значениях переменной x имеет смысл выражение:
$ а) sqrt{x+2} + sqrt{4-x} $
$ {left{ begin{array}{c} x+2 ge 0 \ 4-x ge 0 end{array} right.} iff {left{ begin{array}{c} x ge -2 \ x le 4 end{array} right.} iff -2 le x le 4 $
$x in [-2;4]$
$ б) sqrt{2x+3} + frac{1}{x-4}$
$ {left{ begin{array}{c} 2x+3 ge 0 \ x-4 neq 0 end{array} right.} iff {left{ begin{array}{c} x ge -1,5 \ x neq 4 end{array} right.}$
$x in [-1,5;4) cup (4;+ infty) $
$ в) frac{1}{sqrt{x-5}} + frac{1}{sqrt{1-x}}$
$ {left{ begin{array}{c} x-5 gt 0 \ 1-x gt 0 end{array} right.} iff {left{ begin{array}{c} x gt 5 \ x lt 1 end{array} right.} iff x in varnothing$
$x in varnothing $ — решений нет
$ г) {sqrt{x+3}} + frac{1}{sqrt{x+1}}$
$ {left{ begin{array}{c} x+3 ge 0 \ x+1 gt 0 end{array} right.} iff {left{ begin{array}{c} x ge -3 \ x gt -1 end{array} right.} iff x>-1$
$x in (-1;+ infty) $
Пример 3*. У космического пирата Шутзема несколько затруднительное финансовое положение и только 510 астротугриков в кармане. Однако ему нужно пополнить запасы топлива и продовольствия. Одна капсула с топливом стоит 50 астротугриков, а одна капсула с едой – 30 астротугриков. Какой вариант покупок есть у Шутзема на всю сумму без сдачи, если топлива нужно не менее 4 капсул, а еды – не менее 5?
Пусть x — количество капсул с топливом, y – количество капсул с едой.
По условию задачи:
$$ {left{ begin{array}{c} 50x+30y le 500 \ x ge 4 \ y ge 5 \ x,y in Bbb N end{array} right.} iff {left{ begin{array}{c} 5x+3y le 50 \ x ge 4 \ y ge 5 \ x,y in Bbb N end{array} right.} $$
Изобразим полученные полуплоскости графически и найдём их пересечение.
Прямая сверху – это бюджетное ограничение.
На этой прямой в области допустимых значений (закрашенный треугольник, стороны включительно) есть только одно целое решение: $ {left{ begin{array}{c} x = 6 \ y = 7 end{array} right.} $
Ответ: 6 капсул топлива и 7 капсул еды.
В данной статье я отвечаю на очередной вопрос от моих подписчиков. Вопросы приходят разные. Не все из них корректно сформулированы. А некоторые из них сформулированы так, что не сразу получается понять, о чём хочет спросить автор. Поэтому среди огромного множества присылаемых вопросов приходится отбирать действительно интересные, такие «жемчужины», отвечать на которые не просто увлекательно, но ещё и полезно, как мне кажется, для других моих читателей. И сегодня я отвечаю на один из таких вопросов. Как изобразить множество решений системы неравенств?
Это действительно хороший вопрос. Потому что метод графического решения задач в математике — это очень мощный метод. Человек так устроен, что ему удобнее воспринимать информацию с помощью различных наглядных материалов. Поэтому если вы овладеете этим методом, то поверьте, он для вас окажется незаменимым как при решении заданий из ЕГЭ, особенно из второй части, других экзаменов, так и при решении задач оптимизации и так далее, и так далее.
Так вот. Как же нам ответить на этот вопрос. Давайте начнём с простого. Пусть в системе неравенств содержится только одна переменная .
Упростим эту систему. Для этого прибавим к обеим частям первого неравенства 7 и поделим обе части на 2, не меняя при этом знак неравенства, так как 2 — положительное число. К обеим частям второго неравенства прибавим 4. В результате получим следующую систему неравенств:
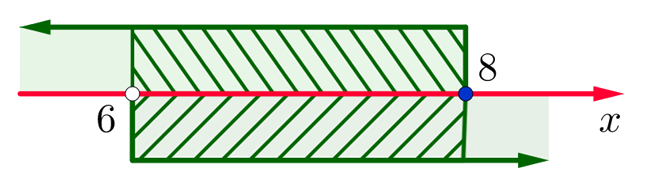
Обычно такую задачу называют одномерной. Почему? Да потому что для того, чтобы изобразить множество её решений, достаточно прямой. Числовой прямой, если быть точным. Отметим точки 6 и 8 на этой числовой прямой. Понятно, что точка 8 будет находиться правее, чем точка 6, потому что на числовой прямой большие числа находятся правее меньших. Кроме того, точка 8 будет закрашенной, так как согласно записи первого неравенства она входит в его решение. Наоборот, точка 6 будет незакрашенной, так как она не входит в решение второго неравенства:
Отметим теперь стрелочной сверху значения , которые меньше или равны 8, как того требует первое неравенство системы, а стрелочкой снизу — значения
, которые больше 6, как того требует второе неравенство системы:
Осталось ответить на вопрос, где на числовой прямой находятся решения системы неравенств. Запомните раз и навсегда. Знак системы — фигурная скобка — в математике заменяет союз «И». То есть, переводя язык формул на человеческий язык, можно сказать, что от нас требуется указать значения , которые больше 6 И меньше или равны 8. То есть искомый промежуток лежит на пересечении отмеченных промежутков:
Вот мы и изобразили множество решений системы неравенств на числовой прямой в случае, если в системе неравенств содержится только одна переменная. В этот заштрихованный промежуток входят все значения , при которых все неравенства, записанные в системе, выполняются.
Рассмотрим теперь более сложный случай. Пусть в нашей системе содержатся неравенства с двумя переменными и
. В этом случае обойтись только прямой для изображения решений такой системы не получится. Мы выходим за рамки одномерного мира и добавляем к нему ещё одно измерение. Здесь нам понадобится уже целая плоскость. Рассмотрим ситуацию на конкретном примере.
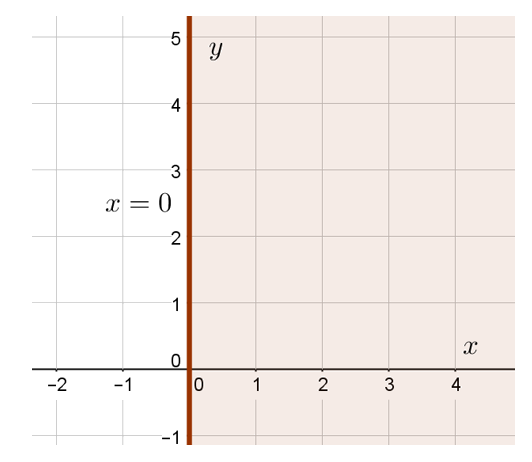
Итак, как же можно изобразить множество решений данной системы неравенств с двумя переменными в прямоугольной системе координат на плоскости? Начнём с самого простого. Зададимся вопросом, какую область этой плоскости задаёт неравенство . Уравнение
задаёт прямую, проходящую перпендикулярно оси OX через точку (0;0). То есть фактически это прямая совпадает с осью OY. Ну а раз нас интересуют значения
, которые больше или равны 0, то подойдёт вся полуплоскость, лежащая справа от прямой
:
Причём все точки, которые лежат на оси OY, нам тоже подходят, потому что неравенство — нестрогое.
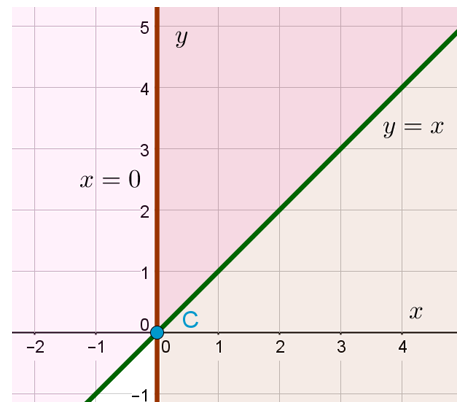
Чтобы понять, какую область на координатной плоскости задаёт третье неравенство, нужно построить график функции . Это прямая, проходящая через начало координат и, например, точку (1;1). То есть фактически это прямая, содержащая биссектрису угла, образующего первую координатную четверть.
А теперь посмотрим на третье неравенство в системе и подумаем. Какую область нам нужно найти? Смотрим: . Знак «больше или равно». То есть ситуация аналогична той, что была в предыдущем примере. Только здесь «больше» означает не «правее», а «выше». Потому что OY — это у нас вертикальная ось. То есть область, задаваемая на плоскости третьим неравенством, — это множество точек, находящихся выше прямой
или на ней:
С первым неравенством системы чуть менее удобно. Но после того, как мы смогли определить область, задаваемую третьим неравенством, я думаю, что уже понятно, как нужно действовать.
Нужно представить это неравенство в таком виде, чтобы слева находилась только переменная , а справа — только переменная
. Для этого вычтем из обеих частей неравенства
и поделим обе части на 2, не меняя при этом знак неравенства, потому что 2 — это положительное число. В результате получаем следующее неравенство:
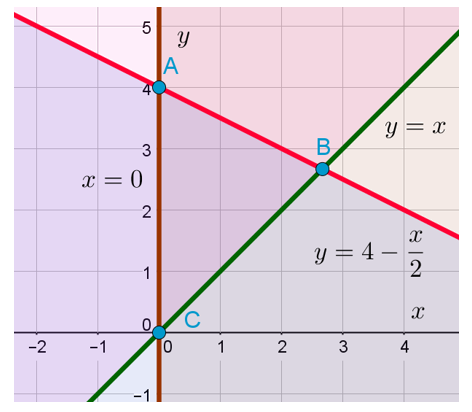
Осталось только изобразить на координатной плоскости прямую , которая пересекает ось OY в точке A(0;4) и прямую
в точке
. Последнее я узнал, приравняв правые части уравнений прямых и получив уравнение
. Из этого уравнения находится координата
точки пересечения, а координата
, я думаю вы догадались, равна координате
. Для тех, кто всё-таки не догадался, это потому что у нас уравнение одной из пересекающихся прямых:
.
Как только мы нарисовали эту прямую, сразу можно отметить искомую область. Знак неравенства у нас здесь «меньше или равно». Значит, искомая область находится ниже или непосредственно на изображённой прямой:
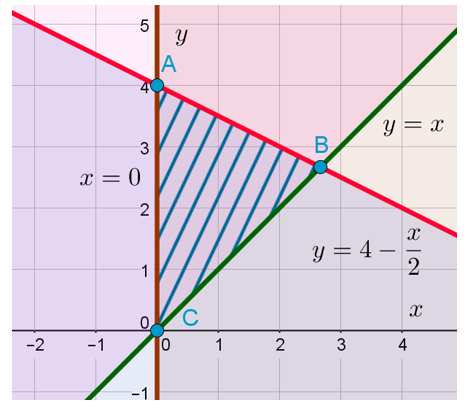
Ну и последний вопрос. Где же всё-таки находится искомая область, удовлетворяющая всем трём неравенствами системы? Очевидно, что она находится на пересечении всех трёх отмеченных областей. Опять пересечение! Запомните: знак системы в математике означает пересечение. Вот она, эта область:
Ну и последний пример. Ещё более общий. Предположим теперь что у нас не одна переменная в системе и ни две, а аж целых три!
Поскольку переменных целых три, то для изображения множества решений такой системы неравенств нам потребуется третье измерение в добавок к двум, с которыми мы работали в предыдущем примере. То есть мы вылезаем из плоскости в пространство и изображаем уже пространственную систему координат с тремя измерениями: X, Y и Z. Что соответствует длине, ширине и высоте.
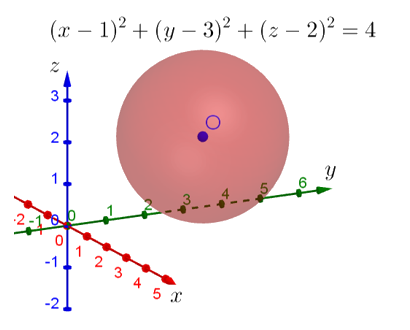
Начнём с того, что изобразим в этой системе координат поверхность, задаваемую уравнением . По форме оно очень напоминает уравнение окружности на плоскости, только добавляется ещё одно слагаемое с переменной
. Несложно догадаться, что это уравнение сферы с центром в точке (1;3;2), квадрат радиуса которой равен 4. То есть сам радиус равен 2.
Тогда вопрос. А что тогда задаёт само неравенство? Для тех, кого этот вопрос ставит в тупик, предлагаю рассудить следующим образом. Переводя язык формул на человеческий, можно сказать, что требуется указать все сферы с центром в точке (1;3;2), радиусы которых меньше или равны 2. Но тогда все эти сферы будут находиться внутри изображённой сферы! То есть фактически данным неравенством задаётся вся внутренняя область изображённой сферы. Если хотите, задаётся шар, ограниченный изображённой сферой:
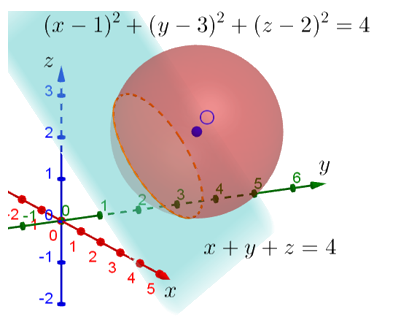
Поверхность, которую задаёт уравнение x+y+z=4 — это плоскость, которая пересекает оси координат в точках (0;0;4), (0;4;0) и (4;0;0). Ну и понятно, что чем больше будет число справа от знака равенства, тем дальше от центра координат будут находиться точки пересечения этой плоскости с осями координат. То есть второе неравенство задаёт полупространство, находящееся «выше» данной плоскости. Используя условный термин «выше», я имею ввиду дальше в сторону увеличения значений координат по осям.
Данная плоскость пересекает изображённую сферу. При этом сечение пересечения — это окружность. Можно даже посчитать, на каком расстоянии от центра системы координат находится центр этой окружности. Кстати, кто догадается, как это сделать, пишите свои решения и ответы в комментариях. Таким образом исходная система неравенств задаёт область пространства, которая находится дальше от этой плоскости в сторону увеличения координат, но заключённая в изображённую сферу:
Вот таким образом изображают множество решений системы неравенств. В случае, если переменных в системе больше, чем 3 (например, 4), наглядно изобразить множество решений уже не получится. Потому что для этого потребовалась бы 4-х мерная система координат. Но нормальный человек не способен представить себе, как могли бы располагаться 4 взаимно перпендикулярные оси координат. Хотя у меня есть знакомый, который утверждает, что может сделать это, причём с лёгкостью. Не знаю, правду ли он говорит, может быть и правду. Но всё-таки нормальное человеческое воображение этого сделать не позволяет.
Надеюсь, сегодняшний урок оказался для вас полезным. Чтобы проверить, насколько хорошо вы его усвоили, выполните записанное ниже домашнее задание.
Изобразите множество решений системы неравенств:
Материал подготовил репетитор по математике и физике в Москве, Сергей Валерьевич
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.


9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 





20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.
Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:
-5<x<12 или
Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Пример:
Решить систему неравенств:
Решим каждое неравенство в отдельности
1) 5x-x2≥0,
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:
2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.
Объединим оба решения:
Ответ: (4; 5].
Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
Решим каждое неравенство в отдельности
1) 5х+6≤1,
5х≤ -5,
х≤ -1.
2) 2х+1≥3,
2х≥2,
х≥1.
Объединим оба решения:
Ответ: (-∞; -1]U[1;+∞).
УПРАЖНЕНИЯ
1. Решите систему неравенств:
Решение:
а)
Ответ: (5; 7]
2. Решите систему неравенств:
Решение:
Ответ: (1; 10].
3. Найдите целые решения системы неравенств:
Решение:
а)
Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.
4. Решите систему неравенств:
Решение:
Ответ: (-1; 3).
5. Решите систему неравенств:
Решение:
Ответ: (-1;2).
6. Решите систему неравенств:
Решение:
Ответ: нет решений.
7. Решите систему неравенств:
Решение:
Ответ: (0; +∞).
8. Решите неравенство:
а) -2<3x+5≤10; б) 2<4x+6≤12.
Решение:
а) -2 < 3x+5 ≤ 10;
-2-5
< 3x ≤ 10-5;
-7
< 3x ≤ 5;
-7:3
< x ≤ 5:3;
-7/3
< x ≤ 5/3.
Ответ: (-2 1/3; 1 2/3].
9. Решите систему неравенств:
Решение:
Ответ: [0,4; 0,5).
10. Решите систему неравенств (№ 3.4.52 [7]):
Решение:
Ответ: (-1; 2).
11. Решите систему неравенств:
Решение:
Ответ: [-9; 3)U(3; 9].
12. Решите систему неравенств:
Решение:
Ответ: (-7; -6)U(1;7).
13. Решите систему неравенств:
Решение:
Ответ: (2; 4).
14. Решите систему неравенств:
Решение:
Ответ: (-7; -2)U(0; 2).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решите систему неравенств:
2. Решите систему неравенств:
3. Решите систему неравенств:
4. Решите систему неравенств:
5. Решите систему неравенств:
6. Решите систему неравенств:
7. Решите систему неравенств:
8. Решите систему неравенств:
9. Решите систему неравенств:
10. Решите систему неравенств:
Проверь себя
Содержание
- Математика по полочкам
- 13. Системы неравенств
- МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
- Как решать систему неравенств
- Основные понятия
- Типы неравенств
- Система неравенств
- Таблица числовых промежутков
- Алгебра. Урок 8. Неравенства, системы неравенств.
- Неравенства
Математика по полочкам
Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования
13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
Источник
Как решать систему неравенств
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Типы неравенств
Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.
a > b и b > и
Система неравенств
Чтобы щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:
Если а > b , то b а.
Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а > b и c b – d.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа .
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а 0, то аc b, где а, b > 0, то а 2 > b 2 , и если а 2 2 . На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то b, где а, b > 0″ height=»37″ src=»https://lh3.googleusercontent.com/LF-ukOvvfm3VyVfIMauqN5t80Q55yYM4nvHAT7F8gLqvUqWPsNtXxG7aRF79Foq7MwyONaIRQCIRGQPToOh2YpQYIp2skOqQnhUydgHSJPHX07U-US5MHuxZpH15nzz2Kxq4mv4u» width=»37″> .
Если а .
Таблица числовых промежутков
Полезна тем, что с ее помощью удобно записывать множество решений.
Источник
Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Неравенства
- Линейные неравенства
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
≥ больше или равно,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a 0 , то знак неравенства меняется на противоположный , неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 6 x ≤ − 1 + 1
Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A ) и подставить её значение в выражение a x 2 + b x + c вместо x .
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0
Это значит, что знак на интервале, в котором лежит точка 2 , будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя .
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя .
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x .
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые .
Если знак неравенства строгий ,
при нанесении на ось x нули числителя выколотые .
Если знак неравенства нестрогий ,
при нанесении на ось x нули числителя жирные .
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x .
- Решить второе неравенство системы, изобразить его графически на оси x .
- Нанести решения первого и второго неравенств на ось x .
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x .
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x .
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
Графическая интерпретация решения:
- Решаем второе неравенство системы
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
Графическая интерпретация решения:
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
Решаем методом интервалов.
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 — два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Источник
Adblock
detector
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x c |

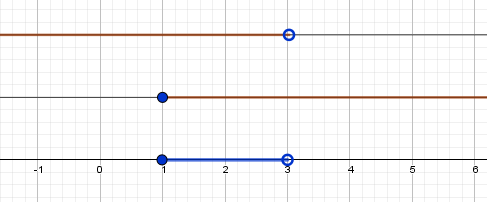










![Rendered by QuickLaTeX.com [ begin{cases} 2x-7leqslant 9 \ x-4>2. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-c2d2fbf06d37908176f7855348bd1ee1_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} xleqslant 8 \ x>6. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-e354e782b309f49f3d2a32ba3ecfdfa7_l3.png)


![Rendered by QuickLaTeX.com [ begin{cases} x+2yleqslant 8 \ xgeqslant 0 \ ygeqslant x. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-2d9632160c48b2777a035f3d176edea6_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} (x-1)^2+(y-3)^2+(z-2)^2leqslant 4 \ x+y+zgeqslant 4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-410af121e91222c804c36bc597b5c082_l3.png)
![Rendered by QuickLaTeX.com [ 1. begin{cases} y-x>-2 \ xgeqslant 0 \ 2x+3y<7 end{cases} 2. begin{cases} x^2+y^2leqslant 9 \ y-2xgeqslant 4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-93c8b684ed39e31068e1d3ae7d10d55a_l3.png)
![Rendered by QuickLaTeX.com [ 3. begin{cases} x^2+y^2leqslant 16 \ (x-5)^2+y^2geqslant 4 . end{cases} 4. begin{cases} x^2+y^2+z^2leqslant 16 \ x>0. end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-702028826923aa849704d859954b2811_l3.png)