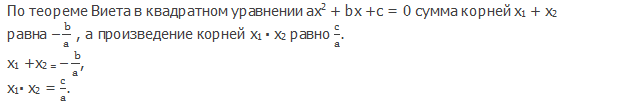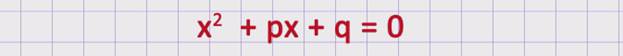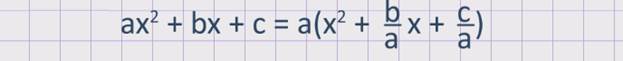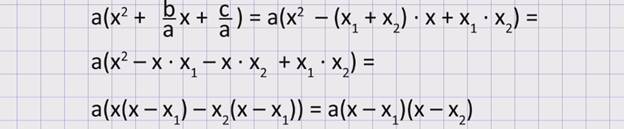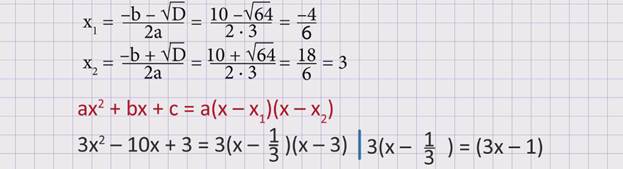После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью
формулы для корней
можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.
Перед тем, как изучить теорему Виета, хорошо потренируйтесь в
определении коэффициентов
«a», «b» и «с» в квадратных уравнениях.
Без этого вам будет трудно применить теорему Виета.
Когда можно применить теорему Виета
Не ко всем квадратным уравнениям имеет смысл использовать эту теорему.
Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.
Запомните!
Приведенное квадратное уравнение — это уравнение, в котором старший
коэффициент «a = 1».
В общем виде приведенное квадратное уравнение выглядит следующим образом:
x2 + px + q = 0
Обратите внимание, что разница с обычным общим видом
квадратного уравнения «ax2 + bx + c = 0» в том, что в
приведённом уравнении «x2 + px + q = 0» коэффициент
«а = 1».
Если сравнить приведенное квадратное уравнение «x2 + px + q = 0» с обычным общим видом квадратного
уравнения «ax2 + bx + c = 0», то становится видно,
что
«p = b», а «q = c».
Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.
| Уравнение | Коэффициенты | Вывод |
|---|---|---|
| x2 − 7x + 1 = 0 |
|
Так как «a = 1» можно использовать теорему Виета. |
|
3x2 − 1 + x = 0
Приведем уравнение к общему виду: 3x2 + x − 1 = 0 |
|
Так как «a = 3» не следует использовать теорему Виета. |
|
−x2 = −3 + 2x
Приведем уравнение к общему виду: −x2 + 3 − 2x = 0 |
|
Так как «a = −1» не следует использовать теорему Виета. |
Как использовать теорему Виета
Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.
Запомните!
Теорема Виета для приведённых квадратных уравнений «x2 + px + q = 0» гласит
что справедливо следующее:
, где «x1» и «x2» — корни этого уравнения.
Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент «p» —
значит плохой, поэтому он берется со знаком минус».
Рассмотрим пример.
x2 + 4x − 5 = 0
Так как в этом уравнении «a = 1», квадратное уравнение
считается приведённым, значит, можно
использовать метод Виета.
Выпишем коэффициенты «p» и «q».
- p = 4
- q = −5
Запишем теорему Виета для квадратного уравнения.
| x1 + x2 = −4 | |
| x1 · x2 = −5 |
Методом подбора мы приходим к тому, что корни уравнения
«x1 = −5» и «x2 = 1». Запишем ответ.
Ответ: x1 = −5; x2 = 1
Рассмотрим другой пример.
x2 + x − 6 = 0
Старший коэффициент «a = 1» поэтому можно применять теорему Виета.
| x1 + x2 = −1 | |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения
«x1 = −3» и «x2 = 2». Запишем ответ.
Ответ: x1 = −3; x2 = 2
Важно!
Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь.
Вы всегда можете решить любое квадратное уравнение, используя
формулу для нахождения корней.
Деление уравнение на первый коэффициент
Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.
2x2 − 16x − 18 = 0
Сейчас в уравнении «a = 2»,
поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы «a = 1».
Для этого достаточно разделить все уравнение на «2».
Таким образом, мы сделаем квадратное уравнение приведённым.
2x2 − 16x − 18 = 0 | (:2)
2x2(:2) − 16x(:2) − 18(:2) = 0
x2 − 8x − 9 = 0
Теперь «a = 1» и можно смело записывать формулу Виета и находить корни методом подбора.
| x1 + x2 = −(−8) | |
| x1 · x2 = −9 |
Методом подбора получим, что корни уравнения
«x1 = 9» и «x2 = −1». Запишем ответ.
Ответ: x1 = 9; x2 = −1
Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.
Корни «x1» и
«x2» квадратного уравнения
«x2 + px + 3 = 0» удовлетворяют
условию «x2 = 3x1».
Найти «p», «x1»,
«x2».
Запишем теорему Виета для этого уравнения.
По условию дано, что
«x2 = 3x1».
Подставим это выражение в систему вместо «x2».
| x1 + 3x1 = −p | |
| x1 · 3x1 = 3 |
Решим полученное квадратное уравнение «x12 = 1»
методом подбора и найдем «x1».
x12 = 1
- (Первый корень) x1 = 1
- (Второй корень) x1 = −1
Мы получили два значения «x1».
Для каждого из полученных значений найдем «p» и запишем все полученные результаты в ответ.
(Первый корень) x1 = 1
Найдем
«x2»
x1 · x2 = 3
1 · x2 = 3
x2 = 3
Найдем «p»
x1 + x2 = −p
1 + 3 = −p
4 = −p
p = −4;
(Второй корень) x1 = −1
Найдем «x2»
x1 · x2 = 3
−1 · x2 = 3
−x2 = 3 | ·(−1)
x2 = −3
Найдем «p»
x1 + x2 = −p
−1 + −3 = −p
−4 = −p
p = 4
Ответ: (x1 = 1; x2 = 3; p = −4) и
(x1 = −1; x2 = −3; p = 4)
Теорема Виета в общем виде
В школьном курсе математики теорему Виета используют только для приведённых уравнений,
где старший коэффициент «a = 1», но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.
В общем виде теорема Виета для квадратного уравнения выглядит так:
Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.
3x2 + 3x − 18 = 0
Используем для него теорему Виета в общем виде.
| x1 + x2 = −1 | |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения
«x1 = −3» и «x2 = 2». Запишем ответ.
Ответ: x1 = −3; x2 = 2
В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.
Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в
которых «a = 1».
Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
- Алгоритм разложения квадратного трёхчлена на множители с помощью дискриминанта
- Алгоритм разложения квадратного трёхчлена на множители по теореме Виета
- Примеры
Алгоритм разложения квадратного трёхчлена на множители с помощью дискриминанта
Данный алгоритм является универсальным.
На входе: квадратный трёхчлен $ax^2+bx+c$
Задача: разложить трёхчлен на множители
Шаг 1. Находим дискриминант $D = b^2-4ac$
Шаг 2. Если $D gt 0, x_1,2 = frac{-b pm sqrt{D}}{2a} $ и $ax^2+bx+c = a(x-x_1 )(x-x_2 )$
Если D = 0, $x_0 = — frac{b}{2a}$ и $ax^2+bx+c = a(x-x_0 )^2$
Если $D lt 0$, разложение на множители невозможно.
Шаг 3. Работа завершена.
Алгоритм разложения квадратного трёхчлена на множители по теореме Виета
Данный алгоритм применяется в частных случаях.
Если один (или оба) корня квадратного уравнения целые, то полезным навыком становится разложение на множители «в уме», с помощью теоремы Виета.
Навык этот не простой, и если у вас сразу не получится, не расстраивайтесь.
Рассмотрим следующий трёхчлен: $x^2+8x+15$
b = 8, c = 15
Если корни трёхчлена существуют, то их произведение равно 15.
Прикинем «в уме» соответствующие пары натуральных чисел:
(1;15),(3;5)
В трёхчлене $c gt 0$, значит корни одного знака, и в построении b участвует сумма этих корней. Из пары (1;15) сумма 8 не выходит, а вот из пары (3;5) — получается.
Для выбранной пары (3;5) запишем разложение, пока без знаков:
$$ (x…3)(x…5) = x^2+8x+15 $$
Теперь видно, что знаки в скобках – два плюса:
$$ (x+3)(x+5) = x^2+8x+15 $$
Разложение найдено.
Рассмотрим другой трёхчлен: $x^2+2x-35$
b = 2, c = -35
Пары натуральных чисел, дающие произведение 35:
(1;35),(5;7)
В трёхчлене $c lt 0$, значит корни разных знаков, и в построении b участвует разность этих корней. Из пары (1;35) разность 2 не выходит, а вот из пары (5;7) — получается.
Для выбранной пары (5;7) запишем разложение, пока без знаков:
$$ (x…5)(x…7) = x^2+2x-35 $$
Теперь видно, что 7 должно быть с плюсом, а 5 – с минусом:
$$ (x-5)(x+7) = x^2+2x-35 $$
Разложение найдено.
Обобщим алгоритм разложения по теореме Виета.
На входе: приведенный квадратный трёхчлен $x^2+bx+c$
Задача: разложить трёхчлен на множители при гипотезе, что корни — целочисленные
Шаг 1. Записать все пары натуральных чисел (m;n), дающих в произведении c.
Шаг 2. Если $c gt 0$, то из всех пар выбрать ту, сумма которой даёт b.
Если $c lt 0$, то из всех пар выбрать ту, разность которой даёт b.
Если выбрать пару не удаётся, данный алгоритм не подходит, и нужно приступить к разложению с помощью дискриминанта.
Шаг 3. Для выбранной пары записать разложение без знаков в виде:
$$ (x…m)(x…n) = x^2+bx+c $$
Сопоставляя левую и правую части, окончательно расставить знаки в скобках.
Шаг 4. Работа завершена.
Внимание!
Предложенный алгоритм позволяет не только раскладывать на линейные множители трёхчлены, но и находить их корни, т.е. решать соответствующие квадратные уравнения.
Не забывайте менять знаки при записи решений уравнения!
Например:
Решаем $x^2+8x+15 = 0$. Получаем (x+3)(x+5) = 0. Корни $x_1 = -3, x_2 = -5$.
Решаем $x^2+2x-35 = 0$. Получаем (x-5)(x+7) = 0. Корни $x_1 = 5, x_2 = -7$.
При некотором опыте, можно наловчиться раскладывать не только приведенные трёхчлены, например:
$$ 5x^2-14x-3 = (5x+1)(x-3), 3x^2+13x-10 = (3x-2)(x+5), $$
$$ 6x^2+7x-3 = (3x-1)(2x+3) $$
В этих случаях алгоритм усложняется за счёт дополнительных вариантов расстановки коэффициентов при переменной в скобках.
Примеры
Пример 1. Разложите квадратный трёхчлен с помощью дискриминанта:
$а) 2x^2+7x-4$
$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $
$ x = frac{-7 pm 9}{4} = left[ begin{array}{cc} x_1 = -4 \ x_2 = frac{1}{2} end{array} right. $
Получаем: $2x^2+7x-4 = 2(x+4) left(x- frac{1}{2} right)$
Можно также записать: $2x^2+7x-4 = (x+4)(2x-1)$
$б) 3x^2+20x-7$
$ D = 20^2-4 cdot 3 cdot (-7) = 400+84 = 484 = 22^2 $
$x = frac{-20 pm 22}{6} = left[ begin{array}{cc} x_1 = -7 \ x_2 = frac{1}{3} end{array} right.$
Получаем: $3x^2+20x-7 = 3(x+7) left(x-frac{1}{3} right)$
Можно также записать: $3x^2+20x-7 = (x+7)(3x-1)$
$в) 4x^2-19x-5$
$D = 19^2-4 cdot 4 cdot (-5) = 361+80 = 441 = 21^2$
$ x = frac{19 pm 21}{8} = left[ begin{array}{cc} x_1 = -frac{1}{4} \ x_2 = 5 end{array} right.$
Получаем: $4x^2-19x-5 = 4 left(x+ frac{1}{4} right)(x-5)$
Можно также записать: $4x^2-19x-5 = (4x+1)(x-5)$
$г*) x^2- sqrt{2}x+ frac{1}{2}$
$ D = (sqrt{2})^2-4 cdot frac{1}{2} = 2-2 = 0, x = frac{sqrt{2}}{2} $
Получаем: $x^2-sqrt{2} x+ frac{1}{2} = left(x- frac{sqrt{2}}{2} right)^2 $
Пример 2*. Разложите трёхчлены на множители подбором по теореме Виета:
$а) x^2+7x+12$
Пары множителей: (1;12),(2;6),(3;4)
$c = 12 gt 0 Rightarrow$ выбираем из пар ту, что в сумме дает b = 7. Это пара (3;4).
Записываем разложение без знаков: $(x…3)(x…4) = x^2+7x+12$
Расставляем знаки, результат: $x^2+7x+12 = (x+3)(x+4)$
$б) x^2+3x-18$
Пары множителей: (1;18),(2;9),(3;6)
$c = -18 lt 0 Rightarrow$ выбираем из пар ту, разность которой дает b = 3. Это пара (3;6).
Записываем разложение без знаков: $(x…3)(x…6) = x^2+3x-18$
Расставляем знаки, результат: $x^2+3x-18 = (x-3)(x+6)$
в) x+4x-77
Пары множителей: (1;77),(7;11)
$c = -18 lt 0 Rightarrow$ выбираем из пар ту, разность которой дает b=4. Это пара (7;11).
Записываем разложение без знаков: $(x…7)(x…11) = x^2+4x-77$
Расставляем знаки, результат: $x^2+4x-77 = (x-7)(x+11)$
$г*) 2x^2-x-3$
Одна пара множителей (1;3)
Возможные разложения с коэффициентом:
$$ (2x…1)(x…3) = 2x^2-x-3, (2x…3)(x…1) = 2x^2-x-3 $$
$c = -3 lt 0$, в скобках разные знаки.
Перебираем четыре возможных варианта и получаем:
$$2x^2-x-3 = (2x+3)(x-1) = 2 left(x+ frac{3}{2} right)(x-1)$$
Пример 3. Сократите дробь.
Разложение на множители проводим по формулам сокращенного умножения, с помощью дискриминанта или по теореме Виета.
а) $$ frac{x^2-16}{x^2+11x+28} = frac{(x-4)(x+4)}{(x+4)(x+7)} = frac{x-4}{x+7}$$
б) $$ frac{x^2-2x-15}{x^2-10x+25} = frac{(x-5)(x+3)}{(x-5)^2} = frac{x+3}{x-5}$$
в) $$ frac{3y^2-5y+2}{3y^2-y-2} = frac{(3y-2)(y-1)}{(3y+2)(y-1)} = frac{3y-2}{3y+2}$$
г)$$ frac{2y^2-3y+1}{3y^2-4y+1} = frac{(2y-1)(y-1)}{(3y-1)(y-1)} = frac{2y-1}{3y-1}$$
Пример 4. Упростите выражение:
$$ frac{x-16}{(x+2)^2} ∶ left(frac{3x+11}{(3x^2+17x+22)} — frac{2}{x+2} right) = frac{x-16}{(x+2)^2} ∶ left(frac{3x+11}{(3x+11)(x+2)} — frac{2}{x+2} right) = $$
$$ = frac{x-16}{(x+2)^2} ∶ left(frac{1}{x+2} — frac{2}{x+2}right) = frac{x-16}{(x+2)^2} ∶ left(-frac{1}{x+2}right) = -frac{(x-16)(x+2)}{(x+2)^2} = $$
$$ =-frac{x-16}{x+2} = frac{16-x}{x+2}$$
Как разложить квадратное уравнение по теореме виета
Ключевые слова: квадратный трехчлен, разложение на множители, теорема Виета
Квадратный трехчлен раскладывается на множители: ax 2 + bx + c = a ( x – x 1 )( x – x 2 ) ,
где $$x_<1>= frac<-b + sqrt><2a>, x_<2>= frac<-b — sqrt><2a>$$, $$D = b^ <2>- 4ac$$ в том случае, если D > 0.
Если D ax 2 + bx + c не имеет действительных корней.
Если D > 0, то квадратный трехчлен имеет два корня (при D = 0 они совпадают). Если же D x 2 – 4 x + 3.
Решение.
1 способ. По формулам $$x_<1>= frac<-b + sqrt><2a>, x_<2>= frac<-b — sqrt><2a>$$, где $$D = b^ <2>- 4ac$$ найдем корни данной квадратичной функции: $$x_ <1>= 1$$ и $$x_ <2>= 3$$.
Применяя формулу для разложения квадратичной функции на множители, получаем: x 2 – 4 x + 3 = ( x – 1)( x — 3).
2 способ. Применим непосредственное выделение полного квадрата.
x 2 – 4 x + 3 = x 2 – 4 x + 4 – 1 = ( x – 2) 2 – 1 = ( x – 2) 2 – 1 2 = ( x – 2 + 1)( x – 2 – 1) = ( x – 1)( x – 3).
Ответ. ( x – 1)( x – 3).
Пример. Пусть $$x_<1>$$ и $$x_<2>$$ — корни квадратичной функции x 2 + px + q = 0 Найти, чему равно значение выражения $$frac>> + frac>>$$.
Решение. Так как x 1 и x 2 — корни квадратичной функции x 2 + px + q = 0 , то справедливы соотношения: $$x_ <1>+ x_ <2>= — p$$ и $$x_ <1>cdot x_ <2>= q$$. Тогда имеем: $$frac>> + frac>> = frac^ <2>+ x_<2>^<2>>x_<2>>= frac <(x_<1>+ x_<2>)^ <2>- 2x_<1>x_<2>>x_<2>> = frac <(-p)^<2>- 2q> =
frac — 2q> = frac>
— 2$$.
Ответ. $$frac> — 2$$
Теорема Виета для квадратного уравнения
О чем эта статья:
Основные понятия
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Существует три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:
- если D 0, есть два различных корня.
В случае, когда второй коэффициент четный, можно воспользоваться формулой нахождения дискриминанта , где .
В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Рассмотрим квадратное уравнение, в котором первый коэффициент равен 1: . Такие уравнения называют приведенными квадратными уравнениями. Сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Обучение на курсах по математике помогает быстрее разобраться в новых темах и подтянуть оценки в школе.
Доказательство теоремы Виета
Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что следующие равенства верны
- x₁ + x₂ = −b,
- x₁ * x₂ = c.
Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.
-
Объединим числитель и знаменатель в правой части.
Раскроем скобки и приведем подобные члены:
Сократим дробь полученную дробь на 2, остается −b:
Мы доказали: x₁ + x₂ = −b.
Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.
-
Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:
Перемножаем числители и знаменатели между собой:
Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a 2 − b 2 . Получаем:
Далее произведем трансформации в числителе:
Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.
Далее раскроем скобки и приведем подобные члены:
Сократим:
Мы доказали: x₁ * x₂ = c.
Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.
Обратная теорема Виета
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:
Обратная теорема Виета
Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.
Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.
Докажем теорему, обратную теореме Виета
Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.
Зафиксируем, что сумма m и n равна −b, а произведение равно c.
Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.
-
Выразим b из равенства m + n = −b. Это можно сделать, умножив обе части на −1:
Подставим m в уравнение вместо x, выражение −m − n подставим вместо b, а выражение mn — вместо c:
При x = m получается верное равенство. Значит число m является искомым корнем.
- Аналогично докажем, что число n является корнем уравнения. Подставим вместо x букву n, а вместо c подставим m * n, поскольку c = m * n.
При x = n получается верное равенство. Значит число n является искомым корнем.
Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.
Примеры
Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.
Дано: x 2 − 6x + 8 = 0.
Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv» width=»99″>
Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.
Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»57″ src=»https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=»64″>
Неприведенное квадратное уравнение
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:
ax 2 + bx + c = 0, где а = 1.
Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x 2 .
- Получилось следующее приведенное уравнение:
-
Получается, второй коэффициент при x равен, свободный член —. Значит сумма и произведение корней будут иметь вид:
Рассмотрим пример неприведенного уравнения: 4x 2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x 2 , то есть на 4.
Разложение квадратного трёхчлена на множители
Как разложить на множители квадратный трёхчлен
Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
Где левая часть — исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Итак, x1 = 6 , x2 = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x1)(x − x2). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x1 = 6, x2 = 2
Если a равно единице (как в данном примере), то решение можно записать покороче:
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Итак, x1 = 4 , x2 = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x1)(x − x2) , где вместо переменных a , x1 и x2 подстáвим соответствующие значения. В данном случае a = 2
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24
Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x1 + x2 = −b . Для этого можно умножить обе его части на −1
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x2
Далее замечаем, что выражение ( x − x1 ) является общим множителем. Вынесем его за скобки:
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства и
Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1
Теперь из второго равенства выразим c . Для этого умножим обе его части на a
Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:
Здесь вместо переменных b и c были подставлены выражения −ax1 − ax2 и ax1x2 , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax2
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:
Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x1)(x − x2) вместо переменных x1 и x2 .
Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x1 и x2 . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2
Тогда значение −2 в процессе разложения на множители будет подставлено вместо x1 и x2 . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x1)(x − x2) , где вместо a , x1 и x2 подстáвим соответствующие значения:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)
Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x1
Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Теперь из второго равенства выразим k . Так мы найдём его значение.
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
http://skysmart.ru/articles/mathematic/teorema-vieta-formula
Теорема Виета помогает решать квадратные уравнения путём подбора. В этой статье даны определения, доказательства, формулы и примеры решений квадратных уравнений для чайников.
Что такое теорема Виета
Франсуа Виет (1540-1603 гг) – математика, создатель знаменитых формул Виета
Теорема Виета нужна для быстрого решения квадратных уравнений (простыми словами).
Если более подробно, то теорема Виета – это сумма корней данного квадратного уравнения равняется второму коэффициенту, который взят с противоположным знаком, а произведение равно свободному члену. Это свойство обладает любым приведённым квадратным уравнением, у которого есть корни.
При помощи теоремы Виета можно легко решать квадратные уравнения путём подбора, поэтому скажем “спасибо” этому математику с мечем в руках за наш счастливый 7 класс.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Доказательство теоремы Виета
Чтобы доказать теорему, можно воспользоваться известными формулами корней, благодаря которым составим сумму и произведение корней квадратного уравнения. Только после этого мы сможем убедиться, что они равны и, соответственно,
.
Допустим у нас есть уравнение: . У этого уравнения есть такие корни:
и
. Докажем, что
,
.
По формулам корней квадратного уравнения:
,
.
1. Найдём сумму корней:
.
Разберём это уравнение, как оно у нас получилось именно таким:
=
.
Шаг 1. Приводим дроби к общему знаменателю, получается:
=
=
.
Шаг 2. У нас получилась дробь, где нужно раскрыть скобки:
=
=
. Сокращаем дробь на 2 и получаем:
.
Мы доказали соотношение для суммы корней квадратного уравнения по теореме Виета.
2. Найдём произведение корней:
=
= =
=
=
=
.
Докажем это уравнение:
.
Шаг 1. Есть правило умножение дробей, по которому мы и умножаем данное уравнение:
.
Шаг 2. Далее выполняется умножение скобку на скобку (в числителе). Можно воспользоваться формулой сокращённого умножения (ФСУ) – формула разности, откуда получается:
.
Теперь вспоминаем определение квадратного корня и считаем:
=
.
Шаг 3. Вспоминаем дискриминант квадратного уравнения: . Поэтому в последнюю дробь вместо D (дискриминанта) мы подставляем
, тогда получается:
=
.
Шаг 4. Раскрываем скобки и приводим подобные слагаемые к дроби:
.
Шаг 5. Сокращаем «4a» и получаем .
Вот мы и доказали соотношение для произведения корней по теореме Виета.
ВАЖНО! Если дискриминант равняется нулю, тогда у квадратного уравнения всего один корень.
Теорема, обратная теореме Виета
По теореме, обратной теореме Виета можно проверять, правильно ли решено наше уравнение. Чтобы понять саму теорему, нужно более подробно её рассмотреть.
Если числа и
такие:
и
, тогда они и есть корнями квадратного уравнения
.
Доказательство обратной теоремы Виета
Шаг 1. Подставим в уравнение выражения для его коэффициентов:
Шаг 2. Преобразуем левую часть уравнения:
;
.
Шаг 3. Найдём Корни уравнения , а для этого используем свойство о равенстве произведения нулю:
или
. Откуда и получается:
или
.
Примеры с решениями по теореме Виета
Задание
Найдите сумму, произведение и сумму квадратов корней квадратного уравнения , не находя корней уравнения.
Решение
Шаг 1. Вспомним формулу дискриминанта . Подставляем наши цифры под буквы. То есть,
,
– это заменяет
, а
. Отсюда следует:
. Получается:
. Если дискриминант больше нуля, тогда у уравнения есть корни. По теореме Виета их сумма
, а произведение
.
Выразим сумму квадратов корней через их сумму и произведение:
.
Ответ
7; 12; 25.
Задание
Решите уравнение . При этом не применяйте формулы квадратного уравнения.
Решение
У данного уравнения есть корни, которые по дискриминанту (D) больше нуля. Соответственно, по теореме Виета сумма корней этого уравнения равна 4, а произведение – 5. Сначала определяем делители числа , сумма которых равняется 4. Это числа «5» и «-1». Их произведение равно – 5, а сумма – 4. Значит, по теореме, обратной теореме Виета, они являются корнями данного уравнения.
Ответ
и
Задание
Найдите, если это возможно, сумму и произведение корней уравнения:
Решение
. Так как дискриминант меньше нуля, значит у уравнения нет корней.
Ответ
Нет корней.
Задание
Составьте уравнение, каждый корень которого в два раза больше соответствующего корня уравнения:
Решение
По теореме Виета сумма корней данного уравнения равна 12, а произведение = 7. Значит, два корня положительны.
Сумма корней нового уравнения будет равна:
, а произведение
.
По теореме, обратной теореме Виета, новое уравнение имеет вид:
Ответ
Получилось уравнение, каждый корень которого в два раза больше:
Итак, мы рассмотрели, как решать уравнение при помощи теоремы Виета. Очень удобно пользоваться данной теоремой, если решаются задания, которые связаны со знаками корней квадратных уравнений. То есть, если в формуле свободный член
– число положительное, и если в квадратном уравнении имеются действительные корни, тогда они оба могут быть либо отрицательными, либо положительными.
А если свободный член – отрицательное число, и если в квадратном уравнении есть действительные корни, тогда оба знака будут разными. То есть, если один корень положительный, тогда другой корень будет только отрицательный.
Полезные источники:
- Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. Алгебра 8 класс: Москва “Просвещение”, 2016 – 318 с.
- Рубин А. Г., Чулков П. В. – учебник Алгебра 8 класс:Москва “Баласс”, 2015 – 237 с.
- Никольский С. М., Потопав М. К., Решетников Н. Н., Шевкин А. В. – Алгебра 8 класс: Москва “Просвещение”, 2014 – 300
§ 1 Теорема Виета. Разложение квадратного трёхчлена на множители
Познакомимся с теоремой Виета, с соотношениями между корнями квадратного уравнения и его коэффициентами, научимся раскладывать квадратный трёхчлен на множители.
Квадратным уравнением называют уравнение вида ax2 + bx + c = 0, где a, b, c-коэффициенты, х – переменная, причём a ≠ 0. Левая часть квадратного уравнения
ax2 + bx +c – это многочлен второй степени, его называют квадратным трехчленом. Если в квадратном уравнении коэффициент при х2 или, можно сказать, старший коэффициент a равен 1, то такое квадратное уравнение называют приведенным.
Впервые зависимость в виде соотношений между корнями квадратного уравнения и его коэффициентами обнаружил французский математик Франсуа Виет.
Докажем теорему Виета.
Теорема Виета справедлива и для квадратных уравнений, имеющих один корень. В этом случае считают, что уравнение имеет два одинаковых корня.
Теорему Виета удобно применять для приведенного квадратного уравнения:
Приведенное квадратное уравнение можно записать в виде:
Тогда сумма корней х1 +х2 равна второму коэффициенту, взятому с противоположным знаком, то есть – р, а произведение корней х1∙ х2 равно свободному члену q.
х1 +х2 = – р
х1∙ х2 = q
По теореме Виета можно подбором найти корни уравнения.
Например, решим квадратное уравнение х2 – х – 12 = 0.
Уравнение является приведенным, так как коэффициент a равен 1. Тогда сумма корней х1 + х2 = 1, а произведение х1 ∙ х2= –12. Если х1 и х2 целые числа, то они являются делителями числа –12. Нетрудно догадаться, что х1 = –3; х2 = 4.
По теореме обратной теореме Виета можно выполнить проверку правильности нахождения корней квадратного уравнения.
Обратное утверждение теоремы Виета:
Если х1 и х2 – корни квадратного уравнениятакие, чтох1 + х2 = –р, х1 ∙ х2 = q, то эти числа0 – корни уравнения х2 + рх + q = 0.
Решим уравнение 3х2 – 4х – 4 = 0.
Дискриминант D= (-4)2 -4 ∙ 3 ∙ (-4) = 64, D > 0.
Найдем корни:
С помощью теоремы Виета выводится формула разложения квадратного трехчлена на множители.
В квадратном трехчлене ax2 + bx +c вынесем за скобки a. Получим:
Значит, квадратный трехчленможно разложить на множители ax2 + bx + c = a(х– х1) (х –х2),где х1 и х2 – корни квадратного трехчлена, которые можно найти, решая квадратное уравнение ax2 + bx + c = 0.
Если х1 = х2 , т.е. дискриминант квадратного трехчлена равен нулю (D = 0), то доказанная формула будет иметь вид ax2 + bx + c = a(х– х1)2.
Разложим на множители квадратный трехчлен 3х2 – 10х + 3.
Для этого решим квадратное уравнение 3х2 – 10х + 3 = 0.
Дискриминант D = = (-10)2 – 4 ∙ 3 ∙ 3 = 64, D > 0.
Тогда 3х2 – 10х + 3 = (3х – 1)(х – 3).
§ 2 Важно запомнить
Тогда сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком х1 +х2 = –р, а произведение корней равно свободному члену х1∙ х2 = q. Эти соотношения впервые обнаружил французский математик Франсуа Виет.
По теореме Виета можно подбором найти корни уравнения.
Если свободный член q – отрицательное число, то корни имеют разные знаки. По теореме, обратной теореме Виета, можно проверить правильность нахождения корней.
С помощью теоремы Виета выводится формула разложения квадратного трёхчлена на множители a x2 + bx +c= a(х — х1) (х -х2), где х1; х2 – корни квадратного трехчлена.