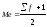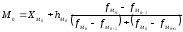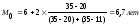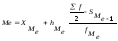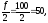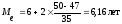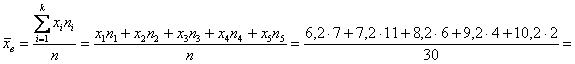Мода
и медиана –
особого рода средние, которые используются
для изучения структуры вариационного
ряда. Их иногда называют структурными
средними, в отличие от рассмотренных
ранее степенных средних.
Мода
– это величина признака (варианта),
которая чаще всего встречается в данной
совокупности, т.е. имеет наибольшую
частоту.
Мода
имеет большое практическое применение
и в ряде случаев только мода может дать
характеристику общественных явлений.
Медиана
– это варианта, которая находится в
середине упорядоченного вариационного
ряда.
Медиана
показывает количественную границу
значения варьирующего признака, которой
достигла половина единиц совокупности.
Применение медианы наряду со средней
или вместо нее целесообразно при наличии
в вариационном ряду открытых интервалов,
т.к. для вычисления медианы не требуется
условное установление границ отрытых
интервалов, и поэтому отсутствие сведений
о них не влияет на точность вычисления
медианы.
Медиану
применяют также тогда, когда показатели,
которые нужно использовать в качестве
весов, неизвестны. Медиану применяют
вместо средней арифметической при
статистических методах контроля качества
продукции. Сумма абсолютных отклонений
варианты от медианы меньше, чем от любого
другого числа.
Рассмотрим
расчет моды и медианы в дискретном
вариационном ряду:
|
Стаж, |
Число |
Накопленные |
|
1 |
2 |
2 |
|
3 |
4 |
6 |
|
4 |
5 |
(11) |
|
8 |
4 |
15 |
|
10 |
1 |
16 |
|
ИТОГО: |
16 |
— |
Определить моду и медиану.
Мода
Мо =
4 года, так как этому значению соответствует
наибольшая частота f
= 5.
Т.е.
наибольшее число рабочих имеют стаж 4
года.
Для
того, чтобы вычислить медиану, найдем
предварительно половину суммы частот.
Если сумма частот является числом
нечетным, то мы сначала прибавляем к
этой сумме единицу, а затем делим пополам:
Ме=16/2=8
Медианой
будет восьмая по счету варианта.
Для
того, чтобы найти, какая варианта будет
восьмой по номеру, будем накапливать
частоты до тех пор, пока не получим сумму
частот, равную или превышающую половину
суммы всех частот. Соответствующая
варианта и будет медианой.
Ме
= 4 года.
Т.е.
половина рабочих имеет стаж меньше
четырех лет, половина больше.
Если
сумма накопленных частот против одной
варианты равна половине сумме частот,
то медиана определяется как средняя
арифметическая этой варианты и
последующей.
Вычисление
моды и медианы в интервальном вариационном
ряду
Мода
в интервальном вариационном ряду
вычисляется по формуле
где ХМ0
— начальная
граница модального интервала,
hм0
– величина модального интервала,
fм0,
fм0-1,
fм0+1
– частота
соответственно модального интервала,
предшествующего модальному и последующего.
Модальным
называется такой интервал, которому
соответствует наибольшая частота.
Пример
1
|
Группы |
Число |
Накопленные |
|
1 |
2 |
3 |
|
До |
4 |
4 |
|
2-4 |
23 |
27 |
|
4-6 |
20 |
47 |
|
6-8 |
35 |
82 |
|
8-10 |
11 |
93 |
|
свыше |
7 |
100 |
|
ИТОГО: |
100 |
— |
Определить
моду и медиану.
Решение.
Модальный
интервал [6-8], т.к. ему соответствует
наибольшая частота f
= 35. Тогда:
Хм0=6,
fм0=35
hм0=2,
fм0-1=20
fм0+1=11
Вывод:
Наибольшее число рабочих имеет стаж
примерно 6,7 лет.
Для
интервального ряда Ме вычисляется по
следующей формуле:
где Хме
–
нижняя граница медиального интервала,
hме
– величина медиального интервала,
–
половина суммы частот,
fме
– частота медианного интервала,
Sме-1
–сумма
накопленных частот интервала,
предшествующего медианному.
Медианный
интервал – такой интервал, которому
соответствует кумулятивная частота,
равная или превышающая половину суммы
частот.
Определим
медиану для нашего примера.
Найдем:
т.к
82>50, то медианный интервал [6-8].
Тогда:
Хме
=6, fме
=35,
hме
=2, Sме-1=47,
Вывод: Половина рабочих имеет стаж
меньше 6,16 лет, а половина имеет стаж
больше, чем 6,16 лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:
Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
Загрузка…
Аннотация: Для получения более полной характеристики вариационного ряда помимо средней величины рассчитываются так называемые структурные показатели. К ним относятся мода, медиана, квартили, децили, перцентили, квартильные и децильные коэффициенты.
8.1. Мода
Мода (Мо) — это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.
8.1.1. Определение моды в дискретных вариационных рядах
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
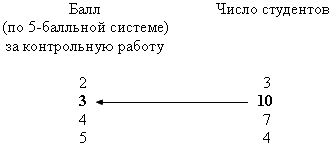
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
Здесь наибольшая частота — 10, она принадлежит варианте со значением 3, значит, Мо = 3. Таким образом, самой распространенной оценкой, полученной студентами за контрольную работу, была «тройка».
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
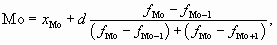
где хМо — нижняя граница модального интервала;
d — величина интервала;
fMo — частота модального интервала;
fMo — 1 — частота интервала, предшествующего модальному;
fMo + 1 — частота интервала, следующего за модальным.
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
- модальным является интервал 60-80, так как ему соответствует наибольшая частота (21);
- нижняя граница модального интервала xМо = 60; величина интервала d = 20 (80 — 60 = 20);
- частота модального интервала fМо = 21; частота интервала, предшествующего модальному, fМо — 1 = 15; частота интервала, следующего за модальным, fМо + 1 = 12.
Подставив в формулу соответствующие величины, получим
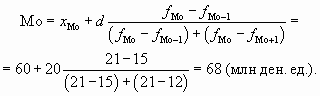
Определить модальное значение признака можно и по графику. Для этого в случае дискретных вариационных рядов строится полигон распределения. Напомним, что у него на оси абсцисс помещаются значения признака (варианты), а на оси ординат — соответствующие им частоты. Значение абсциссы, соответствующее наибольшей вершине полигона, будет значением моды.
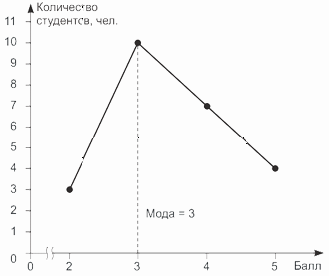
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Рис.
8.1.
Определение моды по полигону распределения
Если имеется интервальный вариационный ряд с равными интервалами, то для определения моды строится гистограмма, у которой на оси абсцисс находятся значения границ интервалов, а на оси ординат — соответствующие интервалам частоты. На гистограмме модальный интервал будет иметь наибольшую высоту столбца. Затем надо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса точки пересечения будет значением моды. Продемонстрируем это на примере.
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).
Рис.
8.2.
Определение моды по гистограмме распределения
Вариационный ряд может содержать несколько модальных значений. Чаще всего это происходит, когда в один ряд объединяют разнородные единицы наблюдения, которые желательно разделить на подгруппы и анализировать по отдельности. Вариационный ряд, имеющий одну моду, называется унимодальным, две — бимодальным, три и более — мультимодальным.
Структурные средние — мода, медиана, квантиль, дециль
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода — величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
— величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили —
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Медиана —
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
— нижняя граница медианного интервала
— величина медианного интервала
— сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили — это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% —
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
— накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1.5 |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд — значения дохода жильцов распределены по возрастанию.
Мода
— наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
— такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
— значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% — между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
|
Удельный вес вкладов, % |
5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода — варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
—
начало модального интервала
—
величина интервала
—
частота модального интервала
—
частота интервала, предшествующего модальному
—
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана — варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина — более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 | 0.2 |
| 12-15 | 0.05 |
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.
3.1.4. Как вычислить среднюю, моду и медиану интервального ряда?
Начнём опять с ситуации, когда нам даны первичные статические данные:
Пример 10
По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.):
– это в точности числа из Примера 6. Но теперь нам нужно найти среднюю, моду и медиану.
Решение: чтобы найти среднюю по первичным данным, нужно
просуммировать все варианты и разделить полученный результат на объём совокупности:
ден. ед.
Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то,
конечно, забиваем в любую свободную ячейку:
=СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.
Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел
одинаковые, но среди них запросто может найтись так 5-6-7 вариант с одинаковой максимальной частотой, например, частотой 2.
Поэтому модальное значение рассчитывается по сформированному интервальному ряду (см. ниже).
Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем
скобку ) и жмём Enter: . Причём, здесь даже ничего
не нужно сортировать.
Но в Примере 6 я проводил сортировку совокупности по возрастанию (вспоминаем и сортируем), и это хорошая возможность
повторить формальный алгоритм отыскания медианы.
Делим объём выборки пополам:
, и поскольку она состоит из чётного
количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного
ряда:
ден. ед.
Ситуация вторая. Когда даны не первичные данные, а готовый интервальный ряд (что в учебных задачах бывает чаще).
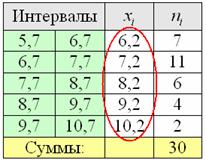
Продолжаем анализировать этот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины интервалов:
– чтобы воспользоваться знакомой формулой дискретного случая:
– и это отличный результат! Расхождение с
более точным значением (), вычисленным по
первичным данным, составило всего 0,04!
Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось
весьма эффективным. Впрочем, с современными программами не составляет особого труда вычислить точное значение даже по
очень большому массиву первичных данных. Если они нам известны 
С другими центральными показателями всё занятнее.
Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в нашей задаче
это интервал с частотой 11, и воспользоваться
следующей страшненькой формулой:
, где:
– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.
Таким образом:
ден. ед. – как видите, «модная» цена на
ботинки заметно отличается от среднего арифметического значения .
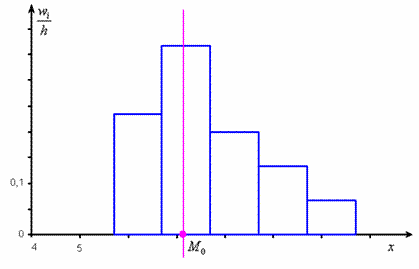
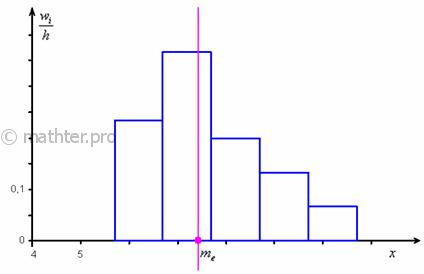
Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот
и отмечу :
откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала
с бОльшей частотой. По той причине, что дешёвых ботинок больше. И, возможно, они тоже вполне себе модные.
Справочно остановлюсь на редких случаях:
– если модальный интервал крайний, то либо
;
– если обнаружатся два смежных модальных интервала, например, и
,
то рассматриваем модальный интервал , при этом
близлежащие интервалы (слева и справа) по возможности тоже укрупняем в два раза;
– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым две
или бОльшее количество мод.
Вот такой вот депеш мод 
И медиана. Она рассчитывается чуть по менее страшной формуле. Для её применения
нужно найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две
равные части.
Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты
, здесь же сподручнее рассчитать
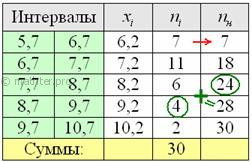
«обычные» накопленные частоты . Вычислительный
алгоритм такой же – первое значение сносим слева (красная стрелка), а каждое следующее получается как сумма
предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера):
Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопится» на всех «пройденных»
интервалах, включая текущий.
Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит -ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко
прийти к выводу, что эти варианты содержатся в интервале .
Формула медианы:
, где:
– объём статистической совокупности;
– нижняя граница медианного
интервала;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота
предыдущего интервала.
Таким образом:
ден. ед. – заметим, что медианное
значение, в отличие от моды, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:
Справочно особые случаи:
– если медианным является крайний левый интервал, то ;
– если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то
объединяем эти интервалы, и по возможности удваиваем предыдущий интервал.
Ответ: ден. ед.
По сравнению с предыдущей задачей ,
центральные показатели оказались заметно отличны друг от друга. Это говорит об асимметрии
(«скошенности») распределения цен, что хорошо видно по гистограмме и совершенно логично –
ботинок низкого и среднего ценового сегмента много, а премиального – мало.
Задание для тренировки:
Пример 11
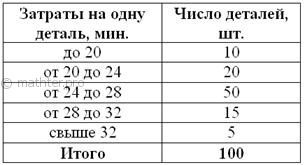
Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено
следующее статистическое распределение:
…да, тот самый завод Петровского 
Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на
калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце книги. Это, кстати, уже
каноничная «интервальная» задача, в которой исследуется непрерывная величина – время.
Что ещё можно сказать по теме?
Несмотря на разнообразия рассмотренных показателей, их всё равно бывает не достаточно. Существуют крайне неоднородные
совокупности, у которых варианты «кучкуются» во многих местах, и по этой причине средняя, мода и
медиана плохо характеризуют положение дел.
В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в упоротых специализированных исследованиях – и с
помощью перцентилей.
Квартили упорядоченного вариационного ряда – это варианты , которые делят его на 4 равные (по количеству вариант) части. Из чего
автоматически следует, что 2-я квартиль – есть в точности медиана: .
В тяжёлых случаях проводится разбиение на 10 частей – децилями – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по
количеству вариант) частей.
И в очень тяжелых случаях в ход пускается 99 перцентилей .
После разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние и другие
показатели.
В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для
самостоятельного изучения.
Ну а сейчас мы переходим к изучению второй группы статистических показателей:


| Оглавление |