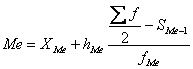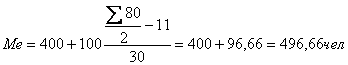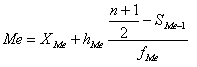Дискретный вариационный ряд и его характеристики
- Классификация рядов распределения
- Дискретный вариационный ряд, полигон частот и кумулята
- Выборочная средняя, мода и медиана
- Степень асимметрии вариационного ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования дискретного вариационного ряда
- Примеры
п.1. Классификация рядов распределения
Статистический ряд распределения – это количественное распределение единиц совокупности на однородные группы по некоторому варьирующему признаку.
В зависимости от природы признака различают атрибутивные и вариационные ряды.
Атрибутивный ряд распределения построен на качественном признаке.
Вариационный ряд распределения построен на количественном признаке.
Например:
Качественными признаками, которые не поддаются измерению, являются: профессия, пол, национальность и т.п.
Количественными признаками, которые можно подсчитать или измерить, являются: количество людей в группе, число повторений в опыте, возраст, вес, рост, скорость, температура и т.п.
По упорядоченности вариационные ряды делятся на упорядоченные (ранжированные) и неупорядоченные. Упорядочить ряд можно по возрастанию или убыванию исследуемого признака.
По характеру непрерывности признака вариационные ряды делятся на дискретные и интервальные.
Например:
Дискретными признаками, которые принимают отдельные значения, являются: количество людей в группе, число детей в семье, количество домов, число опытов и т.п.
Непрерывными признаками, которые могут принимать любые значения в интервале, являются: возраст, вес, рост, скорость, температура и т.п.
Варианты – это отдельные значения признака, которые он принимает в вариационном ряду.
Частоты – это численности отдельных вариант.
Например:
Распределение учеников по оценкам за контрольную работу
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
В данном ряду признак – это оценка, варианты признака (x_i) – это множество {2;3;4;5}, частоты (f_i) – это количество учеников, получивших каждую из оценок.
п.2. Дискретный вариационный ряд, полигон частот и кумулята
Дискретный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся прерывно и принимающему конечное множество значений.
Общий вид дискретного вариационного ряда
| Варианты, (x_i) | (x_1) | (x_2) | … | (x_k) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k — число вариант исследуемого признака.
Тогда общее количество исходов (число единиц в совокупности): (N=sum_{i=1}^k f_i)
Полигон частот – это ломаная, которая соединяет точки ((x_i,f_i)).
Например:
| Для распределения учеников по оценкам из нашего примера получаем такой полигон: |  |
Относительная частота варианты (x_i) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$ Относительная частота (w_i) является эмпирической оценкой вероятности варианты (x_i) в исследуемом ряду.
Полигон относительных частот – это ломаная, которая соединяет точки ((x_i,w_i)).
Полигон относительных частот является эмпирическим законом распределения исследуемого признака.
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)).
Ступенчатая кривая (F(x_i)), построенная по точкам ((x_i,S_i)), является эмпирической функцией распределения исследуемого признака.
Например:
Проведем необходимые расчеты и построим полигон относительных частот, кумуляту и эмпирическую функцию распределения учеников по оценкам.
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (w_i) | 0,0909 | 0,4545 | 0,3030 | 0,1515 | 1 |
| (S_i) | 0,0909 | 0,4545 | 0,8485 | 1 | — |
Полигон относительных частот (эмпирический закон распределения)
Кумулята (красная ломаная) и эмпирическая функция распределения (ступенчатая синяя кривая).
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 2\ 0,0909, 2lt xleq 3\ 0,5455, 3lt xleq 4\ 0,8485, 4lt xleq 5\ 1, xgt 5 end{cases} $$
п.3. Выборочная средняя, мода и медиана
Выборочная средняя дискретного вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Мода дискретного вариационного ряда – это варианта с максимальной частотой: $$ M_o=x*, f(x*)=underset{i=overline{1,k}}{max}f_i $$ Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
На полигоне частот мода – это абсцисса самой высокой точки.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
Алгоритм:
1. Отсортировать ряд по возрастанию.
2а. Если общее количество измерений N нечётное, найти (m=lceilfrac N2rceil) и округлить в сторону увеличения. (M_e=x_m) — искомая медиана.
2б. Если общее количество измерений N чётное, найти (m=frac N2) и вычислить медиану как среднее (M_e=frac{x_m+x_{m+1}}{2}).
На графике кумуляты медиана – это абсцисса первой точки слева, ордината которой превысила 0,5.
Например:
1) Найдем выборочную среднюю для распределения учеников по оценкам:
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (x_if_i) | 6 | 45 | 40 | 25 | 116 |
$$ X_{cp}=frac{6+45+40+25}{33}=frac{116}{33}approx 3,5 $$ Средняя оценка за контрольную – 3,5.
2) Найдем моду. Максимальная частота – 15 человек – у троечников. Значит: (M_o=3).
3) Найдем медиану. Общее количество измерений N=33 — нечетное.
Находим: (m=lceilfrac N2rceil=17)
Смотрим на ряд слева направо. Сначала у нас идет 3 двоечника, затем 15 троечников.
Вместе их 18, и 17-й человек в ряду — троечник. Группа троечников является медианной: (M_e=3).
Также, медиану можно найти по графику кумуляты. (3;0,5455) – это первая слева точка, в которой ордината больше 0,5. Значит, медиана равна абсциссе этой точки, т.е. (M_e=3).
п.4. Степень асимметрии вариационного ряда
В рядах с асимметрией или выбросами выборочная средняя не отражает в полной мере особенности исследуемого признака. Типичный случай – значение среднего уровня доходов в странах с высоким индексом Джини, где 5% населения получает 95% доходов. Или анекдотичный случай со «средней температурой по больнице».
Поэтому, кроме средней, в статистическом исследовании всегда следует определять моду и медиану.
Мода, медиана и выборочная средняя совпадут, если вариационный ряд является симметричным: $$ X_{cp}=M_o=M_e $$ Если вершина распределения сдвинута влево и правая часть ветви длиннее левой (длинный правый хвост), такая асимметрия называется правосторонней. При правосторонней асимметрии: $$ M_olt M_elt X_{cp} $$ Если вершина распределения сдвинута вправо и левая часть ветви длиннее правой (длинный левый хвост), такая асимметрия называется левосторонней. При левосторонней асимметрии: $$ M_ogt M_egt X_{cp} $$ Для умеренно асимметричных рядов (по Пирсону) модуль разности между модой и средней не более 3 раз превышает модуль разности между медианой и средней: $$ frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}geq 3 $$
Например:
Для распределения учеников по оценкам мы получили (X_{cp}=3,5; M_o=3; M_e=3).
Т.к. средняя оказалась больше моды и медианы, наше распределение имеет правостороннюю асимметрию (что видно на полигоне частот – правый хвост длиннее).
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{0,5}{0,5}=1lt 3), т.е. распределение умеренно асимметрично.
п.5. Выборочная дисперсия и СКО
Выборочная дисперсия дискретного вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac{(x_1-X_{cp})^2 f_1+(x_2-X_{cp})^2 f_2+…+(x_k-X_{cp})^2 f_k}{N}=\ =frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
1) Найдем выборочную дисперсию для распределения учеников по оценкам:
| Оценка, (x_i) | 2 | 3 | 4 | 5 | Всего |
| К-во учеников, (f_i) | 3 | 15 | 10 | 5 | 33 |
| (x_i^2) | 4 | 9 | 16 | 25 | — |
| (x_i^2 f_i) | 12 | 135 | 160 | 125 | 432 |
$$ D=frac{12+135+160+125}{33}-3,5^2=frac{432}{33}-3,5^2approx 0,73 $$ 2) Значение СКО: (sigma=sqrt{D}approx 0,86)
п.6. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия дискретного вариационного ряда определяется как: begin{gather*} S^2=frac{1}{N-1}sum_{i=1}^k(x_i-X_{cp})^2 f_i=frac{N}{N-1}D end{gather*}
В теоретической статистике доказывается, что выборочная дисперсия D является смещенной оценкой дисперсии при распространении на генеральную совокупность.
А именно, выборочная дисперсия D всегда меньше математического ожидания для дисперсии генеральной совокупности.
Исправленная выборочная дисперсия S2 является несмещенной оценкой.
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Если показатель вариации V<33%, то выборка считается однородной, т.е. большинство полученных в ней вариант находятся недалеко от средней, и выборочная средняя хорошо характеризует среднюю генеральной совокупности.
В противном случае, выборка неоднородна. Варианты в выборке находятся далеко от средней, есть выбросы. А значит, и в генеральной совокупности они возможны. Т.е., распространять результаты выборки на генеральную совокупность нельзя.
Если исследуется не выборка, а вся генеральная совокупность, дисперсию «исправлять» не нужно.
Например:
Для распределения учеников по оценкам получаем:
1) Исправленная выборочная дисперсия $$ S^2=frac{N}{N-1}D=frac{33}{32}cdot 0,73approx 0,76 $$ 2) Стандартное отклонение $$ x=sqrt{S^2}approx 0,87 $$ 3) Коэффициент вариации: $$ V=frac{0,87}{3,5}cdot 100text{%}approx 24,8text{%}lt 33text{%} $$ Выборка является однородной.
Это означает, что согласно коэффициенту вариации полученные результаты контрольной работы можно рассматривать в качестве «типичных» и распространить их на генеральную совокупность, т.е. на всех школьников, которые будут писать эту работу.
п.7. Алгоритм исследования дискретного вариационного ряда
На входе: таблица с вариантами (x_i) и частотами (f_i, i=overline{1,k})
Шаг 1. Составить расчетную таблицу. Найти (w_i,S_i,x_if_i,x_i^2,x_i^2f_i)
Шаг 2. Построить полигон относительных частот (эмпирический закон распределения) и график кумуляты с эмпирической функцией распределения. Записать эмпирическую функцию распределения.
Шаг 3. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 4. Найти выборочную дисперсию и СКО.
Шаг 5. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.8. Примеры
Пример 1. На площадке фриланса была проведена выборка из 100 фрилансеров и подсчитано количество постоянных заказчиков, с которыми они работают.
В результате было получено следующее распределение:
| Число постоянных заказчиков | 0 | 1 | 2 | 3 | 4 | 5 |
| Число фрилансеров | 22 | 35 | 27 | 11 | 3 | 1 |
Исследуйте полученный вариационный ряд.
1) Вариационный ряд является дискретным.
Исследуемый признак – «число постоянных заказчиков».
Варианты признака (x_iinleft{0;1;..;5right}). Количество вариант k=6.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | ∑ |
| (f_i) | 23 | 35 | 27 | 11 | 3 | 1 | 100 |
| (w_i) | 0,23 | 0,35 | 0,27 | 0,11 | 0,03 | 0,01 | — |
| (S_i) | 0,23 | 0,58 | 0,85 | 0,96 | 0,99 | 1 | — |
| (x_if_i) | 0 | 35 | 54 | 33 | 12 | 5 | 139 |
| (x_i^2) | 0 | 1 | 4 | 9 | 16 | 25 | — |
| (x_i^2f_i) | 0 | 35 | 108 | 99 | 48 | 25 | 315 |
2) Полигон относительных частот (эмпирический закон распределения):
Кумулята и эмпирическая функция распределения:
$$ F(x)= begin{cases} 0, xleq 0\ 0,23, 0lt xleq 1\ 0,58, 1lt xleq 2\ 0,85, 2lt xleq 3\ 0,96, 3lt xleq 4\ 0,99, 4lt xleq 5\ 1, xgt 5 end{cases} $$ 3) Выборочная средняя: $$ X_{cp}=frac1Nsum_{i=1}^k x_if_i= frac{1}{100}cdot 139=1,39 $$ Мода (абсцисса самой высокой точки на полигоне частот): (M_0=1).
Медиана (абсцисса первой слева точки на кумуляте, где значение превысило 0,5): точка (1;0,58), (M_e=1).
(X_{cp}gt M_e=M_0) – распределение асимметрично, с правосторонней асимметрией.
При этом (frac{|M_0-X_{cp}|}{|M_e-X_{cp}|}=frac{0,39}{0,39}=1lt 3), т.е. распределение умеренно асимметрично.
4) Выборочная дисперсия: $$ D=frac1Nsum_{i=1}^k x_i^2f_i-X_{cp}^2=frac{1}{100}cdot 315-1,39^2=1,2179approx 1,218 $$ CKO: $$ sigma=sqrt{D}approx 1,104 $$
5) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{100}{99}cdot 1,218approx 1,230 $$ Стандартное отклонение выборки: $$ s=sqrt{S^2}approx 1,109 $$ Коэффициент вариации: $$ V=frac{s}{X_{cp}}cdot 100text{%}=frac{1,109}{1,39}cdot 100text{%}approx 79,8text{%}gt 33text{%} $$ Представленная выборка неоднородна. Полученное значение средней (X_{cp}=1,39) не может быть распространено на генеральную совокупность всех фрилансеров.
Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике — мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Имеется выборка из генеральной совокупности
Исходные данные к задаче
№ вар. Выборка
4 14 13 10 11 4 9 12 9 11 1 5 11 14 5 12 8 10
7 12 11 12 13 6 5 2 1 8 1 8 10 7 10 12 12
11 13 16 3 13 8 6 11 5 14 12 8 10 10 12 11 12
а) Построить статистический ряд распределения, полигон частот, определить размах, моду, медиану.
б) Выполнить группировку, разбив на равные интервалы шириной h=2, построить гистограмму и график эмпирической функции распределения вероятностей.
в) найти точечные оценки математического ожидания, дисперсии, ско.
г) Определить доверительные интервалы для неизвестных математического ожидания и дисперсии , отвечающей заданной доверительной вероятности
() в предположении, что выборка взята из нормальной генеральной совокупности;
д) Построить графики теоретической функции распределения вероятностей и плотности распределения вероятности в предположении, что генеральная совокупность распределена по нормальному закону. Сравнить эти графики с гистограммой и эмпирической функцией распределения вероятностей. Сделать вывод.
е) Проверить гипотезу о нормальном законе распределения генеральной совокупности, используя критерий Пирсона при уровне значимости .
По результатам сформировать отчет, сделать выводы.
Отчет
а) Построить статистический ряд распределения, полигон частот, определить размах, моду, медиану.
Входные данные
14 13 10 11 4 9 12 9 11 1 5 11 14 5 12 8 10
7 12 11 12 13 6 5 2 1 8 1 8 10 7 10 12 12
11 13 16 3 13 8 6 11 5 14 12 8 10 10 12 11 12
Вариационный ряд (расположенные в порядке возрастания варианты):
1, 1, 1, 2, 3, 4, 5, 5, 5, 5, 6, 6, 7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 16.
Статистический ряд
xi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16
ni
3 1 1 1 4 2 2 5 2 6 7 9 4 3 1
Объем выборки n=ni=51
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1;n1), (x2;n2)… (xi;ni), где xi– варианты выборки и ni—соответствующие им частоты.
Отложим на оси абсцисс варианты xi, а на оси ординат – соответствующие частоты. Соединив точки (xi;ni), отрезками прямых, получим искомый полигон частот.
Наименьшее значение в выборке xmin=1, наибольшее значение в выборке xmax=16.
Размах выборки: R=xmax-xmin=16-1=15.
Мода – наиболее часто встречаемая варианта – xMod=12
Медиана – середина вариационного ряда для n=51 xMed=10
б) Выполнить группировку, разбив на равные интервалы шириной h=2, построить гистограмму и график эмпирической функции распределения вероятностей.
Выполним группировку, разбив на равные интервалы
Шаг одного интервала h=2, тогда получим группированный статистический ряд
xi
1, 3
(3, 5]
(5, 7] (7, 9] (9, 11] (11, 13] (13, 15] (15, 17]
ni
5 5 4 7 13 13 3 1
Заполним таблицу 1, используя следующие формулы:
Середина интервала: ,
относительные частоты ,
Эмпирическая функция распределения .
Плотность относительной частоты .
Таблица 1
Номер интервала Границыинтервала Середина интервала Абсолютная частота Относительная частота Эмпирическая функция распределения Плотность относительной частоты
N
1 1, 3
2 5 0,10 0,10 0,05
2 (3, 5]
4 5 0,10 0,20 0,05
3 (5, 7] 6 4 0,08 0,27 0,04
4 (7, 9] 8 7 0,14 0,41 0,07
5 (9, 11] 10 13 0,25 0,67 0,13
6 (11, 13] 12 13 0,25 0,92 0,13
7 (13, 15] 14 3 0,06 0,98 0,03
8 (15, 17] 16 1 0,02 1,00 0,01
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению wi/h (плотность относительной частоты). Площадь частичного i-гo прямоугольника равна hwih=wi—сумме относительных частот вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям относительной частоты. Например, над интервалом 1, 3 проведем отрезок, параллельный оси абсцисс и находящийся от нее на расстоянии, равном 0,05; аналогично строят остальные отрезки.
Объем выборки n=51.
Наименьшая варианта равна 2, поэтому F*(x)=0 при x≤2.
Значение X<4, а именно x1=2 наблюдалось 5 раз, следовательно, F*(x)=5/51=0,1 при 2<x≤4.
Значения x<6, а именно x1=2 и x2=4, наблюдались 5+5=10 раз, следовательно, F*(x)=10/51=0,2 при 4<x≤6.
Значения x<8, а именно x1=2, x2=4 и x3=6, наблюдались 5+5+4=14 раз, следовательно, F*(x)=14/51=0,27 при 6<x≤8.
Значения x<10, а именно x1=2, x2=4, x3=6, x4=8 наблюдались 5+5+4+7=21 раз, следовательно, F*(x)=21/51=0,41 при 8<x≤10.
Значения x<12, а именно x1=2, x2=4, x3=6, x4=8, x5=10 наблюдались 5+5+4+7+13=34 раза, следовательно, F*(x)=34/51=0,67 при 10<x≤12.
Значения x<14, а именно x1=2, x2=4, x3=6, x4=8, x5=10 и x6=12 наблюдались 5+5+4+7+13+13=47 раз, следовательно, F*(x)=47/51=0,92 при 12<x≤14.
Значения x<16, а именно x1=2, x2=4, x3=6, x4=8, x5=10, x6=12, x7=14 наблюдались 5+5+4+7+13+13+3=50 раз, следовательно, F*(x)=50/51=0,98 при 14<x≤16.
Так как x=16 наибольшая варианта, то F*(x)=1 при x>16.
Искомая эмпирическая функция:
F*(x)=0 при x≤2; 0,10 при 2<x≤4;0,20 при 4<x≤6;0,27 при 6<x≤8;0,41 при 8<x≤10;0,67 при 10<x≤12;0,92 при 12<x≤14;0,98 при 14<x≤16;1 при x>16
График эмпирической функции распределения:
F*(x)
1
0,98
0,92
0,67
0,41
0,27
0,2
0,1
0 2 4 6 8 10 12 14 16
x
в) найти точечные оценки математического ожидания, дисперсии, ско.
Точечные оценки искомых числовых характеристик определяются по следующим формулам
, .
Для удобства расчетов последовательно заполним столбцы следующей таблицы.
Таблица 2
N
1 2 5 10 4 20
2 4 5 20 16 80
3 6 4 24 36 144
4 8 7 56 64 448
5 10 13 130 100 1300
6 12 13 156 144 1872
7 14 3 42 196 588
8 16 1 16 256 256
51 454
4708
На основании приведенных в таблице 2 данных можно найти точечные оценки: математического ожидания
.
Дисперсии
.
СКО:
.
г) Определить доверительные интервалы для неизвестных математического ожидания и дисперсии , отвечающей заданной доверительной вероятности () в предположении, что выборка взята из нормальной генеральной совокупности.
Для построения доверительного интервала для математического ожидания
используем формулы:
,,
– квантиль распределения Стьюдента с (n-1) степенью свободы;
В нашем случае для получим
,,
,
для дисперсии
,
д) Построить графики теоретической функции распределения вероятностей и плотности распределения вероятности в предположении, что генеральная совокупность распределена по нормальному закону. Сравнить эти графики с гистограммой и эмпирической функцией распределения вероятностей. Сделать вывод.
Для того, чтобы проверить гипотезу о том, что выборка из нормальной генеральной совокупности, подставим точечные оценки в место неизвестных параметров в плотность распределения вероятности и функцию распределения вероятности. Нормальная плотность распределения вероятности
.
Будем считать, что
.
Результаты расчетов будем заносить в таблицу 3.
Сначала найдем и занесем в третий столбец с округлением до сотых.
Далее по таблице ищем значения функции , соответствующие рассчитанным ранее значениям . При этом пользуемся четностью функции : . Результат заносим в четвертый столбец таблицы 3.
Найдем значения теоретической функции плотности вероятности . Результат заносим в пятый столбец таблицы 3.
Находим значения теоретической функции распределения , где . Значения функции находятся по таблице с учетом того, что . Результаты заносим в последний столбец таблицы 3.
Таблица 3
N
1 2 -1,89 0,0669 0,018 0,029
2 4 -1,34 0,1626 0,044 0,090
3 6 -0,79 0,2920 0,080 0,215
4 8 -0,25 0,3867 0,106 0,401
5 10 0,30 0,3814 0,104 0,618
6 12 0,85 0,2780 0,076 0,802
7 14 1,39 0,1518 0,041 0,918
8 16 1,94 0,0608 0,017 0,974
Строим на основании расчетов графики теоретических плотности вероятности и функции вероятности .
Гистограмма немного асимметрична, но можно сделать предположение, что совокупность распределена по нормальному закону. По графикам эмпирической и теоретической функции также можно сделать предположение, что данное распределение близко к нормальному.
е) Проверить гипотезу о нормальном законе распределения генеральной совокупности, используя критерий Пирсона при уровне значимости .
Методом Пирсона проверим гипотезу Н0 – генеральная совокупность распределена по нормальному закону. Альтернативная гипотеза НА – это не так.
Результаты расчетов будем сводить в таблицу 4.
Критерий использует тот факт, что приближенно нормальная величина. Чтобы это условие выполнялось в достаточной мере, необходимо, чтобы в каждом интервале было не менее пяти точек. Для этого интервалы, в которых это условие не выполняется, следует объединить с соседними. В таблице 4 пятый и шестой интервалы из таблицы 1 объединены в один интервал.
Определяем длину интервалов, середины, абсолютную и относительную частоты. По результатам расчета заполняем первые шесть колонок таблицы 4.
Рассчитываем значения и . Результаты заносим в седьмую и восьмую колонки таблицы 4.
Оценим теоретические вероятности попадания нормальной случайной величины с указанными параметрами в интервал .
.
Заполняем девятую колонку таблицы 4.
Далее считаем и заполняем десятую колонку таблицы 4.
Значения заносим в последний столбец таблицы 4.
№ Интервал Длина интервала Середина интервала Абсолютная частота Относительная частота
Теор. плотность вероятности Теоретич. вероятность
1 1, 3
2 2 5 0,1 -1,89 0,018 0,037 0,063 0,1101
2 (3, 7]
4 5 9 0,18 -1,07 0,062 0,246 0,066 0,017712
3 (7, 9] 2 8 7 0,14 -0,25 0,106 0,211 0,071 0,024066
4 (9, 11] 2 10 13 0,25 0,30 0,104 0,208 0,042 0,008297
5 (11, 17] 6 14 17 0,33 1,39 0,041 0,249 0,081 0,026461
51 1
0,186636
Таблица 4
Вычисляем , здесь r – число интервалов табл. 4. Для данной выборки .
.
По таблице находим квантиль , где l – число оцениваемых параметров. В нашем случае ( и ). находим из условия .
,
.
И так, по таблице находим .
Если , то справедлива гипотеза Н0. Если , то НА. В нашем случае , то есть гипотеза Н0 не принимается
Предположение о нормальном законе распределения не принимается.
Выводы: По данным выборки построили статистический ряд, определили моду, медиану и размах выборки, построили полигон частот. Составили интервальный статистический ряд, разбив данную выборку на 8 равных интервалов, шириной h=2, построили гистограмму относительных частот, которая оказалась немного асимметричной, но по ее виду можно сделать предположение, что данная совокупность распределена по нормальному закону. Построили график эмпирической функции распределения по накопленным относительным частотам. Нашли несмещенные точечные оценки параметров распределения:
x=8,9, и . Полученные результаты говорят о том, что среднее значение равно 8,9 с разбросом порядка 3,66, то есть примерно в 70% случаев значение должно попадать в интервал от 5,24 до 12,56 (в выборке в этот интервал попадает 73% значений).
Определили доверительные интервалы для математического ожидания и дисперсии с доверительной вероятностью 0,9. Доверительный интервал для математического ожидания: 7,87<m<9,93. Это означает, что среднее значение с вероятность 90% заключено в интервале 7,87-9,93.
Доверительный интервал для дисперсии: 9,9<σ2<19,22. Иными словами, среднее квадратическое отклонение величины X, характеризующее ее разброс относительно математического ожидания m=8,9, с вероятностью 90% заключено в пределах от 3,15 до 4,38.
Построили графики теоретической функции распределения вероятностей и плотности распределения вероятности. Сравнили полученные графики с эмпирическими. Сделали предположение о том, что данное распределение близко к нормальному. Но, проверив с помощью критерия Пирсона при уровне значимости гипотезу о нормальном распределении генеральной совокупности, пришли к выводу, что эмпирические и теоретические частоты различаются значимо, то есть, нулевую гипотезу о нормальном распределении генеральной совокупности отвергаем в пользу альтернативной.
20.
Биноминальный закон распределения и
его числовые характеристики.
Биноминальный закон
распределения описывает случайные
величины, значения которых определяют
количество «успехов» и «неудач» при
повторении опыта N раз. В каждом опыте
«успех» может наступить с вероятностью
p, «неудача» — с вероятностью q=1-p. Закон
распределения в этом случае определяется
формулой Бернулли:
,
где 0<p<1; q=1-p; k=0,
1, 2, …, n.
Биномиальный закон
распределения представляет собой закон
распределения числа X=k
наступлений события A в n независимых
испытаниях, в каждом из которых оно
может произойти с одной и той же
вероятностью p.
Ряд распределения
биномиального закона имеет вид:
|
xi |
0 |
1 |
2 |
… |
m |
… |
n |
|
pi |
qn |
|
|
… |
|
… |
pn |
Вероятности любого
числа событий соответствуют членам
разложения бинома Ньютона в степени,
равной числу испытаний:
где pn
— вероятность того, что при n
испытаниях событие А наступит n
раз;
qn
— вероятность того, что при n
испытаниях событие А не наступит ни
разу;
—
вероятность того, что при n
испытаниях событие А наступит m
раз, а событие Ā наступит n-m
раз;
—
число сочетаний (комбинаций) появления
события А и Ā.
На рисунке приведены
многоугольники (полигоны) распределения
случайной величины X,
имеющей биномиальный закон распределения
с параметрами n=5
и p
(для p=0,2;
0,3; 0,5; 0,7; 0,8).
Числовые характеристики
биноминального распределения:
Теорема. Математическое
ожидание случайной величины X,
распределённой по биномиальному закону,
M(X)=np,
а её дисперсия D(X)=npq.
Следствие. Математическое
ожидание частости события в n
независимых испытаниях, в каждом из
которых оно может наступить с одной и
той же вероятностью p,
равно p,
т. е.
а её дисперсия
Наивероятнейшее число
наступлений события A
в n
независимых испытаниях, в каждом из
которых оно может произойти с одной и
той же вероятностью p,
удовлетворяет неравенству
np-q≤m0≤np+p.
Это означает, что мода случайной величины,
распределённой по биномиальному закону,
— число целое — находится из того же
неравенства np-q≤M0(X)≤np+p.
Биномиальный закон
широко используется в теории и практике
статистического контроля качества
продукции, при описании функционирования
систем массового обслуживания, в теории
стрельбы и в других областях.
ИЛИ
М(m)=np — математическое
ожидание частоты появления события А
при n независимых испытаниях;
D(m)=npq — дисперсия частоты
появления события. А;
—
среднее квадратическое отклонение
частоты.
Пример 1.
В рекламных целях торговая фирма
вкладывает в каждую пятую единицу товара
денежный приз размером 100 тенге. Найти
закон распределения числа сотен тенге,
полученных при четырёх сделанных
покупках.
Решение.
Вероятность того, что в случайно сделанной
покупке окажется денежный приз, равна
p=1/5=0,2. Случайная величина X — число
покупок, в которые вложен денежный приз,
имеет биномиальный закон распределения
с параметрами n=4 и p=0,2. Ряд распределения
X имеет вид:
|
xi |
0 |
1 |
2 |
3 |
4 |
|
pi |
0,4096 |
0,4096 |
0,1536 |
0,0256 |
0,0016 |
значения pi=P(X=m),
(m=0, 1, 2, 3, 4) вычислены по формуле
Пример 2.
В среднем по 10% договоров страховая
компания выплачивает страховые суммы
в связи с наступлением страхового
случая. Определить среднее (прогнозируемое)
число договоров которым компании
придётся выплатить страховые суммы в
связи с наступлением страхового случая
и оценить меру отклонения числа таких
договоров от ожидаемого среднего
значения (риск компании), если заключено
2000 договоров.
Решение.
Вероятность того, что случайно выбранному
договору страховая компания выплачивает
страховую сумму в связи с наступлением
страхового случая, равна
Случайная величина X — число договоров,
по которым страховая компания выплачивает
страховые суммы в связи с наступлением
страхового случая, имеет биномиальный
закон распределения с параметрами
n=2000 и p=0,1. Среднее (прогнозируемое) число
договоров, по которым страховая компания
выплачивает страховые суммы — математическое
ожидание случайной величины X находим
по формуле M(X)=np=2000·0,1=200. Меру отклонения
числа договоров по которым компания
должна будет выплатить страховые суммы
от ожидаемого среднего значения (риск
компании) можно оценить, определив
дисперсию или среднее квадратическое
отклонение случайной величины X.
D(X)=npq=2000·0,1·0,9=180
Таким образом,
прогнозируемое число договоров, по
которым страховая компания выплатит
страховые суммы в связи с наступлением
страхового случая, вероятнее всего
будет находится пределах диапазона
200±13.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.
Расчёт структурных характеристик
вариационного ряда распределения.
Студент
должен:
знать:
— область применения и методику расчёта структурных
средних величин;
уметь:
— исчислять структурные средние величины;
— формулировать вывод по полученным результатам.
Методические указания
В
статистике исчисляются мода и медиана, которые относятся к структурным средним,
так как их величина зависит от строения статистической совокупности.
Расчёт моды
Модой называется значение признака
(варианта), чаще всеговстречающееся в изучаемой
совокупности. В дискретном ряду распределения модой будет варианта с наибольшей
частотой.
Например: Распределение проданной женской обуви по размерам характеризуется
следующим образом:
|
Размер |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
|
Количество |
8 |
19 |
34 |
108 |
72 |
51 |
6 |
2 |
В этом ряду
распределения модой является 37 размер,
т.е. Мо=37 размер.
Для
интервального ряда распределения мода определяется по формуле:
где ХMo —
нижняя граница модального интервала;
hMo — величина модального интервала;
fMo –
частота модального интервала;
fMo—1 и
fMo+1 – частота интервала соответственно
предшествующего модальному и следующего за ним.
Например:
Распределение рабочих по стажу работы характеризуется следующими данными.
|
Стаж работы, лет |
до 2 |
2-4 |
4-6 |
6-8 |
8-10 |
10 и более |
|
Число рабочих, чел. |
4 |
23 |
20 |
35 |
11 |
7 |
Определить моду
интервального ряда распределения.
Мода интервального ряда составляет
Мода всегда бывает
несколько неопределённой, т.к. она зависит от величины групп и точного
положения границ групп. Мода широко применяется в коммерческой практике при
изучении покупательского спроса, при регистрации цен и т.п.
Расчёт медианы
Медианой в статистике называется варианта,
расположенная в середине упорядоченного ряда данных, и которая делит
статистическую совокупность на две равные части так, что у одной половины
значения меньше медианы, а у другой половины – больше её. Для определения
медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания
или убывания индивидуальных значений признака.
В дискретном
упорядоченном ряду с нечётным числом членов медианой будет варианта,
расположенная в центре ряда.
Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7
лет, т.е. Ме=7 лет
Если дискретный
упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя
арифметическая из двух смежных вариант, стоящих в центре ряда.
Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду
имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя
арифметическая из этих значений и будет медианой ряда
Чтобы определить медиану для
сгруппированных данных, необходимо считать накопленные частоты.
Например: По имеющимся данным определим медиану размера обуви
|
Размер обуви |
Количество проданных пар |
Сумма накопленных частот |
|
34 |
8 |
8 |
|
35 |
19 |
8+19=27 |
|
36 |
34 |
27+34=61 |
|
37 |
108 |
61+108=169 |
|
38 |
72 |
— |
|
39 |
51 |
— |
|
40 |
6 |
— |
|
41 |
2 |
— |
|
Итого |
300 |
Для
определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание
итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот
ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная
сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е.
37 и есть медиана ряда.
Если
же сумма накопленных частот против одной из вариант равна точно половине суммы
частот ряда, то медиана определяется как средняя арифметическая этой варианты и
последующей.
Например: По имеющимся данным определим медиану заработной платы рабочих
|
Месячная заработная плата, тыс.руб. |
Число рабочих, чел. |
Сумма накопленных частот |
|
14,0 |
2 |
2 |
|
14,2 |
6 |
2+6=8 |
|
16,0 |
12 |
8+12=20 |
|
16,8 |
16 |
— |
|
18,0 |
4 |
— |
|
Итого: |
40 |
— |
Медиана будет равна:
Медиана
интервального вариационного ряда распределения определяется по формуле:
Где ХМе – нижняя граница медианного интервала;
hMe –
величина медианного интервала;
∑f
— сумма частот ряда;
fМе – частота медианного интервала;
Например: По имеющимся данным о распределении предприятий по численности
промышленно – производственного персонала рассчитать медиану в интервальном
вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
7 |
4+7=11 |
|
400-500 |
30 |
11+30=41 |
|
500-600 |
19 |
— |
|
600-700 |
15 |
— |
|
700-800 |
5 |
|
|
Итого: |
80 |
Определим, прежде всего,
медианный интервал. В данном примере сумма накопленных частот, превышающих половину
суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный
интервал, т.е. интервал, в котором находится медиана ряда. Определим её
значение
Если же сумма накопленных частот
против одного из интервалов равна точно половине суммы частот ряда, то медиана
определяется по формуле:
где n – число
единиц в совокупности.
Например: По имеющимся данным о распределении предприятий по
численности промышленно – производственного персонала рассчитать медиану в
интервальном вариационном ряду
|
Группы предприятий по численности ППП, чел. |
Число предприятий |
Сумма накопленных частот |
|
100-200 |
1 |
1 |
|
200-300 |
3 |
1+3=4 |
|
300-400 |
6 |
4+6=10 |
|
400-500 |
30 |
10+30=40 |
|
500-600 |
20 |
40+20=60 |
|
600-700 |
15 |
— |
|
700-800 |
5 |
|
|
Итого: |
80 |
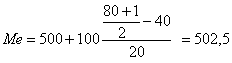
Моду и медиану в
интервальном ряду можно определить
графически:
моду
в дискретных рядах — по полигону распределения, моду в интервальных рядах — по
гистограмме распределения, а медиану — по кумуляте.
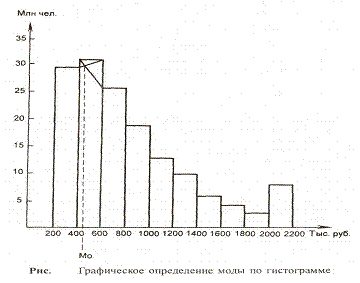
Мода интервального ряда распределения
определяется по гистограмме распределения определяют
следующим образом. Для этого выбирается самый высокий прямоугольник, который
является в данном случае модальным. Затем правую вершину модального
прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.
Медиана рассчитывается по
кумуляте. Для её определения из точки на шкале
накопленных частот (частостей), соответствующей 50%,
проводится прямая, параллельная оси абсцисс, до
пересечения с кумулятой. Затем из точки пересечения
указанной прямой с кумулятой опускается перпендикуляр
на ось абсцисс. Абсцисса точки пересечения является медианой.
Кроме моды и медианы в вариантных рядах могут быть
определены и другие структурные характеристики – квантили. Квантили
предназначены для более глубокого изучения структуры ряда распределения.
Квантиль – это значение
признака, занимающее определенное место в упорядоченной по данному признаку
совокупности. Различают следующие виды квантилей:
— квартили – значения признака, делящие упорядоченную
совокупность на четыре
равные части;
— децили
– значения признака, делящие упорядоченную совокупность на десять
равных частей;
— перцентели —
значения признака, делящие упорядоченную совокупность на сто равных частей.
Таким образом, для характеристики положения центра ряда распределения
можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя
центра распределения необходимо исходить из следующих рекомендаций:
—
для устойчивых социально-экономических
процессов в качестве показателя центра используют среднюю
арифметическую. Такие процессы характеризуются симметричными распределениями, в
которых ;
—
для неустойчивых процессов положение
центра распределения характеризуется с помощью Mo
или Me. Для асимметричных процессов предпочтительной
характеристикой центра распределения является медиана, поскольку занимает
положение между средней арифметической и модой.