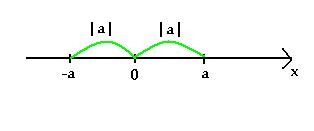
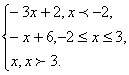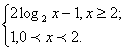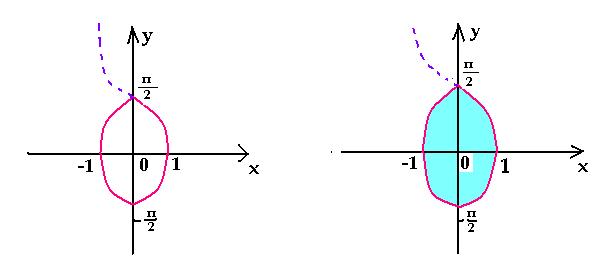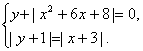Для любого действительного числа (x) можно вычислить (|x|), т. е. можно говорить о функции (y=|x|).
Запишем:
y=x,еслиx≥0−x,еслиx<0
.
График будем строить «по частям». Сначала построим прямую (y=x) и выделим её часть на луче
0;+∞
.
Затем построим прямую (y=-x) и выделим её часть на открытом луче
−∞;0
.
Теперь полученные лучи построим в одной системе координат; это и есть график функции (y=|x|).
Значение квадратного корня — неотрицательное число, поэтому:
если (a < 0), то
a2
(=- a) (действительно, (- a > 0) и
−a2=a2
).
Итак,
a2=a,если a≥0−a,если a<0
.
В правой части равенства получили модуль числа (a):
a=a,если a≥0−a,если a<0
.
Значит,
a2
и (| a |) — тождественные выражения.
Вместо (a) может стоять любое выражение.
На этой странице вы узнаете
- Как перевернуть график модуля?
- Одной ногой тут, другой там: к какому промежутку относить граничные точки?
- Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0?
Модуль числа — это великая математическая мудрость, которая показывает дружбу и соперничество противоположных знаков: минуса и плюса. О том, что держит число в рамках, узнаем в статье.
Модуль
Мы легко можем найти расстояние от точки до точки, достаточно просто измерить его линейкой. Но можно ли найти расстояние от 0 до любого числа?
Представим, что наш дом находится посередине между школой и магазином. И до школы, и до магазина 500 метров, но они стоят по разные стороны от дома.
Расположим их на координатной прямой. Поскольку и школа, и магазин располагаются на одинаковом расстоянии, то от дома до них мы будем идти 500 метров. Но на координатной прямой до школы мы пройдем −500 метров, поскольку движемся против направления оси, а до магазина 500 метров.

Будет ли являться полученный результат противоречием? Нет, поскольку когда мы ищем расстояние, нам неважно направление движения и знак. В математике существует специальное определение — это модуль, или абсолютная величина.
Модуль — расстояние от любой точки на координатной прямой до начала координат.
Поскольку на координатной прямой мы можем отложить расстояние в две стороны, то такое расстояние можно найти и с отрицательными точками, и с положительными. Расстояние измеряет длину отрезка, то есть оно всегда будет положительно.
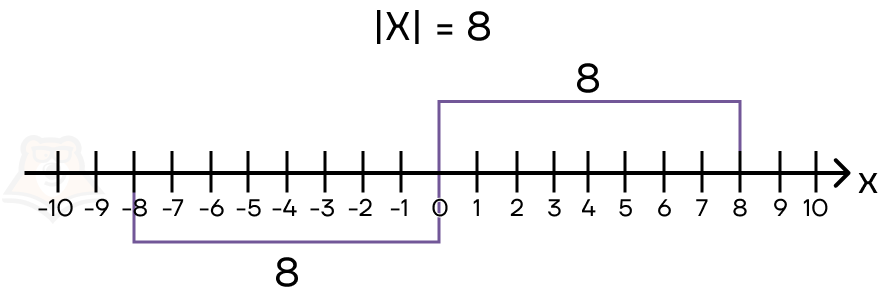
Можно сказать, что от любого числа модуль берет только цифры, а на знаки не обращает внимания. Например, |−8| = 8 и |8| = 8.
Может возникнуть вопрос: куда исчезает минус? Чтобы избавиться от минуса, достаточно умножить число на −1: (-8) * (-1) = 8. Значит, модуль просто умножает число на -1.
Отсюда получается, что модулем числа а называют выражение:

Возьмем два случая: a = 8 и a = -8. Для первого получаем |8| = 8, а для второго |-8| = -(-8) = 8, то есть определение выполняется.
Можно ли взять модуль функции? Да. Модулем произвольной функции называют выражение:
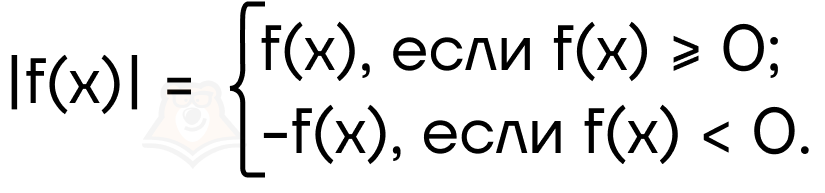
Свойства модуля
Модуль, как и все понятия в математике, обладает своими свойствами.
Свойство 1. |a| >= 0.
Как мы уже говорили, модуль всегда будет положительным числом, поскольку он не обращает внимания на знак числа.

Свойство 2. |a| = |-a|.
Это свойство также подтверждает рассуждения выше. Модули противоположных чисел, то есть чисел с разными знаками, равны.
Свойство 3. |a| >= a.
Если число а будет положительным, например, 5, то неравенство |5| >= 5 (rightarrow) 5 >= 5 выполняется, поскольку знак неравенства нестрогий.
Если число а будет отрицательным, например, -5, то неравенство |-5| >= -5 (rightarrow) 5 >= -5 выполняется, поскольку положительное число всегда больше отрицательного.
Свойство 4. |a * b| = |a| * |b|.
Пусть a = 5, b = -2, тогда |5 * (-2) | = |-10| = 10, и |5| * |-2| = 5 * 2 = 10, то есть выражения равны между собой.
Свойство 5. (|frac{a}{b}| = frac{|a|}{|b|}).
Рассуждения такие же, как и в предыдущем свойстве. Пусть a = 10, b = -5, тогда (|frac{10}{(-5)}| = |-2| = 2 и frac{|10|}{|-5|} = frac{10}{5} = 2).
Свойство 6. |a + b| <= |a| + |b|.
Почему появилось неравенство, а не уравнение, как в предыдущих двух свойствах? Разберем два примера.
Пусть a = 1, b = 2, тогда |1 + 2| = |3| = 3 и |1| + |2| = 1 + 2 = 3 — неравенство выполняется, поскольку знак нестрогий.
Но если a = -1, b = 2, тогда |-1 +2| = |1| = 1 и |-1| + |2| = 1 + 2 = 3, откуда получаем 1 < 3.
Свойство 7. (sqrt{a^2} = |a|).
Докажем это свойство. Пусть (sqrt{a^2} = x), тогда x0, поскольку квадратный «Корень» не может быть отрицательным. Возведем полученное уравнение в квадрат: a2 = x2
a2 — x2 = 0
(a — x)(a + x) = 0
Из уравнения x = a, из-за ограничений на x получаем a >= 0.
И x = -a, из-за ограничений на x получаем a < 0.
То есть получается выражение модуля.
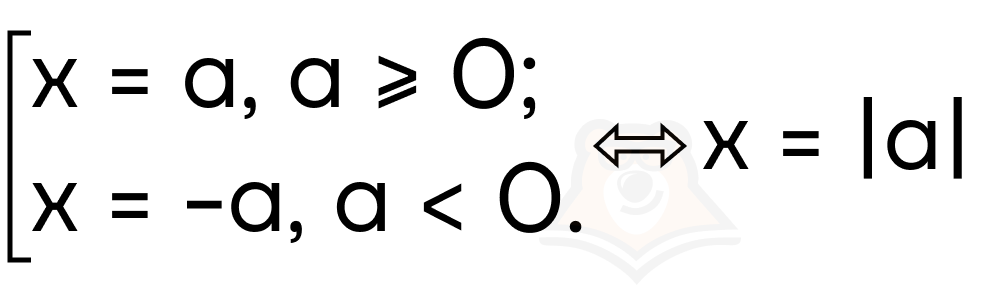
Свойство 8. |a|2 = a2.
Поскольку и модуль, и квадрат числа дают положительный результат, модуль в квадрате можно заменить просто квадратом числа.
График модуля
Как изобразить функцию с модулем? Для начала разберемся, что делает модуль с графиком функции.
Рассмотрим функцию y = x — это прямая. При этом у может быть и положительным, и отрицательным.
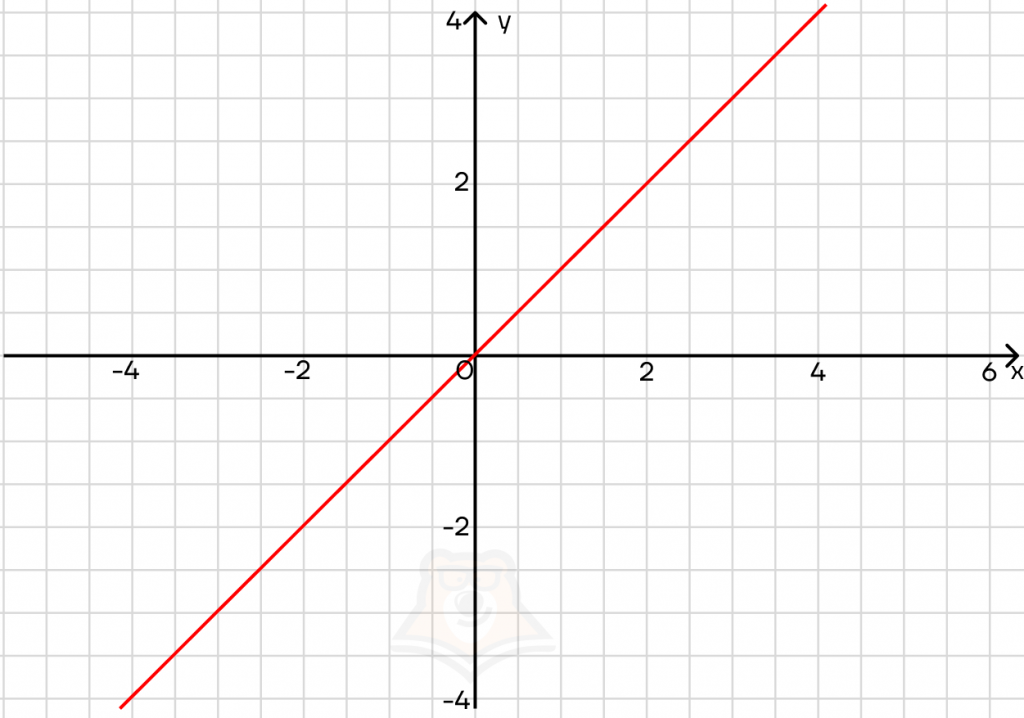
Занесем х под знак модуля: y = |x|. Теперь у может быть только положительным. Что происходит с частью графика, которая лежит ниже оси х? Она зеркально отражается. В итоге мы получаем галочку:
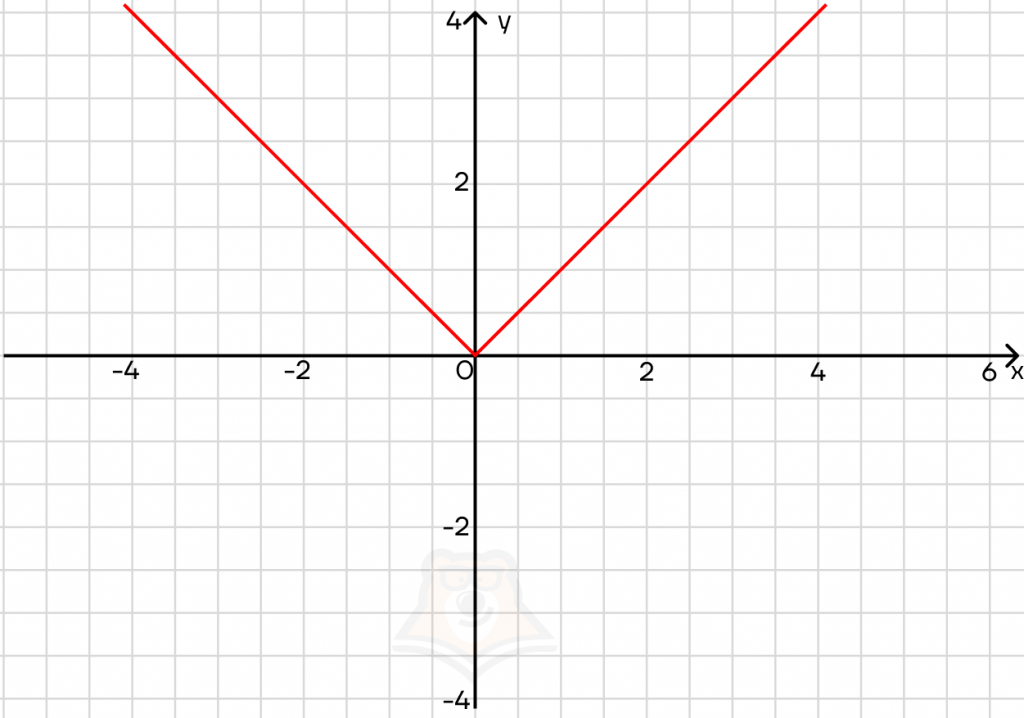
Модуль отражает любой график относительно оси х.
Что будет, если перед х будет стоять коэффициент? Построим графики:
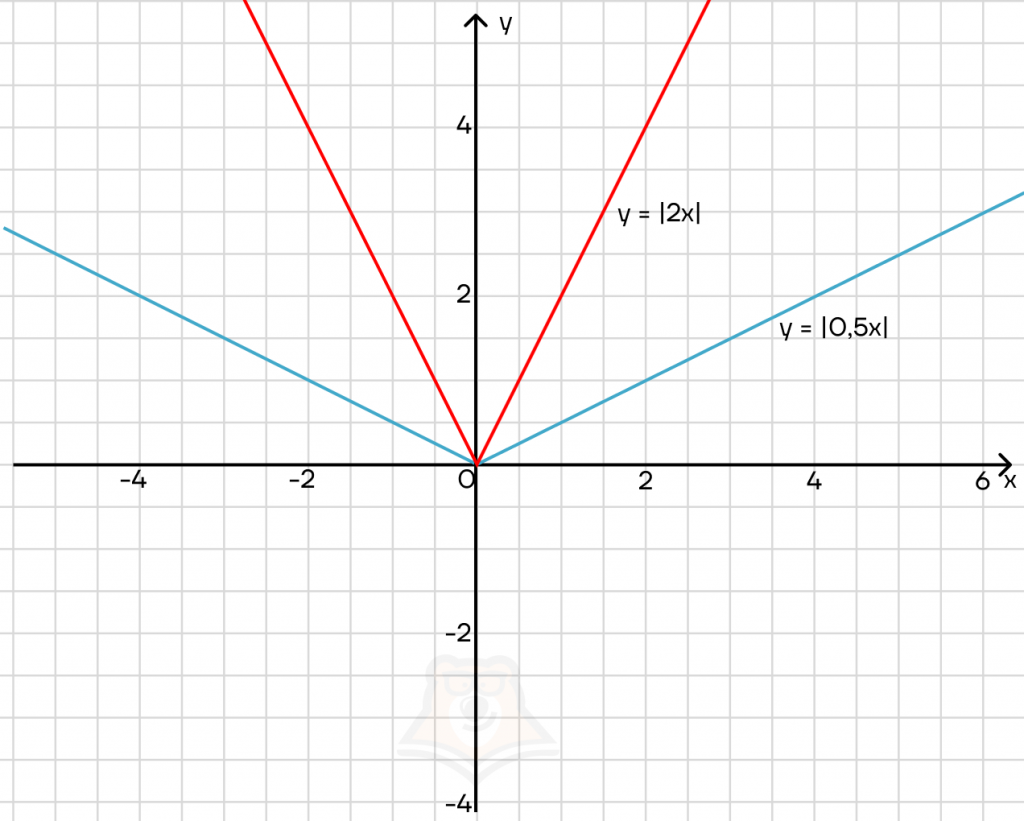
Галочка будет сужаться и расширяться. Причем чем больше коэффициент перед х, тем ýже будет галочка.
Попробуем добавить слагаемое к подмодульному выражению.
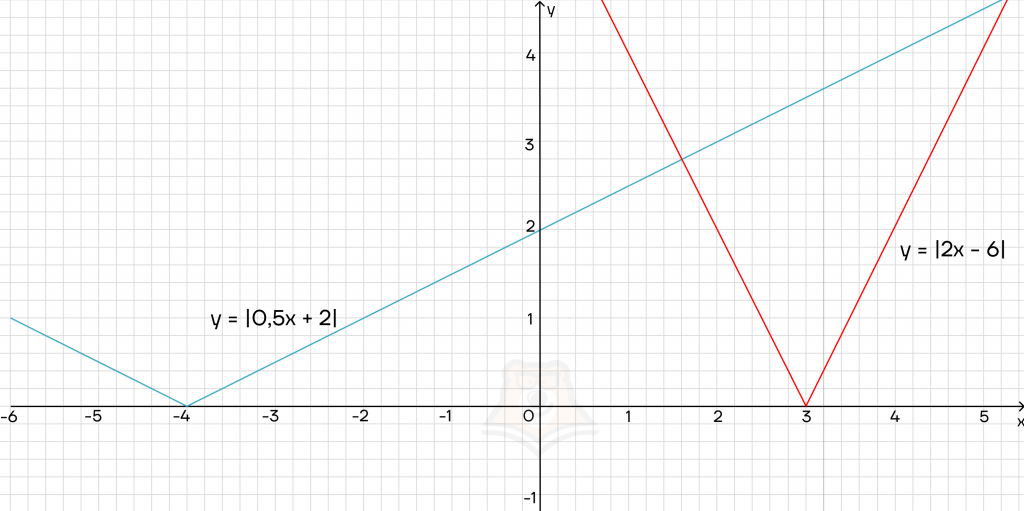
График модуля будет двигаться вдоль оси х. Причем:
- если мы прибавляем число, то график сдвигается влево;
- если мы вычитаем число, то график сдвигается вправо.
Добавим число к модулю, а не подмодульному выражению:
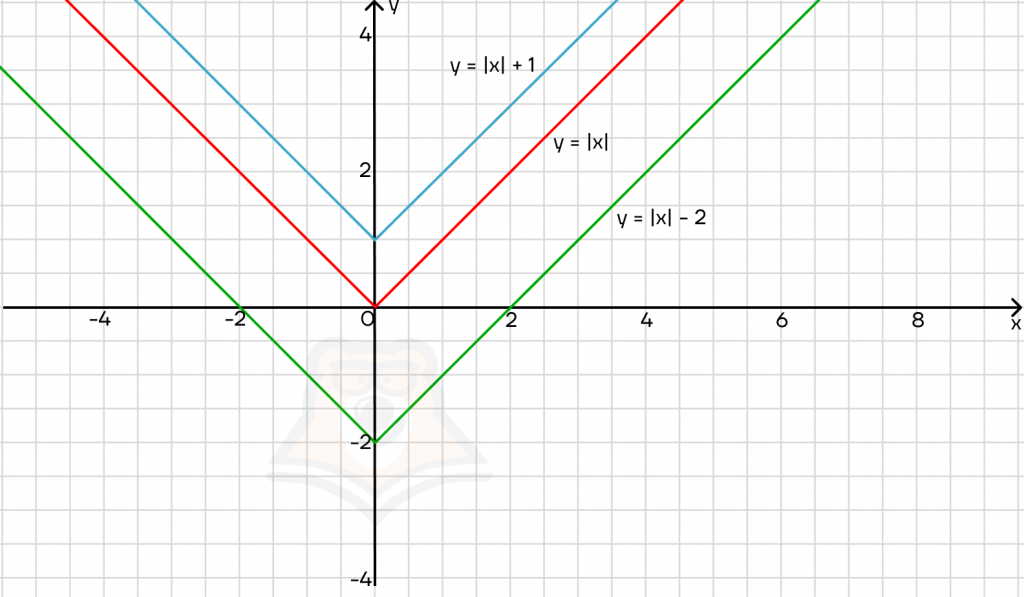
График будет двигаться вдоль оси у.
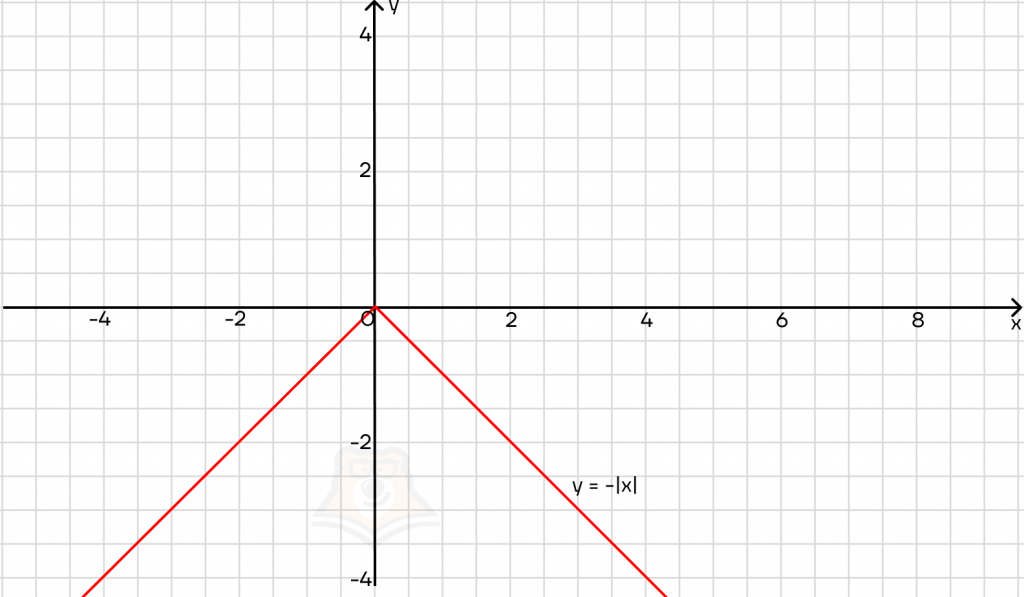
Для этого достаточно добавить перед модулем минус. Важно, чтобы минус стоял именно перед модулем, а не внутри него. Тогда график будет отзеркален относительно оси х и лежать только ниже нее.
Это легко проследить с помощью уравнений: если y = -|x|, то, при x = 3 получаем:
y = -|3| = -3
Уравнения с модулем
1. Возьмем уравнение вида |f(x)| = a. Поскольку модуль не может быть отрицательным, то и а не может быть отрицательным. Получаем следующий переход:
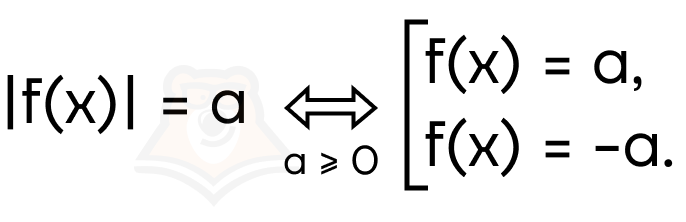
Пример 1. Решите уравнение |4x + 5| = 7.
Решение. В уравнении f(x) = 4x + 5, a = 7. Воспользуемся переходом:
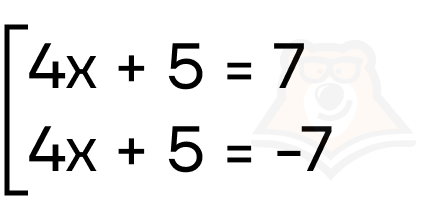
Из первого уравнения x = 0,5, а из второго уравнения x = -3.
Ответ: 0,5: -3.
2. В уравнениях и неравенствах можно встретить два разных модуля. Как быть в этом случае?
Шаг 1. Находим нули подмодульных выражений.
Шаг 2. Чертим числовую прямую и ищем знаки на промежутках для каждого модуля. Если подмодульное выражение отрицательно на промежутке, то ставится минус, если положительно — ставится плюс.
Шаг 3. Для каждого промежутка раскрываем модули. Если подмодульное выражение на промежутке отрицательно, то модуль раскрывается со знаком минус. Если положительно — модуль раскрывается со знаком плюс. Важно: полученные корни должны принадлежать промежуткам, на которых раскрывается модуль, иначе они не будут решениями уравнения.
Шаг 4. Записать все полученные корни в ответ.
Пример 2. Решите уравнение |x — 2| — |x + 2| = 4x — 5.
Решение. Найдем, в каких точках модули будут равны 0. Для этого подмодульное выражение также должно быть равно 0:
x — 2 = 0 (rightarrow) x = 2
x + 2 = 0 (rightarrow) x = -2
Нарисуем числовую прямую с этими точками:
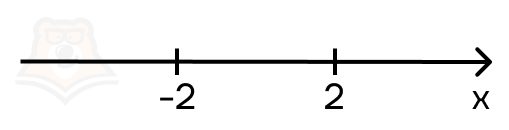
У нас получилось три промежутка:
- (-(infty);-2)
- [-2;2)
- [2;+(infty))
Обратим внимание, какие знаки имеет первый модуль на промежутках: x — 2 > 0 при x > 2. Следовательно, на первых двух промежутках модуль будет отрицательным, а на третьем положительным. Расставим его знаки красным цветом.
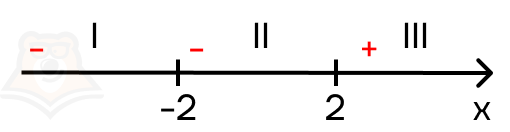
Проанализируем второй модуль: x + 2 > 0 (rightarrow) x>-2. Получается, подмодульное выражение будет положительно на втором и третьем промежутке, и отрицательным на первом промежутке. Расставим его знаки синим цветом.
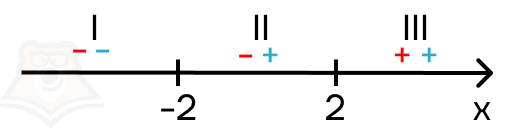
Теперь мы можем рассмотреть уравнение на всех трех промежутках. Однако для этого обязательно ввести ограничения: полученные точки должны принадлежать только этому промежутку, поскольку на следующем модули будут раскрываться уже по-другому.
2. Рассмотрим первый промежуток: x<-2. Оба модуля раскрываются с отрицательным знаком, и мы получаем следующее уравнение:
-(x — 2) — (-(x + 2)) = 4x — 5
-x + 2 + x + 2 = 4x — 5
4 = 4x — 5
4x = 9
x = 2,25
Точка не удовлетворяет ограничению, поскольку не лежит в промежутке (-(infty);-2):
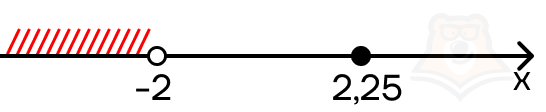
Рассмотрим второй промежуток: [-2;2). Первый модуль раскрывается с минусом, а второй с плюсом:
-(x — 2) — (x + 2) = 4x — 5
-x + 2 — x — 2 = 4x — 5
-2x = 4x — 5
6x = 5
(x = frac{5}{6})
Эта точка лежит в заданном промежутке и является решением уравнения.
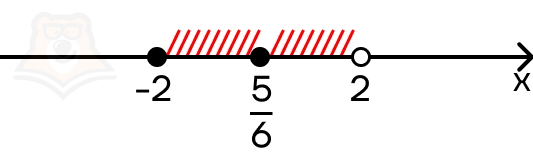
Рассмотрим третий промежуток [2;+(infty)). Оба модуля раскрываются со знаком плюс, мы получаем уравнение:
(x — 2) — (x + 2) = 4x — 5
x — 2 — x — 2 = 4x — 5
-4 = 4x — 5
4x = 1
x = 0,25 — эта точка не лежит в промежутке, то есть не является решением уравнения.
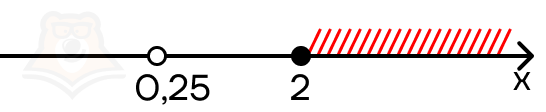
Решением уравнения будет только (x = frac{5}{6}).
Ответ: (frac{5}{6})
Разбивая прямую на промежутки, может возникнуть вопрос: а что делать с точками, в которых модуль равен 0? Их обязательно нужно проверять. Можно сделать это как отдельно, подставив точки в уравнение, так и сразу включить их в условие раскрытия модуля.
Если точки включаются в условие раскрытия модуля, то достаточно включить их только в один из двух промежутков. Включать их в два промежутка нецелесообразно: одна и та же точка будет проверяться дважды.

3. Уравнения вида |f(x)| = g(x)
Поскольку вместо функций могут стоять любые выражения, раскрыть модуль можно двумя способами. Выбор одного из них зависит от того, какая функция проще: f(x) или g(x).
Как можно раскрыть модуль?
- Можно раскрыть его в зависимости от знаков подмодульного выражения: если подмодульное выражение отрицательное, то модуль раскрывается с минусом, если положительное, то с плюсом.
- Можно возвести уравнение в квадрат. Но здесь необходимо ввести ограничения на g(x) — поскольку функция равна модулю, она не может быть отрицательной.
Для удобства можно пользоваться следующей схемой:
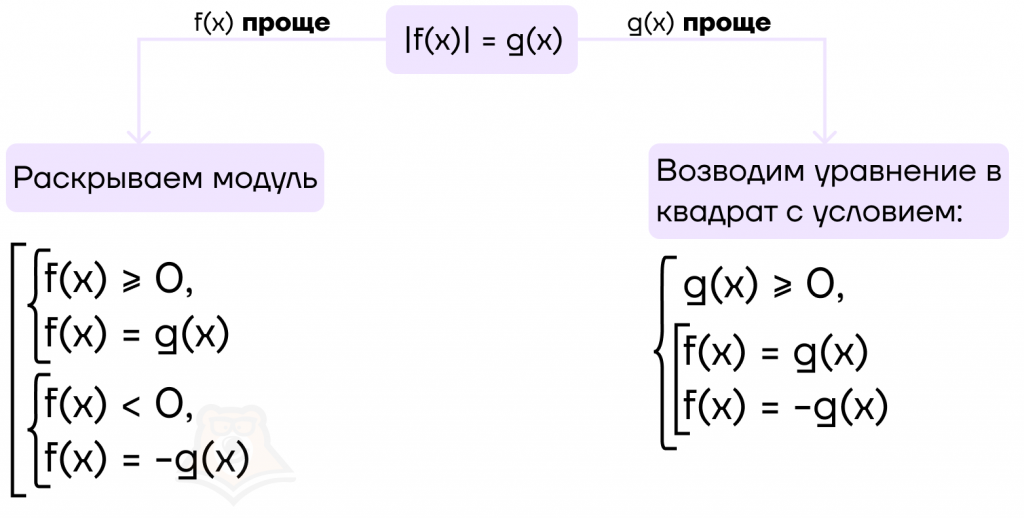
Пример 3. Решите уравнение |8 — x| = x2 — 5x + 11.
Решение. Заметим, что подмодульное выражение значительно проще функции справа, в этом случае удобнее будет раскрыть модуль. Получаем совокупность двух систем:
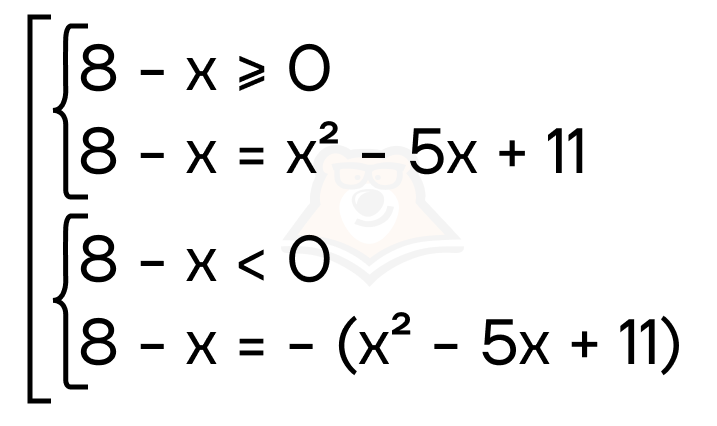
Рассмотрим первую систему.
8 — x >= 0 (rightarrow) x <= 8
Решим уравнение:
8 — x = x2 — 5x + 11
x2 — 4x + 3 = 0
D = 16 — 12 = 4
(x_1 = frac{4 + 2}{2} = 3)
(x_2 = frac{4 — 2}{2} = 1)
Оба корня уравнения удовлетворяют условию x <= 8, значит, решением системы будут 1 и 3.
Рассмотрим вторую систему.
8 — x < 0 (rightarrow) x > 8
Решим уравнение:
8 — x = -x2 + 5x — 11
x2 — 6x + 19 = 0
D = 36 — 76 = -40 — при отрицательном дискриминанте решения уравнений нет.
Решением всего уравнения будут x = 1 и x = 3.
Ответ: 1, 3
4. Разберем еще один тип уравнений, когда модуль равен модулю. Неужели придется рассматривать целых 4 случая раскрытия модуля? Нет, достаточно будет возвести в квадрат обе части уравнения. Таким образом, мы получаем следующий переход:
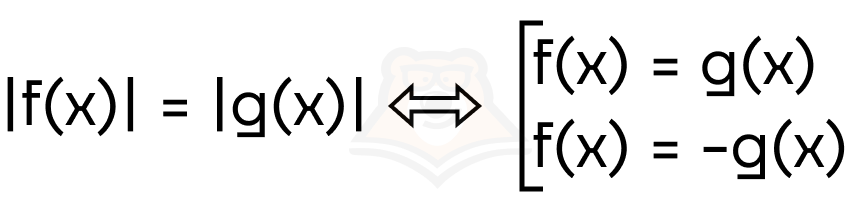
Пример 4. Решите уравнение |x — 2| = |2x + 8|.
Решение. Возведем обе части уравнения в квадрат. Для этого воспользуемся свойством 8.
(x — 2)2 = (2x + 
(x — 2)2 — (2x + 
Воспользуемся формулой сокращенного умножения:
((x — 2) — (2x + 8))((x — 2) + (2x + 
Если произведение множителей равно 0, то каждый множитель равен 0. Тогда:
x — 2 — (2x + 
x — 2 + (2x + 

Получаем совокупность:
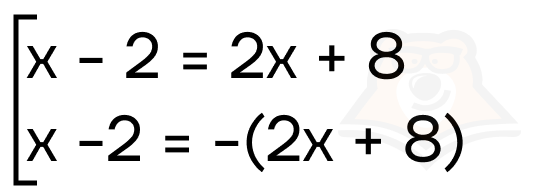
Решим первое уравнение совокупности:
x — 2 = 2x + 8
x = -10
Решим второе уравнение совокупности:
x — 2 = -2x — 8
3x = -6
x = -2
Решением уравнения будут x = -10 и x = -2
Ответ: -2, -10
Неравенства с модулем
Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам.
Пример 5. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 (rightarrow) (x = frac{7}{3}).
Определим, с какими знаками модуль будет раскрываться на каждом промежутке.
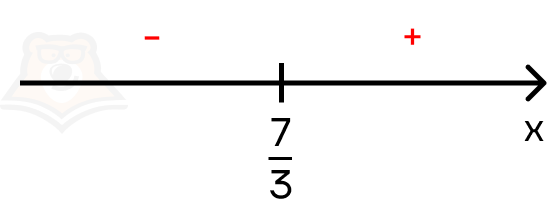
Осталось рассмотреть неравенство на двух промежутках.
1. (x leq frac{7}{3}), тогда
x2 — (-(3x — 7)) + 7 >= 0
x2 + 3x — 7 + 7 >= 0
x2 + 3x >= 0
x(x + 3) >= 0
Решим это неравенство «Методом интервалов». Сразу учтем ограничение (x leq frac{7}{3}).
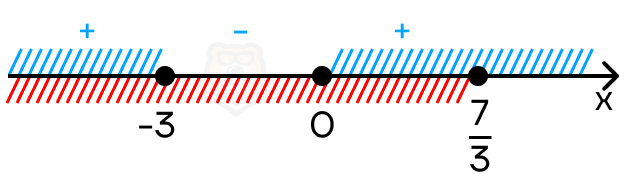
Получаем, что решением неравенства на заданном промежутке будет (x in (-infty; -3] U[0; frac{7}{3}]).
2. (x > frac{7}{3}), тогда
x2 — 3x + 7 + 7 >= 0
x2 — 3x + 14 >= 0
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней на заданном отрезке не будет.
Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график.
Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.
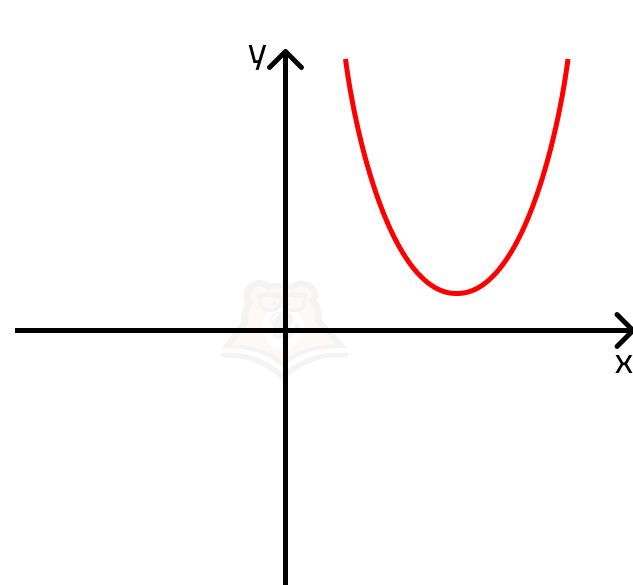
Однако не стоит забывать про ограничение (x > frac{7}{3}). Накладывая его, получаем решение ((frac{7}{3}; + infty)).
Осталось только объединить полученные на промежутках решения:
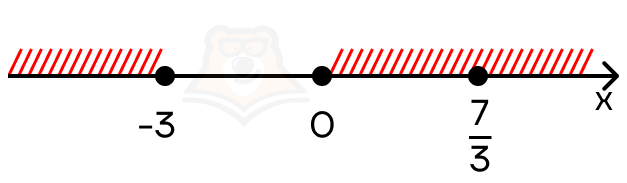
Получаем, что (x in (-infty;- 3] U [0; +infty)).
Ответ: (x in (-infty;- 3] U [0; +infty))
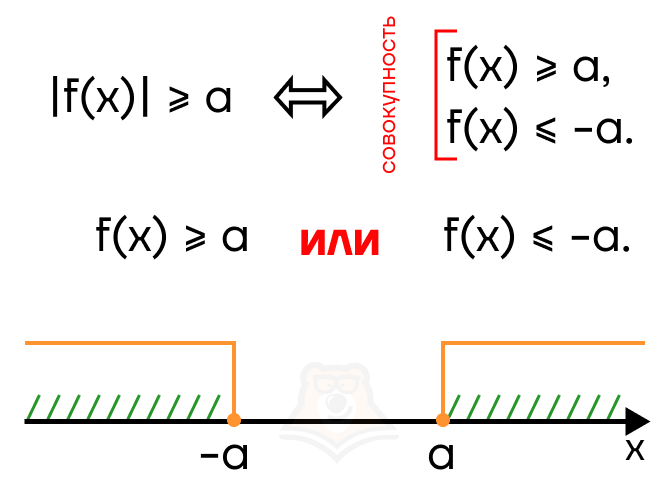
Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?
Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как:
f(x) > a и -f(x) > a (rightarrow) f(x) < -a.
Отметим эти промежутки на числовой прямой:
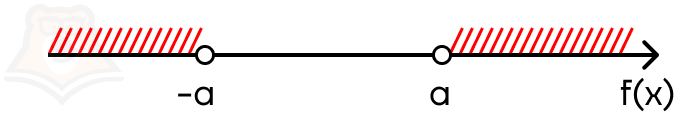
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности.
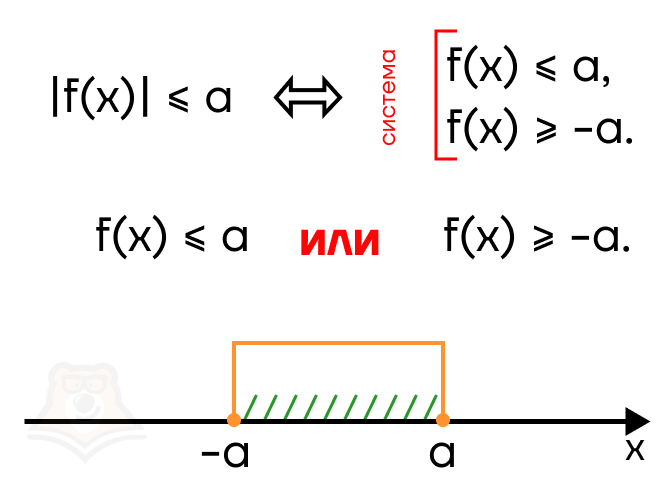
Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a (rightarrow) f(x) > -a. На числовой прямой это будет выглядеть следующим образом:

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки.
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат.
|f(x)| ⋁ a | (uparrow) 2 — вместо ⋁ может стоять любой знак неравенства.
f2(x) ⋁ a2
f2(x) — a2 ⋁ 0
Воспользуемся формулой сокращенного умножения:
(f(x) — a)(f(x) + a) ⋁ 0
Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0.
Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:
- |f(x)| ⋁ g(x) (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат.
- |f(x)| ⋁ |g(x)| (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому.
Пример 6. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Перенесем модуль в другую часть неравенства:
|3x — 7| <= x2 + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно.
Повторим действия, чтобы прийти к равносильному переходу:
(3x — 7)2 <= (x2+7)2
(3x-7)2 — (x2 + 7)2 <= 0
(3x — 7 — (x2 + 7))(3x — 7 + x2 + 7) <= 0
(3x — 7 — x2 — 7)(3x + x2) <= 0
(-x2 + 3x — 14) * x(3 + x) <= 0
-(x2 — 3x + 14) * x(3 + x) <= 0
(x2 — 3x + 14) * x(3 + x) <= 0
Рассмотрим первую скобку:
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:
x(3 + x) <= 0

Тогда (x in (-infty;- 3] U [0; +infty))
Ответ: (x in (-infty;- 3] U [0; +infty))
При решении можно сразу использовать равносильный переход, не расписывая его.
Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.
Фактчек
- Модуль — расстояние от любой точки на координатной прямой до начала координат. Модуль обозначается двумя вертикальными черточками: |a| = a и |-a| = a.
- Модулем числа называют выражение:

- График модуля представляет собой “галочку”, которая лежит выше оси х. Модуль отражает график любой функции зеркально оси х так, что значения у всегда больше 0.
- Модуль можно раскрыть двумя способами. Этим свойством можно пользоваться при решении уравнений с модулем.
- При решении неравенств с модулем можно раскрывать его, либо воспользоваться равносильным переходом, если в неравенстве выполняются все условия для него.
Проверь себя
Задание 1.
Чему равно выражение |-16 * 2|?
- 32
- −32
- −16
- 16
Задание 2.
Какой график имеет функция y = |x|?
- Парабола
- Гипербола
- Прямая
- Галочка
Задание 3.
Решите уравнение |x| = -3.
- 3
- −3
- Решений нет
- 3 и −3
Задание 4.
Решите уравнение |x + 2| = 15.
- −13
- 17
- 13 и -17
- Решений нет
Задание 5.
Какой равносильный переход можно использовать для неравенства вида |f(x) |⋁ |g(x)|?
- f(x) ⋁ g(x)
- f(x) ⋀ g(x)
- f2(x) — 2 * f(x) * g(x) + g2(x) ⋁ 0
- (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Ответы: 1. — 1 2. — 4 3. — 3 4. — 3 5. — 4
Функция модуля — это функция, заданная формулой y=|х|.
По определению модуля,
Соответственно, при x≥0 график модуля — прямая пропорциональность y=x, при x<0 — y= -x. То есть график функции y=|х| состоит из двух лучей — биссектрисы I и биссектрисы II координатных углов.
Для построения графика функции модуля x достаточно в I и II координатных четвертях провести из точки O лучи через диагональ каждой клеточки.
Можно отметить пару точек, например, (5; 5) и (-5; 5), и провести через них лучи с началом в точке O (0; 0) (лучше брать точки подальше от О, тогда график получится более точным).
Свойства функции y=|х|
1) Область определения — множество действительных чисел:
D: x∈(-∞; ∞).
2) Область значений —множество неотрицательных чисел:
E: y∈[0; ∞).
3) Функция имеет один нуль:
y=0 при x=0.
4) График функции модуль x симметричен относительно оси Oy (противоположным значениям x соответствуют равные значения y:|-х|=|х|, то есть y=|х| — чётная функция).
5) Функция модуля убывает при x∈(-∞; 0) и возрастает при x∈(0; ∞).
Определение модуля
Алгебрагическое определение: | x |
=
Геометрическое определение: модулем
числа называется расстояние от точки,
изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7
классе рассматривается линейная функция и ее
график и уже можно показывать построение
несложных графиков функций, содержащих модуль.
Далее, по мере изучения различных функций, их
свойств, каждую такую тему можно заканчивать
рассмотрением более сложных графиков, в том
числе с модулем. В этой статье рассматриваются
основные приемы построения графиков таких
функций.
I. На алгебрагическом определении основан метод
«раскрытия модуля на промежутках».
Например: | x + 2 | = | x + 2 | =
метод можно применять при построении графиков
функций, содержащих один или более модулей.
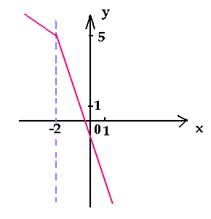
Например, построим график функции у = | x + 2 | –
2x + 1 , предварительно упростив ее.
у = у
=
Если модулей несколько, то каждый из них
раскрываем на промежутках относительно точек,
обращающих каждый из них в нуль. Например,
построим график функции у = | 3 – x | – x
+ | x + 2 | + 1.
1. Если х < – 2, то у = 3 – х – х
– (х + 2) + 1, у = – 3х + 2.
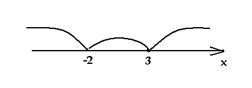
< х < 3, то у = 3 – х – х + х
+ 2 + 1, у = – х + 6.
3. Если х > 3, то у = – (3 – х) – х
+ х + 2 + 1, у = х.
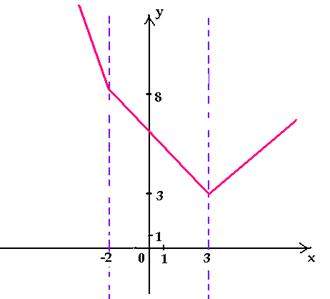
записываем как кусочно-заданную:
у =
Подобно тому, как числовая прямая точками – 2 и 3
разбивается на промежутки, координатная
плоскость прямыми х = – 2 и х = 3
разбивается на части («полосы»), в каждой из
которых строим свой график. Заметим, что данная
функция непрерывна, поэтому на «границах» части
графика должны соединяться.
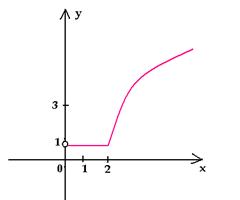
метод можно применять к функциям разных видов.
Например, построим график функции у = | log2
x – 1 | – log0,5 x.
Заметим, что х > 0.
1. Пусть log2x – 1 > 0, log2x >
1, x > 2, тогда у = log2 x – 1 +
log2 x; y = 2 log2 x – 1.
2. Пусть log2 x – 1 < 0, 0 < x < 2,
тогда у = – log2 x + 1 + log2 x; y
= 1.
Запишем функцию как кусочно-заданную:
у =
III. Рассмотрим некоторые частные случаи
функций, содержащих модуль.
1) у = | f(x) |.
По определению модуля имеем: | f(x) | =
Таким образом , для того, чтобы построить график
такой функции, необходимо взять часть графика,
лежащую не ниже оси абсцисс, а часть графика,
лежащую ниже этой оси отобразить относительно
нее в верхнюю полуплоскость. (Заметим, что «–»,
стоящий перед функцией означает симметричное
отображение графика относительно оси абсцисс).
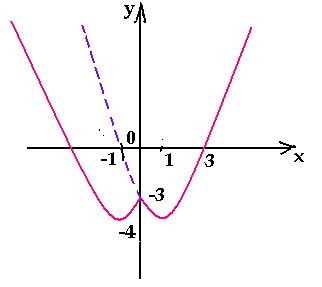
Например, построим график функции у = | x2
– 2х – 3 |.
Построим сначала график функции у = х2
– 2х – 3. Графиком этой функции является
парабола, ветви которой направлены вверх.
Координаты ее вершины: х = 1, у = – 4. Точки
пересечения параболы с осями координат: (0; – 3); (–
1; 0); (3; 0). Далее выполняем отображение части
графика, лежащей в нижней полуплоскости,
относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(|
x |) =
Чтобы построить график такой функции строим
график функции у = f(x) и берем ту его
часть, где х > 0 (в правой полуплоскости).
Затем эту часть симметрично отображаем в левую
полуплоскость, где х < 0. (Заметим, что
построение графика функции f(– x) и
состоит в отображении части графика, лежащей в
правой полуплоскости в левую относительно оси
ординат).
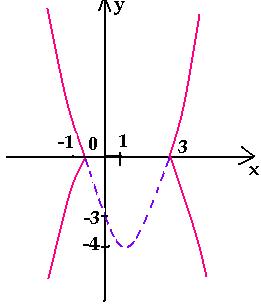
Например, построим график функции у = х2
– 2| х | – 3. Сначала строим график функции у
= х2 – 2х – 3, далее выполняем
указанные преобразования.
3) Построим график функции y = | f(| x
|)|, например, y = | x2 – 2| х | – 3 |,
выполним последовательно преобразования,
рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x).
Ее нельзя назвать функцией, так как не
выполняется условие: каждому значению х должно
соответствовать единственное значение у.
Рассмотрим построение графика такой
зависимости (можно говорить «графика
уравнения»). Используем определение модуля: у
= f(x), если у > 0, – у = f(x),
y = – f(x), если у < 0
Получаем, чтобы построить такой график, сначала
строим график функции у = f(x) и
берем ту его часть, которая лежит в верхней
полуплоскости, где у > 0; чтобы
построить график в нижней полуплоскости (где у
< 0), нужно построенную часть отобразить
симметрично относительно оси абсцисс (знак «–»
перед функцией и означает такое отображение)
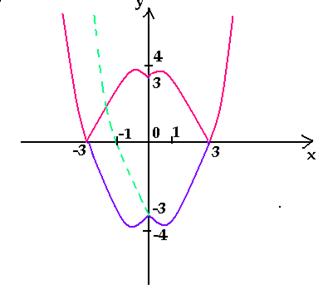
Например, построим график уравнения | y | = x2
– 2х – 3
Заметим, что графики, не относящиеся к
рассмотренным частным случаям, следует строить «
раскрывая модули на промежутках».
| x |
1 |
0 |
– 1 |
|
y |
0 |
|
|
IV. Приведем некоторые примеры
1. Построим график уравнения | y | = arccos| x
|.
2. Графическим способом можно решать и
неравенства с двумя переменными. Например,
решением неравенства | y | < arccos| x |
являются координаты точек закрашенной части
плоскости, включая границы.
Решим еще одно задание, предлагавшееся на ЕГЭ:
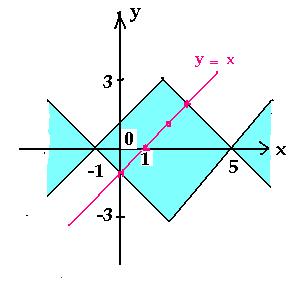
найти все целочисленные решения неравенства | y
| < | | x – 2 | – 3 | (х0; у0),
для которых х0 = у0. Построим
сначала график уравнения | y | = | | x – 2 | –
3 |. Решением данного неравенства будут являться
координаты точек закрашенной части плоскости,
включая границы.
Пары чисел (х0; у0),
являющиеся решениями неравенства, для которых y0
= x0, являются координатами точек,
лежащих на прямой у = х. Выберем точки с
целыми координатами: (0; – 1); (1; 0); (2; 1); (3; 2), они и
будут являться решениями данной задачи.
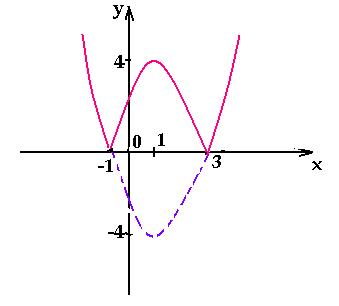
3. Определить, сколько корней имеет уравнение | 3
– x | + log3| x | = 2 – x.
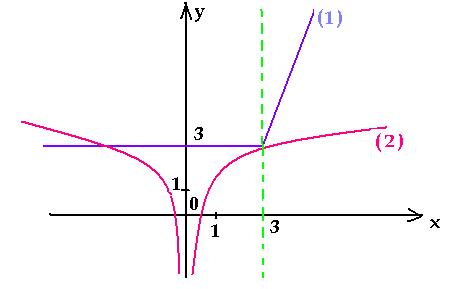
Запишем уравнение в виде | 3 – x | + x = log3|
x | + 2. В одной системе координат построим
графики функций y = | 3 – x | = x (1) и y
= log3| x | = 2 (2). Функцию (1) запишем как
кусочно-заданную, раскрывая модуль на
промежутках:
y =
График функции (2) построим, выполняя
отображение графика y = log3x + 2
относительно оси ординат ( один из рассмотренных
частных случаев ).
Графики имеют две общие точки, следовательно,
данное уравнение имеет два корня.
V. Для повторения материала, его закрепления
предлагаем выполнить следующие задания.
1. Постройте графики функций и уравнений: y =
| y | =
; y = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = + 1.
2. Решите графически уравнения c одной и двумя
переменными: | 3 – x | – 3 = 2| x | – x2;
| y | = 2| x | – x2; = | x – 2,5 | –1,5.
3. Решите графически неравенства с двумя
переменными: | y | > x24x + 3;
| x | + | y | < 3.
4. Решите графически систему уравнений:
5. Найдите все значения а, при каждом из которых
уравнение | x + a | + | | x – 3 | – 4 | = 1
имеет ровно два корня.
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
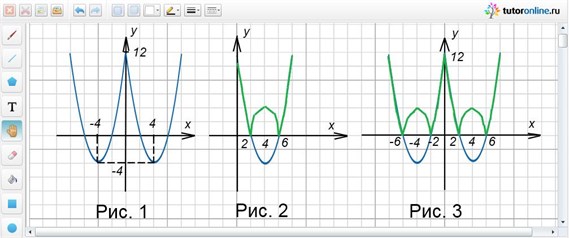
Построить график функции y = x2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x2 – 8|x| + 12| проводят комбинацию преобразований:
y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
|
Функция |
Преобразование |
|
f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
|
|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
|
|f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
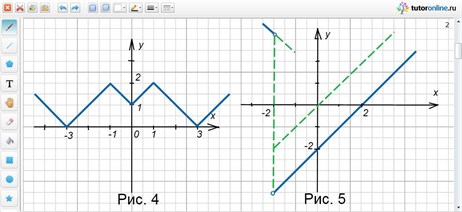
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x2 – 4)/√(x + 2)2.
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x2 – 4)/√(x + 2)2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x < -2, y = -(x – 2).
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x < -1 и x < 2;
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x < 2;
{-x – 1 – x + 2 = -2x + 1, при x < -1 и x ≥ 2 – пустое множество.
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x < -1;
{2x – 1, при -1 ≤ x < 2.
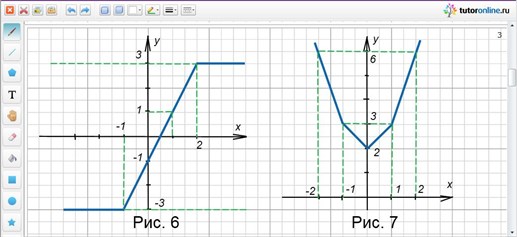
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.