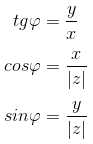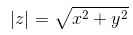Как найти модуль комплексного числа калькулятор

Калькулятор комплексных чисел. Вычисление выражений с комплексными числами

Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.

Как пользоваться калькулятором

1. Введите в поле ввода выражение с комплексными числами
2. Укажите, требуется ли вывод решения переключателем «С решением»
3. Нажмите на кнопку «Построить»

Ввод комплексных чисел

комплексные числа можно вводить в следующих трёх форматах:

• Только действительная часть: 2, 2.5, -6.7, 12.25
• Только мнимая часть: i, -i, 2i, -5i, 2.16i, -12.5i
• Действительная и мнимая части: 2+i, -5+15i, -7+2.5i, -6+i
• Математические константы: π, e

Поддерживаемые операции и математические функции

• Арифметические операции: +, -, *, /, ^
• Получение абсолютного значения числа: abs
• Базовые математические функции: exp, ln, sqrt
• Получение действительной и мнимой частей: re, im
• Тригонометрические функции: sin, cos, tg, ctg
• Гиперболические функции: sh, ch, th, cth
• Обратные тригонометрические функции: arcsin, arccos, arctg, arcctg
• Обратные гиперболические функции: arsh, arch, arth, arcth

Примеры корректных выражений

• (2+3i)*(5-7i)
• sh(i)
• (4+i) / (3 — 4i)
• sqrt(2i)
• (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.75)

Комплексные числа

Комплексные числа — это числа вида x+iy, где x, y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.

Примеры комплексных чисел

• 4+3i — действительная часть = 4, мнимая = 3
• -2+i — действительная часть = -2, мнимая = 1
• i — действительная часть = 0, мнимая = 1
• -i — действительная часть = 0, мнимая = -1
• 10 — действительная часть = 10, мнимая = 0

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi² = (ac — bd) + (bc + ad)i
• деление: = = + i

Примеры

Найти сумму чисел 5+7i и 5.5-2i:
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i + 5.5-2i = 10.5 + 5i

Найти разность чисел 12-i и -2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом:12-i — (-2i) = 12 + i

Найти произведение чисел 2+3i и 5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом:2+3i * (5-7i) = 31 + i

Найти отношение чисел 75-50i и 3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом:75-50i / (3+4i) = 1 - 18i

Другие действия над комплексными числами

Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:

• Получение действительной части числа: Re(z) = a
• Получение мнимой части числа: Im(z) = b
• Модуль числа: |z| = √(a2 + b2)
• Аргумент числа: arg z = arctg(b / a)
• Экспонента: ez = ea·cos(b) + i·ea·sin(b)
• Логарифм: Ln(z) = ln |z| + i·arg(z)
• Тригонометрические функции: sin z, cos z, tg z, ctg z
• Гиперболические функции: sh z, ch z, th z, cth z
• Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
• Обратные гиперболические функции: arsh z, arch z, arth z, arcth z

Примеры

Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(4² + (-3)²) = √25 = 5

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: x+iy, где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

Решение:

• Найдём радиус (модуль) комплексного числа r: r = √(1² + 1²) = √2
• Найдём аргумент числа: φ = arctan() = = 45°
• Запишем результат в тригонометрической форме: √2·(cos(45°) + isin(45°))
• Запишем результат в показательной форме: √2·eπi/4

Начиная с 16 века математики столкнулись с необходимостью введения комплексных чисел, то есть чисел вида a+bi, где a,b — вещественные числа, i — мнимая единица — число, для которого выполняется равенство: i²=-1.

Интересно проследить, как менялось представление о комплексных числах с течением времени. Вот некоторые цитаты из древних трудов:

• XVI век : Эти сложнейшие величины бесполезны, хотя и весьма хитроумны. ¹
• XVII век : Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием. ²
• XVIII век : Квадратные корни из отрицательных чисел не равны нулю, не меньше нуля и не больше нуля. Из сего видно, что квадратные корни из отрицательных чисел не могут находиться среди возможных чисел. Поэтому, нам не остается ничего другого, как признать их невозможными числами. Это ведет нас к понятию таких чисел, которые по своей природе невозможны и обычно называются мнимыми или воображаемыми, потому что их только в уме представить можно. ³
• XIX век Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы и иероглифы нелепых количеств. ⁴

Известно три способа записи комплексного числа z:

Алгебраическая запись комплексного числа

,
где a и b — вещественные числа, i — мнимая единица. a — действительная часть, bi — мнимая часть.

Тригонометрическая запись комплексного числа

,
где r — модуль комплексного числа:

, который соответствует расстоянию от точки на комплексной плоскости до начала координат, а φ — угол наклона вектора 0-z к оси действительных значений или аргумент комплексного числа.

Показательная запись комплексного числа

была введена Леонардом Эйлером для сокращения тригонометрической записи.

Значение аргумент комплексного числа определяется с точностью до , для всех целых k. Главный аргумент — это значение аргумента, лежащее в диапазоне (-π..π].
Главный аргумент вычисляется как арктангенс двух аргументов мнимой и действительной части комплексного числа:
, см Арктангенс с двумя аргументами

Над комплексным числом возможны все алгебраические операции:

Сложение комплексных чисел

Комплексные числа складываются ровно так же, как и многочлены:

Умножение комплексных чисел

Помня о том, что i*i=-1, легко выразить формулу для умножения комплексных чисел:

Деление комплексных чисел

Формулу деления комплексных чисел проще всего вывести, путем умножения числителя и знаменателя на сопряженное комплексное число, для того, чтобы избавиться от мнимой единицы в знаменателе:

Сопряженное комплексное число, это число вида:

Раскрывая скобки получаем:

Возведение в целую степень

Проще всего комплексное число возводить в степень используя показательную форму:

формула вытекает из формулы Муавра:

Вычисление корня степени n

Из формулы Муавра вытекает решение для корней степени n из комплексного числа:
,
всего получается n корней, где k = 0..n-1 — целое число, определяющее индекс корня. Корни располагаются на комплексной плоскости, как вершины правильного многоугольника.

Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки,
соответствующей данному комплексному числу и обозначается Arg(z) = φ

Из определения следуют следующие формулы:

Для числа z = 0 аргумент не определен.

Главным значением аргумента называется такое значение φ, что .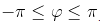
Обозначается: arg(z).

Свойства аргумента:

Модулем комплексного числа z = x + iy называется вещественное число |z| равное:

Для любых комплексных чисел z, z₁, z₂ имеют место следующие свойства модуля:

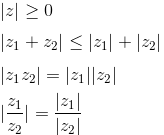
для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости.