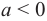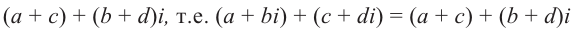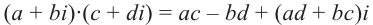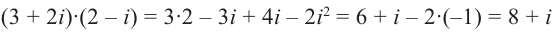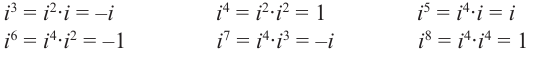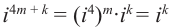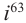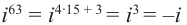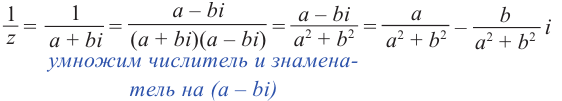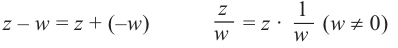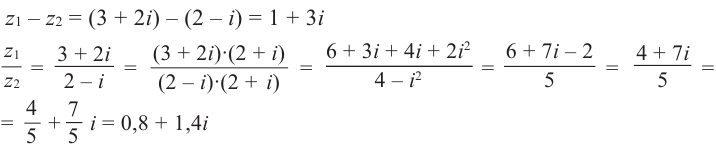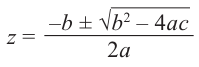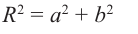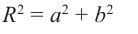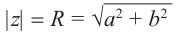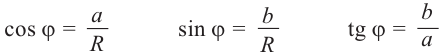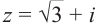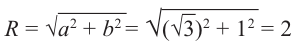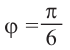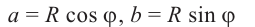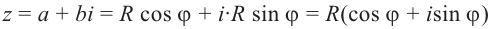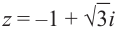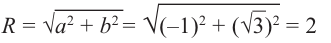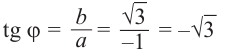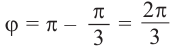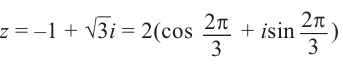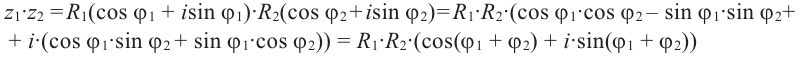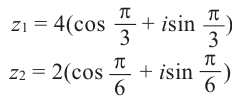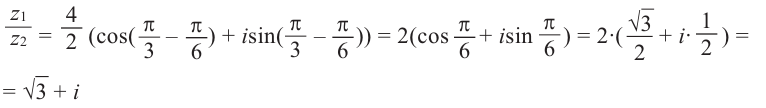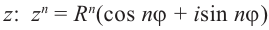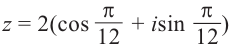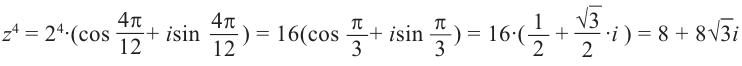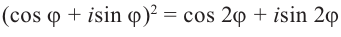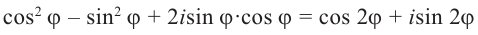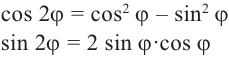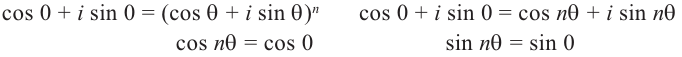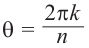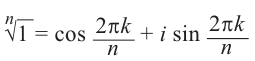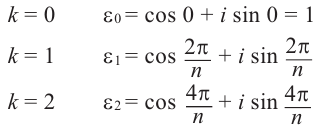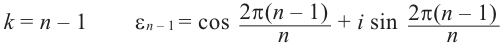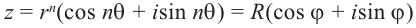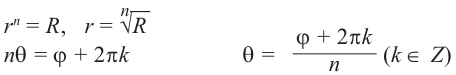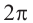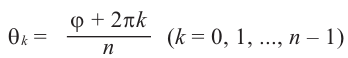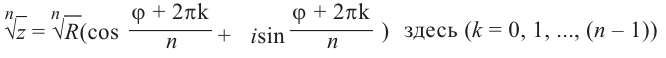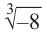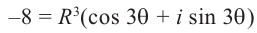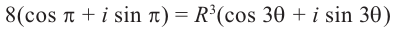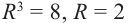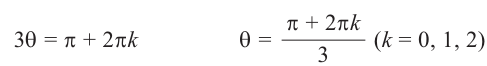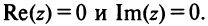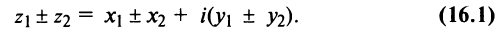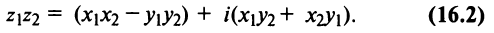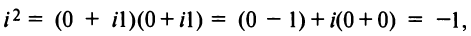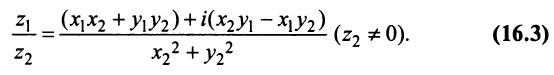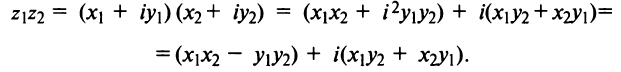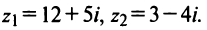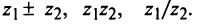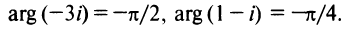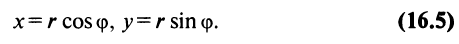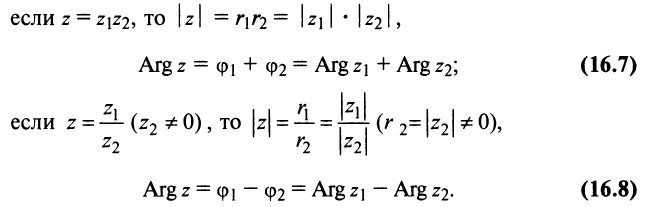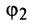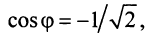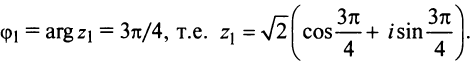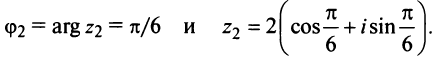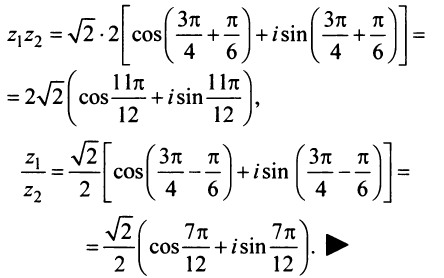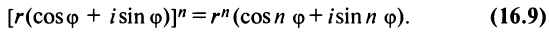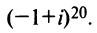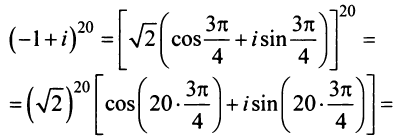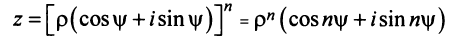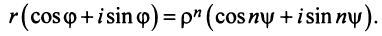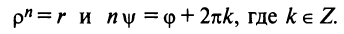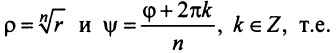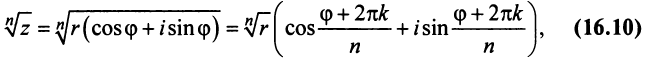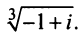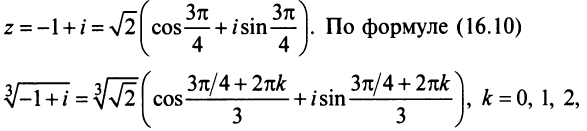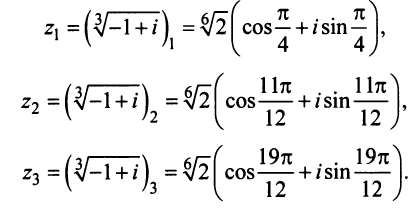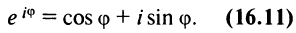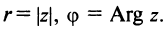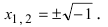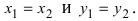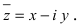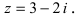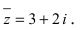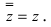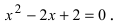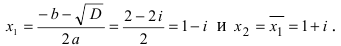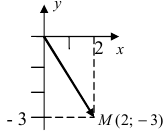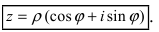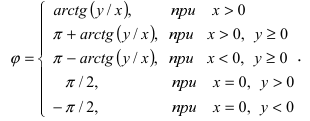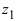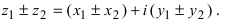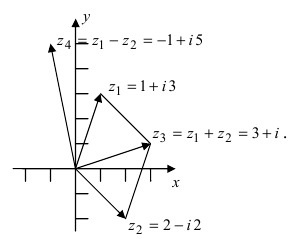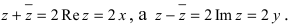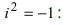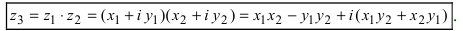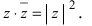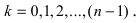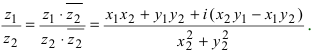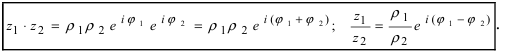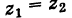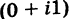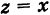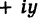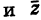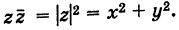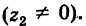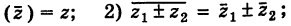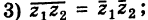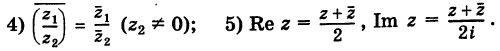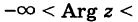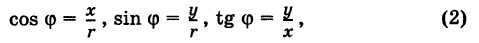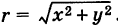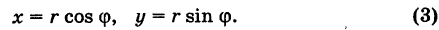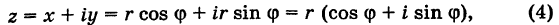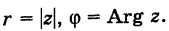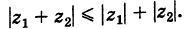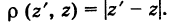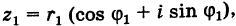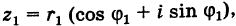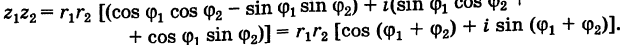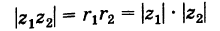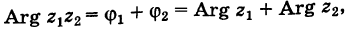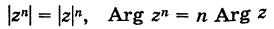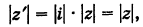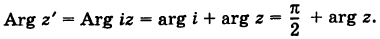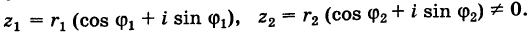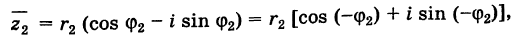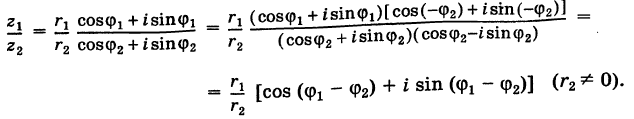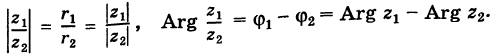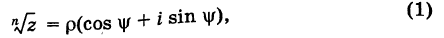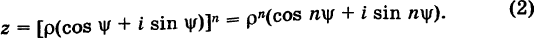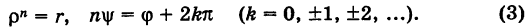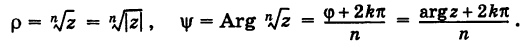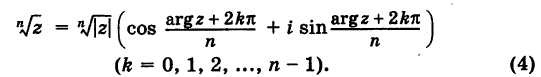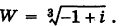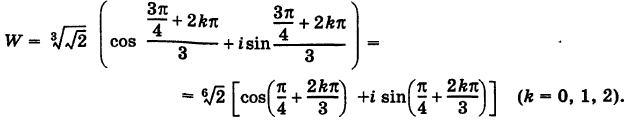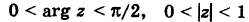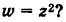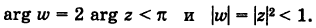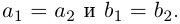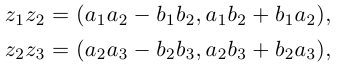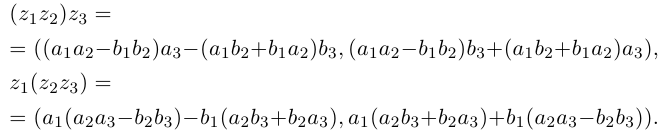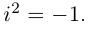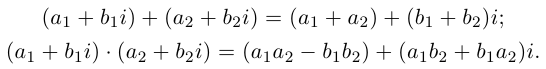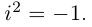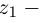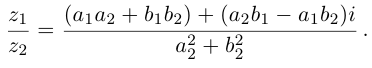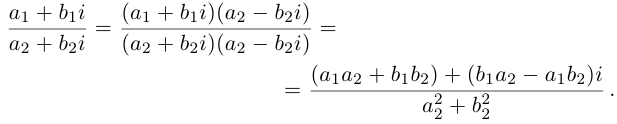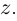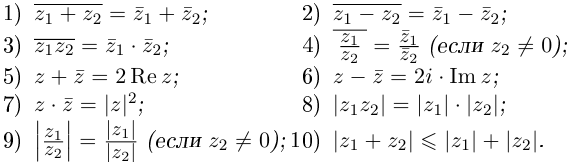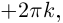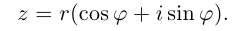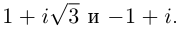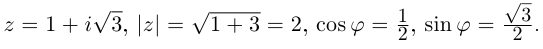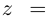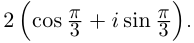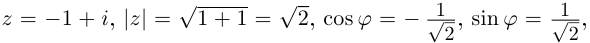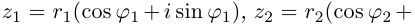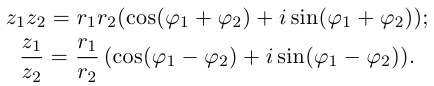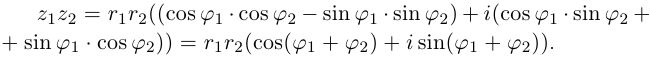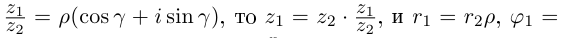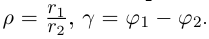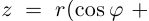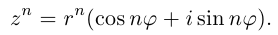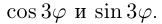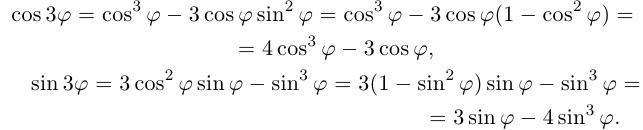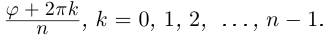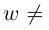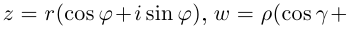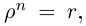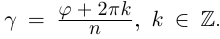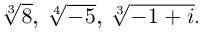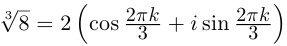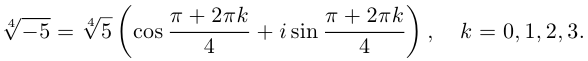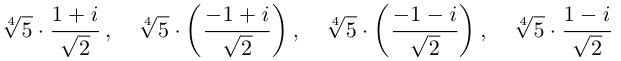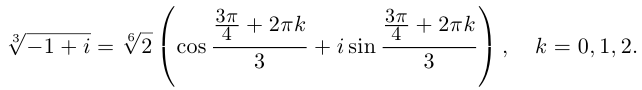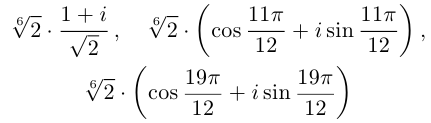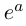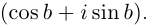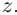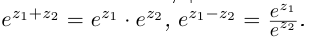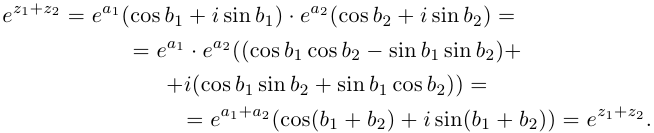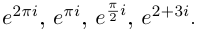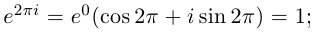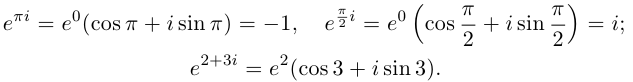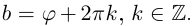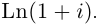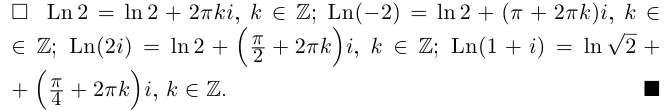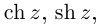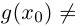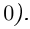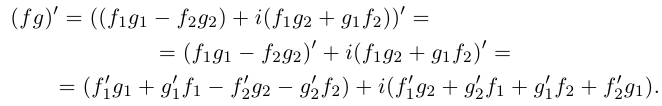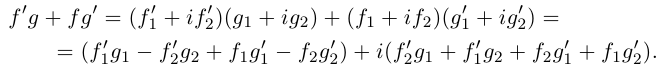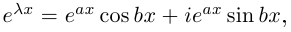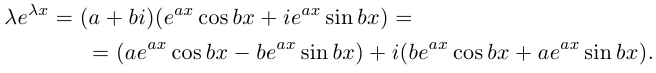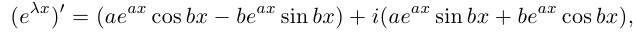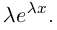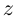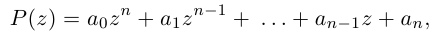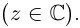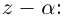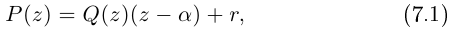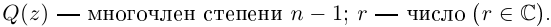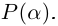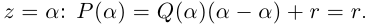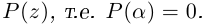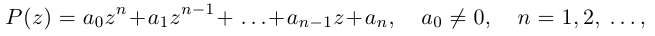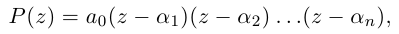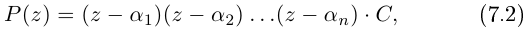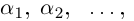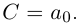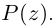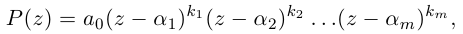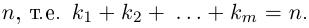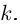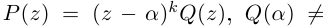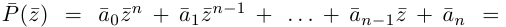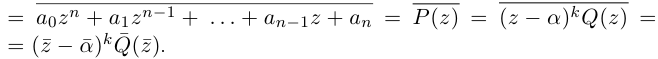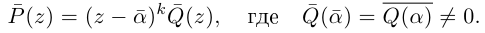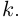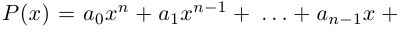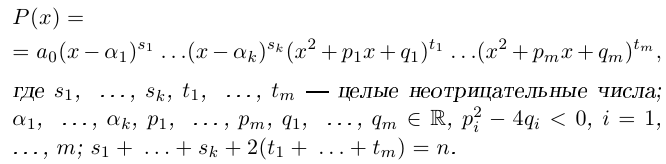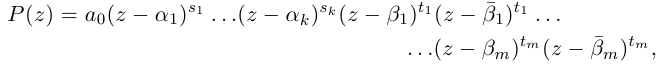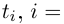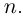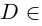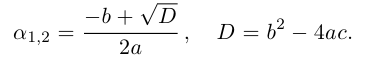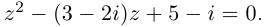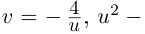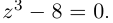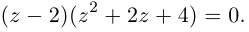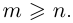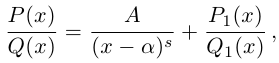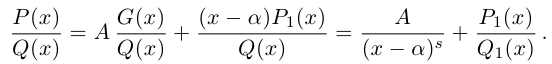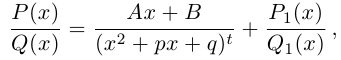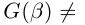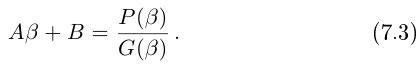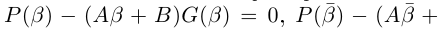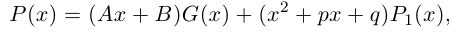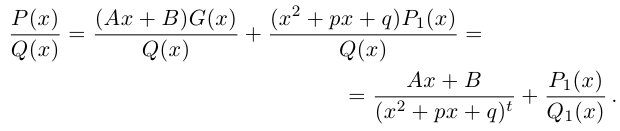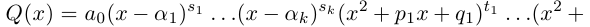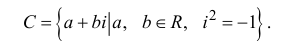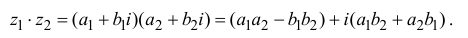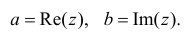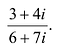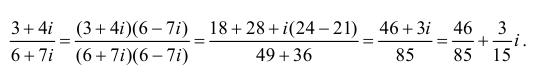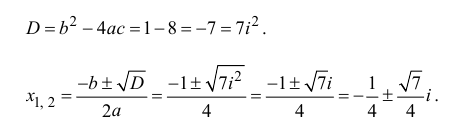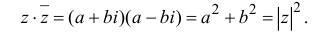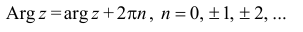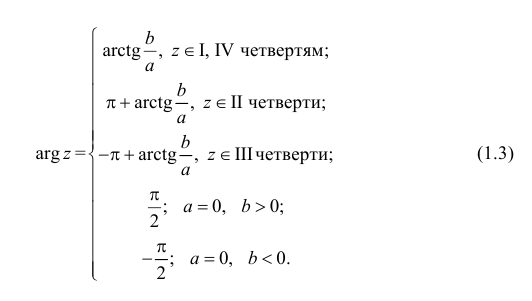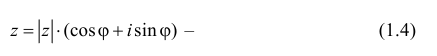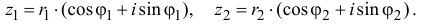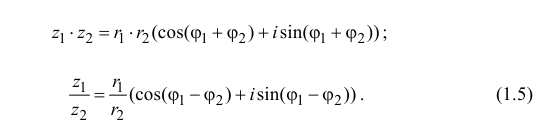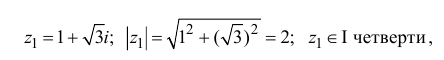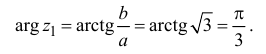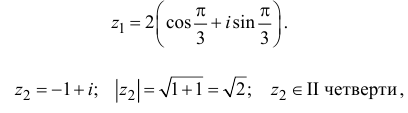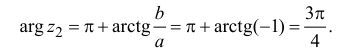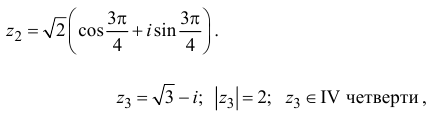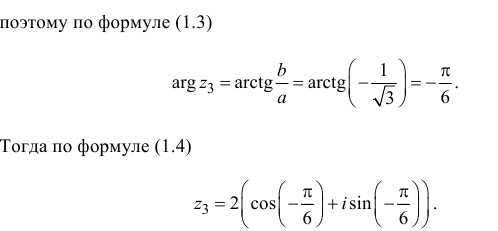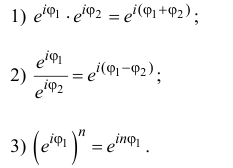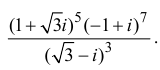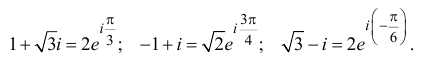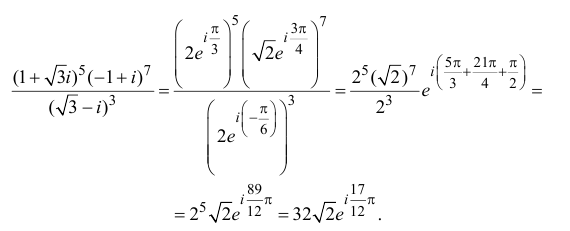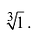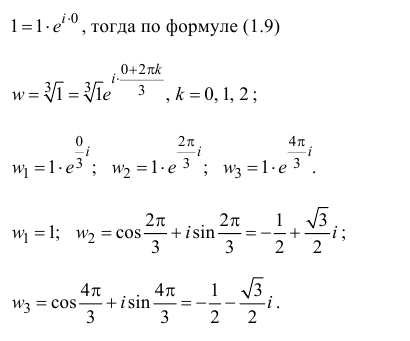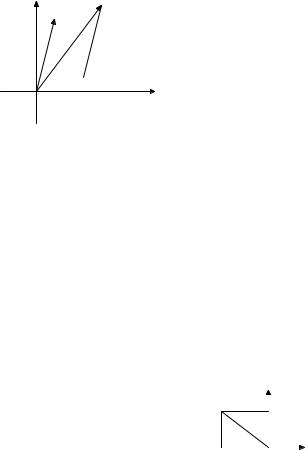

Рис. 28.2. Сложение комплексных чисел.
Умножение комплексных чисел также имеет геометрический смысл; мы выясним его в следующем параграфе.
§ 29. Модуль и аргумент комплексного числа
Повторить: § 25: отбор чисел на круге.
В этом параграфе мы выясним геометрический смысл умножения комплексных чисел. Сначала — небольшая подготовка.
|
Расстояние на комплексной плоскости |
||||||||
|
от начала координат (точки O) до точки z |
||||||||
|
называется модулем комплексного числа z. |
||||||||
|
Модуль комплексного числа z обозначает- |
||||||||
|
ся |z|, как и модуль действительного числа. |
||||||||
|
Такое совпадение обозначений не приводит |
||||||||
|
к путанице, поскольку модуль действитель- |
Рис. 29.1. |
|||||||
|
ного числа также равен расстоянию от со- |
||||||||
|
ответствующей точки на числовой оси до |
√ |
|||||||
|
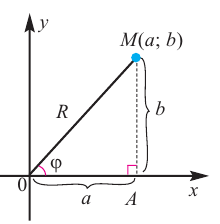
точки O. Если z = a + bi, то, очевидно, |z| = |
a2 + b2 |
(рис. 29.1). |
Задача 29.1. Докажите, что для любых комплексных чисел z и w верно неравенство |z + w| 6 |z| + |w|.
Теперь соединим точку z с точкой O. Угол, образуемый полученным отрезком с действительной осью (точнее говоря, с поло-
169

|
а) |
б) |
||||||
|
Рис. 29.2. |
жительным направлением действительной оси), называется аргументом числа z (рис. 29.2а). Этот угол принято выражать в радианах.
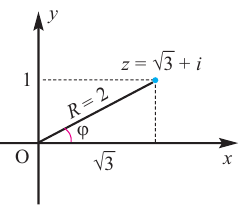
Если z = a + bi, |z| = r, аргумент z равен ϕ, то, очевидно,
a = r cos ϕ; b = r sin ϕ.
Стало быть, z = r cos ϕ + ir sin ϕ = r(cos ϕ + i sin ϕ).
Запись комплексного числа в виде r(cos ϕ + i sin ϕ), где r > 0, называется тригонометрической формой комплексного числа. В тригонометрической форме можно записать любое комплексное число, кроме нуля (аргумент нуля мы не определяем).
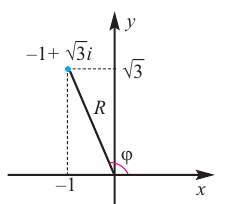
Запишем, например, в√тригонометрической форме число z = = −1 −i. Очевидно, |z| = 2, и из рис. 29.2б видно, что в качестве аргумента можно взять 5π/4:
−1 − i = 2 cos 54π + i sin 54π .
Впрочем, с тем же успехом можно было бы сказать, что аргумент −1 − i равен −34π : ведь равенство −1 − i = √2 cos −34π +
+i sin −34π также верно. Вообще, аргумент комплексного числа определен не однозначно, а с точностью до прибавления 2πn, где n — целое число. В качестве аргумента числа z можно взять любое число ϕ, для которого z = |z|(cos ϕ + i sin ϕ).
170

Задача 29.2. Найдите аргументы следующих чисел, после чего за-
|
пишите эти числа в тригонометрической форме: а) i; б) −1; в) |
|||||
|
√ |
√ |
||||
|
3 + i; г) |
3 − i; д) −(cos ϕ + i sin ϕ); е) cos ϕ − i sin ϕ. |
Задача 29.3. Докажите, что
1
cos ϕ + i sin ϕ = cos ϕ − i sin ϕ.
Пусть теперь нам даны комплексные числа z1 = r1(cos ϕ1 + + i sin ϕ1) и z2 = r2(cos ϕ2 + i sin ϕ2). Давайте их перемножим:
z1z2 = r1(cos ϕ1 + i sin ϕ1)r2(cos ϕ2 + i sin ϕ2) =
=r1r2(cos ϕ1 + i sin ϕ1)(cos ϕ2 + i sin ϕ2) =
=r1r2(cos ϕ1 cos ϕ2 − sin ϕ1 sin ϕ2)+
+i(sin ϕ1 cos ϕ2 + cos ϕ1 sin ϕ2) =
=r1r2(cos(ϕ1 + ϕ2) + i sin(ϕ1 + ϕ2)).
(мы воспользовались формулами синуса и косинуса суммы). Как видите, если перейти к тригонометрической форме, то
умножение комплексных чисел запишется простой формулой:
r1(cos ϕ1 + i sin ϕ1)r2(cos ϕ2 + i sin ϕ2) =
= r1r2(cos(ϕ1 + ϕ2) + i sin(ϕ1 + ϕ2)).
Или словами:
При умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Поскольку деление — действие, обратное к умножению, то:
При делении комплексных чисел их модули делятся, а аргументы вычитаются.
Итак, мы придали геометрический смысл умножению комплексных чисел, рассматриваемых как векторы на плоскости. На первый взгляд это противоречит сказанному в § 17, где мы говорили, что геометрически
171
определить умножение векторов на плоскости невозможно. Представьте себе, однако, что у нас даны два вектора и мы хотим их умножить «как комплексные числа»— тут же выяснится, что для того, чтобы сложить аргументы, надо сначала иметь ось, от которой эти аргументы отсчитывать, причем если выбрать «действительную ось» по-другому, то произведение изменится!
Рассматривая умножение комплексных чисел, записанных в тригонометрической форме, мы убедились, что при умножении комплексных чисел их модули перемножаются. Запишем это свойство комплексных чисел в виде формулы
Задача 29.4. Докажите формулу (29.1), исходя из определения умножения комплексных чисел.
Задача 29.5. а) Докажите, что |z| = z · z¯; б) выведите из этой формулы тождество (29.1).
Формулу (29.1) можно переписать и не используя комплексных чисел. В самом деле, если z = a1 + b1i и w = a2 + b2i, то, возводя (29.1) в квадрат, получаем такое тождество:
|
(a12 + b12)(a22 + b22) = (a1a2 − b1b2)2 + (a1b2 + b1a2)2. |
(29.2) |
Разумеется, это тождество легко проверить и непосредственно.
Задача 29.6. Докажите, что число
32858969712941053630927296788431704044342041015625 = 531 ·1325
является суммой квадратов двух целых чисел.
Задача 29.7. Докажите, что число
73734314159378042035384049570 = = 2 ·5 ·13 ·29 ·37 ·41 ·53 ·61 ·73 ·89 ·97 ·101 ·113 ·137 ·149 ·157 ·173
также является суммой квадратов двух целых чисел.
172
Указание. 2 = 12 + 12; 5 = 12 + 22. . .
Существует аналог тождества (29.2) для сумм четырех квадратов, показывающий, что произведение двух сумм четырех квадратов также равно сумме четырех квадратов:
(a21 + a22 + a23 + a24)(b21 + b22 + b23 + b24) =
=(a1b1 − a2b2 − a3b3 − a4b4)2 + (a1b2 + a2b1 + a3b4 − a4b3)2 +
+(a1b3 + a3b1 − a2b4 + a4b2)2 + (a1b4 + a4b1 + a2b3 − a3b2)2.
Задача 29.8. Докажите это тождество.
Имеется также аналог этих двух тождеств для сумм восьми квадратов, но на этом все и кончается: при n 6= 2, 4, 8 тождеств типа «произведение двух сумм n квадратов равно сумме n квадратов» не существует.
Теперь посмотрим, что вытекает из того, что аргументы комплексных чисел при умножении складываются.
Если возвести комплексное число в степень n, то есть умножить его на себя n раз, то его модуль возведется в степень n, а аргумент умножится на n:
(r(cos ϕ + i sin ϕ))n = rn(cos nϕ + i sin nϕ).
В частности, при r = 1 получится вот что:
(cos ϕ + i sin ϕ)n = cos nϕ + i sin nϕ.
Эта формула называется формулой Муавра.
Из формулы Муавра легко вывести формулы, выражающие cos nϕ и sin nϕ через cos ϕ и sin ϕ. Для этого надо в ее левой части раскрыть скобки и привести подобные. При n = 5, например, получится вот что:
(cos ϕ + i sin ϕ)5 = (cos5 ϕ − 10 cos3 ϕ sin2 ϕ + 5 cos ϕ sin4 ϕ) +
+i(5 cos4 ϕ sin ϕ − 10 cos2 ϕ sin3 ϕ + sin5 ϕ) =
=cos 5ϕ + i sin 5ϕ.
173

Так как выражения слева и справа равны, то равны по отдельности их вещественные и мнимые части, откуда:
cos 5ϕ = cos5 ϕ − 10 cos3 ϕ sin2 ϕ + 5 cos ϕ sin4 ϕ, sin 5ϕ = 5 cos4 ϕ sin ϕ − 10 cos2 ϕ sin3 ϕ + sin5 ϕ.
Чтобы получить такие формулы для произвольного n, надо раскрывать скобки в (cos ϕ + i sin ϕ)n, а для этого требуется общая формула для раскрытия скобок в выражении (a + b)n. Мы выпишем эту формулу, но не будем ее доказывать. Выглядит она так:
(a + b)n = an + nan−1b
+ n(n − 1)(n − 2) an−3 1 · 2 · 3
|
+ |
n(n − 1) |
an−2b2 + |
|||
|
1 · 2 |
n(n − 1)(n − 2) . . . 2 |
||||
|
b3 + . . . + |
a1bn−1 |
+ bn. |
|||
|
1 · 2 · . . . (n − 1) |
Иными словами, в правой части коэффициент при an−kbk равен
n(n − 1) . . . (n − k + 1) : в знаменателе стоит произведение первых
1 · 2 · · · · · k
k натуральных чисел, а в числителе — произведение k идущих подряд целых чисел в убывающем порядке, начиная с n. Хотя коэффициенты в нашей формуле записаны как дроби, на самом деле все они — целые числа.
Формула для (a+ b)n, которую мы выписали, называется формулой бинома Ньютона.
Задача 29.9. Проверьте формулу бинома Ньютона для n = 3, 4, 5.
Задача 29.10. а) Выпишите формулу бинома Ньютона для n = 6. б) Выпишите формулы для cos 6ϕ и sin 6ϕ.
Задача 29.11. Убедитесь, что в формуле бинома Ньютона коэффициент при abn−1 равен n.
Задача 29.12. Докажите, что в формуле бинома Ньютона коэффициенты при an−kbk и akbn−k равны (что и не удивительно: если левая часть тождества не меняется, когда меняешь местами a и b, то такой же должна быть и правая часть).
174

Другое приложение формулы Муавра — еще один вывод формулы для суммы косинусов или синусов углов, образующих арифметическую прогрессию (§ 22). В самом деле, пусть нам надо вычислить сумму
cos α + cos(α + β) + cos(α + 2β) + . . . + cos(α + nβ).
Рассмотрим комплексные числа a = cos α + i sin α, b = cos β + + i sin β. Тогда, очевидно, abk = cos(α + kβ) + i sin(α + kβ). Следовательно,
a + ab + ab2 + . . . + abn = (cos + cos(α + β) + . . . + cos(α + nβ)) + + i(α sin + sin(α + β) + . . . + sin(α + nβ)).
Однако правую часть можно вычислить по формуле для суммы геометрической прогрессии:
a + ab + ab2 + . . . + abn = a1 − bn+1 = 1 − b
= (cos α + i sin α) 1 − cos(n + 1)β − i sin(n + 1)β .
1 − cos α − i sin α
(Если вас смущает, что мы применяем эту формулу к комплексным числам, посмотрите в вашем школьном учебнике, как она доказывается, и убедитесь, что дословно то же доказательство годится и для комплексных чисел.)
Теперь осталось упростить выражение в правой части (для этого, как обычно при делении комплексных чисел, надо умножить числитель и знаменатель дроби на (1−cos α)+i sin α и выделить в полученном выражении действительную и мнимую части). Действительная часть будет равна cos α+ cos(α+ β)+ . . .+ cos(α+
+nβ), а мнимая часть будет равна sin α + sin(α + β) + . . . + sin(α +
+nβ).
Задача 29.13. Проведите эти выкладки и убедитесь, что ответы совпадают с полученными в § 22.
Раз с помощью тригонометрической формы комплексные числа удобно возводить в степень, естественно надеяться, что та же
175
тригонометрическая форма поможет и в выполнении обратной операции — извлечения корней из комплексных чисел. Покажем на примере, какие новые явления при этом возникают.
Давайте извлечем корень пятой степени из 32, то есть найдем число, которое, будучи возведенным в пятую степень, даст 32. Среди действительных чисел такое число одно — это число 2. Посмотрим, что будет, если рассматривать любые комплексные числа. Мы ищем такие числа z, что z5 = 32. Проще всего найти модуль числа z: если z5 = 32, то |z5| = |z|5 = 32 (при перемножении чисел модули перемножаются), откуда |z| = 2 (уж |z|-то — это обычное действительное число, так что тут никаких разночтений не будет). Осталось найти аргумент z. Для этого запишем z в тригонометрической форме: z = 2(cos ϕ + i sin ϕ). Тогда z5 = 32(cos 5ϕ + i sin 5ϕ), откуда 32(cos 5ϕ + i sin 5ϕ) = 32, cos 5ϕ + i sin 5ϕ = 1, что, в свою очередь, равносильно системе тригонометрических уравнений
(
cos 5ϕ = 1;
sin 5ϕ = 0.
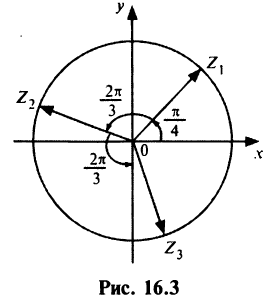
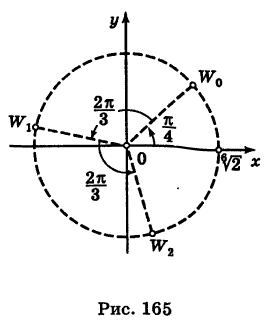
Этой системе, очевидно, удовлетворяют в точности те и только те числа ϕ, для которых числу 5ϕ соответствует начало отсчета на тригонометрической окружности, то есть 5ϕ = 2kπ, или ϕ = 2πk/5 (k Z). Стало быть, решения уравнения z5 = 32 — это числа вида 2(cos 2πk/5 + i sin 2πk/5), где k Z. Не все эти числа различны: так как комплексные числа с аргументами, отличающимися на 2π, совпадают, то разные комплексные числа получаются только при k = 0, 1, 2, 3, 4, а дальше значения z будут повторяться. Итак, все корни уравнения z5 = 32 или, если угодно, все корни пятой степени из 32 таковы:
z1 = 2(cos 0 + i sin 0);
z2 = 2(cos 2π/5 + i sin 2π/5); z3 = 2(cos 4π/5 + i sin 4π/5); z4 = 2(cos 6π/5 + i sin 6π/5); z5 = 2(cos 8π/5 + i sin 8π/5);
176

|
Здесь z1 — это просто число 2, действитель- |
||||
|
ный корень уравнения z5 = 32. Прочие кор- |
||||
|
ни этого уравнения действительными уже |
||||
|
не являются. Если изобразить все корни |
||||
|
пятой степени из 32 на комплексной плос- |
||||
|
кости, то окажется, что они расположены |
||||
|
в вершинах правильного пятиугольника. |
||||
|
В наших рассуждениях не играло ника- |
Рис. 29.3. |
|||
|
кой роли ни то, что мы извлекали корень |
||||
|
именно степени 5, ни то, что мы извлекали его из 32. На самом |
||||
|
деле для всякого |
комплексного числа a = 0 существует ровно |
|||
|
n |
6 |
|||
|
n решений уравнения z |
= a (эти решения называются корня- |
|||
|
ми степени n из a). При изображении на комплексной плоскости |
||||
|
корни степени n из a располагаются в вершинах правильного n- |
||||
|
угольника с центром в точке 0. |
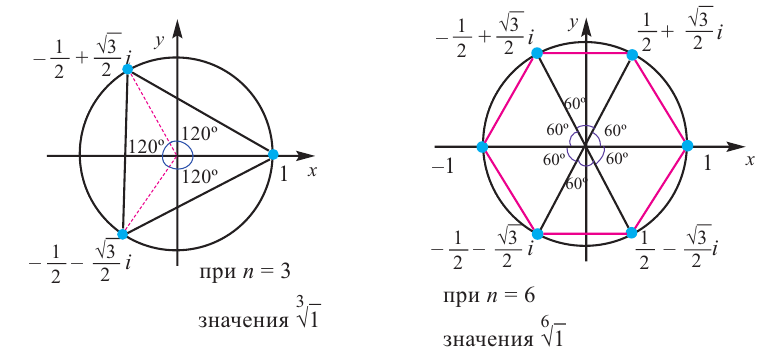
Задача 29.14. Найдите: а) все три кубических корня из i; б) все шесть корней степени 6 из 1 и изобразите их на комплексной плоскости.
Задача 29.15. а) Докажите, что произведение двух корней степени n из 1 — тоже корень степени n из 1.
б*) Пусть z1, z2, . . . , zn — все корни степени n из 1, k — целое число. Докажите, что
|
z1k + z2k + |
· · · |
+ znk = |
0, |
если k не делится на n; |
|
n, |
если k делится на n. |
|||
Мы добавили к обычным вещественным числам число i для того, чтобы можно было извлекать квадратные корни из отрицательных чисел; при этом оказалось, что в комплексных числах можно решить любое квадратное уравнение. Замечательно, что и вообще любое алгебраическое уравнение имеет корень в комплексных числах: никаких новых чисел помимо i ради этого вводить не надо. Этот важный факт, который по традиции называют основной теоремой алгебры, доказал в конце 18 века великий немецкий математик К. Ф. Гаусс.
177
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Комплексные числа
Краткая теория
Комплексным числом
называется
выражение вида
, где
и
– действительные
числа, а символ
удовлетворяет
условию
.
Число
называется
действительной частью комплексного
числа и обозначается
,
–
мнимой частью и обозначается
,
–
мнимой единицей.
Комплексные числа
и
называется
комплексно-сопряженными. Так, если
, то
.
Сложение, вычитание и умножение
комплексным чисел, заданных в алгебраической форме, выполняются по правилам
сложения, вычитания и умножения двучленов вида
с заменой
каждый раз
на
. Деление выполняется по формуле:
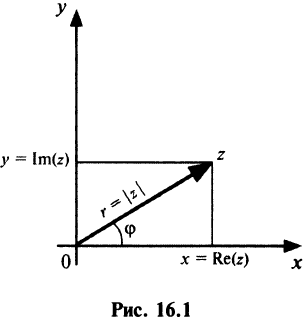
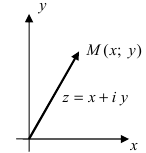
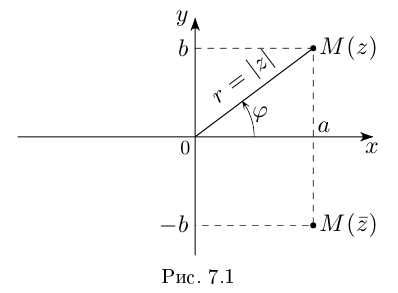
Геометрически комплексное число
изображается
точкой
на координатной
плоскости или радиус-вектором
этой точки.
Тригонометрическая форма комплексного числа
имеет вид:
где
– модуль числа
;
– его аргумент
– величина угла
между положительным направлением оси
и
радиусом-вектором
(см. рисунок),
причем величина угла считается положительной, если отсчет ведется против
часовой стрелки, и отрицательной – если по часовой стрелке.
Величина угла
определяется из
системы уравнений:
Значение
(или
) обозначается
и называется
главным.
Действия над комплексными числами в тригонометрической форме
Если
то
то есть при умножении комплексных
чисел, заданных в тригонометрической форме, их модули перемножаются, аргументы
складываются, а при делении модули делятся, а аргументы вычитаются.
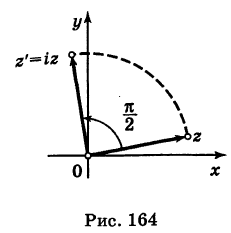
Геометрический умножение данного комплексного числа на другое комплексное
число, отличное от нуля, означает поворот радиус-вектора, изображающего данное
число, против часовой стрелки на угол, равный аргументу другого числа.
Аналогично деление означает поворот радиуса-вектора данного числа по часовой
стрелке на угол, равный аргументу другого числа, и деление этого вектора на
модуль другого числа.
При возведении в степень
используется формула Муавра
Все значения корня степени
из комплексного
числа
находятся по
формуле
Показательная форма комплексного числа
имеет вид
, где
– формула
Эйлера.
Действия над комплексными числами в показательной форме
Если
то
Если
то
Примеры решения задач
Задача 1
Даны комплексные числа
.
Вычислить
Решение
Последовательно вычисляем:
Окончательно получаем:
Ответ:
Задача 2
1) Записать число
в
алгебраической форме;
2) изобразить его на
координатной плоскости;
3) записать число
в
тригонометрической и показательной формах;
4) вычислить
;
5) найти все корни
уравнения
Решение
1) Запишем число
в
алгебраической форме:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
2) Изобразим число
на
координатной плоскости:
3) Запишем
число
в
тригонометрической и показательной формах
Модуль комплексного числа:
Вектор
лежит в 4-й четверти. Аргумент комплексного
числа:
Комплексное число в тригонометрической форме:
Комплексное число в показательной форме:
4) Возведем
комплексное число в заданную степень:
5) Найдем корни
уравнения
.
Получаем:
Тогда корни уравнения:
Задача 3
Даны три комплексных числа
,
и
:
1) выполните действия в
алгебраической, тригонометрической и показательной формах;
2) найдите расстояние
между точками
и
на
комплексной плоскости.
Решение
1) Запишем числа в тригонометрической форме:
Вектор
лежит в
2-й четверти
Число в показательной форме:
Число в тригонометрической форме:
Вектор
лежит в
4-й четверти
Число в показательной форме:
Число в тригонометрической форме:
Вектор
лежит в
3-й четверти
Число в показательной форме:
Число в тригонометрической форме:
Выполним действия в алгебраической форме:
Выполним действия в тригонометрической форме:
Выполним действия в
показательной форме:
2) Найдем расстояние между
точками
и
на
комплексной плоскости:
Содержание:
Хроника возникновения комплексных чисел:
Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b — натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 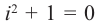
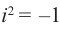
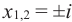
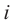
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 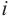
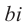
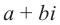
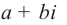
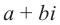
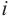
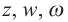
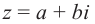
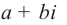
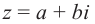
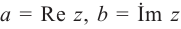
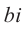
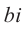
Следствие: для комплексных чисел а + 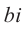
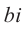
а + 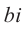
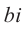
Пример. Из равенства 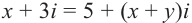
Решение: Из равенства действительных и мнимых частей получаем: х = 5
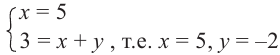
Суммой комплексных чисел 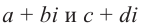
Действия над комплексными числами
Произведением комплексных чисел 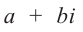
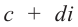
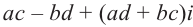
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 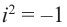
Пример №1
Рассмотрим частные случаи степеней мнимых единиц:
Как видно, натуральные степени мнимой единицы 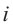
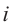
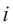
Пример №2
Вычислите: а) 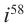
Решение: а) 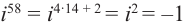
Число 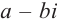
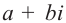
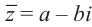
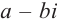
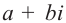
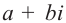
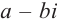
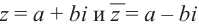
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 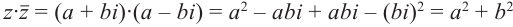
В частном случае, сопряжённым для действительного числа является само число, для мнимого — произведение числа и (-1).
Для каждого комплексного числа 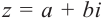
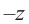
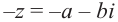
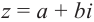
Вычитание и частное комплексных чисел определяется равенствами:
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 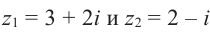
Решение:
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел 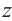
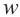
Квадратный корень комплексного числа
Число, квадрат которого равен 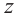
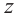
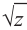
Пример №4
Найдём квадратный корень комплексного числа
Решение: Пусть 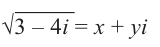
Из равенства действительных и мнимых частей имеем:
Отсюда получаем решение (2; -1) и (-2; 1). Значит,
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 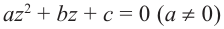
Пример №5
Решим уравнение 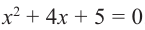
Решение:
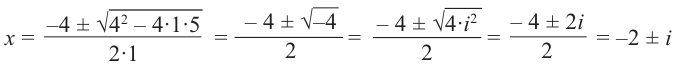
Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 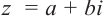
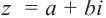
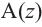
Пример:
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 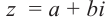
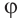
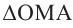
Отсюда:
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как: 
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом 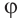
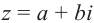
Из 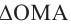
Модуль числа 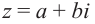
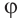
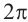
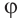
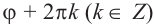
Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0; 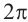
Пример №6
Найдём модуль и аргумент комплексного числа
Решение: Из того, что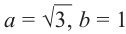
и принимая внимание, что угол 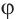
получим:
Из формул 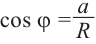
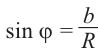
Тогда
Для комплексного числа 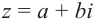
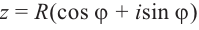
В частном случае для модуля и аргумента числа 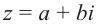
Пример №7
Запишем комплексное число
в тригонометрической форме.
Решение:
Так как угол 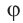
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 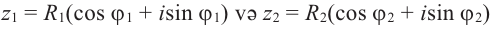
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
Теперь найдём отношение
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
Возвести число 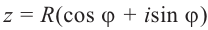
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
Формулу 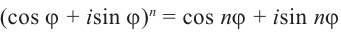
Отсюда
Из равенства двух комплексных чисел имеем:
Аналогичным образом можно написать формулы для 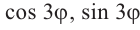
Корень n-ой степени комплексного числа
Найдём значение выражения 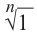
Запишем в виде 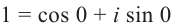
виде 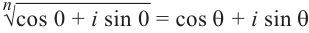
Возведём каждую из двух сторон в n-ую степень:
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 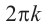
Это значит,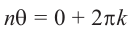
Таким образом,
Отсюда при 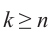
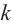

Обозначим корни 
Как видно, модули корней 
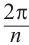

Корнем 
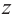
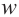
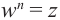
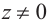


Запишем 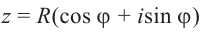
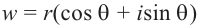
Для 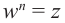
Из равенства двух комплексных чисел получим:
Значения при 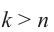

Поэтому, должно соблюдаться следующее:
Формула корни n-ой степени комплексного числа
Если 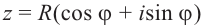
Пример №8
Найдём все значения
Решение: пусть 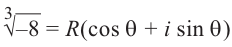
Отсюда
При
При
При
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида 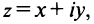
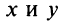
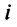
Число 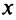
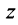
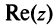
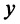
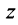
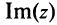
Действительное число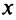
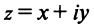
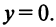
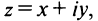
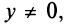
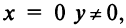
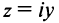
Числа 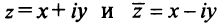
Два комплексных числа 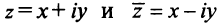
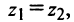
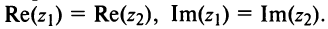
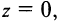
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
2. Умножение комплексных чисел
В частности,
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 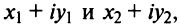
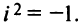
Пример №9
Даны комплексные числа
Найти
Решение:
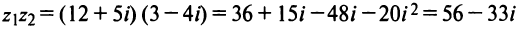
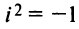
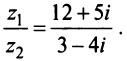
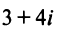
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости
Плоскость называется комплексной, если каждому комплексному числу 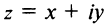
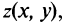
Оси 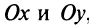
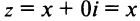
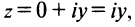
Тригонометрическая и показательная формы комплексного числа
С каждой точкой 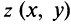
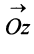
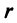
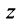
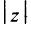
Угол 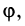
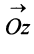
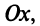
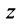
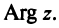
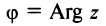
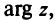
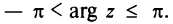
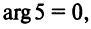
Очевидно (см. рис. 16.1), что
Следовательно, комплексное число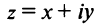
Представление комплексного числа в виде (16.6), где 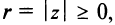
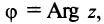
Сформулируем некоторые свойства арифметических операций над комплексными числами.
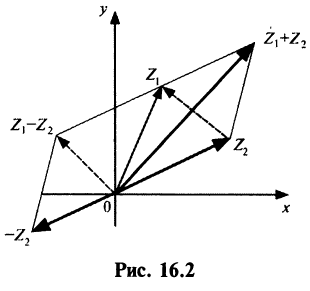
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел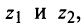
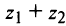
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
Геометрически умножение числа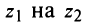
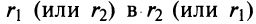
Пример №10
Комплексные числа 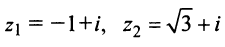
Решение:
По формуле (16.4) найдем модуль комплексного числа 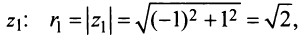
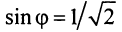
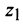
Аналогично 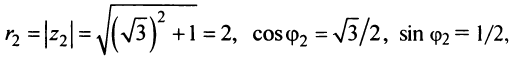
Теперь по формулам (16.7) и (16.8)
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 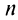
Пример №11
Найти
Решение:
По формуле Муавра (16.9)
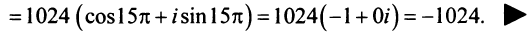
Пусть
Тогда, используя определение корня и формулу Муавра (16.9), получим
или
Отсюда следует, что
Итак,
где
При 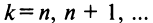
Таким образом, корень 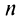
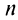
Пример №12
Найти
Решение:
В примере 16.2 было получено
откуда получаем три значения корня
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки 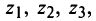
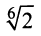
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
Отсюда следует показательная форма комплексного числа.
где
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 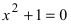
Определение: Выражение 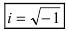
Определение: Комплексным числом называется выражение вида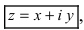
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 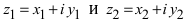
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 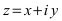
Пример №13
Записать комплексно-сопряженное число к комплексному числу
Решение:
Согласно определению комплексно-сопряженного числа получаем
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е.
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение
Решение:
Вычислим дискриминант уравнения 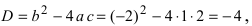
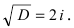
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
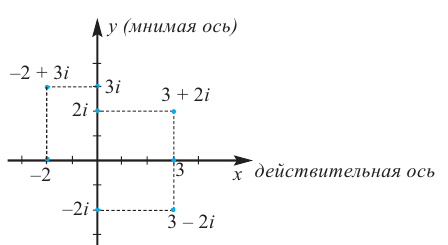
Комплексное число 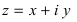
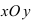
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3).
Решение:
Рис. 3. Изображение комплексного 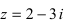
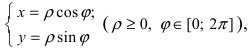
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: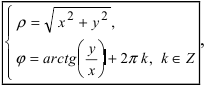
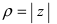
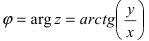
Замечание: Аргумент комплексного числа 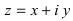
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 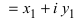
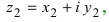
Пример №16
Найти сумму и разность чисел 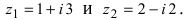
Решение:
Найдем сумму заданных комплексных чисел 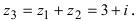
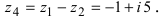
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что
2. Для того чтобы найти произведение двух комплексных чисел 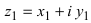
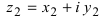
Замечание: Отметим, что
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 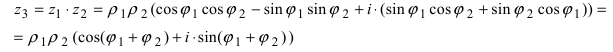
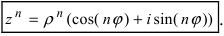
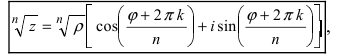
3. Деление комплексного числа 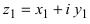
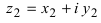
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 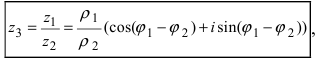
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например,
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 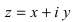
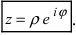
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
где х и у — действительные числа, a i — мнимая единица.
Числа вида 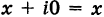
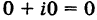
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
Под модулем комплексного числа z понимается неотрицательное число
Сопряженным числом 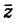
Таким образом,
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
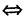
В частности, z = 0 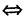
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) — Re z1 ± Re z2,
Im (z1 ± z2) — Imz1 ± 1mz2
III. z1z2 = (x1x2 — y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
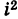
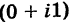
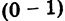
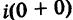
Заметим, что правило умножения III получается формально путем умножения двучленов 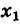
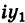
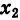
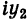
Очевидно также, что для 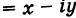
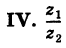
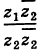
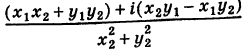
Легко проверить следующие свойства:
1)
- Заказать решение задач по высшей математике
Комплексная плоскость
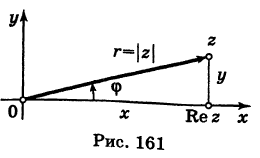
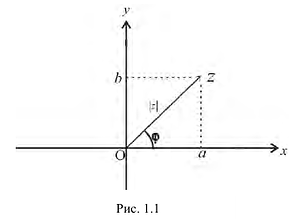
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
На оси Ох расположены действительные числа: z =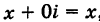
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
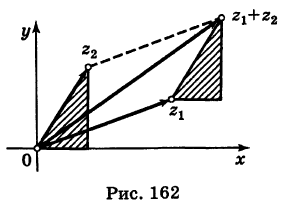
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 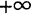
Для аргумента ср имеем (рис. 161)
где
Примеры: 1) arg 2 = 0; 2) arg (-1) = 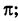
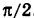
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
Таким образом, имеем тригонометрическую форму комплексного числа
где
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число 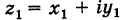
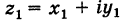
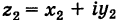
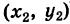
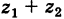
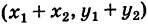
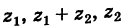
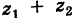
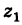
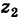
Следствие. Так как 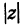
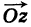
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 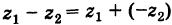

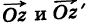
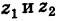
Следствие. Расстояние между двумя точками 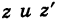
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
то имеем
Отсюда
и
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
(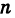
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
Пример №17
Построить точку 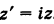
Решение:
Имеем
Следовательно, при умножении на i вектор 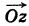
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
Так как
то на основании теоремы 1 имеем
Отсюда
Извлечение корня из комплексного числа
Пусть
где 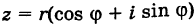
Отсюда получаем
Таким образом,
Заметим, что здесь под 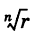
Здесь в качестве числа k достаточно брать лишь значения 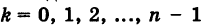
Из формулы (4) следует, что корень 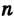
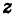
Пример №18
Найти
Решение:
Так как 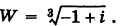
Отсюда
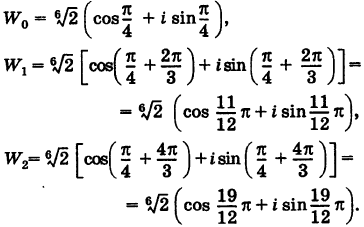
Точки 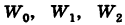
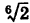
Понятие функции комплексной переменной
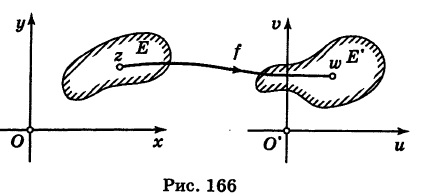
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z 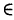
с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут
Множества Е и Е’ можно изображать на одной комплексной плоскости.
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
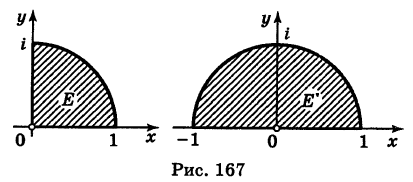
Пример:
Во что переходит сектор Е
(рис. 167, а) при отображении
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 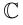
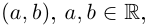
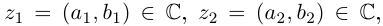
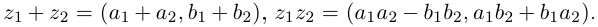
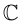
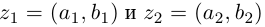
Операции сложения и умножения на множестве 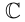
Лемма 7.1. Для любых комплексных чисел 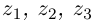
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 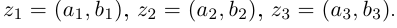
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
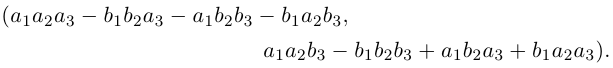
Определение 7.2. Комплексное число 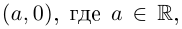
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар 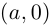
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой
Легко видеть, что 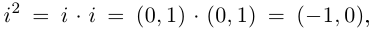
Далее, так как 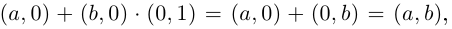
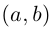
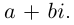
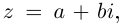
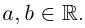
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что
Определение 7.4. Разностью двух комплексных чисел 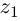
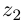
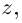
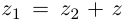
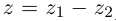
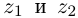
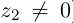
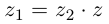
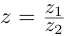
Проверим, что эти операции однозначно определены.
□ Пусть 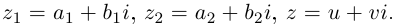
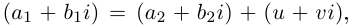
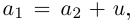
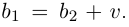
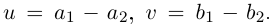
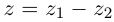
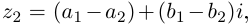
Для частного имеем: 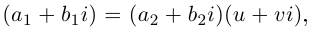
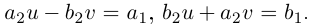
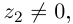
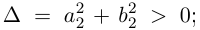
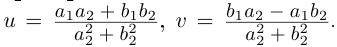
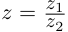
Такое деление можно осуществлять непосредственно:
Комплексное число 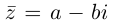
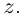
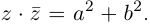
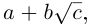
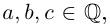

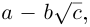
Определение 7.5. Пусть 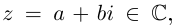
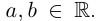
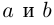
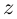
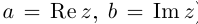
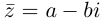
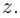
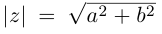
Лемма 7.2. Для любых комплексных чисел 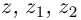
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел 
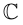
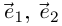
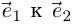
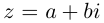
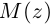
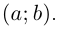
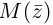
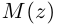
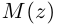
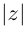
Аргументом числа 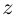
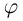
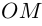
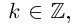
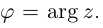
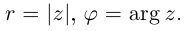
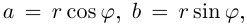
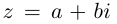
Пример:
Записать в тригонометрической форме числа
□ 1)
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 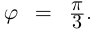
2) 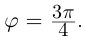
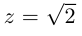
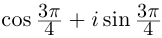
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 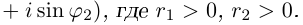
Если
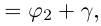
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 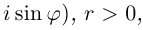
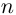
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для
□ Имеем: 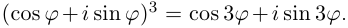
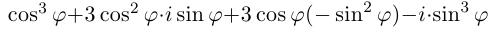
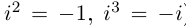
Определение 7.6. Пусть 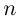
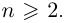
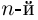
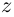
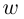
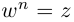
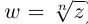
Лемма 7.4. Если 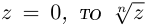
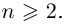
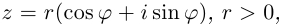
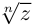
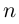
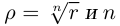
□ Правая часть леммы очевидна, так как 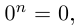
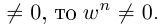
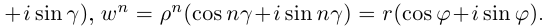
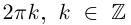
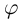
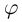
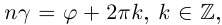
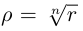
При замене 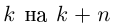
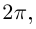
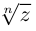
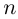
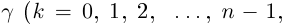
Замечание. 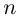
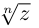
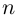
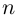
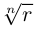
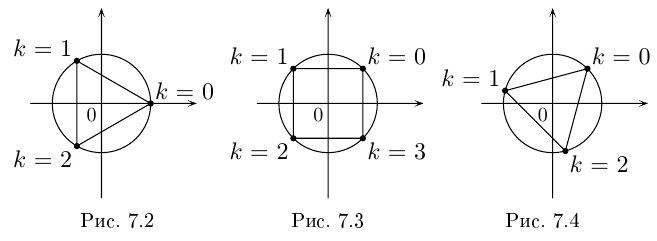
Пример №19
Найти все значения
□ 1) 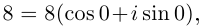
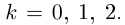
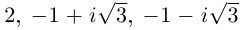
Первое из них — арифметическое значение кубического корня из положительного числа 8.
2) 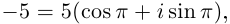
Получим 4 значения:
(см. рис. 7.3). 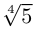
3) 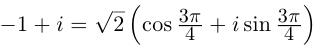
Получим 3 значения:
(см. рис. 7.4). ■
Определение 7.7. Пусть 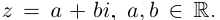
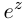
Если 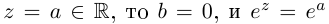
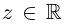
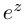
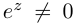
Лемма 7.5. Для любых 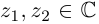
□ Пусть 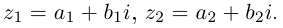
Далее, так как 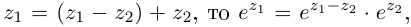
Пример №20
Вычислить
□ Имеем:
Так как при всех 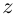
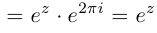
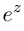
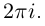
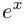
Определение 7.8. Логарифмом комплексного числа 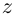
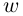
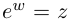
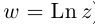
Лемма 7.6. Если 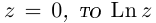
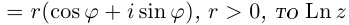
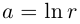
□ Первая часть леммы следует из того, что 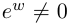
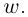
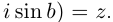
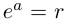
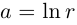
Таким образом, множество значений функции 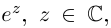
Пример №21
Найти все значения 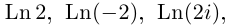
Определение 7.9. Для любых 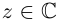
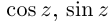
Если
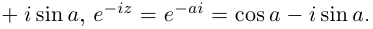
Аналогично,
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 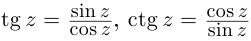
Так как
Легко видеть, что 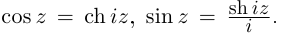
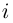
Комплекснозначные функции действительной переменной
Рассмотрим функцию 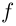
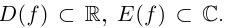
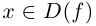
Так как 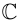
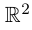
Определение 7.10. Комплекснозначная функция действительной переменной 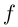
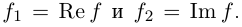
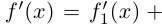
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной 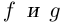
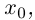
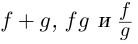
в точке 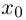
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 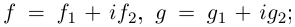
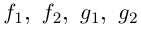
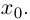
Функция 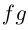
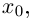
Легко видеть, что это выражение совпадает с
Пример №22
Доказать, что при любом 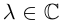
т.е. привычная для действительных 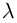
□ Пусть
Тогда
С другой стороны,
что совпадает с
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной
где 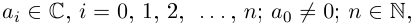
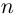
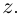
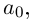
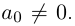
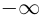
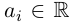
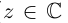
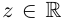
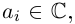
Если 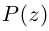
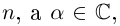
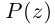
где
Теорема 7.1 (Безу). Остаток от деления многочлена 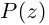
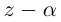
□ Из (7.1) имеем при
Следствие. Многочлен 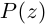

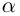
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число 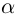
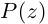
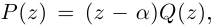
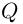
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени 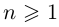
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
раскладывается в произведение линейных множителей
где 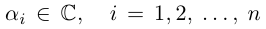
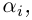
□ По основной теореме алгебры 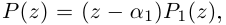
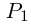
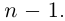
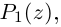
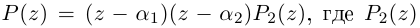
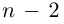
где 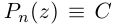
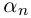
Если раскрыть скобки в правой части (7.2), то коэффициент при 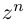
Определение 7.11. Комплексное число 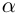
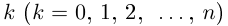
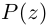
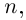
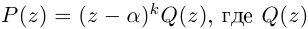
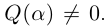
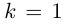
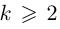
Если 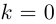
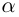
В общем случае, учитывая кратность корней, многочлен 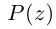
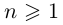
где все комплексные числа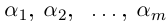
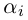
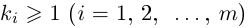
Лемма 7.8. Пусть 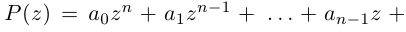
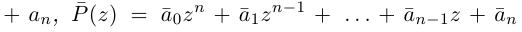
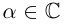
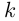
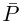
□ Так как 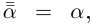
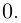
Так как 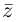
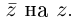
Это и означает, что 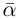
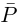
Следствие. Если 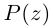
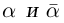
□ Это очевидно из леммы 7.8, так как 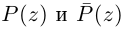
Теорема 7.4. Многочлен степени 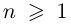
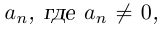
□ По теореме 7.3 и лемме 7.8
где 
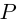


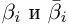

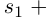
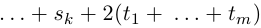
Пусть 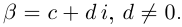
Получили квадратный трёхчлен с действительными коэффициентами 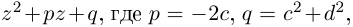
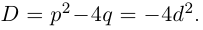
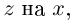
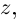
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
Корни 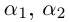
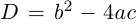
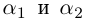
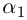
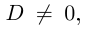
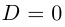
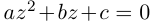
Если 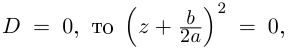
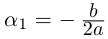
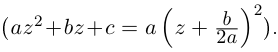
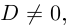
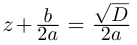
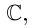
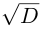
Пример №23
Решить уравнение
□ 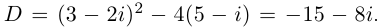
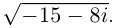
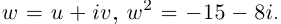
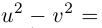
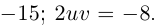
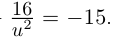
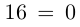
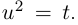
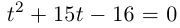
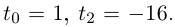
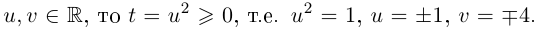
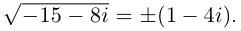
Пример №24
Найти все значения 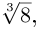
□ Левая часть раскладывается на множители:
Поэтому один из корней равен 2. Квадратный трёхчлен 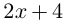
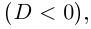
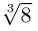
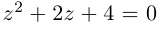
Во множестве комплексных чисел 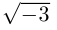
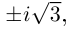
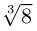
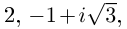
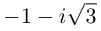
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 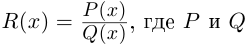
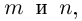
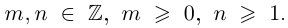
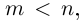
Лемма 7.9. Если 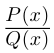
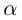
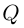
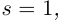
где 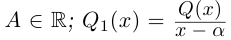
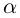
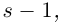
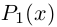
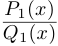
□ Так как 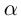
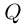
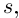
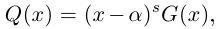
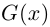
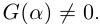
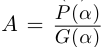
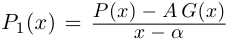
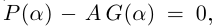
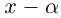
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень 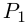
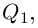
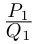
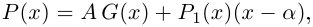
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть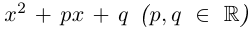
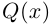
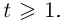
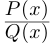
где 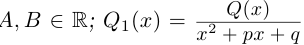
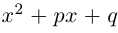
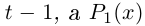
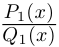
□ Пусть 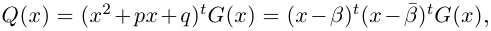
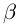
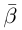
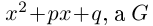
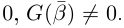
Такие числа А и В определены единственным образом, так как если 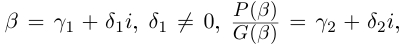
и числа А, В находятся из системы 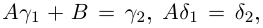
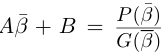
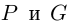
Рассмотрим многочлен 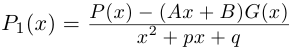
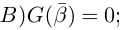
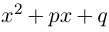
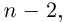
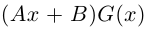
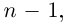
Значит, степень 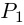
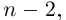
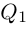
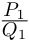
откуда
Последовательно выделяя из многочлена 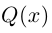
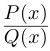
(здесь
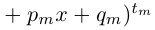
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом 
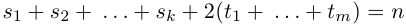
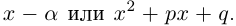
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
а) 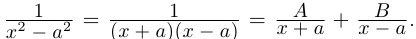
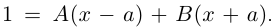
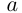
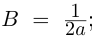
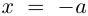
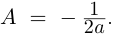
б)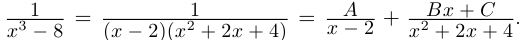
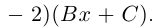
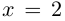
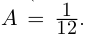
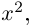
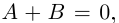
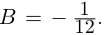
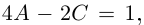
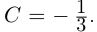
в)
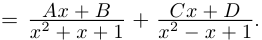
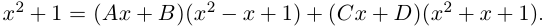
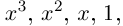
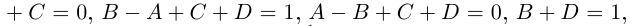
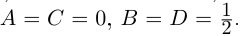
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
где
х – переменная.
Корнем многочлена (1.1) называется любое число 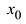
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например:
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 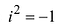
Тогда ±i – два корня уравнения
Определение 1.2. Множеством комплексных чисел называется множество
Суммой двух комплексных чисел 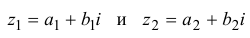
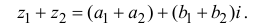
Произведением двух комплексных чисел 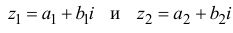
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения:
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти
Решение:
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
Решение:
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 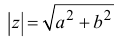
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
При этом 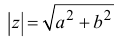
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 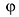
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 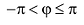
главным и обозначается argz.
Замечание.
При этом
Если 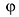
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть
Доказательство
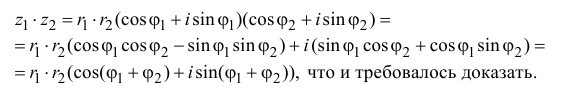
Из формул (1.5) следует, в частности, что 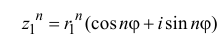
Пример №28
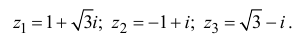
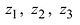
Решение:
поэтому по формуле (1.3)
Тогда по формуле (1.4)
поэтому по формуле (1.3)
Тогда
Из формул (1.5), (1.6) видно, что аргумент 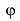
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 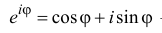
Тогда из теоремы 1.2 следует, что
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 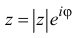
Пример №29
Вычислить
Решение:
Согласно примеру 1.3
Поэтому
Определение 1.5. Корнем n-й степени из числа z 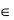
число 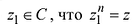
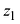
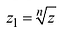
Из формулы (1.8) видно что 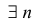
если 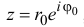
Пример №30
Найти
Решение:
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
Комплексные числа в тригонометрической
и показательной формах
Тригонометрическая форма комплексного числа
Каждому комплексному числу геометрически соответствует точка
на плоскости
. Но положение точки на плоскости, кроме декартовых координат
, можно зафиксировать другой парой — ее полярных координат
в полярной системе (рис. 1.3,a).
Величина является неотрицательной и для данной точки определяется единственным образом, а угол
может принимать бесчисленное множество значений (при этом
): если точке соответствует некоторое значение
, то ей также соответствуют значения
. Например, если для точки
(см. рис. 1.1) выбрать
, то ей соответствует любое
, в частности
при
. Если же выбрать
, то
, а при
получаем
.
Используя связь декартовых и полярных координат точки (рис. 1.3,б), из алгебраической формы записи комплексного числа
получаем тригонометрическую форму:
(1.3)
Показательная форма комплексного числа
Если обозначить комплексное число , у которого
, а
, через
, то есть
, то из (1.3) получим показательную форму записи комплексного числа:
(1.4)
Равенство называется формулой Эйлера.
Заметим, что геометрически задание комплексного числа равносильно заданию вектора
, длина которого равна
, то есть
, а направление — под углом
к оси
(рис. 1.3,б).
Модуль комплексного числа
Число — длина радиуса-вектора точки
называется модулем комплексного числа
. Обозначение:
.
Из рис. 1.3,б получаем формулу для нахождения модуля числа, заданного и алгебраической форме
(1.5)
Очевидно, что и
только для числа
.
С помощью правила вычитания запишем модуль числа , где
и
А это, как известно, есть формула для расстояния между точками и
.
Таким образом, число есть расстояние между точками
и
на комплексной плоскости.
Пример 1.13. Найти модули комплексных чисел:
Решение
Аргумент комплексного числа
Полярный угол точки
называется аргументом комплексного числа
. Обозначение:
.
В дальнейшем, если нет специальных оговорок, под будем понимать значение
, удовлетворяющее условию
. Так, для точки
(см. рис. 1.1)
.
Формулу для нахождения аргумента комплексного числа , заданного в алгебраической форме, получаем, используя связь декартовых и полярных координат точки
(см. рис. 1.3,б). Для точек, не лежащих на мнимой оси, т.е. для
, у которых
, получаем
; для точек мнимой положительной полуоси, т.е. для
, у которых
, имеем
; для точек мнимой отрицательной полуоси, т.е. для
, у которых
, соответственно
.
Аргумент числа — величина неопределенная.
Нахождение аргумента при сводится к решению тригонометрического уравнения
. При
, т.е. когда
— число действительное, имеем
при
и
при
. При
решение уравнения зависит от четверти плоскости
. Четверть, в которое расположена точка
, определяется по знакам
и
. В результате получаем:
(1.6)
При решении примеров удобно пользоваться схемой, которая изображена на рис. 1.5.
Пример 1.14. Найти аргументы чисел из примера 1.13.
Решение
Пример 1.15. Найти модуль и аргумент числа .
Решение. Находим . Так как
, т.е. точка расположена в четвертой четверти, то из равенства
получаем
(рис. 1.5).
Главное значение аргумента комплексного числа
Аргумент комплексного числа определяется неоднозначно. Это следует из неоднозначности задания величины угла для данной точки, а также из тригонометрической формы записи комплексного числа и свойства периодичности функций
и
.
Всякий угол, отличающийся от на слагаемое, кратное
, обозначается
и записывается равенством:
(1.7)
где — главное значение аргумента,
.
Пример 1.16. Записать и
для чисел
.
Решение. Числа и
— действительные, расположены на действительной оси (рис. 1.6), поэтому
числа и
— чисто мнимые, расположены на мнимой оси (рис. 1.6), поэтому
Пример 1.17. Записать комплексные числа из примера 1.16:
а) в тригонометрической форме;
б) в показательной форме.
Решение
Модули всех чисел, очевидно, равны 1. Поэтому, используя решение предыдущего примера и формулы (1.3) и (1.4), получаем:
а)
б) .
Пример 1.18. Записать в тригонометрической форме числа .
Решение
Числа и
записаны в алгебраической форме (заметим, что заданная запись числа
не является тригонометрической формой записи (сравните с (1.3)). Находим модули чисел по формуле (1.5):
Далее находим аргументы. Для числа имеем
и, так как
(точка расположена в третьей четверти), получаем
(см. рис. 1.5). Для числа
имеем
, или
, и, так как
(точка расположена в четвертой четверти (см. рис. 1.5)), получаем
.
Записываем числа и
в тригонометрической форме
Заметим, что для числа решение можно найти иначе, а именно используя свойства тригонометрических функций:
.
Число является произведением двух чисел. Выполнив умножение, получим алгебраическую форму записи (найдем
и
):
. Здесь, как и для числа
, при решении удобно использовать преобразования тригонометрических выражений, а именно
.
Рассуждая, как выше, найдем . Для числа
, записанного в алгебраической форме, получаем тригонометрическую форму:
Равенство комплексных чисел в тригонометрической форме
Условия равенства комплексных чисел получаем, используя геометрический смысл модуля и аргумента комплексного числа, заданного в тригонометрической форме. Так, для чисел
из условия
. очевидно, следует:
или
(1.8)
Аргументы равных комплексных чисел либо равны (в частности равны главные значения), либо отличаются на слагаемое, кратное .
Для пары сопряженных комплексных чисел и
справедливы следующие равенства:
(1.9)
Умножение комплексных чисел в тригонометрической форме
Зададим два комплексных числа в тригонометрической форме и
и перемножим их по правилу умножения двучленов:
или
Получили новое число , записанное в тригонометрической форме:
, для которого
.
Правило умножения. При умножении комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
(1.10)
В результате умножения чисел может получиться аргумент произведения, не являющийся главным значением.
Пример 1.19. Найти модули и аргументы чисел:
Решение
Каждое из заданных чисел записано в виде произведения. Найдем модули и аргументы сомножителей и воспользуемся правилом (1.10) умножения чисел, заданных в тригонометрической форме:
Для чисел и
находим модули и аргументы:
. Используя формулы (1.10), получаем
б) . Для числа
имеем:
; для числа
, и так как
(точка расположена в четвертой четверти), то
. Используя формулы (1.10), получаем
.
Заметим, что для решения этой задачи можно раскрыть скобки, записать каждое число в алгебраической форме, а затем найти и
, используя формулы (1.5), (1.6).
Деление комплексных чисел в тригонометрической форме
Рассмотрим частное комплексных чисел , заданных в тригонометрической форме. Из определения частного
имеем
и, применяя к произведению правило умножения (формулы (1.10)), получаем
.
Правило деления. Модуль частного, полученного в результате деления чисел, заданных в тригонометрической форме, равен частному от деления модуля числителя на модуль знаменателя, а аргумент частного равен разности аргументов делимого и делителя:
(1.11)
В результате деления чисел по формуле (1.11) может получиться аргумент честного, не являющийся главным значением.
Пример 1.20. Записать в тригонометрической форме комплексное число .
Решение. Обозначим . Для чисел
и
находим модули и аргументы:
(см. пример 1.19). По формуле (1.11) получаем
и
Возведение в степень комплексного числа в тригонометрической форме
Из определения степени и правила умножения чисел, записанных в тригонометрической форме (формула (1.10)), получаем
, где
.
Правило возведения в степень. При возведении в степень комплексного числа в эту степень возводится модуль числа, а аргумент умножается на показатель степени:
(1.12)
Записывая число в тригонометрической форме
, получаем формулу возведения в степень:
(1.13)
При это равенство принимает вид и называется формула Муавра
(1.14)
Пример 1.21. Найти модуль и аргумент комплексного числа .
Решение. Обозначим . Находим модуль и аргумент числа
. Поэтому
и
. Так как по определению для главного значения аргумента выполняется условие
, то
.
Пример 1.22. Записать в тригонометрической форме число .
Решение
Пример 1.23. Используя формулу Муавра, найти выражения для и
через тригонометрические функции угла
.
Решение
Из формулы (1.14) при имеем
. Возведем левую часть в степень, учитывая, что
(см. пример 1.8):
Используя условие равенства комплексных чисел, получаем:
Извлечение корня из комплексного числа в тригонометрической форме
Рассмотрим задачу извлечения корня из комплексного числа, заданного в показательной или тригонометрической форме , или
. Искомое число
также запишем в показательной форме:
. Используя определение операции извлечения корня
и условия (1.8), получаем соотношения
или
(1.15)
Правило извлечения корня. Чтобы извлечь корень из комплексного числа, нужно извлечь корень (арифметический) той же степени из модуля данного числа, а аргумент разделить на показатель корня:
(1.16)
Теперь можно записать число в показательной форме:
Если записать это соотношение в тригонометрической форме, то, учитывая периодичность тригонометрических функций, нетрудно убедиться, что выражение принимает только
различных значений. Для их записи достаточно в формуле (1.15) взять
последовательных значений
, например
. В результате получаем формулу извлечения корня из комплексного числа в тригонометрической форме, где
:
(1.17)
Замечания 1.1
1. Рассмотренная задача извлечения корня степени из комплексного числа равносильна решению уравнения вида
, где, очевидно,
.
Для решения уравнения нужно найти значений
, а для этого необходимо найти
и использовать формулу извлечения корня.
2. Исследование формулы (1.17) показывает, что все комплексные числа (значения
) имеют равные модули, т.е. геометрически расположены на окружности радиуса
. Аргументы двух последовательных чисел отличаются на
, так как
, т.е. каждое последующее значение
может быть получено из предыдущего
поворотом радиуса-вектора точки
на
.В этом заключается геометрический смысл формулы (1.17), что можно сформулировать следующим образом.
Точки, соответствующие значениям , расположены в вершинах правильного n-угольника, вписанного в окружность с центром в начале координат, радиус которой
, причем аргумент одного из значений
равен
(рис. 1.7).
Алгоритм решения комплексных уравнений вида z^n-a=0
1. Найти модуль и аргумент числа .
2. Записать формулу (1.17) при заданном значении .
3. Выписать значения корней уравнения , придавая значения
.
Пример 1.24. Решить уравнения: a) ; б)
.
Решение
Задача равносильна задаче нахождения всех значений корня из комплексного числа. Решаем в каждом случае по алгоритму.
а) Найдем .
1. Определим модуль и аргумент числа .
2. При полученных значениях и
записываем формулу (1.17):
Заметим, что справа стоит — арифметический корень, его единственное значение равно 1.
3. Придавая последовательно значения от 0 до 5, выписываем решения уравнения:
Геометрически соответствующие точки расположены в вершинах правильного шестиугольника, вписанного в окружность радиуса , одна из точек (соответствует
)
. Строим шестиугольник (рис. 1.8,в). Отметим свойства корней этого уравнения с действительными коэффициентами — его комплексные корни являются попарно сопряженными:
и
— действительные числа.
б) Найдем .
1. Определим модуль и аргумент числа .
2. По формуле (1.17) имеем
3. Выписываем корни .
Для геометрического представления решения уравнения достаточно изобразить одно значение, например (при
) — это точка окружности
, лежащая на луче
. После этого строим правильный треугольник, вписанный в окружность
(рис. 1.8,б).
Пример 1.25. Найти корень уравнения , для которого
.
Решение
Задача равносильна задаче нахождения при условие
.
1. Находим модуль и аргумент числа .
2. По формуле (1.17) имеем: .
3. Для нахождения искомого решения нет необходимости выписывать все значения корня. Нужно выбрать значение , при котором выполняется условие
(соответствующая точка — точка второй четверти). Удобно при этом использовать чертеж (рис. 1.9).
Условию поставленной задачи удовлетворяет корень (при
):
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.