Как найти модуль обыкновенной дроби - Исправление недочетов и поиск решений вместе с Examum.ru

Введем понятие абсолютное величины или модуля дроби. Эти понятия нужны для вычисления действий дробей.

Модуль положительной дроби.

Понятие модуля числа или что такое модуль числа можно посмотреть нажав на ссылку.

Определение:
Модулем положительной дроби – это сама дробь.

Например:
Модуль дроби (frac{1}{2}) будет равна дроби (frac{1}{2}), то есть той же самой дроби.

(Bigl|frac{1}{2} Bigl| =frac{1}{2})

Модуль отрицательной дроби.

Определение:
Модулем отрицательной дроби является противоположная ей дробь или положительная ей дробь.

Рассмотрим пример:
Модуль дроби (-frac{2}{3}) будет равна дроби с противоположным знаком, то есть с плюсом (frac{2}{3}).

(Bigl|-frac{2}{3} Bigl| =frac{2}{3})

Определение:
Модуль нуля равен нулю.
|0|=0

Определение:
У противоположных чисел модули равны.

Рассмотрим пример:
Модуль дроби (frac{4}{7}) равен (frac{4}{7}) и модуль противоположной дроби (-frac{4}{7}) равен (frac{4}{7}).

(Bigl|-frac{4}{7} Bigl| = Bigl|frac{4}{7} Bigl| =frac{4}{7})

Вопросы по теме:
Назовите модуль положительного числа?
Ответ: то же положительное число.

Назовите модуль отрицательного числа?
Ответ: противоположное число отрицательному числу.

Назовите модуль 0?
Ответ:0

Пример №1:
Решите модули дробей: а) (frac{4}{5}) б) (-frac{2}{7}) в) (frac{-0}{3}) г) (frac{3}{-8}) е) 0 ж) (frac{0}{-2})

Решение:
а) (Bigl|frac{4}{5} Bigl| =frac{4}{5})
б) (Bigl|- frac{2}{7} Bigl| =frac{2}{7})
в) (Bigl|frac{-0}{3} Bigl| =frac{0}{3}=0)
г) (Bigl|frac{3}{-8} Bigl| =frac{3}{8})
е) |0|=0
ж) (Bigl|frac{0}{-2} Bigl| =frac{0}{2}=0)

Пример №2:
Сравните модули дробей: а) (Bigl|-frac{1}{3} Bigl|) и (Bigl|frac{1}{3} Bigl|) б) (Bigl|-frac{9}{2} Bigl|) и (Bigl|-frac{6}{11} Bigl|)

Решение:
а) Чтобы сравнить модули дробей нужно их посчитать:

(Bigl|-frac{1}{3} Bigl| = frac{1}{3}) и (Bigl|frac{1}{3} Bigl| = frac{1}{3})

Видно, что дроби одинаковы, поэтому ставим знак равно.

(Bigl|-frac{1}{3} Bigl| = Bigl|frac{1}{3} Bigl|)

б)Раскроем модули дробей.

(Bigl|-frac{9}{2} Bigl| = frac{9}{2}) и (Bigl|-frac{6}{11} Bigl| = frac{6}{11})

Получили две дроби (frac{9}{2}) и (frac{6}{11}). Дробь (frac{9}{2}) неправильная, поэтому эта дробь больше 1. А дробь правильная, поэтому меньше 1. Получаем: (frac{9}{2}>frac{6}{11})

(Bigl|-frac{9}{2} Bigl| > Bigl|-frac{6}{11} Bigl|)

Источник

Напомним, что два числа, равные по модулю, но противоположные по
знаку, называются противоположными.

Натуральные числа, противоположные им числа и число 0 составляют
вместе множество целых чисел. Множество целых чисел обозначается .

Число вида , где , называется обыкновенной дробью. Число называется числителем дроби, число — знаменателем.

Дробь называется правильной, если её числитель меньше
знаменателя , и неправильной, если её числитель больше знаменателя или
равен ему .

Основное свойство дроби: если
числитель и знаменатель дроби умножить или разделить на одно и то же число, не
равное нулю, то получится дробь, равная данной.

Число вида , где , , называется рациональным. Множество рациональных чисел
обозначается .

А теперь вспомним правила выполнения арифметических действий над
рациональными числами:

1. Сложение рациональных чисел:

2. Вычитание рациональных чисел:

3. Умножение рациональных чисел:

4. Частное двух рациональных чисел:.

Десятичные дроби — это такие
обыкновенные дроби, у которых знаменатель — единица с нулями, то есть 10; 100;
1000 и так далее.

Десятичные дроби записывают без знаменателей. Сначала пишут целую
часть числа, справа от неё ставят запятую; первая цифра после запятой означает
число десятых (то есть десятых долей единицы), вторая — сотых, третья —
тысячных и так далее.

Цифры, стоящие после запятой, называются десятичными знаками.

Бесконечной называется десятичная
дробь, у которой после запятой бесконечно много цифр.

Каждое рациональное число может быть представлено в виде конечной или бесконечной десятичной
дроби. Это достигается делением числителя на знаменатель.

Обыкновенная несократимая дробь может быть записана конечной десятичной дробью тогда и только
тогда, когда её знаменатель не содержит никаких других простых множителей, кроме
2 или 5.

Бесконечную десятичную дробь называют периодической, если у
неё, начиная с некоторого места, одна цифра или группа цифр повторяется,
непосредственно следуя одна за другой. Повторяющуюся цифру или группу цифр
называют периодом и записывают в скобках.

Например, .

Если период начинается сразу после запятой, то дробь называют чисто
периодической; если же между запятой и периодом есть другие десятичные
знаки, то дробь называют смешанной периодической.

Правила обращения периодической дроби в обыкновенную:

1. Для обращения чистой периодической дроби в обыкновенную в
числителе оставляют период десятичной дроби, а в знаменателе — число, состоящее
из девяток, взятых столько раз, сколько знаков в периоде десятичной дроби.

Например:

2. Для обращения смешанной периодической десятичной дроби в
обыкновенную в числителе берут число, стоящее в десятичной дроби до второго
повторения периода, минус число, стоящее в десятичной дроби до периода; в
знаменателе нужно написать столько девяток, сколько цифр в периоде, и приписать
к ним столько нулей, сколько цифр в исходной десятичной дроби от запятой до
периода.

Например:

Бесконечная десятичная непериодическая дробь называется иррациональным
числом.

Рациональные и иррациональные числа образуют множество
действительных чисел. Множество действительных чисел обозначают заглавной
латинской буквой .

Модулем (абсолютной величиной)
действительного числа называют само это число , если , и противоположное число , если .

Геометрически модуль числа означает расстояние на координатной
прямой от точки до точки .

Модуль действительного числа обладает свойствами.

При имеем:

1. тогда и только тогда, когда или ;

2. тогда и только тогда, когда ;

3. тогда и только тогда, когда или .

Основные моменты мы с вами повторили, а теперь давайте перейдём к
практической части занятия.

Задание первое. Найдите значение
выражения .

Решение.

Задание второе. Расположите в порядке
возрастания числа:

; ; ; ; .

Решение.

Задание третье. Найдите целые числа и такие, что .

Решение.

Задание четвёртое. При каких
натуральных значениях дробь является целым числом?

Решение.

Задание пятое. Укажите наибольшее
целок , при котором дробь является целым числом.

Решение.

Источник

Дроби, модуль числа, рациональные числа
- - - Урок 2. Подготовка к ЕГЭ по математике
  - Конспект урока «Дроби, модуль числа, рациональные числа»
  - Получите полный комплект видеоуроков, тестов и презентаций
    Подготовка к ЕГЭ по математике
Модуль fractions, рациональные числа в Python.
- - - Создание рациональных чисел.
  - Математические операции над рациональными числами.
Fraction в Python
- Python3
- Python3
- Python
- Python3
- Python
- Python3
Модуль дробей в Python — PythonForBeginners.
- Как использовать модуль дробей в Python?
- Как округлять дроби?
- Получение числителя и знаменателя из дроби
- Арифметические операции над дробями
- Получить приблизительное рациональное значение из числа с плавающей запятой, используя модуль дробей
- Заключение

Дроби, модуль числа, рациональные числа

Урок 2. Подготовка к ЕГЭ по математике

В данном видеоуроке мы напомним, какие числа называют целыми, рациональными и действительными. Повторим правила выполнения арифметических действий над рациональными числами. Вспомним правило обращения периодической дроби в обыкновенную. Напомним, что называют модулем действительного числа, а также основные свойства модуля.

Конспект урока «Дроби, модуль числа, рациональные числа»

Напомним, что два числа, равные по модулю, но противоположные по
знаку, называются противоположными.

Число вида , где , , называется рациональным. Множество рациональных чисел
обозначается .

А теперь вспомним правила выполнения арифметических действий над
рациональными числами:

1. Сложение рациональных чисел:

2. Вычитание рациональных чисел:

3. Умножение рациональных чисел:

4. Частное двух рациональных чисел:.

Цифры, стоящие после запятой, называются десятичными знаками.

Бесконечной называется десятичная
дробь, у которой после запятой бесконечно много цифр.

Например, .

Если период начинается сразу после запятой, то дробь называют

чисто
периодической; если же между запятой и периодом есть другие десятичные
знаки, то дробь называют смешанной периодической.

Правила обращения периодической дроби в обыкновенную:

Например:

Бесконечная десятичная непериодическая дробь называется иррациональным
числом.

Геометрически модуль числа означает расстояние на координатной
прямой от точки до точки .

Модуль действительного числа обладает свойствами.

При имеем:

1. тогда и только тогда, когда или ;

2. тогда и только тогда, когда ;

3. тогда и только тогда, когда или .

Основные моменты мы с вами повторили, а теперь давайте перейдём к
практической части занятия.

Задание первое. Найдите значение
выражения .

Решение.

Задание второе. Расположите в порядке
возрастания числа:

; ; ; ; .

Решение.

Задание третье. Найдите целые числа и такие, что .

Решение.

Задание четвёртое. При каких
натуральных значениях дробь является целым числом?

Решение.

Задание пятое. Укажите наибольшее
целок , при котором дробь является целым числом.

Решение.

Предыдущий урок 1
Числа и их свойства

Следующий урок 3
Прогрессии

Получите полный комплект видеоуроков, тестов и презентаций
Подготовка к ЕГЭ по математике

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Модуль fractions, рациональные числа в Python.

Модуль fractions обеспечивает поддержку арифметики рациональных чисел.

Создание рациональных чисел.

Экземпляр fractions.Fraction() может быть создан из пары целых чисел, другого рационального числа или строки.

Самый простой способ создать дробь это указать числитель numerator и знаменатель denominator. По умолчанию numerator=0, denominator=1:

>>> from fractions import Fraction
>>> Fraction()
# Fraction(0, 1)
>>> Fraction(numerator=1, denominator=2)
# Fraction(1, 2)
>>> Fraction(1, 2)
# Fraction(1, 2)
# Если числитель и знаменатель имеют общий 
# делитель, то числа они будут сокращены:
>>> Fraction(2, 4)
# Fraction(1, 2)
>>> Fraction(3, 6)
# Fraction(1, 2)

В качестве числителя и/или знаменателя могут быть указаны другие экземпляры Fraction():

>>> from fractions import Fraction
>>> Fraction(10, Fraction(1, 2))
# Fraction(20, 1)
>>> Fraction(Fraction(1, 2), 3)
# Fraction(1, 6)
>>> Fraction(Fraction(1, 2), Fraction(1, 4))
# Fraction(2, 1)

Целое число и вещественное число, так же можно преобразовать в дробь:

>>> from fractions import Fraction
>>> Fraction(5)
# Fraction(5, 1)
>>> Fraction(1. 5)
# Fraction(3, 2)

Создание рационального числа из десятичного числа:

>>> from fractions import Fraction
>>> from decimal import Decimal
>>> Fraction(Decimal('1.5'))
# Fraction(3, 2)
>>> Fraction(Decimal('3'))
# Fraction(3, 1)

Создание дроби из строки:

>>> from fractions import Fraction
>>> Fraction('1.2')
# Fraction(6, 5)
>>> Fraction('1.2e+5')
# Fraction(120000, 1)
>>> Fraction('-7/12')
# Fraction(-7, 12)
>>> Fraction('-0.12')
# Fraction(-3, 25)
>>> Fraction('-.12')
# Fraction(-3, 25)
>>> Fraction('  3/4  ')
# Fraction(3, 4)
>>> Fraction('  3.4  ')
# Fraction(17, 5)

Дроби могут быть приведены к основным типам языка Python.

>>> from fractions import Fraction
>>> x = Fraction('3/4')
>>> y = Fraction(1.5)
>>> int(y)
1
>>> float(y)
1.5
>>> str(y)
'3/2'
>>> str(x)
'3/4'

Математические операции над рациональными числами.

Рациональные числа поддерживают Все арифметические операции, однако невозможно выполнить действие над типами

Fraction() и Decimal() в одном математическом выражении:

>>> from fractions import Fraction
>>> x = Fraction('3/4')
>>> y = Fraction(1.5)
>>> x + y
# Fraction(9, 4)
>>> x - y
# Fraction(-3, 4)
>>> x * y
# Fraction(9, 8)
>>> x / y + 5
# Fraction(11, 2)
>>> x / y * 2.5
# 1.25
>>> x ** y
# 0.649519052838329
>>> from decimal import Decimal
>>> z = Decimal('1.5')
>>> z + x
# Traceback (most recent call last):
#   File "<stdin>", line 1, in <module>
# TypeError: unsupported operand type(s) for +: 'decimal.Decimal' and 'Fraction'

Дроби могут работать с некоторыми функциями модуля math, т. к. могут быть преобразованы к float:

>>> from fractions import Fraction
>>> from math import *
>>> x = Fraction('3/4')
>>> y = Fraction(1.
 5)
>>> modf(x)
# (0.75, 0.0)
>>> fabs(x)
# 0.75
>>> sqrt(x)
# 0.8660254037844386
>>> exp(y)
# 4.4816890703380645

Модуль

Fraction в Python

Сохранить статью

Уровень сложности:
Easy
Последнее обновление:
16 мая, 2022

Читать

Обсудить

Улучшить статью

Сохранить статью

Этот модуль обеспечивает поддержку арифметики рациональных чисел. Это позволяет создать экземпляр Fraction из целых чисел, чисел с плавающей запятой, чисел, десятичных знаков и строк. Экземпляры фракции: Экземпляр Fraction может быть создан из пары целых чисел, другого рационального числа или из строки. Экземпляры дробей можно хэшировать, и их следует рассматривать как неизменяемые.

класс фракций. Дробь (числитель = 0, знаменатель = 1) : Для этого требуется, чтобы числитель и знаменатель были экземплярами чисел. Rational , и возвращается экземпляр дроби со значением = (числитель/знаменатель). Ошибка деления на ноль возникает, если знаменатель = 0.

Python3

from fractions import Fraction

print (Fraction( 11 , 35 ))

Печать (Фракция ( 10 , 18 ))

Печать (Fraction ()


 .0042

Вывод:

 11/35
5/9
0

класс фракций. Дробь (other_fraction) : Для этого требуется, чтобы other_fraction была экземпляром чисел. Rational и экземпляр дроби с тем же значением возвращается.
дроби класса. Дробь (плавающая) : Для этого требуется экземпляр с плавающей запятой , и возвращается экземпляр дроби с тем же значением.

Python3

from fractions import Fraction

print (Fraction( 1.13 ))

Output :

 1272266894732165/11258992624

класс фракций. Дробь (десятичная) : Для этого требуется десятичный экземпляр , и возвращается экземпляр дроби с тем же значением.

Python

from fractions import Fraction

print (Fraction( '1.13' ))

Выходные данные:

 113/100

класс фракций. Фракция (строка) : Для этого требуется строка или экземпляр Unicode , и возвращается экземпляр дроби с тем же значением. Форма для этого экземпляра: [знак] числитель [‘/’ знаменатель] Здесь знак представляет собой «+» или «-», а числитель и знаменатель представляют собой строки из одиночных цифр.

Python3

from fractions import Fraction

print (Fraction( '8/25' ))

печать (дробь ( '1. 13' ))

Печать (фракция ( '3/7' )

9003

404042 ))

9003

40404040404141400400400400400400400400400400400400400400400400400400400400400400400400400400400400400400400400 400400 )) '1.414213 tn' ))

Вывод:

 8/25
113/100
3/7
1414213/1000000

limit_denominator(max_denominator=1000000) :
- Этот метод полезен для поиска рациональных приближений к заданному числу с плавающей запятой.
- Этот модуль находит и возвращает ближайшую к себе дробь, знаменатель которой не превышает max_denominator.
- Этот модуль также можно использовать для возврата числителя заданной дроби в наименьшем члене с использованием свойства числителя и знаменателя с использованием свойства знаменателя .

Выполнение математических операций с дробями

Python

из fractions import Fraction

print (Fraction( 113 , 100 ) + Fraction( 25 , 18 ))

Печать (Фракция ( 18 , 5 ) / 5 ) / ) / ) / )0042 18 , 10 ))


  print   (Fraction(   18   ,   5   )   *   Fraction(   16   ,   19   ))  
  print   (Fraction(   18   ,   5   )   *   Fraction(   15   ,   36   ))  
  print   (Fraction(   12   ,   5   )   *   *   Fraction(   12   ,   10   ))

Выход :

/0267
2
288/95
3/2
2. 8592589556

Вычисления на основе дробей с использованием различных функций математического модуля

Python3

import math

from fractions import Fraction

print (math.sqrt(Fraction( 25 , 4 )))

Печать (Математика.0042 )))


  print   (math.floor(Fraction(   3558   ,   1213   )))  
  print   (Fraction (math. 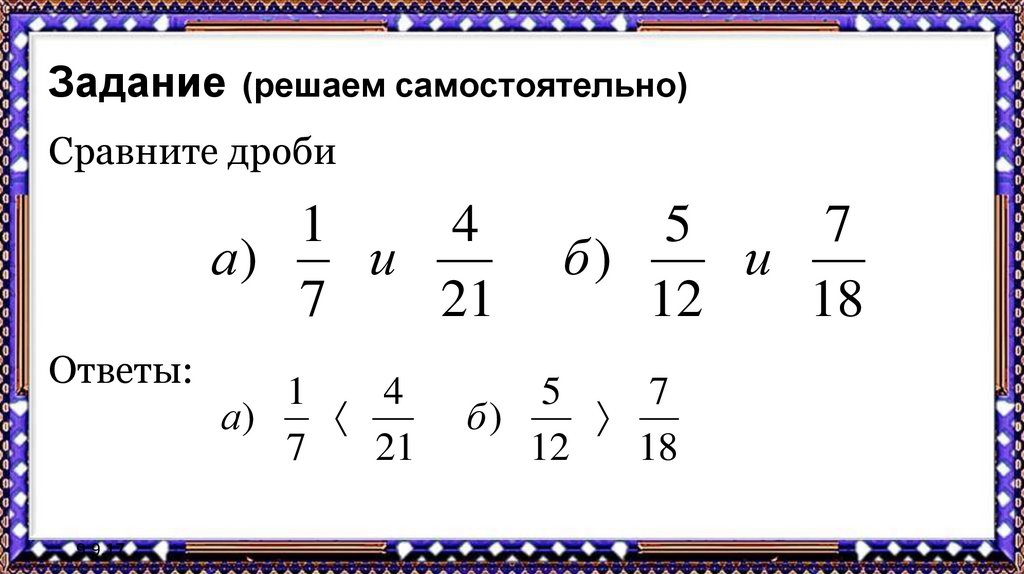sin(math.pi   /   3   )))  
  print   (Fraction(math.sin(math.pi   /   3   )) .limit_знаменатель(   10   ))

Выход:

 2,5
3.0550504633
2.0
31685776981/4503599627370496
6/7

Эта статья предоставлена Адити Гупта . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.

Статьи по теме

Модуль дробей в Python — PythonForBeginners.

com

Вы должны были использовать числовые типы данных, такие как целые числа и числа с плавающей запятой в Python. Но использовали ли вы дроби в их реальной форме? В этой статье мы изучим дроби и будем выполнять операции с дробями, используя модуль дробей в python.

Как использовать модуль дробей в Python?

Мы можем использовать метод Fraction из модуля Fractions в Python для создания рациональных чисел в виде дробей. Мы можем импортировать модуль следующим образом.

импортировать дроби

Мы можем преобразовать целое число, число с плавающей запятой или строку в дробь в python. Чтобы преобразовать отношение двух целых чисел в дробь, мы используем метод модуля дробей Fraction() и передаем числитель в качестве первого аргумента и знаменатель в качестве второго аргумента. Функция возвращает дробный объект следующим образом.

импортные фракции мойInt1=1 мойИнт2=2 print("Целое число 1(числитель) равно:",myInt1) print("Целое число 2(знаменатель) равно:",myInt2) мояфракция = дроби. Фракция (myInt1, myInt2) print("Значение дроби:",myFraction)

Вывод:

Целое число 1 (числитель): 1 Целое число 2 (знаменатель): 2 Значение дроби: 1/2

Мы можем получить значение дроби из числа с плавающей запятой, используя метод дроби модуля дробей. Когда мы передаем число с плавающей запятой методу Fraction() в качестве входных данных, он возвращает соответствующее значение дроби следующим образом.

импортные фракции мой поплавок = 0,5 print("Число с плавающей запятой:",myFloat) myFraction=фракции.Дробь(myFloat) print("Значение дроби:",myFraction)

Вывод:

Число с плавающей запятой: 0,5 Значение дроби: 1/2

Мы также можем преобразовать строку в дробь, используя метод Fraction(). Мы можем передать строковое представление дроби или литерал с плавающей запятой в строке в качестве входных данных для метода Fraction, который возвращает соответствующие значения дроби следующим образом.

импортные фракции мояСтр1="0,5" print("Строковый литерал:",myStr1) myFraction1=фракции. Дробь(myStr1) print("Значение дроби:",myFraction1) мояСтр2="1/2" print("Строковый литерал:",myStr2) myFraction2=фракции.Дробь(myStr2) print("Значение дроби:",myFraction2)

Вывод:

Строковый литерал: 0,5 Значение дроби: 1/2 Строковый литерал: 1/2 Значение дроби: 1/2

Как округлять дроби?

Мы можем округлять дроби в Python в соответствии с количеством цифр, необходимых в знаменателе дроби, используя метод round(). Метод round() принимает округляемую дробь в качестве первого аргумента и количество цифр, до которого должен быть округлен знаменатель, в качестве второго аргумента. Функция возвращает дробь с желаемым количеством цифр в знаменателе. Это можно понять следующим образом.

импортные фракции мойInt1=50 мойInt2=3 мояфракция = дроби. Фракция (myInt1, myInt2) print("Значение дроби:",myFraction) округленный = круглый (моя фракция, 2) print("Округленное значение равно:", округлено)

Вывод:

Дробное значение: 50/3 Округленное значение: 1667/100

Если мы не передаем число цифр, до которого должен быть округлен знаменатель, в качестве второго аргумента, метод round() преобразует дробь в ближайшее целое число. Это можно увидеть следующим образом.

импортные фракции мойInt1=50 мойInt2=3 мояфракция = дроби. Фракция (myInt1, myInt2) print("Значение дроби:",myFraction) округленный = круглый (моя фракция) print("Округленное значение:", округлено)

Вывод:

Дробное значение: 50/3 Округленное значение: 17

Получение числителя и знаменателя из дроби

Мы также можем извлечь числитель и знаменатель из дроби. Чтобы извлечь числитель, мы используем поле «числитель» объекта дроби. Точно так же для извлечения знаменателя мы используем поле «знаменатель» объекта дроби. Это можно понять из следующего примера.

импортные фракции мойInt1=50 мойInt2=3 мояфракция = дроби. Фракция (myInt1, myInt2) print("Значение дроби:",myFraction) print("Числитель:",myFraction.numerator) print("Знаменатель:",myFraction.denominator)

Вывод:

Дробное значение: 50/3 Числитель: 50 Знаменатель: 3

Арифметические операции над дробями

Мы можем выполнять арифметические операции, такие как сложение, вычитание, умножение и деление над дробями, используя модуль Fractions в Python так же, как мы выполняем эти операции над другими числовыми типами данных, такими как целые числа и числа с плавающей запятой. .

Мы можем выполнить арифметические операции над двумя заданными дробями в python следующим образом.

импортные фракции myFraction1=фракции.Дробь(50,3) myFraction2=фракции.Дробь(1,2) print("Значение первой дроби:",myFraction1) print("Значение второй дроби:",myFraction2) print("Дробь1 + Дробь2:", myFraction1 + myFraction2) print("Дробь1 - Дробь2:",мояДробь1 - мояДробь2) print("Дробь1 * Дробь2 это:",мояДробь1 * мояДробь2) print("Дробь1 / Дробь2:", myFraction1 / myFraction2)

Вывод:

Значение первой дроби: 50/3 Значение второй дроби: 1/2 Фракция1 + Фракция2: 103/6 Фракция1 - Фракция2: 97/6 Фракция1 * Фракция2: 25/3 Fraction1 / Fraction2: 100/3

Получить приблизительное рациональное значение из числа с плавающей запятой, используя модуль дробей

Мы можем получить рациональное число в виде дроби из любого числа с плавающей запятой или десятичного числа. Чтобы получить дробь из десятичного числа, мы можем передать десятичное число методу Fraction(), который преобразует их в рациональное число следующим образом.

импортные фракции мой поплавок = 22/7 print("Значение с плавающей запятой:",myFloat) myFraction=фракции.Дробь(myFloat) print("Значение дроби:",myFraction)

Вывод:

Значение с плавающей запятой: 3,142857142857143 Значение дроби: 7077085128725065/2251799813685248

После получения дроби в указанном выше формате мы можем ограничить наибольшее значение знаменателя с помощью метода limit_denominator(). Метод limit_denominator() при вызове дроби принимает максимально допустимое значение знаменателя в качестве входных данных и возвращает соответствующую дробь. Это можно понять из следующего примера.

импортные фракции мой поплавок = 22/7 print("Значение с плавающей запятой:",myFloat) myFraction=фракции.Дробь(myFloat) print("Значение дроби:",myFraction) мояфракция1=мояфракция.limit_знаменатель(100) print("Приблизительное значение дроби со знаменателем, ограниченным 100:",myFraction1)

Вывод:

Значение с плавающей запятой: 3,142857142857143 Значение дроби: 7077085128725065/2251799813685248 Приблизительное значение дроби со знаменателем, ограниченным 100: 22/7

Заключение

В этой статье мы изучили тип данных дроби и реализовали его с помощью модуля дробей в Python.

Источник

Дробь — форма представления числа в математике. Дробная черта обозначает операцию деления. Числителем дроби называется делимое, а знаменателем — делитель. Например, в дроби $frac{5}{7}$ числителем является число 5, а знаменателем — 7.

Правильной называется дробь, у которой модуль числителя больше модуля знаменателя. Если дробь является правильной, то модуль её значения всегда меньше 1. Все остальные дроби являются неправильными.

Дробь называют смешанной, если она записана как целое число и дробь. Это то же самое, что и сумма этого числа и дроби:

$[5frac{2}{3}=5+frac{2}{3}.]$

Основное свойство дроби

Если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится, то есть, например,

$[frac{3}{5}=frac{4 cdot 3}{4 cdot 5}=frac{12}{20}.]$

Приведение дробей к общему знаменателю

Чтобы привести две дроби к общему знаменателю, нужно:

Числитель первой дроби умножить на знаменатель второй
Числитель второй дроби умножить на знаменатель первой
Знаменатели обеих дробей заменить на их произведение

Действия с дробями

Сложение. Чтобы сложить две дроби, нужно

Привести дроби к общему знаменателю
Сложить новые числители обеих дробей, а знаменатель оставить без изменений

Пример:

$[frac{3}{5}+frac{1}{2}=frac{6}{10}+frac{5}{10}=frac{11}{10}=1frac{1}{10}.]$

Вычитание. Чтобы вычесть одну дробь из другой, нужно

Привести дроби к общему знаменателю
Вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений

Пример:

$[frac{3}{5}-frac{1}{2}=frac{6}{10}-frac{5}{10}=frac{1}{10}.]$

Умножение. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели:

$[frac{5}{3} cdot frac{1}{2} = frac{5 cdot 1}{3 cdot 2} = frac{5}{6}.]$

Деление. Чтобы разделить одну дробь на другую, следует числитель первой дроби умножить на знаменатель второй, а знаменатель первой дроби умножить на числитель второй:

$[frac{5}{3} : frac{1}{2} = frac{5 cdot 2}{3 cdot 1} = frac{10}{3} = 3 frac{1}{3}.]$

Источник

Обыкновенные дроби

Наглядное представление
дроби

Обыкновенная (или
простая) дробь — запись рационального
числа в виде

или

.
Горизонтальная или косая черта обозначает
знак деления, в результате чего получается
частное. Делимое
называется числителем дроби, а делитель —
знаменателем.

Обозначения обыкновенных
дробей

Есть несколько видов записи обыкновенных
дробей в печатном виде:

½
1/2 или

(наклонная
черта называется «солидус»^[2])
выключная формула:

(горизонтальная
черта называется Винкулиум (англ.))
строчная формула:

Рациональное число

Рациональное число (лат. ratio —
отношение, деление, дробь) — число,
представляемое несократимой обыкновенной
дробью

,

—
целое
число, а знаменатель

—
натуральное
число. Понятие дроби возникло
несколько тысяч лет назад, когда,
сталкиваясь с необходимостью измерять
некоторые вещи (длину, вес, площадь и
т.п.), люди поняли, что не удаётся обойтись
целыми числами и необходимо ввести
понятие доли:
половины, трети и т.п. Дробями и операциями
над ними пользовались, например, шумеры,
древние египтяне и греки.

Множество рациональных чисел

Множество рациональных чисел обозначается

и
может быть записано таком в виде:

При этом оказывается, что разные записи
могут представлять одну и ту же дробь,
например,

и

,
(все дроби, которые можно получить друг
из друга умножением или делением на
одно и то же натуральное число, представляют
одно и то же рациональное число). Поскольку
делением числителя и знаменателя дроби
на их наибольший
общий делитель можно получить
единственное несократимое представление
рационального числа, то можно говорить
об их множестве как о множестве
несократимых дробей со взаимно
простыми целым числителем и
натуральным знаменателем:

Здесь

—
наибольший общий делитель чисел

Множество рациональных чисел является
естественным обобщением множества
целых
чисел. Легко видеть, что если у
рационального числа

знаменатель

,
то

является
целым числом. Множество рациональных
чисел располагается на числовой оси
всюду плотно: между любыми двумя
различными рациональными числами
расположено хотя бы одно рациональное
число (а значит, и бесконечное множество
рациональных чисел). Тем не менее,
оказывается, что множество рациональных
чисел имеет счётную
мощность
(то есть все его элементы можно
перенумеровать). Заметим, кстати, что
ещё древние греки убедились в существовании
чисел, не представимых в виде дроби
(например, они доказали, что не существует
рационального числа, квадрат которого
равен 2).

Терминология

Формальное определение

См. также: Кольцо
частных

Формально рациональные числа определяются
как множество классов эквивалентности
пар

по
отношению
эквивалентности

,
если

.
При этом операции сложения и умножения
определяются следующим образом:

[Связанные определения

Правильные, неправильные
и смешанные дроби

Правильной называется дробь, у
которой модуль
числителя меньше модуля знаменателя.
Правильные дроби представляют рациональные
числа, по модулю меньшие единицы.
Дробь, не являющаяся правильной,
называется неправильной и представляет
рациональное число, большее или равное
единице по модулю.

Неправильную дробь можно представить
в виде суммы
целого числа и правильной дроби,
называемой смешанной дробью.
Например,

.
Подобная запись (с пропущенным знаком
сложения), хотя и употребляется в
элементарной арифметике,
избегается в строгой математической
литературе из-за схожести обозначения
смешанной дроби с обозначением
произведения целого числа на дробь.

[править]
Высота дроби

Высота обыкновенной дроби —
это сумма модуля числителя и знаменателя
этой дроби. Высота рационального
числа — это сумма модуля числителя
и знаменателя несократимой обыкновенной
дроби, соответствующей этому числу.

Например, высота дроби

равна

.
Высота же соответствующего рационального
числа равна

,
так как дробь сокращается на

.

[править]
Комментарий

Термин дробное число (дробь)
иногда^[^{уточнить}^]
используется как синоним к термину
рациональное число, а иногда синоним
любого нецелого числа. В последнем
случае, дробные и рациональные числа
являются разными вещами, так как тогда
нецелые рациональные числа — всего
лишь частный случай дробных.

Свойства

[ Основные свойства

Множество рациональных чисел удовлетворяют
шестнадцати основным свойствам,
которые легко могут быть получены из
свойств целых
чисел.^[1]

Упорядоченность.
Для любых рациональных чисел

и

существует
правило, позволяющее однозначно
идентифицировать между ними одно и
только одно из трёх отношений:
«
»,
«
»
или «
».
Это правило называется правилом
упорядочения и формулируется следующим
образом: два положительных числа

и

связаны
тем же отношением, что и два целых числа

и

;
два неположительных числа

и

связаны
тем же отношением, что и два неотрицательных
числа

и

;
если же вдруг

неотрицательно,
а

—
отрицательно, то

.

Суммирование дробей

Операция
сложения. Для любых
рациональных чисел

и

существует
так называемое правило суммирования,
которое ставит им в соответствие
некоторое рациональное число

.
При этом само число

называется
суммой
чисел

и

и
обозначается

,
а процесс отыскания такого числа
называется суммированием. Правило
суммирования имеет следующий вид:

.

Операция
умножения. Для любых
рациональных чисел

и

существует
так называемое правило умножения,
которое ставит им в соответствие
некоторое рациональное число

.
При этом само число

называется
произведением
чисел

и

и
обозначается

,
а процесс отыскания такого числа также
называется умножением. Правило
умножения имеет следующий вид:

.

Транзитивность
отношения порядка. Для любой тройки
рациональных чисел

,

и

если

меньше

и

меньше

,
то

меньше

,
а если

равно

и

равно

,
то

равно

.

Коммутативность
сложения. От перемены мест рациональных
слагаемых сумма не меняется.

Ассоциативность
сложения. Порядок сложения трёх
рациональных чисел не влияет на
результат.

Наличие нуля.
Существует рациональное число 0, которое
сохраняет любое другое рациональное
число при суммировании.

Наличие противоположных чисел.
Любое рациональное число имеет
противоположное рациональное число,
при суммировании с которым даёт 0.

Коммутативность умножения. От
перемены мест рациональных множителей
произведение не меняется.

Ассоциативность умножения. Порядок
перемножения трёх рациональных чисел
не влияет на результат.

Наличие единицы.
Существует рациональное число 1, которое
сохраняет любое другое рациональное
число при умножении.

Наличие обратных
чисел. Любое ненулевое
рациональное число имеет обратное
рациональное число, умножение на которое
даёт 1.

Дистрибутивность
умножения относительно сложения.
Операция умножения согласована с
операцией сложения посредством
распределительного закона:

Связь отношения порядка с операцией
сложения. К левой и правой частям
рационального неравенства можно
прибавлять одно и то же рациональное
число.

Связь отношения порядка с операцией
умножения. Левую и правую части
рационального неравенства можно
умножать на одно и то же положительное
рациональное число.

Аксиома
Архимеда. Каково бы ни
было рациональное число

,
можно взять столько единиц, что их сумма
превзойдёт

.

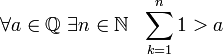
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Модуль положительной дроби.

Модуль отрицательной дроби.

Дроби, модуль числа, рациональные числа

Урок 2. Подготовка к ЕГЭ по математике

Конспект урока «Дроби, модуль числа, рациональные числа»

Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ЕГЭ по математике

Модуль fractions, рациональные числа в Python.

Создание рациональных чисел.

Математические операции над рациональными числами.

Fraction в Python

Python3

Python3

Python

Python3

Python

Python3

Модуль дробей в Python — PythonForBeginners.

Как использовать модуль дробей в Python?

Как округлять дроби?

Получение числителя и знаменателя из дроби

Арифметические операции над дробями

Получить приблизительное рациональное значение из числа с плавающей запятой, используя модуль дробей

Заключение

Основное свойство дроби

Приведение дробей к общему знаменателю

Действия с дробями

Множество рациональных чисел

Получите полный комплект видеоуроков, тестов и презентаций
Подготовка к ЕГЭ по математике