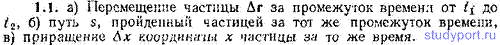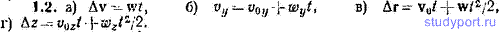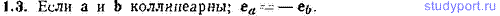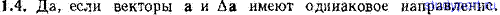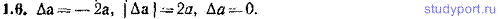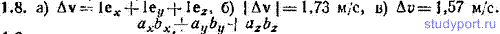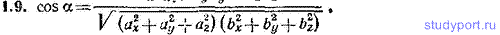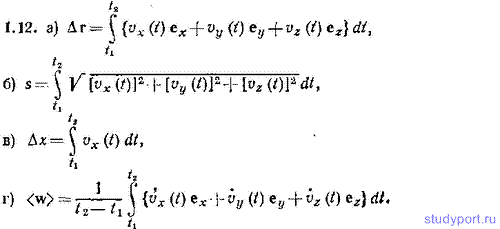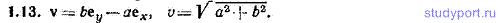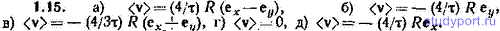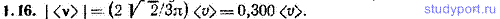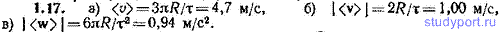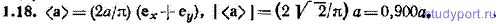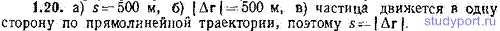Как найти модуль относительной скорости частицы

Спрятать решение

Подставив V = 0 в уравнение (6.36), находимM =2m1 − v 2 / c2.Заметим, что M > 2m , т.е. в данном процессе масса системы несохраняется. Например, если v = 0,6 c , то M = 2,5m .§6. Релятивистская механика92Задание для самостоятельной работы6.8. Две частицы движутся навстречу друг другу с одинаковыми по модулюскоростями v0. Найти модуль относительной скорости частиц v. Вычислить, c ; v0 = 0,5c ; v0 = 0,9c .v для следующих значений v0: v0 = 016.9. Две частицы движутся с одинаковыми по модулю скоростями v0 вовзаимно перпендикулярных направлениях. Найти модуль относительной, c;скорости частиц v. Вычислить v для следующих значений v0: v0 = 01v0 = 0,5c ; v0 = 0,9c .6.10.

На частицу массой m действует сила F. Каково ускорение частицы a,если ее скорость v = 0,8c , а направление силы перпендикулярнонаправлению скорости?6.11. На частицу, движущуюся со скоростью v = 0,5c , действует сила,направленная под углом α = 45° к вектору скорости. Найти угол β междунаправлениями скорости и ускорения частицы.6.12. Пусть в некоторой системе отсчета S декартовы проекции импульса иэнергия частицы равны, соответственно, px , py , pz и E.

Каковы декартовыпроекции импульса px′ , p′y , pz′ и энергия E ′ этой частицы в системе S’,движущейся относительно S как показано на рис. 6.1?6.13. Найти соотношение между энергией E и импульсом p частицы, массакоторой равна нулю. Какова скорость v такой частицы?6.14. Пусть при скорости частицы v0 ее импульс равен p0.

Во сколько раз ηнужно увеличить скорость частицы, чтобы ее импульс стал равным 2p0?Найти значение η для v0 / c = 0,1; 0,5; 0,9.6.15. Частица, движущаяся со скоростью v1 = 0,8c , налетает на покоящуюсячастицу, имеющую такую же массу. В результате столкновения частицыслипаются. Определить скорость v образовавшегося тела.§7. Неинерциальные системы отсчета93§7. Неинерциальные системы отсчетаКраткие теоретические сведенияЛежащие в основе механики законы Ньютона (см.

§4) справедливытолько в инерциальных системах отсчета. Относительно всех инерциальныхсистем данное тело имеет одно и то же ускорение a. Поскольку любая неинерциальная система отсчета движется относительно инерциальной с некоторым ускорением, ускорение тела в неинерциальной системе a ′ отличается от a.

Таким образом, переход в неинерциальную систему отсчета приводит к появлению у тела добавочного ускорения, причиной которого является не действие на него других тел, а движение самой системы отсчета. Вто же время, необходимость такого перехода часто диктуется практическими потребностями решения задач механики в ускоренно движущихся системах отсчета.Для того, чтобы можно было применять в неинерциальных системах уравнения динамики в обычной форме, вводят так называемые силыинерции, действие которых вызывает у тел добавочное ускорение. В соответствии с этим, уравнение движения материальной точки (второй законНьютона) в неинерциальной системе приобретает видma′ = F + Fин .(7.1)Здесь m – масса материальной точки, a ′ – ее ускорение относительно неинерциальной системы отсчета, F – сумма сил, действующих на материальную точку со стороны других тел, Fин – сила инерции, определяемая формулойFин = −m(a − a′) ,(7.2)§7.

Неинерциальные системы отсчета94где a = F / m – ускорение материальной точки в инерциальной системе отсчета.Входящая в определение силы инерции величина (a − a ′) представляет собой разность ускорений одной и той же точки относительно двухсистем отсчета: неподвижной и движущейся. Нахождение этой разностиявляется задачей кинематики относительного движения. Воспользовавшисьформулами, приведенными в §3, получаем:(a − a′) = a п + a к ,(7.3)где aп – переносное ускорение, aк – кориолисово ускорение.

Следовательно,сила инерции может быть представлена в виде суммы двух слагаемых:Fин = Fп + Fк ,(7.4)Fп = −ma п(7.5)где– переносная сила инерции,Fк = − ma к(7.6)– кориолисова сила инерции. Формулы, приведенные в §3, позволяют выразить эти силы через характеристики движения неинерциальной системыотсчета и кинематические характеристики движения точки относительнонеинерциальной системы, а именно,Fп = − ma 0 + mω 2 r⊥′(7.7)Fк = −2m[ω, v ′] .(7.8)и§7. Неинерциальные системы отсчета95Здесь a0 – ускорение начала отсчета неинерциальной системы, ω – угловаяскорость вращения неинерциальной системы, r⊥′ – составляющая радиусвектора материальной точки в неинерциальной системе отсчета, перпендикулярная оси вращения системы, v′ – скорость материальной точки относительно неинерциальной системы.Второе слагаемое в правой части формулы (7.7) носит названиецентробежной силы инерции:Fцб = mω2r⊥′ .(7.9)Центробежная сила направлена от оси вращения неинерциальной системы.Переносная сила инерции образует потенциальное силовое поле.Заметим, что силы инерции отличаются от «обычных» сил (силвзаимодействия между телами) рядом особенностей.

Во-первых силы инерции не инвариантны относительно перехода от одной неинерциальной системы отсчета к другой. Во-вторых, нельзя указать конкретные тела, со стороны которых действуют силы инерции. Иначе говоря, силы инерции неподчиняются третьему закону Ньютона. В остальном это обычные силы,которые способны вызывать ускорения тел, совершать работу, изменятьэнергию и импульс тел, деформировать тела и т.п. Использование сил инерции позволяет решать задачи механики непосредственно по отношению кускоренно движущимся системам отсчета, что часто оказывается значительно проще, чем анализ движения в инерциальной системе.Примеры решения задачПример 7.1. На резиновом жгуте подвешено тело массой m.

Известно, чтопри увеличении длины жгута вдвое по сравнению с его собственной длинойl0 на концах жгута возникает сила f0. Система вращается вокруг вертикальной оси так, что тело движется в горизонтальной плоскости по окружностис угловой скоростью ω.

Найти длину шнура при движении тела и угол, накоторый отклонится шнур от вертикали.§7. Неинерциальные системы отсчета96Решение. Перейдем в неинерциальную систему отсчета, вращающуюся сугловой скоростью ω (рис. 7.1). В этой системе тело m находится в равновесии под действием трех сил:mg + Fцб + T = 0 .(7.10)Здесь через T обозначена сила натяжения шнура,Fцб = mω2 R ′ – центробежная сила инерции. ЗаписываяРис. 7.1соотношение (7.10) в проекциях на горизонтальную и вертикальную оси, имеемm ω 2 R ′ = T sin α ,(7.11)mg = T cos α .(7.12)Согласно закону Гука, натяжение жгутаT = k (l − l0 ) ,где k – коэффициент жесткости, l – длина жгута в растянутом состоянии.

Поусловию задачи T = f 0 при l = 2l0 . Отсюда k = f 0 / l0 иT =f0(l − l0 ) .l0(7.13)Объединяя (7.11) – (7.13) и учитывая, что R ′ = l sin α , находим ответ:cosα = gf 0 − m ω 2 l0ω 2 l0 f 0,(7.14)⎛ m ω l0⎞l = l0 ⎜⎜+ 1⎟⎟ .2⎝ f 0 − m ω l0 ⎠2§7. Неинерциальные системы отсчета97Пример 7.2. Небольшое тело поместили на вершину полусферы радиусомR. Затем полусфере сообщили постоянное ускорение a0 в горизонтальном направлении (рис.7.2). Пренебрегая трением, найти угол ϑ0 междувертикалью и радиус-вектором, проведеннымиз центра полусферы в точку, где происходитРис.

7.2отрыв тела.Решение. Перейдем в неинерциальную систему отсчета, связанную с полусферой. В этой системе отсчета вплоть до момента отрыва от полусферытело движется под действием трех сил:m&r& = mg + N + Fин ,(7.15)где N – сила реакции со стороны полусферы. Поскольку траектория тела доточки отрыва представляет собой дугу окружности радиусом R,&&rn = − nv2,R(7.16)где n – нормаль к поверхности сферы в точке нахождения тела. Для силыинерции имеем выражениеFин = −ma 0 .(7.17)Проектируя (7.15) на направление нормали n и учитывая (7.16), (7.17), получаем−mv2= − mg cos ϑ + ma0 sin ϑ + N .R(7.18)§7. Неинерциальные системы отсчета98В точке отрыва сила реакции N обращается в нуль.

Из уравнения (7.18) находимv02= g cos ϑ 0 − a0 sin ϑ 0 .R(7.19)Для того чтобы связать скорость тела с углом ϑ, воспользуемся закономизменения энергии тела в неинерциальной системе отсчета:mv2= mgR (1 − cos ϑ) + ΔA ,2(7.20)где ΔA – работа силы инерции. Работа силы инерции на перемещенииdS = R dϑ равна (см. рис. 7.3):dA = Fин dS cos ϑ = ma0 R cos ϑdϑ .ОтсюдаРис. 7.3ϑ∫ΔA = ma0 R cos ϑ dϑ = ma0 R sin ϑ .(7.21)0Используя (7.20) и (7.21), находимv2= g(1 − cos ϑ) + a0 sin ϑ .2R(7.22)Это равенство справедливо и в точке отрыва. Используя формулы (7.19) и(7.22), получаем условие для угла ϑ в точке отрыва:cos ϑ 0 − α sin ϑ 0 −2= 0.3(7.23)§7.

Неинерциальные системы отсчета99Здесь введено обозначениеα=a0.g(7.24)Найдем решение уравнения (7.23). Для этого представим его в виде⎛⎞ 21α1 + α2 ⎜cos ϑ 0 −sin ϑ 0 ⎟ − = 0⎜⎟ 31 + α2⎝ 1 + α2⎠и введем угол ϕ такой, чтоcos ϕ =11+ α2, sin ϕ =α1 + α2.(7.25)Тогдаcos( ϑ 0 + ϕ) =23 1 + α2и, следовательно,⎞⎛2⎟ −ϕ.ϑ 0 = arccos⎜⎜⎟⎝ 3 1 + α2 ⎠С учетом формул (7.25) полученное решение можно представить в видеcos ϑ 0 =2 + α 5 + 9α 23(1 + α 2 ).Пример 7.3. Какую форму следует придать куску проволоки, вращающемуся вокруг вертикальной оси с угловой скоростью ω, чтобы надетая на проволоку маленькая бусинка в любой точке проволоки могла находиться вравновесии? Трением бусинки о проволоку пренебречь.§7. Неинерциальные системы отсчета100Решение.

Вы зашли на страницу вопроса «Первая частица движется со скоростью V1 = 4ex, а вторая со скоростью V2 = 8ey Найти модуль относительной скорости первой частицы V?, который относится к
категории Физика. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.

Страница 1 из 3

1.1. Частица движется с постоянной скоростью v. Что определяет выражение: a) v(t₂-t₁), б) v(t₂-t₁), в) v_x(t₂-t₁)?

1.2. Частица движется с постоянным ускорением w. В начальный момент времени она находилась в точке с радиус-вектором r0 и имела скорость v0. Написать выражение для: а) приращения скорости частицы dv за время t, б) проекции скорости частицы на ось у в момент времени t, в) перемещения частицы за время t, г) приращения координаты z частицы за время.

1.3. В каком случае векторы а и b могут быть связаны соотношением a = αb, где α — скаляр? Как соотносятся их орты, если а₀?

1.4. Может ли приращение модуля вектора Δа оказаться равным модулю приращения вектора |Δа|?

1.5. В каком соотношении находятся приращение модуля вектора и модуль приращения вектора |Δа|, если векторы а и Δа направлены в противоположные стороны?

1.6. Вектор а изменил направление на обратное. Найти: Δa, |Δa|, Δa.

1.7. Вектор а повернулся без изменения «длины» на малый угол δφ. а) Написать приближенное выражение для |Δа|. б) Чему равно Δа?

1.8. Начальное значение скорости равно v₁=1e_x+3e_y+5e_z (м/с), конечное v₂=2e_x+4e_y+6e_z (м/с). Найти: а) приращение скорости Δv, б) модуль приращения скорости |Δv|, в) приращение модуля скорости Δv.

1.9. Написать выражение для косинуса угла α между векторами с компонентами a_x, a_y, a_z и b_x, b_y, b_z.

1.10. Компоненты одного вектора равны (1, 3, 5), другого — (6, 4, 2). Найти угол α между векторами.

1.11. Преобразовать к виду, содержащему только модули векторов и угол α, выражение a [bc], в котором векторы а и с взаимно перпендикулярны, а вектор b образует с нормалью к плоскости, в которой лежат векторы а и с, угол α.

1.12. Заданы функции v_x(t), v_y(t) и v_z(t), определяющие в некоторой системе координат скорость частицы v. Написать выражение для: а) перемещения частицы Δr за промежуток времени от t₁ до t₂, б) пути s, пройденного частицей за тот же промежуток времени, в) приращения Δх координаты х частицы за время от t₁ до t₂. г) среднего значения ускорения частицы <w> за то же время.

1.13. Частица 1 движется со скоростью v₁ = ae_x, частица 2 — со скоростью v₂=be_y (a и b — константы). Найти скорость v второй частицы относительно первой и модуль v этой скорости.

1.15. Частица движется равномерно по часовой стрелке по окружности радиуса R, делая за время τ один оборот. Окружность лежит в координатной плоскости x, y, причем центр окружности совпадает с началом координат. В момент t = 0 частица находится в точке с координатами x = 0, y = R. Найти среднее значение скорости точки за промежуток времени: а) от 0 до τ/4, б) от 0 до τ/2, в) от 0 до 3τ/4, г) от 0 до τ, д) от τ/4 до 3τ/4.

1.16. Частица прошла за некоторое время 3/4 окружности со средним значением модуля скорости (v). Найти модуль средней скорости частицы |<v>| за то же время.

1.17. Первоначально покоившаяся частица прошла за время 10,0 с полторы окружности радиуса 5,00 м с постоянным тангенциальным ускорением. Вычислить соответствующие этому промежутку времени значения: а) среднего модуля скорости <v>, б) модуля средней скорости |<v>|, в) модуля среднего ускорения |<w>|.

1.18. Постоянный по модулю вектор а, равномерно поворачиваясь против часовой стрелки в плоскости х, у, переходит за время из положения, при котором он совпадает по направлению с осью х, в положение, при котором он совпадает по направлению с осью у. Найти среднее за время значение вектора а и модуль этого среднего.

1.19. Радиус-вектор точки r изменяется: а) только по модулю, б) только по направлению. Что можно сказать о траектории?

1.20. Радиус-вектор частицы определяется выражением: r=3t²e_x+4t²e_y+7e_z (м). Вычислить: а) путь s, пройденный частицей за первые 10 секунд движения, б) модуль перемещения |Δr| за то же время, в) объяснить полученные результаты.