Как найти модуль перемещения тела по окружности

Как найти модуль перемещения тела по окружности

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ​ ( T ) ​ — время, в течение которого тело совершает один полный оборот. Единица периода — ​ ( [,T,] ) ​ = 1 с.

Частота обращения ​ ( (n) ) ​ — число полных оборотов тела за одну секунду: ​ ( n=N/t ) ​. Единица частоты обращения — ( [,n,] ) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.

Связь между частотой и периодом обращения выражается формулой: ​ ( n=1/T ) ​.

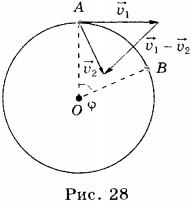
Пусть некоторое тело, движущееся по окружности, за время ​ ( t ) ​ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ​ ( varphi ) ​.

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ​ ( omega ) ​ — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ​ ( omega=varphi/t ) ​. Единица угловой скорости — радиан в секунду, т.е. ​ ( [,omega,] ) ​ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ​ ( 2pi ) ​. Поэтому ​ ( omega=2pi/T ) ​.

Линейная скорость тела ​ ( v ) ​ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ​ ( vec =l/t ) ​. За один оборот точка проходит путь, равный длине окружности. Поэтому ​ ( vec =2pi!R/T ) ​. Связь между линейной и угловой скоростью выражается формулой: ​ ( v=omega R ) ​.

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ​ ( vec=frac > ) ​ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ​ ( a=frac ) ​. Так как ​ ( v=omega R ) ​, то ​ ( a=omega^2R ) ​.

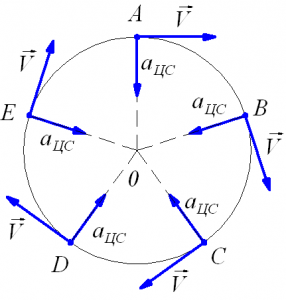
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ​ ( R_1 ) ​ от центра вращающегося колеса, равна ​ ( v_1 ) ​. Чему равна скорость ​ ( v_2 ) ​ точки 2, находящейся от центра на расстоянии ​ ( R_2=4R_1 ) ​?

1) ​ ( v_2=v_1 ) ​
2) ​ ( v_2=2v_1 ) ​
3) ​ ( v_2=0,25v_1 ) ​
4) ​ ( v_2=4v_1 ) ​

3. Период обращения точки по окружности можно вычислить по формуле:

1) ​ ( T=2pi!Rv ) ​
2) ( T=2pi!R/v ) ​
3) ( T=2pi v ) ​
4) ( T=2pi/v ) ​

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ​ ( omega=a^2R ) ​
2) ( omega=vR^2 ) ​
3) ( omega=vR )
4) ( omega=v/R ) ​

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ​ ( 1/T ) ​
2) ​ ( v^2/R ) ​
3) ​ ( v/R ) ​
4) ​ ( omega R ) ​
5) ​ ( 1/n ) ​

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ​ ( T ) ​ — время, в течение которого тело совершает один полный оборот. Единица периода — ​ ( [,T,] ) ​ = 1 с.

Частота обращения ​ ( (n) ) ​ — число полных оборотов тела за одну секунду: ​ ( n=N/t ) ​. Единица частоты обращения — ( [,n,] ) = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.

Связь между частотой и периодом обращения выражается формулой: ​ ( n=1/T ) ​.

Пусть некоторое тело, движущееся по окружности, за время ​ ( t ) ​ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ​ ( varphi ) ​.

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ​ ( omega ) ​ — физическая величина, равная отношению угла поворота ( varphi ) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ​ ( omega=varphi/t ) ​. Единица угловой скорости — радиан в секунду, т.е. ​ ( [,omega,] ) ​ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ​ ( 2pi ) ​. Поэтому ​ ( omega=2pi/T ) ​.

Линейная скорость тела ​ ( v ) ​ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ​ ( vec=l/t ) ​. За один оборот точка проходит путь, равный длине окружности. Поэтому ​ ( vec=2pi!R/T ) ​. Связь между линейной и угловой скоростью выражается формулой: ​ ( v=omega R ) ​.

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ​ ( vec=frac<Deltavec> ) ​ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ​ ( a=frac ) ​. Так как ​ ( v=omega R ) ​, то ​ ( a=omega^2R ) ​.

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ​ ( R_1 ) ​ от центра вращающегося колеса, равна ​ ( v_1 ) ​. Чему равна скорость ​ ( v_2 ) ​ точки 2, находящейся от центра на расстоянии ​ ( R_2=4R_1 ) ​?

1) ​ ( v_2=v_1 ) ​
2) ​ ( v_2=2v_1 ) ​
3) ​ ( v_2=0,25v_1 ) ​
4) ​ ( v_2=4v_1 ) ​

3. Период обращения точки по окружности можно вычислить по формуле:

1) ​ ( T=2pi!Rv ) ​
2) ( T=2pi!R/v ) ​
3) ( T=2pi v ) ​
4) ( T=2pi/v ) ​

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ​ ( omega=a^2R ) ​
2) ( omega=vR^2 ) ​
3) ( omega=vR )
4) ( omega=v/R ) ​

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ​ ( 1/T ) ​
2) ​ ( v^2/R ) ​
3) ​ ( v/R ) ​
4) ​ ( omega R ) ​
5) ​ ( 1/n ) ​

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Перемещение тел по окружности достаточно распространено в нашей жизни и в природе. Яркими примерами этого типа перемещения являются вращения ветровых мельниц, планет вокруг своих звезд и колес транспортных средств. В данной статье рассмотрим, какими формулами движение по окружности тел описывается.

Перемещение по окружности и по прямой линии в физике

В физике вопросами движения занимается кинематика. Она устанавливает связь между величинами, описывающими этот процесс. В динамике также уделяется внимание движению, однако она ориентирована на описание причин его возникновения. Другими словами, если для кинематики главными физическими величинами являются путь и скорость, то для динамики — это действующие на тела силы.

Вам будет интересно:Интерес: определение, понятие, типы и функции

В физике принято выделять два идеальных типа траекторий движения:

• прямая линия;
• окружность.

Математический аппарат для описания движения по обоим типам траекторий развит настолько хорошо, что понимание формул, например для прямолинейного движения, автоматически приводит к пониманию выражений для движения по окружности. Единственная принципиальная разница между формулами указанных типов перемещения заключается в том, что для движения по окружности удобно использовать угловые характеристики, а не линейные.

Вам будет интересно:Педагогическая система Макаренко: принципы и компоненты

Далее в статье будем рассматривать исключительно кинематические формулы движения по окружности тел, не вдаваясь в подробности динамики.

Угловые характеристики движения: угол поворота

Прежде чем записывать формулы движения по окружности в физике, следует ввести величины, которые будут фигурировать в этих формулах.

Начнем с угла поворота. Будем обозначать его греческой буквой θ (тета). Поскольку вращение предполагает движение точки вдоль одной и той же окружности, то значение угла поворота θ за определенный промежуток времени можно использовать для определения количества оборотов, которое сделала эта точка. Напомним, что вся окружность равна 2*pi радиан, или 360o. Тогда формула для числа оборотов n через угол θ примет вид:

Вам будет интересно:Академик Рыбаков Б.А.: биография, археологическая деятельность, книги

n = θ/(2*pi)

Здесь и далее во всех формулах угол выражается в радианах.

Пользуясь известным углом θ, также можно определить линейное расстояние, которое точка прошла вдоль окружности. Это расстояние будет равно:

L = θ*r

Здесь r — радиус рассматриваемой окружности.

Угловая скорость и ускорение

Кинематические формулы движения по окружности точки предполагают также использование понятий угловой скорости и углового ускорения. Обозначим первую буквой ω (омега), а вторую буквой α (альфа).

Физический смысл угловой скорости ω прост: эта величина показывает, на какой угол в радианах поворачивается точка за каждую секунду времени. Данное определение имеет следующее математическое представление:

ω = dθ/dt

Эта формула скорости движения по окружности записана в дифференциальной форме. Полученная с ее помощью величина ω называется мгновенной скоростью. Ее удобно использовать, если движение не является равномерным, то есть происходит с переменной скоростью.

Угловое ускорение α — это величина, которая описывает быстроту изменения скорости ω, то есть:

α = dω/dt

Угловое ускорение измеряется в радианах в секунду квадратную (рад/с2). Так, 1 рад/с2 означает, что тело увеличивает за каждую секунду времени скорость на 1 рад/с.

Учитывая выражение для ω, записанное выше, равенство можно представить в такой форме:

α = d2θ/dt2

В зависимости от особенностей движения по окружности величина α может быть постоянной, переменной или нулевой.

Равномерное движение

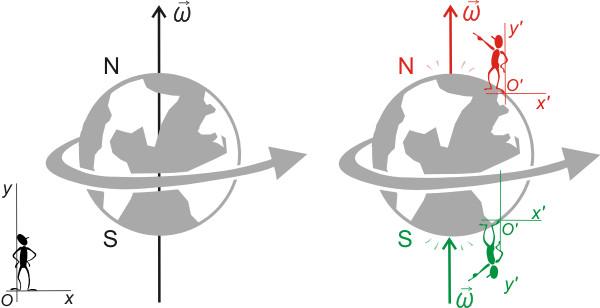
Когда на вращающееся тело не действует никакая внешняя сила, то угловая скорость будет оставаться постоянной сколь угодно длительное время. Такое движение получило название равномерного вращения. Оно описывается следующей формулой:

θ = ω*t

В этом выражении переменными являются всего две величины: t и θ. Скорость ω = const.

Следует отметить один важный момент: нулю равна лишь равнодействующая внешних сил на тело, внутренние же силы, действующие в системе, нулю не равны. Так, внутренняя сила заставляет вращающееся тело изменять свою прямолинейную траекторию на криволинейную (окружность). Эта сила приводит к появлению центростремительного ускорения. Последнее не изменяет ни скорость ω, ни линейную скорость v, оно лишь изменяет направление движения.

Равноускоренное движение по окружности

Формулы для этого типа перемещения можно получить непосредственно из приведенных математических выражений для величин ω и α. Равноускоренное движение предполагает, что за более-менее длительный промежуток времени модуль и направление ускорения α не изменяются. Благодаря этому можно проинтегрировать дифференциальное выражение для α и получить следующие две формулы:

ω = ω0 + α*t;

ω = ω0 — α*t

Очевидно, что в первом случае движение будет равноускоренным, во втором — равнозамедленным. Величина ω0 здесь — это некоторая начальная скорость, которой вращающееся тело обладало до появления ускорения.

Для равноускоренного движения не существует конечной скорости, поскольку она может возрастать сколь угодно долго. Для равнозамедленного движения конечным состоянием будет прекращение вращения, то есть ω = 0.

Теперь запишем формулы для определения угла θ при движении с постоянным ускорением. Эти формулы получаются, если произвести двойное интегрирование по времени для выражения α через θ. Получаются следующие выражения:

θ = ω0*t + α*t2/2;

θ = ω0*t — α*t2/2

То есть центральный угол θ, на который тело повернется за время t, будет равен сумме двух слагаемых. Первое слагаемое — это вклад в θ равномерного движения, второе — равноускоренного (равнозамедленного).

Связь между угловыми и линейными величинами

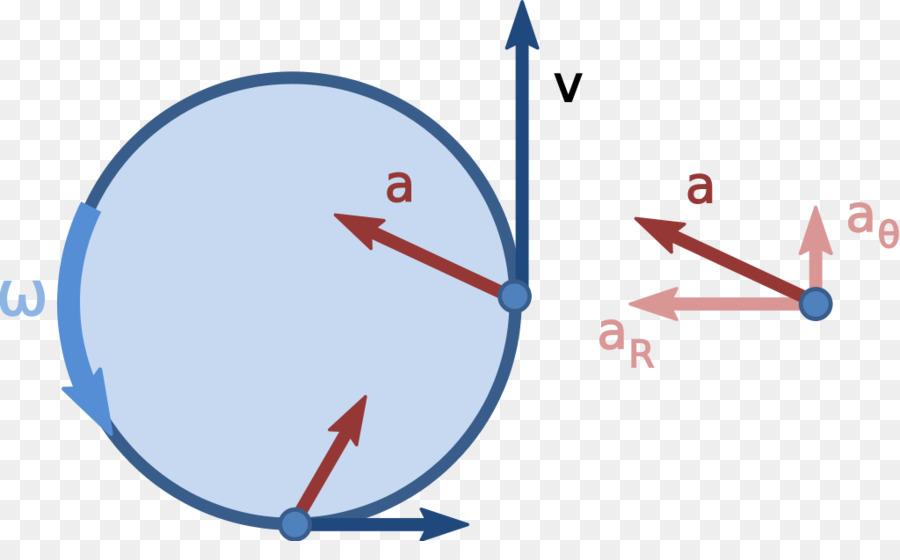
При рассмотрении понятия угла поворота θ уже была приведена формула, которая его связывает с линейным расстоянием L. Здесь же рассмотрим аналогичные выражения для скорости ω и ускорения α.

Линейная скорость v при равномерном движении определяется как расстояние L, пройденное за время t, то есть:

v = L/t

Подставляя сюда выражение для L через θ, получаем:

v = L/t = θ/t*r = ω*r

Мы получили связь между линейной и угловой скоростью. Важно отметить, что удобство использования угловой скорости связано с тем, что она не зависит от радиуса окружности. В свою очередь, линейная скорость v возрастает линейно с увеличением r.

Остается записать связь между линейным ускорением a и его угловым аналогом α. Чтобы это сделать, запишем выражение для скорости v при равноускоренном движении без начальной скорости v0. Получаем:

v = a*t

Подставляем сюда полученное выражение связи между v и ω:

ω*r = a*t =>

a = ω/t*r = α*r

Как и скорость, линейное ускорение, направленное по касательной к окружности, зависит от радиуса.

Ускорение центростремительное

Выше уже было сказано несколько слов об этой величине. Здесь приведем формулы, которые можно использовать для ее вычисления. Через скорость v выражение для центростремительного ускорения ac имеет вид:

ac = v2/r

Через угловую скорость его можно записать так:

ac = ω2*r2/r = ω2*r

Величина ac не имеет никакого отношения к тангенциальному ускорению a. Центростремительное ускорение обеспечивает поддержание вращающегося тела на одной окружности.

Задача на определение угловой скорости вращения планеты

Известно, что ближе всего к солнцу находится Меркурий. Полагая, что он вращается по окружности вокруг светила, мы можем определить его угловую скорость ω.

Для решения задачи следует обратиться к справочным данным. Из них известно, что планета делает полный оборот вокруг светила за 87 дней 23,23 часа земных. Это время называется периодом обращения. Учитывая, что движение происходит с постоянной угловой скоростью, запишем рабочую формулу:

θ = ω*t =>

ω = θ/t

Остается перевести время в секунды, подставить значение угла θ, соответствующее полному обороту (2*pi), и записать ответ: ω = 8,26*10-7 рад/c.

Человек регулярно сталкивается с разными видами движения. Перемещение тела по окружности позволяет понять многие физические процессы. На основе закономерностей такого явления работают разнообразные механизмы. Рассчитать характеристики движения по окружности достаточно просто, если знать и уметь применять несколько основных формул.

Движение тела по окружности — какими законами описывается

Движением по окружности в теории называют вращение какой-либо материальной точки или тела относительно оси, неподвижной в выбранной системе отсчета и не проходящей через центр тела.

Тело может двигаться по окружности двумя способами:

• равномерно;
• неравномерно.

Равномерное движение тела характеризуется постоянной угловой скоростью. Для описания такого перемещения применяют следующие формулы:

• угловая скорость: (omega =frac{2pi }{T})
• скорость движения: (V =frac{2pi R}{T}=omega R)
• угол поворота: (phi =2pi frac{t}{T}=omega t)
• ускорение: (frac{2pi v}{T}=omega ^{2}R)

Неравномерное движение возможно при переменной угловой скорости тела. В данном случае применимы формулы:

• тангенциальное ускорение: (a_{t}=frac{dv}{dt})
• центростремительное ускорение: (a_{n}=frac{v^{2}}{R}=omega ^{2}R)

В представленных уравнениях используются такие параметры, как:

• Т — период вращения;
• t — время;
• ω — угловая скорость;
• R — радиус;
• a_t — тангенциальное ускорение;
• a_n — центростремительное или полное ускорение.

При отсутствии специальных оговорок, в процессе решения задач движение тела по окружности принимают за равномерное. Для расчета пройденного пути используют формулу:

(S=frac{v}{t})

где:

• S является расстоянием, которое преодолело тело;
• v представляет собой скорость движения тела;
• t определяет время движения.

Таким образом, справедливы выражения:

(v=frac{S}{t})

(t =frac{v}{S})

Величины, которые применяют для решения задач, характеризуются положительными значениями:

S > 0, v > 0, t > 0

При решении задач принято все величины переводить в единицы измерения, согласно системе СИ.

Секретом заданий на движение тела по окружности является то, что обгоняющий будет преодолевать на 1 круг больше при первом обгоне. Данное расстояние считается на n кругов больше, если первый объект обогнал другого в n-ый раз.

Задачи на движение по окружности от простых до сложных

Задачи на движение тела по окружности отличаются по степени сложности. Можно рассмотреть примеры простых заданий.

Задача 1

Длина круговой трассы составляет 8 километров. Из ее точки в один момент времени в одинаковом направлении выехали два автомобиля. Первый автомобиль развил скорость 114 км/ч и, спустя 20 минут после начала движения, обогнал второй автомобиль на один круг. Требуется определить скорость, с которой двигался второй автомобиль. Ответ необходимо представить в км/ч.

Решение

Известно, что старт произошел одновременно для обоих автомобилей. Через 20 минут после начала движения первое транспортное средство опережало второе на один круг. Таким образом, в течение 20 минут или 1/3 часа первый автомобиль преодолел на 1 круг больше, то есть на 8 км больше. За час первый автомобиль проехал на 8*3=24 км больше, чем второй. Скорость второго транспортного средства на 24 км/ч меньше по сравнению с первым, и равна 114-24=90 км/ч.

Ответ: второй автомобиль двигался со скоростью 90 км/ч.

Задача 2

Из пункта А круговой трассы выехал велосипедист, а спустя полчаса стартовал мотоциклист. Через 10 минут после начала пути водитель мотоцикла догнал велосипедиста в первый раз. Спустя еще 30 минут мотоциклист догнал велосипедиста повторно. Требуется определить, какова скорость мотоциклиста, в том случае, когда длина трассы составляет 30 км. Ответ необходимо представить в км/ч.

Решение

В первую очередь требуется перевести минуты в часы. Скорости мотоциклиста и велосипедиста можно обозначить х и у. В первый раз водитель мотоцикла обогнал велосипедиста, спустя 10 минут или 1/6 часа после начала движения. До этого момента велосипедист находился в движении 40 минут или 2/3 часа.

Можно упростить запись условий задачи:

велосипедист: v = х, t = 2/3, S = 2/3*х;

мотоциклист: v = у, t = 1/6, S = 1/6*у.

Велосипедист и мотоциклист преодолели одинаковый путь:

(frac{1}{6}y=frac{2}{3}x)

Спустя 30 минут или 1/2 часа после первого обгона мотоциклист выполнил второй обгон велосипедиста.

Таким образом:

велосипедист: v = х, t = 1/2, S = 1/2*х;

мотоциклист: v = у, t = 1/2, S = 1/2*у.

Требуется определить расстояния, которые преодолели гонщики. Мотоциклист обогнал велосипедиста, то есть проехал больше на один круг. Это является ключевым моментом в данной задаче. Один круг составляет 30 километров. Второе уравнение будет иметь вид:

(frac{1}{2}y-frac{1}{2}x=30)

Далее необходимо решить полученную систему:

у = 4х

у – х = 60

Таким образом, х = 20, у = 80.

Ответ: скорость мотоциклиста равна 80 км/ч.

Бывают задания на движение тела по окружности с повышенной степенью сложности. Как правило, подобные примеры при невозможности проведения экспериментов требуют сложных вычислений.

Задача 3

На часах со стрелками время 8 часов 00 минут. Требуется определить, через сколько минут минутная стрелка в четвертый раз догонит часовую стрелку.

Решение

Спустя один час минутная стрелка преодолевает один круг, а часовая проходит лишь 1/12 циферблата. Допустим, что скорости равны 1 круг в час и 1/12 круга в час соответственно. Начало движения приходится на 8.00. Необходимо определить время, в течение которого минутной стрелке в первый раз удастся догнать часовую.

Минутная стрелка преодолеет на 2/3 круга больше. Исходя из этого, можно записать уравнение:

(1*t-frac{1}{12}t=frac{2}{3})

Таким образом, спустя 8/11 часа стрелки совпадут. Предположим, что через время z стрелки совпадут повторно. Минутная стрелка преодолеет расстояние 1*z, а часовая 1/12*z. При этом минутной стрелкой будет пройдено на один круг больше. Можно записать уравнение:

(1*z-frac{1}{12}z=1)

Решение данного уравнения будет таким:

(z=frac{12}{11})

Таким образом, через 12/11 часа стрелки совпадут повторно. Спустя еще 12/11 часа они встретятся вновь и так далее. Поэтому при старте в 8.00 в четвертый раз минутная стрелка догонит часовую через:

(frac{8}{11}+3frac{12}{11}) часа

Ответ: минутная и часовая стрелки совпадут в четвертый раз через (frac{8}{11}+3frac{12}{11})часа.

Нередко при решении задач на движение по окружности требуется рассчитать среднюю скорость тела. Важно, что данная величина не совпадает со средним арифметическим скоростей. Средняя скорость определяется с помощью формулы:

(v=frac{S_{0}}{t_{0}})

где v является средней скоростью;

S₀ представляет собой общий путь;

t₀ определяет общее время.

При наличии двух участков пути средняя скорость рассчитывается по формуле:

(v=frac{S_{1}+S_{2}}{t_{1}+t_{2}})

Наиболее сложными задачами считаются примеры с пятизначными дискриминантами. Рассмотрим алгоритм действий в таком случае.

Задача 4

Пара гонщиков участвует в соревновании. Путь, который требуется преодолеть, равен 60 кругам кольцевой трассы в 3 км. После одновременного старта первый гонщик пересек финиш раньше, чем второй на 10 минут. Требуется рассчитать среднюю скорость второго гонщика. Известно, что впервые первый участник обогнал второго на круг, спустя 15 минут после начала движения. Ответ требуется записать в км/ч.

Решение

Первый участник гонки, находясь в движении 15 минут, догнал второго гонщика на первом круге. Таким образом, в течение 15 минут он преодолел на 1 круг или на 3 км больше, чем второй. За час первый гонщик проехал 3*4=12 километров больше. При этом скорость его движения на 12 км/ч превышает скорость второго гонщика. 10 минут соответствует ¼ часа. Можно записать уравнение:

(frac{180}{x}-frac{180}{x+12}=frac{1}{6})

Далее необходимо преобразовать выражение к квадратному уравнению:

(x^{2}+12x-12960=0)

Таким образом, получен пятизначный дискриминант. Есть более простой вариант решения задачи. Можно записать уравнение:

(frac{180}{x}-frac{180}{x+12}=frac{1}{6})

В нем 180 можно поделить на 12. Заменим х=12z:

(frac{180}{12z}-frac{180}{12z+12}=frac{1}{6})

(frac{15}{z}-frac{15}{z+1}=frac{1}{6})

(frac{90}{z}-frac{90}{z+1}=1)

Данное равенство можно преобразить в квадратное уравнение. Целый положительный корень такого выражения z=9. Тогда получим:

(х=12z=108)

Ответ: средняя скорость второго гонщика равна 108 км/ч.

Нахождение линейной скорости при движении по окружности

Любая точка, находящаяся на окружности, перемещается с некоторой скоростью. Данная величина называется линейной скоростью. Вектор линейной скорости всегда совпадает по направлению с касательной к окружности. К примеру, стружка из точильного станка движется, повторяя направление мгновенной скорости.

Можно рассмотреть какую-то точку на окружности, совершившую один оборот. При этом было затрачено время равное периоду Т. Расстояние или путь, пройденный точкой, представляет собой длину рассматриваемой окружности.

Задачи на тему равномерное движение по окружности

Задача 1

Радиус выпуклого моста равен 90 м. Требуется определить скорость, с которой автомобиль должен пройти его середину, чтобы пассажир на мгновение ощутил невесомость.

Решение

Согласно условиям задачи:

R = 90 м

N = 0

Сила реакции опоры обладает нулевым значением, так как пассажир в состоянии невесомости не оказывает давление на сиденье автомобиля.

Решение задачи необходимо представить в системе отсчета, которая связана с Землей. Человек совершает движение вместе с автомобилем. Ускорение при этом направлено вниз. На пассажира действует сила притяжения Земли, которая будет центростремительной:

(mg=mfrac{v^{2}}{R})

Таким образом:

(v=sqrt{frac{Rmg}{m}}=sqrt{Rg}=sqrt{90*10}=30) м/с

Ответ: скорость автомобиля составляет 30 м/с.

Задача 2

Масса девочки 40 кг. Она качается на качелях, длина подвеса которых составляет 4 м. Требуется определить силу, с которой девочка давит на сиденье при прохождении среднего положения со скоростью 5 м/с.

Решение

На девочку действует сила тяжести (mvec{g}) и сила реакции опоры (vec{N}).

Качели находятся под действием силы давления  (vec{F_{g}}), которая направлена вниз. Согласно третьему закону Ньютона, данная сила соответствует взятой со знаком минус силе реакции опоры:

(vec{F_{g}}=-vec{N})

Таким образом, решением задачи является определение силы реакции опоры. Исходя из закона динамики:

(mvec{g}+vec{N}= mvec{a})

В проекции на ось Х:

(N-mg=mfrac{v^{2}}{R})

Из чего следует вывод:

(F_{g}=left|N right|=m(g+frac{v^{2}}{R}))

(F_{g}=40(10+frac{5^{2}}{4})=650) Н

Ответ: сила равна 650 Н.

Задача 3

Шарик привязали с помощью нити к подвесу. Он описывает в горизонтальной плоскости окружность, совершая движение с постоянной скоростью. Нить обладает длиной 0,6 м и составляет с вертикалью угол в 60 градусов. Необходимо рассчитать, какова скорость шарика.

Решение

Сумма сил (mvec{g}) и натяжения (vec{F_{n}}), исходя из правила параллелограмма, соответствует результирующей силе, направленной в центр вращения (sum_{i}^{}{vec{F}_{i}}):

(sum_{i}^{}{vec{F}_{i}}= mvec{g}+vec{F_{n}}= mvec{a})

Силы в сумме определяются из прямоугольного треугольника с углом α равным 60 градусам. Исходя из того, что (vec{F_{n}}) является противолежащим катетом, получим:

(vec{F_{n}}=mg*tg α)

Таким образом:

(mg*tg α= mvec{a}= mfrac{v^{2}}{R})

(v^{2}=frac{mg*tan alpha *R}{m}=gR*tan alpha)

R включен в прямоугольный треугольник, в котором длина нити представляет собой гипотенузу. R является катетом, противолежащий углу α в 60 градусов.

(R=l*sin alpha)

Преобразив формулу квадрата скорости шарика с помощью подстановки выражения для радиуса, получим:

(v^{2}=gl*sin alpha *tan alpha )

(v=sqrt{gl*sin alpha *tan alpha }=sqrt{10*0.6*frac{sqrt{3}}{2}*sqrt{3}}=3) м/с

Ответ: скорость шарика составляет 3 м/с.

Задача 4

Необходимо определить максимальную скорость мотоцикла по горизонтальной плоскости, который описывает при этом дугу окружности с радиусом 100 м. Коэффициент трения резины о плоскость составляет 0,4.

Решение

Во время поворота мотоцикл наклоняется к центру поворота. На транспортное средство оказывают действие:

• сила тяжести (mvec{g});
• сила реакции опоры (vec{N});
• сила трения (vec{F_{tr}});
• сила тяги (vec{F_{t}});
• сила сопротивления (vec{F_{c}}).

Данные силы в сумме составляют:

(mvec{g}+vec{N}+vec{F_{tr}}+vec{F_{t}}+vec{F_{c}}= mvec{a})

Согласно выражениям:

(mvec{g}+vec{N}=0)

(vec{F_{t}}+vec{F_{c}}=0)

Получим:

(vec{F_{tr}}= mvec{a})

Сила трения составляет:

(F_{tr}= mu mg)

Таким образом:

(mu mg=ma= mfrac{v^{2}}{R})

(v=sqrt{frac{mu mgR}{m}}=sqrt{mu gR}=sqrt{0.4*10*100}=20) м/с

Ответ: максимальная скорость равна 20 м/с.

Задачи разной сложности по теме движения тела по кружности часто встречаются не только в школьной программе, но и во время обучения в вузе. Знание основных закономерностей позволит быстро найти решение примера любой сложности. Если в процессе расчетов возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.

Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.

При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (a_r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) a_n или а_ЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.

Модуль центростремительного ускорения равен

a_ЦС=v² / R

Где v – линейная скорость, R – радиус окружности

Рис. 1.22. Движение тела по окружности.

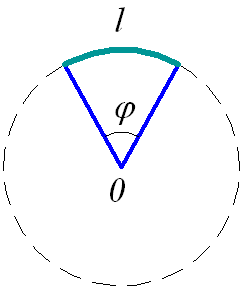
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то

1 радиан= l / R

Так как длина окружности равна

l = 2πR

то

360^о = 2πR / R = 2π рад.

Следовательно

1 рад. = 57,2958^о = 57^о18’

Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:

ω = φ / t

Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:

v= l / t

Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением

l = Rφ

где R – радиус окружности.

Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:

v = l / t = Rφ / t = Rω или v = Rω

Рис. 1.23. Радиан.

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.

n = 1 / T

За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда

T = 2π / ω

То есть угловая скорость равна

ω = 2π / T = 2πn

Центростремительное ускорение можно выразить через период Т и частоту обращения n:

a_ЦС = (4π²R) / T² = 4π²Rn²

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---