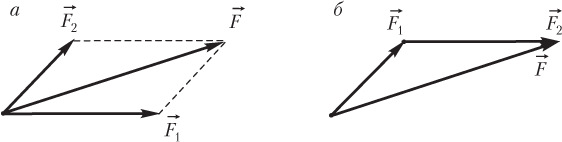Как найти модуль равнодействующей горизонтальных сил

Формула модуля равнодействующей силы

Сила является вектором, то есть обладает как модулем (величиной) так и направлением. Однако чаще всего приходится иметь дело с телами, на которые действуют не одна, а несколько сил. Тогда рассматривают сумму всех сил, оказывающих действие на тело, такую сумму сил называют равнодействующей силой ():

   

Равнодействующая сила – это гипотетический (искусственный) параметр, который вводят для того, чтобы удобнее было производить расчеты. Следует учитывать, что равнодействующая сила (как и любая сила) – это векторная величина, имеющая модуль и направление.

Модуль равнодействующей двух сил

Допустим, тело находится под воздействием двух сил. Они направлены по одной прямой (рис.1).

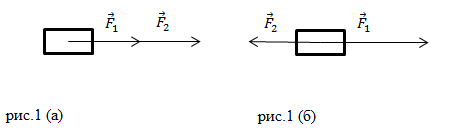
Если силы имеют одинаковые направления (рис.1 (а)), то модуль равнодействующей вычисляется как:

   

На рис 1(б) силы направлены по одной прямой, но имеют противоположные направления. Формулой для вычисления модуля равнодействующей в таком случае будет выражение:

   

Рассмотрим случаи, когда две силы, действующие на тело, направлены под углом друг другу (рис.2).

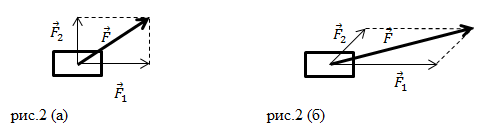
В случае, который представлен на рис.2 (а) силы и направлены под углом 900 по отношению друг к другу. Модуль равнодействующей силы можно найти по теореме Пифагора:

   

Если угол между векторами сил и отличен от прямого угла, то модуль равнодействующей силы находят по теореме косинусов:

   

где – угол между векторами и

Модуль равнодействующей нескольких сил

Пусть на тело действуют силы: , тогда равнодействующая этих сил () находится в соответствии с формулой (1). Для того чтобы вычислить модуль равнодействующей нескольких сил приложенных к телу выполняют следующую последовательность действий:

1. Вводят декартову систему координат, выбирают направления осей (X,Y).
2. Записывают проекции сил, действующих на тело на избранные оси:

      

3. Вычисляют проекции равнодействующей силы на оси X и Y, при этом складывают проекции сил по осям. Необходимо отметить, что суммирование проводят алгебраическое, то есть учитывают знаки проекций:

      

4. И в заключении модуль равнодействующей силы находят, применяя теорему Пифагора:

      

Примеры решения задач по теме «Модуль равнодействующей силы»

На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.

Формула равнодействующей всех сил

Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.

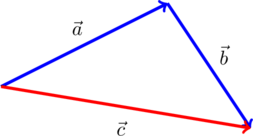
Складывают векторы, используя правило треугольника (рис.1)

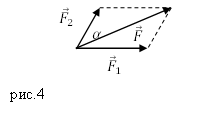
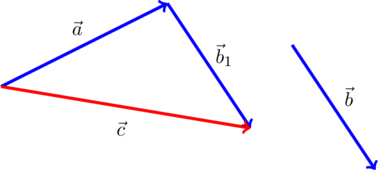
правило параллелограмма (рис.2).

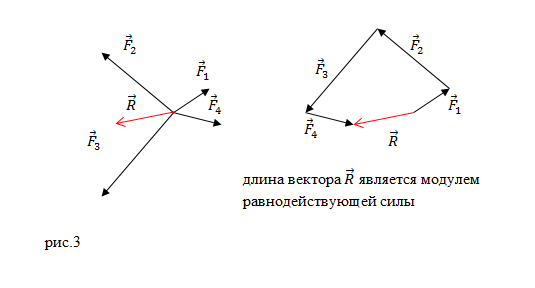
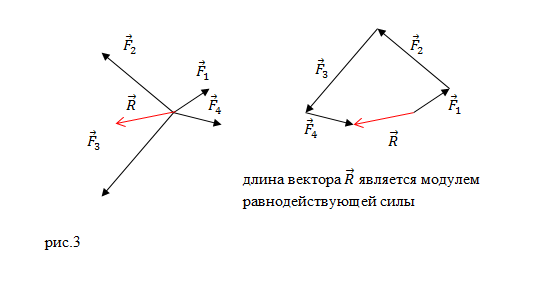
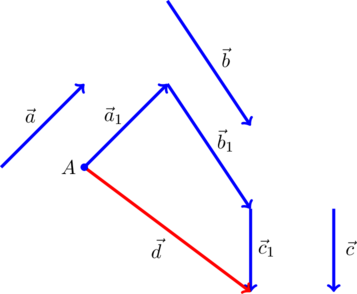
или многоугольника (рис.3):

Второй закон Ньютона и формула модуля равнодействующей

Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:

$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач с решением

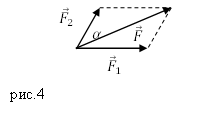
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?

Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Н
ight).]

Ответ. $F=52,92$ Н

Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?

Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:

Следовательно, модуль силы можно найти как:

Ускорение точки будем искать, используя связь между ним и перемещением точки:

Первая производная от $s$ по времени равна:

Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:

Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:

О причинах изменений

Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.

Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.

Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).

Сложение сил

В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:

$mvec a = sumlimits_^n vec F_i$.

Рис. 1. Равнодействующая сил.

Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:

$F = sumlimits_^n vec F_i$

А силу $F_i$ представим в виде:

Тогда суммой двух сил будет новый вектор $F_ = (F_ + F_, F_ + F_, F_ + F_)$.

Рис. 2. Покомпонентное сложение векторов.

Абсолютное значение равнодействующей можно рассчитать так:

Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.

Разберем правила треугольника и параллелограмма. Графически это выглядит так:

Рис. 3. Правило треугольника и параллелограмма.

Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.

Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.

Задачи

• На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.

Решение

Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.

$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:

Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.

Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.

Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:

• На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?

Решение

Достаточно сложить иксовые компоненты векторов:

Что мы узнали?

В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.

Силу, заменяющую собой действие на тело нескольких сил, называют равнодействующей ; равнодействующая сила равна векторной сумме сил, приложенных к данному телу:

F → = F → 1 + F → 2 + . + F → N ,

где F → 1 , F → 2 , . F → N — силы, приложенные к данному телу.

Равнодействующую двух сил удобно находить графически по правилу параллелограмма (рис. 2.14, а ) или треугольника (рис. 2.14, б ).

Для сложения нескольких сил (вычисления равнодействующей) используют следующий алгоритм :

1) вводят систему координат и записывают проекции всех сил на координатные оси:

F 1 x , F 2 x , . F Nx ,

F 1 y , F 2 y , . F Ny ;

2) вычисляют проекции равнодействующей как алгебраическую сумму проекций сил:

F x = F 1 x + F 2 x + . + F Nx ,

F y = F 1 y + F 2 y + . + F Ny ;

3) модуль равнодействующей вычисляют по формуле

F = F x 2 + F y 2 .

Рассмотрим частные случаи равнодействующей.

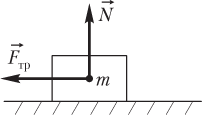
Силу взаимодействия тела с горизонтальной опорой , по которой может происходить движение тела, рассчитывают как равнодействующую силы трения и силы реакции опоры (рис. 2.15):

F → вз = F → тр + N → ,

ее модуль вычисляется по формуле

F вз = F тр 2 + N 2 ,

где F → тр — сила трения скольжения или покоя; N → — сила реакции опоры.

Частные случаи равнодействующей:

Силу взаимодействия тела с комбинированной опорой (например, креслом автомобиля, самолета и т.п.) рассчитывают как равнодействующую сил давления на вертикальную и горизонтальную части опоры (рис. 2.16):

F → вз = F → гор + F → верт ,

где F → гор — сила давления, действующая на тело со стороны горизонтальной части опоры (численно равная весу тела); F → верт — сила давления, действующая на тело со стороны вертикальной части опоры (численно равная силе инерции).

Частные случаи равнодействующей:

Равнодействующая силы тяжести и силы Архимеда называется подъемной силой (рис. 2.17):

F → под = F → А + m g → ,

ее модуль вычисляется по формуле

F под = F А − m g ,

где F → А — сила Архимеда (выталкивающая сила); m g → — сила тяжести.

Частные случаи равнодействующей:

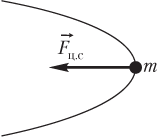
Если под влиянием нескольких сил тело равномерно движется по окружности, то равнодействующая всех приложенных к телу сил является центростремительной силой (рис. 2.18):

F → ц .с = F → 1 + F → 2 + . + F → N .

где F → 1 , F → 2 , . F → N — силы, приложенные к телу.

Модуль центростремительной силы, направленной по радиусу к центру окружности, может быть вычислен по одной из формул:

F ц .с = m v 2 R , F ц .с = m ω 2 R , F ц .с = m v ω ,

где m — масса тела; v — модуль линейной скорости тела; ω — величина угловой скорости; R — радиус окружности.

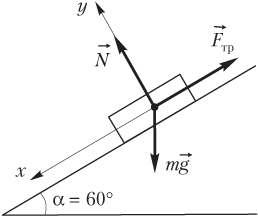
Пример 21. По дну водоема, наклоненному под углом 60° к горизонту, начинает скользить тело массой 10 кг, полностью находящееся в воде. Найти модуль равнодействующей всех сил, приложенных к телу, если между телом и дном водоема воды нет, а коэффициент трения составляет 0,15.

Решение. Так как между телом и дном водяная прослойка отсутствует, то сила Архимеда на тело не действует.

Искомой величиной является модуль векторной суммы всех сил, приложенных к телу:

F → = F → тр + m g → + N → ,

где N → — сила нормальной реакции опоры; m g → — сила тяжести; F → тр — сила трения. Указанные силы и система координат изображены на рисунке.

Вычисление модуля результирующей силы F проведем в соответствии с алгоритмом.

1. Определим проекции сил, приложенных к телу, на координатные оси:

проекция силы трения

F тр x = − F тр = − μ N ;

проекция силы тяжести

( m g ) x = m g sin 60 ° = 0,5 3 m g ;

проекция силы реакции опоры

проекция силы трения

проекция силы тяжести

( m g ) y = − m g cos 60 ° = − 0,5 m g ;

проекция силы реакции опоры

где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения.

2. Вычислим проекции равнодействующей на координатные оси, суммируя соответствующие проекции указанных сил:

F x = F тр x + ( m g ) x = − μ N + 0,5 3 m g ;

F y = ( m g ) y + N y = − 0,5 m g + N .

Движение по оси Oy отсутствует, т.е. F y = 0, или, в явном виде:

Отсюда следует, что

что позволяет получить формулу для расчета силы трения:

F тр = μ N = 0,5 μ m g .

3. Искомое значение равнодействующей:

F = F x 2 + F y 2 = | F x | = − 0,5 μ m g + 0,5 3 m g = 0,5 m g ( 3 − μ ) .

F = 0,5 ⋅ 10 ⋅ 10 ( 3 − 0,15 ) = 79 Н.

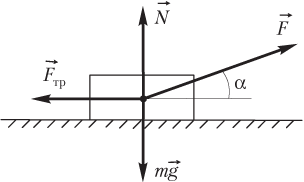
Пример 22. Тело массой 2,5 кг движется горизонтально под действием силы, равной 45 Н и направленной под углом 30° к горизонту. Определить величину силы взаимодействия тела с поверхностью, если коэффициент трения скольжения равен 0,5.

Решение. Силу взаимодействия тела и опоры найдем как равнодействующую силы трения F → тр и силы нормальной реакции опоры N → :

F → вз = F → тр + N → ,

модуль которой определяется формулой

F вз = F тр 2 + N 2 .

Силы, приложенные к телу, показаны на рисунке.

Модуль силы нормальной реакции опоры определяется формулой

N = m g − F sin 30 ° ,

а модуль силы трения скольжения —

где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения; F — модуль силы, вызывающей движение тела.

С учетом выражений для N и F тр формула для расчета искомой силы принимает вид:

F вз = ( μ N ) 2 + N 2 = N μ 2 + 1 = ( m g − F sin 30 ° ) μ 2 + 1 .

F вз = ( 2,5 ⋅ 10 − 45 ⋅ 0,5 ) ( 0,5 ) 2 + 1 ≈ 2,8 Н.

Пример 23. Во сколько раз изменится подъемная сила, если с аэростата сбросить балласт, равный половине его массы? Плотность воздуха считать равной 1,3 кг/м 3 , массу аэростата с балластом — 50 кг. Объем аэростата составляет 50 м 3 .

Решение. Подъемная сила, действующая на аэростат, является равнодействующей силы Архимеда F → А и силы тяжести m g → :

F → под = F → А + m g → ,

модуль которой определяется формулой

где F A = ρ возд gV — модуль силы Архимеда; ρ возд — плотность воздуха; g — модуль ускорения свободного падения; V — объем аэростата; m — масса аэростата (с балластом или без него).

Модуль подъемной силы может быть рассчитан по формулам:

• для аэростата с балластом

F под 1 = ρ возд g V − m 1 g ,

• для аэростата без балласта

F под 2 = ρ возд g V − m 2 g ,

где m 1 — масса аэростата с балластом; m 2 — масса аэростата без балласта.

Искомое отношение модулей подъемных сил составляет

F под 2 F под 1 = ρ возд V − m 2 ρ возд V − m 1 = 1,3 ⋅ 50 − 25 1,3 ⋅ 50 − 50 ≈ 2,7 .

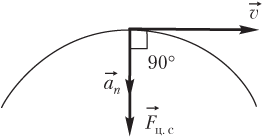
Пример 24. Модуль равнодействующей всех сил, действующих на тело, равен 2,5 Н. Определить в градусах угол между векторами скорости и ускорения, если известно, что модуль скорости остается постоянным.

Решение. Скорость тела не изменяется по величине. Следовательно, тело обладает только нормальной составляющей ускорения a → n ≠ 0 . Такой случай реализуется при равномерном движении тела по окружности.

Равнодействующая всех сил, приложенных к телу, является центростремительной силой и показана на рисунке.

Векторы силы, скорости и ускорения имеют следующие направления:

• центростремительная сила F → ц .с направлена к центру окружности;
• вектор нормального ускорения a → n направлен так же, как и сила;
• вектор скорости v → направлен по касательной к траектории движения тела.

Следовательно, искомый угол между векторами скорости и ускорения равен 90°.

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2 -х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

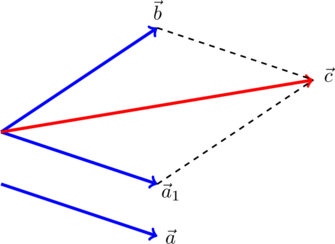
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

Как построить векторы сил

Простейшие примеры векторов в физике — скорость и сила.

1. Всякое движение можно представить как результат сложения нескольких движений, его составляющих. Скорость результирующего движения изображается по величине и направлению диагональю параллелограмма, построенного на отрезках, изображающих составляющие скорости, как на сторонах. Рассмотрим конкретный пример.

Рыбак переправляется на лодке `A` через реку, которая течёт в сторону, указанную стрелкой (рис. 18). Пусть скорость течения воды `vec(v_1)` изображается по величине и направлению отрезком `AB`, а скорость `vec(v_2)` движения лодки относительно воды под влиянием усилий гребца изображается отрезком `AC` (в стоячей воде лодка двигалась бы по направлению `AC` со скоростью `vec(v_2)`). Лодка будет двигаться относительно берега по направлению `AM` со скоростью `vec v`, изображаемой диагональю `AD` параллелограмма, постро­енного на векторах `vec(v_1)` и `vec(v_2)` (в данном случае параллелограмм `ABCD` является прямоугольником).

2. Сила — как векторная величина — всегда имеет определённое направление, модуль, а также точку приложения.

Часто встречаются случаи, когда на тело действуют несколько сил. Тогда бывает удобно заменить их одной силой, которая производит на тело такое же действие, как и несколько одновременно действующих сил. Такую силу (если она существует) называют равнодействующей. Нахождение равнодействующей нескольких сил осуществляется с по­мощью правил векторного сложения, при этом слагаемые силы назы­вают составляющими.

Так, несколько сил, действующих на одну и ту же точку тела, всегда можно заменить одной равнодействующей, как бы ни были направлены силы и каковы бы ни были их величины. Пусть, например, на тело действуют четыре силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и `vec(F_4)`, приложенные к одной точке `O` и лежащие в одной плоскости (рис. 19). Тогда их равнодействующая `vec F` будет равна векторной сумме этих сил, найденной по правилу многоугольника (рис. 20).

Найти равнодействующую `vec R` трёх равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми силами равны между собой.

`F_1 = F_2 = F_3 = F`.

См. рис. 21. Углы между парами векто ров `vec(F_1)` и `vec(F_2)`, `vec(F_2)` и `vec(F_3)`, а также между векторами `vec(F_1)` и `vec(F_3)`, равны друг другу и равны `120^@` . Сложим силы `vec(F_2)` и `vec(F_3)` по правилу параллелограмма. Вследствие равенства модулей сил `vec(F_2)` и `vec(F_3)` этот параллелограмм есть ромб. Сумма сил `vec(F_2) + vec(F_3)` есть диагональ ромба, поэтому углы между парами векторов `vec(F_2)` и `vec(F_2) + vec(F_3)`, а также `vec(F_3)` и `vec(F_2) + vec(F_3)` равны по `60^@` , т. е. векторы `vec(F_1)` и `vec(F_2) + vec(F_3)` направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах `vec(F_2)` и `vec(F_3)`, состоит из двух равносторонних треугольников, поэтому модуль силы

`|vec(F_2) + vec(F_3)| = F_2 = F_3 = F = F_1`, т. е `vec F_1 = — (vec(F_2) + vec(F_3))`,

откуда следует `vec(F_1) + vec(F_2) + vec(F_3) = 0`.

К телу приложено `6` сил, лежащих в одной плоскости и составляющих друг с другом углы в `60^@`. Силы последовательно равны `1`, `2`, `3`, `4`, `5` и `6 Н`. Найти равнодействующую `vec R` этих шести сил.

Сложение сил по правилу многоугольника здесь нецелесообразно. Поступим иначе. Сложим сначала попарно силы, направленные вдоль одной прямой (см. рис. 22 а, б, в).

`|vec(F_2) + vec(F_4)| = 4 — 1 = 3`,

аналогично `|vec(F_2) + vec(F_5)| = 5 — 2 = 3` и `|vec(F_3) + vec(F_6)| = 6 — 3 = 3`.

Сумма сил `vec(F_2) + vec(F_5)` направлена вдоль вектора `vec(F_5)`. Туда же направлена и сумма сил `vec(F_1) + vec(F_4) + vec(F_3) + vec(F_6)`, причём модуль этой силы равен `3`. В итоге получаем, что сумма всех шести сил `vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)` направлена вдоль направления силы `vec(F_5)`, а модуль этой силы `|vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)| = 3 + 3 = 6 Н`.

Найти равнодействующую `vec R` пяти равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой (см. рис. 23). (Эти углы, разумеется, равны `360^@ //5 = 72^@`.)

В отличие от предыдущего примера здесь мы имеем нечётное число сил, поэтому невозможно образовать из них целое число пар. Поступим иначе. Возьмём какую-нибудь силу, например, `vec(F_1)`, а остальные сгруппируем в пары и попарно сложим их (см. рис. 24):

`vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`.

Почему удобна именно такая группировка сил в пары? Дело в том, что обе суммы сил (и `vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`) направлены вдоль линии действия силы `vec(F_1)`. Ясно, что равнодействующая всех сил будет направлена вдоль линии действия силы `vec(F_1)`. Модули сумм сил легко найти из геометрии. Например, в силовом параллелограмме, построенном на векторах `vec(F_2)` и `vec(F_5)`, который является ромбом, длина диагонали ромба (модуль силы `vec(F_2) + vec(F_5)`) равна удвоенной половинке диагонали, а та легко ищется из любого из четырёх прямоугольных треугольников, на которые ромб разбивается диагоналями. В результате

`|vec(F_2) + vec(F_5) | = 2F cos 72^@`,

где `F` — модуль любой из пяти исходных сил. Аналогично

`|vec(F_3) + vec(F_4)| = 2F cos 36^@`.

В итоге для модуля искомой силы получаем формулу

`R = F(1 + 2 cos 72^@ — 2 cos 36^@)` (*).

Для углов `72^@` и `36^@` нет таких простых формул, как для углов `30^@`, `45^@` или `60^@`. Пользуясь калькулятором, можно, однако, показать, что согласно формуле (*) `R = 0`.

Имеется и более красивое доказательство того, что результирующий вектор есть нулевой вектор. В самом деле, мы довольно произвольно взяли в качестве силы, которой не хватило пары, силу `vec(F_1)`. Если бы в качестве такой взять силу `vec(F_2)`, а в пары объединить `vec(F_1)` и `vec(F_3)` (одна пара) и `vec(F_4)` и `vec(F_5)`, то, повторив рассуждения, получим, что равнодействующая всех пяти сил `vec R` должна быть направлена вдоль линии действия силы `vec(F_2)`. Возможно ли, чтобы вектор был одновременно направлен вдоль двух несовпадающих друг с другом направлений (и `vec(F_1)`, и `vec(F_2)`; а на самом деле, как догадался читатель, ещё и вдоль направления действия сил `vec(F_3)`, `vec(F_4)` и `vec(F_5)`!)? Ненулевым вектор не может быть! Остаётся одна возможность: суммарный вектор – нулевой!

В примерах 10 и 11 мы искали по правилу параллелограмма суммы сил.

В примере 12 нас интересовала лишь проекция равнодействующей силы на направление (например, силы `vec(F_1)`).

В следующих примерах наш интерес будет также скорее не к равнодействующей силе, а только к каким-то её проекциям.

Электрический фонарь весом `Q = 16 Н` укреплён, как показано на рис. 25.

Определите отношение натяжений `T_1` и `T_2` в проволоках `BA` и `BC`, углы наклона которых даны на рисунке.

В условиях равновесия сумма всех сил, приложенных к точке `B`, равна нулю. Поэтому проекция равнодействующей всех сил на горизонтальное направление тоже равна нулю. Проекция силы со стороны проволоки, идущей к фонарю, на это направление равна нулю (эта сила вертикальна). Остаются вклады от двух натяжений со стороны проволок `BA` и `BC`. Горизонтальную ось направим слева направо. Тогда имеем: T 1 , гор + T 2 , гор = 0 T_<1,;mathrm<гор>>+T_<2,;mathrm<гор>>=0 (см. рис. 26), т. е.

`T_1 * cos 60^@ — T_2 cos 45^@ = 0`

(или `T_1 * sin 30^@ — T_2 sin 45^@ = 0`), откуда получаем `T_1//T_2 = sqrt2`.

Однородная массивная верёвка подвешена за два конца на разных высотах (см. рис. 27). Масса верёвки `m`. Углы, которые составляет верёвка с вертикалью в точках закрепления, равны `30^@` и `60^@`.

Определите силы натяжения верёвки вблизи её точек крепления.

Задача кажется очень трудной, т. к. не ясно, какую роль играет неизвестная нам форма верёвки, которую она примет под действием сил тяжести всех частей верёвки. (В предыдущем примере мы не интересовались провисанием проволок под действием силы тяжести, молчаливо считая провисание малым.) И всё же задача в той постановке, в какой дана, имеет простое решение. Мысленно проведём горизонтальную ось слева направо. Поскольку верёвка находится в равновесии, то сумма проекций всех сил на горизонтальное направление равна нулю. Сила тяжести верёвки имеет нулевую проекцию на это направление (эта сила направлена вертикально). Снова остаются вклады от двух натяжений (см. рис. 28):

Полагая `sin 30^@ = 1//2` и `sin 60^@ = sqrt3 //2`, находим `T_1 // T_2 = sqrt3`. Мысленно проведём ещё и вертикальную ось, направив её вниз. Сумма проекций всех сил на эту ось также равна нулю:

`mg — T_1 cos 30^@ — T_2 cos 60^@ = 0`.

Учитывая найденное ранее соотношение между `T_1` и `T_2` и значения `cos 60^@ = 1//2` и `cos 30^@ = sqrt3 //2`, получаем:

`mg — sqrt3 * T_2 * sqrt3 //2 — T_2 //2 = 0`,

`T_2 = mg//2` и `T_1 = sqrt3 mg//2`.

На гладкой наклонной плоскости с углом наклона `alpha` лежит брусок массой `m`. Какую горизонтальную силу нужно приложить к бруску, чтобы он находился в покое (рис. 29)?

Определите также модуль нормальной силы реакции на брусок со стороны наклонной плоскости.

Брусок по условию задачи покоится. Значит, сумма всех сил, приложенных к бруску, равна нулю. Равны нулю и суммы проекций сил на любые направления, в частности, на направление вдоль наклонной плоскости и перпендикулярное ему. Нормальная сила реакции `vec N` со стороны наклонной плоскости имеет равную нулю составляющую вдоль наклонной плоскости.

Проекция сила тяжести `m vec g` на ось `Ox` вдоль наклонной плоскости (рис. 30) равна `- mg sin alpha`, а проекция горизонтальной силы `F` на эту ось равна `F cos alpha`. Других сил вдоль наклонной плоскости не действует (плоскость, по условию задачи, гладкая, т. е. сила трения пренебрежимо мала). Приравнивая нулю сумму проекций на ось `Ox` всех сил, действующих на тело, получаем: `- mg sin alpha + F cos alpha = 0`, откуда находим

`F = mg (sin alpha)/(cos alpha) = mg * bbb»tg» alpha`.

Для отыскания `N` обратимся к проекциям сил на направление `Oy`. Приравняем нулю и сумму проекций на ось `Oy`:

`N — mg cos alpha — F sin alpha = 0`,

откуда `N = mg cos alpha + F sin alpha`, или с учётом найденного значения `F`:

`N = mg cos alpha + mg (sin^2 alpha)/(cos alpha) = mg (cos^2 alpha + sin^2 alpha)/(cos alpha)`,

тогда с учётом основного тригонометрического тождества, `sin^2 alpha + cos^2 alpha = 1`, получаем окончательно

На шероховатой поверхности доски лежит брусок массой `m`. К нему приложена сила, направленная под углом `alpha` к горизонту (см. рис. 31).

Определите модуль нормальной силы реакции со стороны поверхности.

Поскольку брусок не проваливается и не подскакивает вверх, то сумма проекций сил на вертикальную ось равна нулю:

`N + F * sin alpha — mg = 0`,

(см. рис. 32), откуда находим

`N = mg — F * sin alpha`.

Часто совершенно безосновательно приравнивают силу реакции `N` силе тяжести `mg`. Мы видим, что даже в случае горизонтальной поверхности это в общем случае не так. Для наклонной плоскости это тоже не так. В предыдущем примере нормальная сила реакции равнялась `mg//cos alpha`. Кстати, если бы удерживающая сила `F` действовала там не вдоль горизонтали, а вдоль наклонной плоскости, то для удержания бруска на наклонной плоскости потребовалась бы сила величиной `F = mg sin alpha`, а нормальная сила реакции была бы равна `N = mg cos alpha` (и снова не равнялась бы `mg`!)

Докажите это самостоятельно.

(См. рис. 33). В данном примере мы имеем дело с весьма простым случаем разложения скорости на два взаимно перпендикулярных направления:

`vec v = vec(v _sf»гор») + vec(v_sf»верт»)`,

(См. рис. 34). В данном случае мы имеем дело со сложением движений: `vec(v_sf»с») = vec(v_sf»св») + vec(v_sf»в»)`, где `vec(v_sf»св»)` — скорость самолёта относительно воздуха (модуль которой равен скорости самолёта относительно земли в безветренную погоду), а `vec(v_sf»в»)` — скорость воздуха. Далее по теореме Пифагора получаем:

Как и в примере 9, мы также имеем дело со случаем сложения движений. Но там было проще: не требовалось выбирать никакой стратегии, рыбак лишь наблюдал, как снесёт его лодку течением воды в реке. Если бы вода в реке покоилась, то, направив корпус лодки под углом `alpha` к нормали, мы заставили бы её двигаться в направлении вектора `vec V` (см. рис. 35). В действительности, вода в реке не стоячая, а имеет скорость `vec u` Поэтому сносимая течением лодка будет двигаться в направлении вектора `vec v` таком, что `vec v = vec V + vec u`. Учитывая, что оба треугольника в параллелограмме на рис. 35 прямоугольные (по условию, лодка должна двигаться перпендикулярно берегам), находим

`sin alpha = u//V = 3//5`, `alpha

а по теореме Пифагора v = V 2 — u 2 = 4 м / с v=sqrt=4;mathrm м/mathrm с .

В данном примере скорость лодки относительно воды меньше, чем скорость воды в реке, `V *

Лодку вытягивают из воды, стоя на крутом берегу и выбирая верёвку, которая привязана к носу лодки, со скоростью `v` (см. рис. 37).

Какой будет скорость лодки `u` в момент, когда верёвка будет составлять угол `alpha` с горизонтом? Верёвка нерастяжима.

Традиционная ошибка решающих эту задачу состоит в том, что пытаются разложить движение лодки на два направления – горизонтальное и вертикальное, делая (неправильное!) построение, как показано на рис. 38а и получая неверный ответ `u = v * cos alpha`. Что здесь неправильно? В отличие от самолёта из примера 17, который двигался под отличным от нуля углом к горизонту (см. рис. 33), здесь лодка движется горизонтально ! Сделаем другое разложение скорости лодки `vec u` по двум направлениям – вдоль верёвки (в данный момент времени!) и перпендикулярно ей (см. рис. 38б).

Проекция вектора `vec u` на направление верёвки будет равна скорости `v`, с которой выбирают верёвку: `v = u cos alpha`, поэтому `u = v/(cos alpha)`.

Поясним ещё, почему проекция вектора `vec u` на направление верёвки будет равна скорости `v` с которой выбирают верёвку. Если мы имеем абсолютно твердое тело (АТТ), деформациями в котором можно пренебречь, или нерастяжимую нить (но уже максимально натянутую), то как бы ни двигались АТТ или нерастяжимая нить, они будут обладать следующим свойством. Возьмём две произвольные точки `A` и `B` нити или АТТ и мысленно соединим их прямой. Тогда составляющие скоростей выбранных точек вдоль этой прямой в любой момент времени будут равны друг другу: v A ∥ → = v B ∥ → overrightarrow>=overrightarrow> (см. рис. 39). В противном случае изменялось бы расстояние между точками `A` и `B`. Составляющие скорости, перпендикулярные отрезку прямой `AB`, могут быть при этом любыми.

Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 40). В некоторый момент времени силы натяжения тросов, идущих от лодок 1 и 2, равны друг другу по модулю и равны `F`. Угол между тросами равен `2 alpha`. Какая равнодействующая сила приложена к буксируемой лодке со стороны тянущих её лодок? Чему будет равна эта сила в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?

Две силы нужно сложить по правилу параллелограмма, который в данном случае будет ещё и ромбом с перпендикулярными друг другу диагоналями, разбивающими его на четыре равных прямоугольных треугольника. Из геометрии рис. 41 видно, что модуль равнодействующей силы `R` равен удвоенной длине прилежащего катета: `R = 2F cos alpha`. При стремлении угла между направлениями тросов к нулю `R -> 2F` (`cos alpha -> 1` при `alpha -> 0`).

Хитрее оказывается похожая задача, когда заданы не силы, а скорости.

Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 42). В некоторый момент времени модули скоростей лодок 1 и 2 равны друг другу и равны `v_1 = v_2 = v`. Найти модуль и направление скорости буксируемой лодки `u`. Тросы нерастяжимы. Чему будет равна эта скорость в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?

Ясно, что «решение» `u = 2v cos alpha` (как в предыдущем примере) не подходит, т. к. при `alpha -> 0` мы получили бы, что `u -> 2v`, чего не может быть. Если, например, две собаки в упряжке бегут с одинаковыми скоростями `v` в одном направлении, то и скорость упряжки будет равна этой же скорости `v` (если, конечно, упряжка не отцепилась или к ней не подключили дополнительно мотор).

Решение задачи такое же, как в примере 21. В данном примере важнейшими словами являются «Тросы нерастяжимы». Ясно, что правильное построение, учитывающее это условие, должно быть таким, как на рис. 43, откуда немедленно получаем `v = u cos alpha`, поэтому `u = v/(cos alpha)`. Тогда в предельном случае, когда `alpha -> 0`, имеем `u -> v`, как и должно быть.

Заметим, что четырёхугольник на рис. 43 весьма мало похож на параллелограмм из предыдущего примера. Еще меньше будет похож на параллелограмм этот четырёхугольник, когда модули скоростей `v_1 != v_2` (см. рис. 44).

Две лодки буксируют третью с помощью двух тросов (рис. 45). В некоторый момент времени скорость 2-ой лодки в 2 раза больше, чем скорость 1-ой, `v_2 = 2v_1 = 2v`, а угол между тросами равен `90^@`. В каком направлении и с какой скоростью движется в этот момент буксируемая лодка? Тросы нерастяжимы.

В данном случае четырёхугольник на рис. 44 будет прямоугольником — см. рис. 46 (т. е. всё же параллелограммом).

По определению тангенса угла `»tg»varphi _1 = v_2 //v_1 = 2`, откуда, пользуясь калькулятором, находим `varphi _1

63^@`; `varphi _2 = 90^@ — varphi _1

Модуль скорости буксируемой лодки найдём по теореме Пифагора (раз уж у нас «случайно» появились прямоугольные треугольники):

`u = sqrt(v_1^2 + v_2^2) = sqrt(v^2 + (2v)^2) = sqrt5 * v

Как составить силовые уравнения

В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.

Что такое равнодействующая

Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.

Результат сложения может дать:

1. вектор, имеющий длину,
2. или вектор, не имеющий длины.

Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.

Длина вектора содержит сумму квадратов всех его проекций на оси.

Где ( a_ ) и ( a_ ) — это проекции вектора (ссылка) ( vec ) на оси Ox и Oy.

Когда вектор равен нулю, равна нулю каждая его проекция на осях.

Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.

Левая часть силового уравнения

В левой части силового уравнения записываем силы, действующие на тело.

Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.

Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».

Правая часть силового уравнения

В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.

Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.

Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.

Тогда в правой части уравнения запишем:

• (ma), если ускорение направлено туда же, куда направлена ось;
• (- ma), если ускорение направлено противоположно оси;

А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.

В правой части уравнения запишем ноль (0 = ускорения нет).

Векторы сил параллельны

В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.

Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.

Проведем на рисунке ось, направим ее вверх.

Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.

Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:

Сила ( F_<text<сопр>>) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.

В правую часть уравнения поместим равнодействующую.

Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.

Математики запишут, что ускорение есть, но оно – нулевое (vec=0).

То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.

Примечания:

1. На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec>). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
2. На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.

Итоговое силовое уравнение имеет вид:

[large F_<text<сопр>> — m cdot g = 0 ]

Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.

Векторы сил не параллельны

Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.

Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).

Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.

Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.

Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.

Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.

Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.

Так выглядит уравнение для горизонтальной оси

Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.

Для вертикальной оси уравнение выглядит так:

[large N — m cdot g = 0 ]

Система, пригодная для решения задачи, состоит из двух уравнений

Куда направить оси

Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).

Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.

Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.

Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.

Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.

При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.

Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.

Выводы:

1. Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
2. Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.

Движение по наклонной плоскости

Составим систему уравнений для решения такой задачи:

Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.

Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.

Выражение для ускорения

Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)

Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.

Пользуясь осями координат, составляем теперь уравнения в проекциях.

Уравнение для проекций векторов на ось Ox:

[ large — F_<text<трен>> – m cdot g_ = — m cdot a ]

Уравнение для проекций векторов на ось Oy:

[ large N – m cdot g_ = 0 ]

Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.

[ large begin m cdot g_ = mg cdot cos left(alpha right) \ m cdot g_ = mg cdot sin left(alpha right) end ]

Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений

[ large begin — F_<text<трен>> – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end ]

Дополним эту систему выражением для силы трения.

Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.

[ large begin N = mg cdot cos left(alpha right) \ F_<text<трен>> = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end ]

Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:

[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]

Выражение для пройденного пути

Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:

[ large begin 0 = v_ <0>— a cdot t \ S = v_ <0>cdot t — a cdot frac <2>end ]

Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.

Упрощенная система для решения задачи теперь включает всего два уравнения

[ large begin mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_ <0>cdot frac> — frac> <2>cdot frac> end ]

Подставив в эту систему известные значения начальной (v_<0>) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.

Формула модуля равнодействующей силы в физике

Формула модуля равнодействующей силы

На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.

Формула равнодействующей всех сил

Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(1right).]

Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.

Складывают векторы, используя правило треугольника (рис.1)

правило параллелограмма (рис.2).

или многоугольника (рис.3):

Второй закон Ньютона и формула модуля равнодействующей

Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:

[overline{F}=sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(2right).]

$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач с решением

Читать дальше: формула периода колебаний математического маятника.

Модуль равнодействующей силы

Четверг, 24 декабря, 2015

В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.

Как найти модуль равнодействующей силы

Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку.

Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.

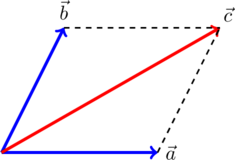
1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы и . Суммарный вектор есть вектор :

Если векторы и не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор заменен на равный ему вектор , и :

2. Правило треугольника. На рисунке по правилу треугольника складываются векторы и . В сумме получается вектор :

Если вектор отложен не от конца вектора , нужно заменить его равным и отложенным от конца вектора , после чего воспользоваться правилом треугольника. Например, на рисунке вектор заменен равным ему вектором , и :

3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки в конец последнего отложенного вектора. На рисунке :

Задача на нахождение модуля равнодействующей силы

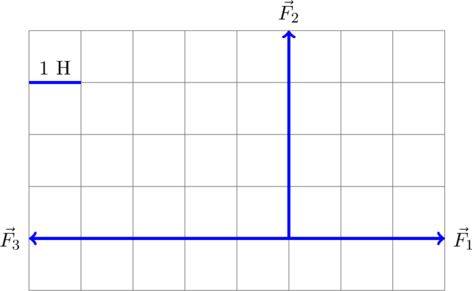
Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.

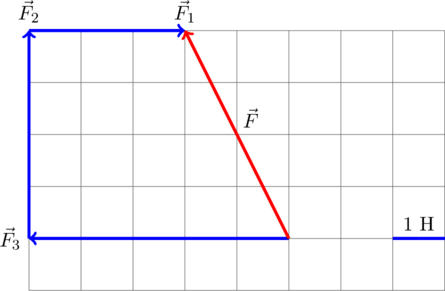
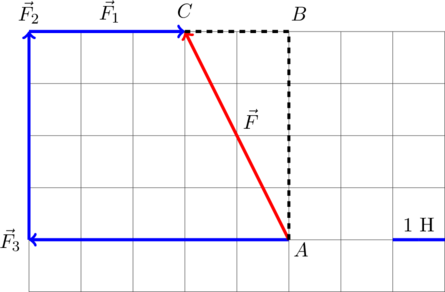
Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:

Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник :

Требуется найти гипотенузу этого треугольника. «По клеточкам» находим длину катетов: Н, Н. Тогда по теореме Пифагора для этого треугольника получаем: Н. То есть искомый модуль равнодействующей сил равен Н.

Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!

Репетитор по физике на Юго-Западной
Сергей Валерьевич