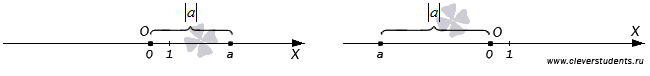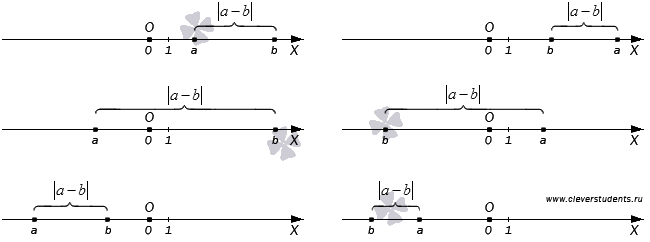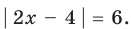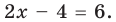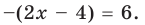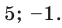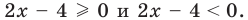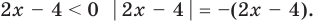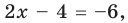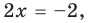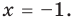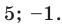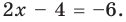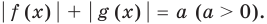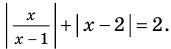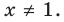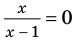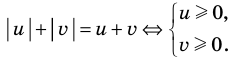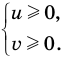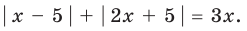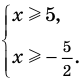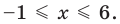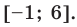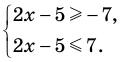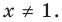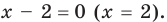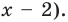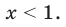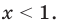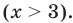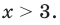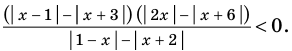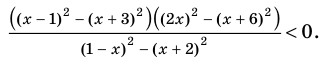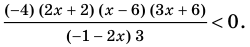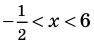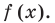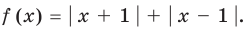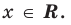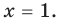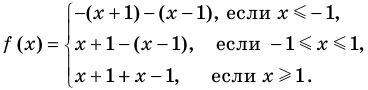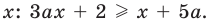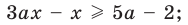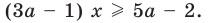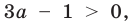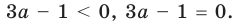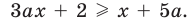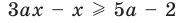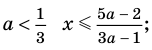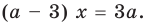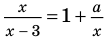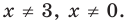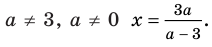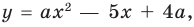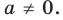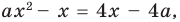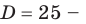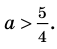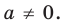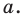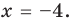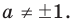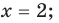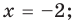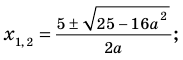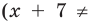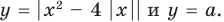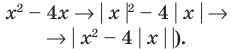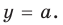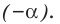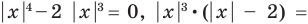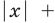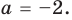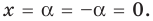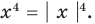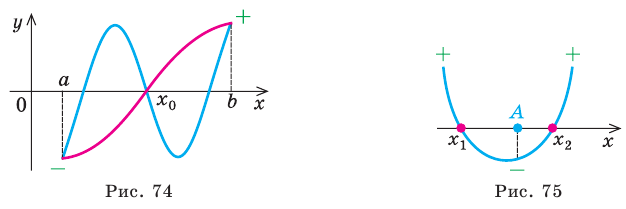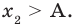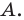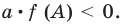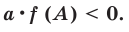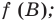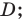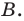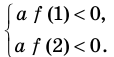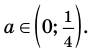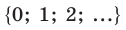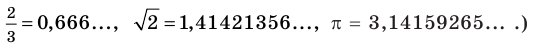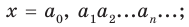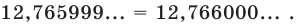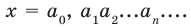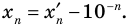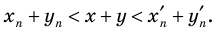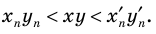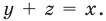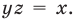Существуют следующие свойства модуля действительных чисел:
Проведем доказательства, рассматривая различные случаи значений a и b .
Доказательство 1) |a + b| ≤ |a| + |b|:
Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b . Из этого следует, что |a + b| = |a| + |b| .
Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a| . Выражение же |a| + |b| равно сумме абсолютных значений a и b , что больше, чем b – a . Поэтому |a + b| .
Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b| , что также меньше суммы модулей |a| + |b| .
Если a и b – отрицательные числа, то получим |–a – b| . Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b| ). Но уже было доказано, что |a + b| = |a| + |b| , следовательно и |–a – b| = |a| + |b| .
Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.
Доказательство 3) , a ≠ 0:
Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/ a .
Доказательство 4) |a – b| ≥ |a| – |b|:
Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b| , потому что можно не брать модули вообще и тогда с двух сторон получим a – b .
Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b| , что больше, чем |a| – |b| .
Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b| , что больше, чем |a| – |b| .
В этой статье мы детально разберем модуль числа. Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.
Навигация по странице.
Модуль числа – определение, обозначение и примеры
Сначала введем обозначение модуля числа. Модуль числа a будем записывать как 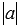
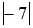
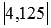

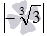
Так мы определились с обозначением, теперь пришло время дать определение модуля числа. Чтобы хорошо понять определение модуля числа необходимо хорошо владеть материалом статьи положительные и отрицательные числа, а также статьи противоположные числа.
Следующее определение модуля относится к действительным числам, а следовательно, и к натуральным числам, и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в последнем пункте этой статьи.
Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .
Озвученное определение модуля числа часто записывают в следующем виде 



Запись 




Также имеет место и запись 

Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и 







В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака, а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа. Так модуль числа и абсолютная величина числа – это одно и то же.
Модуль числа как расстояние
Геометрически модуль числа можно интерпретировать как расстояние. Приведем определение модуля числа через расстояние.
Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.
Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.
Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому 
Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.
Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .
То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.
Определение модуля числа через арифметический квадратный корень
Иногда встречается определение модуля через арифметический квадратный корень.
Модуль числа a – это арифметический квадратный корень из квадрата числа a , то есть, 
Для примера вычислим модули чисел −30 и 
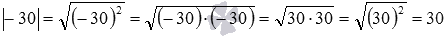
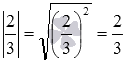
Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда 


Свойства модуля
Модулю присущ ряд характерных результатов — свойства модуля. Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.
Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом. В буквенном виде это свойство имеет запись вида 
Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль. Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.
Идем дальше. Противоположные числа имеют равные модули, то есть, 
Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел, то есть, 




Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, 





Следующее свойство модуля записывается в виде неравенства: 





Только что доказанное неравенство намного чаще встречается в виде 


Модуль комплексного числа
Дадим определение модуля комплексного числа. Пусть нам дано комплексное число, записанное в алгебраической форме 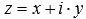

Модулем комплексного числа z=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.
Модуль комплексного числа z обозначается как 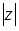
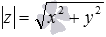
Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа 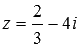
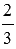
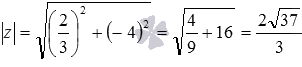
Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.
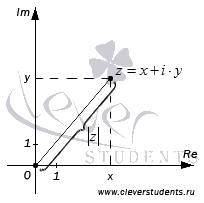
Модуль комплексного числа z – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.
По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как 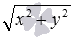
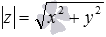
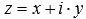
Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z , если оно записано в тригонометрической форме как 





Можно также заметить, что произведение комплексного числа 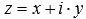
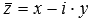
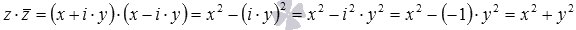
Модуль комплексного числа z – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, 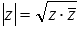
В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Модуль числа — это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности.
А между тем она проста как апельсин. Но чтобы ее понять, давай сначала разберемся зачем нужен модуль.
Вот смотри, ситуация первая.
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, неважно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая.
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией Lays, если они тебе недовесили?
Нет. Потому что Lays устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» — это и есть модуль.
Ситуация третья.
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч — это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от нуля в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее.
Что же такое модуль числа?
Представь, что это ты. 
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления . 
Итак, ты делаешь шага вперёд и оказываешься в точке с координатой . 
Это означает, что ты удалился от места, где стоял на шага ( единичных отрезка). То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно .
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой сделать шага в обратную сторону, то окажешься в точке с координатой . 
Какое расстояние было пройдено в первом и во втором случае? Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки ( и ), в которых ты оказался одинаково удалены от точки, из которой было начато движение ( ). 
Таким образом, мы приблизились к понятию модуля . Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа будет . Модуль числа также равен , потому что расстояние не может быть отрицательным !
Модуль – это абсолютная величина
Обозначается модуль просто:
Итак, найдём модуль числа и :
Основные свойства модуля
Вот мы и приблизились к первому свойству модуля:
Модуль не может быть выражен отрицательным числом.
То есть, если – число положительное, то его модуль будет равен этому же числу:
если ext< >mathbf<0>,»> то .
Если – отрицательное число, то его модуль равен противоположному числу:
А если ? Ну, конечно! Его модуль также равен :
Из этого следует, что модули противоположных чисел равны, то есть:
А теперь потренируйся:
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда?
А если перед тобой вот такое число:
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль :
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим :
Если , то какой знак имеет ? Ну конечно, !
А, значит, знак модуля раскрываем, меняя знак у выражения:
Разобрался? Тогда попробуй сам:
Какими же ещё свойствами обладает модуль?
Если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
А что, если нам нужно разделить два числа (выражения) под знаком модуля?
Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
при условии, что (так как на ноль делить нельзя).
Стоит запомнить ещё одно свойство модуля:
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:
Почему так? Всё очень просто!
Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению.
Рассмотрим на примере:
Выражения также равны, если оба числа отрицательны:
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.
Что если перед нами такое выражение:
Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что , а значит .
Число больше нуля, а значит можно просто записать:
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
А чему равно такое выражение:
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства. И что же получается? А вот что:
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
Ну, и почему сомнения? Действуем смело!
Во всем разобрался? Тогда вперед тренироваться на примерах!
1. Найдите значение выражения , если .
2. У каких чисел модуль равен ?
3. Найдите значение выражений:
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Итак, подставим значения и в выражение
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и .
Все уловил? Тогда пора перейти к более сложному!
Попробуем упростить выражение
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
Получается, значение первого выражения под модулем .
, следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно: 
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Во втором случае просто отбросим знак модуля:
Упростим данное выражение целиком:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа — это само число , если , и число , если :
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Как найти модуль разности корней
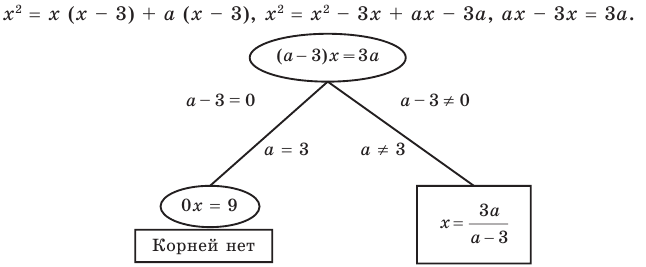
Из курса школьной математики многие помнят, что корень – это решение уравнения, то есть те значения Х, при которых достигается равенство его частей. Как правило, задача нахождения модуля разности корней ставится в отношении квадратных уравнений, ведь именно они могут иметь два корня, разность которых вы сможете вычислить.
Для начала решите уравнение, то есть найдите его корни или докажите, что они отсутствуют. Перед вами уравнение второй степени: посмотрите, имеет ли оно вид AX2 + BX + C = 0, где А, В и С – простые числа и А не равно 0.
Если уравнение не равно нулю или во второй части равенства присутствует неизвестная Х, приведите его к стандартному виду. Для этого перенесите все числа в левую часть, заменив стоящий перед ними знак. Например, 2Х^2 + 3X + 2 = (-2X). Привести это уравнение можно следующим образом: 2Х^2 + (3Х + 2Х) + 2 = 0. Теперь, когда ваше уравнение приведено к стандартному виду, можно приступить к нахождению его корней.
Вычислите дискриминант уравнения D. Он равен разности B, возведенного в квадрат, и А, умноженного на С, и на 4. Приведенное в пример уравнение 2Х^2 + 5Х + 2 = 0 имеет два корня, так как его дискриминант равен 5^2 + 4 х 2 х 2 = 9, то есть больше 0. Если же дискриминант равен нулю, вы сможете решить уравнение, но оно иметь всего один корень. Отрицательный дискриминант свидетельствует об отсутствии корней уравнения.
Найдите корень из дискриминанта (√D). Для этого вы можете воспользоваться калькулятором с алгебраическими функциями, онлайн-кулькулятором или специальной таблицей корней (обычно она приводится в конце учебников и справочников по алгебре). В нашем случае √D = √9 = 3.
Чтобы вычислить первый корень квадратного уравнения (X1), подставьте в выражение (-В + √D) полученное число и разделите результат на А, умноженное на 2. То есть Х1 = (-5 + 3)/ (2 х 2)= -0,5.
Найти второй корень квадратного уравнения X2 можно заменив в формуле сумму на разность, то есть Х2 = (-В — √D) / 2A. В приведённом примере Х2 = (-5 — 3)/ (2 х 2) = -2.
Отнимите от первого корня уравнения второй, то есть X1 – X2. При этом абсолютно не имеет значения то, в каком порядке вы подставите корни: конечный результат будет тот же. Полученное число – это разность корней, и вам осталось только найти модуль этого числа. В нашем случае X1 – X2 = -0,5 – (-2) = 1,5 или Х2 – Х1 = (-2) – (-0,5) = -1,5.
Модуль – эторасстояние на оси координат от нуля до точки N, измеряемое в единичных отрезках, поэтому модуль любого числа не может быть отрицательным. Найти модуль числа можно следующим образом: модуль положительного числа равен ему самому, а модуль отрицательного – противоположное ему число. То есть|1,5| = 1,5 и |-1,5| = 1,5.
Разность модулей и модуль разности
Существуют следующие свойства модуля действительных чисел:
Проведем доказательства, рассматривая различные случаи значений a и b .
Доказательство 1) |a + b| ≤ |a| + |b|:
Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b . Из этого следует, что |a + b| = |a| + |b| .
Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a| . Выражение же |a| + |b| равно сумме абсолютных значений a и b , что больше, чем b – a . Поэтому |a + b| .
Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b| , что также меньше суммы модулей |a| + |b| .
Если a и b – отрицательные числа, то получим |–a – b| . Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b| ). Но уже было доказано, что |a + b| = |a| + |b| , следовательно и |–a – b| = |a| + |b| .
Доказательство 2) |ab| = |a| × |b|:
Здесь, в отличие от сложения, рассматривать все случаи особо не требуется, т. к. абсолютное значение произведения любых чисел (положительных ли, отрицательных ли) не зависит от знаков множителей. В выражении |ab| мы сначала перемножаем числа, а потом «отбрасываем» знак (отрицательный, если он есть), в выражении |a| × |b| сначала избавляемся от знаков, а потом перемножаем. Но от того, в какой момент был взят модуль (до или после умножения), не зависит абсолютное значение произведения.
Доказательство 3) , a ≠ 0:
Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/ a .
Доказательство 4) |a – b| ≥ |a| – |b|:
Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b| , потому что можно не брать модули вообще и тогда с двух сторон получим a – b .
Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b| , что больше, чем |a| – |b| .
Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b| , что больше, чем |a| – |b| .
В этой статье мы детально разберем модуль числа. Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.
Навигация по странице.
Модуль числа – определение, обозначение и примеры
Сначала введем обозначение модуля числа. Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль целого числа −7 можно записать как ; модуль рационального числа 4,125 записывается как , а модуль иррационального числа имеет запись вида .
Так мы определились с обозначением, теперь пришло время дать определение модуля числа. Чтобы хорошо понять определение модуля числа необходимо хорошо владеть материалом статьи положительные и отрицательные числа, а также статьи противоположные числа.
Следующее определение модуля относится к действительным числам, а следовательно, и к натуральным числам, и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в последнем пункте этой статьи.
Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .
Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0 , , если a=0 , и , если a .
Запись можно представить в более компактной форме . Эта запись означает, что , если ( a больше или равно 0 ), и , если a .
Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0 . В этом случае имеем , но −0=0 , так как нуль считают числом, которое противоположно самому себе.
Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как — отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .
В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака, а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа. Так модуль числа и абсолютная величина числа – это одно и то же.
Модуль числа как расстояние
Геометрически модуль числа можно интерпретировать как расстояние. Приведем определение модуля числа через расстояние.
Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.
Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.
Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому .
Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.
Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .
То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.
Определение модуля числа через арифметический квадратный корень
Иногда встречается определение модуля через арифметический квадратный корень.
Модуль числа a – это арифметический квадратный корень из квадрата числа a , то есть, .
Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .
Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0 , то .
Свойства модуля
Модулю присущ ряд характерных результатов — свойства модуля. Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.
Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом. В буквенном виде это свойство имеет запись вида для любого числа a . Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.
Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль. Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.
Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a . Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.
Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел, то есть, . По определению модуль произведения чисел a и b равен либо a·b , если , либо −(a·b) , если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.
Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.
Следующее свойство модуля записывается в виде неравенства: , a , b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника. Чтобы это стало понятно, возьмем точки A(a) , B(b) , C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС , у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ , — длине отрезка АС , а — длине отрезка СВ . Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .
Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b , и принять c=0 .
Модуль комплексного числа
Дадим определение модуля комплексного числа. Пусть нам дано комплексное число, записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z , а – мнимая единица.
Модулем комплексного числа z=x+i·y называется арифметический квадратный корень из суммы квадратов действительной и мнимой части данного комплексного числа.
Модуль комплексного числа z обозначается как , тогда озвученное определение модуля комплексного числа может быть записано в виде .
Данное определения позволяет вычислить модуль любого комплексного числа в алгебраической форме записи. Для примера вычислим модуль комплексного числа . В этом примере действительная часть комплексного числа равна , а мнимая – минус четырем. Тогда по определению модуля комплексного числа имеем .
Геометрическую интерпретацию модуля комплексного числа можно дать через расстояние, по аналогии с геометрической интерпретацией модуля действительного числа.
Модуль комплексного числа z – это расстояние от начала комплексной плоскости до точки, соответствующей числу z в этой плоскости.
По теореме Пифагора расстояние от точки O до точки с координатами (x, y) находится как , поэтому, , где . Следовательно, последнее определение модуля комплексного числа согласуется с первым.
Данное определение также позволяет сразу указать, чему равен модуль комплексного числа z , если оно записано в тригонометрической форме как или в показательной форме . Здесь . Например, модуль комплексного числа равен 5 , а модуль комплексного числа равен .
Можно также заметить, что произведение комплексного числа на комплексно сопряженное число дает сумму квадратов действительной и мнимой части. Действительно, . Полученное равенство позволяет дать еще одно определение модуля комплексного числа.
Модуль комплексного числа z – это арифметический квадратный корень из произведения этого числа и числа, комплексно сопряженного с ним, то есть, .
В заключение отметим, что все свойства модуля, сформулированные в соответствующем пункте, справедливы и для комплексных чисел.
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Модуль числа — это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности.
А между тем она проста как апельсин. Но чтобы ее понять, давай сначала разберемся зачем нужен модуль.
Вот смотри, ситуация первая.
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, неважно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая.
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией Lays, если они тебе недовесили?
Нет. Потому что Lays устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» — это и есть модуль.
Ситуация третья.
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч — это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от нуля в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления .
Итак, ты делаешь шага вперёд и оказываешься в точке с координатой .
Это означает, что ты удалился от места, где стоял на шага ( единичных отрезка). То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно .
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой сделать шага в обратную сторону, то окажешься в точке с координатой .
Какое расстояние было пройдено в первом и во втором случае? Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки ( и ), в которых ты оказался одинаково удалены от точки, из которой было начато движение ( ).
Таким образом, мы приблизились к понятию модуля . Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа будет . Модуль числа также равен , потому что расстояние не может быть отрицательным !
Модуль – это абсолютная величина
Обозначается модуль просто:
Итак, найдём модуль числа и :
Основные свойства модуля
Вот мы и приблизились к первому свойству модуля:
Модуль не может быть выражен отрицательным числом.
То есть, если – число положительное, то его модуль будет равен этому же числу:
если ext mathbf ,»> то .
Если – отрицательное число, то его модуль равен противоположному числу:
А если ? Ну, конечно! Его модуль также равен :
Из этого следует, что модули противоположных чисел равны, то есть:
А теперь потренируйся:
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда?
А если перед тобой вот такое число:
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль :
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим :
Если , то какой знак имеет ? Ну конечно, !
А, значит, знак модуля раскрываем, меняя знак у выражения:
Разобрался? Тогда попробуй сам:
Какими же ещё свойствами обладает модуль?
Если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
А что, если нам нужно разделить два числа (выражения) под знаком модуля?
Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
при условии, что (так как на ноль делить нельзя).
Стоит запомнить ещё одно свойство модуля:
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:
Почему так? Всё очень просто!
Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению.
Рассмотрим на примере:
Выражения также равны, если оба числа отрицательны:
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.
Что если перед нами такое выражение:
Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что , а значит .
Число больше нуля, а значит можно просто записать:
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
А чему равно такое выражение:
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства. И что же получается? А вот что:
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
Ну, и почему сомнения? Действуем смело!
Во всем разобрался? Тогда вперед тренироваться на примерах!
1. Найдите значение выражения , если .
2. У каких чисел модуль равен ?
3. Найдите значение выражений:
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Итак, подставим значения и в выражение
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и .
Все уловил? Тогда пора перейти к более сложному!
Попробуем упростить выражение
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
Получается, значение первого выражения под модулем .
, следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Во втором случае просто отбросим знак модуля:
Упростим данное выражение целиком:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа — это само число , если , и число , если :
Квадратное уравнение. Парабола
Квадратичная функция
$s=frac<2>$ — путь, которое проходит свободно падающее тело за время t с нулевой начальной скоростью.
В общем виде эту зависимость можно записать так: $y=ax^2$. График этой функции — парабола, вершина которой находится в точке (0,0). Ветви направлены вверх. Четная функция.
Квадратичной называется функция, которую можно задать формулой y=ax² + bx + c, причем а отлично от 0. Здесь a,b,c — некоторые числа, x — переменная.
Корень — это значение переменной, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.
Vertex form
Можно выделить квадратный двучлен, поэтому это тоже парабола со сдвигом и растяжением.
Вершина параболы в точке (m,n), $m = frac<-b><2a>, n = frac<-D><4a>$
Квадратное уравнение
a — первый или старший коэффициент
b — второй коэффициент или средний или коэффициент при x
c — свободный член
Дискриминант $D = b^2-4ac$
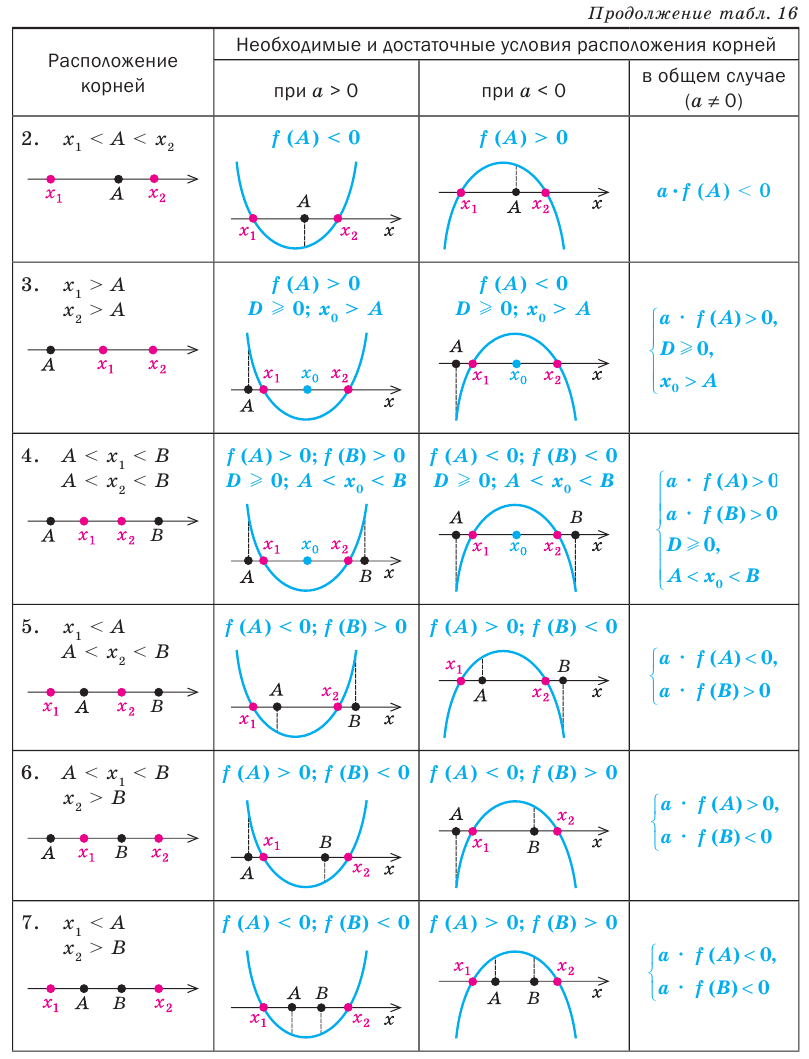
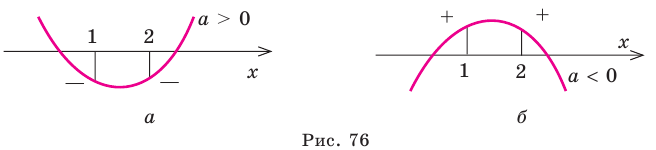
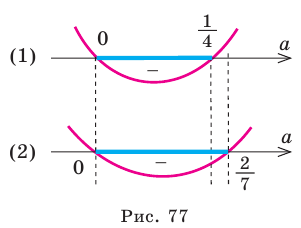
Схематическое расположение параболы в зависимости от знаков первого коэффициента и дискриминанта.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент.
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю.
Теорема Виета
Теорема. Cумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Если приведенное квадратное уравнение $x^2 + px + q = 0$ имеет действительные корни, то их сумма равна $-p$, а произведение равно $q$, то есть
$$x_1 + x_2 = –p, \ x_1 cdot x_2 = q$$
Примечание. Любое квадратное уравнение можно привести к такому виду делением на a.
Пример. Найти сумму корней уравнения $x^2-7x+13=0$. Корней нет, поэтому ответ «сумма корней равна 7» — неверный. Для определения количества корней необходимо найти дискриминант.
Таким образом, в формулировку теоремы Виета необходимо добавить условие: если корни существуют, то … Или если дискриминант неотрицателен. Заметим, что при нулевом дискриминанте теорема Виета тоже работает (считать, что уравнение имеет два равных корня).
Пример. (Мерзляк, Алгебра 8 углубл, 2016)
Применения теоремы Виета
Теорема Виета позволяет угадывать целые корни квадратного трехчлена (не решая уравнение).
Так, находя корни квадратного уравнения x² – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: $$6 = 2 cdot 3, , 2 + 3 = 5. $$
Отсюда должно следовать, что числа 2 и 3 являются искомыми корнями.
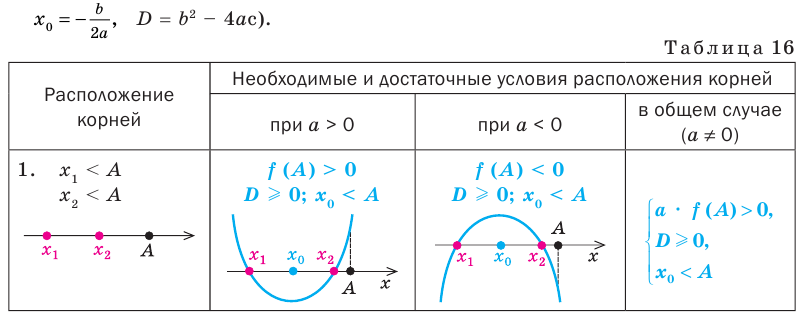
Определение знаков корней
Определение знаков корней без решения уравнения (при условии что D > 0).
| p > 0 | p 0 | Корни имеют одинаковые знаки |
|---|---|---|
| оба корня отрицательны | оба корня положительны | |
| Свободный член q 0 |
Геометрический смысл теоремы Виета
Мы привыкли произносить «икс квадрат», «квадрат суммы», «удвоенный квадрат», не придавая этим выражениям геометрического смысла. На самом деле все они отражают взгляд на алгебру, который сложился еще в глубокой древности, потому что людям приходилось решать геометрические задачи на вычисление площадей.
В клинописных текстах древнего Вавилона (около 2000 лет до нашей эры) обнаружена такая задача. «Площадь 1000 состоит из суммы двух квадратов, и сторона меньшего составляет две трети стороны другого, уменьшенные на 10. Какова сторона бóльшего квадрата?»
Решить такую задачу — это все равно, что решить уравнение $x^2+(frac 2 3 x-10)^2=1000$. В клинописном тексте нет формулы для решения этого уравнения, но перечисляются необходимые этапы вычисления, которые приводят к корню $x = 30$.
Фактически вавилонский метод дает решение системы $beginx+y=p \ xy= qend$,
которая представляет собой запись задачи нахождения сторон прямоугольника с данным периметром и площадью. Теорема Виета, с изучения которой начинается этот параграф, связывает решение этой системы с решением квадратного уравнения.
Обобщение теоремы Виета
Теорема Вієта для зведеного многочлена $f(x)=x^n+a_x^+ldots+a_1x+a_0$ формулюється так: «Якщо $x_1, x_2, x_3, ldots, x_, x_n$ — всі комплексні корені (включаючи рівні) цього многочлена степеня n, то мають місце рівності:
$$ x_1+x_2+ldots+x_n=-a_ $$ $$ x_1x_2+x_1x_3+ldots+x_1x_n+x_2x_3+ldots+x_x_n=a_ $$ $$ x_1x_2x_3+x_1x_2x_4+ldots+x_1x_x_n+ldots+x_x_x_n=-a_ $$ $$x_1x_2x_3 ldots x_n=(-1)^n a_0$$
Разность корней квадратного уравнения
Для приведенного уравнения $$ x_1-x_2 = sqrt $$
$$ <(x_1-x_2)^2>= x_1^2 — 2x_1x_2 + x_2^2 = (x_1+x_2)^2-4x_1x_2$$
Для приведенного уравнения с учетом теоремы Виета:
$$(x_1-x_2)^2 = (-b)^2-4c = b^2-4ac = D$$
Таким образом, если корни квадратного уравнения существуют, то расстояние между ними равно корню из дискриминанта. Грубо говоря, чем больше дискриминант, тем больше расстояние между корнями.
Обобщение дискриминанта
Дискриминантом многочлена $p(x)$ называется функция, задаваемая его коэффициентами.
Если точнее, то дискриминант — это произведение квадратов разностей корней многочлена, умноженное на старший коэффициент в степени на 2 меньше удвоенной степени многочлена.
1. Любая точка параболы равноудалена от некоторый точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
2. Если вращать параболу вокруг ее оси симметрии (например, параболу $y = x^2$ вокруг оси Oy), то получается очень интересная поверхность, которая называется параболоидом вращения.
Поверхность жидкости, вращающейся в сосуде, имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе.
4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола.
5. В парках культуры устраивают иногда забавный аттракцион «Параболоид чудес». Каждому из стоящих внутри вращающегося параболоида кажется, что он стоит на полу, а остальные люди каким-то чудом держатся на стенках.
6. В зеркальных телескопах тоже применяют параболические зеркала: свет от далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокусе.
7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи света, отразившись от параболического зеркала, образуют параллельный пучок.
Опыты, описанные в пунктах 2 и 5, основаны на одном и том же свойстве параболоида: если вращать параболоид с подходящей скоростью вокруг его оси, расположенной вертикально, то равнодействующая центробежной силы и силы тяготения в любой точке параболоида направлена перпендикулярно к его поверхности.
Солнечные концентраторы
Солнечные концентраторы используют энергию солнечной радиации, которая попадает на параболическую поверхность зеркала, в фокусе которой обычно располагается трубка с циркурирующим по ней теплоносителем. Как правило в качестве теплоносителя выступает масло. Теплоноситель нагревает воду, которая испаряясь поступает в турбогенератор в виде пара.
Параболические концентраторы с двигателем Стирлинга представляют собой СЭС с параболическими концентраторами, которые фокусируются на двигатель Стирлинга. Такие электростанции характеризуются высоким КПД (более 31%). В качестве рабочего тела двигателя Стирлинга используется, как правило, водород, или гелий.
Согласно известной исторической легенде, Архимед почти полностью сжег флот римского полководца Марка Марцелла, используя медные параболические зеркала.
8-этажное сооружение, включающее около 10 тысяч отдельных параболических зеркал. На сегодняшний день Солнечная Печь, выстроенная в 1970 году в Восточных Пиренеях – крупнейшая в мире. Массив зеркал действует в качестве параболического отражателя. Свет фокусируется в одном центре. И температура там может достигать 3500 градусов по Цельсию. При такой температуре можно плавить сталь. Но температуру можно регулировать, устанавливая зеркала под разными углами.
Подвесные мосты
Вантовый мост — тип висячего моста, состоящий из одного или более пилонов, соединённых с дорожным полотном посредством прямолинейных стальных тросов — вантов. В отличие от висячих мостов, где дорожное полотно поддерживается вертикальными тросами, прикреплёнными к протянутым по всей длине моста основным несущим тросам, у вантовых мостов тросы (ванты) соединяются непосредственно с пилоном.
Русский мост (Владивосток) — вантовый мост с самым длинным основным пролётом в мире (1104 м), при общей длине в 1886 м
Висячий мост — мост, в котором основная несущая конструкция выполнена из гибких элементов (кабелей, канатов, цепей и др.), работающих на растяжение, а проезжая часть подвешена.
Висячие мосты находят наиболее удачное применение в случае большой длины моста, невозможности или опасности установки промежуточных опор (например в судоходных местах).
Золотые Ворота (Сан-Франциско) — один из самых узнаваемых мостов в мире. Мост был самым большим висячим мостом в мире с момента открытия в 1937 году и до 1964 года. Общая длина моста — 2737 м, длина основного пролёта — 1280 м, высота опор — 227 м над водой, масса — 894 500 т. В среднем, по мосту проезжают сто тысяч автомобилей в сутки. 6 полос.
Основные несущие тросы (или цепи) подвешивают между установленными по берегам пилонами. К этим тросам крепят вертикальные тросы или балки, на которых подвешивается дорожное полотно основного пролёта моста. Основные тросы продолжаются за пилонами и закрепляются на уровне земли. Продолжение тросов может использоваться для поддержки двух дополнительных пролётов.
Под действием сосредоточенной нагрузки несущая конструкция может изменять свою форму, что уменьшает жёсткость моста. Для избежания прогибов в современных висячих мостах дорожное полотно усиливают продольными балками или фермами, распределяющими нагрузку.
Используются также конструкции, в которых дорожное полотно поддерживается системой прямолинейных канатов, закреплённых непосредственно на пилонах. Такие мосты называются вантовыми.
Основной пролёт можно сделать очень длинным при минимальном количестве материала. Поэтому использование такой конструкции очень эффективно при строительстве мостов через широкие ущелья и водные преграды. В современных висячих мостах широко применяют проволочные тросы и канаты из высокопрочной стали с пределом прочности около 2—2,5 ГПа(200-250 кгс/мм²), что существенно снижает собственный вес моста.
Отсутствует необходимость ставить промежуточные опоры, что даёт большие преимущества, например, в случае горных разломов или рек с сильным течением.
Будучи относительно податливыми, висячие мосты могут, без ущерба для целостности конструкции, изгибаться под действием сильного ветра или сейсмических нагрузок, тогда как более жёсткие мосты нужно строить более крепкими и тяжёлыми.
Полотно моста сильно прогибается, если на одном участке сосредоточена нагрузка существенно больше, чем на других. Из-за этого висячие мосты реже используются в качестве железнодорожных, чем другие типы.
Основные напряжения в висячем мосте — это напряжения растяжения в основных тросах и напряжения сжатия в опорах, напряжения в самом пролёте малы. Почти все силы в опорах направлены вертикально вниз и стабилизируются за счёт тросов, поэтому опоры могут быть очень тонкими. Сравнительно простое распределение нагрузок по разным элементам конструкции упрощает расчёт висячих мостов.
Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе. Ненагруженный трос, подвешенный между двумя опорами, принимает форму т. н. «цепной линии», которая близка к параболе в почти горизонтальном участке. Если весом тросов можно пренебречь, а вес пролёта равномерно распределён по длине моста, тросы принимают форму параболы. Если вес троса сравним с весом дорожного полотна, то его форма будет промежуточной между цепной линией и параболой.
Клифтонский мост близ Бристоля (инженер Изамбард Кингдом Брюнель, 1864).
Акаси-Кайкё — самый длинный подвесной мост в мире. Полная длина составляет 3911 м. Пилоны имеют высоту 298 м, что выше 90-этажного дома.
Вначале были построены два бетонных основания для пилонов на дне пролива Акаси. Для строительства этого моста был разработан специальный бетон, который не растворяется в воде при заливке. Следующим этапом было протягивание тросов. Для этого нужно было с одного пилона на другой протянуть направляющий канат. Он был протянут с помощью вертолёта. Когда в 1995 году оба троса были протянуты, и можно было приступать к монтажу дорожного полотна, произошло непредвиденное: город Кобе стал жертвой крупного землетрясения магнитудой в 7,3 балла. Пилоны выдержали землетрясение, но из-за изменения рельефа дна пролива один из пилонов сдвинулся на 1 м в сторону, таким образом нарушив все расчёты. Инженеры предложили удлинить балки дорожного полотна и увеличить расстояние между вантами, свисающими с основных тросов. Строительные работы, задержанные не более чем на месяц, возобновились. Монтаж дорожного полотна закончился в 1998 году.
В конструкции моста имеется система двухшарнирных балок жёсткости, позволяющая выдерживать скорости ветра до 80 м/с, землетрясения магнитудой до 8,5 и противостоять сильным морским течениям. Для уменьшения действующих на мост нагрузок имеется система динамических гасителей колебаний.
Если вытянуть в длину все стальные нити (диаметром 5,23 мм) несущих тросов моста Акаси-Кайкё, то ими можно опоясать земной шар более семи раз.
Модель параболы
Легко получить параболу с помощью обычного карманного фонарика. Световое пятно от вертикально расположенного фонаря будет кругом. Немного повернём его, и пятно будет иметь форму эллипса. При дальнейшем повороте фонарика эллипс будет всё больше и больше вытягиваться, а в некоторый момент его наиболее удалённая точка уйдёт в бесконечность. Кривая, ограничивающая такое пятно, называется параболой. Неограниченные кривые, которые получаются при дальнейшем вращении фонарика, называются гиперболами. Все получившиеся кривые – окружность, эллипс, парабола, гипербола – конические сечения. Такое название они получили заслуженно, поскольку световой столб, выходящий из фонарика, является конусом.
Парабола, как огибающая
Параболу можно рассматривать, как огибающую семейства прямых.
См. также Конические сечения — Параболическое зеркало. Параболический бильярд
Цепочки окружностей, вписанных в кривую 2-го порядка
Если радиус окружности, вписанной в параболу $y=x^2$ равен 1, то радиус второй окружности, вписанной в эту же параболу и касающейся первой окружности, равен 2, радиус аналогичной 3-й окружности равен 3 и т. д.
Интересно, что радиусы подобной цепочки окружностей, вписанных в угол, образуют геометрическую прогрессию.
Фокус и директриса параболы
Задача. Постройте график функции $y = x^2$. Масштаб возьмите покрупней: 1 = 4 клетки. Отметьте на оси Oy точку F(0; 1/4). Полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс. Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?
Результат мы Вам сможем сказать заранее: какую бы точку на параболе вы ни взяли, расстояние от этой точки до точки (0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число — на 1/4. Можно сказать иначе: расстояние от любой точки параболы $y = x^2$ до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = −1/4, параллельной оси Ox.
Замечательная точка F(0; 1/4) называется фокусом параболы, а прямая y = −1/4 — директрисой (по-русски направляющая) этой параболы. Директриса и фокус есть у всякой параболы.
Геометрический смысл параболы
Парабола — это множество точек, равноудалённых от данной прямой (директрисы параболы) и не лежащей на директрисе данной точки (фокуса параболы).
Парабола — это множество центров окружностей, касающихся данного круга и данной прямой, касающейся этого круга.
Источник — подробнее, больше картинок
Задача. Свободно падающее тело
Тело, свободно падающее без начальной скорости с некоторой высоты, за последнюю секунду падения проходит путь в 7 раз больший чем за первую секунду движения. Найдите высоту, с которой падает тело.
За первую секунду тело пройдёт расстояние равное: $S=frac<2>=10 cdot 1/2=5 $ м.
Тогда за последнюю секунду тело пройдёт расстояние равное 35 м. С другой стороны, за последнюю секунду тело пройдет расстояние: $$ frac <2>- frac<2>= 35$$
Решив это уравнение получим t = 4 с, откуда S = 80 м
| t, с | 1 | 2 | 3 | 4 | 5 | 6 |
| s общий, м | 5 | 20 | 45 | 80 | 125 | 180 |
| s за последнюю секунду | 5 | 15=20-5 | 25=45-20 | 35=80-45 | 45=125-80 | 55 |
Таким образом, любое падающее тело за первую секунду проходит 5м, за вторую секунду — в 3 раза больше, за третью — в 5 раз больше, за четвертую — в 7 раз больший путь, за пятую — в 9 раз, за шестую — в 11 раз. Арифметическая прогрессия, физики называют это закон нечетных чисел. Путь, пройденный за секунду, тоже образует арифметическую прогрессию с разность 10, что соответствует ускорению свободного падения g.
Задача. Тело, падающее без начальной скорости, за последнюю секунду падения прошло путь s = 35 м. Какую скорость имело тело в момент падения на землю? Сопротивлением воздуха пренебречь.
Решение. Время падения = 4 с. Скорость $v = s’ = gt = 40$ м/с.
http://planshet-info.ru/kompjutery/raznost-modulej-i-modul-raznosti
http://xlench.bget.ru/doku.php/mat/algebra/sq-equ?do=export_xhtml
Уравнения с модулем
-
Слева модуль, справа число
-
Слева модуль, справа выражение, зависящее от переменной
-
Квадратные уравнения с заменой
-
Модуль равен модулю
-
Два или несколько модулей
-
Модуль в модуле
Эта статья посвящена приёмам решения уравнений, содержащих переменную под знаком модуля.
Если на экзамене вам попадётся уравнение с модулем, его можно решить, вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда, занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним определение модуля.
Если число x неотрицательное, то модуль x равен самому числу x.
А для отрицательного числа x модуль равен противоположному ему положительному числу -x.
Рассмотрим различные типы уравнений с модулем.
Начнем с простых заданий.
к оглавлению ▴
Слева модуль, справа число
Это самый простой случай. Нам поможет геометрический смысл модуля.
Модуль числа — это расстояние от нуля до данного числа. Очевидно, расстояние не может быть отрицательным. Оно или положительно, или равно нулю. Например, . Другими словами, расстояние от точки -2 до нуля равно 2. Этим мы пользуемся при решении уравнений.
1. Решим уравнение:
Решение:
На числовой прямой есть ровно две точки, расстояние от которых до нуля равно двум. Это точки 2 и -2. Значит, у уравнения есть два решения:
и
.
Ответ: -2; 2.
2. Решите уравнение:
Решение:
Ответ:
3. Решите уравнение:
Решение:
Мы получили совокупность двух квадратных уравнений. А затем решили отдельно каждое из них.
Вот что мы делали, решая квадратные уравнения:
— применили теорему Виета и нашли корни.
корней нет.
Ответ:
4. Решим уравнение:
Решение:
Задача похожа на предыдущую.
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение равносильно совокупности двух простых:
или
Второе уравнение не имеет корней. Решения первого: x = 0 и x = 5.
Ответ: 0; 5.
к оглавлению ▴
Слева модуль, справа выражение, зависящее от переменной
Здесь приходится раскрывать модуль по определению. . . или соображать!
5.
Решение:
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.
6.
Решение:
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения.
Второй случай: x < 3. Снимаем модуль:
Число . больше, чем
, и потому не удовлетворяет условию x < 3. Проверим
:
Значит, . является корнем исходного уравнения.
Ответ:
7. Решите уравнение: = x.
Если уравнение имеет несколько корней, в ответе запишите меньший корень
Решение:
ОДЗ уравнения: x≠3. Так как в левой части уравнения — неотрицательная величина, должно также выполняться условие Возведем обе части уравнения в квадрат
= x
(разность квадратов),
Так как — это посторонний корень. Уравнение имеет два корня:
или
Меньший корень: 1.
Ответ: 1.
8.
Решение:
Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не полный квадрат.
Давайте воспользуемся следующим правилом:
Уравнение вида равносильно совокупности двух систем:

То же самое, но немного по-другому:
Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию
Приступаем. Сначала решаем первое уравнение:
Затем решаем второе уравнение:
Теперь в каждом случае проверяем знак правой части:
Подходят только и
.
Ответ:
Еще одно уравнение того же типа.
9. Решите уравнение: .
Это уравнение вида Вспомним, что оно равносильно системе:
Получим:
Решим отдельно каждое уравнение совокупности.
по теореме Виета.
Система примет вид:
Сравним и
Для сравнения мы будем использовать вот такой символ:
.
Умножим обе части этого неравенства на 2: .
Прибавим 5 к обеим частям выражения: Обе части выражения неотрицательны, поэтому возведем их в квадрат и сравним квадраты. Очевидно, 17
9. Это значит, что
и
Остальные корни, очевидно, меньше, чем -1.
Ответ: .
к оглавлению ▴
Квадратные уравнения с заменой 
Замена переменной — универсальный способ решения всевозможных уравнений. И этот способ помогает нам решать квадратные уравнения, содержащие переменную под знаком модуля.
10. Решим уравнение:
Решение:
Поскольку , удобно сделать замену |x| = t. Получаем:

Ответ: ±1.
к оглавлению ▴
Модуль равен модулю
Речь идёт об уравнениях вида Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Как мы получили это равенство? Покажем на примере задачи.
11. Решите уравнение:
Решение:
Возведем обе части в квадрат, поскольку они неотрицательны.
Перенесем все в левую часть и воспользуемся формулой разности квадратов:
Ответ:
12. Решим уравнение: .
Решение:
Уравнение равносильно следующей совокупности:
Решим каждое из уравнений совокупности и запишем ответ.
1)
— корни первого квадратного уравнения.
2)
— корни второго квадратного уравнения.
В ответ запишем все 4 корня.
Ответ:
к оглавлению ▴
Два или несколько модулей
13. Решим уравнение:
Решение:
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении).
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются с «плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается с «минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются с «минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Ответ: [1; 2] ∪ {5}.
к оглавлению ▴
Модуль в модуле
14. Решим уравнение:
Решение:
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
2) x ≥ 3. Имеем:
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается с «плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Ответ: 4.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Часто в решении уравнений и неравенств с модулем используется график функции Он строится согласно определению модуля:
.
Для получаем участок графика y = x.
Для получаем участок графика y = −x. Вот этот график:
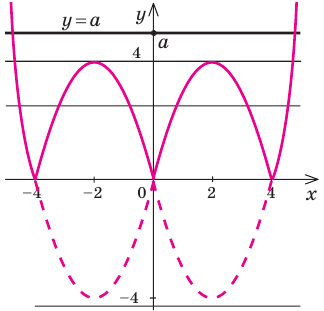
15. Решите уравнение:
Решение:
Сделаем замену переменной:
Тогда
Получим:
Мы помним, что
Решим уравнение графически. В левой части — график функции
Построим этот график. Сначала изобразим графики функций (точка минимума (3; 0)) и
(точка минимума ( -3; 0)). Можно сказать, что график функции
сдвинут относительно графика
на 3 единицы вправо, а график
— на 3 единицы влево.
И построим график суммы функций и
В точке с абсциссой 3 значение одного из слагаемых равно 0, другое слагаемое равно 6, сумма равна 6.
В точке с абсциссой -3 аналогично.
При х = 0 оба слагаемых равны 3, сумма равна 6.
Легко доказать, что сумма двух линейных функций есть линейная функция.
Поэтому при — получим горизонтальный участок. При x
3 получим луч с угловым коэффициентом, равным 2, а при x
— 3 — луч с угловым коэффициентом, равным — 2.
Решения нашего уравнения — все принадлежащие отрезку от
до
значит,
Ответ:
Мы рассмотрели все основные типы уравнений с модулями.
Читайте также о том, как решать неравенства с модулем.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Уравнения с модулем» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание:
Уравнения и неравенства, содержащие знак модуля
Объяснение и обоснование:
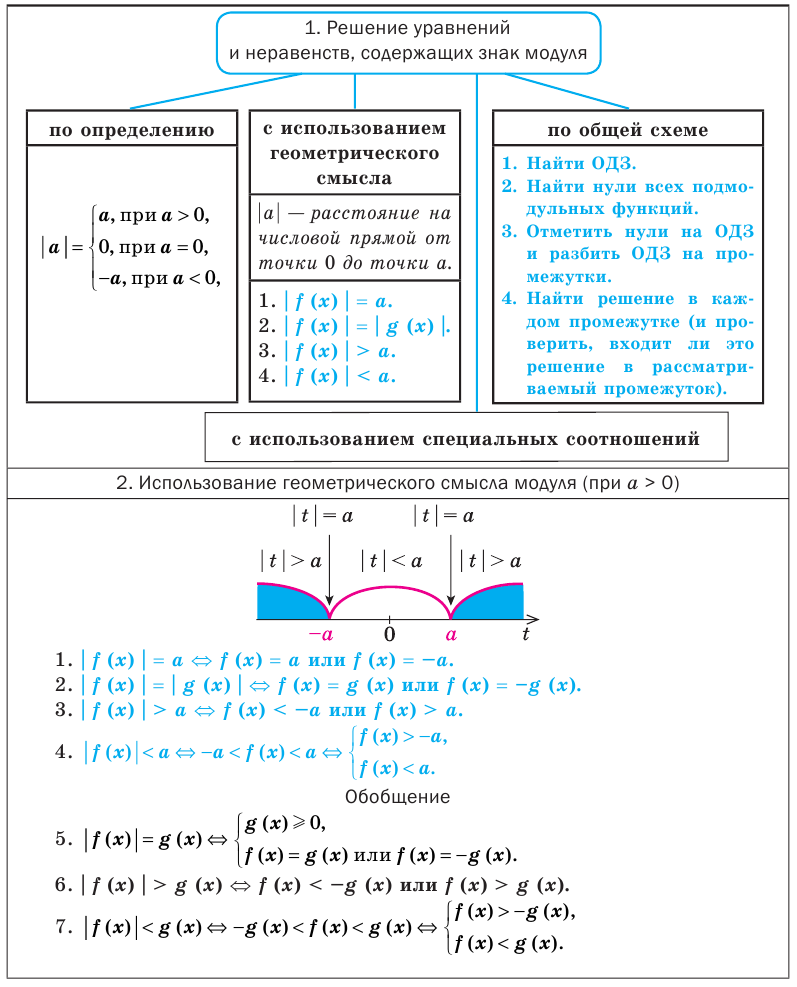
Решать любое уравнение или неравенство, содержащее знак модуля можно одним из трех основных способов: по определению модуля, исходя из геометрического смысла модуля или по общей схеме. Некоторые уравнения или неравенства, содержащие знак модуля, могут быть также решены с использованием специальных соотношений (табл. 15).
В зависимости от выбранного способа решения получаем разные записи решения.
Пример №441
Решите уравнение
I способ (по определению модуля)
Решение:
► 1) Если
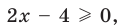
то получаем уравнение
Тогда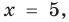
2) Если
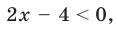
то получаем уравнение
Тогда 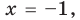
Ответ:
Комментарий:
Чтобы раскрыть знак модуля по определению, рассмотрим два случая:
По определению модулем положительного (неотрицательного) числа является само это число, а модулем отрицательного числа является противоположное ему число. Поэтому при 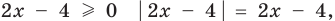
В каждом случае решаем полученное уравнение и выясняем, удовлетворяет ли каждый из найденных корней тому условию, при котором мы его находили.
II способ (использование геометрического смысла модуля)
Решение:
► 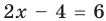
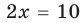
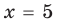
Ответ:
Комментарий:
С геометрической точки зрения 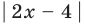

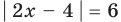
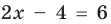
Замечание. При решении уравнения с использованием геометрического смысла модуля знак модуля раскрывается неявно, то есть определение модуля в явном виде не применяется.
Общая схема решения уравнений и неравенств, содержащих знак модуля, — это фактически немного измененный метод интервалов. Поясним содержание этой схемы на примере уравнения с двумя модулями вида
Чтобы решить это уравнение, необходимо раскрыть знаки модулей, а для этого необходимо знать, где функции 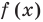
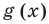
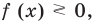
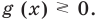
Каждое из этих неравенств мы умеем решать методом интервалов. Перестроим прием решения неравенств методом интервалов таким образом, чтобы он давал возможность одновременно решать каждое из последних неравенств. Как известно, решение неравенства (1) методом интервалов начинается с нахождения его ОДЗ (то есть области определения функции 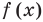
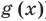
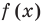
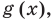
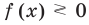
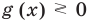
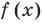
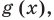
В каждом из полученных промежутков знаки функций 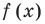
Примеры решения задач:
Пример №442
Решите уравнение
Решение:
► 1. ОДЗ:
2. Нули подмодульных функций:
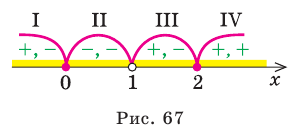
3. Нули 0 и 2 разбивают ОДЗ на четыре промежутка, в которых подмодульные Рис. 67 функции имеют знаки
4. Находим решения данного уравнения в каждом из промежутков (поскольку знаки подмодульных функций одинаковы на промежутках I и III, удобно для решения объединить эти промежутки). Промежутки I и III: 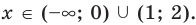
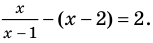
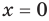
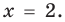
Промежуток II: 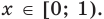
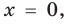
промежутке получаем уравнение 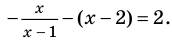
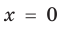
Промежуток IV: 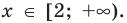
забыть значение 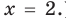
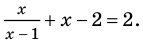
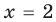
Ответ: 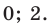
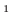
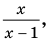
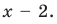
отметить на числовой прямой ОДЗ, а потом нули подмодульных функций на ОДЗ.
Проиллюстрируем также получение и использование специальных соотношений, приведенных в таблице 15.
Обоснуем, например, соотношение 5:
Запишем заданное равенство в виде 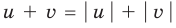
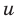
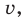
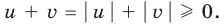
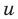
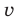
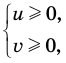
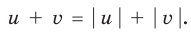
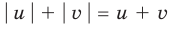
Пример №443
Решите уравнение
Решение:
► Поскольку 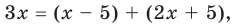
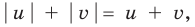
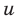
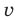
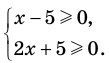
Таким образом,
Ответ:
Комментарий:
Если обозначить 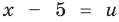
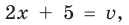
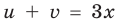
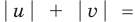
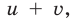
Заметим, что данное уравнение можно решать и по общей схеме, но тогда решение будет более громоздким.
При решении неравенств, содержащих знак модуля, рассуждения, связанные с раскрытием знаков модулей, полностью аналогичны рассуждениям, которые использовались при решении уравнений, содержащих знак модуля.
Пример №444
Решите неравенство
Решение:
► Учитывая геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству
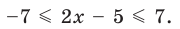
Тогда 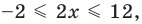
Ответ:
Комментарий:
Неравенство вида 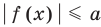
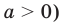
Поскольку заданное неравенство — это неравенство вида 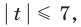
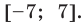
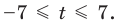
Пример №445
Решите неравенство 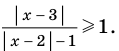
Решение:
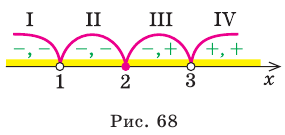
► 1. ОДЗ: 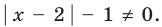
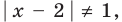
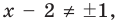
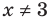
2. Нули подмодульных функций: 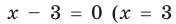
3. Нуль 2 разбивает ОДЗ на четыре промежутка, на которых подмодульные функции имеют знаки, показанные на рисунке 68 (на каждом из промежутков первый знак — это знак функции 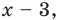
4. Находим решения заданного неравенства в каждом из промежутков (поскольку знаки подмодульных функций являются одинаковыми на промежутках I и II, удобно для решения объединить эти промежутки). Промежутки I и II: 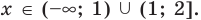
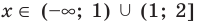
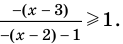
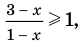
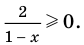
В промежутки, которые мы рассмотрели, входят все значения 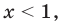
Промежуток III: 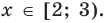
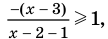
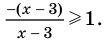
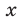
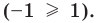
Промежуток IV: 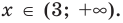
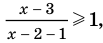
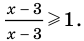
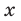
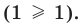
есть любое число из этого промежутка
Объединяя все решения, полученные в каждом из промежутков, имеем решение данного неравенства на всей ОДЗ: 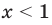
Ответ:
Укажем, что для решения некоторых неравенств, содержащих знак модуля, удобно применять также специальные соотношения, приведенные в таблице 15.
Пример №446
Решите неравенство
Решение:
► Поскольку 
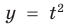
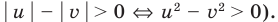
Раскладывая на множители все разности квадратов, имеем:
Далее методом интервалов получаем 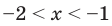
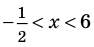
Ответ: 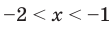
Общая схема, предложенная в таблице 15, может быть использована не только при решении уравнений или неравенств, содержащих знак модуля, но и при преобразовании выражений, содержащих знак модуля.
Например, для построения графика функции 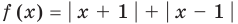
Оформление решения подобного примера может быть таким.
Пример №447
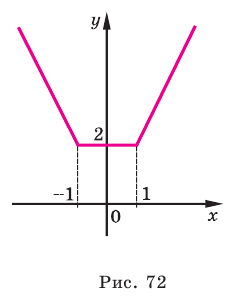
Постройте график функции
► 1. Область определения функции: все
2. Нули подмодульных функций: 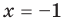
3. Отмечаем нули на области определения и разбиваем область определения на промежутки (на рисунке 71 также указаны знаки подмодульных функций в каждом из промежутков).
4. Тогда
Таким образом,
Строим график этой функции (рис. 72).
Уравнения и неравенства с параметрами
Решение уравнений и неравенств с параметрами
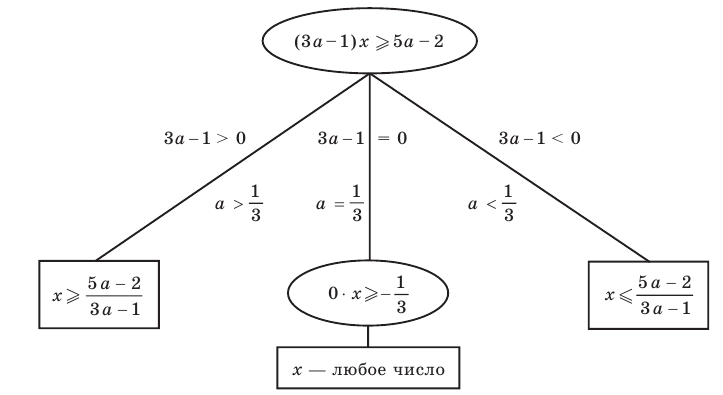
Если в запись уравнения или неравенства, кроме переменной и числовых коэффициентов, входят также буквенные коэффициенты — параметры, то при решении таких уравнений можно пользоваться следующим ориентиром.
Любое уравнение или неравенство с параметрами можно решать как обычное уравнение или неравенство до тех пор, пока все преобразования или рассуждения, необходимые для решения, можно выполнить однозначно. Если какое-то преобразование нельзя выполнить однозначно, то решения необходимо разбить на несколько случаев, чтобы в каждом из них ответ через параметры записывался однозначно.
На этапе поиска плана решения уравнения или неравенства с параметрами или в ходе решения часто удобно сопровождать соответствующие рассуждения схемами, по которым легко проследить, в какой момент мы не смогли однозначно выполнить необходимые преобразования, на сколько случаев пришлось разбить решение и чем отличается один случай от другого. Чтобы на таких схемах (или в записях громоздких решений) не потерять какой-то ответ, целесообразно помещать окончательные ответы в прямоугольные рамки. Записывая окончательный ответ, следует учитывать, что ответ должен быть записан для всех возможных значений параметра.
Пример №448
Решите неравенство с переменной
Комментарий:
Заданное неравенство является линейным относительно переменной 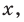
1) переносим члены с переменной 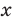
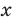
2) выносим в левой части за скобки общий множитель 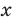
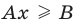
Для решения последнего неравенства мы хотели бы разделить обе его части на 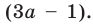
Приведенные выше рассуждения можно наглядно записать так:
Решение:
►
Ответ: 1) при 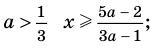
3) при 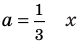
При решении более сложных уравнений или неравенств следует помнить, что уравнения и неравенства с параметрами чаще всего решают с помощью равносильных преобразований, а все равносильные преобразования уравнений или неравенств выполняют на области допустимых значений (ОДЗ) заданного уравнения или неравенства (то есть на общей области определения для всех функций, которые входят в запись уравнения или неравенства). Поэтому, прежде чем записать ответ, нужно обязательно учесть ОДЗ заданного уравнения или неравенства.
Пример №449
Решите уравнение 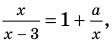
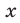
Комментарий:
Заданные дробные выражения существуют тогда и только тогда, когда знаменатели заданных дробей не равны нулю, следовательно, ОДЗ уравнения:
Умножим обе части заданного уравнения на выражение 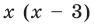
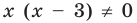
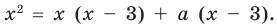
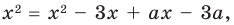
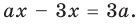
Для того чтобы найти значение переменной 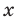
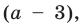
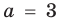
Решение в соответствии с приведенными выше рассуждениями можно наглядно записать в виде схемы.
Решение:
► ОДЗ:
Выясним, при каких значениях 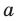
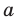
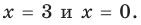
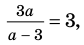
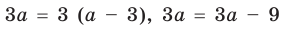
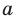
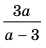
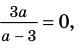
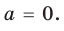
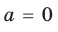
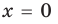
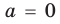
Ответ: 1) при 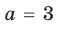
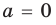
Пример №450
Решите уравнение 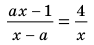
Комментарий:
Будем выполнять равносильные преобразования заданного уравнения. Для этого найдем его ОДЗ (знаменатели дробей не равны нулю). Если теперь обе части уравнения умножить на произведение выражений, которые стоят в знаменателях дробей (и которое не равно нулю на ОДЗ уравнения), то получим уравнение 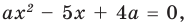
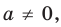
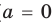
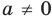
Если 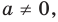
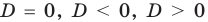
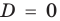
то есть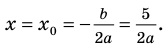

Поскольку корни уравнения (1) записываются достаточно громоздкими формулами (см. решение), то вместо подстановки полученных корней в ограничение ОДЗ можно подставить «запрещенные» значения 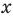
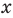
Решение:
► ОДЗ: 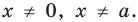
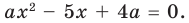
1. Если 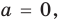
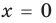
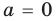
2. Если 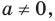
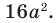
1) 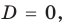
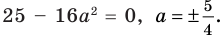
значение корня: 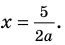
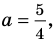
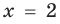
входит в ОДЗ и является корнем заданного уравнения. Если 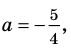
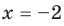
2) 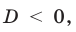
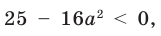
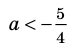
Тогда уравнение (1) не имеет корней.
3) 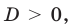
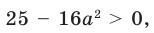
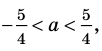
Тогда уравнение (1) имеет два корня:
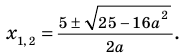
Выясним, при каких значениях 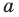
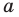
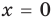
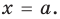
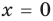
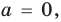
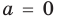
Подставляя в уравнение (1) 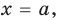

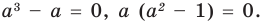
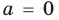
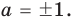
При 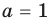
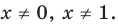
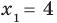
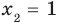
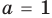
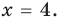
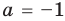
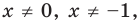
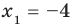
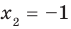
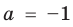
Таким образом, формулу корней (2) можно использовать, если 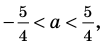
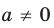
Ответ: 1) если 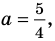
2) если 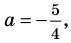
3) если 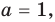
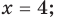
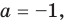
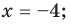
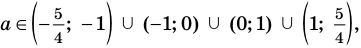
6) если 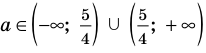
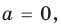
Замечание. Чтобы облегчить запись ответа в этом и аналогичных примерах, можно пользоваться таким приемом. Перед записью ответа в сложных или громоздких случаях изобразим ось параметра (а) и отметим на ней все особые значения параметра, которые появились в процессе решения. Под осью параметра (левее от нее) выпишем все полученные решения (кроме решения «корней нет») и напротив каждого ответа отметим, при каких значениях параметра этот ответ можно использовать (рис. 73). После этого ответ записывают для каждого из особых значений параметра и для каждого из полученных промежутков оси параметра. В частности, перед записью ответа в рассмотренном примере, на черновике удобно изобразить такую схему (рис. 73).
Исследовательские задачи с параметрами
Некоторые исследовательские задачи с параметрами удается решить по такой схеме: 1) решить заданное уравнение или неравенство; 2) исследовать полученное решение.
Пример №451
Найдите все значения 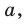
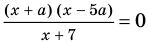
Решение:
► ОДЗ: 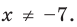
Тогда 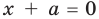
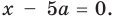
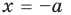
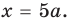
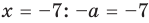
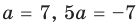
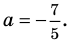
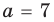
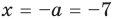
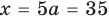
При 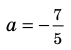
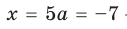
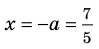
единственный корень. Также заданное уравнение будет иметь единственный корень, если 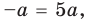
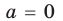
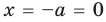
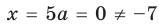
Ответ:
Комментарий:
Поскольку дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю, то на ОДЗ 
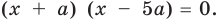
После этого выясним, при каких значениях 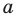
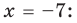
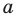
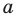
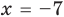
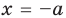
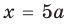
Исследование количества решении уравнении и их систем
При решении некоторых задач с параметрами можно пользоваться таким ориентиром: если в задаче с параметрами речь идет о количестве решений уравнения (неравенства или системы), то для анализа заданной ситуации часто удобно использовать графическую иллюстрацию решения.
Наиболее простым соответствующее исследование является в том случае, когда заданное уравнение можно преобразовать к виду 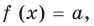
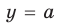
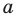
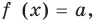
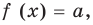
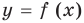
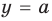
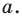
- Заказать решение задач по высшей математике
Пример №452
Сколько корней имеет уравнение 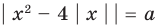
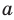
Решение:
► Построим графики функций
Анализируя взаимное размещение полученных графиков, получаем ответ:
1) при 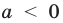
2) при 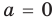
3) при 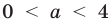
4) при 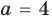
5) при 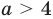
Комментарий:
Поскольку в этом задании речь идет о количестве решений уравнения, то для анализа заданной ситуации попробуем использовать графическую иллюстрацию решения.
1. Строим график функции (учитывая, что 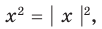
2) Строим график функции
3) Анализируем взаимное размещение полученных графиков и записываем ответ (количество корней уравнения 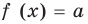
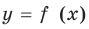
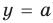
Отметим, что значительное количество исследовательских заданий не удается решить путем непосредственных вычислений (или такие вычисления являются очень громоздкими). Поэтому часто приходится сначала обосновывать какое-то свойство заданного уравнения или неравенства, а затем, пользуясь этим свойством, уже давать ответ на вопрос задачи.
Например, принимая во внимание четность функций, которые входят в запись заданного уравнения, можно использовать такой ориентир.
Если в уравнении 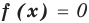
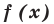
Пример №453
Найдите все значения параметра 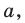
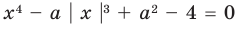
Решение:
► Функция 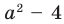
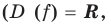
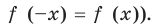
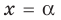
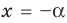
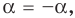
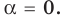
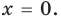
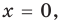
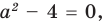
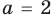
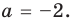
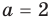
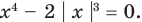
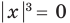
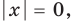
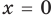
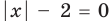
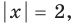
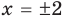
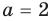
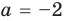
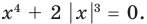
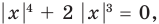
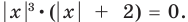
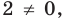
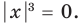
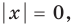
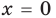
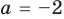
Ответ:
Комментарий:
Замечаем, что в левой части заданного уравнения стоит четная функция, и используем ориентир, приведенный выше. Действительно, если 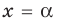
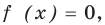
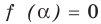
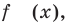
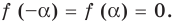
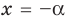
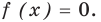
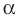
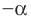
Выясним, существуют ли такие значения параметра 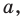
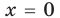
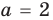
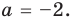
Поскольку значение 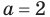
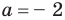
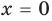
Использование условий расположения корней квадратного трехчлена
Использование условий расположения корней квадратного трехчлена 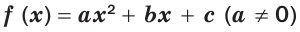
Решение некоторых исследовательских задач с параметрами можно свести к использованию необходимых и достаточных условий расположения корней квадратного трехчлена. Основные из этих условий приведены в таблице 16 (в таблице использованы традиционные обозначения:
Объяснение и обоснование:
Для обоснования указанных условий достаточно воспользоваться тем, что график функции 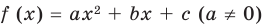
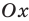
Например, для того чтобы два различных корня квадратного трехчлена 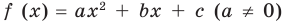

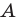
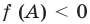
Действительно, график квадратичной функции 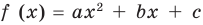
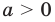
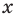

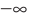
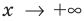
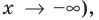
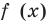
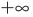
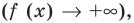
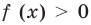
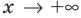
Если выполняется условие 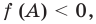
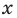
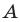
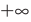
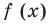
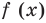
Точно так же с изменением значения аргумента 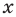
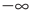
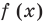
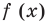
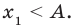
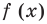

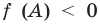
Аналогичные рассуждения при 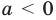
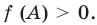
Действительно, 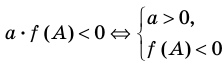
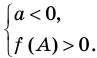
квадратный трехчлен 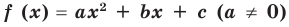
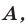
Аналогично можно обосновать и другие условия, приведенные в таблице 16.
Заметим, что приведенные условия не обязательно запоминать: для их записи можно пользоваться графиком квадратичной функции (изображенным для нужного расположения корней) и таким ориентиром.
Для того чтобы корни квадратного трехчлена 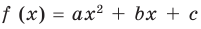
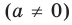
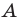
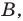
1) знак коэффициента при старшем члене;
2) знаки значений 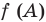
3) знак дискриминанта
4) положение абсциссы вершины параболы 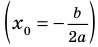
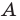
Отметим, что для случаев, в которых хотя бы одно из данных чисел расположено между корнями квадратного трехчлена (см. вторую, пятую, шестую и седьмую строки табл. 16), достаточно выполнения первых двух условий этого ориентира, а для других случаев приходится рассматривать все четыре условия. Заметим также, что, записывая каждое из указанных условий, следует выяснить, будет ли выполняться требование задачи в том случае, когда в этом условии будет записан знак нестрогого неравенства.
Пример №454
Найдите все значения параметра 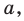
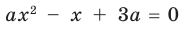
Комментарий:
Поскольку заданное уравнение имеет два различных корня, то оно квадратное (то есть 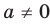
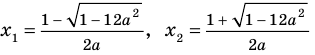
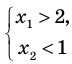
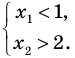
Попробуем воспользоваться условиями расположения корней квадратного трехчлена. Для этого можно непосредственно использовать соответствующие условия, зафиксированные в таблице 16, или получить их с помощью предложенного ориентира. В частности, обозначим 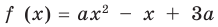
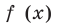
Для того чтобы корни квадратного трехчлена располагались по разные стороны от чисел 1 и 2, необходимо и достаточно выполнения совокупности условий 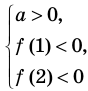
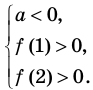
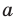
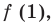
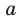
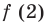
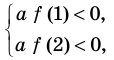
Решение:
► Поскольку заданное уравнение имеет два различных корня, то оно является квадратным (то есть 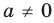
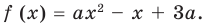
Получаем систему
Решаем неравенства (1) и (2) и находим общее решение системы (рис. 77).
Ответ: заданное уравнение имеет один корень больше двух, а второй — меньше единицы при
Сведения из истории:
Напомним, что алгебра — раздел математики, посвященный изучению буквенных выражений и уравнений. Долгое время алгебра была частью науки о числе — арифметики. Значительное количество задач, возникающих в процессе практической деятельности человека, решают одинаковыми способами. Используя вместо чисел буквы, математики научились решать такие задачи в общем виде. Так и образовалась математическая наука — алгебра.
Исторически зачатки алгебры были известны вавилонянам, египтянам и грекам задолго до нашей эры. Сохранился египетский папирус Ахмеса (XVII в. до н. э.) с решением алгебраических задач. Ученые Вавилона (более 4000 лет назад) умели находить приближенное значение квадратного корня из любого натурального числа, а также решать квадратные уравнения. Это было связано с решением задач на нахождение площадей земельных участков и с развитием астрономии. Однако у вавилонян еще не было понятия отрицательного числа, и поэтому корень квадратного уравнения мог быть только положительным.
Диофант, греческий математик, живший в III в. в Александрии, написал трактат «Арифметика», в котором он уже решал линейные и другие уравнения. В Средние века особенно активно алгебра развивалась в арабских странах и Средней Азии.
Задачи, связанные с квадратными уравнениями, можно найти и в трудах индийских математиков V в. Квадратные уравнения классифицировал в трактате «Алгебра» аль-Хорезми. Он же привел и способы их решения.
В течение многих веков развитие алгебры сильно тормозилось, потому что математикам долго не удавалось ввести в свои исследования удобные обозначения. Поэтому изложение математических работ выглядело громоздко. Только начиная с XVI в. постепенно в математику начали вводить современные обозначения. Символы 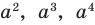
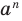
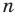
Благодаря исследованиям французского математика Франсуа Виета (1540-1603) уравнения второй степени, третьей и четвертой степеней впервые стали рассматривать в буквенных обозначениях. Он ввел буквенные обозначения для неизвестных величин и коэффициентов уравнений. Особенно ценил открытые им формулы, названные впоследствии формулами Виета. Однако Виет признавал только положительные корни. Лишь в XVII в., после работ Г. Декарта, И. Ньютона и других математиков, решение квадратных и других уравнений приобрело современный вид.
Идея зависимости величин тоже берет начало от древнегреческой науки. Но греки рассматривали лишь величины, которые имеют «геометрическую» природу, и не ставили вопрос об общем изучении разных зависимостей. Графическое изображение зависимостей между величинами широко использовали Г. Галилей (1564-1642), П. Ферма (1601-1665) и Г. Декарт, который ввел понятие переменной величины. Развитие механики и техники привело к необходимости введения общего понятия функции, что сделал немецкий философ и математик Г. Лейбниц (1646-1716). Большие классы функций изучал в ходе своих исследований И. Ньютон.
В 1718 г. ученик Лейбница, И. Бернулли (1667-1748), дал определение функции, лишенное геометрических образов. Следующий шаг в развитии понятия функции сделал его ученик, член Петербуржской академии наук Л. Ейлер (1707-1783).
После работ ряда математиков (Ж. Фурье (1768-1830), М. И. Лобачевский, П. Дирихле и др.) было дано следующее определение: «Переменная величина 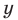
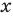
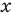
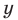
На современном этапе к словам «каждому значению величины л:» добавляют «принадлежащему некоторому множеству», а вместо переменных величин говорят об элементах этих множеств. Такой подход позволяет рассматривать с единой точки зрения как числовые функции, так и, например, геометрические преобразования и т. п.
Несоизмеримость стороны квадрата и его диагонали была открыта в V в. до н. э. в Древней Греции. Это открытие показало, что для измерения геометрических величин недостаточно рациональных чисел. Поэтому греческие математики отказались от обозначения геометрических величин числами и стали развивать геометрическую алгебру (поэтому и сейчас говорят «квадрат числа», «куб числа» и т. п.).
Греческий математик Евдокс (IV в. до н. э.) разработал теорию отношений геометрических величин, которая заменяла для древнегреческих математиков современную теорию действительных чисел. В основе теории Евдокса лежит идея о бесконечной делимости отрезков и других фигур.
Р. Декарт ввел произвольно выбранный единичный отрезок, что позволило ему выразить все действия над числами через действия над отрезками. В сущности, он уже работал с положительными действительными числами. Лишь во второй половине XIX в. теория действительных чисел была приведена к теории натуральных чисел.
О понятии действительного числа
Первые представления о числах формировались постепенно под влиянием практики. С давних времен числа применялись в ходе счета и измерения величин.
Ответ на вопрос «Сколько элементов содержит данное конечное множество?» всегда выражается или натуральным числом, или числом «нуль». Следовательно, множество
всех неотрицательных чисел обслуживает все потребности счета.
Иначе с измерением величин. Расстояние между двумя пунктами может равняться 3,5 километра, площадь комнаты — 16,45 квадратных метра и т. п.
Исторически положительные действительные числа появились как отношение длин отрезков. С открытием несоизмеримости диагонали единичного квадрата с его стороной стало понятным, что отношение длин отрезков не всегда можно выразить не только натуральным, но и рациональным числом. Чтобы числовое значение каждого отрезка при фиксированной единице измерения было определено, необходимо было ввести новые числа — иррациональные.
Все практические измерения величин имеют только приближенный характер. Их результат с необходимой точностью можно выразить с помощью рациональных дробей или конечных десятичных дробей.
Например, измеряя диагональ квадрата со стороной 1 м с точностью до 1 см, мы выясним, что ее длина приближенно равна 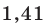
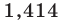
Однако в математике часто уклоняются от приближенного характера практических измерений. Последовательный теоретический подход к измерению длин отрезков приводит к необходимости рассмотрения бесконечных десятичных дробей. (Именно такими дробями являются числа
Отношение длины любого отрезка к длине отрезка, принятого за единицу измерения, всегда можно выразить числом, представленным в виде бесконечной десятичной дроби.
Полная теория действительных чисел достаточно сложна и не входит в программу средней школы. Она обычно рассматривается в курсах математического анализа. Однако с одним из способов ее построения мы ознакомимся в общих чертах.
1. Пусть:
а) каждому действительному числу соответствует (как его запись) бесконечная десятичная дробь:
б) каждая бесконечная десятичная дробь является записью действительного числа.
Но при этом естественно считать десятичную дробь, оканчивающуюся бесконечной последовательностью девяток, только другой записью числа, представленного десятичной дробью, оканчивающей бесконечной последовательностью нулей: 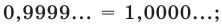
Только исключив из рассмотрения десятичные дроби с девяткой в периоде, получим взаимно однозначное соответствие между множеством действительных чисел и множеством бесконечных десятичных дробей. Число 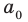
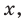
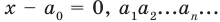
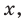
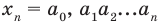
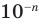
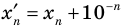
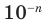
Если число 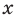
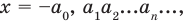
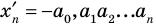
2. Вводят правило сравнения двух действительных чисел. По определению число 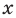
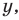
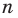
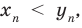
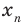
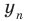
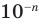
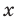
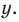
3. Определяют арифметические действия над действительными числами (при этом также пользуются тем, что эти действия уже определены для конечных десятичных дробей).
Суммой двух действительных чисел 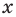
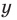
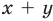
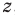
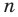
В курсах математического анализа доказывается, что такое число существует и оно единственное.
Аналогично произведением двух неотрицательных чисел 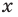
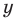
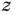
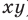
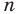
Такое число существует, и оно единственное.
Напомним, что примеры выполнения таким образом определенных действий сложения и умножения действительных чисел было рассмотрено в курсе алгебры 8 класса.
Воспользовавшись тем, что произведение неотрицательных чисел 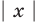
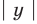
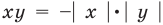
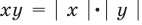
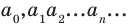
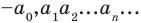
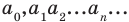
Вычитание определяется как действие, обратное сложению: разностью 
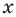
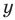
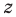
Деление определяется как действие, обратное умножению: частным 
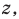
4. Показывают, что неравенства и арифметические операции, определенные выше, сохраняют основные свойства, присущие им во множестве рациональных чисел.
Теория действительного числа была построена сразу в нескольких формах немецкими математиками Р. Дедекиндом (1831-1916), К. Вейерштрассом (1815-1897) и Г. Кантором (1845-1918).
- Уравнение
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Прямые и плоскости в пространстве
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства