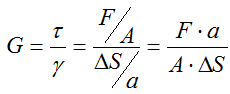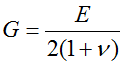Модулем сдвига (упругости II рода) – называется физическая величина, характеризующая упругие свойства материалов и их способность сопротивляться сдвигающим деформациям.
Обозначается латинской буквой G,
единица измерения – Паскаль [Па] (гигапаскаль [ГПа])
В сопромате данный модуль используется в расчетах на сдвиг, срез и кручение.
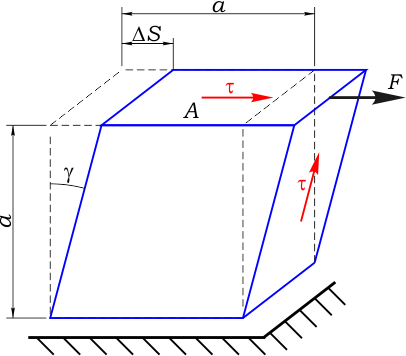
Рис. 1 Деформация сдвига
Теоретически определяется отношением касательных напряжений τ к углу сдвига γ (рис. 1)
где
τ=F/A — касательные напряжения;
γ — угол сдвига;
F — сдвигающая сила;
A — площадь приложения силы F;
ΔS — величина сдвига;
a — размер элемента.
Опытное значение определяется по результатам эксперимента по определению модуля упругости II рода.
Таблица 1. Сравнительные значения модуля для некоторых материалов
|
Материал |
Модуль сдвига |
|
Сталь |
80 |
|
Чугун |
45 |
|
Медь |
40 |
|
Титан |
40 |
|
Алюминий |
27 |
|
Стекло |
26,2 |
Модуль упругости II рода можно определить с помощью известных модуля Юнга E и коэффициента Пуассона ν:
Модуль сдвига является коэффициентом пропорциональности в законе Гука при сдвиге:
τ=Gγ
При расчетах на кручение, GIp – жесткость поперечного сечения вала, где Ip — полярный момент инерции поперечного сечения.
Механические характеристики материалов >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Что такое модуль сдвига?
На чтение 5 мин. Просмотров 425 Опубликовано 25.06.2021
Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига. Он также известен как модуль жесткости и может обозначаться G или, реже, S или μ . Единицей измерения модуля сдвига в системе СИ является паскаль (Па), но значения обычно выражаются в гигапаскалях (ГПа). В английских единицах измерения модуль сдвига выражается в фунтах на квадратный дюйм (PSI) или в килограммах (тысячах) фунтов на квадрат в (ksi).
- Большое значение модуля сдвига указывает на высокую жесткость твердого тела. Другими словами, для создания деформации требуется большая сила.
- Небольшое значение модуля сдвига указывает на то, что твердое тело является мягким или гибким. Для его деформации требуется небольшая сила.
- Одно определение жидкости – это вещество с нулевым модулем сдвига. Любая сила деформирует его поверхность.
Содержание
- Уравнение модуля сдвига
- Пример расчета
- Изотропные и анизотропные материалы
- Влияние температуры и давления
- Таблица значений модуля сдвига
- Источники
Уравнение модуля сдвига
Модуль сдвига определяется путем измерения деформации твердое тело от приложения силы, параллельной одной поверхности твердого тела, в то время как противоположная сила действует на его противоположную поверхность и удерживает твердое тело на месте. Думайте о сдвиге как о толкании одной стороны блока с трением как противодействующей силе. Другой пример – попытка отрезать проволоку или волосы тупыми ножницами.
Уравнение для модуля сдвига:
G = τ xy /γ xy = F/A/Δx/l = Fl/AΔx
Где:
- G – модуль сдвига или модуль жесткости
- τ xy – напряжение сдвига
- γ xy – деформация сдвига
- A – площадь, на которую действует сила
- Δx – поперечное смещение
- l – начальная длина
Деформация сдвига равна Δx/l = tan θ или иногда = θ, где θ – угол, образованный деформацией, вызванной приложенной силой.
Пример расчета
Например, найдите модуль сдвига образца при напряжении 4×10 4 Н/м 2 испытывает напряжение 5×10 -2 .
G = τ/γ = (4×10 4 Н/м 2 )/(5×10 -2 ) = 8x 10 5 Н/м 2 или 8×10 5 Па = 800 кПа
Изотропные и анизотропные материалы
Некоторые материалы изотропны по отношению к сдвигу, что означает, что деформация в ответ на силу одинакова независимо от ориентации. Другие материалы анизотропны и по-разному реагируют на напряжение или деформацию в зависимости от ориентации. Анизотропные материалы гораздо более восприимчивы к сдвигу по одной оси, чем по другой. Например, рассмотрим поведение деревянного блока и то, как он может реагировать на силу, приложенную параллельно волокну древесины, по сравнению с его реакцией на силу, приложенную перпендикулярно волокну. Рассмотрим, как алмаз реагирует на приложенную силу.. Скорость сдвига кристалла зависит от ориентации силы по отношению к кристаллической решетке.
Влияние температуры и давления
Как и следовало ожидать, реакция материала на приложенную силу изменяется в зависимости от температуры и давления. В металлах модуль сдвига обычно уменьшается с повышением температуры. Жесткость уменьшается с увеличением давления. Для прогнозирования влияния температуры и давления на модуль сдвига используются три модели: модель напряжения пластического течения при механическом пороговом напряжении (MTS), модель модуля сдвига Надаля и Лепоака (NP) и модуль сдвига Стейнберга-Кохрана-Гинана (SCG). модель. Для металлов обычно существует область температуры и давления, в которой изменение модуля сдвига является линейным. За пределами этого диапазона поведение моделирования сложнее.
Таблица значений модуля сдвига
Это таблица образцов модуля сдвига значения при комнатной температуре. Мягкие, гибкие материалы, как правило, имеют низкие значения модуля сдвига. Щелочноземельные и основные металлы имеют промежуточные значения. Переходные металлы и сплавы имеют высокие значения. Алмаз, твердое и жесткое вещество, имеет чрезвычайно высокий модуль сдвига.
| Материал | Модуль сдвига (ГПа) |
| Резина | 0.0006 |
| Полиэтилен | 0,117 |
| Фанера | 0,62 |
| Нейлон | 4.1 |
| Свинец (Pb) | 13,1 |
| Магний (Mg) | 16,5 |
| Кадмий (Cd) | 19 |
| Кевлар | 19 |
| Бетон | 21 |
| Алюминий (Al) | 25.5 |
| Стекло | 26.2 |
| Латунь | 40 |
| Титан (Ti) | 41,1 |
| Медь (Cu) | 44,7 |
| Железо (Fe) | 52.5 |
| Сталь | 79.3 |
| Dia mond (C) | 478.0 |
Обратите внимание, что значения для Янга модуль следуют аналогичной тенденции. Модуль Юнга – это мера жесткости твердого тела или линейного сопротивления деформации. Модуль сдвига, модуль Юнга и объемный модуль – это модули упругости, все они основаны на законе Гука и связаны друг с другом уравнениями.
Источники
- Крэндалл, Даль, Ларднер (1959). Введение в механику твердого тела . Бостон: Макгроу-Хилл. ISBN 0-07-013441-3.
- Guinan, M; Стейнберг, Д. (1974). «Производные по давлению и температуре модуля изотропного поликристаллического сдвига для 65 элементов». Журнал физики и химии твердого тела . 35 (11): 1501. DOI: 10. 1016/S0022-3697 (74) 80278-7
- Ландау Л.Д., Питаевский Л.П., Косевич А.М., Лифшиц Е.М. (1970). Теория упругости , т. 7. (Теоретическая физика). 3-е изд. Пергамон: Оксфорд. ISBN: 978-0750626330
- Варшни Ю. (1981). «Температурная зависимость упругих постоянных». Физическая проверка Б . 2 (10): 3952.
-
-
Что такое объемный модуль?
-
-
Что такое геологическое напряжение?
-
Определение давления и примеры
-
Эластичность: определение и примеры
-
Физические свойства материи
-
Напряжение, деформация и усталость металла
-
Определение, единицы измерения и примеры давления
-
-
Объяснение пластичности: растягивающее напряжение и металлы
-
Килопаскаль (кПа) Определение
-
Все, что вам нужно знать о литосфере
-
-
Какова плотность воздуха в STP?
-
46.Основные
механические свойства. Модуль сдвига
Механические
свойства материалов,
совокупность
показателей, характеризующих сопротивление
материала воз действующей на него
нагрузке, его способность деформироваться
при этом, а также особенности его
поведения в процессе разрушения. В
соответствии с этим М. с. м. измеряют
напряжениями (обычно
в кгс/мм2 или Мн/м2), деформациями
(в %), удельной работой деформации и
разрушения (обычно
в кгс×м/см2 или Мдж/м2), скоростью
развития процесса разрушения при
статической или повторной нагрузке
(чаще всего в мм за
1 сек или
за 1000 циклов повторений нагрузки, мм/кцикл). М.
с. м. определяются при механических
испытаниях образцов различной формы.
В
общем случае материалы в конструкциях
могут подвергаться самым различным по
характеру нагрузкам (рис.
1):
работать нарастяжение,
сжатие, изгиб, кручение,
срез и т. д. или подвергаться совместному
действию нескольких видов нагрузки,
например растяжению и изгибу. Также
разнообразны условия эксплуатации
материалов и по температуре, окружающей
среде, скорости приложения нагрузки и
закону её изменения во времени. В
соответствии с этим имеется много
показателей М. с. м. и много методов
механических испытаний. Для металлов
и конструкционных пластмасс наиболее
распространены испытания на
растяжение, твёрдость,
ударный изгиб; хрупкие конструкционные
материалы (например, керамику,
металлокерамику) часто испытывают на
сжатие и статический изгиб; механические
свойства композиционных материалов
важно оценивать, кроме того, при
испытаниях на сдвиг.
Диаграмма
деформации. Приложенная
к образцу нагрузка вызывает его деформацию.
Соотношения между нагрузкой и деформацией
описываются т. н. диаграммой деформации
(рис.
2).
Вначале деформация образца (при
растяжении — приращение длины Dl )
пропорциональна возрастающей нагрузке Р,
затем в точке n эта
пропорциональность нарушается, однако
для увеличения деформации необходимо
дальнейшее повышение нагрузки Р;
при Dl >
Dlв деформация
развивается без приложения усилия
извне, при постепенно падающей нагрузке.
Вид диаграммы деформации не меняется,
если по оси ординат откладывать
напряжение
а
по оси абсцисс — относительное удлинение
(F0 и l0 —
соответственно начальная площадь
поперечного сечения и расчётная длина
образца).
Сопротивление
материалов измеряется напряжениями,
характеризующими нагрузку, приходящуюся
на единицу площади поперечного сечения
образца
в кгс/мм2. Напряжение
при
котором нарушается пропорциональный
нагрузке рост деформации, называется
пределом пропорциональности. При
нагрузкеР < Рn разгрузка
образца приводит к исчезновению
деформации, возникшей в нём под действием
приложенного усилия; такая деформация
называется упругой. Небольшое превышение
нагрузки относительно Рn может
не изменить характера деформации —
она по-прежнему сохранит упругий
характер. Наибольшая нагрузка, которую
выдерживает образец без появления
остаточной пластической деформации
при разгрузке, определяет предел
упругости материала:
У
конструкционных неметаллический
материалов (пластмассы, резины)
приложенная нагрузка может вызвать
упругую, высокоэластическую и остаточную
деформации. В отличие от упругой,
высокоэластическая деформация исчезает
не сразу после разгрузки, а с течением
времени. Высокопрочные армированные
полимеры (стеклопластики, углепластики
и др.) разрушаются при удлинении 1—3%.
На последних стадиях нагружения у
некоторых армированных полимеров
появляется высокоэластическая
деформация. Высокоэластический модуль
ниже модуля упругости, поэтому диаграмма
деформации в этом случае имеет тенденцию
отклоняться к оси абсцисс.
Упругие
свойства. В
упругой области напряжение и деформация
связаны коэффициентом пропорциональности.
При растяжении s = Еd, где Е —
т. н. модуль нормальной упругости,
численно равный тангенсу угла наклона
прямолинейного участка кривой s = s(d) к
оси деформации (рис.
2).
При испытании на растяжение цилиндрического
или плоского образца одноосному (s1>0;
(s2 =
s3 =
0) напряжённому состоянию соответствует
трёхосное деформированное состояние
(приращение длины в направлении действия
приложенных сил и уменьшение линейных
размеров в двух других взаимно
перпендикулярных направлениях): d1>0;
d2 =
d3 <
0. Соотношение между поперечной и
продольной деформацией (коэффициент
Пуассона)
в
пределах упругости для основных
конструкционных материалов колеблется
в довольно узких пределах (0,27—0,3 для
сталей, 0,3—0,33 для алюминиевых сплавов).
Коэффициент Пуассона является одной
из основных расчётных характеристик.
Зная m и Е,
можно расчётным путём определить и
модуль сдвига
и
модуль объёмной упругости
Для
определения Е,
G,
и m пользуются тензометрами.
Сопротивление
пластической деформации. При
нагрузках Р > Рв наряду
со всё возрастающей упругой деформацией
появляется заметная необратимая, не
исчезающая при разгрузке пластическая
деформация. Напряжение, при котором
остаточная относительная деформация
(при растяжении — удлинение) достигает
заданной величины (по ГОСТ — 0,2 %),
называется условным пределом текучести
и обозначается
Практически
точность современных методов испытания
такова, что sп и
sе определяют
с заданными допусками соответственно
на отклонение от закона пропорциональности
[увеличение ctg(90 — a) на 25—50 %] и на величину
остаточной деформации (0,003—0,05 %) и
говорят об условных пределах
пропорциональности и упругости. Кривая
растяжения конструкционных металлов
может иметь максимум (точка в на рис.
2)
или обрываться при достижении наибольшей
нагрузки Рв’.
Отношение
характеризует
временное сопротивление (предел
прочности) материала. При наличии
максимума на кривой растяжения в области
нагрузок, лежащих на кривой левее в,
образец деформируется равномерно по
всей расчётной длине l0,
постепенно уменьшаясь в диаметре, но
сохраняя начальную цилиндрическую или
призматическую форму. При пластической
деформации металлы упрочняются, поэтому,
несмотря на уменьшение сечения образца,
для дальнейшей деформации требуется
прикладывать всё возрастающую нагрузку.
sв,
как и условные s0,2,
sn и
sе,
характеризует сопротивление металлов
пластической деформации. На участке
диаграммы деформации правее в форма
растягиваемого образца изменяется:
наступает период сосредоточенной
деформации, выражающейся в появлении
«шейки». Уменьшение сечения в шейке
«обгоняет» упрочнение металлов,
что и обусловливает падение внешней
нагрузки на участке Рв —
Pk.
У
многих конструкционных материалов
сопротивление пластической деформации
в упруго-пластической области при
растяжении и сжатии практически
одинаково. Для некоторых металлов и
сплавов (например, магниевые сплавы,
высокопрочные стали) характерны заметные
различия по этой характеристике при
растяжении и сжатии. Сопротивление
пластической деформации особенно часто
(при контроле качества продукции,
стандартности режимов термической
обработки и в др. случаях) оценивается
по результатам испытаний на твёрдость
путём вдавливания твёрдого наконечника
в форме шарика (твёрдость по Бринеллю
или Роквеллу), конуса (твёрдость по
Роквеллу) или пирамиды (твёрдость по
Виккерсу). Испытания на твёрдость не
требуют нарушения целостности детали
и потому являются самым массовым
средством контроля механических
свойств. Твёрдость по Бринеллю (HB) при
вдавливании шарика диаметром D под
нагрузкой Р характеризует
среднее сжимающее напряжение, условно
вычисляемое на единицу поверхности
шарового отпечатка диаметром d:
Характеристики
пластичности. Пластичность
при растяжении конструкционных
материалов оценивается удлинением
или
сужением
при
сжатии — укорочением
(где h0 и hk —
начальная и конечная высота образца),
при кручении — предельным углом
закручивания рабочей части образца
Q,рад или
относительным сдвигом g = Qr (где r —
радиус образца). Конечная ордината
диаграммы деформации (точка k на рис.
2)
характеризует сопротивление разрушению
металла Sk,
которое определяется
(Fk —
фактическая площадь в месте разрыва).
Модуль
сдвига-величина,
характеризующая деформацию сдвига.
Модуль
сдвига равен отношению касательного
напряжения к величине угла сдвига.

части диаграмма сдвига (на рисунке)
линейная, т.е. угол сдвига пропорционален
касательному напряжению .
Закон пропорциональности, называемый
законом Гука при сдвиге, может быть
записан:
где
коэффициент пропорциональности G называется
модулем сдвига сдвига или модулем
упругости 2-го рода. Он характеризует
сопротивление материала упругим
деформациям и является его упругой
постоянной.
Модуль упругой деформации
Определение и модуль упругой деформации
Деформация в твердом теле называется упругой, если она пропадает после того, как нагрузку с тела сняли.
В общем случае модуль упругости (E) определяют как
где – напряжение;
– относительная деформация. Надо помнить, что данное определение справедливо для линейного отрезка диаграммы напряжений, то есть когда деформацию можно считать упругой. На данном участке диаграммы величина E определена тангенсом угла наклона прямолинейного участка диаграммы.
В зависимости от типа деформации, направления действия деформирующей силы различают несколько модулей упругости. Наиболее часто используемые:
- модуль Юнга;
- модуль сдвига;
- модуль объемной упругости;
- коэффициент Пуассона и др.
Модуль Юнга
Модуль Юнга используют при характеристике деформация растяжения (сжатия) упругого тела, при этом деформирующая сила действует по оси тела. Модуль Юнга чаще всего определяют используя закон Гука:
Модуль Юнга, равен напряжению, появляющемуся в стержне, если его относительное удлинение равно единице (или при двойном удлинении длины тела). На практике кроме резины при упругой деформации двойного удлинения невозможно достичь, тело рвется.
Коэффициент упругости и модуль Юнга связаны как:
где – длина тела до деформации; S – площадь поперечного сечения.
Единицей измерения модуля Юнга служит паскаль.
Модуль сдвига
При помощи модуля сдвига (G) характеризуют способность тела оказывать сопротивление изменению формы тела (при этом объем сохраняется). Находят модуль сдвига как:
– абсолютный сдвиг слоев параллельных по отношению друг к другу; h — расстояние между слоями; F – сила, вызывающая сдвиг, параллельная сдвигающимся слоям тела.
Если вещество является однородным и изотропным, то модуль сдвига связан с модулем Юнга выражением:
где – коэффициент Пуассона для материала, который зависит от природы вещества. Иногда обозначается буквой
.
Модуль объемной упругости
Модуль объемной упругости (модуль объемного сжатия) (K) – отражает способность тела к изменению объема при действии объемного напряжения, которое одинаково по всем направлениям. Его определяют выражением:
где V – объем тела; p – давление, оказываемое на тело.
Если тело является изотропным, то:
Примеры решения задач
Вы здесь
Модуль сдвига
Содержание
- Модуль сдвига
- Металлы
- Пластмассы
- Резины
- Различные материалы
- Литература
Модуль сдвига
Сдвигом называют деформацию, при которой все слои тела, параллельные некоторой плоскости, смещаются друг относительно друга. При сдвиге объем деформируемого образца не меняется.
Модуль сдвига (N) – одна из нескольких величин, характеризующих упругие свойства материала.
Модуль сдвига связан с модулем Юнга через коэффициент Пуассона:
1 кгс/мм2 = 10-6 кгс/м2 = 9,8·106 Н/м2 = 9,8·107 дин/см2 = 9,81·106 Па = 9,81 МПа.
| Материал | Модуль сдвига | ||
|---|---|---|---|
| кгс/мм2 | Н/м2 | МПа | |
| Металлы | |||
| Алюминий | 2300-2700 | 2250-2650 | 22500-26500 |
| Алюминий отожженный | 2500 | 2450 | 24500 |
| Бронза | 4400 | 4320 | 43200 |
| Бронза алюминиевая, литье | 4180 | 4100 | 41000 |
| Бронза фосфористая катаная | 4180 | 4100 | 41000 |
| Висмут | 1200-1400 | 1180-1370 | 11800-13700 |
| Висмут литой | 1220 | 1200 | 12000 |
| Вольфрам | 13300 | 13050 | 130500 |
| Вольфрам отожженный | 8970-21910 | 8800-21500 | 88000-215000 |
| Дюралюминий | 2750 | 2700 | 27000 |
| Дюралюминий катаный | 2650 | 2600 | 26000 |
| Железо кованое | 8000-8300 | 7850-8150 | 78500-81500 |
| Железо литое | 3570-5400 | 3500-5300 | 35000-53000 |
| Золото | 2600-3900 | 2550-3830 | 25500-38300 |
| Золото отожженное | 2970 | 2910 | 29100 |
| Инвар | 5600 | 5500 | 55000 |
| Кадмий | 1940 | 1900 | 19000 |
| Кадмий литой | 1960 | 1920 | 19200 |
| Константан | 6200 | 6080 | 60800 |
| Латунь | 2700-3700 | 2650-3630 | 26500-36300 |
| Латунь корабельная катаная | 3670 | 3600 | 36000 |
| Латунь холоднотянутая | 3470-3670 | 3400-3600 | 34000-36000 |
| Манганин | 4700 | 4610 | 46100 |
| Медь | 4000-4800 | 3920-4700 | 39200-47000 |
| Медь деформированная | 4230 | 4150 | 41500 |
| Медь прокатанная | 3980 | 3900 | 39000 |
| Медь холоднотянутая | 4890 | 4800 | 48000 |
| Нейзильбер | 4000 | 3920 | 39200 |
| Никель | 7500 | 7360 | 73600 |
| Олово | 1700 | 1670 | 16700 |
| Олово литое | 1670-1810 | 1640-1780 | 16400-17800 |
| Палладий | 4000-5000 | 3920-4900 | 39200-49000 |
| Палладий литой | 5200 | 5110 | 51100 |
| Платина | 6000-7200 | 5880-7060 | 58800-70600 |
| Платина отожженная | 6200 | 6090 | 60900 |
| Свинец | 550-600 | 540-580 | 5400-5800 |
| Свинец литой | 575 | 562 | 5620 |
| Серебро | 2500-2900 | 2450-2840 | 24500-28400 |
| Серебро отожженное | 2640 | 2590 | 25900 |
| Сталь инструментальная | 8000-8500 | 7850-8340 | 78500-83400 |
| Сталь легированная | 8150 | 8000 | 80000 |
| Сталь специальная | 8500-8800 | 8340-8630 | 83400-86300 |
| Титан | 4480 | 4400 | 44000 |
| Цинк | 3000-4000 | 2940-3920 | 29400-39200 |
| Цинк катаный | 3160 | 3100 | 31000 |
| Чугун | 2900-3500 | 2840-3430 | 28400-34300 |
| Чугун белый, серый | 4480 | 4400 | 44000 |
| Чугун ковкий | 4000 | 3920 | 39200 |
| Пластмассы | |||
| Плексиглас | 151 | 148 | 1480 |
| Целлулоид | 66 | 65 | 650 |
| Резины | |||
| Каучук | 0,28 | 0,27 | 2,7 |
| Резина мягкая вулканизированная | 0,05-0,15 | 0,05-0,15 | 0,5-1,5 |
| Различные материалы | |||
| Бетон | 715-1730 | 700-1700 | 7000-17000 |
| Гранит | 1430-4490 | 1400-4400 | 14000-44000 |
| Известняк плотный | 1530 | 1500 | 15000 |
| Кварцевая нить (плавленая) | 3160 | 3100 | 31000 |
| Мрамор | 1430-4490 | 1400-4400 | 14000-44000 |
| Стекло | 1780-2950 | 1750-2900 | 17500-29000 |
Литература
- Краткий физико-технический справочник. Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с.
- Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
- Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.
- 14912 просмотров